Abstract
This paper examines the folding mechanism of an individual β-hairpin in the presence of other hairpins by using an off-lattice model of a small triple-stranded antiparallel β-sheet protein, Pin1 WW domain. The turn zipper model and the hydrophobic collapse model originally developed for a single β-hairpin in literature is confirmed to be useful in describing β-hairpins in model Pin1 WW domain. We find that the mechanism for folding a specific hairpin is independent of whether it folds first or second, but the formation process are significantly dependent on temperature. More specifically, β1-β2 hairpin folds via the turn zipper model at a low temperature and the hydrophobic collapse model at a high temperature, while the folding of β2-β3 hairpin follows the turn zipper model at both temperatures. The change in folding mechanisms is interpreted by the interplay between contact stability (enthalpy) and loop lengths (entropy), the effect of which is temperature dependent.
INTRODUCTION
The folding mechanisms of β-hairpins have been known to be determined by the interplay between hydrophobic interactions and hydrogen-bonding interactions.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 One mechanism was proposed by Muñoz and co-workers based on the temperature-jump experiments and a statistical mechanical model of the GB1 hairpin, a 16-residue peptide.21, 22 In this model, folding is initiated from the turn nucleation, followed by zipping the hairpin from the turn region to the end.21, 22 This mechanism was later called the turn zipper mechanism.23 The second mechanism was postulated by Dinner et al. based on their multicanonical Monte Carlo simulations.24 Their simulations revealed that a hydrophobic collapse occurs prior to the hairpin formation,24 and it was called the hydrophobic collapse mechanism.23
While the folding of a single β-hairpin has been studied in detail, it is not yet clear regarding how an individual β-hairpin would fold in the presence of other β-hairpins in the same protein. This paper focuses on the individual folding mechanism of each β-hairpin in a two-hairpin polypeptide by using Pin1 WW domain as the model. The WW domain family, named after two highly conserved tryptophans in the strands, is a triple-stranded antiparallel β-sheet protein with 30–50 residues. The WW domain family, which is stable in monomer and amenable to extensive mutagenesis,25, 26, 27, 28, 29, 30 is regarded as one of the simplest β-sheet models for testing a variety of hypotheses regarding β-sheet folding.31, 32, 33, 34, 35 Pin1 WW domain, one of the best characterized peptide of this family, is the N-terminal (residues 1–39) of a two-domain protein hPin1, in which the C-terminal cis∕trans-isomerase domain (residues 45–167) is weakly connected to the WW domain by a flexible linker.36 The truncation of residues 1–5 of Pin1 WW domain has no substantial influence on its function or stability.37 The structure of residues 6–39 is shown in Fig. 1. The overall topology of the Pin1 WW domain is made of three strands (β1, residues 11–15; β2, residues 22–26; and β3, residues 31–34) connected by two loops (loop 1, residues 16–21 and loop 2, residues 27–30). The protein could tolerate mutations almost expanding all strands and loops. The abnormal large ϕ-values (>1) of loop 1 have been interpreted that the nucleation of loop 1 is the driving force to form β1-β2 hairpin,27 analogous to a turn zipper mechanism proposed by Muñoz and co-workers.21, 22 Recent NMR measurements of Pin1 WW and other WW domains (hYAP56 and FBP28) indicated that loop 1 was dynamic38, 39, 40, 41 at the folded state. Meanwhile, the unfolding simulation of FBP28 indicated that loop 1 was more like a hinge to bring the long-range hydrophobic residues together,29, 38 although ϕ-values of residues in loop 1 are larger than 1.
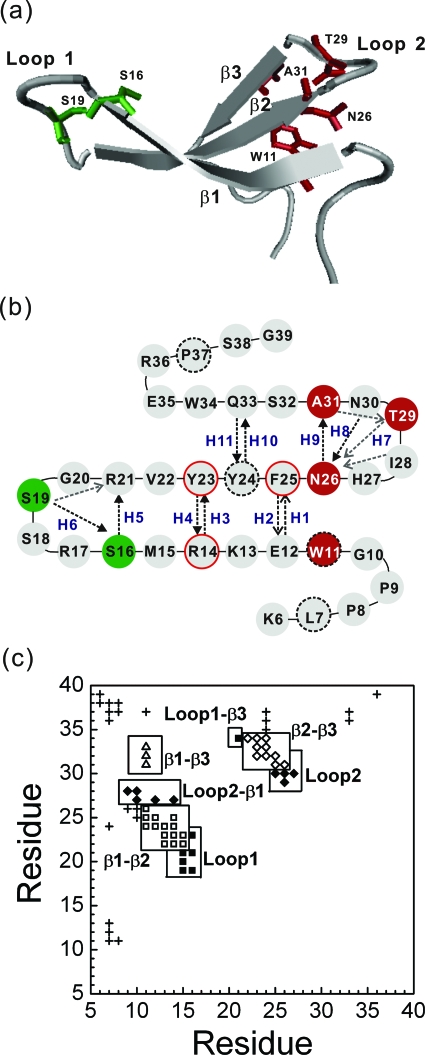
Figure 1.
(a) A cartoon display of the native structure of Pin1 WW domain (K6 to G39) ) along with several key residues (S16 and S19 in green, and W11, N236, T29, and A31 in red). Drawn with software VMD (Ref. 57). (b) Two-dimensional presentation of the Pin1 WW domain. In addition to the secondary-structure elements, the main-chain H-bonds and side-chain H-bonds are illustrated by the black and gray dashed lines, respectively. Each H-bond is indicated by an arrow from a hydrogen donor to the associated hydrogen accepter. Ten main-chain H-bonds (H1-H6, H8-H11) and a side-chain H7 are labeled. The hydrophobic core 1 (L7, W11, Y24, and P37) and core 2 (R14, Y23, and F25) are specifically highlighted with a black dashed-line border and a red solid-line border, respectively. (c) The contact map of the global-minimum-energy structure of the model protein. A residue is in contact with another residue if there is at least one square-well atomic contact between them. Square symbols denote β1-β2 contacts; diamonds, β2-β3 contacts; triangles, β1-β3 contacts; the filled squares indicate contacts between loop 1 residues and other residues; the filled diamonds refer to contacts between loop 2 residues and other ones; and other contacts are labeled with crosses. The total number of native residue-residue contacts (∣i−j∣⩾3) is 65.
The folding kinetics of Pin1 WW domains has been studied theoretically on the molecular and atomic levels. With a three-letter code residue sequence (the hydrophobic, hydrophilic, and neutral), Cecconi et al. studied the thermodynamics of Pin1 WW domain. They reported that the folding and unfolding were essentially reversible. Its folding started from collapsed hydrophobic cores in the middle of β1-β2 hairpin and β2-β3 hairpin.32 Karanicolas et al., on the other hand, found that the β2-β3 hairpin of Pin1 WW domain folded prior to hairpin β1-β2 by using an improved Cα-based model.42 Moreover, the difference in side-chain packing leads to the biphasic kinetics observed in FBP28 WW domain, in contrast to single-exponential kinetics in Pin1 WW domain.43 In addition, our own studies, based on an all-atom Gō model, revealed the temperature-dependent folding pathways.44 At the transition temperature, the β1-β2 hairpin forms first because the stabilities of the hydrophobic interactions in β1-β2 hairpin are sufficiently strong to resist the thermal fluctuation. At low temperatures, the dominant pathway is the formation of β2-β3 hairpin because it is stable at low temperatures and, more importantly, it has a much shorter connecting loop than loop 1 that connects β1 and β2.44
While the relative sequential folding of the two hairpins in a WW domain38, 42, 44 has been studied in detail, little attention was paid to the detailed folding mechanisms for individual hairpins. Several fundamental questions are yet to be addressed. For instance, can the folding mechanism of a single β hairpin be applied to a β-hairpin within a protein (i.e., in the presence of other secondary-structure elements)? Can different β hairpins in a protein have different folding mechanisms? Is the folding mechanism of a β hairpin dependent on whether it is formed first or second? The purpose of this paper is to address these questions by folding and unfolding simulations of an all-atom Gō model of Pin 1 WW domain.
METHODS AND SIMULATIONS
Model
The initial heavy-atom positions of residues 6–39 of the native state were obtained from the x-ray structure coded 1pin.pdb36 in Protein Data Bank and the positions of the polar hydrogen atoms were generated by CHARMM program45 and minimized for 100 steps to remove bad contacts using the CHARMM polar hydrogen parameter set 19 with distance-dependent dielectric constants.46 The total number of all heavy atoms and polar hydrogen atoms is 361.
The interaction of two bonded atoms, as well as any 1,3 angle-constrained atomic pair and 1,4 aromatic carbon pair, i and j, is described as an infinitely deep square-well potential
| (1) |
where σij is the atomic distance obtained by the CHARMM energy minimization as mentioned above. The bond-length tolerance of 0.1 is introduced to decouple multibody collisions into binary collisions.47
The square-well nonbonded i, j pair interactions are represented as follows:
| (2) |
where is the van der Waals distance obtained from the CHARMM polar hydrogen parameter set 19 (Ref. 46) and Bij is the square-well depth. The factor of 0.8 is the typical ratio between the hard-core diameters and the van der Waals parameters in the Weeks–Chandler–Andersen perturbation theory,48 while a ratio of 1.5 between the square-well and hard-core diameters is typical for small molecular systems.49
The L-form chirality about a tetrahedral extended heavy atom (ω0=35.26439°) as well as the plane of aromatic atoms (ω0=0°) are maintained by a “bondlike” potential for improper dihedral angels. A 20° fluctuation is used to increase the flexibility and folding rate
| (3) |
The CHARMM minimized structure generated as the above further undergoes a short discontinuous molecular dynamics (MD) simulation to remove all initial hard-core overlaps. The square-well interactions Bij for the original native contacts found in the x-ray structure are set to be −100, which is a large negative energy in order to ensure that these interactions are maintained throughout the simulation. During the process, we modify the initially overlapped hard-core diameters found in the CHARMM minimized structure until the true hard-core diameters are reached. The resulting structure has a main-chain root-mean-squared deviation (RMSD) from the original x-ray structure of 0.69 Å and is regarded as the global minimum structure for the model protein [Fig. 1a]. A hydrogen bond (H-bond) is defined by a cutoff distance of 2.88 Å between a donor H atom and an accepter O atom. Ten backbone H-bonds as well as a side-chain H-bond of the native structure are labeled in Fig. 1b; other native side-chain H-bonds are mainly located in two loop regions [Fig. 1b, and also see Refs. 27, 44]. The global minimum structure has 2398 square-well atom-atom overlaps. Henceforth, they shall be regarded as native atomic contacts.
To ensure that the native structure [Fig. 1a] has the global minimum energy, a Gō interaction50 is applied. In a Gō model, Bij=−1 for a native contact, and Bij=0 otherwise. Henceforth, all parameters and quantities are scaled in units of ε, the reduced internal energy E* (=E∕ε), the reduced temperature T* (=kBT∕ε, in which kB is the Boltzmann constant), the reduced time unit t* (=t, where M is the average mass of the atoms and σL is 1 Å). The total number of all native residue-residue contacts (∣i–j∣⩾3) is 65 [in Fig. 1c].
Simulations
The discontinuous MD simulations of an isolated model Pin1 WW domain are carried out in the canonical ensemble. In contrast to the normal continuous MD simulation, a discontinuous one adopts square-well interactions between atoms or particles and it is time-saving by using the efficient search algorithms.51 Ghost-solvent particles are employed to maintain the constant temperature by their collisions with protein atoms.52, 53 Thermodynamics studies indicate that the folding transition temperature of the model Pin1 WW domain is around T*=3.6.44 For folding kinetics, the initial coil-like configurations were sampled from equilibrium simulations at T*=4.0. 135 kinetic simulations were performed for t*=200 000 at a low temperature T*=3.0. At the approximate transition temperature T*=3.6, only limited folding and unfolding events were obtained after long equilibrium simulations, and these trajectories were also used to investigate the folding mechanisms. A progress variable Q, the fraction of nonlocal native contacts (∣i−j∣⩾3) between residues [total number is 65, shown in Fig. 1c], is used to monitor the folding process. Two residues are in contact if there is any square-well atomic overlap between them.
RESULTS
Refolding at a low temperature T*=3.0
The folding process of the model protein was triggered by a sudden drop of temperature from the equilibrium simulation at T*=4.0 to T*=3.0. We found that 102 out of 135 independent runs folded within the cutoff time of t*=200 000. Here, a trajectory is considered as “folded” if the main-chain RMSD values of more than 20 configurations saved at an interval of t*=100 during simulations are smaller than 2.5 Å.
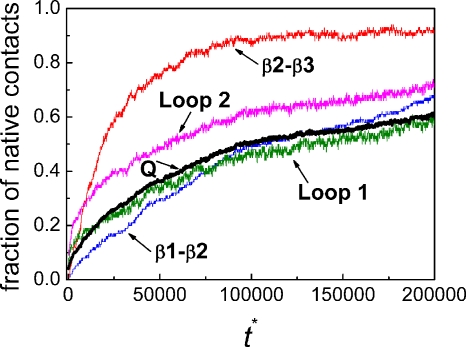
The average fractions of total native contacts Q and the native contacts between β1 and β2, between β2 and β3, within loop 1 and between loop 1 and other residues, and within loop 2 and between loop 2 and other residues (averaged over all of 135 folding trajectories) are shown as a function of the reduced time in Fig. 2. There is an initial formation of the native contacts in loop 2 which appears to trigger the quick formation of the contacts between β2 and β3. The formation of the native contacts of loop 1 is more gradual and faster than that of the contacts between β1 and β2 for t*<125 000. However, it is only an average picture.
Figure 2.
The average fractions of native contacts over all 135 trajectories (including 102 folded and 33 unfolded trajectories) as a function of reduced time at T*=3.0. The fraction for the total contacts (Q) is shown in thick black line. The fractions of the native contacts between β1 and β2 (blue), between β2 and β3 (red), within loop 1 and between loop 1 and other residues (olive), and within loop 2 and between loop 2 and other residues (magenta) are also given.
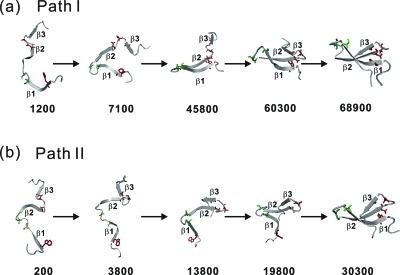
A detailed inspection of individual folding trajectories indicated that in the 102 folded runs, 80 trajectories fold with β2-β3 hairpin formed first, which we call path II, and 22 trajectories fold with β1-β2 hairpin formed first, which we call path I. The typical snapshots in path I and path II are illustrated in Fig. 3. We also inspected the 33 unfolded runs (untill t*=200 000) and found that those trajectories can also be classified either with a mostly formed β2-β3 hairpin or β1-β2 hairpin. This suggests that those trajectories will, if running for a sufficiently long time, fold in similar folding pathways as those folded.
Figure 3.
Structural snapshots at the marked reduced times for two typical folded trajectories at T*=3.0. (a) path I and (b) path II. Several key residues (S16 and S19 in green, and W11, N26, T29, and A31 in red) are shown.
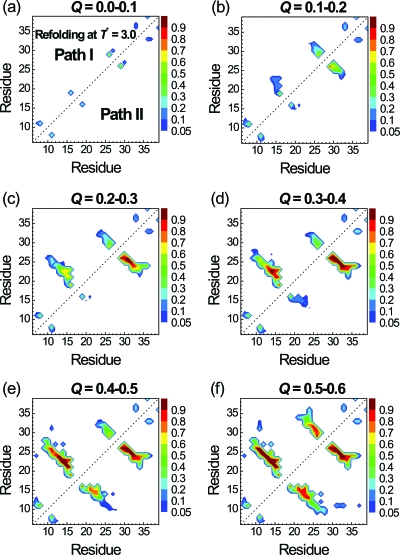
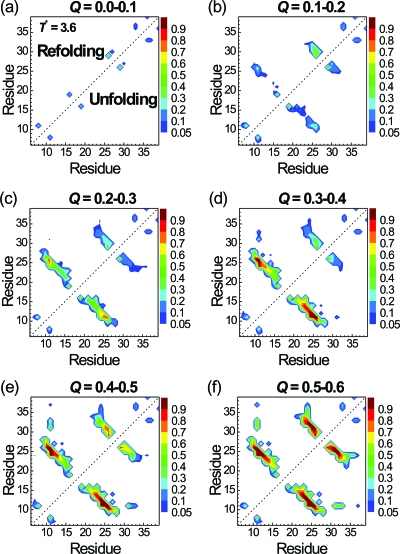
To further understand which contacts trigger the folding, we plot the probabilities of contacts at different stages of folding (Q between 0.0 and 0.6) for path I (in the upper triangle) and path II (in the lower one) in Fig. 4. All 102 folded trajectories in paths I and II are used to make the plot in Fig. 4. We did not show the result for Q>0.6 because folding is essentially completed for Q>0.6. We first take a look at the β1-β2 hairpin in path I. At 0.1<Q<0.2, the contact pair between the S16 and S19 (loop 1) has the highest contact probability (0.63). This was followed by the contact probability of 0.22 between S16 and R21. At 0.2<Q<0.3, the contact probability between S16 and S19 further increases to 0.85 along with increased probabilities of other contacts within loop 1 (S16-R21) and between β1 and β2 (M15-V22 and R14-Y23). At 0.3<Q<0.4, the central contact between β1 and β2 (R14-Y23) becomes stabilized and the folding of the β1-β2 hairpin is mostly completely. On the other hand, although the contact probability of pair N26-T29 in the β2-β3 hairpin is already 0.54 for 0.0<Q<0.1, it does not change much during the folding process from Q∼0.1 to Q∼0.4. Thus, in path I and at T*=3.0, the S16-S19 contact triggers the formation of β1-β2 hairpin, while the N26-T29 contact initiates the formation of hairpin β2-β3 after the formation of β1-β2 hairpin. Both S16-S19 and N26-T29 are located at the turns of the two hairpins, as shown in Fig. 1b. Hence, both hairpins in path I can be viewed as folded via the turn zipper mechanism.
Figure 4.
Probabilities of native residue-residue contacts at various stages of folding according to the Q values. Results for the folded trajectories via path I (22 trajectories) and path II (80 trajectories) are shown in the upper and lower triangles, respectively. The reduced folding temperature T* is 3.0.
Path II is the dominant pathway at T*=3.0 and the contact maps at different stages of folding are showed in the lower triangle of Fig. 4. The formation of the β2-β3 hairpin is early essentially completed as 0.2<Q<0.3. In contrast, the formation of the β1-β2 hairpin did not occur until 0.4<Q<0.6. Although the β2-β3 hairpin folded much earlier than the β1-β2 hairpin in path II, the folding processes of individual hairpins in paths I and II are the same (triggered by the same key contacts).
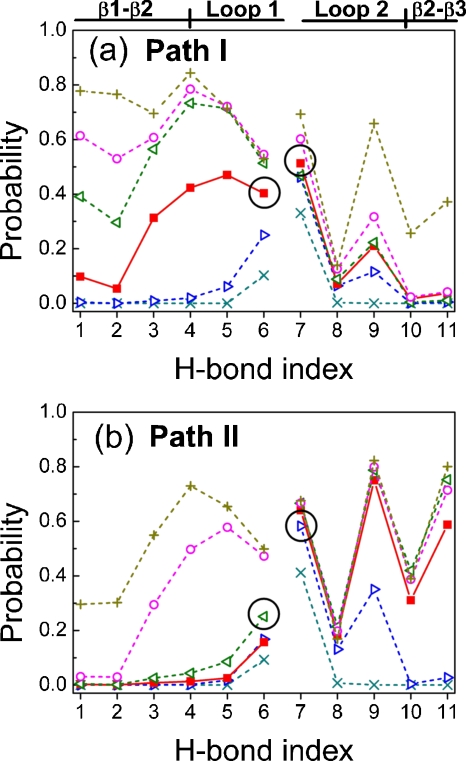
Figure 5 further analyzes the folding processes according to ten main-chain H-bond contacts and one side-chain H-bond at different folding stages (Q values). There are H1–H4 for the contacts between β1 and β2, H5 and H6 within loop 1, H8 within loop 2, H9–H11 between β2 and β3, and H7, the side-chain H-bond between the N–H of T29 and the O=CNH2 group of N26 [Fig. 1b].
Figure 5.
Probabilities of 11 H-bonds at various folding stages according to the Q values of the 102 folded trajectories via (a) path I or (b) path II at T*=3.0. The H-bond indices are defined in Fig. 1b. The secondary-structure regions are also labeled in Fig. 5a. The circles indicate the key H-bonds (H6 in loop 1 and H7 in loop 2) that would be initiated at first in the folding process. Lines serve as guides for the eye and are broken to separate the region of β1-β2 hairpin from the region of β2-β3 hairpin: Q=0.0–0.1 (×), Q=0.1–0.2 (▷), Q=0.2–0.3 (◼), Q=0.3–0.4 (◁), Q=0.4–0.5 (○), and Q=0.5–0.5 (+).
In path I, the probability of H6 in the β1-β2 hairpin is the highest from 0.0<Q<0.2. This is followed by H5 at 0.2<Q<0.3, and then H4 at 0.3<Q<0.6. Similarly, the side-chain H7 in loop 2 of the β2-β3 hairpin has the highest contact probability in path I. The main-chain H8 (N–H of N30 to O=C of N26) at the end of loop 2 is always lower than 0.2 because N30 has a very weak interaction with all other residues. In path II, Fig. 5b also shows that H6 is the first formed H-bond in the β1-β2 hairpin, and H7 is the first formed one in the β2-β3 hairpin. This confirms the turn zipper mechanism for two hairpins in two different folding paths.
Refolding and unfolding around the critical transition temperature T*=3.6
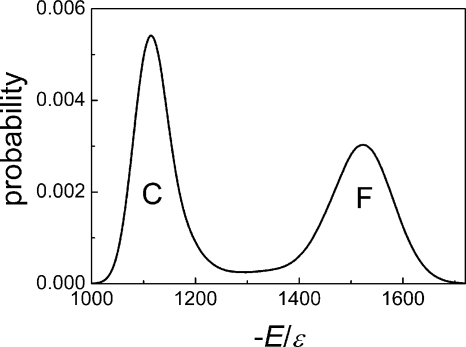
We further explored the folding and unfolding events at T*=3.6, the folding transition temperature, at which the energy exhibited a bimodal distribution, as seen in Fig. 6, indicating a cooperative two-state transition between a coil state and a folded state. These events are difficult to observe at the transition temperature because of the equal stabilities of the folded and unfolded states. We obtained eight folding and unfolding equilibrium trajectories after very long simulations (on average, 40 days of CPU 2.8G for one trajectory lasting at t*=4 000 000). Only path I (β1-β2 hairpin folds first) and the reverse of path I (β1-β2 hairpin unfolds last) were observed in these trajectories.
Figure 6.
Probability distribution of the absolute value of the reduced energy (−E∕ε) at the transition temperature T*=3.60. C, coil state; F, folded state.
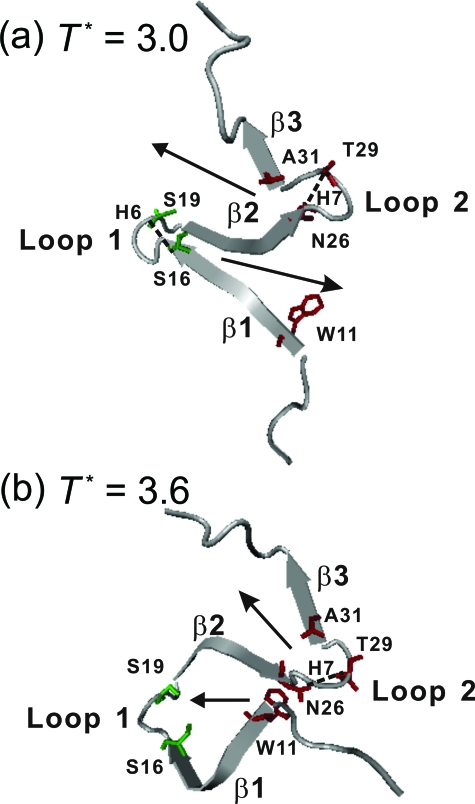
The contact maps of the configurations collected from folding and unfolding events at the transition temperature are shown in Fig. 7. To increase the statistics, we included 500 configurations before and after each folding (or unfolding) event. We found that the folding processes at the transition temperature essentially follow the reverse processes of unfolding. This is expected because the equilibrium folding∕unfolding simulations should be reversible. Although S16-S19 in loop 1 of β1-β2 hairpin has the highest contact probability at 0.0<Q<0.1, it is the contact between W11 and N26 that emerges with the second highest contact probability at 0.1<Q<0.2 and has the highest probability for Q>0.2. So, the W11-N26 contact serves as the nucleation site for the growth and final folding of β1-β2, unlike the low-temperature folding that starts from loop 1. On the other hand, the folding mechanism of β2-β3 hairpin is the same as that observed at low temperatures: N26-T29 is the first contact pair to trigger the formation of β2-β3. The difference of the folding mechanisms of β1-β2 hairpin at different temperatures is highlighted in Fig. 8.
Figure 7.
Probabilities of native residue-residue contacts at various folding stages according to the Q values for the equilibrium folding trajectories via path I (in the upper triangle) and unfolding trajectories via the reverse of path I (in the lower triangle) at the proximate transition temperature T*=3.6.
Figure 8.
Typical snapshots showing the key step in Pin1 WW domain through path I. (a) At low temperature (T*=3.0), folding of β1-β2 and β2-β3 hairpins are initiated from loop 1 and loop 2, respectively, and the zipping directions are indicated by the arrows. (b) At the transition temperature (T*=3.6), the folding of β1-β2 hairpin is initiated from the contact between W11 and N26, and the directions of the sheet formation are also indicated by the arrows. Several key residues (S16 and S19 in green, and W11, N26, T29, and A31 in red) are shown.
DISCUSSION
Folding mechanisms for individual hairpins
The folding pathways of Pin 1 WW domain can be classified into two different paths based on the early formation of either β1-β2 hairpin (path I) or β2-β3 hairpin (path II). Path II dominates at low temperatures, while only path I prevails at the transition temperature. Detailed examinations indicate that the folding mechanism of an individual β hairpin is independent of whether it folds first or second (i.e., in path I or path II). Instead, it is somewhat dependent on the temperature of the folding simulation. While β2-β3 hairpin folds via a turn zipper mechanism at low or high temperatures, β1-β2 hairpin folds via a turn zipper mechanism at low temperatures but a hydrophobic collapse mechanism at the folding-transition temperature.
The above change in the mechanism can be understood as follows. At high temperatures, a high kinetic energy allows a protein to explore more conformational space and only those native contacts that are sufficiently stable to withstand thermal fluctuation can serve as the nucleation sites for folding. There are 55 native atomic interactions for the residue pair W11-N26 for stabilizing β1-β2 hairpin, the strongest residue-residue interaction in the model Pin1 WW domain. By comparison, the strongest residue-residue interaction in β2-β3 hairpin (between Y24 and Q33) has only 26 atomic interactions. This explains the collapse mechanism for the first formation of β1-β2 at the relatively high temperature (T*=3.6). Once β1-β2 hairpin is formed, β2-β3 hairpin can be assembled with the least entropic cost via the turn zipper mechanism. At low temperatures, each native contact is less likely broken as soon as it is formed. As a result, the contacts between the nearest neighbors might form first and trigger the folding event. This explains the turn zipper mechanism for both hairpins at the low temperature (T*=3.0). It also explains the dominance of path II at the low temperature: β2-β3 hairpin has a shorter loop and its assembly is entropically more favorable than β1-β2 hairpin with a longer loop.
Comparison with experimental results
The above interpretation agrees with the experiments that reducing the length of loop 1 and substituting with high turn-propensity residues lead to fast folding and more stabilized proteins.26, 54 The difficulty of folding loop 1 found in simulations is consistent with the lack of strong interactions of loop 1 residues with other residues27, 36 and the functional role of a flexible loop 1 for ligand binding.54 The theoretical finding that V22 and M15 are not important in folding agrees with the weaker preference for Met and Val as cross-strand neighbors in β-sheets found by experiments and statistics.55, 56 The proposed nucleating W11-N26 contact is found to be critical for stabilizing Pin 1 WW domain.27
Based on mutation experiments and ϕ-value analysis, Gruebele and co-workes suggested two distinct kinds of residues in Pin1 WW domain:25, 27 loop 1 is responsible for folding rate and hydrophobic clusters for thermodynamic stability. At high temperatures, the hydrophobic clusters come into play but do not fully dominate the folding rate.25, 27 Our simulations at different temperatures are consistent with these findings: at low temperatures, path II dominates and the folding of β1-β2 hairpin is the rate determining step, while at high temperatures, the hydrophobic contact between N26 and W11 becomes the most important nucleation contact. In our simulations, the contacting pair N26-T29 plays an important role in initiating the folding of the loop 2 (Figs. 457). This is also consistent with the experimental observation that N26 is the structural gatekeeper27 in the WW domain. This may explain, in part, why the residue N26 is highly conserved in WW domain family.27, 37
It should be emphasized, however, that a Gō model has its limitation because it contains only the native contact interactions. For example, it unlikely provides a good description of unfolded conformations where non-native contacts often play an important role. The purpose of this paper is to show the behavior of individual hairpins of Pin 1 WW domain if its native contact energies dominate over non-native energies. This assumption is supported by the above-described consistency with some experimental results. However, it may not hold up as more experimental data become available. Nevertheless, the interplay between contact stability (enthalpy) and loop lengths (entropy) likely plays an important role in folding of many proteins.
Comparison with other simulation results
By analyzing the thermodynamic free energy profile based on a Cα model, Karanicolas and Brooks III42 predicted that the β2-β3 hairpin of Pin1 WW domain folded prior to β1-β2 hairpin. We found this pathway as the dominant path II in our low-temperature folding simulations. The unfolding all-atom simulations of FBP (Ref. 29) indicated that β2-β3 hairpin was dissociated first and the hydrophobic contacts in β1-β2 hairpin were more stable than those in loop 1.29 This is similar to the reverse of path I discovered in our simulation. Cecconi et al.32 suggested that the first contacts formed during folding were located in the middle of the two hairpins. During the unfolding reaction, the contacts of loop 1 and loop 2 disappeared at last. We did not find a similar pathway in our simulations. This is likely caused by the difference in models (a Cα model used by Cecconi et al.32 versus an all-atom model used in this study).
CONCLUSIONS
This paper has confirmed that the present two models of β-hairpin formation, the turn zipper model proposed by Moñuz and co-workers21, 22 and hydrophobic collapse model proposed by Dinner et al.24 in their studies of a single hairpin in a rather short polypeptide, are still justified in description of kinetic processes of individual hairpins in a two-hairpin protein. We also found that two β-hairpins in the Gō model of Pin1 WW domain obeyed different and temperature-dependent folding mechanisms: at a low temperature, both hairpins fold via the turn zipper model; however, it is the hydrophobic interaction at the end of β1-β2 hairpin that initiates the folding of β1-β2 hairpin at the folding-transition temperature (thus following the hydrophobic collapse model). The result highlights the interplay of the entropic and enthalpic effects on folding at different temperatures.
ACKNOWLEDGMENTS
The authors are grateful for the financial supports from NSF of China (Grants Nos. 50533010, 20574013, 20774020, and a Two-Base grant), Chinese Ministry of Education (key Grant No. 305004), Chinese Ministry of Science and Technology (973 Project No. 2005CB522700), Science and Technology Developing Foundation of Shanghai (Grant No. 07JC14005), Shanghai Education Committee (Project No. B112), and Senior Visiting Scholar Foundation of Key Laboratory. Partial computer support from NHPCC of Shanghai is appreciated. Y. Zhou also thanks the supports from National Institutes of Health (R01 GM 966049 and R01 GM 068530).
References
- Smith A. W. and Tokmakoff A., Angew. Chem., Int. Ed. 10.1002/anie.200701172 46, 7984 (2007). [DOI] [PubMed] [Google Scholar]
- Zhou Y. Q. and Linhananta A., Proteins 10.1002/prot.10065 47, 154 (2002). [DOI] [PubMed] [Google Scholar]
- Espinosa J. F., Muñoz V., and Gellman S. H., J. Mol. Biol. 10.1006/jmbi.2000.4349 306, 397 (2001). [DOI] [PubMed] [Google Scholar]
- Dyer R. B., Maness S. J., Peterson E. S., Franzen S., Fesinmeyer R. M., and Andersen N. H., Biochemistry 10.1021/bi049177m 43, 11560 (2004). [DOI] [PubMed] [Google Scholar]
- Klimov D. K. and Thirumalai D., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.97.6.2544 97, 2544 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans D. A. and Wales D. J., J. Chem. Phys. 10.1063/1.1759317 121, 1080 (2004). [DOI] [PubMed] [Google Scholar]
- Wei G. H., Derreumaux P., and Mousseau N., J. Chem. Phys. 10.1063/1.1613642 119, 6403 (2003). [DOI] [Google Scholar]
- Wei G. H., Mousseau N., and Derreumaux P., Proteins 10.1002/prot.20127 56, 464 (2004). [DOI] [PubMed] [Google Scholar]
- Pande V. S. and Rokhsar D. S., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.96.16.9062 96, 9062 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lwin T. Z. and Luo R., Protein Sci. 10.1110/ps.062438006 15, 2642 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolinski A., Ilkowski B., and Skolnick J., Biophys. J. 77, 2942 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imamura H. and Chen J. Z. Y., Proteins 10.1002/prot.20846 63, 555 (2006). [DOI] [PubMed] [Google Scholar]
- Ferrara P. and Caflisch A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.190324897 97, 10780 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrara P. and Caflisch A., J. Mol. Biol. 10.1006/jmbi.2000.4400 306, 837 (2001). [DOI] [PubMed] [Google Scholar]
- Wang H. W. and Sung S. S., J. Am. Chem. Soc. 10.1021/ja992359x 122, 1999 (2000). [DOI] [Google Scholar]
- Pitera J. W., Haque I., and Swope W. C., J. Chem. Phys. 10.1063/1.2190226 124, 141102 (2006). [DOI] [PubMed] [Google Scholar]
- Tsai J. and Levitt M., Biophys. Chem. 10.1016/S0301-4622(02)00198-9 101, 187 (2002). [DOI] [PubMed] [Google Scholar]
- Lei H. X., Dastidar S. G., and Duan Y., J. Phys. Chem. B 10.1021/jp063716a 110, 22001 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gellman S. H., Curr. Opin. Chem. Biol. 10.1016/S1367-5931(98)80109-9 2, 717 (1998). [DOI] [PubMed] [Google Scholar]
- Hughes R. M. and Waters M. L., Curr. Opin. Struct. Biol. 10.1016/j.sbi.2006.06.008 16, 514 (2006). [DOI] [PubMed] [Google Scholar]
- Muñoz V., Thompson P. A., Hofrichter J., and Eaton W. A., Nature (London) 10.1038/36626 390, 196 (1997). [DOI] [PubMed] [Google Scholar]
- Muñoz V., Henry E. R., Hofrichter J., and Eaton W. A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.95.11.5872 95, 5872 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muñoz V., Ghirlando R., Blanco F. J., Jas G. S., Hofrichter J., and Eaton W. A., Biochemistry 10.1021/bi052556a 45, 7023 (2006). [DOI] [PubMed] [Google Scholar]
- Dinner A. R., Lazaridis T., and Karplus M., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.96.16.9068 96, 9068 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deechongkit S., Nguyen H., Powers E. T., Dawson P. E., Gruebele M., and Kelly J. W., Nature (London) 10.1038/nature02611 430, 101 (2004). [DOI] [PubMed] [Google Scholar]
- Nguyen H., Jäger M., Kelly J. W., and Gruebele M., J. Phys. Chem. B 10.1021/jp052373y 109, 15182 (2005). [DOI] [PubMed] [Google Scholar]
- Jäger M., Nguyen H., Crane J. C., Kelly J. W., and Gruebele M., J. Mol. Biol. 10.1006/jmbi.2001.4873 311, 373 (2001). [DOI] [PubMed] [Google Scholar]
- Ferguson N., Pires J. R., Toepert F., Johnson C. M., Pan Y. P., Volkmer-Engert R., Schneider-Mergener J., Daggett V., Oschkinat H., and Fersht A., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.221467398 98, 13008 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrovich M., Jonsson A. L., Ferguson N., Daggett V., and Fersht A. R., J. Mol. Biol. 10.1016/j.jmb.2006.05.050 360, 865 (2006). [DOI] [PubMed] [Google Scholar]
- Crane J. C., Koepf E. K., Kelly J. W., and Gruebele M., J. Mol. Biol. 10.1006/jmbi.2000.3665 298, 283 (2000). [DOI] [PubMed] [Google Scholar]
- Russ W. P., Lowery D. M., Mishra P., Yaffe M. B., and Ranganathan R., Nature (London) 10.1038/nature03990 437, 579 (2005). [DOI] [PubMed] [Google Scholar]
- Cecconi F., Guardiani C., and Livi R., Biophys. J. 10.1529/biophysj.105.069138 91, 694 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karanicolas J. and Brooks C. L., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0731771100 100, 3954 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mu Y. G., Nordenskiöld L., and Tam J. P., Biophys. J. 10.1529/biophysj.105.076406 90, 3983 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibragimova G. T. and Wade R. C., Biophys. J. 77, 2191 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranganathan R., Lu K. P., Hunter T., and Noel J. P., Cell 10.1016/S0092-8674(00)80273-1 89, 875 (1997). [DOI] [PubMed] [Google Scholar]
- Jäger M., Nguyen H., Dendle M., Gruebele M., and Kelly J. W., Protein Sci. 10.1110/ps.072775507 16, 1495 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharpe T., Jonsson A. L., Rutherford T. J., Daggett V., and Fersht A. R., Protein Sci. 10.1110/ps.073004907 16, 2233 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowalski J. A., Liu K., and Kelly J. W., Biopolymers 10.1002/bip.10020 63, 111 (2002). [DOI] [PubMed] [Google Scholar]
- Jacobs D. M., Saxena K., Vogtherr M., Bernado P., Pons M., and Fiebig K. M., J. Biol. Chem. 10.1074/jbc.M300796200 278, 26174 (2003). [DOI] [PubMed] [Google Scholar]
- Peng T., Zintsmaster J. S., Namanja A. T., and Peng J. W., Nat. Struct. Mol. Biol. 10.1038/nsmb1207 14, 325 (2007). [DOI] [PubMed] [Google Scholar]
- Karanicolas J. and Brooks C. L., J. Mol. Biol. 10.1016/j.jmb.2003.09.047 334, 309 (2003). [DOI] [PubMed] [Google Scholar]
- Karanicolas J. and Brooks C. L., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0304825101 101, 3432 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Z. L., Ding J. D., and Zhou Y. Q., Biophys. J. 10.1529/biophysj.106.102095 93, 2152 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks B. R., Bruccoleri R. E., Olafson B. D., States D. J., Swaminathan S., and Karplus M., J. Comput. Chem. 10.1002/jcc.540040211 4, 187 (1983). [DOI] [Google Scholar]
- Neria E., Fischer S., and Karplus M., J. Chem. Phys. 10.1063/1.472061 105, 1902 (1996). [DOI] [Google Scholar]
- Bellemans A., Orban J., and Vanbelle D., Mol. Phys. 10.1080/00268978000100671 39, 781 (1980). [DOI] [Google Scholar]
- Weeks J. D., Chandler D., and Andersen H. C., J. Chem. Phys. 10.1063/1.1674820 54, 5237 (1971). [DOI] [Google Scholar]
- Sherwood A. E. and Prausnitz J. M., J. Chem. Phys. 10.1063/1.1725884 41, 429 (1964). [DOI] [Google Scholar]
- Taketomi H., Ueda Y., and Gō N., Int. J. Pept. Protein Res. 7, 445 (1975). [PubMed] [Google Scholar]
- Smith S. W., Hall C. K., and Freeman B. D., J. Comput. Phys. 10.1006/jcph.1996.5510 134, 16 (1997). [DOI] [Google Scholar]
- Andersen H. C., J. Chem. Phys. 10.1063/1.439486 72, 2384 (1980). [DOI] [Google Scholar]
- Zhou Y. Q., Karplus M., Wichert J. M., and Hall C. K., J. Chem. Phys. 10.1063/1.474186 107, 10691 (1997). [DOI] [Google Scholar]
- Jäger M., Zhang Y., Bieschke J., Nguyen H., Dendle M., Bowman M. E., Noel J. P., Gruebele M., and Kelly J. W., Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0600511103 103, 10648 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wouters M. A. and Curmi P. M. G., Proteins 10.1002/prot.340220205 22, 119 (1995). [DOI] [PubMed] [Google Scholar]
- Smith C. K. and Regan L., Science 10.1126/science.270.5238.980 270, 980 (1995). [DOI] [PubMed] [Google Scholar]
- Humphrey W., Dalke A., and Schulten K., J. Mol. Graphics 10.1016/0263-7855(96)00018-5 14, 33 (1996). [DOI] [PubMed] [Google Scholar]