Abstract
An anatomically realistic computational model of the pelvic floor and anal canal regions was used in this study to examine the mechanics of normal defecatory function within the female pelvic floor. This subject-specific, MRI-based model enabled mechanical simulations to be performed and quantitatively assessed against experimental data retrieved from the same volunteer. The levator ani muscle group mesh was used as the domain over which the governing equations of finite elasticity were solved using the finite element method with a Mooney-Rivlin material law. Deformation of the levator ani was simulated during a ‘bear down’ maneuver in order to visualize the way this muscle group functions in an asymptomatic subject. A pressure of 4 kPa was imposed on the mesh and the computed mesh displacements were compared to those obtained from dynamic MR images with an average, experimentally consistent, downwards displacement of 27.2 mm being achieved. The RMS error for this movement was 0.7 mm equating to a percentage error of 2.6% in the supero-inferior direction and 13.7 mm or 74.5% in the antero-posterior direction.
Keywords: Computational model, Finite elasticity, Finite element, Mooney-Rivlin, Validation, levator ani
I. Introduction
One in every ten women will, at some point in their lives, suffer a form of pelvic floor dysfunction so severe that it will require surgery, with one third of these undergoing repeated surgical procedures (Olsen, Smith, Bergstrom, Colling & Clark 1997). Pelvic floor dysfunction (PFD) results from specific damage to, or atrophy of, the muscles, fascial structures and nerves of the pelvic floor. The spectrum of dysfunction is vast, and abnormalities of the pelvic floor can lead to defecation disorders such as fecal incontinence or obstructed defecation (Smith & Witherow 2000). Fecal incontinence is a disorder that affects people of all ages. It is, however, more common in women and in older adults, but is not considered a normal part of the aging process. It remains unclear whether muscle damage or neuropathy is the primary mechanism for the development of PFD, but some authors believe that the PFD is largely caused by damage to the connective tissues (ligaments and fascia) and muscles of the pelvic floor. The combined action of ligaments, fascia and muscles anchors the pelvic organs, and the urethra, vagina and anal canal. The normal function of the pelvic organs is thus dependent on the integrity of the pelvic floor (Petros 2004).
Normal defecatory control requires the complex integration of neurological pathways and four main muscle groups in the pelvic floor and anal canal: the internal anal sphincter, external anal sphincter, puborectalis and the levator ani muscle group. It also requires the ability to adequately determine anorectal contents, and the ability to access the necessary facilities to evacuate the rectum. In particular, the LA is important in controlling defaecation as it acts together with the striated muscle of the anterior abdominal wall, to generate intra-abdominal pressure. Any increase in intra-abdominal pressure (e.g., caused by sneezing or coughing) is applied equally to all sides of the pelvic and abdominal walls. If the LA is pathologically weakened or temporarily inactivated, the pressure on one side of a pelvic organ may become greater than that on the other, allowing the organ to descend (genital prolapse). If this movement carries the organ outside the pelvic cavity, pressure acting on the content of that organ will be directed unequally and in the case of the bladder or rectum could cause urinary or faecal incontinence (Janda, van der Helm & de Blok 2003). The shape of the levator ani and regional thickening during different levels of physiological loading can provide an indication of pelvic floor dysfunction (Lee, Horkaew, Darzi & Yang 2004).
In the past, the poor selection of patients, insufficient baseline investigations and poorly audited surgical techniques, have led to unacceptable levels of surgical failure. In many cases, patients and their symptoms were not adequately assessed, which may have led to a delay in diagnosis, with prolonged morbidity and unnecessary or inappropriate surgical procedures (Smith & Witherow 2000). The ability to accurately simulate levator ani muscle function will enable clinicians to better understand the anatomical and physiological defects which may be affecting normal defecatory function in patients and thereby select the most appropriate treatment for each individual.
Few of the currently available geometric pelvic floor models are suitable for finite element analysis. One of the most advanced numerical models to date is the d’Aulignac, Martins, Pires, Mascarenhas & Jorge (2005) model which uses shell finite elements to reconstruct the levator ani muscle in three dimensions. Muscle fiber direction and tissue incompressibility were included in the model to help simulate the muscle under pressure and with active contraction. However, the geometry for the d’Aulignac et al. (2005) model was constructed using data from a 72 year old female cadaver and therefore may not be representative of live subjects.
The purpose of this study is to present simulation results of levator ani muscle function using the finite element method on computational meshes based on live subject data.
II. Pelvic Floor Model
An anatomically realistic female pelvic floor model, based on live subject MRI data (previously described in detail in Noakes, Bissett, Pullan & Cheng (2008)), was used as the basis of the simulation environment. The model was constructed from 120 cross-sectional T2 weighted MRI images, with a base resolution of 384 × 384 pixels with a 1 mm slice separation. The subject was a healthy, nulliparous, 32 year old female volunteer. Ethical approval and informed consent were obtained for the MRI data to be used in this study.
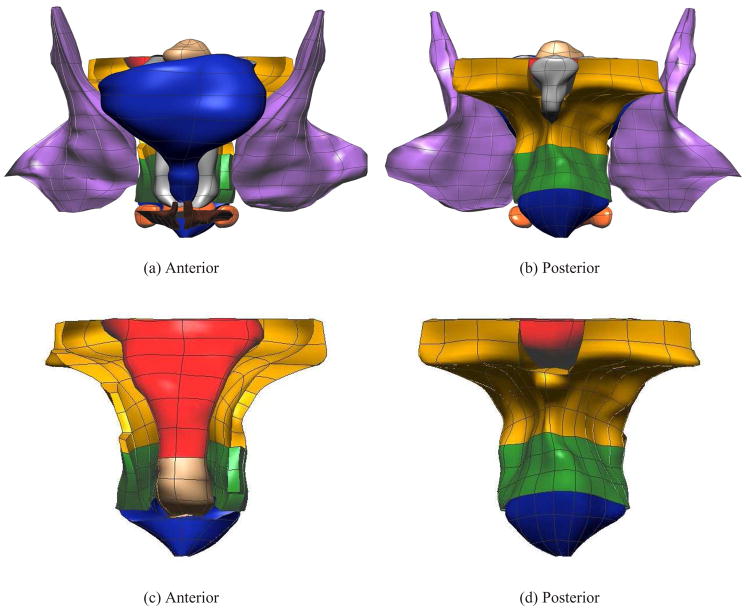
The boundaries of each of the pelvic structures in the model were delineated via manual data point placement on each MR image. A total of 19, 678 data points were traced around 13 components of interest including the rectum, vagina, uterus and bladder (including urethra), the puborectalis (PR) muscle, the levator ani muscle group (LA), the internal and external anal sphincter (IAS and EAS respectively), the transverse perineae (TP) muscles, obturator internus (OI) muscles, the bulbospongiosus muscle, the coccyx bone and the perineal body (PB). Initial trilinear finite elements were constructed around each data cloud. A least squares iterative fitting technique was then used to minimize the distances between each data point and its orthogonal position on the initial mesh (Bradley, Pullan & Hunter 1997, Cheng, Sands, French, Withy, Wong, Legget, Smith & Pullan 2005). The final fitted surface and volume meshes (shown in Figure 1) were interpolated using tricubic Hermite basis functions to give a realistic appearance to the anatomical geometries and had an average RMS error of less than 0.75 mm between the data points and final fitted mesh surfaces.
Fig. 1.
The final fitted models from the MRI data set. Shown are (a) anterior and (b) posterior views showing 12 of the 13 components – levator ani (LA) (gold), puborectalis (PR) (green), external anal sphincter (EAS) (blue), internal anal sphincter (IAS) (beige), rectum (red), transverse perineae (orange), perineal body (orange), coccyx (silver), uterus (beige), vagina (silver), obturator internus (purple) and bulbospongiosus (brown). Also shown are enlarged views of the (c) anterior and (d) posterior of the LA, PR, EAS, IAS and rectum. For clarity the lumen has not been shown in these views.
III. Mechanical Modelling: Valsalva Pressure on the Levator Ani Muscle
The levator ani muscle was presented using 160 nodes and 58 tricubic Hermite elements. The finite elasticity deformation simulations were performed using the CMISS1 software package. For simulation purposes the levator ani (LA) muscle group was created with the local coordinate system (ξ1, ξ2, ξ3) defined as follows: ξ1 running (subject’s) right to left around the muscle, ξ2 running in a superior/inferior direction and ξ3 running in a medio-lateral direction.
Pressure was applied orthogonally to the anterior surface of each of the muscle elements to simulate the deformation experienced by the LA muscle during a ‘bearing down’ abdominal squeeze maneuver, performed by increasing intra-abdominal pressure while relaxing the pelvic floor muscles, as is carried out in the process of evacuation of the bowel or during the delivery of a baby (Parente, Jorge, Mascarenhas, Fernandes & Martins 2007).
Understanding and predicting the deformation of a material under varying distributions of applied stresses and strains is fundamental to understanding its function. Biological materials present nonlinear mechanical behavior and so a finite deformation elasticity framework must be employed.
Continuum models of mechanical function have two preliminary requirements: (a) an appropriate representation of the 3D geometry of the pelvic floor, and (b) information about the mechanical behavior of the muscle tissue. On this basis, it is possible to solve governing equations that obey well-established physical laws of conservation of mass, momentum, and energy subject to pressure and displacement boundary conditions (Hunter, Pullan & Smaill 2003). Because regional stresses cannot be measured, models can be validated only by comparing displacement and strain fields observed during contraction or relaxation with predicted behavior. At present, the accuracy of continuum modelling is constrained much more by incomplete knowledge of the constitutive relations and associated material parameters that govern the 3D mechanical behavior of skeletal and smooth muscle than by the precision of the modelled anatomic description.
A. Material Parameters
Soft biological tissues are generally modeled as incompressible elastic solids for which the components of the second Piola-Kirchhoff stress tensor are given by the derivatives of the strain energy function, W. The functional form the strain energy function can be inferred from experimental data, and the material parameters may then be estimated using well-established fitting techniques. The Mooney-Rivlin material law (Mooney 1940), commonly used in biomechanical simulations (see Equation 1), was used in this study. This simple material law utilizes a non-linear relationship between stress and strain to describe incompressible hyperelastic materials that exhibit near-isotropic behavior.
| (1) |
where W is the strain energy function and c1 and c2 are material parameters which have dimensions of stress but no physical interpretation (Humphrey 2002), and must be determined from experiments on the particular material being modelled, and I1 and I2 are principal strain invariants of the right Cauchy-Green tensor.
As it is difficult to test the material behaviour of the levator ani muscle in vivo, a two-parameter Mooney-Rivlin (Mooney 1940) hyperelastic material model was initially adopted with the same parameters as those used in the work of Lee, Darzi & Yang (2005) who also modelled the levator ani. In that work they used coefficients of c10 = 2.5 kPa, c20 = 0.625 kPa, however these material parameters were found to be too compliant in our case. Previous hyperelastic material models from Gérard, Wilhelms-Tricarico, Perrier & Payan (2003) (tongue), Meier & Blickhan (2000), Ionescu, Guilkey, Berzins, Kirby & Weiss (2005) and Teran, Sifakis, Blemker, Hing, Lau & Fedkiw (2005) (skeletal muscle and tendons) were used as a guide to increase the Mooney-Rivlin parameters to c10 =4.5 kPa and c20 =2 kPa in order to increase the material stiffness. The Mooney-Rivlin model in our simulation hence approximates the strain energy function W as defined in Equation 2:
| (2) |
B. Boundary Conditions
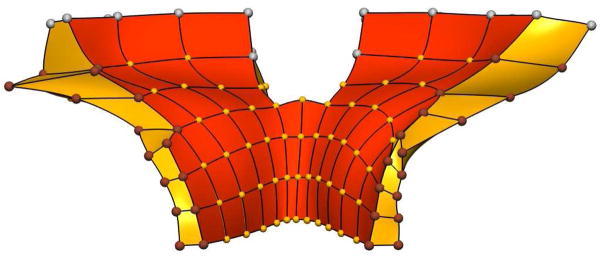
To simulate the deformation of the levator ani muscle, boundary conditions were imposed on the model to incorporate the existence of the surrounding supporting structures. The elements which experienced the applied pressures, and the displacement boundary constraints are illustrated in Figure 2. We applied fixed displacement boundary conditions (including nodal values and their derivatives) to twenty nodes on the undeformed mesh. These zero-displacement nodes were located along the top of the muscle and those located posteriorly on the muscle where the LA is firmly attached to the coccyx bone. A further 32 nodes, corresponding to those portions of the LA which attach to the fasciae of obturator internus (laterally), were constrained to move only in the z (inferior-superior) direction. This is because the presence of the obturator internus muscle prevents lateral movement (x direction) and any antero-posterior movement is minimized due to the close attachment of the LA with the pubis bone. All other nodal parameters (and derivatives) in the mesh were left unconstrained.
Fig. 2.
Anterior view of the levator ani computational mesh showing the boundary conditions applied to the model. The superior surface (shaded red) shows the elements which experienced the applied pressure. The nodes in silver are those which remain fixed. The brown nodes are constrained to move only in the vertical (z) direction whilst the remaining (gold) nodes may move and rotate freely under load.
Intra-abdominal pressure (IAP) has been measured at rest by Schaer, Perucchini, Munz, Peschers, Koechli & Delancey (1999), Sanchez, Tenofsky, Dort, Shen, Helmer & Smith (2001), Cobb, Burns, Kercher, Matthews, Norton & Heniford (2005) and Chionh, Wei, Martin & Opdam (2006) with an average of approximately 0.48 kPa. IAP during valsalva (forced exhalation against a closed glottis) has also been measured under different conditions by Sugrue (1995), Howard, Miller, Delancey & Ashton-Miller (2000), Cobb et al. (2005), Hemat (2003) and Brandt, Lorenzato, Nobrega, Albuquerque, Falcao & Júnior (2006) with average values of 4.76 kPa for subjects lying supine, while standing subjects gave valsalva pressures of approximately 9.65 kPa (see Table I).
TABLE I.
Intra-abdominal (IAP) Pressure Recordings from Previous Research
| Author | IAP Valsalva-Supine (kPa) | IAP Valsalva-Standing (kPa) |
|---|---|---|
| Sugrue (1995) | 4.22 | – |
| Howard et al. (2000) | – | 10.89 |
| Hemat (2003) | – | 8 – 10.67 |
| Cobb et al. (2005) | 5.29 (sitting) | 8.65 |
| Brandt et al. (2006) | – | 9.74 |
|
| ||
| Average IAP | 4.76 | 9.65 |
| Values used in this study | 4.5† | ★ |
Takes into account the slightly higher IAP contribution produced by the sitting position in Cobb et al. (2005).
Patient was supine when performing the valsalva maneuver, so standing values were not required.
Because the model was based on images taken of the subject in a supine position and in a resting state, the muscles already incorporate resting tone. Therefore, the mean resting pressure (0.5 kPa) was subtracted from the approximated average supine valsalva pressure (4.5 kPa) to give the final pressure (4 kPa) to be applied to the LA model in the simulation.
C. Simulation Results
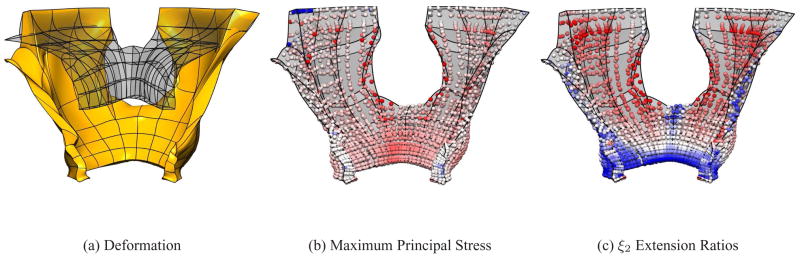
In order to compute the final deformation of the LA muscle, twenty load steps, each providing 5% of the total load, were used to solve the nonlinear equations via Newton’s method. Loading of all 58 elements in the model with 4 kPa produced an average downwards displacement of 27.2 mm and an average posterior displacement of 18.4 mm of the mesh. The shape of the muscle was shown to have deformed during the simulation from a ‘seagull-like’ shape (when viewed posteriorly) into a shape with a more concave, ‘bowl’ type appearance. The deformation of the muscle, and its relative movement compared to the original reference mesh at rest, are shown in Figure 3a. Figure 3(b) and Figure 3(c) show the stresses and extension ratios located at each of the computational Gauss points at the final deformed state. Figure 3(b) shows the maximum principal stresses at each of the Gauss points ranging from −10–200 kPa (−10 kPa is denoted blue, 0 kPa is denoted white, 200 kPa is denoted red). Figure 3(c) shows the extension ratios in the ξ2 direction (i.e., the superior-inferior direction) ranging from 0.7–2 (0.7 is denoted blue, 1 is denoted white and 2 is denoted red).
Fig. 3.
Results of finite elasticity simulations. Anterior view (a) of the levator ani (gold surface) deforming under ‘bear down’ pressure compared to the muscle geometry (transparent surface) at rest. The (b) stress and (c) extension ratio distributions are shown at the computational Gauss points in the deformed state. The stresses varied from −10 – 200 kPa (with blue representing maximum negative stress, white representing zero stress and red representing maximum positive stress), while the extension ratios in the ξ2 direction varied from 0.7 – 2 (with blue representing maximum compression, white representing zero extension and red representing maximum extension).
D. Comparison with Dynamic MRI
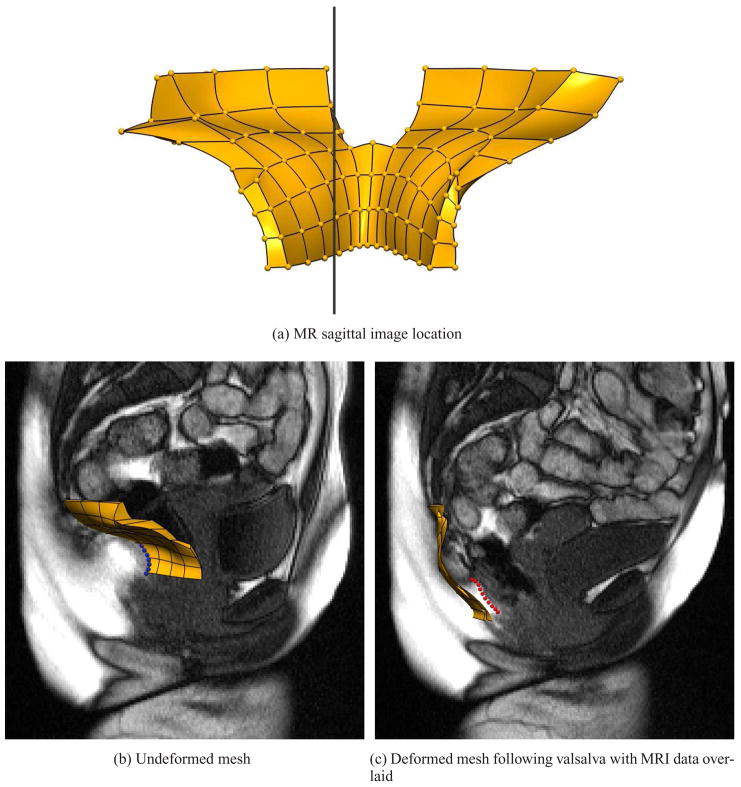
Dynamic T2 weighted sagittal MR images, were taken of the same subject during a ‘bear down’ maneuver. These images were used to determine the actual displacement of the subject’s levator ani muscle during ‘bear down’ by digitizing the posterior surface of the levator ani muscle on the MR images at rest, and then again at the final stage of the ‘bear down’ when the displacement of the muscles was greatest. Figure 4(a) shows the location of the dynamic sagittal slices in relation to the LA muscle mesh. Three points on the posterior surface of the LA muscle mesh were tracked during its simulated deformation and compared to the movement of 3 similarly positioned locations identified on the digitized surface of the muscle in the dynamic MR image sequence. The displacement of the muscle during ‘bear down’ (as measured on the MR images) had an average inferior movement of 27.9 mm and an average posterior movement of 4.7 mm.
Fig. 4.
Location of (a) the dynamic slice overlaid against the reference LA mesh. The LA mesh can be directly compared with the overlaid sagittal slice in the (b) rest position and (c) deformed position. In (b) the LA muscle has been highlighted on the MR image by the blue points and in (c) by the red points.
Figure 4(b) shows the undeformed levator ani muscle mesh (gold) overlaid on the dynamic sagittal MR image at rest. The blue points on the image outline the posterior surface of the levator ani on the image which closely corresponds with the undeformed muscle mesh.
The ‘bear down’ simulation produced an average (over the 3 tracked points) downwards displacement of 27.2 mm and an average posterior displacement of 18.4 mm in the deformed mesh. The inferior movement of the deformed mesh was similar, 0.7 mm less than that seen in the dynamic MRI scans of the subject (see Figure 4(c) and Table II). However, the posterior displacement was on average 13.7 mm greater, in the posterior direction, than the movement shown in the MR images.
TABLE II.
Average LA Muscle Mesh Displacement Compared with MRI Experimental Findings Following Bear Down Deformation. Positive y direction is in the anterior direction while positive z direction is in the inferior direction.
| Displacement axis | LA displacement from MR images (mm) | LA mesh displacement (mm) | Difference (mm) | % error |
|---|---|---|---|---|
| Antero-Posterior (y) | 4.7 | 18.4 | 13.7 | 74.5 |
| Supero-Inferior (z) | −27.9 | −27.2 | 0.7 | 2.6 |
IV. DISCUSSION
We have presented results of finite elasticity simulation of a subject specific finite element model of the levator ani muscle. The research of Hill (2006) recorded approximately half of the asymptomatic nulliparous subjects having the posterior LA deforming into a ‘bowl’ shape as it descended during valsalva loading. The LA model therefore appears to represent this type of individual.
The finite elasticity simulation attempted to represent a ‘bear down’ maneuver. The simulation results have been directly compared against dynamic MR images of the same subject. The RMS error between the simulated results and the MR images was was 0.7 mm equating to a percentage error of 2.6% in the supero-inferior direction and 13.7 mm or 74.5% in the antero-posterior direction. There are a number of reasons for the larger than expected movement of simulated LA muscle in the posterior direction; many related to assumptions and simplifications in the finite element model.
The extension ratios showed that maximum compression in the ξ2 direction occurred at the bottom of the levator ani muscle and around the bottom coccyx region, whiles highest extension in the in the ξ2 direction was obtained in the upper portions of the muscle. However, it is uncertain whether this distribution of extensions are an accurate representation of deformation of the levator muscle in the in vivo case and further investigation is warranted.
One reason for the large posterior displacement error is the fact that the model does not restrict the change in length in the posterior portion of the muscle which, Hill (2006) and Kruger, Murphy & Heap (2005) believe, changes shape during a ‘bear down’ but does not stretch like the anterior portions of the muscle which are fixed anteriorly at the pubis bone via a close connection with the puborectalis. The simulation was performed on the LA muscle mesh in isolation and therefore ignored (except for the boundary conditions) physical relationships with surrounding musculature, bone and skin. The simulation could be further extended by including the surrounding pelvic structures which apply a force on the movement of the muscle during ‘bear down’ and the constraints provided by the MRI table to restrict excessive movement in the posterior direction. In addition, the relatively simple material law assumes isotropy in the muscle. Our model also lacks any explicit fibre distributions known to be in the musculature.
In this study, passive mechanics was used to simulate the deformation of the LA muscle, therefore, the mesh was assumed to react passively to the applied pressure with no natural (or active) contractile response included in the simulation. We believe this assumption is realistic when the LA is loaded with pressure during an abdominal squeeze ‘bear down’, because intra-abdominal pressure is primarily generated by the abdominal muscles which sit above the pelvic floor. However, during a valsalva maneuver, muscles within the pelvic floor also produce some contraction and thereby contribute to the IAP. Further information about the tone of the LA muscle is required to better understand the contractile behavior of the LA muscle when a subject evacuates their bowel. This is important for future studies since, if the muscle contracts and relaxes in a non-uniform fashion during ‘bear down’ (as is hypothesized by Hill (2006)) then incorporating this irregularity into the simulation would require the use of an active mechanics model and most likely change the deformation results which currently show the entire muscle in a relaxed state deforming passively under pressure.
In the ‘bear down’ simulation, the dynamic sagittal slice sequence used for comparison was only taken at one position in the subject. This practical limitation arose due to the short time frame in which the subject could perform the ‘bear down’ whilst being imaged, and only provided a tiny snapshot of what the deformed muscle shape might look like at any stage during the maneuver. It was not possible to deduce the entire shape from a such a small (1 mm) interval and so, whilst the deformation produced in the simulations was approved by an anatomist and appears to follow previous research findings, more slices through the muscle would be needed to verify the simulation. We hope that advances in MRI technology in the future will allow for high-resolution 3D dynamic MRI scans.
V. CONCLUSIONS
The overall objective of this study was to model one of the mechanical process occurring within the female pelvic floor in order to improve the understanding of normal defecatory function in the pelvic floor and anal canal.
The levator ani muscle group mesh was used as a realistic, geometric domain over which the governing equations of finite elasticity were solved using the finite element method. A simple valsalva deformation, with an applied pressure of 4 kPa, was simulated on the levator ani muscle mesh and caused the original ‘seagull-like’ shape to deform into a concave, ‘bowl’ shape with an average, experimentally consistent, downwards displacement of 27.2 mm measured at the nodes. An average posterior displacement (13.7 mm greater than that measured experimentally) of 18.4 mm was also recorded.
The subject-specific MRI model was used as a framework to examine the mechanics of normal function of the levator ani muscle group during a valsalva maneuver. The functional simulation performed on the pelvic musculature produced promising results which were consistent with live experimental data taken from the subject. The benefits of the inclusion of a detailed anisotropic material laws and more realistic boundary conditions are unknown at this stage, but may enable improved simulation accuracy.
Acknowledgments
The authors would like acknowledge the assistance of Drs Vijay Rajagopal and Jae-Hoon Chung from the Bioengineering Institute for helpful discussions on mechanics theory and analysis. The authors would also like to thank Professor Stuart Heap from Mercy Hospital in assisting with pelvic floor anatomy identification, Jenny Kruger and Bernadette Murphy from The University of Auckland Sports Science Department for providing the MRI data. The authors are grateful to the subject for volunteering to be part of this study and allowing the results to be published.
This project was funded in part by a National Institutes of Health Grant (R01 DK64775). The first author would also like to acknowledge the financial assistance of NZIMA (New Zealand Institute of Mathematics and its Applications) Masters Scholarship.
Footnotes
Conflict of Interest
The authors declare that there is no conflict of interest present.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bradley CP, Pullan AJ, Hunter PJ. Geometric modeling of the human torso using cubic Hermite elements. Ann Biomed Eng. 1997;25:96–111. doi: 10.1007/BF02738542. [DOI] [PubMed] [Google Scholar]
- Brandt FT, Lorenzato FRB, Nobrega LV, Albuquerque CDC, Falcao R, Júnior AA. Intra-abdominal pressure measurement during ultrasound assessment of women with stress urinary incontinence: a novel model. Acta Cirúrgica Brasileira. 2006;21(4):237–241. doi: 10.1590/s0102-86502006000400009. [DOI] [PubMed] [Google Scholar]
- Cheng LK, Sands GB, French RA, Withy SJ, Wong SP, Legget ME, Smith WM, Pullan AJ. Rapid construction of a patient specific torso model from 3D ultrasound for noninvasive imaging of cardiac electrophysiology. Med Biol Eng Comput. 2005;43:1–6. doi: 10.1007/BF02345808. [DOI] [PubMed] [Google Scholar]
- Chionh JJL, Wei BPC, Martin JA, Opdam HI. Determining normal values for intra-abdominal pressure. ANZ Journal of Surgery. 2006;76:1106–1109. doi: 10.1111/j.1445-2197.2006.03849.x. [DOI] [PubMed] [Google Scholar]
- Cobb WS, Burns JM, Kercher KW, Matthews BD, Norton HJ, Heniford BT. Normal intraabdominal pressure in healthy adults. Journal of Surgical Research. 2005;129:231–235. doi: 10.1016/j.jss.2005.06.015. [DOI] [PubMed] [Google Scholar]
- d’Aulignac D, Martins JAC, Pires EB, Mascarenhas T, Jorge RMN. A shell finite element model of the pelvic floor muscles. Comput Methods Biomech Biomed Engin. 2005;8(5):339–47. doi: 10.1080/10255840500405378. [DOI] [PubMed] [Google Scholar]
- Gérard J, Wilhelms-Tricarico R, Perrier P, Payan Y. A 3d dynamical biomechanical tongue model to study speech motor control. Recent Researh and Developments in Biomechanics. 2003;1:49–64. [Google Scholar]
- Hemat RAS. Principles of Modern Urology. Urotext: 2003. [Google Scholar]
- Hill RG. Master’s thesis. The University of Auckland; New Zealand: 2006. The structure and function of the pelvic floor muscles: A pilot magnetic resonance imaging study. [Google Scholar]
- Howard D, Miller JM, Delancey JOL, Ashton-Miller JA. Differential effects of cought, valsalva, and continence status on vesical neck movement. Obstet Gynecol. 2000;95:535–540. doi: 10.1016/s0029-7844(99)00618-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer-Verlag; New York, US: 2002. [Google Scholar]
- Hunter PJ, Pullan AJ, Smaill BH. Modelling total heart function. Annual Review of Biomedical Engineering. 2003;5:147–177. doi: 10.1146/annurev.bioeng.5.040202.121537. [DOI] [PubMed] [Google Scholar]
- Ionescu I, Guilkey J, Berzins M, Kirby RM, Weiss J. Computational simulation of penetrating trauma in biological soft tissues using the material point method. Studies in Health Technology and Informatics. 2005;111:213–218. [PubMed] [Google Scholar]
- Janda S, van der Helm FCT, de Blok SB. Measuring morphological parameters of the pelvic floor for finite element modelling purposes. J Biomech. 2003;36(6):749–757. doi: 10.1016/s0021-9290(03)00008-3. [DOI] [PubMed] [Google Scholar]
- Kruger JA, Murphy BA, Heap SW. Alterations in levator ani morphology in elite nulliparous athletes: A pilot study. Australian and New Zealand Journal of Obstetrics and Gynaecology. 2005;45:42–47. doi: 10.1111/j.1479-828X.2005.00349.x. [DOI] [PubMed] [Google Scholar]
- Lee S, Darzi A, Yang G. Subject specific finite element modelling of the levator ani. Medical Image Computing and Computer-Assisted Intervention. 2005;8:360–367. doi: 10.1007/11566465_45. [DOI] [PubMed] [Google Scholar]
- Lee S, Horkaew P, Darzi A, Yang G. Statistical shape modelling of the levator ani with thickness variation. In: Barillot PHC, Haynor DR, editors. Lecture Notes in Computer Science. Springer Berlin/Heidelberg; 2004. pp. 258–265. [Google Scholar]
- Meier P, Blickhan R. Fem-simulation of skeletal muscle: The influence of inertia during activation and deactivation. In: Herzog W, editor. Skeletal Muscle Mechanics: From Mechanisms to Function. John Wiley & Sons, Ltd; 2000. pp. 207–224. [Google Scholar]
- Mooney. A theory of large elastic deformation. J Appl Phys. 1940;11:582–592. [Google Scholar]
- Noakes KF, Bissett IP, Pullan AJ, Cheng LK. Anatomically based three-dimensional models of the pelvic floor and anal canal for finite element analysis. Ann Biomed Eng. 2008 doi: 10.1007/s10439-008-9471-6. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsen AL, Smith VJ, Bergstrom JO, Colling JC, Clark L. Epidemiology of surgically managed pelvic organ prolapse and urinary incontinence. Obstet Gynecol. 1997;89:501–506. doi: 10.1016/S0029-7844(97)00058-6. [DOI] [PubMed] [Google Scholar]
- Parente MP, Jorge RM, Mascarenhas T, Fernandes AA, Martins JA. Deformation of the pelvic floor muscles during a vaginal delivery. Int Urogynecol J Pelvic Floor Dysfunct. 2007;19(1):65–71. doi: 10.1007/s00192-007-0388-7. [DOI] [PubMed] [Google Scholar]
- Petros PEP. The Female Pelvic Floor. Springer Verlag; Berlin: 2004. [Google Scholar]
- Sanchez NC, Tenofsky PL, Dort JM, Shen LY, Helmer SD, Smith RS. What is normal intra-abdominal pressure? Am Surg. 2001;67:243–248. [PubMed] [Google Scholar]
- Schaer GN, Perucchini D, Munz E, Peschers U, Koechli OR, Delancey JOL. Sonographic evaluation of the bladder nech in continent and stress-incontinent women. Obstet Gynecol. 1999;93:412–416. doi: 10.1016/s0029-7844(98)00420-7. [DOI] [PubMed] [Google Scholar]
- Smith CA, Witherow RON. The assessment of female pelvic floor dysfunction. BJU International. 2000;85:579–587. doi: 10.1046/j.1464-410x.2000.00474.x. [DOI] [PubMed] [Google Scholar]
- Sugrue M. Intra-abdominal pressure. Clinical Intensive Care. 1995;6:76–79. doi: 10.1007/s00134-002-1253-2. [DOI] [PubMed] [Google Scholar]
- Teran J, Sifakis E, Blemker S, Hing VNT, Lau C, Fedkiw R. Creating and simulating skeletal muscle from the visible human data set. IEEE TVCG.0. 2005 doi: 10.1109/TVCG.2005.42. [DOI] [PubMed] [Google Scholar]