Use of ¹³C^α Chemical-Shifts in Protein Structure Determination

Abstract

A physics-based method, aimed at determining protein structures by using NOE-derived distances together with observed and computed ¹³C chemical shifts, is proposed. The approach makes use of ¹³C^α chemical shifts, computed at the density functional level of theory, to obtain torsional constraints for all backbone and side-chain torsional angles without making a priori use of the occupancy of any region of the Ramachandran map by the amino acid residues. The torsional constraints are not fixed but are changed dynamically in each step of the procedure, following an iterative self-consistent approach intended to identify a set of conformations for which the computed ¹³C^α chemical shifts match the experimental ones. A test is carried out on a 76-amino acid all-α-helical protein, namely the B. Subtilis acyl carrier protein. It is shown that, starting from randomly generated conformations, the final protein models are more accurate than an existing NMR-derived structure model of this protein, in terms of both the agreement between predicted and observed ¹³C^α chemical shifts and some stereochemical quality indicators, and of similar accuracy as one of the protein models solved at a high level of resolution. The results provide evidence that this methodology can be used not only for structure determination but also for additional protein structure refinement of NMR-derived models deposited in the Protein Data Bank.

Introduction

Traditional NMR investigations of protein structure in solution make use of the ¹³C chemical shifts to identify secondary-structure regions in a coarse-grained manner, and quantitative use of NOEs, vicinal coupling constants, and backbone dipolar couplings to obtain three-dimensional structures. We present a method which exploits distances derived from Nuclear Overhauser Effects¹ (NOEs) and ¹³C^α chemical shifts without resorting to other experimental data (such as vicinal coupling constants or backbone residual dipolar couplings) to determine protein structure; the method can also be used for further refinement of structures that have already been determined by the traditional methods. In the methodology presented here, the ¹³C^α chemical shifts are computed at the Density Functional Theory (DFT) level to identify conformations whose chemical shifts match the experimental ones.

This methodology, validated on 10,564 residues from 139 conformations of the human protein ubiquitin,² relies on the fact that the ¹³C^α chemical shifts of a given residue are insensitive to neighboring residues in the amino acid sequence,^3,4 that their values depend on both the backbone torsional (ϕ,ψ) and the side-chain torsional (χ’s) angles of a given residue,^5–9 that the ¹³C^α chemical shifts differ between α-helical and β-sheet conformations,^10,11 and that the ¹³C^α nucleus, among all nuclei, is the only one with such properties that are ubiquitous in proteins, making the ¹³C^α nucleus an attractive candidate for theoretical chemical shift predictions at the quantum chemical level of theory. Actually, ¹³C^α and ¹³C^β chemical shifts have been used, together with other types of measurements, in protein structure determinations based on traditional NMR procedures.^12–16

Since chemical shifts can generally be measured with less effort than either NOEs or ³J_HNα coupling constants,¹⁷ it is highly desirable to develop procedures that can use chemical-shift information for protein structure determination in an effective manner, i.e., by predicting the ¹³C^α chemical shifts at the quantum chemical level of theory, without use of information derived from conformational-shifts [Δδ(¹³C)], which are defined as the deviation of the observed ¹³C^α and ¹³C^β chemical shifts from their corresponding statistical-coil values,¹⁰ or empirical-shielding-surface-derived,¹³ or pre-computed shielding-surface-derived information.¹⁸ Such a procedure is presented here.

Since torsional constraints can be obtained for all backbone (ϕ,ψ) and side-chain torsional angles (not only χ¹) in the procedure proposed here, this method is expected to lead to a more precise characterization of the conformational distributions for the backbone, as well as for the side chains of the amino acid residues on both the surface and the interior of a protein. Moreover, this procedure does not restrict the assignment of ¹³C-based torsional constraints to residues that may exhibit low mobility, such as those in α-helices and β-strands. Finally, we provide evidence that the new self-consistent methodology can be used not only for structure determination but also for additional protein structure refinement of NMR-derived models deposited in the Protein Data Bank (PDB) provided that both experimental NOE-derived distances and ¹³C^α chemical shifts in solution are available for comparison with calculated values.

Methods

Structure determination using calculated ¹³C chemical shifts and NOEs

The proposed method obtains constraints for all backbone and side-chain torsional angles (including cis-trans isomerization for proline residues), i.e., not only for the ~40% of the amino acid residues in α-helices and β-sheets in proteins, but also for the ~60% of the amino acids in non-regular structures.⁸ The method is physics-based, and makes no use of knowledge-based information such as conformational preferences of a Ramachandran map. The constraints are not fixed but are changed dynamically in each step of the procedure (only the NOE-derived constraints are preserved, not the original torsional constraints), following an iterative self-consistent approach.

A set of observed NOEs and backbone (ϕ,ψ)-torsional constraints, traditionally derived from the conformational shifts [Δδ(¹³C)],¹⁰ are considered as the input experimental data. The procedure, illustrated in the flow chart of Figure 1, consists of the following steps:

Figure 1.

Flow chart illustrating the steps of the computational procedure, as described in the Methods section Structure determination using calculated ¹³C^α chemical shifts and NOEs. VTF is the acronym for the Variable-Target-Function approach.¹⁹ The variable ξ represent the convergence criterion (see Methods, section: A criterion for assessing the quality of protein models).

(1) The proposed methodology starts with the application of the Variable-Target-Function (VTF) approach¹⁹ to a given amino acid sequence to produce an ensemble of conformations that are required to obey the distance constraints derived from experimental NOEs and the torsional constraints derived from conformational shifts (the latter identifying the α-helical and β-sheet regions). The VTF approach generates conformations of polypeptides by random sampling of torsional angles; thus, all backbone and side-chain torsional angles are chosen randomly between 180° and −180° with the exception of the torsional angles ω of the peptide groups, which are always chosen in the planar trans (180°) conformation. When proline is present in the sequence, both up (U) and down (D) puckering conformations of the pyrrolidine ring are considered; this notation pertains to the following torsional angles: ϕ = −53.0° and χ¹ = −28.1° and ϕ = −68.8° and χ¹ = 27.4°, respectively, for the C^γ atom of the proline residue.²⁰

Repetitive application of the VTF approach, which makes use of the input constraints, generates a set of conformations, e.g., six conformations that are free of steric overlaps and, therefore, closely match the observed NOEs and a set of torsional constraints for the backbone (ϕ,ψ). A set of structures, rather than a single one, is obtained because the number of constraints is usually insufficient to define a unique structure.

(2) The ¹³C chemical shifts are computed at the DFT level for each conformation of the set obtained in step (1). To apply the DFT procedure, each amino acid X in the amino acid sequence is treated as a terminally-blocked tripeptide with the sequence Ac-GXG-NMe in the conformation of each generated protein structure. Residue X of a given amino acid in a particular protein conformation is kept fixed, and the conformations of the remaining residues of the terminally-blocked tripeptide are optimized with the ECEPP/3 force field.²⁰ The ¹³C^α chemical shifts are computed with a 6–311+G(2d,p) locally-dense basis set²¹ for each amino acid residue X, while the remaining residues in the tripeptide are treated with a 3-21G basis set. As noted previously,² computation of all ¹³C^α chemical shifts for a protein with n amino acid residues requires, on average, about 7 hours with a Beowulf class cluster with n (Athlon 2800+) processors. This is the largest computational requirement in the current methodology. During the computation of the shielding, all the ionizable groups are assumed to be uncharged because there is theoretical evidence⁴ indicating that it is better to use uncharged rather than charged side chains if the charge state of the side chain is unknown.

Although chemical shifts are sensitive to bond-length and bond-angle variations, no geometry optimization at the ab initio level was carried out because there is evidence^22,23 that a geometry-optimized structure, starting from an ECEPP-geometry, has only a very small effect on the computed shielding.

The isotropic shielding values, calculated by using the Gaussian 98 package,²⁴ are referenced with respect to a tetramethylsilane (TMS) ¹³C chemical shift scale (δ), as described previously.²² Conversion of the predicted TMS-referenced values for the ¹³C chemical shifts to 2,2-dimethyl-2-silapentane-5-sulfonic acid (DSS), used as a reference for the observed values,²⁵ is carried out by raising the computed values by 1.7 ppm.²⁶

(3) Examination of the chemical shifts of all the amino acids in, say, the six conformations of the set considered in steps (1) and (2) identifies the amino acid at each position in the sequence whose computed chemical shifts most closely match the observed ones among the six at that position. This identified set of individual amino acid conformations corresponds to (only) one conformation of the whole chain, defining a new set of ϕ,ψ,χ’s torsional constraints

(4) The VTF procedure of step (1) is repeated but the initial torsional constraints used in step (1) are now replaced by the new set of ϕ,ψ and χ’s torsional constraints derived in step (3). At this stage of the procedure, a tolerance range for the torsional constraints of ± 30° was adopted. Variation of the torsional angles within this tolerance range is considered acceptable and hence is not subject to energetic penalties. In this repetition of step (1), rather than obtaining a set of conformations, only one conformation is selected, viz., the one with the closest match to both the NOEs and the new set of ϕ,ψ,χ’s torsional constraints derived in step (3);

(5) Starting from the conformation selected in step (4), and with use of both the NOEs and the new set of ϕ,ψ,χ’s torsional constraints derived in step (3), a conformational search (e.g., Monte Carlo with minimization)^27,28 is carried out, but this time by using a complete force-field that contains contributions from: (a) the internal potential energy, as described by the ECEPP/3 force field;²⁰ (b) the solvent free-energy contribution, by using a solvent-accessible surface area model approach;²⁹ and (c) additional energy terms aimed at penalizing violations of the distance and torsional constraints.^30,31

(6) While constraints for all the amino acid residues in the sequence are imposed, not all the NOEs and the torsional constraints derived in step (3) can always be satisfied simultaneously. Thus, the conformational search of step (5) produces an ensemble rather than a single conformation. A selection of a subset of structures is now performed by a clustering procedure, i.e., by using the Minimal Spanning Tree (MST) method,³² assuming a specific rmsd cutoff for all heavy atoms and no cutoff in energy, leading to five conformations (see Results and Discussion section)

(7) Steps (2) and (3) are repeated for the selected subset of five structures obtained in step (6), giving rise to an updated set of ϕ,ψ,χ torsional constraints.

(8) The best model of the subset obtained in step (6), with step (5) being repeated using the existing NOEs and the updated set of ϕ,ψ,χ torsional constraints obtained in step (7), is selected. The best model is defined as the one possessing the largest number of amino acid residues closely matching the observed ¹³C^α chemical shifts. It is important to note that, during this stage of the procedure, the selected tolerance range for the torsional constraints is reduced, e.g., from the ±30° used in step (4) to ±20° or ±10°, aimed at narrowing down the allowed changes for the torsional angles. Steps (5–8) are iterated until convergence is achieved. In particular, the protein structure determination procedure is finished (as indicated in Figure 1) if the following criterion is satisfied: ca-rmsd^α < ξ, where ca-rmsd^α is a new scoring function, and ξ is some adopted limit for this function. A discussion of these parameters follows in the next two sub-sections.

Chemical shifts in the presence of conformational averaging

Based on the hypothesis that the ¹³C^α chemical shifts depend mainly on the secondary structure,^10,11 with no influence of amino acid sequence,^3–5 a new scoring function (ca-rmsd^α), namely, the conformationally-averaged root-mean-square-deviation was recently proposed² as a criterion to assess the quality of protein models (see next sub-section) Ca-rmsd ^α is defined as

$$ca-\text{rmsd}={[(1/N){\displaystyle \sum _{\mu =1}^N({{\mathrm{\Delta }}^{\mathrm{\alpha }}}_{\mathrm{\mu }})}]}^{1/2}$$ (1)

with 1 ≤ μ ≤ N and N being the number of observed ¹³C^α chemical shifts. Under the assumption of fast conformational averaging, the following expression was derived for Δ^α_μ with

$${{\mathrm{\Delta }}^{\mathrm{\alpha }}}_{\mathrm{\mu }}\cong {(}^{13}{{\mathrm{C}}^{\mathrm{\alpha }}}_{\text{observed},\mathrm{\mu }}-{<}^{13}{{\mathrm{C}}^{\mathrm{\alpha }}}_{\text{predicted}>\mu })$$ (2)

with

$${<}^{13}{{\mathrm{C}}^{\mathrm{\alpha }}}_{\text{predicted}>\mu }=1/\mathrm{\Omega }{\displaystyle \sum _{i=1}^{\mathrm{\Omega }}{{\mathrm{C}}^{\mathrm{\alpha }}}_{\text{predicted},\mu ,i}}$$ (3)

with 1 ≤ i ≤ Ω; where ¹³C^α_{predicted,μ,i} are the computed chemical shifts for amino acid μ in model i out of a total of Ω models, and ¹³C^α_predicted,μ represents the observed ¹³C chemical shift for the amino acid μ.

A criterion for assessing the quality of protein models

A common practice to assess the quality of NMR structures is to compare its structural properties with those obtained from the corresponding experimentally-determined X-ray structure. However, adoption of such a criterion involves two problems: (a) the X-ray structure may not be available, or (b) it may not provide the optimal representation of the structure in solution² that is consistent with the observed ¹³C^α chemical shifts. As an alternative to surmount these problems, here we propose to use the values of the computed ca-rmsd^α of a reference protein solved at a high-level of quality, as a standard measure of the quality of the predicted ¹³C^α chemical shifts. In other words, the ca-rmsd^α (indicated with the symbol ξ in Figure 1) provides a rapid assessment of the quality of the models, i.e., the computations are judged to have converged, for the protein under study, if its ca-rmsd^α is less than, or equal to ξ.

The protein Ubiquitin, solved by NMR methods by Cornilescu et al.³³ (PDB code: 1D3Z), has been adopted here as a reference model because of its high quality. This protein has also been solved by X-ray diffraction at 1.8 Å resolution³⁴ (PDB code: 1UBQ). In particular, evidence of the high quality of the NMR-derived protein models by Cornilescu et al.³³ is provided by several studies, among others, the following: (1) a theoretical analysis comparing the back-calculated backbone residual dipolar couplings and side-chain scalar couplings with the corresponding observed values for both the 10 NMR-derived structures of 1D3Z and a new set of 128 models⁹ (PDB code: 1XQQ); (2) the results of Sun et al.,¹⁸ who carried out a comparison between the ¹³C^α shielding computed at the ab initio Hartree-Fock level (for the averaged NMR structure of 1D3Z) and the observed values; and (3) the analysis of Vila et al.,² showing theoretical evidence indicating that the 1D3Z ensemble provides a better representation of the observed ¹³C^α chemical shifts in solution than the X-ray structure³⁴ (PDB code: 1UBQ). Based on this evidence, the ca-rmsd^α computed² for the ten refined conformations of ubiquitin obtained by Cornilescu et al.³³ are adopted here as standard values of the quality of the predicted ¹³C chemical shifts, and hence as a criterion for monitoring convergence of the structure determination procedure described in the section Structure determination using calculated ¹³C chemical shifts and NOEs.

Application to B. Subtilis Acyl Carrier Protein

We chose the B. Subtilis Acyl Carrier (SAC) protein²⁵ as a test of the procedure proposed here because this is a small protein with only 76 amino acid residue and no disulfide bonds, for which all the ¹³C^α chemical shifts and the NOE-derived distances are available from the Biological Magnetic Resonance Data Bank (BMRB),³⁵ under accession number 4989. The NMR structure of the SAC protein has been solved by Xu et al.,²⁵ using traditional methods, and the coordinates of the average-minimized structure are deposited in the Protein Data Bank with the code 1HY8.

For comparison of our computed structures with the experimental (average-minimized) 1HY8 structure, we have calculated the chemical shifts of this experimental structure. In order to be able to apply step (3) to compute chemical shifts, using tripeptides in the conformation of the experimentally-determined 1HY8 structure, we first regularized the experimental structure of 1HY8, i.e., all residues were replaced by the standard ECEPP/3 residues²⁰ in which bond lengths and bond angles are fixed (rigid geometry approximation), and hydrogen atoms are added.

Results and Discussion

1.- Structure determination of the SAC protein

Starting with the amino acid sequence, we applied the proposed procedure to determine the structure of the SAC protein. Neither the deposited coordinates of the minimized average structure for the SAC protein (PDB code 1HY8) nor any information derived from this structure was used at any stage of the structure determination procedure. ¹³C chemical shifts were computed for the regularized deposited experimentally-determined structure, and were used only for the purpose of comparison (a) with the experimentally observed values of the ¹³C chemical shifts (row 4 in Table 1), and (b) with the values computed by the proposed procedure (rows 2 and 3 in Table 1).

Table 1.

Ca-rmsd^α values for Predictions of the ¹³C^α Chemical Shifts of the SAC Protein^a

Protein Model	ca-rmsdα (ppm)
Preliminary Set of Structuresb (PSS)	3.3
Final Set of Structuresc (FSS)	2.9 [2.5]
1HY8d	3.9

^a)Values of ca-rmsd^α are computed as described in the Methods section.

^b)Values of ca-rmsd^α computed from the five protein models of the PSS obtained in step (6) by using the ¹³C^α-derived torsional constraints, as explained in the Results and Discussion section.

^c)Values of ca-rmsd^α computed from the nine protein models of the FSS obtained in step (8) with ¹³C^α-derived torsional constraints, as explained in the Results and Discussion section. In brackets, the values of ca-rmsd^α computed² for the 10 NMR structures of the protein ubiquitin³³ deposited in the PDB under the code 1D3Z.

^d)Values of ca-rmsd^α computed with the coordinates of the minimized-average NMR structure²⁵ (PDB code 1HY8).

Although the proposed methodology for protein structure determination, in general, allows for the prediction of all the torsional angles based on the computation of the ¹³C^α chemical shifts, the ω torsional angles for all residues, other than proline, are always restricted in this procedure to the following range: 180° ± 8°. The reason to adopt this criterion is that there is evidence indicating that ω torsional angles are on average, except for proline residues, within a range of 178° ± 5.5°.³⁶ In addition, it is possible to use ¹³C-based predictions to determine whether the peptide group of proline is in the cis or trans conformation³⁷ and to explore the cis-trans isomerization during the conformational search. However, since there are no prolines in the SAC protein, this capability was not needed here. Whereas all χ values can be predicted, in the current application, only χ¹ to χ³ are used. The reason for this simplification is that the ¹³C^α chemical shifts seem to have a weak dependence on the torsional angles beyond χ³.^4,5

Protein structure determination of the SAC protein was carried out following the steps described in the section Structure determination using calculated ¹³C chemical shifts and NOE’s.

During the application of step (1), the original NMR-derived constraints reported by Xu et al.,²⁵ that include sequential, long- and short- distance NOEs and backbone torsional angles, were used. These original torsional constraints were applied only to the α-helical portions of the sequence. In the original implementation of the data of Xu et al.,²⁵ the following ranges of the torsional constraints were assumed: ϕ=−60° ± 30° and ψ = −40° ± 30° and there was no constraint for the side-chain torsional angles. At the end of step (1), six conformations satisfying the torsional constraints mentioned above were obtained. These conformations possessed the lowest constraint energies, satisfied the original torsional constraints for the backbone, and had a maximum violation of the NOE-derived distances constraints lower than 1.0 Å.

Application of steps (2) and (3) enabled us to identify a new set of ϕ, ψ and χ’s torsional-angle constraints. Use of the NOEs and the new set of ϕ, ψ and χ’s obtained from the ¹³C^α-derived torsional constraints during step (3) led to a single conformation. The allowed range of variation for the torsional constraints used was ±30°. The conformation selected during this step showed a maximum distance violation of 0.63Å, computed from the NOEs. Starting from this conformation, application of step (5) led to an ensemble of 118 conformations. Clustering of these conformations [step (6)] by using the Minimal Spanning Tree method³² with an all-heavy-atom rmsd-cutoff of 0.7 Å and no cutoff in energy, led to a subset of five families. The leading member of each family, i.e., the lowest-energy conformation, was extracted and the selected five conformations were used to compute the predicted ¹³C chemical shifts. The rmsd^α for each of the five conformations is shown in light-grey filled bars in Figure 2, and the computed ca-rmsd^α from the five conformations are reported in Table 1 as the Preliminary Set of Structures (PSS).

Figure 2.

Grey filled bars indicate the rmsd^α value computed as described in the Methods section for each of the five PSS of the SAC protein obtained with the ¹³C^α-derived torsional constraints. Black filled bar indicates the rmsd^α value (3.9 ppm) computed for the NMR average minimized structure (1HY8). The solid horizontal line (3.3 ppm) indicates the ca-rmsd^α value computed from the five PSS obtained with the ¹³C^α-derived torsional constraints (as explained in Result and Discussion section).

Remainder of the procedure

By using the subset of five conformations obtained with the ¹³C^α-derived torsional constraints, step (7) was applied and gave rise to an updated set of backbone (ϕ,ψ and side-chain (χ¹, χ² and χ³) torsional constraints. Step (8) was carried out twice, i.e., by using two different ranges for the new torsional constraints, namely Set 1: ±20°, and Set 2: ±10°. Set 1 and Set 2 led to and 42 conformations, respectively. Clustering, using the MST method with a cut off of 0.8 Å and 0.2 Å, for the first- and second-set, respectively, with no cutoff in energy, produced five and four families, respectively. The leading member of each family was extracted, and the selected nine conformations were used to compute the predicted ¹³C chemical shifts. The rmsd^α for each conformation of the two sets is shown in light- and dark-grey filled bars, respectively, in Figure 3, and the computed ca-rmsd^α from the nine conformations are reported in Table 1 as the Final Set of Structures (FSS).

Figure 3.

Light- and dark-grey filled bars indicate the rmsd^α (ppm) value computed as described in the Result and Discussion section for each of the nine FSS for the SAC protein. Black filled bar indicates the rmsd^α (3.9 ppm) value computed for the NMR minimized average structure (1HY8). The solid horizontal line (2.9 ppm) indicates the ca-rmsd^α value computed from the nine models of the FSS (as explained in Result and Discussion section).

2.- Evaluation of the predicted structures in terms of the ¹³C^α chemical shifts

Table 1 shows the computed values for the ca-rmsd^α for (i) the deposited average minimized structure of the SAC protein (1HY8); (ii) the five PSS; and (ii) the nine FSS. From Table 1, we can conclude that the ensembles of conformations obtained with the ¹³C^α-derived torsional constraints in the PSS and the FSS are better representations of the observed ¹³C^α chemical shifts in solution than the average minimized structure deposited in the PDB (1HY8). Figure 2 and Figure 3 show (as grey-filled bars) a comparison of the computed rmsd^α for: (a) the five PSS; and (b) the nine FSS; the value obtained for the average minimized structure (1HY8) in Figure 2 and Figure 3 are indicated as black-filled bars. The solid horizontal line in these Figures denotes the computed values for the ca-rmsd^α which, as noted before,² is lower than any of the rmsd^α computed from the conformations in the ensembles, except for model 1 shown in Figure 2. It is important to note that no test was carried out to identify unambiguously whether additional torsional constraints on larger side- chains such as Lys and Arg might improve the agreement shown in Figure 3. In addition, from Figure 3 it is not feasible to obtain a definite conclusion about which is the most appropriate tolerance range that should be adopted for the variation of all (non-omega) torsional constraints. It may happen that the tolerance range depends on the type and percentage of secondary structure element and the architecture of the protein.

3.- Structural differences among the 9 models and the average minimized structure (1HY8)

Figure 4 shows the distribution of the average rmsd (Å) for all-heavy atoms computed from the nine FSS, with respect to the average minimized structure (1HY8) as a function of the amino acid sequence. The black filled bars denote the four α-helices characteristic of this protein and the light-grey filled bars indicate the loops connecting such α-helices. Not surprising, most of the structural disagreements come from the loop regions. In fact, the rmsd computed from the α-helices H1 (residues 3–14), H2 (residues 37–49), H3 (58–60), and H4 (residues 65–75) are: 1.8 ± 0.8 Å, 2.2 ± 0.5 Å, 3.3 ± 1.0 Å, and 1.5 ± 0.6 Å, respectively, while the corresponding values for the loops L1 (residues 15–36), L2 (residues 50–57), and L3 (61–64) are: 2.7 ± 1.0Å, 3.5 ± 1.7 Å, and 2.1 ± 0.9Å, respectively. The rmsd computed over all 76 residues is 2.4 ± 1.1Å. Among all the residues in α-helices, the highest rmsd (4.5±1.8 Å) is observed for residue Glu-60, in H3. Unlike, the other residues in α-helices, this residue is observed to be non-helical in 2 out of 9 models.

Figure 4.

For each amino acid residue in the sequence, the bars indicate the averaged value of the rmsd for all heavy atoms rmsd (Å), computed from all nine FSS of the SAC protein, with respect to the NMR average minimized structure (1HY8). Black-filled bars denote the portion in α-helical conformation, while the grey-filled bars denote the loops connecting the helices. Only half of the standard deviations, computed for each amino acid residue, are displayed by the symbol ( ) [to facilitate visualization].

For each amino acid residue in Figure 4, the vertical line denotes the computed standard deviation (σ) from the nine FSS. Clearly, the σ values observed for some amino acid residues in the loops are greater than those in the α-helical regions. In particular, most of the amino acid residues with values of σ exceeding 1.0 Å are in the loop regions, viz., residues 19, 20, 23, 55–57, 59–61, as shown in Figure 4. Notably, 6 out of these 9 residues are ionizable, namely, Glu-19, Lys-23, Asp-56, Glu-57, Glu-60 and Lys-61. By contrast, 5 other ionizable residues, namely Glu-5, Arg-6, Lys-9, Asp-13 and Arg-14, in the H1 α-helix have, on average, σ values lower than 0.4 Å. The flexibility of the ionizable residues in the loops suggests that a representation of the experimental structure of the SAC protein by using a single conformation might be a poor one. This observation should constitute a concern for spectroscopists since, on average, ~60% of the amino acid residues in proteins are not expected to be in α-helix or β-sheet secondary-structure elements.⁸ The fact that, by chance, 30% out of these 60% are likely to be ionizable only exacerbates the problem. Figure 5 shows a superposition of the nine FSS and the average minimized structure 1HY8. As noted above, the main differences are observed in the loop regions connecting the helices.

Figure 5.

Ribbon diagram of the superposition of nine models of the FSS for the SAC protein (in yellow color) and the minimized average NMR structure (1HY8) [in red].

4.- Analysis of the ¹³C^α chemical shift error distributions for the FSS

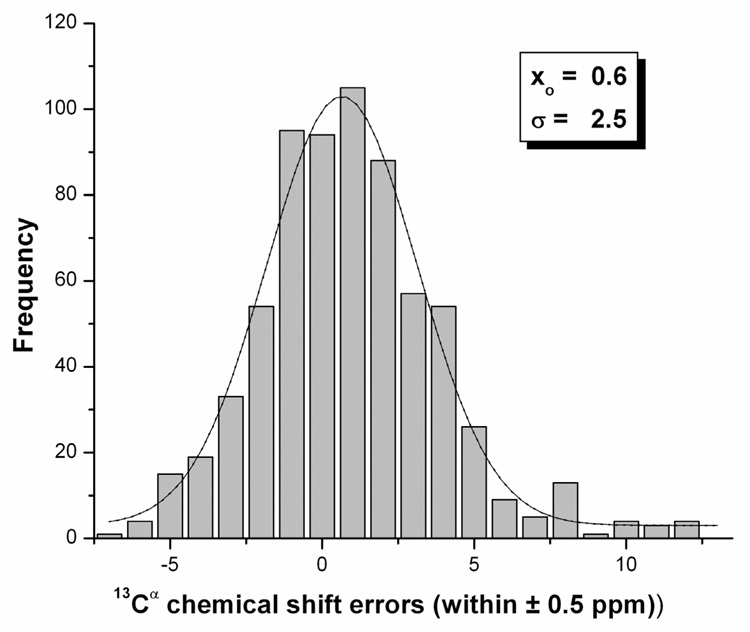
An analysis of the error distributions of the computed ¹³C^α chemical shifts was carried out for the 9 conformations of the FSS. The error between computed and observed ¹³C^α chemical shifts, for each residue (μ) of each conformation of these proteins, was evaluated as Δ^α_μ from equation (2). The accumulated error distribution (shown in Figure 6) can be modeled by a Normal (or Gaussian) function with a characteristic mean (x_o = 0.6 ppm) and standard deviation (σ = 2.5 ppm). Because of the Gaussian nature of the distribution, ~70% of the errors are within one standard deviation (σ = 2.5 ppm) from the mean (x_o). In particular, the σ value obtained here is practically within the range of the standard deviation (0.90 ppm ≤ σ ≤ 2.25 ppm) observed by Wang and Jardetzky³⁸ for ¹³C^α chemical shifts (from a database containing more than 6,000 amino acid residues in α-helix, β-sheet and statistical-coil conformations).

Figure 6.

Grey filled bars indicate the frequency of the error distribution, computed assuming a correction factor of 1.7 ppm as explained in the Methods section, within a ± 0.5 ppm interval between predicted and computed ¹³C^α chemical shifts from the nine FSS for the SAC protein. The distribution was generated by binning the data between −7.5 and 12.5 ppm.

Many factors could contribute to the origin of such errors, as noted in a previous analysis of ubiquitin², such as the use of different methods and standards for chemical-shift referencing, ^2,3 or residues exhibiting high mobility. In this respect, the Δ^α errors are higher for residues in the loop, rather than in the α-helix regions of the molecule, because the FSS shows considerable variability for the backbone in the loop regions (see Figure 4 and Figure 5). A quantitative analysis of the errors for helical and loop regions follows.

5.- Influence of the ¹³C^α-derived constraints on the modeling of the α-helix and loop regions

The α-helical regions of the single deposited structure (1HY8), and of the FSS ensemble of the SAC protein models (shown as black-filled bars in Figure 4), have the following features in common: (a) the number and identity of the residues belonging to each of the four α-helical regions are the same in both the 1HY8 and FSS models; (b) there is good agreement, in terms of all the heavy-atom rmsds, between different models for each of these regions, as discussed in section 3; and (c) the four α-helical regions of both 1HY8 and the FSS satisfied 100% of the conformational-shift-derived backbone (ϕ,ψ) constraints, namely −60° ± 30°, and −40° ± 30°, except for Glu-60 in H3, as was discussed in section 3. However, an important distinction concerning the α-helical regions comes from the fact that the FSS ensemble, but not the single 1HY8, were derived by using additional ¹³C^α-derived torsional constraints, namely for both the backbone and the side chains. As a consequence, a comparative analysis of the errors will shed light on the role of such additional constraints on the accuracy of the ¹³C^α chemical-shift predictions. To carry out this analysis, we computed the average of the absolute errors for all the SAC protein models as follows:

$$<|{\mathrm{\Delta }}^{\mathrm{\alpha }}|>=1/\mathrm{\lambda }{\displaystyle \sum _{\mu \in \mathrm{\Gamma }}|{{\mathrm{\Delta }}^{\mathrm{\alpha }}}_{\mathrm{\mu }}|}$$ (4)

with Δ^α_μ given by equation (2); Γ is an ensemble that contains all the amino acid residues, μ, belonging to α-helix regions, namely, residues 3–14; 37−49; 58–60; 65–75 from the H1, H2, H3 and H4 regions, respectively; and λ represents the total number of residues in these regions, namely 39. Computation of <|Δ^α|> for FSS and 1HY8 conformations, gives: 1.6 ± 1.0 ppm and 2.1 ± 2.2 ppm, respectively. Conceivably, the better agreement obtained for the FSS when compared to that for 1HY8, is due to the additional ¹³C^α-derived side-chain torsional constraints since all of these conformations satisfy the backbone torsional constraints. As an additional test, the corresponding <|Δ^α|> was also computed for the initial six structures obtained after step (1), as described in the Results and Discussion section 1, which were derived by using only the original constraints used by Xu et al.²⁵ The resulting <|Δ^α|> obtained for the α-helical regions of the six structures 2.1 ± 0.7 ppm) is quite similar to that obtained for 1HY8 (2.1 ± 2.2 ppm). This analysis indicates that inclusion of the ¹³C^α-derived constraints, rather than the force-field used, has led to conformations with lower errors and hence, to an improved accuracy of the prediction in terms of the ca-rmsd.

Finally, the average of the absolute error was computed by using equation (4) for all residues of the FSS, the 1HY8, and the six structures obtained after step (1) that do not pertain to α-helical regions. For each set of structures, the following values for <|Δ^α|> were obtained: 2.4±0.8 ppm, for FSS; 3.2±2.2 ppm, for 1HY8; and 3.1±1.7 ppm, for the six structures from step (1). These results are fully consistent with the conclusion derived from the analysis of the α-helical regions, i.e., that inclusion of the ¹³C^α-derived constraints contributes to obtain conformations with lower errors in terms of predicted and observed ¹³C^α chemical shifts.

6.- Analysis of the constraints violations

(a) NOEs distance violations

On average, the nine FSS satisfied 957±12 out of 1050 NOE-derived distance constraints. Figure 7 shows the distribution of the distance-constraint violations in terms of black- and grey-filled bars, denoting short and long NOE-derived distances, respectively. From Figure 7, we conclude that: (i) more than 90% of the total NOE-derived distance violations lie in the range of ≤ 0.2 Å, and (ii) about 70% of the total number of violations per conformation (~90) are short range (see black-filled bars in Figure 7).

Figure 7.

Black- and Grey-filled bars denote the average number of short and long NOEs-derived-distances violations, respectively, computed from the nine models of the FSS. The violations are in the range 0.0–1.0 Å, within intervals of 0.1 Å. At a given interval, e.g., 0.3 Å, the height of the bars represent the accumulated value of distance violations (X) which are in the range, 0.2 Å < X ≤ 0.3 Å.

On the other hand, Xu et al.²⁵ reported, for the average minimized structure (1HY8), that there were no constraint violations greater than 0.2 Å; but, they did not report the total number of distance violations lower than this cutoff, and hence a quantitative comparison is not possible. Furthermore, adopting the same criterion that Xu et al.²⁵ used, i.e., considering as distance violations those that are greater than 0.2 Å, we conclude that our nine FSS satisfied more than 99% of the NOEs constraints.

(b) Torsional constraint violations

Within an allowed tolerance range of ± 20° for the torsional constraints, we found that, on average, 371 out of 403 ¹³C^α–derived backbone and side-chain torsional angles constraints were satisfied for the nine FSS. On the other hand, Xu et al.²⁵ reported that all the torsional constraints were satisfied during the generation of the 22 structural models, from which the average minimized structure (1HY8) was derived. However, because they used a traditional approach, only 92 torsional constraints were used, viz., those encompassing only backbone constraints, i.e., 46 ϕ and 46 ψ dihedral constraints. In addition, the allowed tolerance ranges of deviation for these angle constraints used by Xu et al.²⁵ were less strict than in our applications, namely, in the range of ± 30° to ± 40°, compared with our ± 10° to ± 20° used for the determination of the FSS.

7.- Assessment of the quality of the derived molecular models for SAC protein

(a) A comparison with a high quality protein

The progress of the methodology is monitored here by computing the ca-rmsd^α,² and compared with the values obtained from a high quality protein set, namely, from results obtained from the protein ubiquitin.² The 10 refined conformations of ubiquitin obtained by Cornilescu et al.³³ were generated by using 2,727 distances derived from observed NOEs, 98 dihedral angle constraints derived from observed homo- and heternonuclear J couplings, and 372 dipolar coupling constraints. On the other hand, determination of the protein models derived here for the SAC protein makes use of 1,050 NOE-derived distances and 433 ¹³C^α–derived torsional angle constraints, i.e., with an average of ~5.7 torsional angle constraints per residue. In spite of the use of a smaller set of constraints in our approach, compared to the one used by Cornilescu et al.,³³ a similar quality in terms of the ca-rmsd^α is obtained (see values reported in the fourth row of Table 1).

(b) A comparison based on some stereochemical quality indicators

Table 2 shows a comparison of some stereochemical quality indicators,^{36, 39} computed for (a) the nine FSS for the SAC protein models; and (b) the 22 final structures of the ensemble and the average minimized structure (1HY8) from Xu et al.²⁵ From the values listed in Table 2, we can conclude that both structures, namely the nine FSS and the average minimized structure 1HY8 show comparable stereochemical quality in terms of distribution of residues in the Ramachandran map. However, better agreement is observed for the nine FSS than that for average minimized structure (1HY8) in terms of other structural parameters, such as: (a) the number of abnormally short interatomic distances, namely 74 for 1HY8 and 22 ± 4 for the FSS (these values should be compared with the ideal value³⁶ of 0); and (b) the standard deviation of the planarity (ω dihedral angle) of the peptide bond (as shown in Table 2), namely 0.65° for 1HY8 and 5.8° ± 0.3° for the FSS (these values should be compared with the ideal one³⁶ of 5.5°).

Table 2.

Statistics for Some Structural Quality Indicators for the SAC Protein^a

Structural Quality Indicators	Final Set of Structuresb	1HY8c
Residues in Allowed Regionsd (%)	92 ± 1.0	93.8 ± 2.2 ( 95.8 )
Residues in Generously Allowed Regionse (%)	4.3 ± 0.9	3.4 ± 0.5 ( 2.8 )
Residues in Disallowed Regions f (%)	1.5 ± 0.5	2.8 ± 1.0 ( 1.4 )
Number of Abnormally Short Interatomic Distances g	22.2 ± 3.8	n/a ( 74 )
Standard Deviation of Omega Valuesh (degrees)	5.8° ± 0.3°	n/a ( 0.65° )

^a)Based on PROCHECK ³⁹ or WHAT_IF. ³⁶ Because we adopted the rigid geometry approximation, i.e., fixed bond lengths and bond angles, departures from values for the idealized covalent geometry are not reported.

^b)All the values reported in this column were computed from the final nine protein models obtained after step (8), as explained in Results and Discussion section.

^c)All the values reported in this column, except those from the last two rows, are obtained from Table 1 of Xu et al. ²⁵ The reported standard deviation is based on the averaged values computed for the final ensemble of 22 structures. The values for the minimized average structure (PDB code 1HY8), obtained by averaging the Cartesian coordinates of 22 individual structures of the ensemble, are in parenthesis.

^d)The reported Residues in Allowed Region are based on a sum of the residues in the ‘most favored regions’ and in the ‘additional allowed regions’, as defined in PROCHECK.³⁹

^e)By using PROCHECK.³⁹

^f)By using PROCHECK. ³⁹

^g)By using WHAT_IF.³⁶ According to Vriend³⁶ “…two atoms have an abnormally short interatomic distance if they are closer than the sum of their van der Waals radii minus 0.4 Angstrom. For hydrogen-bonded pairs, a tolerance of 0.5 Angstrom is used…” The value reported for 1HY8 was computed by using the deposited averaged-minimized structure. n/a means that the corresponding values cannot be reported because the 22 final structures of the ensemble are not available.

^h)By using WHAT_IF.³⁶ According to Vriend³⁶ “…the omega angles for trans-peptide bonds in a structure are expected to give a Gaussian distribution with the average around 178 degrees and a standard deviation around 5.5 degrees…”. Structures with values for the standard deviation lower than 4° are considered too tightly constrained.³⁶

To test whether the computed numbers of abnormally short interatomic distances (~22 as shown in Table 2) or ~0.3 per-residue, for the FSS, compares with other NMR-solved structures deposited in the PDB, we carried out an additional comparison involving seven small proteins, namely 1BDD, 1D3Z, 1E0L, 1FSD, 1GAB, 1HDN and 1 VII (listed in alphabetic order following their PDB code). The computed, per-residue, average of the abnormally short interatomic distances for these 7 proteins is: ~0.8, which is ~3 times higher than our computed value of ~0.3. However, additional effort should be expended to reach the ~0, number of abnormally short interatomic distances constrained by refinement in X-ray-derived structures.

Concluding Remarks

The current methodology, whose prediction capabilities have already been tested,² has been used to determine a set of conformations for the SAC protein by the combined use of NOE-derived distances together with observed and computed ¹³C^α chemical shifts. This application led to results that show better agreement, in terms of the ca-rmsd^α and some stereochemical quality indicators, than traditional methods. These results are in line with qualitative evidence showing that, given two structures that satisfy all observed NMR-derived constraints, the one showing better agreement between predicted and observed ¹³C^α chemical shifts also possesses better stereochemistry quality factors.^2,18 Of particular interest are the results showing that inclusion of ¹³C^α-derived constraints for both backbone and side-chains seems to lead to more accurate predictions and, hence, lower ca-rmsd^α for the whole structure. Without loss of generality, we can conclude that the FSS set is a better representation of the SAC protein in solution than the single deposited structure (1HY8) solved by using traditional method. For structures of an all-α-helical protein, an improvement in terms of the “ca-rmsd^α measure” is an indication of the usefulness of the backbone and side-chain torsional constraints information derived from the ¹³C^α chemical shifts. This conclusion is in line with a probability-based secondary structure identification method showing that the reliability to distinguish an α-helix from a statistical-coil follows the ranking: ¹³C^α > ¹³C′ > ¹H^α > ¹³C^β > ¹⁵H > ¹H^N.³⁸ However, caution should be exercised in the generalization of the results to proteins containing additional motifs such as extended strands because the corresponding reliability ranking to distinguish a β-strand from a statistical coil is the following: ¹H^α > ¹³C^β > ¹H^N ~ ¹³C^α ~ 13C′ ~ ¹⁵H >.³⁸ In other words, further testing and research must be carried out for protein structures containing both α-helical and β-strand regions, in order to reveal whether the ¹³C^α-driven methodology proposed in this article leads to major improvement in the predictions.

Additional conclusions, regarding two different views about the potential use of conformational shifts for determining protein structure, are discussed here. The first view¹⁵ suggested that the conformational shifts can provide a reliable source of information for protein structure refinement. A second view¹⁷ has questioned the use of backbone torsional-angle constraints derived from a conformational-shift-based method for the purpose of refining high-quality NMR structures. As an alternative approach to this problem, instead of the conformational shifts, use is made here of the observed ¹³C chemical shifts in conjunction with the computed ¹³C chemical shifts at the DFT level, to derive backbone and side-chain torsional constraints, without establishing a priori the occupancy of any region of the Ramachandran map by the amino acid residues. In addition, torsional constraints are derived dynamically, i.e., they are re-defined at each step of the determination process. The results obtained here after two iterations of the procedure show lower values for the ca-rmsd^α in a consistent manner, indicating that the current methodology might be used routinely for both protein structure determination and refinement of already known protein structures.

It is worth noting that the use of conformational-shift-derived information at the beginning of the protein structure determination, namely during step (2), appeared to be very useful, viz., to identify the α-helical and β-sheet regions of the protein. This result is in line with a view of Luginbühl et al.¹⁷ that the conformational-shift-derived information “…should focus on the early stages of the structure determination…”

Finally, it should be pointed out that there is a wide range of models for a protein in solution,⁴⁰ as illustrated in Figure 5, while the observed ¹³C^α chemical shifts pertain to an average over all the conformations.