Abstract
Previous work has shown that ultrasonic waves propagating through cancellous bone often exhibit a linear-with-frequency attenuation coefficient, but a decrease in phase velocity with frequency (negative dispersion) that is inconsistent with the causality-imposed Kramers–Kronig relations. In the current study, interfering wave modes similar to those observed in bone are shown to potentially contribute to the observed negative dispersion. Biot theory, the modified Biot–Attenborogh model, and experimental results are used to aid in simulating multiple-mode wave propagation through cancellous bone. Simulations entail constructing individual wave modes exhibiting a positive dispersion using plausible velocities and amplitudes, and then summing the individual modes to create mixed-mode output wave forms. Results of the simulations indicate that mixed-mode wave forms can exhibit negative dispersion when analyzed conventionally under the assumption that only one wave is present, even when the individual interfering waves exhibit positive dispersions in accordance with the Kramers–Kronig relations. Furthermore, negative dispersion is observed when little or no visual evidence of interference exists in the time-domain data. Understanding the mechanisms responsible for the observed negative dispersion could aid in determining the true material properties of cancellous bone, as opposed to the apparent properties measured using conventional data analysis techniques.
INTRODUCTION
There is considerable interest in the use of ultrasound to evaluate bone quality, with investigations of cancellous (trabecular) bone playing a prominent role. Cancellous bone consists of a network of (hard) calcified strands (trabeculae) through which courses (soft) bone marrow. Methods for characterizing bone tissue using ultrasound often consist of measurements of the velocity and attenuation properties of ultrasonic waves transmitted through the trabecular network.1, 2, 3, 4, 5
The intricate structure of cancellous bone tissue can complicate measurements. The material architecture is anisotropic, with the trabeculae predominantly oriented along the direction of stresses experienced by the bone. Consequently, acquired ultrasonic data depend on the angle of insonification relative to the predominant trabecular orientation.6, 7, 8 A large number of ultrasonic investigations of cancellous bone reported in literature are performed on bovine leg bones or on human calcanei. In bovine leg bones, insonification is approximately perpendicular to the trabeculae in the medial-lateral (ML) and anterior-posterior directions, and approximately parallel in the superior-inferior (SI) direction. Human calcanei are typically insonified in the ML direction, corresponding to the perpendicular orientation.
The porous structure of cancellous bone supports the propagation of two compressional ultrasonic waves, often denoted as a fast wave and a slow wave.6, 9, 10 Depending on experimental circumstances, such as the porosity and thickness of the bone sample and the insonification angle relative to the predominant trabecular orientation, the two waves are sometimes separate and visibly distinct in the time-domain radio frequency (rf) data; in other instances, only one wave is observed. One possible contributing factor for the observation of a single wave in certain cases is that the difference in the arrival times of the fast and slow waves is small compared to the temporal extent of the ultrasonic pulse, resulting in a rf trace that appears to be that of a single wave but is, in fact, the sum of interfering fast and slow waves. In their investigations of anisotropy in bovine cancellous bone, Hosokawa and Otani noted that the propagation speeds of the fast and slow waves converge as the incident ultrasonic field becomes aligned perpendicular to the predominant trabecular orientation, resulting in overlap of the fast and slow waves in the received rf trace.6 Padilla and Laugier identified the overlap of fast and slow waves as a complicating factor in their study of a stratified model for bone.9 Lee et al. reported that in the ML direction, fast and slow waves in bovine tibia overlap and “are observed as if one longitudinal wave propagates.”10 Haiat et al. also noted the difficulties associated with multiple-mode propagation.11
In general, investigators have found that the attenuation coefficient of bone varies linearly or quasilinearly with frequency, and typically report attenuation measurements as the rate of change in attenuation coefficient with frequency.1, 12 This parameter is known as broadband ultrasound attenuation or, if normalized by sample thickness, as normalized broadband ultrasound attenuation (nBUA), also known as slope of attenuation. However, despite the consensus on the frequency dependence of attenuation coefficient, there is considerable variation in measurements of the frequency dependence of phase velocity. Many laboratories report that on average the phase velocity of ultrasonic waves propagating through cancellous bone decreases with increasing frequency, a phenomenon known as negative dispersion.1, 2, 4, 13 However, an increase in phase velocity with frequency (positive dispersion) is observed in 10%–20% of investigated sites.1, 2
The observed negative dispersion in the majority of bone samples analyzed is further confounded when one considers the apparent inconsistencies with the causality-imposed Kramers–Kronig (KK) relations that relate attenuation to dispersion.12, 14, 15, 16, 17 According to the nearly local approximation to the KK relations with one subtraction, an increase in phase velocity with frequency is expected for samples exhibiting an approximately linear-with-frequency attenuation coefficient. If the attenuation coefficient varied strictly linearly with frequency, the dispersion curve would be positive and logarithmic.12, 15, 16 The inconsistencies with the KK relations are especially troubling in light of evidence that they are valid even under conditions in which the attenuation coefficient and phase velocity exhibit complicated behavior.18
Currently, dispersion is not a widely used metric for clinical bone quality analysis. However, the negative dispersion measured in cancellous bone suggests that evaluating the material properties of bone using current data analysis techniques may be compromised because they result in the measurement of “apparent” material properties instead of the underlying “true” material properties. Consequently, a better understanding of the dispersion characteristics of cancellous bone, including the mechanisms responsible for the observed negative dispersion, could aid in determining the true material properties of cancellous bone, as opposed to the apparent properties measured using conventional data analysis techniques.
In a previous letter, our laboratory proposed that negative dispersion in cancellous bone can arise when rf signals consisting of overlapped fast and slow waves are analyzed as if they are a single longitudinal wave.19 In the current investigation, we extend and enhance this proposed mechanism by using theoretical and experimental results of ultrasonic wave propagation in bone obtained by previous investigators as a basis to generate simulated fast and slow waves that are consistent with the nearly local approximation to the KK relations. We then use the simulated fast and slow waves to create a “mixed” wave form consisting of overlapping fast and slow waves, and then demonstrate that analyzing the mixed wave forms may contribute to the observed negative dispersion in cancellous bone.
THEORY
We considered theories of wave propagation in bone to aid in determining appropriate input values for the parameters used in our simulations. Ultrasonic wave velocity in bone has been extensively modeled using Biot theory,7, 8, 20, 21, 22, 23, 24, 25, 26, 27, 28 modified Biot–Attenborough theory,7, 10, 29, 30 and stratified media theory.7, 9, 31, 32, 33, 34 Each of these models predicts the existence of fast and slow waves; however, the stratified model predicts that only the fast wave propagates at perpendicular insonification. Because our simulations involve two propagating compressional waves, we elected not to explore the stratified model in this study. We note, however, that actual bone structures are unlikely to be rigorously perpendicular to ultrasound wave propagation at any orientation, resulting in the presence of multiple modes even for nominally perpendicular orientations.
The Biot and modified Biot–Attenborough models are typically used to predict the phase velocities of fast and slow waves as functions of porosity, defined as (1−volume fraction of bone). Each model has been empirically extended to include angle-dependent parameters to account for the anisotropy of cancellous bone.7 Because the existing literature includes slightly different implementations of each theory, details of the theoretical formalisms we use to calculate phase velocities are included below.
Biot theory
Biot theory considers the motions of the fluid and solid components of a porous material. Input parameters consist of physical and mechanical properties of the fluid and solid components of the propagation medium. The input parameters are used to predict fast and slow compressional waves corresponding to in-phase and out-of-phase motions between the fluid and solid. Energy losses are due to viscous interactions at interfaces.
Biot theory gives rise to three elastic parameters P, Q, and R given by
| (1a) |
| (1b) |
| (1c) |
where D=1−βpor−(Kb∕Ks)+βpor(Ks∕Kf) and Ks is the bulk modulus of the solid material, Kf is the bulk modulus of the fluid, Kb is the bulk modulus of the elastic frame, μb is the shear modulus of the elastic frame, and βpor is the porosity (volume fraction of fluid).
If the solid material is assumed to be isotropic, the bulk modulus Ks can be related to the intrinsic elastic parameters of the solid by
| (2) |
where Es and νs are Young’s modulus and Poisson’s ratio for the solid. Young’s modulus of the elastic frame of the porous structure Eb is determined from the porosity and Es through the power law relationship
| (3) |
If the frame is assumed to be isotropic, its bulk and shear moduli Kb and μb can be written as
| (4) |
| (5) |
where νb is Poisson’s ratio for the frame.
Although Biot theory assumes an isotropic medium, it has been empirically extended to apply to anisotropic porous materials through exploitation of the power law relationship between Eb and Es. The exponent n in Eq. 3 depends on the angle of insonification relative to trabecular alignment. Hosokawa and Otani found n=1.46 in the parallel orientation and n=2.14 in the perpendicular direction.6 Williams found that n has a value of 1.23 when cancellous bone is insonified parallel to the trabeculae, and a value of 2.35 when insonification is perpendicular to the trabeculae.26 Those values for n were adopted by Lee et al. to construct an angle-dependent Biot model.7 In the current study, we elected to use the values established by Williams and later employed by Lee et al., so we set n=1.23 and n=2.35 for the parallel and perpendicular directions, respectively.
Biot theory also includes mass coefficients to allow for viscous and inertial drag effects. These coefficients are given by
| (6a) |
| (6b) |
| (6c) |
where ρf and ρs are the densities of the fluid and solid components and αtort(ω) is a structural factor known as the dynamic tortuosity. We have used the subscript tort to distinguish the tortuosity (αtort(ω)) from the attenuation coefficient (α(ω)). The dynamic tortuosity was introduced by Johnson et al. as
| (7) |
in which Λ is the viscous characteristic length and η is the fluid viscosity.35 The tortuosity parameter α∞ is given by
| (8) |
where s is a parameter derived from a microscopic model of a frame moving in a fluid. Other investigators have consistently let s=0.25.6, 7, 25, 26
The elastic parameters and mass coefficients are used to construct a characteristic equation given by
| (9) |
whose roots are the wave numbers of the fast and slow waves. The solutions are
| (10) |
where
| (11a) |
| (11b) |
| (11c) |
The phase velocities for the fast and slow waves are then calculated by vphase=Re(ω∕k), resulting in
| (12a) |
| (12b) |
where Re( ) returns the real component of a complex number.
Modified Biot–Attenborough model
The modified Biot–Attenborough model, proposed by Roh and Yoon, is a phenomenological approach for modeling wave propagation through a medium with cylindrical pores.7, 10, 29, 30 It allows for both viscous and thermal energy dissipations but requires empirically determined input parameters. We follow the formulation given by Lee et al.7 The equation of continuity for one-dimensional wave propagation through a circular cylindrical pore is
| (13) |
where ρf is the fluid density and ⟨v⟩ is the average particle velocity over the cross section of the pore. The equation of motion is given by
| (14) |
where p is the acoustic pressure and ρc(ω) is the complex density given by
| (15) |
where
| (16) |
in which J0 and J1 are the zeroth-order and first-order cylindrical Bessel functions. The dimensionless parameter λ is related to the size of the viscous boundary layer at the pore wall and may be written as
| (17) |
where a is the pore radius, ν is the kinematic viscosity of the fluid, and s1 is a boundary condition parameter representing the pore frame rigidity.
When thermal effects are considered, the complex compressibility of the fluid Cc(ω) is given by
| (18) |
where cf, γ, and NPr are the compressional speed, specific heat ratio, and Prandtl number of the fluid, respectively. When the model is extended to a material consisting of an ensemble of cylindrical pores, the wave number for the fast wave is given by
| (19) |
where αtort is the tortuosity, βpor is the porosity, ks=ω∕cs is the wave number of the pore frame, s2 is a phase velocity parameter, and kc is the complex frequency-dependent wave number of the pore fluid given by
| (20) |
The wave number for the slow wave is constructed in a similar fashion, under the assumption that the slow wave velocity tends to zero at low porosities. This wave number is given by
| (21) |
where kg=ω∕cg is the wave number of a hypothetical fluid with an extremely low (approaching zero) wave velocity. The phase velocities for the fast and slow waves are found using vphase=Re(ω∕k), resulting in
| (22a) |
| (22b) |
The phase velocity parameter s2 in Eqs. 19, 21 determines the functional form of the phase velocity as a function of porosity. Lee et al. introduced an empirical anisotropy to this parameter and found that s2=0.5 at parallel insonification and 1.7 at perpendicular insonification.7 We adopted those values for s2 in the current study.
Biot and modified Biot–Attenborough model predictions
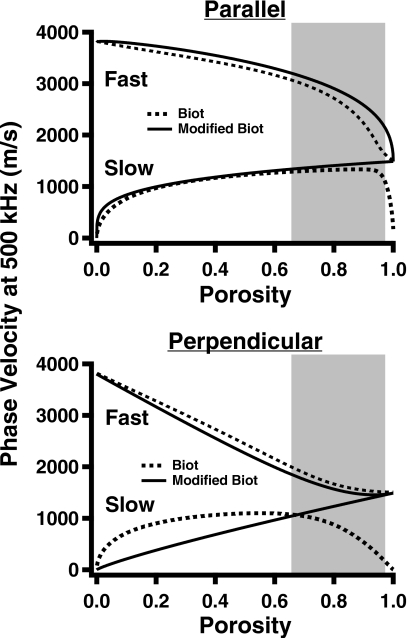
The input parameter values for each model are listed in Table 1, and the resultant phase velocities at 500 kHz for the fast and slow waves as functions of porosity for both perpendicular and parallel insonifications are shown in Fig. 1.
Table 1.
Input model parameters used to generate the curves in Fig. 1.
| Parameter | Biot | Modified Biot |
|---|---|---|
| Solid density (ρs) | 1960 kg∕m3 | 1960 kg∕m3 |
| Fluid density (ρf) | 1000 kg∕m3 | 1000 kg∕m3 |
| Young’s modulus of solid (Es) | 20 GPa | |
| Bulk modulus of fluid (Kf) | 2.28 GPa | |
| Poisson’s ratio for solid (νs) | 0.32 | |
| Poisson’s ratio for skeletal frame (νb) | 0.32 | |
| Tortuosity (αtort) | Equation 7 | 1 |
| Fluid viscosity (η) | 10−3 Pa s | |
| Viscous characteristic length (Λ) | 5 μm | |
| Exponent (n) | 1.23 (parallel) | |
| 2.35 (perpendicular) | ||
| Fluid compressional speed (cf) | 1500 m∕s | |
| Solid compressional speed (cs) | 3800 m∕s | |
| Kinematic viscosity of fluid (ν) | 1×10−6 m2∕s | |
| Specific heat ratio of fluid (γ) | 1.004 | |
| Prandtl number of fluid (NPr) | 7 | |
| Pore radius (a) | 0.5 mm | |
| Boundary condition parameter (s1) | 1.5 | |
| Phase velocity parameter (s2) | 0.5 (parallel) | |
| 1.7 (perpendicular) |
Figure 1.
Predictions of Biot theory (dashed lines) and modified Biot–Attenborough model (solid lines) for fast and slow wave velocities at 500 kHz as functions of porosity. The top panel shows predictions at parallel insonification, and the bottom panel shows predictions at perpendicular insonification. The shaded regions indicate the approximate range of physiological porosities for bovine and human cancellous bone measured by other investigators (Refs. 6, 10, 25).
As indicated in Fig. 1, the angle-dependent Biot and modified Biot models predict that when insonification is parallel to the trabecular orientation, corresponding to the SI direction in bovine leg bones, the velocities of the fast and slow waves remain distinct and moderately different over a wide range of porosities, including those within physiological ranges, and eventually converge toward the same value only at extremely high porosities. At a porosity of 0.85, Biot theory predicts that in the parallel orientation the difference in the velocities of the fast and slow waves is about 1180 m∕s, whereas the modified Biot model predicts a difference of approximately 1320 m∕s. Experimentally, the velocities at parallel insonification were sufficiently different to permit Hosokawa and Otani to observe and measure the velocities of distinct fast and slow waves at porosities above 0.8 in samples approximately 9 mm thick.6
The Biot and modified Biot model predictions differ for the porosity-dependent behavior of the velocities when bone is insonified in the clinically relevant perpendicular direction. In that orientation, and at a porosity of 0.85, Biot theory predicts a velocity difference of 865 m∕s, whereas the modified Biot model predicts a difference of about 200 m∕s. Experiments performed while insonifying in the perpendicular orientation have generally not resulted in the observation of distinct fast and slow waves. Investigations of the anisotropy of cancellous bone have demonstrated that the fast and slow waves become more and more overlapped as the angle of insonification proceeds from parallel to perpendicular.6
SIMULATED WAVE PROPAGATION IN BONE
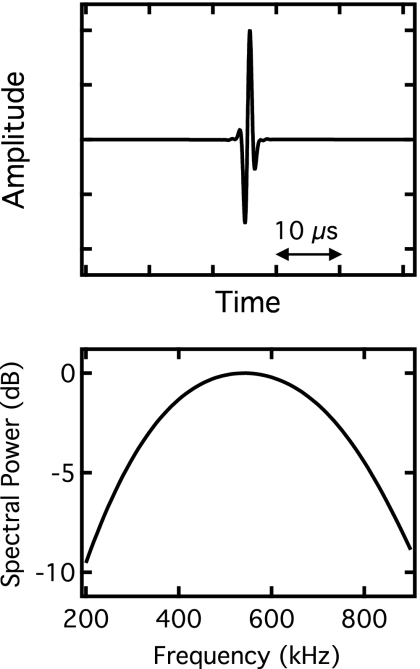
We simulated the propagation of ultrasound through bone by generating fast waves and slow waves independently using phase velocity and attenuation coefficient parameters, and then combined the two waves to form a simulated received signal. The input to the simulation consisted of a simulated broadband reference pulse with a center frequency of 550 kHz and a −6 dB bandwidth of approximately 250–850 kHz (see Fig. 2). An output wave form corresponding to ultrasonic wave propagation through bone was produced by applying linear transfer functions to the input
| (23) |
where output(ω) and input(ω) are the complex frequency-domain representations of the input reference wave form and output mixed wave form. We have assumed that wave propagation through bone and bonelike materials is linear, with speeds of sound and attenuation coefficients independent of amplitude. Hfast(ω) and Hslow(ω) are the transfer functions for the individual fast and slow waves given by
| (24a) |
| (24b) |
in which Afast and Aslow are frequency-independent amplitude compensation factors that correspond to relative initial amplitudes of the fast and slow waves upon encountering the sample, l is the sample thickness, and αfast(ω) and αslow(ω) are the attenuation coefficients given by
| (25a) |
| (25b) |
where βfast and βslow are the values for nBUA. The phase velocities vfast(ω) and vslow(ω) are given by
| (26a) |
| (26b) |
where ω0 is a chosen reference frequency of interest. The linear-with-frequency functional form of the attenuation coefficients [Eqs. 25a, 25b] is taken from the consensus of the published literature. The phase velocities [Eqs. 26a, 26b] are obtained by applying the nearly local form of the KK relations to the linear-with-frequency attenuation coefficients [Eqs. 25a, 25b], under the assumption that this form of the KK relations is valid for the fast and slow waves. These expressions for the phase velocities are valid for small dispersions.
Figure 2.
The time-domain representation of the artificially generated reference pulse used as input to the simulations is displayed in the upper panel, and the power spectrum of the pulse is shown in the lower panel.
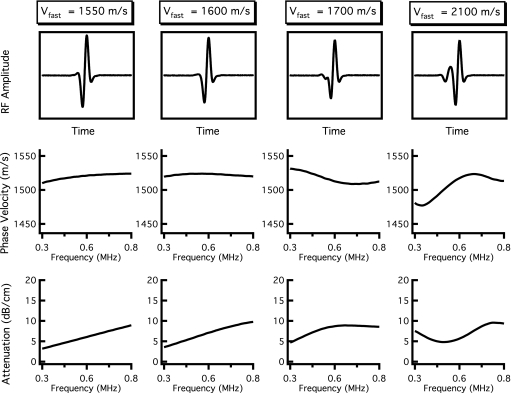
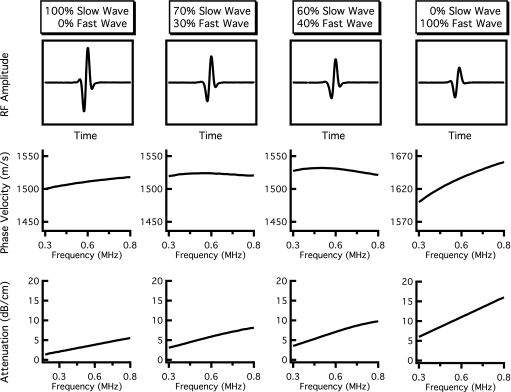
In all simulations, the parameter l was set at 1 cm, a typical thickness of bone samples investigated in vitro. The value for the reference frequency ω0∕2π was set to 300 kHz, and vslow(ω0) was held constant at 1500 m∕s, a velocity near that of sound in water. Based on measurements by Waters and Hoffmeister, the input values for βfast and βslow were set to 20 and 6.9 dB∕cm MHz, respectively.12 Input values for vfast(ω0), Afast, and Aslow were systematically varied. Based on the theoretical predictions displayed in Fig. 1, and the experimental observations of overlapping fast and slow wave modes, we varied vfast(ω0) between 1550 and 2100 m∕s, covering a wide range of velocities that result in the overlap of the fast and slow waves. When vfast was varied, Afast and Aslow were held constant at 0.3 and 0.7, respectively, so that the relative amplitudes of the fast and slow waves were comparable to those observed by other investigators.6, 12 Determining appropriate values for Afast and Aslow is challenging, given the complexity involved in calculating transmission coefficients specific to individual fast and slow waves. We therefore created a second set of simulations in which vfast(ω0) was held constant at 1600 m∕s and Afast and Aslow were varied between 0 and 1 to determine the effects of those parameters on the resultant mixed wave form.
Phase velocities were calculated using a phase unwrapping algorithm previously shown to be valid for experimental data.36
RESULTS
The resulting attenuation coefficients and phase velocities when vfast(ω0) was varied between 1550 and 2100 m∕s are shown in Fig. 3. The relative contributions of the fast and slow waves, Afast and Aslow, were held constant at 0.3 and 0.7, respectively. The left column of Fig. 3 was created with vfast(ω0) set at 1550 m∕s, a velocity only 50 m∕s faster than that of the slow wave. Under such conditions, a visual inspection of the rf signal reveals no explicit evidence of the presence of a second wave; furthermore, the attenuation coefficient and phase velocities do not exhibit suspicious behavior, despite interference taking place in the simulated ultrasonic field. However, as the difference in vfast and vslow becomes more pronounced, as in the remaining columns of Fig. 3, a negative dispersion becomes apparent, in spite of the fact that the frequency-dependent behavior of the attenuation coefficient could be approximated by a linear-with-frequency fit. When vfast(ω0)=1600 m∕s, the magnitude of dispersion (difference in phase velocity) for a twofold increase in frequency is approximately −4 m∕s, based on a linear least squares fit over the bandwidth from 400 to 800 kHz, as in the second column of Fig. 3. When vfast(ω0)=1700 m∕s, the dispersion magnitude is approximately −15 m∕s over the same bandwidth, with a local minimum in phase velocity appearing around 650 kHz. Additionally, the mixed wave form begins to show some evidence of interference under visual inspection. By the time the fast wave velocity reaches 2100 m∕s (right panel), the fast and slow waves are sufficiently separated in time that the dispersion curve obtained by analyzing the mixed wave form using a conventional phase spectroscopy algorithm has large fluctuations, with analogous behavior appearing in the attenuation coefficient.
Figure 3.
Results of independent fast and slow wave propagations when the velocity of the fast wave is varied. The velocity of the fast wave increases from the left column to the right column. The top panels display the resultant mixed rf wave forms, and the center and bottom panels show the corresponding dispersion curves and attenuation coefficients obtained when the mixed wave form is analyzed as if it contained only one wave. When vfast is only 50 m∕s greater than vslow (far left panels), the mixed wave form exhibits positive dispersion and a nearly linear attenuation coefficient. As vfast becomes increasingly greater than vslow (middle panels), the dispersion becomes negative. When vfast is significantly larger than vslow (far right panels), the dispersion curve and attenuation coefficient have complicated frequency-dependent behavior.
Results for varying Afast and Aslow are shown in Fig. 4. In the leftmost panel, the only contribution to the mixed wave form is the slow wave, and the resulting attenuation coefficient and phase velocity corresponding to this wave form are representative of the slow wave input parameters with positive dispersion. As the contribution of the fast wave increases (that is, Afast becomes proportionally more important compared to Aslow), the behavior of the phase velocity changes and begins to decrease with frequency (demonstrates a negative dispersion) over portions of the bandwidth. When (Afast,Aslow)=(0.7,0.3), the magnitude of dispersion is −4 m∕s over the 400–800 kHz bandwidth, but the attenuation coefficient can still be described as reasonably linear. The dispersion becomes approximately −11 m∕s over the same bandwidth when (Afast,Aslow)=(0.6,0.4), with the attenuation coefficient beginning to exhibit a modest degree of not-linear-with-frequency behavior. In each case, the individual fast and slow waves each exhibit a logarithmically increasing (positive) dispersion and a linear-with-frequency attenuation coefficient. Furthermore, the time-domain rf data (top panels) do not show explicit evidence of two-wave interference upon visual inspection. The far right column of Fig. 4 shows the resultant mixed wave and its properties when (Afast,Aslow)=(1,0), corresponding to only fast wave propagation. As expected, the phase velocity and attenuation coefficient of the mixed wave form return to mimicking those of the fast wave with positive dispersion.
Figure 4.
Results of independent fast and slow wave propagations when the relative contributions of the fast and slow waves are varied. The contribution of the fast wave increases from the left column to the right column. The top panels display the resultant mixed rf wave forms, and the center and bottom panels show the corresponding dispersion curves and attenuation coefficients obtained when the mixed wave form is analyzed as if it contained only one wave. The far left-hand panels display only slow wave propagation (Afast=0, Aslow=1), resulting in a positive dispersion and a strictly linear attenuation coefficient. The far right-hand panels show only fast wave propagation (Afast=1, Aslow=0), again corresponding to a positive dispersion and linear attenuation coefficient. The middle panels represent mixed wave forms (nonzero amplitudes for both fast and slow waves) that exhibit negative dispersions while maintaining an approximately linear attenuation coefficient.
DISCUSSION
This study uses a linear system approach, in conjunction with established experimental and theoretical evidence for multiple-wave propagation in cancellous bone, to generate a phenomenological model capable of producing simulated signals that exhibit negative dispersions similar to those observed in cancellous bone. The frequency-domain linear system model has the advantage of simplicity and ease of computation, but this heuristic approach may not adequately account for all features of ultrasonic propagation through cancellous bone. Alternative approaches, including those that take advantage of finite difference time-domain techniques, may prove better for relating the fast and slow waves to the material properties of bone.
We have examined the parameter space for this model, specifically the relative amplitudes and velocities of the fast and slow waves, in the limited manner outlined in Figs. 34. The dispersions become more extreme, and more negative, as the fast and slow waves become closer in magnitude and more disparate in velocity. The detailed nature of the dispersion, however, depends on complicated interdependencies among all the parameters in the model, and a rigorous determination of what regions of the parameter space generate negative dispersion is beyond the scope of this preliminary study.
We have assumed that the attenuation coefficients of cancellous bone rise linearly with frequency. This approximation appears to be adequate for frequencies in the hundreds of kilohertz range currently employed in many clinical devices and is consistent with the general consensus in the published literature. However, this model may not be rigorously valid for bandwidths extending far into the megahertz range, especially if longitudinal-to-longitudinal scattering becomes a significant contributor to the attenuation coefficient at higher frequencies.
The primary focus of this study is simulated propagation of multiple longitudinal waves through cancellous bone. Experimental confirmation of the results presented here would presumably involve analyzing data from bone samples that exhibit a negative dispersion when analyzed under the assumption that one wave was present and recovering two waves when the data are analyzed in a way that permits distinguishing between fast and slow waves. However, differentiating the fast and slow waves can be difficult when they are strongly overlapped temporally. Our laboratory has proposed a Bayesian approach for recovering the properties of each wave and has experimentally confirmed that negative dispersion can arise from two-mode propagation in a simple phantom.37, 38 A better understanding of the physical properties of cancellous bone that contribute to the attenuation and velocity properties of the fast and slow waves may also prove advantageous in predicting the degree of overlap of the two signals, which in turn could provide insight about the dispersion properties of a signal analyzed as if only one wave were present. To that end, Haiat et al. investigated the effects of anisotropy and bone volume fraction on the degree of separation between the fast and slow waves.11
CONCLUSION
Simulated ultrasonic wave propagation of fast and slow waves with phase velocities and attenuation coefficients, similar to those predicted and observed in bone, yielded resultant wave forms consisting of interfering waves that exhibited a decrease in phase velocity with frequency when analyzed conventionally under the assumption that only one wave was present. The underlying “true” ultrasonic characteristics of the fast and slow waves were obscured when analyzed in such a manner. Although the individual wave modes exhibited strictly linear-with-frequency attenuation coefficients and positive logarithmic-with-frequency phase velocities, conventional analysis of the mixed wave forms frequently resulted in complex frequency dependencies of attenuation coefficient and dispersion. In fact, the two-independent mode model used in these simulations produced resultant mixed wave forms characterized by negative dispersion despite the fact that the individual fast and slow waves exhibit positive dispersions in accordance with the Kramers–Kronig relations for attenuation and dispersion. In some simulations, negative dispersion was produced without substantially changing the coarse visual characteristics of either the time-domain signal or the linear-with-frequency behavior of the attenuation coefficient. Although further study is required to determine the validity and role of independent mode simulations for characterizing bone, the interference of multiple waves appears to be a possible source for an apparent negative dispersion of the kind observed in cancellous bone. If the material and structural properties of cancellous bone give rise to multiple interfering wave modes, recovering the ultrasonic characteristics of the individual wave modes, instead of those of the mixed wave form, could provide more robust ultrasonic determinations of bone quality.
ACKNOWLEDGMENTS
This work was supported in part by NSF Grant No. CBET-0717830 Scholar in Residence at the FDA and by NIH Grant No. R37 HL40302.
References
- Droin P., Berger G., and Laugier P., “Velocity dispersion of acoustic waves in cancellous bone,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 10.1109/58.677603 45, 581–592 (1998). [DOI] [PubMed] [Google Scholar]
- Wear K. A., “Measurements of phase velocity and group velocity in human calcaneus,” Ultrasound Med. Biol. 10.1016/S0301-5629(99)00172-6 26, 641–646 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmeister B. K., Whitten S. A., and Rho J. Y., “Low-megahertz ultrasonic properties of bovine cancellous bone,” Bone (N.Y.) 10.1016/S8756-3282(00)00275-1 26, 635–642 (2000). [DOI] [PubMed] [Google Scholar]
- Wear K. A., “Group velocity, phase velocity, and dispersion in human calcaneus in vivo,” J. Acoust. Soc. Am. 10.1121/1.2697436 121, 2431–2437 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Apostolopoulos K. N. and Deligianni D. D., “Influence of microarchitecture alterations on ultrasonic backscattering in an experimental simulation of bovine cancellous bone aging,” J. Acoust. Soc. Am. 10.1121/1.2822291 123, 1179–1187 (2008). [DOI] [PubMed] [Google Scholar]
- Hosokawa A. and Otani T., “Acoustic anisotropy in bovine cancellous bone,” J. Acoust. Soc. Am. 10.1121/1.422790 103, 2718–2722 (1998). [DOI] [PubMed] [Google Scholar]
- Lee K. I., Hughes E. R., Humphrey V. F., Leighton T. G., and Choi M. J., “Empirical angle-dependent biot and mba models for acoustic anisotropy in cancellous bone,” Phys. Med. Biol. 10.1088/0031-9155/52/1/005 52, 59–73 (2007). [DOI] [PubMed] [Google Scholar]
- Hughes E. R., Leighton T. G., White P. R., and Petley G. W., “Investigation of an anisotropic tortuosity in a Biot model of ultrasonic propagation in cancellous bone,” J. Acoust. Soc. Am. 10.1121/1.2387132 121, 568–574 (2007). [DOI] [PubMed] [Google Scholar]
- Padilla F. and Laugier P., “Phase and group velocities of fast and slow compressional waves in trabecular bone,” J. Acoust. Soc. Am. 10.1121/1.1288935 108, 1949–1952 (2000). [DOI] [PubMed] [Google Scholar]
- Lee K. I., Roh H.-S., and Yoon S. W., “Acoustic wave propagation in bovine cancellous bone: Application of the modified Biot-Attenborough model,” J. Acoust. Soc. Am. 10.1121/1.1610450 114, 2284–2293 (2003). [DOI] [PubMed] [Google Scholar]
- Haiat G., Padilla F., Peyrin F., and Laugier P., “Fast wave ultrasonic propagation in trabecular bone: Numerical study of the influence of porosity and structural anisotropy,” J. Acoust. Soc. Am. 10.1121/1.2832611 123, 1694–1705 (2008). [DOI] [PubMed] [Google Scholar]
- Waters K. R. and Hoffmeister B. K., “Kramers-Kronig analysis of attenuation and dispersion in trabecular bone,” J. Acoust. Soc. Am. 10.1121/1.2126934 118, 3912–3920 (2005). [DOI] [PubMed] [Google Scholar]
- Nicholson P. H., Lowet G., Langton C. M., Dequeker J., and Van der Perre G., “A comparison of time-domain and frequency-domain approaches to ultrasonic velocity measurement in trabecular bone,” Phys. Med. Biol. 10.1088/0031-9155/41/11/013 41, 2421–2435 (1996). [DOI] [PubMed] [Google Scholar]
- O’Donnell M., Jaynes E. T., and Miller J. G., “Kramers-Kronig relationship between ultrasonic attenuation and phase velocity,” J. Acoust. Soc. Am. 10.1121/1.385566 69, 696–701 (1981). [DOI] [Google Scholar]
- Waters K., Hughes M., Mobley J., Brandenburger G., and Miller J., “On the applicability of Kramers-Kronig relations for ultrasonic attenuation obeying a frequency power law,” J. Acoust. Soc. Am. 10.1121/1.429586 108, 556–563 (2000). [DOI] [PubMed] [Google Scholar]
- Waters K. R., Mobley J., and Miller J. G., “Causality-imposed (Kramers-Kronig) relationships between attenuation and dispersion,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 10.1109/TUFFC.2005.1503968 52, 822–833 (2005). [DOI] [PubMed] [Google Scholar]
- Mobley J., Waters K. R., and Miller J. G., “Causal determination of acoustic group velocity and frequency derivative of attenuation with finite-bandwidth Kramers-Kronig relations,” Phys. Rev. E 10.1103/PhysRevE.72.016604 72, 016604 (2005). [DOI] [PubMed] [Google Scholar]
- Bauer A. Q., Marutyan K. R., Holland M. R., and Miller J. G., “Is the Kramers-Kronig relationship between ultrasonic attenuation and dispersion maintained in the presence of apparent losses due to phase cancellation?,” J. Acoust. Soc. Am. 10.1121/1.2735803 122, 222–228 (2007). [DOI] [PubMed] [Google Scholar]
- Marutyan K. R., Holland M. R., and Miller J. G., “Anomalous negative dispersion in bone can result from the interference of fast and slow waves,” J. Acoust. Soc. Am. 10.1121/1.2357187 120, EL55–EL61 (2006). [DOI] [PubMed] [Google Scholar]
- Biot M. A., “Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range,” J. Acoust. Soc. Am. 10.1121/1.1908239 28, 168–178 (1956). [DOI] [Google Scholar]
- Biot M. A., “Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range,” J. Acoust. Soc. Am. 10.1121/1.1908241 28, 179–191 (1956). [DOI] [Google Scholar]
- Haire T. and Langton C., “Biot theory: A review of its application to ultrasound propagation through cancellous bone,” Bone (N.Y.) 10.1016/S8756-3282(99)00011-3 24, 291–295 (1999). [DOI] [PubMed] [Google Scholar]
- Fellah Z. E. A., Chapelon J. Y., Berger S., Lauriks W., and Depollier C., “Ultrasonic wave propagation in human cancellous bone: Application of Biot theory,” J. Acoust. Soc. Am. 10.1121/1.1755239 116, 61–73 (2004). [DOI] [PubMed] [Google Scholar]
- Sebaa N., Fellah Z. E. A., Fellah M., Ogam E., Wirgin A., Mitri F. G., Depollier C., and Lauriks W., “Ultrasonic characterization of human cancellous bone using the Biot theory: Inverse problem,” J. Acoust. Soc. Am. 10.1121/1.2335420 120, 1816–1824 (2006). [DOI] [PubMed] [Google Scholar]
- Wear K. A., Laib A., Stuber A. P., and Reynolds J. C., “Comparison of measurements of phase velocity in human calcaneus to Biot theory,” J. Acoust. Soc. Am. 10.1121/1.1886388 117, 3319–3324 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams J. L., “Ultrasonic wave propagation in cancellous and cortical bone: Prediction of some experimental results by Biot’s theory,” J. Acoust. Soc. Am. 10.1121/1.402637 91, 1106–1112 (1992). [DOI] [PubMed] [Google Scholar]
- Hosokawa A. and Otani T., “Ultrasonic wave propagation in bovine cancellous bone,” J. Acoust. Soc. Am. 10.1121/1.418118 101, 558–562 (1997). [DOI] [PubMed] [Google Scholar]
- Chakraborty A., “Prediction of negative dispersion by a nonlocal poroelastic theory,” J. Acoust. Soc. Am. 10.1121/1.2816576 123, 56–67 (2008). [DOI] [PubMed] [Google Scholar]
- Roh H.-S. and Yoon S. W., “Acoustic diagnosis for porous medium with circular cylindrical pores,” J. Acoust. Soc. Am. 10.1121/1.1645247 115, 1114–1124 (2004). [DOI] [PubMed] [Google Scholar]
- Lee K. I., Humphrey V. F., Leighton T. G., and Yoon S. W., “Predictions of the modified Biot-Attenborough model for the dependence of phase velocity on porosity in cancellous bone,” Ultrasonics 46, 323–330 (2007). [DOI] [PubMed] [Google Scholar]
- Hughes E. R., Leighton T. G., Petley G. W., and White P. R., “Ultrasonic propagation in cancellous bone: A new stratified model,” Ultrasound Med. Biol. 10.1016/S0301-5629(99)00034-4 25, 811–821 (1999). [DOI] [PubMed] [Google Scholar]
- Wear K. A., “A stratified model to predict dispersion in trabecular bone,” IEEE Trans. Ultrason. Ferroelectr. Freq. Control 10.1109/58.935726 48, 1079–1083 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin W., Qin Y. X., and Rubin C., “Ultrasonic wave propagation in trabecular bone predicted by the stratified model,” Ann. Biomed. Eng. 10.1114/1.1397787 29, 781–790 (2001). [DOI] [PubMed] [Google Scholar]
- Plona T. J., Winkler K. W., and Schoenberg M., “Acoustic waves in alternating fluid/solid layers,” J. Acoust. Soc. Am. 10.1121/1.395120 81, 1227–1234 (1987). [DOI] [Google Scholar]
- Johnson D. L., Koplik J., and Dashen R., “Theory of dynamic permeability and tortuosity in fluid-saturated porous media,” J. Fluid Mech. 10.1017/S0022112087000727 176, 379–402 (1987). [DOI] [Google Scholar]
- Trousil R. L., Waters K. R., and Miller J. G., “Experimental validation of the use of Kramers-Kronig relations to eliminate the phase sheet ambiguity in broadband phase spectroscopy,” J. Acoust. Soc. Am. 10.1121/1.1365114 109, 2236–2244 (2001). [DOI] [PubMed] [Google Scholar]
- Marutyan K. R., Bretthorst G. L., and Miller J. G., “Bayesian estimation of the underlying bone properties from mixed fast and slow mode ultrasonic signals,” J. Acoust. Soc. Am. 10.1121/1.2401198 121, EL8–EL15 (2007). [DOI] [PubMed] [Google Scholar]
- Bauer A. Q., Marutyan K. R., Holland M. R., and Miller J. G., “Negative dispersion in bone: The role of interference in measurements of the apparent phase velocity of two temporally overlapping signals,” J. Acoust. Soc. Am. 10.1121/1.2839893 123, 2407–2414 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]