An Objective Assessment of Fetal and Neonatal Auditory Evoked Responses

Abstract

Objective

We propose to use cross-correlation function to determine significant fetal and neonatal evoked responses (ERs).

Methods

We quantify ERs by cross-correlation between the stimulus time series and the recorded brain signals. The statistical significance of the correlation is calculated by surrogate analysis. For validation of our approach we investigated a model which mimics the generation of ERs. The model assumes a fixed latency of the ER and contains two parameters, ε and λ. Whether or not the system responds to a given stimulus is controlled by ε. The amount to which the system is excited from the base line (background activity) is governed by λ. We demonstrate the technique by applying it to auditory evoked potentials from four fetuses (21 records) between 27-39 weeks of gestational age and four neonates (eight records).

Results

The method correctly identified the ER and the latency incorporated in the model. A combined analysis of fetuses and neonates data resulted in a significant negative correlation between age and latency.

Conclusions

The analysis of ER, especially for fetal and newborn recordings, should be based on advanced data analysis including the assessment of the significance of responses. The negative correlation between age and latency indicates the neurological maturation.

Significance

The proposed method can be used to objectively assess the ER in fetuses and neonates.

Introduction

The maturation of sensory cortex in newborns and fetuses can be investigated by stimulus evoked responses (ERs) recorded with electroencephalography and magnetoencephalography (e.g. Huottilainen 2005, Eswaran 2005, Chiappa 1990). The major maturation index is the latency of the ER. Because the ERs are elicited by a single stimulus and are much lower in amplitude compared to the background activity, it is difficult to identify them in the cortical signals. For this purpose the stimulus is repeatedly delivered and the ER is quantified by averaging the signals locked to the stimulus delivery time point. In the averaged data, if the post-stimulus amplitude is “higher” than the pre-stimulus amplitude, it is defined as ER. This definition is valid under the following assumptions: (i) the background spontaneous activity averages out to the noise level of (close to) zero amplitude in the presence of sufficiently large number of stimuli and (ii) there are no interfering (biological/measurement) signals. These conditions can be difficult to achieve on fetal and neonatal studies due to issues such as patient comfort, physical state of the fetuses/neonates, and interferences such as breathing and cardiac signals all of which can limit the number of applied stimuli. Hence we need a measure to objectively quantify the ER. Here we propose to use cross-correlation function (CCF) to quantify the ER and subsequently use a bootstrap method to assess its statistical significance. To validate this method we propose a simple stochastic model that mimics ER. Finally, we apply this approach to auditory evoked potentials measured from four fetuses (21 records) between 27-39 weeks of gestational age (GA) and four neonates (eight records one each from right and left stimulations) obtained by a 151-sensor magnetoencephalography (MEG) device.

Method

Quantification of ER

Traditionally ER is quantified by stimulus-locked averaging. Also there has been effort to quantify the fetal ER using wavelet transform, a time and frequency domain approach (Norton et al., 2004).

For our proposed approach, let the time instances of stimuli delivery be κ. Let us define a stimulus series η such that it has a value of one at the time points κ and zero at all other points. For analysis we extract series W and Z. W is related to η and Z represents the cortical recordings. Both time series contain one second of data post the time point κ. The selection of one second is arbitrary, however this should be adequate for evoked responses in fetuses and newborns. If there were N stimuli, and sf was the sampling frequency (in Hz), then W and Z will contain N´= N × sf data points. Now we define the cross-correlation between the series W and Z as follows:

$$C\left(\tau \right)=\frac{\sum _{i=1}^{N^{\prime }-m\tau }[W\left(i\right)-\stackrel{‒}{W}]\cdot [Z(i+\tau )-\stackrel{‒}{Z}]}{\sqrt{\sum _{i=1}^{N^{\prime }-m\tau }{[W\left(i\right)-\stackrel{‒}{W}]}^2}\sqrt{\sum _{i=1}^{N^{\prime }-m\tau }{[Z\left(i\right)-\stackrel{‒}{Z}]}^2}}.$$

Since we are looking for the response elicited by the external stimulus, it is reasonable to shift the MEG data Z backwards in time to identify the ER. Hence we compute C(τ) only forτ = 0 to sf. Shifting the stimulus signal W backwards in time and computing C(τ) would correspond to quantifying the impact of the MEG on the stimulus which does not have any physiological relevance. However, in the conventional stimulus-locked average, this scenario corresponds to the amplitude in the pre-stimulus duration which used to serve as a base line to gauge the signal intensity in the post-trigger duration. In this work we assess the significance of C(τ) by the bootstrap method and hence we did not study the correlation between the two signals in the pretrigger regions. Further, cross-correlation is dependent on the length of the data. For each τ value C(τ) will be estimated for different number of data points and hence there will be an element of bias in this definition. In order to avoid this bias, for each shift (τ) we discard the same number of data points (i.e.) N'-m#x03C4;, where mτ is the maximum value of τ which is one second in our example.

Assessing the statistical significance of CCF

We use bootstrap approach to assess the statistical significance of CCF. If one of the time series is uncorrelated, then assuming that the two time series have Gaussian distribution, we can use ± N^-½ as the confidence limit for C(τ) (Theiler et al., 1992, Timmer et al., 1998), where N is the length of the data. However, in our case neither the trigger series nor the MEG is uncorrelated and hence we need to use a nonparametric approach to assess the statistical significance of CCF. For this purpose the surrogate signals are generated by randomly shuffling the disjoint one-second blocks of the MEG data (Govindan et al., 2006). Shuffling of the entire (trigger) time series has been considered in earlier works (Lv et al., 2007, McCubbin et al., 2007). The advantage of block shuffling over shuffling the entire time series is that the former preserves the (two point) correlation properties of the original signal whereas the later does not. This property is necessary to correctly address a certain type of null hypothesis that is related to biological signals as presented here. For example, if the neuronal data have certain type of correlations and produce spurious C(τ) (i.e. show a high correlation though there is no actual interaction between the two signals), then random shuffling of the entire signal (which destroys the auto-correlations in the signals) would falsify the null hypothesis testing while the surrogates obtained by block shuffling method would correctly address the null hypothesis. Further, we would like to mention that different bootstrap techniques to compute the confidence intervals of the evoked response are known (Kruglikov and Schiff, 2003, Fujioka et al., 2004). While the bootstrap approach proposed by Kruglikov and Schiff is designed for studies involving multiple triggers, the approach proposed by Fujioka et al., assumes a stationary background activity. Hence these methods cannot be applied to the fetal and neonatal data reliably.

To assess the statistical significance of CCF, we make a null hypothesis that the C(τ) computed between η(t) and the MEG data is due to spurious correlations. To test the null hypothesis we synthesize the block shuffled MEG data as discussed above. We compute CCF of the surrogate data as C(τ)_sur. Based on an earlier work (Schreiber and Schmitz, 2000), to reject the null hypothesis at α - level, we synthesize, $\mathit{N}=2\cdot \mathit{K}∕\alpha -1$ number of surrogates, where 2 in this equation denotes the two sided testing to include the positive and negative values (magnitudes) of C(τ) and K is a positive integer. In our calculations we used 50 realizations of surrogate which corresponds to α ≅ 0.04. The null hypothesis can be rejected if the distribution of C(τ)_sur computed from the surrogate realizations is different from C(τ) obtained from original time series (i.e.) if the values of C(τ) are well separated from the values of C(τ)_sur (from all the realizations). Conventionally C(τ)_sur (or any statistic computed for the original data and the surrogate data as well) is assumed to have Gaussian distribution and the confidence limits are defined by computing the number of standard deviations C(τ) that lie outside the distribution of C(τ)_sur. However, in practice, the assumption of Gaussianity may not hold for the chosen measure and hence we might not be able to correctly address the null hypothesis. Instead, we use rank approach to address the null hypothesis (Theiler et al., 1992). We compute the K - th largest value and K - th smallest value of C(τ)_sur for each realization of surrogate. In our calculations we set K = 1 and hence we compute the maximum and minimum of C(τ)_sur for each realization of surrogate. Since we use 50 realizations of surrogates, we will have 50 different maxima and minima. To this end we use the maximum of all the maxima and minimum of all the minima as the upper and lower confidence level of C(τ). The values of τ at which C(τ) exceeds the upper/lower confidence level is considered as the statistically significant response. In this case, the null hypothesis that C(τ) is obtained due to spurious correlations can be rejected at the α level of confidence. Further, the number false positives or specificity of the approach can be improved by decreasing the α value. This can be accomplished by increasing the number of surrogates. However, in this work 50 realizations are chosen to keep the false positives and computational time minimal. Further, one can also increase K which again would result in computational effort and hence we set its value to one in our analysis.

Modeling aspects

One of the fundamental assumptions involved in quantifying ER (based on stimulus-locked averaging) is that the spontaneous brain activity is a zero mean random process. However, in practice, this limit will be reached only when the average is performed over a large number of stimuli. Hence to model the background brain activity Y(t) we use zero mean Gaussian distributed random numbers. Further, we assume the sample frequency to be 312.5 Hz (see below) and generate Y(t) for six minute duration. In an ER study, the externally applied stimuli will usually elicit a response (i.e.) modify the base level activity of the brain, at certain time point later from the onset of stimuli. This time delay is called latency and in our model it is denoted by δ. In an ER study, stimulus is delivered in a pseudo periodic fashion. In our model we use η(t) to represent stimulus series. This series is populated with ones and zeros. The stimulus will be delivered only at time point when η(t) has a value of one. In order to decide the time points (sample numbers) to deliver the stimuli, we generate a sequence κ. In this simulation the time interval between two successive stimuli is assumed to be 2 sec (i.e.) 625 data points (sample frequency based on the real recordings 312.5 Hz). Thus, the sequence κ is generated using Poisson distributed random numbers with mean value of 625. We then compute the cumulative sum of this sequence which gives the continuous time representation of the stimulus points and use it as sequence κ. Thus η(t) will have a value of one at time points dictated by the sequence κ and zero at all other time points. Thus, if t takes on a value in the sequence κ (i.e. where η(t) = 1), the evoked response elicited, X(t + δ), is modeled by modifying (adding a constant λ to) the value of the spontaneous brain activity Y(t) at a latency δ (i.e.) Y(t + δ). λ can be thought of as the parameter which controls the signal to noise ratio of X(t) and is varied between zero and one. For time t that is not in the sequence κ (i.e. where η(t) = 0), X(t) will assume the values of background spontaneous activity Y(t).

The developing brain of the fetus and neonate may not respond to all the externally delivered stimuli with an identical ER. In general it may also be possible that the fetal or neonatal brain does not generate an ER for certain stimuli based on the behavioral state. We incorporate this feature in the model through another time series ϕ(t,ε) and is controlled using the variable ε. When η(t)takes on a value of one, depending on the value of ε, ϕ( t, ε ) dictates whether or not the system should elicit a response to the given stimulus. ϕ( t, ε ) is also populated with ones and zeros based on the (uniformly distributed random) sequence p which contains the same number of points as the sequence κ. If the time t takes on a value in the sequence κ (i.e. when η(t) = 1), ϕ( t, ε ) will take on a value of one if p at this time point is lesser than the chosen tolerance of ε otherwise zero. The parameter ε takes values between zero and one and ε × 100 gives the percentage of stimuli that elicited the response. Based on the above assumptions we propose the following simple stochastic model to describe the ER:

$$\text{X}(t+\delta )=\text{Y}(t+\delta )+\lambda \cdot \varphi (t,\epsilon )\cdot \eta \left(t\right)$$

One of the properties of the ER is that it is small in amplitude and therefore close to the baseline activity. The data simulated from this model should preserve this property.

To summarize we generate three different random series: (i) Gaussian distributed series to model the background brain activity Y(t) ; (ii) Poisson distributed series to model the stimulus series, η( t ) and (iii) uniformly distributed series (p) to adjust the percentage of response ϕ( t,ε ). For the sake of comparison, we generate single realization of all the three random series, and simulate different variants of X(t) by varying the values of ε and λ from zero to one in steps of 0.1. That is we vary the parameter pair ( λ, ε ) from zero to 100 % in steps of 10% and generate a total of 110 different realizations of X(t) from each pair of parameters. Furthermore, in all the simulation, the latency δ was set to 300 milliseconds.

Prior to quantifying the ER we filtered X(t) between 1-10 Hz using 4^th order Butterworth filter so as to make the analysis procedure close to fetal and neonatal MEG data analysis. The ER was quantified using X(t) and η(t) by CCF approach and its statistical significance was also assessed by the aforementioned bootstrap approach.

MEG data

To demonstrate the application of this approach we performed a retrospective analysis of the subgroup of data presented in (Holst et al., 2005). For this purpose we considered four datasets reported by Holst et al., 2005, namely, pat404 (seven fetal, two neonatal records), pat407 (six fetal record and two neonatal records), pat416 (five fetal, two neonatal records) and pat417 (three fetal, two neonatal records).

The details about the data collection can be found in Holst et al., 2005, however for the sake of self-consistency of the paper, we explain it below. Starting at 27 weeks GA, MEG recordings were performed every two weeks until delivery and one time in the newborn period. This study was approved by local Institutional Review Board and all the subjects gave their informed written consent prior to the study. MEG was recorded using an instrument called SARA, an acronym for SQUID Array for Reproductive Assessment, which is installed at University of Arkansas for Medical Sciences. SARA has a 151 primary sensor array curved to fit the shape of the maternal abdomen and is specifically designed to non-invasively record fetal biological magnetic signals. Prior to the MEG recording, the location of the fetal head was identified using ultrasound. Once the subject is positioned on SARA, the position of the fetal head was reconfirmed with the portable ultrasound (Holst et al., 2005). For neonatal recordings, a special cradle was devised to fit the SARA sensor array to record newborn MEG which enabled us to position the neonate so that the head rested against the SARA sensors.

The auditory stimuli were generated using STIM software (Neurosoft, El Paso, TX). The sound stimulation was delivered to the maternal abdomen overlaying the fetal head from the speaker mounted outside the magnetically shielded room through the plastic tubing with an inflated balloon at the distal end (Eswaran et al., 2000). For the newborn studies, the balloon was suspended in the midline over the cradle above the newborn's head (Holst et al., 2005). The auditory stimuli were generated using oddball paradigm (to avoid habituation effects) consisting of random arrangements of tone bursts of 500 Hz frequent stimuli (80%) and 700 or 1000 Hz rare stimuli (20%). The inter stimulus interval was 2 sec. The duration of the tone bursts were 500 milliseconds. The intensity of the sound for fetal stimulation was 120 dB at mother's abdomen and 80 dB for the neonatal stimulation over the cradle (Holst et al., 2005). For newborns, each ear was stimulated separately by turning the baby appropriately with one ear exposed to the direction of the sound. The auditory evoked potentials were sampled at a frequency of 312.5 Hz from 151 magnetic sensors for 6 epochs lasting 1 minute each.

The interfering cardiac signals were removed offline by orthogonal projection technique (McCubbin et al., 2006, Vrba et al., 2004). For further analysis the signals were band pass filtered between 1-10 Hz using 4-th order Butterworth filter with zero phase distortion (Draganova et al., 2005). The ER response was quantified using the CCF approach described above and its statistical significance was assessed using the bootstrap approach. For each MEG data, the latencies were extracted using an automated algorithm from the sensors which passed the bootstrap significance test and any peak which turned out to be statistically significant in 100-900 millisecond range was considered as an ER. The correlation between the latency and GA was assessed using correlation coefficient at the significance level of 0.01.

Results

Model

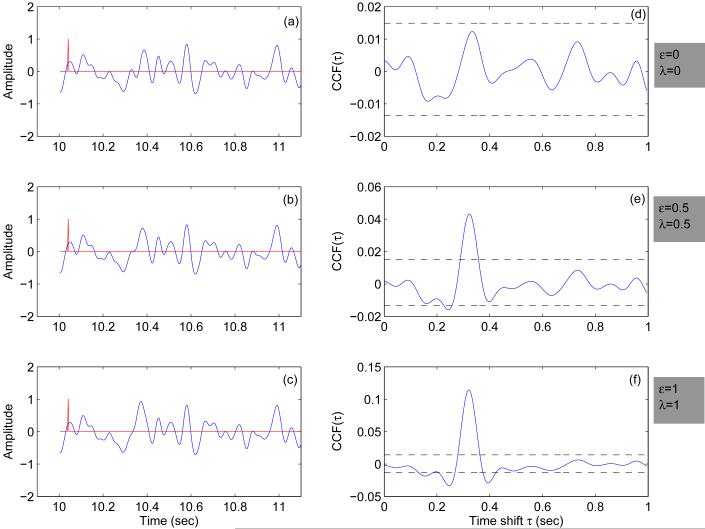
Time traces of simulated data using the model are shown in Figure 1 (a-c) for three different sets of parameters; two extreme cases in Figure 1a and Figure 1c and an intermediate case in Figure 1b. Though the parameter λ governing the SNR of the signal and the number of stimuli eliciting an evoked response (governed by the parameter ε) were increased from Figure 1(a-c), qualitatively all the traces look the same indicating that the ER is almost at the noise level. This property justifies the assumptions involved in the model. Thus, one needs to perform an event related average or use approaches such as CCF to identify the ER. The ER quantified using the CCF approach as discussed in the method section is shown in Figure 1(d-f). The upper and lower confidence limits for the CCF function obtained using bootstrap technique are also given in the same figures. For ε = 0,λ = 0 (Figure 1a) the model does not incorporate any ER and for this scenario the CCF is well within the bootstrap confidence limit as expected. As the percentage of the stimuli (ε) and the signal to noise ratio (λ) increases one would expect the interaction between the stimuli and the brain signal to increase. This is reflected in the CCF shown in Figure 1(d-f). In Figure 1(e-f) the ER is elicited at the latency of 300 milliseconds which was earlier incorporated in the model. For lower values of ε and λ the latency is localized close to the expected value of 300 milliseconds. For higher values of ε and λ, there is a spread in the latencies though the maximum is observed almost at the same time point as observed for the lower values of the parameters. This can be explained as follows: In the simulated data, the ER is incorporated as delta-spike whose frequency response is spectrally white. When applied to the input of a narrow frequency band filter (as done here) the simulated ER is simply the impulse response of the filter, which is well approximated by the sinc function. Thus, for low values of the parameters the amplitude of the ripples are close to the noise level and hence they are insignificant in the CCF. While for the higher values of the parameters, the ripples rise above the noise level and exceed the confidence limits producing spurious amplitude peaks around the fundamental peak of 300 milliseconds. Hence, the spurious peaks seen in CCF for higher values of the parameters ε and λ (Figure 1(d-f)) are almost symmetric around the expected latency of 300 milliseconds and negative in amplitude. These spurious peaks can be minimized by widening the band width of the filter (which is currently kept as 1-10 Hz). In this case one might retain in unwanted high frequency components in the signal which might eventually obscure the ER. In order to check the robustness of our approach we simulated the model for different values of ε and λ starting from zero to one in steps of 0.1. For different sets of parameter values we quantified the ER using the above approach. Our results show that the method has correctly identified the ER for all but two sets of (λ,ε) parameters namely (0.1, 0.1) and (0.1, 0.2). These sets of parameters correspond to low (10% of) SNR value and the response elicited only by 10 to 20 % of the stimuli.

Figure 1.

The snapshot of one second traces of the MEG data simulated using the study model for three different sets of parameters: (a) ε = 0,λ = 0 (b) ε = 0.5,λ = 0.5 and (c) ε = 1,λ = 1 and. The corresponding trigger time series is also shown in the same figures as δ - spike. The evoked response (ER) quantified using the entire datasets shown on the left are given in (d)-(f). The horizontal lines represent the bootstrap confidence limit.

fMEG

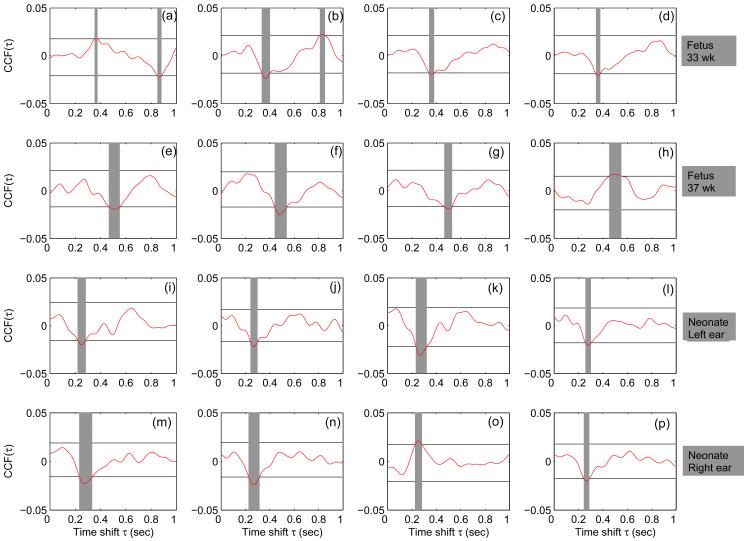
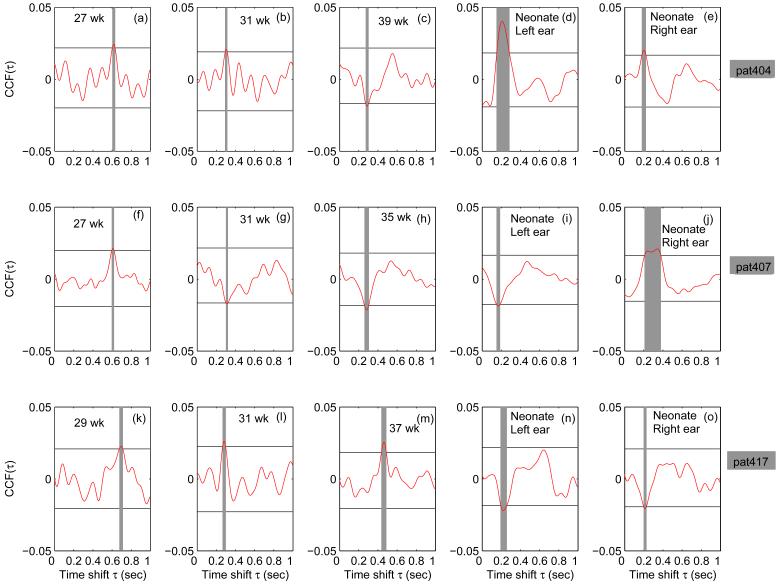
Based on the successful results of theoretical model, we applied the CCF approach to quantify the fetal and neonatal ER. For a single fetus (pat416), the CCFs of four sensors are given in Figure 2(a-d) for 33 weeks and Figure 2(e-h) for 37 weeks. Figure 2(i-l) represents the CCF from four channels during the left ear stimulation of the neonate and Figure 2(m-p) represents the CCF from four channels during the right ear stimulation. The horizontal lines indicate the bootstrap confidence limit. There is an increase in the magnitude of the CCF from 33 weeks to 37 weeks GA. Furthermore, the neonate showed a faster response compared to the fetal counter part. In Figure 3 we present the results of the evoked response of the other three subjects; Figure 3(a-e) represents results from pat404; Figure 3(f-j) from pat407 and Figure 3(k-o) from pat417. We present only the sensors with highest SNR (CCF) from two datasets prior to 34 weeks and two datasets after 34 weeks which include the neonatal data. The horizontal lines in all the plots have the same meaning as in Figure 2. In pat404, Figure 3(a-e) and pat407, Figure 3(f-j) there is a decrement in the latency as a function of gestation, however this decrement is not observed with pat417. As seen in pat416 (Figure 2), the neonates show earlier response compared to the fetuses. Of the 21 fMEG recordings analyzed, we observed significant ER in 18 (approximately 86%) of them which includes six records in pat404, five records in pat407, four records in pat416 and three records in pat417 (see Figure 4). In the case of neonates, we observed ER in all (100%) of them. Further, we would like to mention that the response was observed in the sensor region generally corresponding to the fetal head position as determined by ultrasonography performed immediately prior to the SARA measurement. In the case of neonates the response was mainly observed in the sensors over which the neonatal head was rested during recording.

Figure 2.

ER from four different MEG sensors quantified using CCF for subject pat416 in (a-d) 33 weeks (e-h) 35 weeks of gestation. ER of the neonate are shown in (i-l) for left ear stimulation and (m-p) for right ear stimulation. The horizontal lines represent the bootstrap confidence limit. The time points at which CCF exceeds the confidence limit are highlighted in grey color.

Figure 3.

Results of ER of (a-e) pat404 (h-j) pat407 and (k-o) pat417. Two datasets from below 34 weeks and two datasets after 34 weeks which include the (left and right ear stimulation of) neonatal data are shown. In all the cases only the sensors with highest SNR (CCF) are shown. The horizontal lines represent the bootstrap confidence limit and the vertical grey shaded lines time points exceeding the confidence limit.

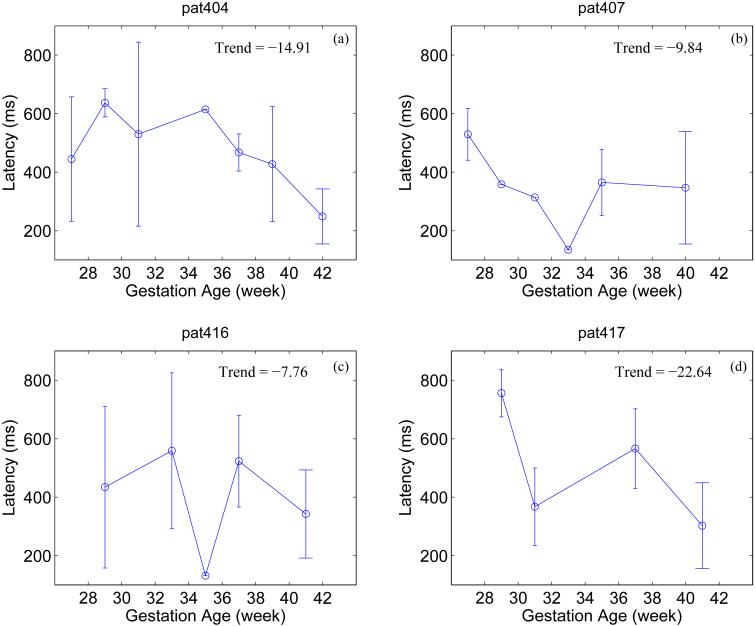
Figure 4.

The average latency values for each gestation age for the four fetuses. Last values in each plot indicate the average latency of the neonates. The error-bars indicate the mean plus/minus one standard deviation. Unit of the trend is millisecond/week.

In less than 5% of our datasets we found multiple (two) components which turned out to be significant as observed in the earlier work (Wakai et al., 1996). For each dataset in which significant fetal or neonatal ER was observed, there was at least one to a maximum of 18 sensors that passed the significance test. The mean value of the latencies for each GA is shown in Figure 4 for all the four fetuses and the last value in each plot corresponds to the latency of the neonate. The error-bar indicates mean plus/minus one standard deviation. There was a negative trend in the latency in all the four cases but it was not statistically significant (p>0.01). However, when the latencies from all the four fetuses and neonates were combined, there was statistically significant decrease in the latency as a function of GA (correlation coefficient = -0.5; p<0.01).

Discussion

We proposed to use CCF to make objective assessment of the ER and suggested a bootstrap approach to judge the statistical significance of the CCF. We tested the performance of the proposed method by applying it to a two parameter model which mimics ER. In the case of model data, except for two sets of parameters corresponding to a low response rate and small signal strength, the CCF method correctly quantified the ER. Furthermore, the method has not falsely identified any response for the parameter values where there should not be any ER. Thus, the CCF analysis with its confidence limit determined by bootstrap approach has a high degree of specificity especially for the particular realization considered in this study. The major difference of this approach to a recently published approach is that we do not take into account the estimate of the noise level during pre stimulus period to determine significant differences between pre and post-stimulus responses (McCubbin et al., 2007).

Earlier studies (Holst et al., 2005, Schleussner et al., 2001, Lengle et al., 2001) found a significant decrease in the latency as a function of gestational age for fetuses on a group level. We did not observe such a trend in fetal data obtained from individual cases, but at the group level, a significant decay was observed in the (combined fetal and neonatal) latencies as a function of GA which could indicate the maturation of the auditory cortex.

In future studies, CCF will be employed to quantify conventional fetal and neonatal ER obtained using single type stimuli. Also, since the proposed method is an objective measure, it can be applied reliably to more complicated scenarios such as habituation behavior (Leader and Baillie, 1988, Leader et al., 1982, Thompson and Spencer, 1966, Sheridan et al., 2008) where multiple types of stimuli limit the total number of stimuli.