Antitumor Efficacy Testing in Rodents

Abstract

The preclinical research and human clinical trials necessary for developing anticancer therapeutics are costly. One contributor to these costs is preclinical rodent efficacy studies, which, in addition to the costs associated with conducting them, often guide the selection of agents for clinical development. If inappropriate or inaccurate recommendations are made on the basis of these preclinical studies, then additional costs are incurred. In this commentary, I discuss the issues associated with preclinical rodent efficacy studies. These include the identification of proper preclinical efficacy models, the selection of appropriate experimental endpoints, and the correct statistical evaluation of the resulting data. I also describe important experimental design considerations, such as selecting the drug vehicle, optimizing the therapeutic treatment plan, properly powering the experiment by defining appropriate numbers of replicates in each treatment arm, and proper randomization. Improved preclinical selection criteria can aid in reducing unnecessary human studies, thus reducing the overall costs of anticancer drug development.

With the worldwide cancer death toll being reported as 7.6 million people in 2007 and current projections suggesting that nearly 1.5 million people living in the United States will be diagnosed with cancer in 2008 (1), there is an obvious need to develop more effective anticancer agents. Unfortunately, the costs of extensive preclinical research and development as well as those associated with generating the human clinical data necessary to support new agent approvals are extremely high. The drug development process includes many steps and requires substantial investments in time and resources, and ultimately requires the recruitment of patients who are willing to participate in human clinical trials (2). A 2003 estimate suggested that a single phase 3 clinical trial of anticancer chemotherapy involving 20 patients requires approximately 4000 person-hours of professional and technical time (3). In addition, the total research and development costs associated with a single compound are estimated to exceed $400 million (4). One contribution to these costs is the expense associated with initial development of compounds that are subsequently abandoned during the drug development process (4).

The typical development plan for a cancer chemotherapy agent involves sequential steps, each of which has associated costs that generally increase as the agent moves down the development path (2,3,5). These steps include in vitro studies to identify test agents; rodent studies to assess the potential activity of these agents; pharmacology studies to define drug absorption, distribution, metabolism, and elimination; and toxicology studies to define a safe starting dose for humans (2). The greatest costs are associated with the preclinical toxicology and pharmacology studies that are required before a drug can be tested in humans. Therefore, the earlier in the process that a compound is deemed unworthy of further development and dropped from consideration, the lower the costs will be for that agent and, ultimately, the lower the overall costs will be for new agents in general.

Although many different in vitro assays, both cell-based and molecular-target driven, have been used to identify lead compounds, the most common step following in vitro assays is efficacy assessments in rodent tumor models (6). Early in the history of cancer therapy development, a large variety of rodent tumors were used in efficacy assessments (7–11). However, in the early 1980s, immunologically compromised mice that are capable of supporting human tumor growth became more widely available (12,13). The availability of these mice resulted in the development of human tumor xenograft models, which are used in the bulk of current preclinical efficacy studies (6,8,11,14,15). Detractors from this approach have suggested that preclinical rodent-based tumor models are not predictive of human clinical outcomes and are therefore unnecessary and can be eliminated (6). However, it is important to note that although some drugs that show activity against human tumor xenografts have failed to show activity in human clinical trials, many of the clinically approved drugs in use today have demonstrated and continue to demonstrate activity in a variety of preclinical models (6,16–23). Because the selection of agents for advancement to human clinical trials has been and continues to be based, in part, on in vivo efficacy studies, their design and interpretation are important both ethically and economically.

In this commentary, I review factors that should be considered during preclinical drug testing to reduce the potential for false-positive conclusions while minimizing the risks of false-negative results. These factors include selecting an optimal preclinical efficacy model, developing a good experimental design, selecting a proper treatment plan, designing an experiment that will provide statistically valuable data, and, finally, presenting the data in a useful format to the research community. It is not my intent to present the pros and cons of the available models (eg, authochthonous vs xenograft, xenograft vs transgenic) because these issues have been discussed extensively elsewhere (6,10,24,25). For clarity, autochthonous models are those in which a tumor of mouse origin is transplanted into a mouse, whereas xenograft models in-volve the transplantation of a tumor from a heterologous species (eg, human) into a mouse. Transgenic models, generated by genetically altering the mouse genome to increase tumor occurrence, are also used in drug studies. Each of these models has unique features; however, the issues discussed here are applicable to all of them.

Identification of an Appropriate Species for Assessing Efficacy

One important consideration in testing new drugs in animal models is the identification of an appropriate species in which to conduct tumor studies, that is, one in which the compound will be effective. In this context, it is important to remember that many compounds are effective across a wide range of species. Indeed, veterinary medicine applies many of the same therapeutic agents across a diverse range of species, and many of these agents (eg, antibiotics, anti-inflammatory agents, analgesics, and anticancer therapies) are clinically relevant in humans. For a variety of reasons, rodent-based models are the most commonly used models for preclinical efficacy testing. In fact, well over 100 clinically approved anticancer compounds are active in rodent tumor models (http://dtp.nci.nih.gov). Nevertheless, important examples exist in which a compound is effective in a rodent model but not in humans. Potential reasons for such discordant results include 1) differences in the pharmacological behavior of drugs in rodents and humans, 2) toxicological differences between rodents and humans, 3) different growth rates of experimental rodent tumors vs spontaneous human tumors, 4) different tumor burden present in experimental models vs humans, 5) differences in objective measurements of outcomes in preclinical models vs humans, and 6) failure to develop and apply stringent evaluation criteria in the preclinical efficacy models (2,6,10,14,17). Although several of these variables can be identified and resolved during pharmacological and toxicological assessments, it is important to design and interpret the results from preclinical models cautiously to avoid sending inappropriate agents down the development pathway. Because issues of pharmacology, toxicology, and interspecies variations in physiology have been discussed elsewhere (6,10,14,17,19,23,25–27), I focus here on the issues specifically associated with selection of a proper model for preclinical experiments.

Selection of a Proper Tumor Model

The first step in preclinical in vivo efficacy evaluations of a chemotherapeutic agent is the selection of a proper tumor model. Early cancer drug development paradigms used a panel of rodent tumor models that were broadly applied to all test agents, that is, model selection was not drug specific (7,8,10). A number of the classical anticancer agents were therefore developed without a full understanding of their mechanism; they were often found to be broadly active in many rapidly growing tumors because of their nonspecific cytotoxic activity (eg, alkylating agents). Many agents that are now under development, by contrast, have been designed to interfere with a specific molecular target or pathway and thus do not possess broad-spectrum cytotoxic or cytostatic characteristics (5,8,10,14). Therefore, to study these agents it is important to identify a model that is capable of responding to alterations in the target pathway. The selection of an appropriate tumor model is commonly based on in vitro sensitivity profiles of the test agent against a panel of target cells or tumors. Alternatively, expression profiling of a panel of human or rodent tumors or transgenic mice can be used to select a potentially sensitive model (14,28–32).

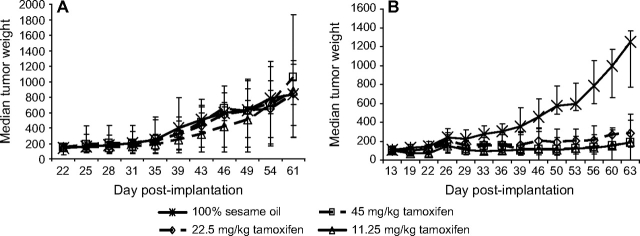
The importance of target (gene or protein) expression for finding antitumor activity can be demonstrated by comparing the effects of the antiestrogen agent tamoxifen on MDA-MB-361 human estrogen receptor (ER)–positive breast cancer xenografts with its effects on MDA-MB-435 ER-negative melanoma (32–34) xenografts. As shown in Figure 1, the growth of MDA-MB-435 xenograft tumors was not inhibited by treatment with tamoxifen, whereas tamoxifen caused marked growth inhibition of the MDA-MB-361 xenograft tumors. The first step in avoiding unnecessary expenditures, as this example shows, is the selection of an efficacy model that is appropriate for the purported mechanism of the test agent—in this case, an antiestrogen would be unlikely to have activity against a tumor that does not express the ER. In addition, for tumors generated from passaged cell lines, it is important to verify the presence of the relevant target in the growing tumors and not just in the cell lines from which they originated, because in vivo cultivation can alter target gene and protein expression through changes in environmental pressures.

Figure 1.

Activity of tamoxifen in human tumor xenografts in mice. A) MDA-MB-435 estrogen receptor–negative melanoma xenografts. B) MDA-MB-361 estrogen receptor–positive breast cancer xenografts. Cells of both lines were implanted orthotopically into the mammary fat pad of athymic nu/nu NCr mice (Animal Production Program, NCI-Frederick), and treatment was initiated when the tumors reached 150–175 mg in size. The MDA-MB-361 tumor-bearing mice were treated weekly with estradiol cypionate (20 μg per mouse) to support tumor growth. Exogenous estradiol is not required for progressive growth of MDA-MB-435 xenografts. For both studies, the vehicle control was 100% sesame oil given by oral gavage once daily for 20 days (n = 20 mice). Tamoxifen was administered by oral gavage once daily for 20 days at a dose of 45, 22.5, or 11.25 mg/kg (n = 10 mice per dose). Individual tumor weights were calculated as weight in mg = (length × width²)/2. Data are plotted as median tumor weight ± the 95% confidence interval of the median.

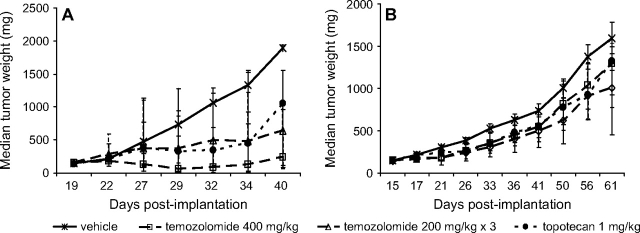
During preclinical efficacy testing, prior knowledge of the sensitivity of the potential tumor models to clinically approved agents is also helpful. This information may strengthen the conclusion that activity in the model reflects the potential for activity in humans; more importantly, this information supports the expectation that the tumor can respond to chemotherapeutic intervention. For example, two clinically approved anticancer agents, temozolomide and topotecan, are effective against A375 melanoma xenograft tumors (temozolomide at a single dose of 400 mg/kg body weight or at three doses of 200 mg/kg, and topotecan at 1 mg/kg on a multidose schedule), whereas both agents are ineffective against human Colo 829 melanoma xenografts at the same doses (Figure 2). During the initial evaluation of a new anticancer agent, it is most productive to select a sensitive model (eg, A375 melanoma) for initial dose, route, and schedule studies and then to evaluate an optimized treatment protocol in more resistant models (eg, Colo 829 melanoma) as part of a sequential efficacy assessment paradigm.

Figure 2.

Activity of temozolomide and topotecan in human tumor xenografts. A) A375 melanoma xenografts. B) Colo 829 melanoma xenografts. Cells of both lines were implanted subcutaneously in female athymic nude (nu/nu NCr) mice (Animal Production Program, NCI-Frederick). Treatment was initiated when the tumors reached 150 mg. Temozolomide was administered by oral gavage as a single dose of 400 mg/kg or as three 200-mg/kg doses given 4 days apart (temozolomide 200 mg/kg × 3) (n = 10 mice per dose group). Topotecan was administered intraperitoneally at 1 mg/kg 5 days per week for 2 weeks (n = 10). The vehicle control group (n = 20) was treated with three doses of saline given 4 days apart. Individual tumor weights were calculated as weight in mg = (length × width²)/2. Data are plotted as median tumor weights ± 95% confidence interval.

Experimental Design Considerations

Selection of a sensitive model is an important first step in carrying out appropriate in vivo efficacy testing; however, developing a good experimental design is also of paramount importance because a poorly designed experiment results in a poorly supported conclusion (10). Important experimental design components include defining the proper controls, treatment protocols, group sizes, and randomization protocols. If these parameters are not considered, the efficacy of a new chemotherapeutic agent may be either over- or underestimated. It is also important to consider the potential impact of the compound formulation on experimental outcomes because of the possibility that the formulation itself may have direct effects on the tumor or the host (eg, unexpected toxic effects). Generally, test compounds are formulated in a carrier or diluent that is believed to be inert and is referred to as the drug vehicle. However, it is possible for the vehicle to be biologically active or to have an unexpected toxicity profile, particularly if new vehicle formulations are developed for the agent undergoing evaluation. Furthermore, experimental manipulation of animals induces a stress response that can alter the experimental outcome. Therefore, vehicle-treated animals should be used as experimental controls instead of untreated animals, even though doing so increases the total number of experimental animals that must be administered treatments during the experiments.

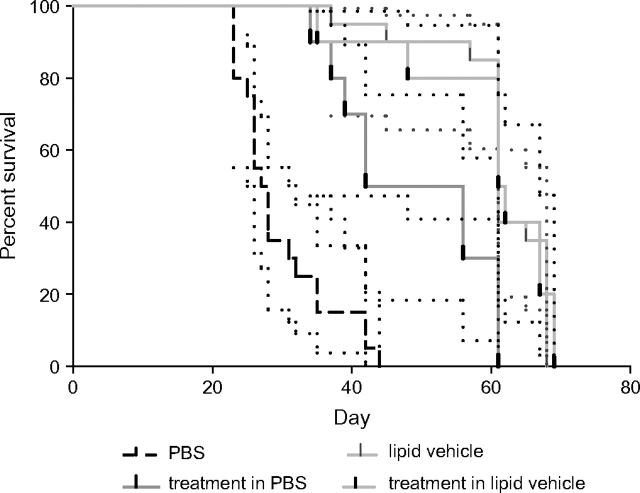
An example of how the selection of an appropriate vehicle and the inclusion of proper vehicle controls are critical to preventing misinterpretation is provided by data from a study in which a therapeutic agent directed against a target expressed in OVCAR-5 human ovarian tumor xenografts was evaluated for tumor growth inhibition (Figure 3). Because the therapeutic agent was found to have the best in vitro activity profile when it was prepared in a lipid-based vehicle, that vehicle was used for administering the drug in the in vivo study. In addition, the therapeutic agent was solubilized in phosphate-buffered saline (PBS) for comparison. In a Kaplan–Meier survival analysis (Figure 3), the lipid-based vehicle alone was as effective at improving survival as the therapeutic agent prepared in it. Furthermore, the vehicle alone was more effective than the therapeutic agent prepared in PBS. If this study had used only untreated or PBS-treated control animals, then the agent would have been assigned greater activity than it actually had. In addition to showing the importance of selecting an appropriate vehicle and including proper vehicle-treated control animals, this example shows the importance of providing the specific details of the control animals as part of the presentation of the experimental data, so that the reader can properly assess the experiment.

Figure 3.

Kaplan–Meier analysis of survival of athymic nude mice bearing intraperitoneal OVCAR-5 human ovarian cancer xenografts. Mice were nu/nu NCr (Animal Production Program, NCI-Frederick). The therapeutic agent was administered at a dose of 1 mg per mouse given intraperitoneally once every other day, for a total of seven doses (n = 10 mice per group) using two different vehicles (lipid vehicle and phosphate-buffered saline [PBS]). The lipid vehicle (n = 20 mice) and PBS (n = 20 mice) were used in separate vehicle control groups following the same dosing schedule. Mice were treated with vehicle alone or with one of the therapeutic agents solubilized in the vehicles. Dotted lines indicate 95% confidence intervals.

Development of a Treatment Plan

Selection of a model and the relevant controls should be straightforward; however, the options for a treatment protocol are limited only by the imagination of the operator. Several important factors should be considered when developing a treatment plan. The most important consideration is whether the experimental agent will be physiologically available to the tumor. Bioavailability is affected by several factors, including the tumor growth site and vascularization of the tumor and surrounding tissues, the vehicle and treatment route, the solubility and stability of the test material, and the uptake, metabolic, and excretion pathways that affect the agent (6,10,14,17). A second critical consideration is the required therapeutic exposure; that is, what is the minimum exposure time required for the agent to affect the tumor cells, and is that effect reversible or irreversible? For example, if a minimum exposure of 48 hours is required to modulate the target, then a single dose of test agent will be unlikely to inhibit tumor growth unless the agent has a long in vivo half-life. Although biologic agents (eg, antibodies) often have long half-lives, most small molecules have short half-lives, particularly in rodents (5). Conversely, a test agent may have a rapid effect on the target, but if that effect is reversible, then antitumor activity will be lost rapidly unless repeated treatments are given.

During development of a treatment protocol, therefore, it is essential to give serious consideration to the likelihood that the tumor will have sufficient exposure to the test agent under the experimental conditions selected. Otherwise, a potentially valuable test agent may be discarded as ineffective during in vivo efficacy studies. A classic example is provided by the early work conducted with paclitaxel (35). In initial studies, paclitaxel was administered intraperitoneally as a suspension in saline rather than as a solution. Activity was modest in these early studies, and the compound was not actively pursued for several years, until subsequent studies using a different vehicle (cremophor, ethanol, and saline) and an intravenous route of administration revealed profound antitumor activity against a wide variety of tumor models (35). The dependence of paclitaxel’s activity on the route of administration was ultimately explained when pharmacology studies unequivocally demonstrated a failure of systemic distribution following intraperitoneal administration (36). It is sobering to consider the impact of losing a compound, such as paclitaxel, that has substantial antitumor activity because of poor experimental design or failure to appreciate the issues associated with its particular biology.

Treatment protocols must have a clear basis for selecting doses and schedules for test agent administration. The goal may be 1) to achieve a target plasma concentration, 2) to maintain a minimum exposure time, or 3) to administer the maximum amount of test agent that does not cause unacceptable toxicity. Therapeutic protocols for anticancer drugs have often depended on the maximum tolerated dose to define the treatment dose and schedule (17). Although this approach may be successful with cytotoxic drugs, it may be less appropriate when assessing cytostatic or target-modulating agents (19,37). These agents are expected to require long-term continuous exposure of the tumor and would likely require similar dosing in humans; thus, administering them at a near-toxic dose is undesirable because it could lead to over-interpreting the activity of the compound, given that comparable doses would be unlikely in humans. Furthermore, target-modulating agents are expected to be of low toxicity because of their specificity. Thus, administration at the maximum tolerated dose would be expected to greatly exceed the necessary exposure, leading to unnecessary consumption of the test agent and thereby increasing the overall costs of testing. For agents with few toxic effects, treatment schedules may be developed using pharmacological endpoints such as plasma concentration and exposure time (19). Whether toxic effects or pharmacologic endpoints define the therapeutic doses and schedules, the conclusions drawn from a particular study are relevant only for the treatment conditions used in the assay. It is essential for the proper interpretation of in vivo therapeutic data that the treatment parameters be provided along with an explanation for their selection because this information is critical to a full understanding of the meaning of the experimental outcomes.

Another consideration in the experimental design is the number of test animals per group. This is another critical feature of efficacy studies because too few animals can result in questionable or invalid results, whereas excessive numbers of animals add costs without producing commensurate benefit. Recommendations from a statistician about the minimum number of animals necessary to achieve appropriate statistical power during development of the experimental protocol can greatly improve the experimental design. If a statistician is not available, then a power calculator should be used to determine the minimum group sizes required to detect differences in measurable outcomes (eg, tumor size, life span) between groups. Such power calculations may be of particular benefit when designing experimental protocols for tumor models in transgenic mice, because these models are heterogeneous in their frequency and time of tumor occurrence. Finally, it is important to determine group sizes based on the efficacy model that is being used rather than relying on the replicate sample paradigm that is typical of in vitro assays, which generally results in groups of insufficient size.

For power calculations, one must know the expected mean values and SDs for the experimental endpoint that is being assessed (eg, tumor size, survival time, target protein expression level). These values can be determined from historical data or from preliminary experiments. For example, growth data (M. G. Hollingshead, unpublished data) for subcutaneous MDA-MB-361 tumors grown from an inoculum of 1 × 10⁷ cells in 0.1 mL given to each of six mice revealed tremendous variability in tumor growth among the mice (Table 1); these data suggest that the subcutaneous MDA-MB-361 tumor xenograft is not an ideal model for studying the therapeutic efficacy of antitumor agents. Using a commercially available power calculator (GraphPad StatMate 2, GraphPad Software, La Jolla, CA), the 95% confidence interval (CI) for the tumor growth data at day 68 (SD of 1401 mg) indicates that achieving a statistically significant difference in tumor growth between two groups would require a difference of 5246 mg if n = 3 mice per group, 3629 mg if n = 5 mice per group, 2945 mg if n = 7 mice per group, 2543 mg if n = 9 mice per group, and 2164 mg if n = 12 mice per group. By contrast, the same cell line inoculated into the mammary fat pad produced tumor growth data with much less variability (Table 2). In this instance, the SD in tumor growth at day 68 was 301 mg. The power calculation for this model indicates that statistically significant differences in tumor growth between the two groups would require a difference of 1127 mg if n = 3 mice per group, 780 mg if n = 5 mice per group, 633 mg if n = 7 mice per group, 546 mg if n = 9 mice per group, and 465 mg if n = 12 mice per group. Thus, intragroup tumor heterogeneity profoundly affects the group size necessary to determine the statistical significance of the difference in tumor growth and should be considered before a tumor model is selected and the experiment is designed. Due to the expense of including sufficient animals to conduct statistically powerful preclinical efficacy studies, many such studies include too few mice, yielding at best an experiment with minimum value and at worst, one with misleading conclusions. These underpowered experiments not only add to the final costs of drug development but also contribute data to reinforce the argument that preclinical models are not predictive of clinical outcomes.

Table 1.

Actual weights of MDA-MB-361 tumors grown subcutaneously in athymic nude (nu/nu Ncr) mice^*

	Experimental day
	5	8	11	15	19	26	29	33	36	40	43	47	54	61	68
Absolute  weight, mg
Mouse 1	14	63	63	63	63	63	63	63	63	75	75	148	211	307	325
Mouse 2	14	14	14	14	14	14	14	14	14	14	14	14	14	63	63
Mouse 3	14	14	14	14	14	14	14	14	63	63	63	81	144	253	425
Mouse 4	14	14	14	14	14	63	63	63	108	158	196	343	666	1276	1744
Mouse 5	14	63	63	63	63	63	81	106	144	343	496	817	1310	2588	3752
Mouse 6	14	14	14	14	14	14	14	14	14	63	63	81	208	425	600
Median tumor weight	14	14	14	14	14	38	39	39	63	69	69	115	210	366	513
Average tumor weight	14	30	30	30	30	38	42	46	68	119	151	247	425	819	1151
SD of average	0	25	25	25	25	27	31	38	51	119	180	301	486	964	1401
SD of median	0	31	31	31	31	27	31	39	52	131	201	334	541	1084	1566
t test vs day 68 values	.07	.08	.08	.08	.08	.08	.08	.08	.09	.10	.11	.15	.26	.64	NA
Relative weight†
Mouse 1	1.0	4.5	4.5	4.5	4.5	4.5	4.5	4.5	4.5	5.4	5.4	10.6	15.1	21.9	23.2
Mouse 2	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	4.5	4.5
Mouse 3	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	4.5	4.5	4.5	5.8	10.3	18.1	30.4
Mouse 4	1.0	1.0	1.0	1.0	1.0	4.5	4.5	4.5	7.7	11.3	14.0	24.5	47.5	91.1	124.6
Mouse 5	1.0	4.5	4.5	4.5	4.5	4.5	5.8	7.6	10.3	24.5	35.5	58.3	93.6	184.8	268.0
Mouse 6	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	1.0	4.5	4.5	5.8	14.9	30.4	42.9
Average	1.0	2.2	2.2	2.2	2.2	2.7	3.0	3.3	4.8	8.5	10.8	17.7	30.4	58.5	82.2
SD	0.0	1.8	1.8	1.8	1.8	1.9	2.2	2.7	3.7	8.5	12.8	21.5	34.7	68.8	100.1

^*Tumor weights were calculated as tumor weight (mg) = (tumor length × tumor width²)/2. Tumors that are shown as weighing 14 mg were estimated as being 3 × 3 mm because they were palpable but too small to be accurately measured with calipers. NA = not applicable.

^†Relative tumor weight = (day T weight/day 5 weight), where day T is each time point beyond the day-5 starting mass.

Table 2.

Actual weights of MDA-MB-361 tumors grown in the mammary fat pad of athymic nude (nu/nu Ncr) mice^*

	Experimental day
	13	19	22	26	29	33	36	39	46	50	53	56	60	63
Absolute weight, mg
Mouse 1	108	117	148	208	196	196	272	343	466	625	756	893	1008	1367
Mouse 2	117	117	117	221	221	361	320	361	225	320	336	425	662	972
Mouse 3	158	225	253	325	288	385	385	550	696	726	756	1055	1172	1310
Mouse 4	108	144	225	361	320	338	416	675	972	1080	1172	1328	1044	1458
Mouse 5	75	98	117	196	225	288	325	429	550	575	600	787	1133	1268
Mouse 6	88	106	126	304	288	239	253	288	320	336	352	425	525	689
Mouse 7	98	117	126	239	225	325	343	405	726	787	893	1268	1458	1504
Mouse 8	125	125	180	211	245	245	336	336	425	486	564	756	847	992
Mouse 9	126	135	144	190	190	201	233	281	336	397	397	650	675	772
Mouse 10	144	144	196	405	405	446	486	564	650	847	926	1080	998	1289
Mouse 11	81	153	153	336	320	272	272	272	325	525	525	550	600	600
Mouse 12	135	272	272	425	361	474	662	725	625	787	817	1044	1172	1248
Mouse 13	81	117	117	225	208	208	208	253	384	662	600	600	756	893
Median	108	125	148	239	425	288	325	361	466	625	600	787	998	1248
Average	111	144	167	280	269	306	347	422	515	627	669	835	927	1105
SD	26	50	54	83	68	92	122	158	211	220	247	303	275	301
SD of the median	26	54	57	93	72	94	124	170	217	220	257	307	285	336
t test vs day-63 values	<.001	<.001	<.001	<.001	<.001	<.001	<.001	<.001	<.001	<.001	<.001	.0323	.129	NA
Relative weight†
Mouse 1	1.0	1.1	1.4	1.9	1.8	1.8	2.5	3.2	4.3	5.8	7.0	8.3	9.3	12.7
Mouse 2	1.0	1.0	1.0	1.9	1.9	3.1	2.7	3.1	1.9	2.7	2.9	3.6	5.7	8.3
Mouse 3	1.0	1.4	1.6	2.1	1.8	2.4	2.4	3.5	4.4	4.6	4.8	6.7	7.4	8.3
Mouse 4	1.0	1.3	2.1	3.3	3.0	3.1	3.9	6.3	9.0	10.0	10.9	12.3	9.7	13.5
Mouse 5	1.0	1.3	1.6	2.6	3.0	3.8	4.3	5.7	7.3	7.7	8.0	10.5	15.1	16.9
Mouse 6	1.0	1.2	1.4	3.5	3.3	2.7	2.9	3.3	3.6	3.8	4.0	4.8	6.0	7.8
Mouse 7	1.0	1.2	1.3	2.4	2.3	3.3	3.5	4.1	7.4	8.0	9.1	12.9	14.9	15.3
Mouse 8	1.0	1.0	1.4	1.7	2.0	2.0	2.7	2.7	3.4	3.9	4.5	6.0	6.8	7.9
Mouse 9	1.0	1.1	1.1	1.5	1.5	1.6	1.8	2.2	2.7	3.2	3.2	5.2	5.4	6.1
Mouse 10	1.0	1.0	1.4	2.8	2.8	3.1	3.4	3.9	4.5	5.9	6.4	7.5	6.9	9.0
Mouse 11	1.0	1.9	1.9	4.1	4.0	3.4	3.4	3.4	4.0	6.5	6.5	6.8	7.4	7.4
Mouse 12	1.0	2.0	2.0	3.1	2.7	3.5	4.9	5.4	4.6	5.8	6.1	7.7	8.7	9.2
Mouse 13	1.0	1.4	1.4	2.8	2.6	2.6	2.6	3.1	4.7	8.2	7.4	7.4	9.3	11.0
Average	1.0	1.3	1.5	2.6	2.5	2.8	3.2	3.8	4.8	5.8	6.2	7.7	8.7	10.3
SD	0.0	0.3	0.3	0.8	0.7	0.7	0.8	1.2	2.0	2.2	2.3	2.8	3.1	3.3

^*Tumor weights were calculated as tumor weight (mg) = (tumor length × tumor width²)/2. NA = not applicable.

^†Relative tumor weight = (day T weight/day 13 weight), where day T is each time point beyond the day 13 starting mass.

In an ideal model, the tumor size distribution at any given observation time will be extremely small, so that subtle differences among groups will be easily detected and statistically significant. Unfortunately, rodent models, whether spontaneous (eg, transgenic) or transplanted, do not result in uniform tumor growth among all tumor-bearing animals. One way to reduce the impact of this variability is to create a large population of tumor-bearing mice and then select a homogeneous subset for randomization into the experimental groups. This approach, referred to as staging the tumor, allows the investigator to select a group of mice whose tumors are homogeneous so that differences in tumor size and age are initially minimized and distributed randomly to each treatment group.

Another often overlooked but important consideration in animal efficacy studies is proper randomization. If animals are assigned to groups on the basis of a biased selection factor rather than a randomization protocol, then the consequence will be experimental bias. For example, in tumor models in which the tumor is generated by implantation of tumor cells or tumor fragments, the inoculum is subject to time-dependent changes in viability, with the result that time to tumor occurrence, initial tumor size, and tumor growth rate will differ between animals implanted at the beginning of the procedure and those inoculated later in the process. If animals are assigned to groups on the basis of inoculation sequence (eg, first six mice to group 1, second six mice to group 2, and so on) instead of randomly, the result will be skewed outcomes. Operator fatigue is also a consideration, particularly with complex or difficult experimental designs (eg, those requiring surgical or intravenous tumor cell inoculation), and the impact of such operator-related bias should therefore be addressed by randomly assigning animals across the experimental groups. With transgenic mice that develop genetically induced tumors and with tumor models that are induced by exposure to chemical carcinogens (eg, skin tumor induction by painting with 7,12-dimethylbenz[a]anthracene and phorbol 12-myristate 13-acetate), there may be heterogeneity in the responses of different litters and age groups that should be considered during protocol development. The use of simple computer programs to randomize animals can avoid this experimental bias without burdening the investigator. The randomization method should be routinely reported as part of a properly described animal model experiment.

Choice of Endpoints

One goal of preclinical tumor models is to define the effect of an experimental treatment on the tumor. This goal requires the selection of an endpoint or set of endpoints. Endpoints should be defined in the experimental design, because selecting the endpoints based on experimental outcomes provides another opportunity to introduce bias. The two most common endpoint categories are antitumor activity and modulation of molecular targets.

Antitumor effectiveness can be defined in various ways, but the ultimate goal of any treatment is to decrease tumor burden, decrease tumor-associated morbidity, improve quality of life, and, where possible, lengthen life span, irrespective of the host species. To reproducibly measure efficacy, response to treatment must be assessed by a set of objective parameters (10,14,15,19,23). Human clinical responses can be defined in several ways. Obviously, the primary goal of cancer therapy is to improve long-term survival while maintaining the patient's quality of life. However, this outcome is difficult to assess in the short term because patients represent a heterogeneous population with a heterogeneous collection of diseases. More commonly, therefore, clinical trials assess time to disease progression, objective response rates, surrogate markers, and quality of life parameters (38). Although not all of these outcomes translate directly to the preclinical models, they do offer an opportunity to define endpoints that may ultimately have clinical relevance (7,10,11).

A variety of endpoints for subcutaneous tumor models have been described in the literature and applied by pharmaceutical companies in their drug development pathway. Within the Developmental Therapeutics Program of the US National Cancer Institute (http://dtp.nci.nih.gov), endpoints for subcutaneous tumors include percent test/control (%T/C) tumor weights calculated on each day that tumors are measured, tumor growth delay, net log cell kill, median days to a defined tumor weight or to a specified number of tumor doublings, and tumor regression (7,11). The lowest calculated %T/C seen over time is defined as the optimal %T/C because it defines the greatest level of activity seen with the test agent. Many pharmaceutical companies use similar endpoints (10,20,39–41). The rate and duration of partial and complete tumor regressions are also considered to be clinically relevant endpoints (42,43), and tumor growth delay serves as a surrogate for disease progression.

The endpoints described here for subcutaneous tumors are calculated based on tumor mass as determined from caliper measurements of the length and width of the subcutaneous tumors. These measurements are subject to operator error and are commonly inaccurate for tumors smaller than 5 mm in either dimension, particularly on haired mice, because the thickness of mouse skin varies among mice and even across the surface of a single mouse and can variably affect caliper measurements. Because of the variability associated with caliper measurements of tumors smaller than 5 × 5 mm, tumor weights of less than 63 mg are unreliable and should be considered suspect when comparing tumor mass (11). In addition, because caliper measurements are operator dependent, it is important that the same operator measure the tumors throughout the course of the experiment. Finally, if the operator can be blinded to the experimental treatment group assignments, there is an even greater reduction in experimental bias.

For tumor models in which tumors grow in sites other than the subcutaneous compartment, an alternate means of tumor measurement must be identified before the therapeutic protocol is initiated. During protocol development, the accuracy and reproducibility of the endpoint measurements must be considered so that the data are properly collected and analyzed. For example, if tumors are to be resected and physically weighed, then the same criteria must be used for determining tumor borders in each mouse, irrespective of whether it was treated with vehicle or test agent. Another important variable is the accuracy of the balance used to weigh the tissues. To remove resection bias, tumors growing within organs can be assessed by resecting and weighing the entire organ. This approach should be used only if an adequate period of time has elapsed between tumor inoculation and measurement so that there is a sufficient tumor mass to provide statistically valid differences between treatment groups. Alternatively, visceral lesions can be assessed by histopathologic evaluation and manual or automated quantitation of the number or volume of lesions. In cases where multiple metastatic lesions occur, quantifying the number and size of lesions may provide an unbiased endpoint. The number of microscopic lesions is a common endpoint for models in which lung or liver metastases are present, such as the murine tumors Lewis lung, B16 melanoma, and M5076 sarcoma (39).

It is worth noting that new imaging technologies (eg, bioluminescence, ultrasound, magnetic resonance imaging) are providing improved, highly sensitive methods for assessing visceral tumor growth that may supplement many of the classical tumor assessments. These technologies also have limitations in that not all of them are equally valuable for all tumor growth sites and, in many cases, the endpoints have not been fully validated. For example, ultrasound can be used to assess tumors growing in the kidney but is not optimal for lesions in the lung (44). For various imaging endpoints, the operator defines the tumor margins when selecting the region of interest for measurement. As stated earlier, the importance of selecting a reproducible, unbiased endpoint is essential because the data generated may be used to make critical drug development decisions. Therefore, when using these technologies for assessing tumor growth, the methods used to define the tumor should be well characterized, reproducible, nonbiased, and validated.

All of these considerations are important to conducting nonbiased experiments; however, the value of the experiment to the research community depends on how the data are presented. Even with staged tumors, growth heterogeneity—particularly for human tumor xenografts—is unavoidable. This heterogeneity led the Developmental Therapeutics Program as well as many pharmaceutical companies to select the group median, rather than the group average, tumor weight for calculation of endpoints (7,8,10,11,20,40,41). The use of the median reduces the impact of an outlying tumor weight on the overall interpretation of the data. For most readers, it is easiest to understand tumor growth data if weights, whether graphed as medians or averages, are presented for each treatment group rather than as a calculated percent of control or starting tumor weight (ie, relative tumor weight). With graphs that show median or average tumor weights, the reader knows the actual tumor weights when treatment was initiated and terminated as well as the continued tumor behavior following cessation of treatment (15). By contrast, when tumor weight data are presented as relative weights, it is more difficult for an observer to assess the real impact of treatment on the tumor. For example, a tumor that is 200% of its starting weight could be 40, 200, or 2000 mg, depending on whether the starting tumor weight was 20, 100, or 1000 mg. Thus, when data are displayed as a relative tumor weight, the observer cannot determine whether the tumor is below the limit of accurate measurement for the assessment method employed. Furthermore, the true impact of treatment on the tumor is more obvious when median or average tumor weights, rather than calculated percentages, are presented visually, because the observer can determine the change in tumor size in terms of actual tumor weight.

Whether average or median tumor weights are presented, the SD, SE, or 95% CI should be provided so that intra- and intergroup variations can be easily ascertained. Although the SE of the median is less commonly encountered, it is defined as 1.253 times the SE of the average (45), which is a common parameter. The 95% CI of the average is also a commonly used parameter; it is easily calculated by standard software programs (eg, Microsoft Excel, GraphPad Prism). Although the 95% CI of the median is less commonly calculated, it can be estimated by ranking the experimental values and then identifying the relevant upper and lower CI values based on their positions in the ranking. Tables for assigning the 95% CI values of the median based on the experimental group size have been published (47,48).

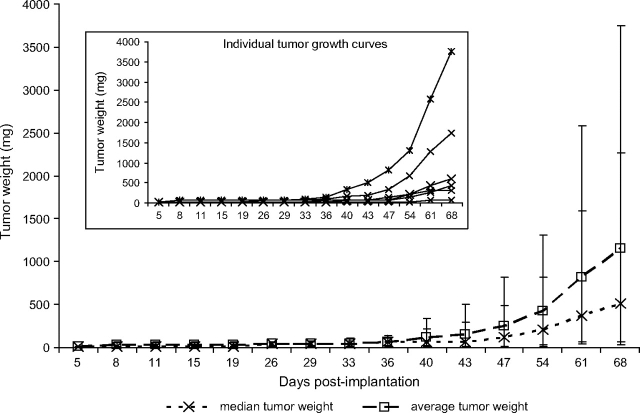
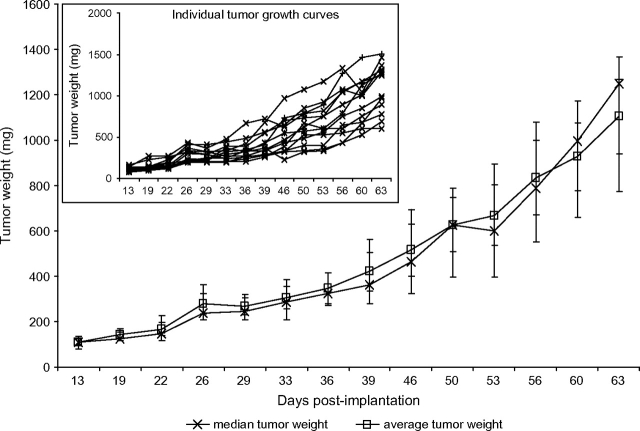
Data (M. G. Hollingshead, unpublished data) from the commonly used MDA-MB-361 subcutaneous tumor model illustrate a number of these issues. For example, an analysis of individual tumor weights for six tumors (Table 1) shows that at day 68 after implantation, the tumors showed substantial size heterogeneity, ranging from 63 to 3752 mg. The median tumor weight was 513 mg on day 68, and the average was 1151 mg. Examination of the individual tumor weights shows that the largest tumor (3752 mg) skewed the average tumor weight upward, whereas the median tumor weight tracked better with the individual tumor weights (Figure 4).

Figure 4.

Tumor weight plots for MDA-MB-361 human breast tumors implanted subcutaneously in athymic nude mice. The data are from Table 1. The main graph presents the median and average tumor weights for a group of six mice (nu/nu Ncr; Animal Production Program, NCI-Frederick), each implanted with 1 × 10⁷ cells in 0.1 mL. The inset presents the individual growth curve for each of the six mice. Individual tumor weights were calculated as weight in mg = (length × width²)/2. The error bars indicate the 95% confidence intervals of the averages or the medians, as appropriate.

The importance of using a homogeneous tumor model is further demonstrated by the P values obtained from t tests comparing each day's tumor weights with the day 68 tumor weights (Table l). With this highly heterogeneous model, the difference between the daily tumor weights never achieved a statistical significance level of .05. Thus, as seen here and in the power calculations described earlier, a tumor model with this degree of heterogeneity could not demonstrate a statistically significant difference, even when compared with the smallest possible tumor size (eg, the starting size of 14 mg). By contrast, data from MDA-MB-361 tumors grown in the mammary fat pad and staged to a starting median tumor weight of approximately 100 mg (Table 2) yielded a tumor size range on day 63 of 600–1504 mg across 13 mice. Although this range is large, the median and average tumor weights (1248 and 1105 mg, respectively) are consistent with each other. Moreover, in contrast to the heterogeneous tumor example, the median and average tumor growth curves (Figure 5) are similar and track well with the individual tumor data. Furthermore, the t test comparisons of tumor weights on day 63 with those on all the other measurement days indicate that the differences are statistically significant at multiple time points. This pattern is consistent with the power calculations described earlier, which had indicated that there was a 50% probability that group sizes of 12 would allow detection of a statistically significant difference between groups if their averages varied by 253 mg. In the example given here, a statistically significant difference was found between the day-53 and day-63 data points, with a P value of .03 and a difference in group averages of 263 mg.

Figure 5.

Tumor weight plots for MDA-MB-361 human breast tumors implanted in the mammary fat pads of athymic nude (nu/nu Ncr; Animal Production Program, NCI-Frederick) mice. The data are from Table 2. The main graph presents the median and average tumor weights for a group of 13 mice, each implanted with 1 × 10⁷ cells in 0.1 mL. The inset presents the individual growth curves for each of the 13 mice. Individual tumor weights were calculated as weight in mg = (length × width²)/2. The error bars are the 95% confidence interval of the average or the median, as appropriate.

Analysis of the individual and average relative tumor weights for these datasets indicates that relative tumor weights can be misleading because they do not provide insight as to the starting tumor mass. For example, the average 4.8 relative tumor weight on day 36 was 3.2 for subcutaneous MDA-MB-361 tumors (Table 1) suggests robust tumor growth. However, the initial tumor weight was 14 mg and the average and median tumor weights on day 36 were only 68 and 63 mg, respectively, which demonstrate that very little tumor growth occurred. Furthermore, the actual tumor weights indicate that the day 36 tumor size was just above the minimum size that can be reliably measured with calipers. By contrast, the relative tumor weight on day 36 was 3.8 for MDA-MB-361 cells implanted in the mammary fat pad (Table 2), and the median and average tumor weights were 325 and 347 mg, respectively. So, whereas comparing the day-36 relative tumor weights between Tables 1 and 2 would suggest that subcutaneously implanted MDA-MB-361 tumors grew more robustly than the same tumors in the mammary fat pad, comparisons of the median and average tumor weights indicate that tumors implanted in the mammary fat pad actually grew more quickly (Table 2).

Appropriate Statistical Evaluation of Tumor Growth Data

Along with the specifics of the experimental protocol, efficacy data should use appropriate statistical evaluations to analyze the differences between the treated and control groups. The statistical tests used will vary with the experimental model, design, and endpoints collected (45). Many methods for selecting a relevant statistical test exist, but the best approach is to seek the assistance of a qualified statistician during the development of the experimental design. Alternatively, commercially available statistical analysis packages provide assistance to the investigator if a statistician is not available. In either case, selecting the statistical evaluation criteria for analyzing the data and defining the criteria for excluding outlying data points before conducting the experiment will remove the temptation to interpret the data in a manner that best supports the original hypothesis. An obvious example of this type of bias occurs when tumors that do not grow in the control group are excluded from the analysis because the operator expected them to grow, whereas tumor-free animals in the treated groups are included because the operator expected the treatment to work. Using a statistical test to identify which outliers should be excluded prevents this type of operator bias.

When selecting the statistical evaluation to be used for a dataset, the first criterion is whether the data have a normal or non-normal distribution. For normally distributed data, parametric tests such as the t test and analysis of variance are likely applicable. By contrast, non-normally distributed data generally require nonparametric tests such as the Wilcoxon, Mann–Whitney, or Kruskal–Wallis tests (46). The specific data to be analyzed will depend on the experimental design. For example, a tumor growing viscerally (eg, in the liver or kidney) may have only a single time point for data collection because the animal may have to be killed to collect and measure the tumor. By contrast, subcutaneously growing tumors have data from multiple time points. A common approach is to assess the statistical significance of differences in tumor size at each of the data collection times and to report the difference at the optimal time point. However, it is important to clarify that the statistical comparison presented is based on data for the optimal time point. A better approach is to present all of the data, along with the statistical differences found at each time point. If data for only a single time point are presented, then an explanation of how that time point was selected—whether because the differences were greatest then or for some other reason—should be provided.

When serial tumor growth data, such as for subcutaneously implanted tumors, are available, an alternative to presenting data for one or more individual time points is to compare the slopes of the tumor growth curves. Such slopes can be calculated readily with commercially available software programs. Although this data presentation method is not commonly used, it allows a statistical comparison of the growth rates for each of the experimental tumors, provided the tumor growth curves are reasonably monophasic. For example, using the data presented graphically in Figure 1, B, for MDA-MB-361 tumor xenografts, the average of the slopes for the vehicle control is 17.3 and that of the 45 mg/kg tamoxifen group is 0.78. The P value from the t test comparison of these slopes is less than .001. By contrast, the vehicle control group for MDA-MB-435 shown in Figure 1, A, had an average tumor growth slope of 20.2, whereas the group treated with 45 mg/kg tamoxifen had an average slope of 21.9, and the P value from the t test comparison of the slopes was .62. This approach is less valuable for tumors with multiphasic growth curves because the slope of the curve from the first to the last tumor measurement is not uniform.

When the experimental endpoint is modulation of molecular markers, then the investigator must determine which samples will be collected and analyzed. Valid samples may include tumor tissue, surrogate tissue (eg, spleen, bone marrow, skin), serum or plasma. Whatever the sample, a critical consideration in the experimental design is the timing of sample collection following exposure to the test agent. The method of collecting and storing the sample may also be critical to a reliable outcome because many markers are unstable and subject to change as a result of experimental conditions (37,49). Performing assay optimization studies before conducting definitive therapeutic protocols will allow the collection method (eg, cryobiopsy, standard needle biopsy, and full or partial tumor resection) to be defined scientifically. In addition, the required sample size (amount of tissue needed to conduct the study) must be considered, along with the impact of the stability of the endpoint on the sample collection methodology. Part of the decision regarding sampling methods must consider the impact of pre- vs postmortem sampling, because some targets may be stable for several minutes postmortem, whereas others may degrade rapidly when respiration and perfusion cease.

If the endpoint being assessed is volatile or easily induced by stress or other manipulation of the host, then sample collection under general anesthesia (eg, using inhalation anesthetics such as isoflurane) may provide a higher quality, clinically relevant sample. Samples preserved in situ by cryobiopsy can be collected with commercially available clinical instruments such as the Cassi cryobiopsy needle. If in situ freezing is not required, then samples obtained by needle biopsy or resection can be placed into liquid fixative (eg, 10% neutral-buffered formalin and RNALater, Ambion, Austin, TX), flash frozen by transfer into a prefrozen cryovial, or stored in another appropriate manner. Whichever method is selected, it must be used consistently both within and across sample groups (37,49). The impact of operator fatigue should also be considered if large numbers of samples must be collected, so that the relative time of collection does not influence the results and subsequent conclusions.

Concluding Thoughts

The conclusions drawn from a series of studies are only as good as the data on which they are based. The impact of high-quality experimental design, methodology, and data interpretation cannot be overstated. To allow others to properly interpret the results of an in vivo efficacy study, it is important to provide a clear explanation of the experimental design, a reasonable overview of the data, and a scientifically justified interpretation of the data. Moreover, if appropriate consideration is given to the experimental design before animal studies are initiated, the number of animals used may ultimately be reduced, because multiple experiments may not be required. Along with a savings in animals there will likely be a concomitant savings in costs and time, contributing to an overall reduction in drug development costs. Conversely, poorly conducted experiments can produce misleading data that result in unnecessary additional studies that consume time, animals, and other resources. Although this in itself is wasteful and adds to the overall cost of drug development, perhaps the greater risk is the diversion of these important resources onto a fruitless course while other, better leads languish owing to a lack of resource availability.