Abstract
We are working to develop beating-heart atrial septal defect (ASD) closure techniques using real-time 3D ultrasound guidance. The major image processing challenges are the low image quality and the processing of information at high frame rate. This paper presents comparative results for ASD tracking in time sequences of 3D volumes of cardiac ultrasound. We introduce a block flow technique, which combines the velocity computation from optical flow for an entire block with template matching. Enforcing adapted similarity constraints to both the previous and first frames ensures optimal and unique solutions. We compare the performance of the proposed algorithm with that of block matching and region-based optical flow on eight in-vivo 4D datasets acquired from porcine beating-heart procedures. Results show that our technique is more stable and has higher sensitivity than both optical flow and block matching in tracking ASDs. Computing velocity at the block level, our technique tracks ASD motion at 2 frames/s, much faster than optical flow and comparable in computation cost to block matching, and shows promise for real-time (30 frames/s). We report consistent results on clinical intra-operative images and retrieve the cardiac cycle (in ungated images) from error analysis. Quantitative results are evaluated on synthetic data with maximum tracking errors of 1 voxel.
Keywords: real-time ultrasound, echocardiography, atrial septal defect, tracking, mutual information, block matching, optical flow, block flow
1. INTRODUCTION
Atrial septal defects (ASD) are congenital heart malformations consisting of openings in the septum between the atria. This allows blood to shunt from the left atrium into the right atrium, which decreases the efficiency of heart pumping. Secundum-type ASD has been reported to account for up to 15% of congenital heart malformations (Benson and Freedom, 1992). Although the surgical intervention for ASD closure is well established and has excellent prognosis, it is performed under cardiopulmonary bypass (CPB), which has widely acknowledged harmful effects.
Recent studies have highlighted the practicability of minimally invasive image-guided beating-heart ASD closure. The patient rehabilitation is improved by avoiding the use of CPB. A compelling review of image-guided surgical applications can be found in (Peters, 2006). There are two alternatives for minimally invasive ASD closure procedures: one using a catheter-based closure, usually under contrast-enhanced fluoroscopy (Faella et al., 2003; Papadopoulou et al., 2005); and another using rigid instruments through the chest wall (Suematsu et al., 2004), demonstrated in animals. Although clinically available, the catheter-based procedure has major disadvantages: it can only be used on a fraction of ASD (Patel et al., 2006), it excludes procedures on small children (Paragios., 2003), and it is generally performed under a high X-ray dose (Papademetris et al., 2003). ASD closure studies using rigid instruments showed the feasibility of the procedures and highlighted their limitations (Downing et al., 2002; Suematsu et al., 2005). Amongst the latter, the difficult visualization of surgical instruments, limited spatial resolution of US imaging, and the large size of the US probe, make the clinical applicability of beating heart surgery difficult. The reliable visualization of structures within the heart remains another major challenge to successful minimally-invasive surgical interventions (Cannon et al., 2003; Suematsu et al., 2004).
Recent advances in ultrasound (US) imaging make this visualization modality an ideal candidate for image-guided interventions. 4D US is simple, cheap and fast, and allows the surgeon to visualize cardiac structures and instruments through the blood pool. US also has some major disadvantages, being extremely noisy with poor shape definition, which makes it confusing and hard to interpret in the operation room. Tracking tissue in 3D US volumes is particularly difficult due to the low spatial resolution caused by interpolation and resampling in image reconstruction (Fenster et al., 2001). Therefore, the development of tracking methods for volumetric data in 4D applications is necessary to assist clinical procedures. In ASD closure procedures, ASD tracking in US images is desirable to guide either the rigid instruments or the catheter.
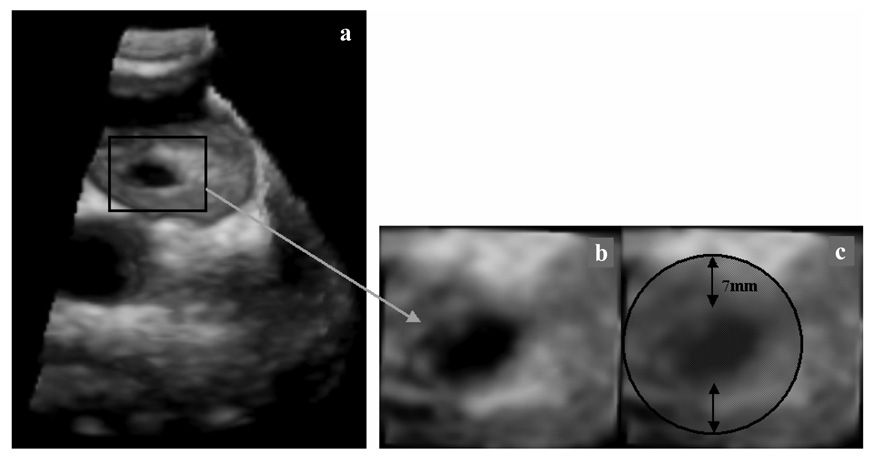
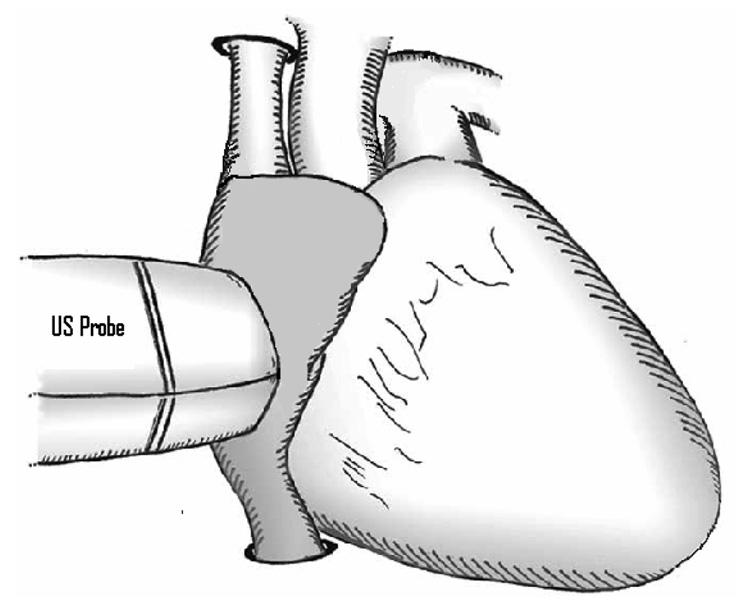
A 3D image of an ASD and its position in the heart is shown in Figure 1. The US probe is placed on the exterior wall of the right atrium, as exemplified in Figure 2. The dynamic nature of ASD is primarily determined by the cardiac cycle with a mean area change of 61% between end-diastolic and end-systolic (Maeno et al., 2000). The change in size is highly variable and present measurements show subjectivity (Handke et al., 2001; Maeno et al., 2000; Podnar et al., 2001). There is little to no correlation between the dynamic changes of ASD and its size, heart rate or age of patient. The motion of the US transducer and the low image quality contribute to the challenges of ASD tracking.
Figure 1.
3D US image of a porcine beating-heart with ASD. The US probe is placed outside the right atrium and the beam oriented toward the left atrium. (a) shows the entire 3D US volume, while (b) presents a magnified view of the ASD. The patch must cover the entire ASD surface, as seen in (c).
Figure 2.
The US probe in relation with the heart. The probe is placed directly to the surface of the right atrium and “looks” through the ASD into the left atrium.
A number of approaches to estimate the motion of cardiac tissue have been tried. They could be separated into two main classes: tracking and segmentation. Block matching is fast and simple (Behar et al., 2004), but estimates velocities at low level and lacks robustness. Optical flow has higher sensitivity and specificity, but is very slow and must find a good compromise between local and global displacements (Boukerroui et al., 2003; Duan et al., 2005). The majority of tracking applications are 2D. An interesting 3D cross-correlation-based approach for speckle tracking on simulated data is proposed in (Chen et al., 2005). Some good examples of temporal segmentation of cardiac US can be found in (Montagnat et al., 2003; Morsy and von Ramm, 1999; Papademetris et al., 2003). Model-based segmentation employing simplex meshes (Montagnat et al., 2003) or finite element models (FEM) (Papademetris et al., 2003) have shown promising results, especially for the left ventricle. The processing speed remains a major challenge. A more detailed overview of previous methods for cardiac motion estimation is provided in the discussion at the end of the paper.
In this paper, we present a 3D block flow approach adapted to ASD tracking that estimates velocities for an entire block using the concept of voxel-based optical flow. The method is aimed at assisting image-guided minimally-invasive beating-heart ASD closures. It provides a fast and reliable ASD position guidance to potentially support the placement of a surgical patch over the atrial septal opening in computer-aided interventions. The method is fast and avoids the problems of traditional block matching, while exploiting the sensitivity of optical flow. The computation is done volumetrically and the displacement optimizes a similarity measure relative to both the previous and original frames. We compare the new results to those obtained by classical implementations of block matching and optical flow.
Section 2 of the paper presents the methodology of the tracking algorithms. We mention block matching, optical flow and similarity measures, and introduce the block flow technique. Comparative results on 4D in-vivo and clinical cardiac US images are shown in Section 3, next to quantitative evaluation on synthetic data.
2. METHODS
Our goal is to follow the motion of ASD across successive heart cycles to facilitate minimally invasive cardiac surgery. In ASD closures using rigid instruments, when the surgical patch is placed over the ASD, a distance of approximately 7mm between the ASD margin and the patch edges is usually ensured (Figure 1). We aim to guide the correct placement of the patch over the ASD surface. At this stage of the algorithm implementation, we assume the initialization of the process is done manually by allowing the user to select a block centered on the ASD in the first frame. This gives a first estimate of the ASD location and a template for the computation of similarity scores, as shown later in the paper.
2.1 Block Matching
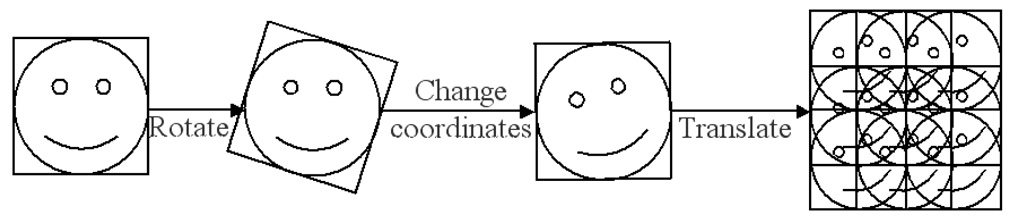
The first approach we considered was single block matching (Ourselin et al., 2000). This multi-scale intensity-based method assumes that there is a global intensity relationship between two images. We are simply interested in matching two blocks, instead of two images, which simplifies the rationale of the algorithm. The principle of single block matching is shown in Figure 3. Given a reference block in the previous frame, this is rotated and translated over a search space in the current frame to find the best fit according to a similarity criterion.
Figure 3.
The principle of single block matching. The reference block is first rotated, its coordinates are changed, and then is translated over the search space of the target image to find the best fit.
During the acquisition of our 4D US images of the heart, the time-gain compensation settings of the US machine are kept constant. However, homogenous objects appear heterogeneous in US images due to attenuation factors. The change of speckle characteristics between frames and the cardiac motion induce more changes in the tissue appearance. Hence, we normalize image intensity before the computation of similarity.
We investigated three types of similarity measures suitable for images of the same modality. First, an identity measure, the sum of squared differences (SSD) of normalized intensities, as seen in
| (1) |
ref is the reference block from the previous frame, tar the target block in the current frame, and n the number of voxels in a block. A linear measure, the inverse Pearson correlation coefficient (PCC), is proposed in
| (2) |
and a statistical measure, based on maximum likelihood (MLE), introduced in (Cohen and Dinstein, 2002) and refined in (Boukerroui et al., 2003), is presented in
| (3) |
An overview of intensity similarity measures can be found in (Roche et al., 2000). For our data, SSD does not cope with relative intensity. PCC minimizes the least square fitting to the original data and is more robust than SSD. However, MLE seems to be the most robust similarity measure for US data (Boukerroui et al., 2003). It assumes that US images are log compressed with Rayleigh speckle noise (Thijssen, 2003), but no change of speckle noise between frames. Minimizing the square error between blocks becomes minimizing the probability distribution function of the additive noise between frames.
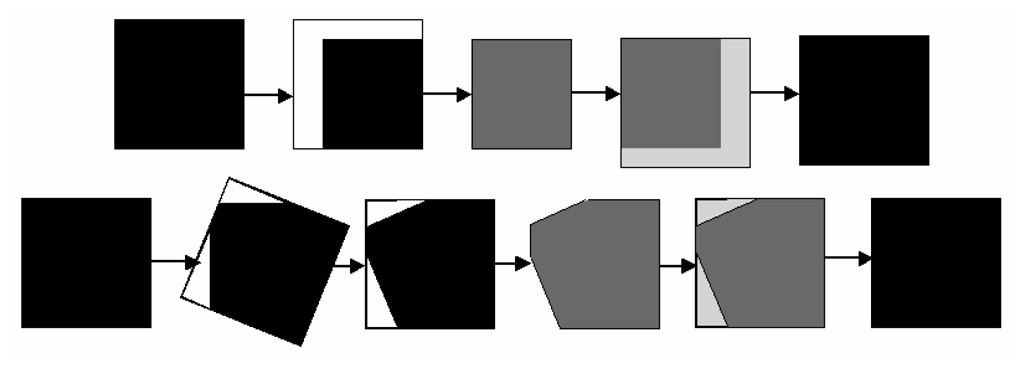
Our implementation uses two steps, from coarse to fine search space to find the block in the target image that is most similar to the given block in the reference image. Typical difficulties in search-space applications are found at margins. Padding at margins is often proposed as a solution, but it influences the response of similarity measures. To avoid padding, we propose reducing the size of the reference block to account for clipping at the edge in the target volume (overflowing the edges). Hence, the similarity score is calculated using two smaller blocks. The best-matched target block is then grown back, on the opposite side of the clipping, to the original size of the reference, using data from the target volume (Figure 4). This element of the algorithm ensures that the ASD is correctly tracked when it reaches or partially crosses the image boundaries.
Figure 4.
Avoiding padding at image margins. The top row shows the change of block size during translation and the bottom row during rotation. ref is shown in black and tar in gray.
2.2 Optical Flow
Secondly, we tested the efficiency of region-based optical flow to track ASD. Optical flow is used to compute motion vectors from spatio-temporal changes in the intensity field of an image. We developed a 3D extension of the 2D method presented in (Boukerroui et al., 2003) and based on (Singh and Allen, 1992). Velocity is computed as the physical shift corresponding to the best match between image regions through time, in terms of minimum energy
| (4) |
where (Singh and Allen, 1992) proposes k=-ln(0.95)/(min(E(u,v,w))). At a first step, the velocities are found weighting the similarity scores within the search space, as in
| (5) |
where x, y and z are the displacements in the three directions. The error of velocity estimation is found from the eigenvalues of the inverse covariance matrix is
| (6) |
At a second step, the velocities of voxels of the same object are linked by imposing neighborhood constraints. The refinement of velocities is performed in a similar way to the first step described above and is not detailed in this paper. Our main contribution to using neighboring information was the extension of the algorithm to 3D. Please refer to (Singh and Allen, 1992) for more information on the 2D approach.
There are other techniques to compute optical flow, such as the first-order differential method (Lucas and Kanade, 1981). They are very sensitive to noise, which is high in US images, and require spatial and temporal smoothing. In a real-time tracking application temporal smoothing can only be performed backwards, as we do not know the data in the next frames. This introduces a bias in the velocity estimation. Another class of optical flow is that of phase-based techniques (Fleet and Jepson, 1990). Although robust to intensity scale, phase-based optical flow requires an optimal search space. In cardiac images, velocities can vary considerably between frames, which makes the estimation of a filter bandwidth difficult. A comparative review of optical flow methods can be found in (Behar et al., 2004).
The major disadvantage of optical flow techniques is the computational load. While the robustness of tracking anatomical structures can be improved by adding movement constraints, smoothing factors and connectivity assumptions, the speed would be decreased and become unsuitable for real-time applications. For a faster implementation, we employ a multi-scale approach from coarse to fine, using MLE. Moreover, the optical flow is estimated only for the contour voxels of ASD, extracted by thresholding, which are then wrapped in the resulting block.
2.3 Block Matching-Optical Flow
We further propose another two-step multi-scale approach, this time using a combination of block matching and optical flow. At both levels, we employed MLE as similarity measure. First, the contour of the ASD is extracted in the first frame and then the velocity of the entire block is estimated. Block matching gives the coarse velocity, common for all the contour voxels. At the finer level, the optical flow is estimated for every contour voxel. The newly estimated voxels in the target image are wrapped in the resulting block. This approach is considerably faster than the multi-scale optical flow.
2.4 Block Flow
We introduce the notion of ‘block flow’, which uses the energy computation for velocity estimation as for optical flow (Singh and Allen, 1992) (and extended to 3D in Section 2.2), but for the entire block, instead of every voxel. For a given reference block ref, we define empirically a maximum displacement md in the new image frame. Within the search space, we compute the estimation error as
| (7) |
Minimizing the energy E is equivalent to minimizing the maximum error in similarity between the target block tar and ref, and between tar and absref, where absref is the user-defined block in the first frame of the 4D sequence. E becomes a value of worst match and obstructs velocities u, v and w to grow in the directions of blocks that are not similar to both the previous frame and the absolute reference. absref acts as a template ensuring that the solution does not diverge from the initial estimate or gold standard. Extending the computation to 3D in a similar manner to (Boukerroui et al., 2003; Singh and Allen, 1992), we obtain the probability distribution R, as in
| (8) |
where τ normalizes the probabilities. The estimate of the three-directional block velocity Vb is presented as a weighted sum of displacements in the three directions in
| (9) |
The block flow algorithm does not use neighborhood information to smooth the block velocity, as the displacement is unique for the entire block. This enforcement is valid for tracking an object like ASD, as the defect remains a compact structure with margins moving together throughout the heart motion. This is not applicable to tracking more complex objects. Once the velocity is calculated, we verify if the new match is on the image margins, as in Figure 4. If that is the case, we grow the block to ensure that it will propagate with the same size as absref.
Compared to block matching, block flow estimates the velocity of the block from a probability distribution function of energy terms corresponding to best matches between blocks. Unlike optical flow, block flow reduces the similarity computations from a set of voxels to one block. Instead of calculating maximum likelihood for every voxel of a contour in typical optical flow, we speed up the computational costs by computing the energy term for only one block. The other major difference between our method and previous approaches is the use of an additional energy term from a predefined block, which can be a standard use of a reference for processing repetitive data.
3. RESULTS
3.1 In Vivo Animal Results
To test the tracking algorithms, we used a database of eight 4D time sequences of porcine beating hearts with artificially created ASD. Available clinical data is sparse; however, we ensured a larger database for our study using animal data. Empirically, we found tracking in animal data more difficult than in clinical studies. This is probably caused by the artificial creation of ASDs when the septum is cut with an instrument in order to create a defect. Artificial ASDs tend to have more jagged edges. Another strong incentive to use animal data is the need for animal studies to design surgery.
The ASDs were created solely under real-time 3D echocardiographic guidance by balloon atrial septectomy and subsequently enlarged by biting off the rim of the ASD with a Kerrison bone punch. (Suematsu et al., 2005). The experimental protocol was approved by the Children’s Hospital Boston Institutional Animal Care and Use Committee. The size of the septal defects varied between 4.8 and 6.5 mm. All the US data were acquired in-vivo with a Sonos 7500 Live 3D Echo scanner (Philips Medical Systems, Andover, MA, USA). The image size is 80×80×176 voxels. For the acquisition of in-vivo data, images were acquired using a streaming mode. The time of acquisition was of 2s/case at a frame rate of 25 volumes/s. We start the search using a larger search space (coarse level) and compute similarity values every two voxels in each direction. Once the best correspondence is found, we refine the search at every voxel with a smaller search space (fine level). The search space is of 10 voxels in each direction, giving a search window of 20×20×20 voxels. At this stage, the implementation of the four tracking algorithms was done in Matlab 7 (The MathWorks, Inc.) We present results on a dual 2.4 GHz processor with 2.5 GB RAM for a block of size 18×18×11 voxels. We chose the smallest block around the ASD that includes its margins and is bigger than the maximum size of ASD.
The performance of the block matching algorithm using two levels (coarse to fine) of combined translation-rotation and MLE is shown on the top row of Figure 5. Each block shown in Figure 5 is a 3D entity visualized from the right atrium looking into the left atrium (from above the block) using a 3D renderer and semi-transparency. In this particular view, a well-tracked ASD will appear as a black hole in the middle of the block, where the surrounding tissue is part of the septum. The rows present the absolute reference in frame 1 and tracking results after 20, 40 and 50 frames (50 frames correspond to 2s). Judging by the small rotations and the rounder shape of ASD, we also tested block matching using only multi-scale translation. The results are almost identical (with an error of maximum 2 voxels) and the speed reaches 0.06 s/frame with PCC similarity criteria and 0.14 s/frame using SSD. Using MLE as similarity measure gives more robustness to the algorithm, but it is more computationally expensive (0.47 s/frame).
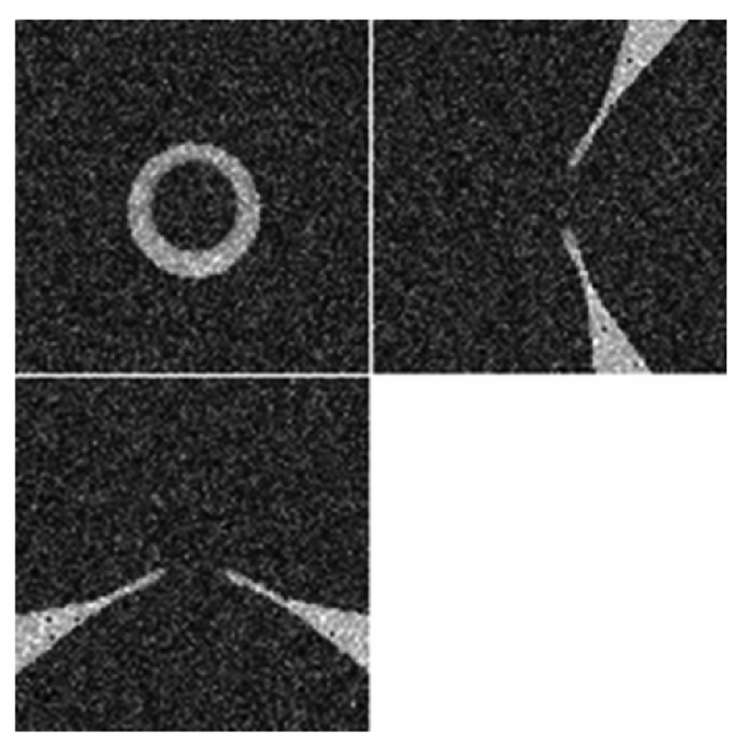
Figure 5.
The comparative performance of the four tracking algorithms. The top row shows results by block matching (BM); the second row by optical flow (OF); the third row by a multi-scale combination of block-matching and optical flow (BMOF); the bottom row by block flow (BF). All blocks are shown equally sized. From left to right, the columns show 3D blocks at frames 1, 20, 40 and 50.
The gold standard for our qualitative assessment of tracking is the expert’s visual judgment of our off-line tracked images, as there is no approved streaming machine yet to be placed in the operating room. Even when all tracking methods provide reasonable results, the ASD can be off-center or only partially found in the tracked block.
The performance of the two level optical flow algorithm was visually more robust than that of simple block matching. Using MLE as similarity criterion, the computational speed was of 25.7 s/frame. The second row in Figure 5 shows tracking results using optical flow. In block matching-optical flow combination, we used some smoothing between neighboring points, but no connectivity was enforced. The contours voxels are enfolded by the resulting block. The speed was increased at 13.32 s/frame using a two level combination of block matching (the coarse level) and optical flow (the fine level), although the technique remains too slow for real-time applications. Results using the block matching-optical flow combination technique are shown on the third row in Figure 5.
Finally, the bottom row in Figure 5 presents tracking results using the new block flow algorithm. Using energy estimation at block level instead of voxel level, the block flow method becomes much faster than optical flow, without losing accuracy. Its processing speed is 0.48 s/frame, comparable to that of single block matching, but with much more robust results. In Figure 6, we present full 3D volumes (the entire frame) of the results obtained by block flow shown in Figure 5.
Figure 6.
Tracking results in full 3D volume for the case shown in Figure 5. (a) presents the first frame and the absolute reference marked as a block; (b) shows tracking results after 25 frames; and (c) after 50 frames.
The block flow technique outperforms both block matching and optical flow for tracking ASD. Block matching is the fastest, but it computes a single similarity measure between successive frames and it stores the best match, ignoring the results in the rest of the search space. Optical flow is more robust, as velocities are computed using similarity measures from the entire search space, but very slow. We tracked ASD contour voxels; without additional motion constrains, the method lacks robustness after approximately one cardiac cycle. The results reported are achieved using a basic implementation to reduce computation time. While more sophisticated optical flow methods would perform better, this is beyond the purpose of this paper. The superior results of the block flow method are due to the combination of measures from the whole search space, as for optical flow, combined with the fast processing for the entire block and the use of a reference block.
3.2 Error Propagation
For a careful characterization of the evolution of errors in time, we defined two components: the absolute error abserr and the conservation error conserr
| (10) |
abserr gives the error of resemblance to absref, as a measure of global variance or cumulative deviation from the model, while conserr shows the energy conservation at every frame, a measure of local variance.
Table 1 shows quantitative results for the compared tracking algorithms. Mean MLE scores are computed for eight 4D image data using the four described methods. The score is normalized between 0 and 100, where 0 corresponds to the perfect match. The block flow algorithm had the conservation scores and in time reaches the best absolute scores as well. For the first 25 frames, block matching has the smallest conservation error (as it minimizes conserr), but block flow stays more robust over time and performs better for the last 25 frames. Regarding the absolute error, block matching performs better than optical flow over the first 25 frames. However, the cumulative error in velocity estimation by block matching increases at a faster pace in time. While being more accurate that optical flow in motion tracking, the block flow method is also 27 times faster. The multi-scale combination of block matching and optical flow starts better and faster than our optical flow implementation, but is the least robust in time. The block flow algorithm performs better than the other techniques with better local and global similarity and the smallest cumulative error.
Table 1.
The mean MLE scores and processing speed for eight ASD 4D images using four tracking techniques. Normalized MLE scores (0–100) were calculated every 25 frames according to Equation (10): 0 for the perfect match to 100 for the worst. The best results are shown in italic.
| Mean/Std conserr | Mean/Std abserr | Speeds/frame | |||
|---|---|---|---|---|---|
| Frames 1–25 | Frames 26–50 | Frames 1–25 | Frames 26–50 | ||
| Block Matching | 2.82±0.98 | 3.77±1.39 | 10.30±4.39 | 16.28±6.12 | 0.47 |
| Optical Flow | 5.36±2.96 | 5.92±3.19 | 13.19±6.14 | 12.82±4.42 | 25.70 |
| Block Matching - Optical Flow | 5.64±2.60 | 6.03±3.43 | 10.18±5.92 | 18.22±3.64 | 13.32 |
| Block Flow | 3.23±1.71 | 3.57±1.74 | 5.32±2.07 | 5.98±2.21 | 0.48 |
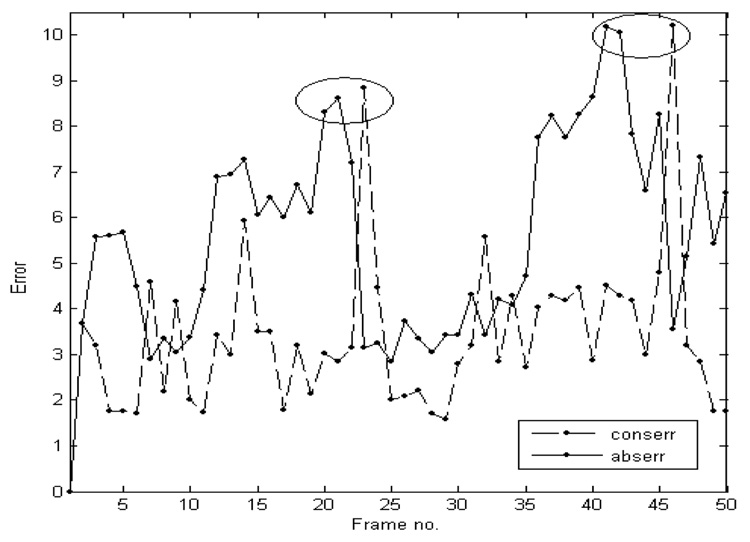
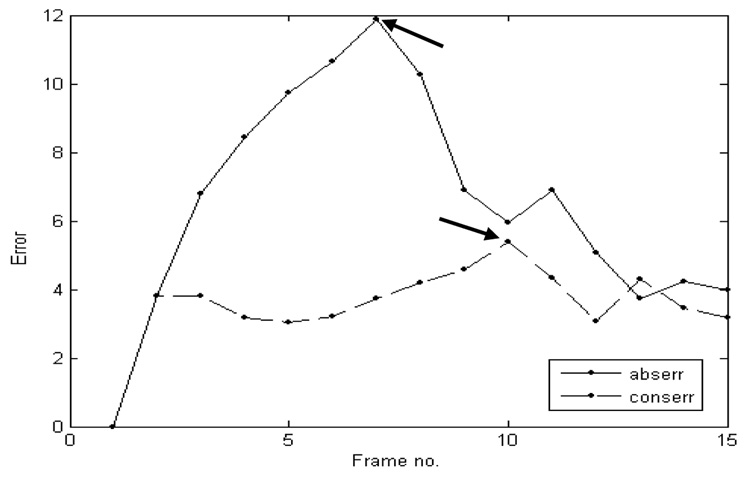
Estimating abserr and conserr at every frame in a typical ASD 4D volume, we obtained the results shown in Figure 7. Our data are ungated, but Figure 7 shows repeatability in the pattern of error variation in time. Under the procedure, a typical porcine heart beats at 70 beat/min. For a data set of 50 frames (2s), the heart goes through approximately two and a half cardiac cycles. Note that each error measure has two peaks in its time evolution and that the peaks are temporally related to each other, as shown by the two ellipses in Figure 7. abserr becomes maximal at times when the ASD exhibits extreme changes of shape in a repetitive way with the heart cycle. conserr shows peaks at sudden movements of the heart septum related to the pumping of the heart. Comparing the error evolution with the cardiac 4D US data, the peaks of abserr are related to the dilation of the left atrium during late diastole, and conserr becomes maximal at the beginning of atrial contraction during systole. These observations are in full agreement with the prevailing literature (Handke et al., 2001; Maeno et al., 2000). The errors also show a small increase in time, a cumulative error that could be corrected using gating information on the repetitiveness of the heart cycle.
Figure 7.
The evolution in time of the absolute and conservation errors. abserr has a mean value of 5.55 and a standard deviation of 2.32. conserr has a mean value of 3.34 and a standard deviation of 1.64. Each error measure has two peaks, which are temporally related to each other, as shown by the two ellipses
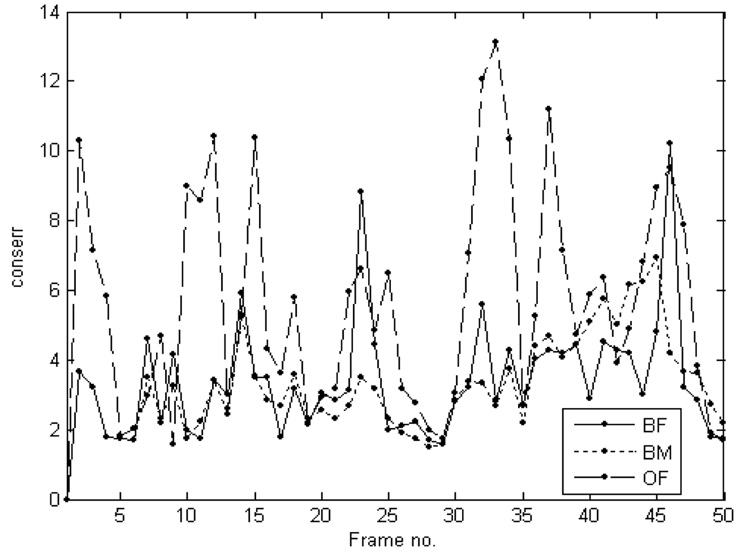
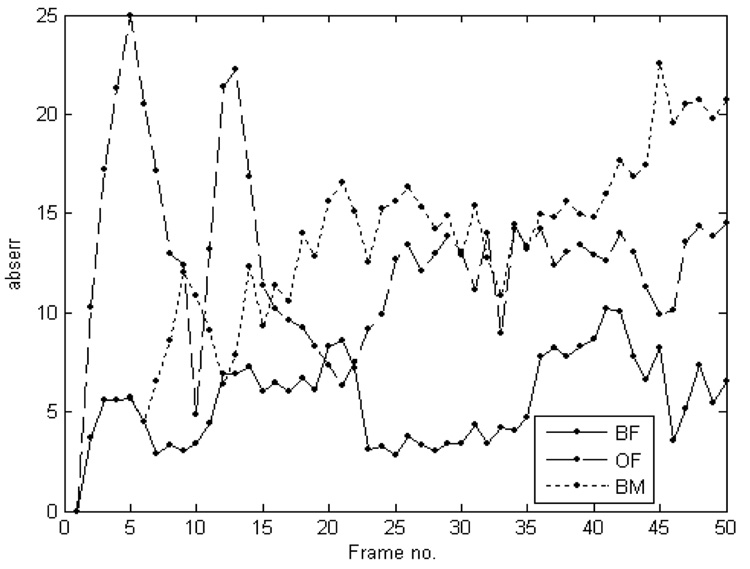
We did not include average error values for the entire dataset, as without gating, different hearts could be at various moments of their heart cycle. However, we compared the evolution of errors in block matching, optical flow and block flow for the case exemplified in Figure 7. The block matching and optical flow techniques do not include a constraint in similarity with absref. Figure 8 shows the evolution of conserr. Block matching, as a technique based on minimizing conserr, has the best local similarity in the first part of the time sequence. Nevertheless, block flow leads on the second part of the sequence. Optical flow has poor local similarity due to the individual migration of contour voxels between frames. Figure 9 shows the evolution of absserr. Optical flow has a difficult initialization due to the migration of each contour voxel. Once stabilized, its error becomes smaller than that of block matching, which has the most rapid growth. The cyclic information contained in block flow is not reflected in the results of the other techniques. The 3D cyclic motion of the block is further observed in Figure 10. The maximum displacement appears on the z-axis, due to the heart contraction/dilation. The x and y displacement from one cycle to the next is partly due to the free-hand probe motion.
Figure 8.
The comparative evolution in time of conserr. BM - block matching; OF - optical flow; BF - block flow.
Figure 9.
The comparative evolution in time of abserr. BM - block matching; OF - optical flow; BF- block flow.
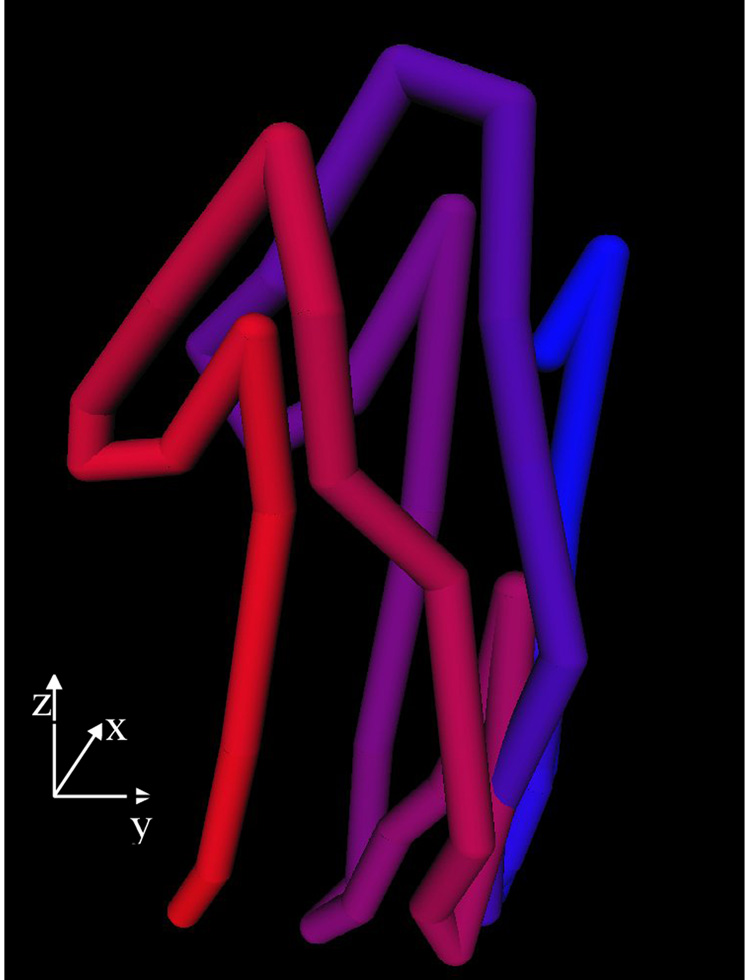
Figure 10.
The 3D motion of the block in a porcine case. Temporal frames start at blue and end at red.
The definition of errors may favor some of the compared methods, as they minimize either abserr or conserr, or both. For instance, block matching minimizes conserr, while block flow uses absref. However, abserr compares the absref with its replica (altered by noise and possible small errors in probe motion) at the end of each cycle. The values of absref after the first cycle are 12.54 (BM), 6.79 (OF) and 2.67 (BF), and after the second cycle are 19.61 (BM), 9.92 (OF) and 2.83 (BF).
We would not expect a significant difference between cardiac cycles, as confirmed both visually and by clinical experts. For the animal sets, the image acquisition stopping criterion is time=2s or 50 frames. Images are acquired by experienced interventional radiologists who aimed at holding the US probe in a locked position relative to ASD. Probe sliding may occur, inducing only minor drifts.
Our data is not ECG-gated, hence we approximate which is the moment when the next heart cycle begins in multi-cycle images; this is a simple task for experienced clinicians. While the ASD dilates/contracts and even changes shape slightly, in theory returns to the same shape and size after one heart cycle. The only difference between heart cycles could appear in the position of ASD, if the ultrasound probe moved. As results show, our algorithm retrieves correctly the new location of the ASD at the end of the heart cycle even if the probe moved. This explains why Figure 10 shows different coordinates for ASD after each cycle, but similar motion patterns within the cycle.
3.3 Clinical Results
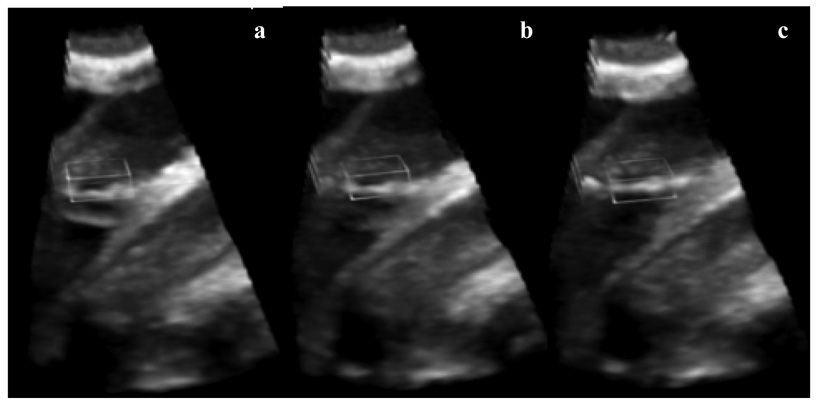
We used for clinical validation three clinical 4D US sequences of infant beating hearts with ASD acquired intra-operationally. The US data were acquired in-vivo with a Sonos 7500 Live 3D Echo scanner (Philips Medical Systems, Andover, MA, USA). The times of acquisition were of 15 and 17 frames/case, corresponding to one heart cycle at a frame rate of 25 volumes/s. The image size is of 160×144×208 voxels. The clinical data has higher resolution than our animal acquisitions. Since the images were acquired intra-operatively, the septum was not orthogonal to the US beam and the ASD appears slanted. This slightly twisted position amplifies the visual effect of change in ASD size, as heart contraction and blood pressure modify the opening between atria. The dilation/contraction of the ASD is shown in Figure 11, where we present tracking results in a clinical ASD case. We ensured that the block enfolding the absolute reference in the first frame is large enough to accommodate the change of size of the ASD. The results are consistent with those from the animal trial and the ASD is tracked as a blood hole in the middle of the septal tissue. The mean errors for the three clinical 4D images associated with the block flow algorithm are 7.09±2.77 for abserr and 4.40±2.14 for conserr. The results are in the same range of values as those obtained in animal data and shown in Table 1, but slightly bigger, as there is a more substantial change of shape between frames in the clinical ASDs when compared to the artificially created animal ASDs. Consistent with our previous observations, abserr and conserr have synchronized peaks, associated with the heart cycle, as in Figure 12. abserr has maximal value at frame 7, when the ASD is fully dilated (late diastole) and furthest from absref (selected at early diastole). conserr is maximal at frame 10 (systole), when the contraction of left atrium changes fast the shape and size of ASD. The 3D cyclic motion of the block is presented in Figure 13. Similar to the porcine cases, the maximum displacement appears on the z axis, due to the heart contraction/dilation. The block is found again at the start position at the end of the heart cycle.
Figure 11.
Clinical ASD tracking. From left to right and top to bottom, the columns show 3D blocks visualized from right atrium to left atrium every two frames between 1 and 15 (the frame number is marked on the upper left corner). The segmented ASD is shown in light gray ellipsoids.
Figure 12.
The evolution in time of the absolute and conservation errors in clinical experiments. The peaks of the two errors are synchronized, as shown the arrows.
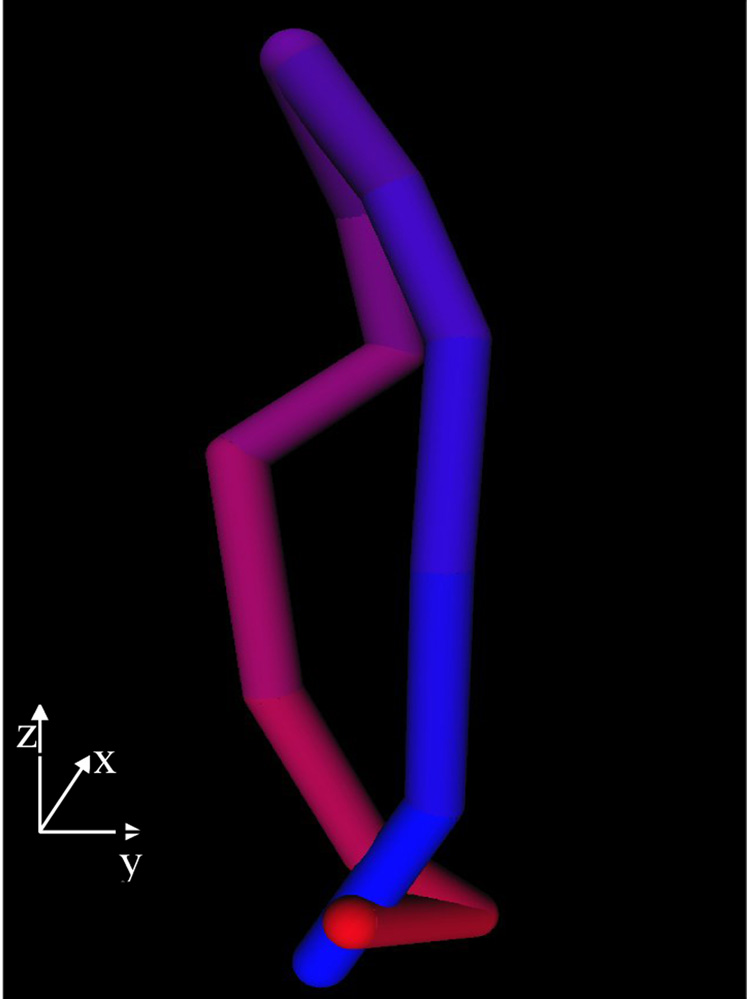
Figure 13.
The 3D motion of the block for a typical clinical case for one heart cycle. Temporal frames start at blue and end at red. At the end of the heart cycle, the block is found at the same position as at the start.
An additional feature of the algorithm is a preliminary segmentation of ASD from tracked blocks. An ample overview of segmentation technique for medical ultrasonic images can be found in (Noble and Boukerroui, 2006). In clinical practice, the ASD is covered with a patch often twice as large in diameter as the ASD. The segmentation that we propose at this stage is basic and fast and aimed to potentially guide the eye of the expert to the position where the real patch would be used to cover the ASD during surgery. The view is operation orientated. The block containing the ASD is projected on the direction that the patch will be placed. We add the intensity values of voxels at every location on the projection plane and the 2D result is thresholded. We correct segmentation errors by morphological closing and keep the maximum connected component. Visually, we present a 2D area at the location and of the size of the ASD to help guiding the placement of the patch and secure that the atrial communication is fully covered, as in Figure 11. A 3D segmentation would provide a better characterization of the 4D dynamic nature of ASD. This is not intended by our application.
3.4 Synthetic Data
It is difficult to evaluate quantitatively the results of ASD tracking without knowledge of the precise 3D position of the anatomical ASD. While we aim to address the automatic 3D segmentation in future work, the golden standard or expert 3D segmentation of ASD remains a delicate task. For a first evaluation of the tracking algorithm, we created a synthetic ASD with known controlled motion. This experiment allows us to obtain quantitative tracking results by comparing the outcome of our algorithm with the known motion of the synthetic ASD block.
The synthetic ASD is designed to have similar characteristics to our real ASD data. For that purpose, we carefully pondered the following parameters that describe the appearance and motion of ASD: image intensity, ASD size, block size, ASD motion (translation and tilt), ASD deformation (scaling), and noise model. The synthetic image is a parallelepiped of size shx x shy x shz. In the center of image we create an artificial hole using the following formulation for the value vh of each pixel
| (11) |
where xh, yh and zh are the x, y and z motions of the artificial ASD. Their directional motions are controlled by parameters a, b and c, with t being the frame number or iteration and φ =(0,t). vh has descending values toward the ASD center and a maximum of 100*π/2 = 157. A Rayleigh noise component with the probability distribution function nh is added to the data. rh is the radius of the artificial ASD and is regulated by parameters α and β. dh is the half width of the septum or ASD membrane.
| (12) |
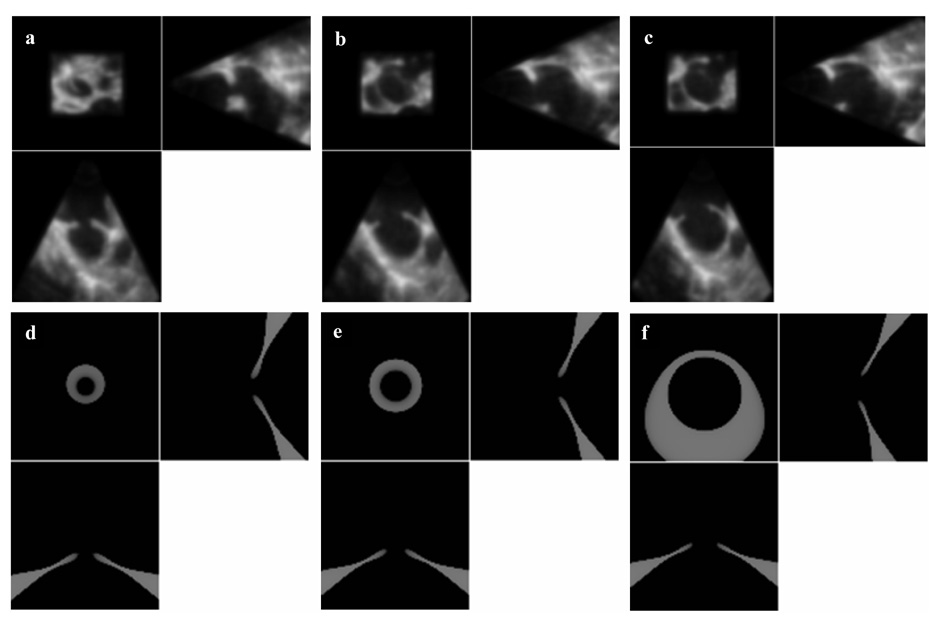
For a numerical example, we used dh=1.5, shx=shy=shz=100, a=b=c=5 (a motion of maximum 10 voxels on either x, y or z;) and α= 1.5 and β=3.5 for rh=(2, 5). The tilt τ is of maximum 10% in the z direction. Figure 14 shows variations in size and tilt of the synthetic ASD next to clinical images at different stages of the heart cycle.
Figure 14.
The synthetic ASD. (a), (b) and (c) show the 2D slices of 3D temporal images of a clinical ASD. (d), (e) and (f) are 2D slices of 3D temporal images of the synthetic ASD; note the change of size and tilt.
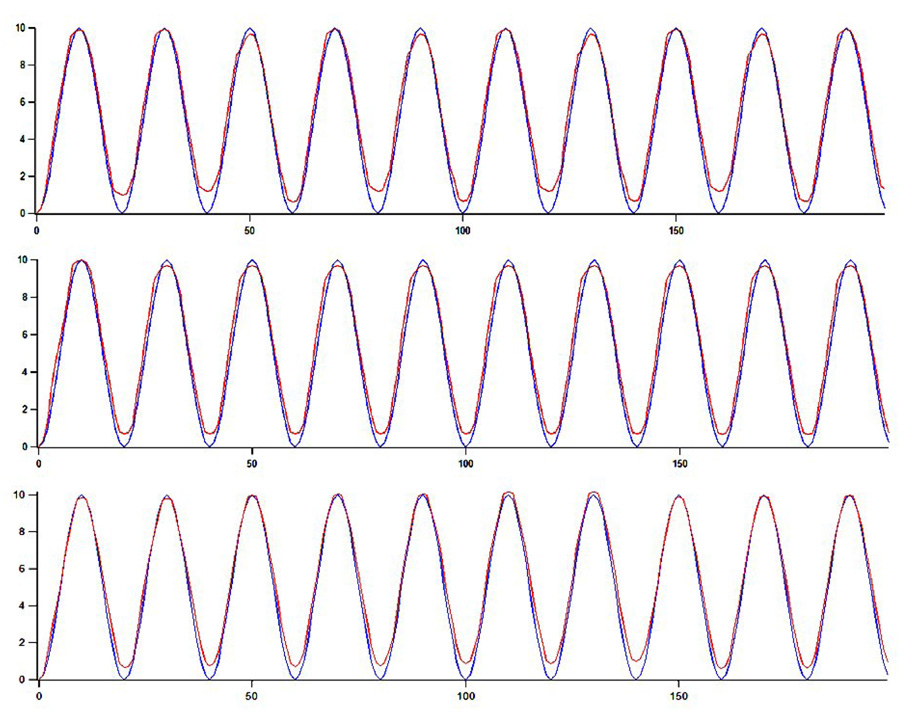
The size of the ASD block is 20×20×10 voxels to resemble the size of blocks in in-vivo data and the entire artificial image has 100×100×100 voxels. The motion is repeated periodically over 200 frames corresponding to 8s of image data and 10 cycles, similar to the heart cycle length in in-vivo data. The noise component is varied between 0 and 20%. Figure 15 shows the synthetic ASD with 20% noise. Tracking results on the synthetic ASD are presented in Figure 16. We show comparatively the real trajectory of the ASD in blue, near the tracked position using block flow in red. For illustration, we present results on the z axis, the main motion component of clinical ASDs. First, we use only a rigid component in the motion (translation and tilt), and then we add scaling, and noise. The maximum digital error is one voxel with mainly subvoxel values for the error in position tracking. Table 2 shows quantitative errors on synthetic data for the compared tracking algorithms, similarly to Table 1.
Figure 15.
The synthetic ASD with 20% Rayleigh noise.
Figure 16.
Tracking results on synthetic ASD over 200 frames and 10 cycles; in blue we show the real ASD trajectory, while in red we present the tracked position of ASD; (a) the z component of tracking when the ASD motion is characterized by rigid motion (translation and tilt) only; (b) rigid motion and scaling; (c) rigid motion, scaling and 20% noise.
Table 2.
The mean MLE scores for synthetic data using four tracking techniques over 50 frames. Normalized MLE scores (0–100) were calculated every 25 frames according to Equation (10): 0 for the perfect match to 100 for the worst. The best results are shown in italic. Results are comparable to those in Table 1 for in-vivo data.
| Mean/Std conserr | Mean/Std abserr | |||
|---|---|---|---|---|
| Frames 1–25 | Frames 26–50 | Frames 1–25 | Frames 26–50 | |
| Block Matching | 2.12±0.19 | 3.29±0.49 | 6.91±5.28 | 7.94±5.06 |
| Optical Flow | 3.96±1.24 | 4.12±1.64 | 7.07±5.12 | 7.02±3.74 |
| Block Matching - Optical Flow | 5.64±2.60 | 6.03±3.43 | 7.18±4.96 | 8.39±4.23 |
| Block Flow | 2.53±0.11 | 2.52± 0.12 | 2.84±0.21 | 2.87±0.15 |
For 50 frames, we estimated the error in position tracking in the z direction, the direction of maximum motion of the ASD block, for the compared tracking methods. The average tracking errors are of 4.04±1.93 (BM), 2.34±1.22 (OF), and 0.20±0.41 (BF) voxels. The errors in position tracking after the first cycle are 4 (BF), 2 (OF) and 1 (BM) voxels, and after the second cycle are 6 (BF), 3 (OF) and 1 (BM) voxels; values are rounded to the closest integer.
In our synthetic case, where the “heart cycle” is perfectly repeatable, the largest tracking errors arise at the position when tar=absref. The value E of energy of block flow (a maximum value) is larger due to identity between tar and absref, as it accounts only for the term MLE (ref, tar), as in Equation (7). This is unlikely to happen in reality, where small differences between tar and absref appear due to the US probe motion and position. Please also note the smoother tracking curve in Figure 16.c compared to Figure 16.a and b, when noise is added. This effect is explained by the use of an MLE function suited to Rayleigh noise distribution, as in Equation (3).
Synthetic data is generated using a simplified noise model, based on US noise distribution (Cohen and Dinstein, 2002; Thijssen, 2003) and on previous publications using Rayleigh distribution models to generate US data (Meunier, 1995; Aysal, 2007). More sophisticated techniques to simulate US data can be found in several recent publications (Duan et al., 2007b; Jensen, 1999; Meunier, 1998; Yu et al., 2006) and will be investigated in future work. One unknown factor is the preprocessing of data by the commercial US machines, which is not accounted by the proposed methods.
4. DISCUSSION
We presented comparative results for the tracking of ASD in 4D echocardiographic images. We introduced a block flow technique, which combines the velocity computation from optical flow for an entire block with template matching. Enforcing similarity constraints to both the previous and first frames, we ensure robust and unique solutions. Computing velocity at the block level, our technique is much faster than optical flow and comparable in computation to block matching. Results on in-vivo 4D datasets demonstrate that our technique is robust and more stable than both optical flow and block matching in tracking ASD. Quantitative results evaluated on synthetic data show maximum tracking errors of 1 voxel.
The absolute reference acts as a template that is used in our energy function to correct motion estimates that drift too far from a repetitive motion pattern. In a similar way, the information from each previous frame corrects for estimates that do not take into account the change in shape of ASD. We chose the ASD in the first frame as absolute reference because it was the first available datum in the image set; the ASD from any other frame could be used in the same way, as every part of the heart cycle is repeated.
The block flow tracking algorithm finds the 3D velocity of an entire block that enfolds the object of interest. In this application, the object is an ASD with an approximate cylindrical shape. The ASD can be extracted from every new block by simple and fast thresholding. Compared to the basic block matching algorithm, our method has higher sensitivity in computing displacements, which gives it more robustness in time. Optical flow is sensitive to very localized changes, which also makes the method prone to errors. Interpolation, smoothing and connectivity constraints improve the performance of optical flow, but also approximate the results. Moreover, the block flow method is much faster than optical flow, finding the tradeoff between accuracy and computational expense.
We first normalized the intensities to reduce the effect of noise and attenuation changes from frame to frame. Then we compared the performance of several similarity measures and found that statistical measures, such as maximum likelihood, are better for our application. A coarse to fine approach is desirable for effectiveness and speed. We used a Rayleigh noise model in the similarity measure (Thijssen, 2003). Although we did not smooth the data, the pre-processing of the commercial ultrasound machines may alter the noise distribution. Our assumption led to robust results, but other noise models may be studied.
The ideal speed of tracking should be equal to that of the US frame rate at 25 frames/s. However, the human eye perceives a quasi-continuous motion at slower frame-rates, such as real-time magnetic resonance images (MR) or real-time computed tomography (CT), which usually display less than 10 frames/s. After visual validation by medical experts, our results have sufficient tracking accuracy to guide the placement of the surgical patch over the ASD.
For research purposes, the implementation of the block flow algorithm was done in Matlab 7 (The MathWorks, Inc.). Its speed on a dual 2.4 GHz processor with 2.5 GB RAM is over 2Hz. We are currently investigating a more speed-effective implementation of the block flow algorithm in C++. Preliminary results indicate that the processing speed will be of 30 frames/s after code optimization.
Processing speed for the robust tracking of cardiac tissues had been addressed in a number of papers. An optical flow approach was proposed in (Duan et al., 2005). and to track endocardiac surfaces. The data points are initialized manually and a finite element surface is fitted to the points. More recently, the authors segment the endocardial borders at 5 frames/s (Duan et al., 2007a). Boukerroui et al. (Boukerroui et al., 2003) use an adapted similarity measure introduced in (Cohen and Dinstein, 2002) to compute region-based optical flow in US image sequences. Their results, although faster, are 2D. The initialization is left out as a separate subject and the authors propose a parameter optimization scheme (Boukerroui et al., 2003). A knowledge-based parametric approach using level sets is proposed in (Paragios., 2003). 2D segmentation and tracking are alternated using shape knowledge, visual information and internal smoothness constraints. An interesting 3D cross-correlation-based approach for speckle tracking on simulated data is proposed in (Chen et al., 2005). However, 3D speckle tracking poses a series of difficulties, from optimization and computational costs, to speckle decorrelation in time and space. A thorough study of decorrelation and the feasibility of speckle-tracking are presented in (Yu et al., 2006) together with an analytical model of echocardiographic imaging.
A different class of algorithms is that of sequential segmentation of echocardiographic images. A good example is presented in (Maeno et al., 2000) combining 4D anisotropic filtering and a model-based segmentation using simplex meshes. The 3D volumes are recreated from 2D acquisitions, which give better in-plane lateral resolution than 3D US, but rely on heavy interpolation between planes. As in the vast majority of cardiac applications, this method segments the left ventricles and creates a model suited for diagnosis and not surgical interventions. The 3D left ventricular motion and tissue deformation from US images is also analyzed in (Papademetris et al., 2003) with a dense Bayesian motion field. A biomechanical model is used for strain information, but the finite element method (FEM) used to solve the equations makes the process very slow. Finally, the trade off between accuracy and computational expense is addressed in (Morsy and von Ramm, 1999) in a method combining correlation search and feature tracking. The speed is increased, compared to conventional correlation, but the feature detector slows down the algorithm for real-time applications (13.3 min/frame).
The dynamic nature of ASD is a subject of on-going interest. Rigid translational motion is an important component of ASD movement, but the change in shape and size was equally noticed. The main components of the motion are translation in the z direction (as in our view) and dilation/contraction. In our animal data, we noticed a more pronounced change in shape, although not pregnant, than in human data, where the change in size due to dilation/translation is more prominent. The difference is most likely related to the artificial creation of animal ASDs.
In closing ASDs with a catheter device it is extremely important to measure the size of the ASD to choose the appropriate device. This is not as important in typical open-heart surgery, but may be very important when aiming to close the ASD on the beating heart when trying to precisely place anchors to close the defect. However, most published papers on the size of ASD used 2D measuring tools, which do not account for the full 3D motion/deformation. Our tracking algorithm, combined with the full 4D segmentation of ASD, will provide valuable information for the full understanding of the dynamic morphology of ASD.
Our method obtained consistent results on in-vivo animal and clinical data. The method was not sensitive to the size of ASD, the change in resolution or the motion of the US probe. An interesting observation was the cyclic evolution of errors in ungated cardiac data. For future work, we will investigate the use of the cardiac cycle for predictive estimation to minimize errors. The automatic detection of the ASD absolute reference will be considered along with more sophisticated and fast methods to segment the ASD in every frame. Other sources of errors, such as free-hand movements will be examined. We will also investigate the consistency constraints for better tracking by linear-elasticity image matching proposed in (Christensen, 1999). The algorithm implementation will be optimized to make it run in real-time and the combination of ASD and instrument segmentation and tracking (Handke et al., 2001; Singh and Allen, 1992) will be exploited for surgical interventions.
ACKNOWLEDGEMENTS
This work is funded by the National Institutes of Health under grant NIH R01 HL073647-01. The authors would like to thank Dr. Alexandre Kabla from the University of Cambridge for informative discussions and Dr. Ivan Salgo from Philips Medical Systems for assistance with image acquisition.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.Aysal TC, Barner KE. Rayleigh-Maximum-Likelihood Filtering for Speckle Reduction of Ultrasound Images. IEEE Transactions on Medical Imaging. 2007;Vol. 26(5):712–727. doi: 10.1109/TMI.2007.895484. [DOI] [PubMed] [Google Scholar]
- 2.Barron JL, Fleet DJ, Beauchemin S. Performance of Optical Flow Techniques. International Journal of Computer Vision. 1994;Vol. 12(1):43–77. [Google Scholar]
- 3.Behar V, Adam D, Lysyansky P, Friedman Z. The Combined Effect of Nonlinear Filtration and Window Size on the Accuracy of Tissue Displacement Estimation using Detected Echo Signals. Ultrasonics. 2004;Vol. 41(9):743–753. doi: 10.1016/j.ultras.2003.09.003. [DOI] [PubMed] [Google Scholar]
- 4.Benson LN, Freedom RM. Atrial Septal Defect. In: Freedom RM, Benson LN, Smallborn JF, editors. Neonatal Heart Disease. London: Springer; 1992. pp. 633–644. [Google Scholar]
- 5.Boukerroui D, Noble JA, Brady M. Velocity Estimation in Ultrasound Images: a Block Matching Approach. Information Processing in Medical Imaging (IPMI) 2003:586–598. doi: 10.1007/978-3-540-45087-0_49. [DOI] [PubMed] [Google Scholar]
- 6.Cannon JW, Stoll JA, Salgo IS, Knowles HB, Howe RD, Dupont PE, Marx GR, del Nido PJ. Real Time 3-Dimensional Ultrasound for Guiding Surgical Tasks. Computer Aided Surgery. 2003;Vol. 8:82–90. doi: 10.3109/10929080309146042. [DOI] [PubMed] [Google Scholar]
- 7.Chen X, Xie H, Erkamp R, Kim K, Jia C, Rubin JM, O’FDonnell M. 3-D Correlation-based Speckle Tracking. Ultrasonic Imaging. 2005;Vol. 27(1):21–36. doi: 10.1177/016173460502700102. [DOI] [PubMed] [Google Scholar]
- 8.Christensen GE. Information Processing in Medical Imaging (IPMI), Lectures notes in computer science. Vol. 1613. New York: Springer; 1999. Consistent Linear-Elastic Transformations for Image Matching; pp. 224–237. [Google Scholar]
- 9.Cohen B, Dinstein I. New Maximum Likelihood Motion Estimation Schemes for Noisy Ultrasound Images. Pattern Recognition. 2002;Vol. 35:455–463. [Google Scholar]
- 10.Downing SW, Herzog WR, Jr., McElroy MC, Gilbert TB. Feasibility of Off-pump ASD Closure using Real-time 3-D Echocardiography. Heart Surgery Forum. 2002;Vol. 5(2):96–99. [PubMed] [Google Scholar]
- 11.Duan Q, Angelini ED, Herz SL, Ingrassia CM, Gerard O, Costa KD, Holmes JW, Laine AF. Evaluation of Optical Flow Algorithms for Tracking Endocardial Surfaces on Three-dimensional Ultrasound Data; SPIE International Symposium, Medical Imaging; 2005. pp. 159–169. [Google Scholar]
- 12.Duan Q, Shechter G, Gutierrez LF, Stanton D, Zagorchev L, Laine AF, Elgort DR. Augmenting CT Cardiac Roadmaps with Segmented Streaming Ultrasound. SPIE Medical Imaging. 2007a;Vol. 6509 6509OV-1-11. [Google Scholar]
- 13.Duan Q, Angelini E, Homma S, Laine A. Validation of Optical-Flow for Quantification of Myocardial Deformations on Simulated RT3D Ultrasound; IEEE International Symposium on Biomedical Imaging (ISBI); 2007b. pp. 944–947. [Google Scholar]
- 14.Faella HJ, Sciegata AM, Alonso JL, Jmelnitsky L. ASD Closure with the Amplatzer Device. Journal of Interventional Cardiology. 2003;Vol. 16(5):393–397. doi: 10.1046/j.1540-8183.2003.01006.x. [DOI] [PubMed] [Google Scholar]
- 15.Fenster A, Downey DB, Cardinal HN. Three-dimensional Ultrasound Imaging. Physics in Medicine and Biology. 2001;Vol. 46(5):R67–R99. doi: 10.1088/0031-9155/46/5/201. [DOI] [PubMed] [Google Scholar]
- 16.Fleet DJ, Jepson AD. Computation of component image velocity from local phase information. International Journal of Computer Vision. 1990;Vol. 5(1):77–104. [Google Scholar]
- 17.Handke M, Schäfer D, Müller G, Schöchlin A, Magosaki E, Geibel A. Dynamic Changes of Atrial Septal Defect Area: New Insights by Three-dimensional Volume-rendered Echocardiography with High Temporal Resolution. European Journal of Echocardiography. 2001;Vol. 2(1):46–51. doi: 10.1053/euje.2000.0064. [DOI] [PubMed] [Google Scholar]
- 18.Linguraru MG, Vasilyev NV, del Nido PJ, Howe RD. Statistical Segmentation of Instruments in 3D Ultrasound Images. Ultrasound in Medicine and Biology. 2007 doi: 10.1016/j.ultrasmedbio.2007.03.003. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lucas B, Kanade T. An Iterative Image Registration Technique with an Application to Stereo Vision. Proc. Image Understanding Workshop. 1981:121–130. [Google Scholar]
- 20.Maeno YV, Benson LN, McLaughlin PR, Boutin C. Dynamic morphology of the secundum atrial defect evaluated by three dimensional septal transoesophageal echocardiography. Heart. 2000;Vol. 83:673–677. doi: 10.1136/heart.83.6.673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Meunier J, Bertrand M. Ultrasonic Texture Motion Analysis: Theory and Simulation. IEEE Transactions on Medical Imaging. 1995;Vol. 14(2):293–300. doi: 10.1109/42.387711. [DOI] [PubMed] [Google Scholar]
- 22.Meunier J. Tissue Motion Assessment from 3D Echographic Speckle Tracking. Physics in Medicine and Biology. 1998;Vol. 43(5):1241–1254. doi: 10.1088/0031-9155/43/5/014. [DOI] [PubMed] [Google Scholar]
- 23.Montagnat J, Sermesant M, Delingette H, Malandain G, Ayache N. Anisotropic Filtering for Model-based Segmentation of 4D Cylindrical Echocardiographic Images. Pattern Recognition Letters. 2003;Vol. 24:815–828. [Google Scholar]
- 24.Morsy AA, von Ramm OT. FLASH Correlation: A New Method for 3-D Ultrasound Tissue Motion Tracking and Blood Velocity Estimation. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 1999;Vol. 46(3):728–736. doi: 10.1109/58.764859. [DOI] [PubMed] [Google Scholar]
- 25.Noble JA, Boukerroui D. Ultrasound Image Segmentation: A Survey. IEEE Transactions on Medical Imaging. 2006;Vol. 25(8):987–1010. doi: 10.1109/tmi.2006.877092. [DOI] [PubMed] [Google Scholar]
- 26.Ourselin S, Roche A, Prima S, Ayache N. Block Matching: A General Framework to Improve Robustness of Rigid Registration of Medical Images. In: DiGioia AM, Delp S, editors. Medical Image Computing and Computer Assisted Intervention (MICCAI 2000), Lectures Notes in Computer Science. Vol. 1935. New York: Springer; 2000. pp. 557–566. [Google Scholar]
- 27.Papademetris X, Sinusas AJ, Dione DP, Duncan JS. Estimation of 3D Left Ventricular Deformation from Echocardiography. Medical Image Analysis. 2001;Vol. 5(1):17–28. doi: 10.1016/s1361-8415(00)00022-0. [DOI] [PubMed] [Google Scholar]
- 28.Papadopoulou DI, Yakoumakis EN, Makri TK, Sandilos PH, Thanopoulos BD, Georgiou EK. Assessment of Patient Radiation Roses During Transcatheter Closure of Ventricular and Atrial Septal Defects with Amplatzer Devices. Catheterization and Cardiovascular Interventions. 2005;Vol. 65(3):434–441. doi: 10.1002/ccd.20353. [DOI] [PubMed] [Google Scholar]
- 29.Paragios N. A Level Set Approach for Shape-driven Segmentation and Tracking of the Left Ventricle. IEEE Trans Med Imaging. 2003;Vol. 22(6):773–786. doi: 10.1109/TMI.2003.814785. [DOI] [PubMed] [Google Scholar]
- 30.Patel A, Cao QL, Koenig PR, Hijazi ZM. Intracardiac Echocardiography to Guide Closure of Atrial Septal Defects in Children less than 15 Kilograms. Catheterization and Cardiovascular Interventions. 2006;Vol. 68(2):287–291. doi: 10.1002/ccd.20824. [DOI] [PubMed] [Google Scholar]
- 31.Peters TM. Image-guidance for Surgical Procedures. Physics in Medicine and Biology. 2006;Vol. 51:R505–R540. doi: 10.1088/0031-9155/51/14/R01. [DOI] [PubMed] [Google Scholar]
- 32.Podnar T, Martanovič P, Gavora P, Masura J. Morphological Variations of Secundum-type Atrial Septal Defects: Feasibility for Percutaneous Closure using Amplatzer Septal Occluders. Catheterization and Cardiovascular Interventions. 2001;Vol. 53(3):386–391. doi: 10.1002/ccd.1187. [DOI] [PubMed] [Google Scholar]
- 33.Roche A, Malandain G, Ayache N. Unifying Maximum Likelihood Approaches in Medical Image Registration. International Journal of Imaging Systems and Technology: Special issue on 3D imaging. 2000;Vol. 11:71–80. [Google Scholar]
- 34.Singh A, Allen P. Image-flow Computation: an Estimation-theoretic Framework and a Unified Perspective. CVGIP: Image Understanding. 1992;Vol. 65(2):152–177. [Google Scholar]
- 35.Stoll JA, Novotny PM, Howe RD, Dupont PE. Real-time 3D Ultrasound-based Servoing of a Surgical Instrument; Proceeding of IEEE International Conference on Robotics and Automation; 2006. pp. 613–618. [Google Scholar]
- 36.Suematsu Y, Marx GR, Stoll JA, DuPont PE, Cleveland RO, Howe RD, Triedman JK, Mihaljevic T, Mora BN, Savord BJ, Salgo IS, del Nido PJ. Three-Dimensional Echocardiography-guided Beating-heart Surgery without Cardiopulmonary Bypass: a Feasibility Study. Journal of Thoracic and Cardiovascular Surgery. 2004;Vol. 128(4):579–587. doi: 10.1016/j.jtcvs.2004.06.011. [DOI] [PubMed] [Google Scholar]
- 37.Suematsu Y, Martinez JF, Wolf BK, Marx GR, Stoll JA, DuPont PE, Howe RD, Triedman JK, del Nido PJ. Three-dimensional Echo-guided Beating Heart Surgery without Cardiopulmonary Bypass: Atrial Septal Defect Closure in a Swine Model. Journal Thoracic Cardiovascular Surgery. 2005;Vol. 130(5):1348–1357. doi: 10.1016/j.jtcvs.2005.06.043. [DOI] [PubMed] [Google Scholar]
- 38.Thijssen JM. Ultrasonic Speckle Formation, Analysis and Processing Applied to Tissue Characterization. Pattern Recognition Letters. 2003;Vol. 24:659–675. [Google Scholar]
- 39.Yu W, Yan P, Sinusas AJ, Thiele K, Duncan JS. Towards Pointwise Motion Tracking in Echocardiographic Image Sequences - Comparing the Reliability of Different Features for Speckle Tracking. Medical Image Analysis. 2006;Vol. 10(4):495–508. doi: 10.1016/j.media.2005.12.003. [DOI] [PubMed] [Google Scholar]