3-D Imaging Based, Radiobiological Dosimetry

Abstract

Targeted radionuclide therapy holds promise as a new treatment against cancer. Advances in imaging are making it possible to evaluate the spatial distribution of radioactivity in tumors and normal organs over time. Matched anatomical imaging such as combined SPECT/CT and PET/CT have also made it possible to obtain tissue density information in conjunction with the radioactivity distribution. Coupled with sophisticated iterative reconstruction algorithims, these advances have made it possible to perform highly patient-specific dosimetry that also incorporates radiobiological modeling. Such sophisticated dosimetry techniques are still in the research investigation phase. Given the attendant logistical and financial costs, a demonstrated improvement in patient care will be a prerequisite for the adoption of such highly-patient specific internal dosimetry methods.

1. Introduction

Systemically delivered radionuclide therapy of cancer may be accomplished by targeting the tumor itself (1), the tumor-associated vasculature (2), or the tumor-associated stroma (3). In each case, either because of the spatial distribution of the targets or the anatomic and physiological transport and penetration characteristics of the carrier, the spatial distribution of radionuclide within the tumor or normal organs is rarely uniform. Advances in imaging technology, accompanied by advances in image reconstruction and processing methodologies, as well as the availability of positron-emitting analogues of therapeutic radionuclides that allow PET imaging for therapy treatment planning, have made it possible to measure the non-uniformity in radionuclide distribution in patients. Currently, the resolution for nuclear medicine imaging is in the mm to cm range. This makes it possible to detect macroscopic non-uniformities in the activity distribution.

Such information, combined with information regarding tissue properties that may be obtained from anatomical imaging, makes it possible to perform dosimetry calculations that account for the non-uniformity in activity distribution over time and space. In turn, this makes it possible to take a first tentative step towards providing a radiobiological interpretation of absorbed dose (and dose-rate) distributions. The objective of such an approach is to translate absorbed dose to tumor control or normal organ toxicity probability. This paper reviews recent advances in imaging-based 3-D dosimetry that incorporate radiobiological modeling.

2. Overview of imaging-based dosimetry methods

Patient-specific, three dimensional (3D)-image based internal dosimetry involves using the patient’s own anatomy and spatial distribution of radioactivity over time to obtain an absorbed dose calculation that provides as output the spatial distribution of absorbed dose. The results of such a patient-specific 3-D imaging-based calculation can be represented as a 3-D parametric image of absorbed dose, as dose –volume histograms over user-defined regions of interest or as the mean, and range of absorbed doses over such regions (4–10)

A number of groups have pursued and contributed to 3-D Imaging-based patient-specific dosimetry (6, 7, 9, 11–19). Several efforts utilized the basic MIRD formalism as applied to a standard phantom geometry (20, 21). The standard phantom geometry was modified to include on-line Monte Carlo calculation and therefore the ability to introduce tumors and adjust organ masses and shapes.

The software package, MABDOSE (12, 13) uses a three-dimensional lattice in which to conduct radiation transport, scoring energy deposition in discrete voxels. The dosimetry system uses the same algorithm used by the MIRD committee for photon transport, and assumes local deposition of particulate energy.

Clairand, et al., described a dosimetry program, DOSE3D, (15) which calculates dosimetric parameters for anthropomorphic phantoms defined with combinatorial geometry. DOSE3D allows the user to add spheres within the phantom for simulating tumors, to change the shape of one or more organs and, for organs defined by pair, to calculate individual dosimetric parameters for each organ. The program was validated for I-131 and Tc-99m by calculating S values for the Medical Internal Radiation Dose (MIRD) adult male phantom and comparing these results with data provided by MIRDOSE3 (now OLINDA (22–24)).

The software package, OLINDA/EXM, which implements the MIRD standard phantom based methodology (23, 24) and is the nuclear medicine community standard for phantom-based dosimetry calculations allows the user to adjust standard phantom organ masses and also includes a module for estimation of spherical tumor self-dose.

Patient-specific dosimetry software that is not based on standard phantom geometries is briefly described below.

The Royal Marsden Dosimetry Package (RMDP) (11), uses manual, marker- or voxel-based registration to register images from different modalities and the sequence of SPECT studies required for 3-D dosimetry calculations. The 3-D patient-specific dosimetry routines use either a beta-kernel or voxel S-factors. Phase-fitting each voxel's activity series enables more robust maps to be generated in the presence of imaging noise, such as is encountered during late, low-count scans or when there is significant redistribution within the VOI between scans. Error analysis can be applied to each generated dose-map. Patients receiving I-131-mIBG, I-131-NaI, and Re-186-HEDP therapies have been analyzed using RMDP. A Monte-Carlo package, developed specifically to address the problems of I-131 quantification by including full photon interactions in a hexagonal-hole collimator and the gamma camera crystal, has been included in the dosimetry package.

A dosimetry tool called OEDIPE (4, 25, 26) has been developed by the group at Nantes, France to carry out personalized internal dosimetry calculations for nuclear medicine and for radiation safety (in the case of internal contamination). The software creates anthropomorphic voxel-based phantoms from computed tomography (CT) and magnetic resonance imaging (MRI) patient images through the use of a friendly graphical user interface (GUI). Several tools have been built-in to allow for image segmentation. Source data, including VOI localization and cumulated activities, are assessed by single photon emission computed tomography (SPECT) images, and the source may be specified in any number of organs either as a point source or a homogeneously distributed source. It is also possible to choose the dosimetric parameters required for the study (mean organ dose or a dose distribution). Phantom, source, and dosimetric parameters are automatically written into a file. That file is then processed by the Monte Carlo code MCNPX (LANL) to perform the actual dose calculation. OEDIPE can compute either the absorbed dose in each organ (in a few minutes), or the absorbed dose in each voxel of the phantom (i.e. the spatial dose distribution at a tissue level) in a few hours or more. OEDIPE automatically reads the MCNPX output file and processes results to give a list of absorbed doses in each organ or a plot of isodose curves superimposed onto the phantom. Because of the long calculation times required to compute an absorbed dose within an entire whole-body phantom at a spatial resolution of a few millimeters, modifications were made to reduce computational times to reasonable values. More recently, this group has been investigating use of the GATE Monte Carlo code which is based on the GEANT4 Monte Carlo software libraries developed at CERN, the high energy physics center in Geneva, Switzerland (27, 28).

MINERVA, an extension of the external beam treatment planning package, PEREGRINE, developed at the Lawrence Livermore National Laboratory has been used for internal dosimetry calculations (18, 29–31). The goal of the MINERVA dose calculation system is to provide 3-D Monte Carlo simulation-based dosimetry for radiation therapy, focusing on experimental and emerging applications. For molecular targeted radionuclide therapy applications, MINERVA calculates patient-specific radiation dose estimates using computed tomography to describe the patient anatomy, combined with a user-defined 3-D radiation source. The new MINERVA system will ultimately incorporate capabilities for a comprehensive list of radiation therapies including boron neutron capture therapy (BNCT), brachytherapy and proton therapy. Using the open application programming interface (API), other groups can add their own modules and share them.

The DOSIMG software (9) has been used with mathematical anthropomorphic phantoms to examine the impact of different quantitative SPECT algorithms on Monte Carlo–derived absorbed dose calculations. Mathematical phantom–derived CT and SPECT images were generated, and dose calculations derived from these were compared with “true” dose results derived from the actual mathematical phantom data (32). The SPECT quantitation methodologies derived from this work were subsequently applied to 111In/90Y dosimetry (33).

The earliest 3-D imaging based targeted radionuclide dosimetry package described in the literature (34) was heavily influenced by treatment planning techniques developed for external radiotherapy treatment planning (35). The 3D-ID (3D-Internal Dosimetry) software package takes the distribution of radionuclide for a given patient (e.g., from SPECT or PET) and combines it with anatomical information (e.g., CT or MRI) to yield absorbed dose estimates that are specific to a particular patient’s biodistribution and anatomy (7, 10, 34, 36–38). This work introduced the concept of dose-volume histograms for internally administered radionuclides (39). The software package, 3D-ID, may be used to carry out both Monte Carlo and point-kernel-based calculations. It has been used to examine the impact of different radionuclides on the dose distribution, given a fixed cumulated activity distribution (6). 3D-ID has been used to perform a detailed analysis of tumor dose vs. response in the treatment of Non-Hodgkin’s Lymphoma using ¹³¹I-anti-B1 antibody (38). The point-kernel module in 3D-ID, and data from a clinical trial of I-131 labeled anti-B1 antibody were used. More recently, 3D-ID has been used in thyroid cancer patients using I-124 PET imaging data with CT for tumor dosimetry (40). This study demonstrated use of multiple PET image studies which were registered across time and integrated, voxel-by-voxel, to provide a 3-D cumulated activity image used in the dosimetry calculation. The same data set and general approach was also used to perform normal organ dosimetry (41).

A next generation version of 3D-ID, named 3D-RD for 3D-Radiobiological Dosimetry (42), has been developed that incorporates radiobiological modeling. 3D-RD is described in detail in section 6.

3. Quantitative imaging input

Accurate imaging-based dosimetry requires accurate quantitative imaging information. In PET, the imaging data are typically corrected for scatter and attenuation by the camera vendor software. Depending on the characteristics of the positron-emitting radionuclide, additional corrections may be required (43). In SPECT, a number of corrections are needed. A tremendous amount of work has been performed in this area and readers are referred to recent books in this area (44, 45) as well as to a number of key individual contributions (46–57). The work of Frey and co-workers in this area is described below (58–64).

Physical phantom experiments using ¹¹¹In in the RSD torso phantom and Monte Carlo simulation experiments simulating ¹¹¹In in the NonUniform Rational B-Spline (NURBS)-based cardiac torso (NCAT) phantom (65, 66) have been used to evaluate quantitative imaging. In the physical phantom experiment, activities were placed in the heart, lungs, liver, and background with activity concentration ratios of 19:5:20:1. Two spherical lesions with diameters 25 mm and 35 mm were placed in the phantom. The spheres had activity concentrations relative to the background of 20:1 for the larger sphere and 110:1 for the smaller. The total activity used was 5 mCi. A GE Millenium VH SPECT system with Hawkeye x-ray CT, a 1” thick crystal and a MEGP collimator were used for data acquisition. Planar whole body anterior and posterior images were obtained using a pixel size of 2.2 mm. SPECT projections were acquired into 128×128 matrices with a 4.4 mm pixel size at 180 views over 360° using two 14% wide energy windows centered at 171 and 245 keV. The SPECT acquisitions were followed by an X-Ray CT scan. Two SPECT studies were performed: one covering the upper part of the phantom and one the lower part. Long acquisitions were used in order to obtain low noise data. A calibration image using a syringe containing 18.5 MBq (500µCi) of ¹¹¹In was also obtained.

The projections were reconstructed using OSEM reconstructions with compensation for various combinations of attenuation (A), scatter (S), Geometric Response Function (G) and Collimator-Detector Response Function (D) (62). Regions of interest (ROIs) around the various organs were manually defined using the SPECT and CT slices. For the spheres, the axial resolution was insufficient to draw accurate ROIs, so spherical ROIs were created with the correct size and aligned with the centers of the lesions. For the planar studies, ROIs were drawn manually and made smaller than the actual organs to avoid overlap. For the SPECT, the reconstructed pixel values were converted to activity concentration using the calibration factor. For the planar studies, TEW scatter compensation was performed prior to computing the geometric mean. The geometric mean values were converted to activity using a scale factor based on the whole body geometric mean counts and the known activity in the phantom. Relative error in the total activity in each ROI was determined and the results are shown in Table 1 (negative signs indicate underestimation compared to the true activity).

Table 1.

Relative error in organ activities for SPECT with various compensations and planar imaging.

METHOD	Heart	Lung	Liver	Large Sphere	Small Sphere
OSEM-NC	−75.56%	−62.06%	−70.78%	−74.76%	−78.22%
OSEM-A	31.73%	38.49%	42.79%	−1.11%	−11.75%
OSEM-AS	−8.36%	−1.60%	0.04%	−20.30%	−22.42%
OSEM-AGS	−4.58%	3.34%	4.65%	−2.38%	3.85%
OSEM-ADS	−5.22%	2.48%	4.11%	0.74%	9.06%
Planar	−5.16%	18.9%	−2.51%	14.5%	−21.3%

Note that, with full compensation, the quantitative accuracy for SPECT was relatively good. Accuracy was greatly improved by the addition of attenuation and scatter compensation, and for the case of the spheres, Geometric Response Function (GRF) compensation. For ¹¹¹In and this particular collimator, Collimator-Detector Response Function (CDRF) compensation provided only modest improvements. This likely is a result of the fact that the collimator penetration and scatter fraction is only about 11% and is relatively independent of distance. Thus, the calibration procedure effectively accounted for collimator effects. Also note that planar imaging is generally worse than the SPECT methods, especially for the spheres and the lung region.

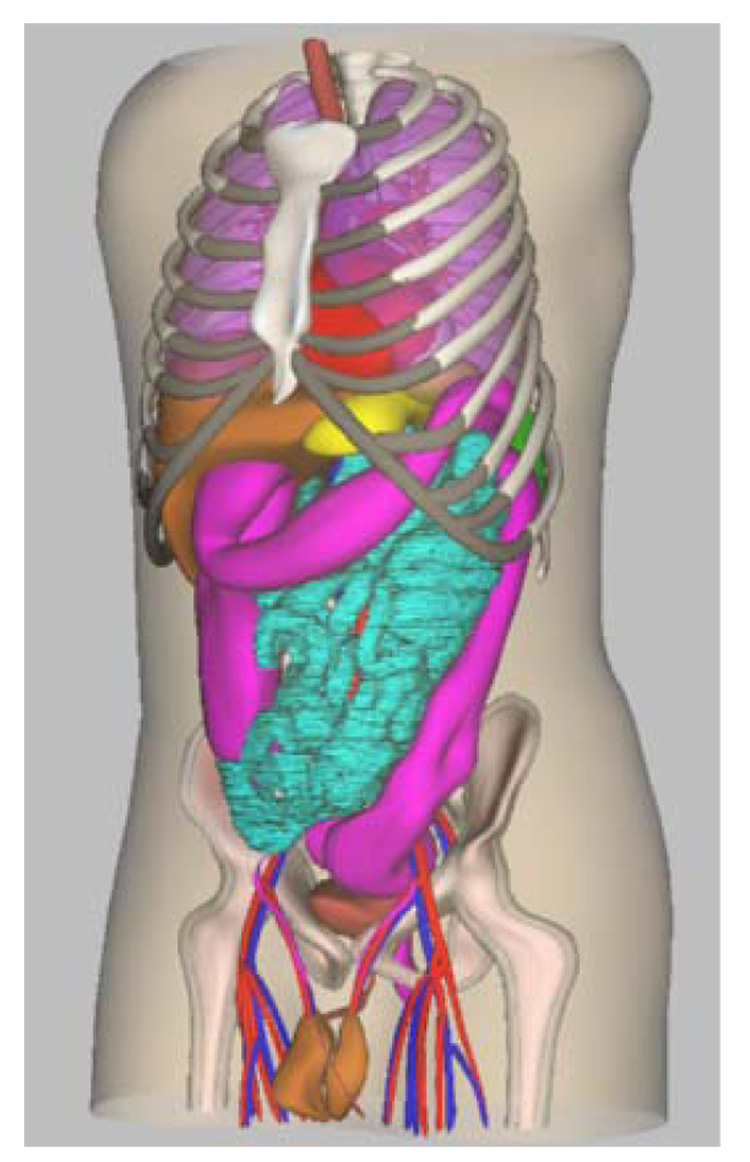
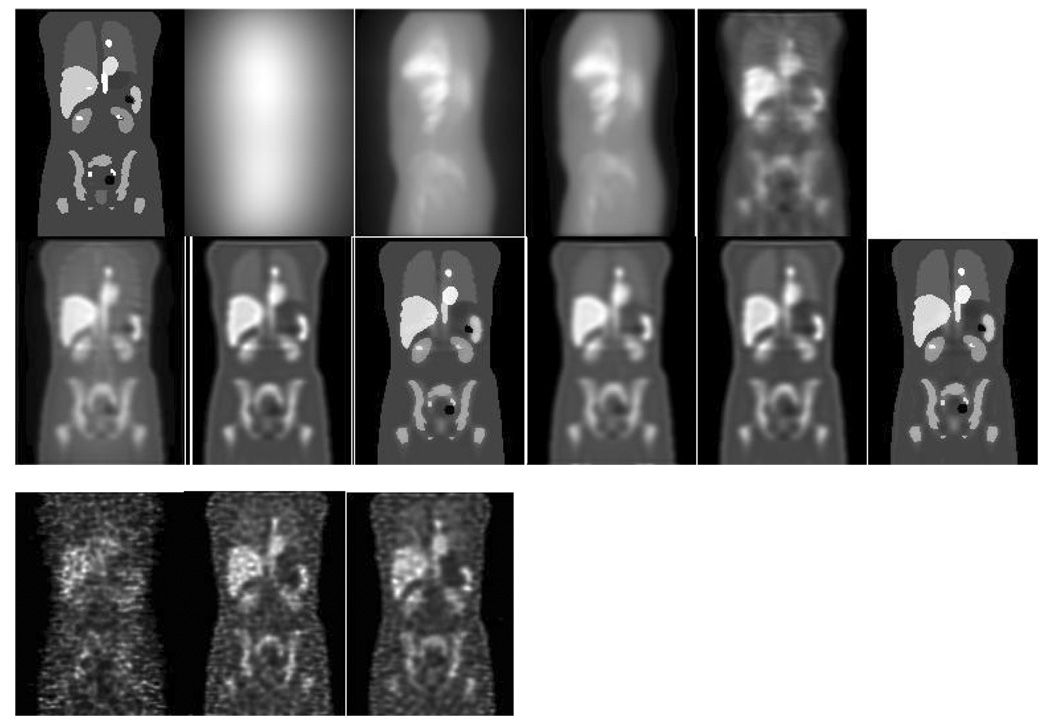
A simulation experiment for a single phantom anatomy and biodistribution was performed to further demonstrate the efficacy of the corrections outlined above. In this study, the NURBS-based cardiac torso (NCAT) phantom (Figure 1) was used as a model of human anatomy. The SimSET Monte Carlo (MC) simulation code (University of Washington (67)) combined with a method for modeling the CDRF was used for imaging simulation (68). Noise modeling was neither clinically realistic nor Poisson distributed. Projection data of the kidneys, liver, and the remainder of the body (including lungs, heart, pelvic marrow, large blood vessels in the chest and abdomen, and spleen) were separately generated. A GE VG camera with 1” crystal and a Medium Energy General Purpose (MEGP) collimator was simulated. Both ¹¹¹In photopeaks were simulated. The uptake in the liver, lungs, blood, bone marrow, kidneys, spleen and body at 0 hr was based on the values determined from a patient study using Zevalin (69). Each organ, and the body individually, were then scaled to model the observed kinetics for that organ. Using this procedure, both simulated SPECT and anterior and posterior planar datasets at 0, 5, 24, 72, and 144 hr post injection, were generated. The SPECT images were reconstructed using Ordered-Subsets Expectation Maximization (OSEM) with no compensation (NC) and with (Attenuation, Collimator-Detector Response Function and Scatter) ADS compensation. The images (see Figure 2) were also reconstructed with an ordered subsets MAP (OSMAP) algorithm using ADS compensation with a prior that penalizes deviations from the region mean in the major blood vessels, marrow, heart, lungs, liver, kidneys, and spleen. For the OSMAP reconstructions, the true regions were used as the regions in which to enforce the prior (the region means were estimated during the reconstruction).

Figure 1.

Depiction of the non-uniform rational b-splines (NURBS) NCAT mathematical phantom.

Figure 2.

The leftmost image is the coronal slice through NCAT phantom with activity distribution modeling an ¹¹¹In Zevalin distribution at 24 hours. The second image to the right is the simulated anterior planar image from the same time point. The right five images are the same coronal slice as the phantom but reconstructed using OSEM-NC, OSEM-ADS, OSMAP-ADS with β=0.1; OSMAP-ADS with β=0.01; and OSMAP-ADS with β=0.001.

Note the good resolution in the OSEM-ADS images compared to OSEM-NC, which is due to the CDRF compensation. The last 3 images in Figure 2 are from the OSMAP-ADS reconstruction. Note that the intensity inside the organs is very uniform, and that the degree of uniformity is controlled by the prior. Also note that the edges are very sharp. Further, the background region is not smooth, as the prior was not applied in this region.

Using these simulated images the exponential clearance curve in each organ was integrated. This was done both for conjugate-view planar (C-Planar) and Q-Planar, a planar quantitation method wherein scatter and attenuation are corrected by Monte Carlo modeling using CT images to define organ anatomy and composition (70, 71). OSMAP-ADS (with β=0.1) reconstruction was used to obtain Q-SPECT. Also, planar/SPECT methods where the half-life was determined from the planar images and the fraction of injected activity (FIA) at time zero was determined by extrapolating the FIA for the 24 hour SPECT image back to time zero were used. The resulting residence times were compared to the true values and the results are shown in Table 2. Note that, once again, negative values represent underestimates. The SPECT residence times for the planar/SPECT method were generally good compared to those from the purely planar method, but there were still significant discrepancies.

Table 2.

Relative error in estimated residence time for planar and SPECT.

Residence Time (h)	Heart	lung	liver	kidney	spleen	marrow	vessels
C-Planar	20±2%	−2±0.8%	29±1%	−21±3%	−12±1%	−24±1%	−36±1%
Q-Planar	−6.5±1%	10±1%	−4±1%	−7±3%	−5±3%	−1±2%	−3.5±3%
Q-SPECT	−3.6±0.5%	2±0.8%	−4.6±0.4%	−5±1%	−3±1%	−0.5±0.8%	6.4±0.8%
C-Planar/Q-SPECT	−9±1%	−10±0.8%	−8±0.7%	−21.5±3%	−17±3%	−18±1.3%	−9±2%
Q-Planar/Q-SPECT	−5±1%	−0.6±1%	−5±1%	−3±0.5%	−2.5±3%	−0.5±2%	5±3%

The results of this simulation study indicate improved accuracy of quantitative SPECT methods as compared to planar and even planar/SPECT methods in estimating the residence times. Since the residence times are directly related to organ dose estimates, the organ dose estimates will be similarly better. These data also point out that the accuracy of planar imaging-based methods commonly used depends strongly on patient-specific factors. Improved planar methods or the use of quantitative SPECT are required in order to obtain more accurate organ dose estimates.

The efficacy of SPECT with compensation for physical image degrading factors in obtaining quantitative activity estimates for ¹³¹I imaging has also been investigated. The same phantom (including the same relative organ activities) as in the ¹¹¹In analysis, above, was used. To highlight the power of iterative reconstruction approaches that simulate the collimator and detector response physics, collimators having thinner septa than traditionally used for ¹³¹I imaging were also included in the study. The simulations were performed using Low Energy High Resolution (LEHR), MEGP, and High Energy General Purpose (HEGP) collimators. To reduce simulation time, only the 364 keV photon (and not higher energy photons) was modeled; noise was not included.

The noise characteristics of CDRF compensation were also investigated. To do this, the counts in the HEGP image were scaled so that the number of geometrically collimated photons was at the same count level as for clinical ¹¹¹In Zevalin images and simulated Poisson noise. For the other collimators, the projection data were scaled by the same factor as for the HEGP images times the relative sensitivity of the collimator with respect to the HEGP collimator. Thus, the total number of counts in the LEHR projection data was greater by a factor of more than 70. However, CDRF compensation was shown to require more iterations and the CDRF deconvolution resulted in noise amplification. This is illustrated in the last row of images in Figure 3. Note that the noise is clearly greater in the LEHR image, resulting from noise amplification during CDRF and the need to use 100 iterations.

Figure 3.

Top row, left to right: coronal slice through phantom; left lateral projection with LEHR collimator; left lateral projection with MEGP collimator; left lateral projection with HEGP collimator; coronal SPECT reconstruction with LEHR collimator and ADS compensation (100 iterations of OSEM with 8 subsets). Middle Row, left to right, SPECT reconstructions from 20 iterations of: MEGP and OSEM-AGS; MEGP and OSEM-ADS; MEGP and OSMAP-ADS; HEGP and OSEM-AGS; HEGP and OSEM-ADS; HEGP and OSMAP-ADS. Bottom row, left to right, reconstructions from noisy projections using same number of iterations as for noise-free images: LEHR and OSEM-ADS; MEGP and OSEM-ADS; HEGP and OSEM-ADS.

From Figure 3, we see that, despite the very poor quality of the LEHR projections, the reconstructed image with ADS is quite good. The image quality for both the MEGP and HEGP images was also significantly improved by ADS compared to AGS. Also, note that the use of OSMAP results in images with very good resolution and very sharp edges. Table 3 shows the relative errors in the organ activity estimates using the images obtained with these different collimators and compensation methods. The perturbation-based Geometric Transfer Matrix (pGTM)-based partial volume compensation (PVC) was also applied and the results are shown. For the LEHR collimator, 100 iterations were used while 20 were used for the MEGP and HEGP collimators. Note that, despite the very poor projection image, the ADS reconstruction for the LEHR collimator has relatively good quantitative accuracy, especially compared to the abysmal accuracy with AGS, indicating the potential efficacy of CDRF compensation. Also note that, despite significantly higher levels of penetration and scatter, the MEGP collimator provides, in general, more accurate quantification. These data also demonstrate the importance of PVC: use of either the pGTM method or OSMAP resulted in significantly improved quantitative accuracy, especially for small structures like the blood and bone marrow, but also for organs like the spleen that are near organs with high uptake (such as the blood or heart). In the columns that include a “±”, the values are the mean and standard deviation over 50 realizations of noisy projections. As indicated by the noise in the image, the activity estimates from the LEHR collimator are less precise than those for the MEGP or HEGP collimators despite having ~70 times more counts. For the MEGP and HEGP collimators, the precisions are similar. Though these results are not for an optimal number of iterations they are suggestive that the choice of collimators with thick septa for ¹³¹I imaging is not as obvious when the goal is accurate quantification and when CDRF compensation is used.

Table 3.

Relative error (in %) in organ activity estimates for the 3 collimators and various reconstruction methods.

Organ/ROI	LEHR Collimator		MEGP Collimator				HEGP Collimator
	OSEM ADS	OSEM AGS	OSEM ADS	OSEM ADS PVC	OSMAP ADS	OSEM AGS	OSEM ADS	OSEM ADS PVC	OSMAP ADS	OSEM AGS
Blood	−60.2±1.1	1704	−41.9±51	−9.67±84	−24.63	−14.43	−44.6±52	−4.20±96	−25.17	−35.43
Marrow	−37.5±1.4	3343	−19.6±50	−1.08±61	−8.48	32.60	−20.7±47	1.54±60	−8.09	−0.63
Heart	−12.1±98	2545	−8.66±37	−0.53±41	−0.97	48.05	−9.24±28	0.02±31	−0.64	18.24
Kidney	−19.9±2.7	4384	−10.9±85	2.1±99	−2.71	55.19	−11.4±90	4.0±1.1	−2.11	15.67
Liver	−7.5±55	2927	−5.60±22	−0.22±24	0.09	56.46	−5.98±25	0.23±27	0.34	24.03
Lung	6.6±1.2	5100	1.46±37	6.60±42	−0.15	88.03	1.98±36	7.45±42	0.30	39.41
Spleen	−25.6±2.4	2378	−12.9±64	−0.56±73	−7.30	31.74	−13.4±64	0.83±66	−7.69	7.25

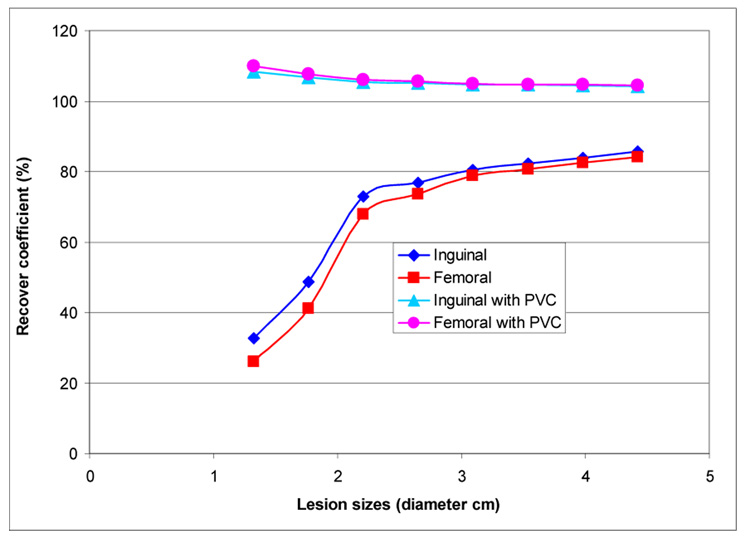
The question of quantification of structures of different sizes was examined by introducing spheres of different diameters in the femoral and inguinal regions of the phantom (Figure 4). The results were generated using OSEM-ADS, with and without PVC; 20 iterations w/ 8 subsets per iteration were used. The pixel and bin size were 0.442 cm. HEGP collimation was simulated; the phantom was 128 × 128 × 200. One hundred and twenty 128² projections spanning 360 degrees were collected. The phantom organ activity concentration was chosen to match that of a recent NHL imaging simulation study (72): background = 4; blood = 48; bone marrow = 4; heart = 48; kidneys = 80; liver = 28; lung = 28; spleen = 52; tumor = 100. The results show 20 to 30% quantitative accuracy when the lesion size is >2.5 cm and results are obtained without PVC. Partial volume correction leads to a 5 to 10 % overestimate of the activity. Because of the lower photon energy and reduced scatter, ¹¹¹In images are expected to yield better results for small lesions.

Figure 4.

Recovery coefficient as a function of lesion size for two lesions placed at the inguinal and femoral vessels. The effect of partial volume correction (PVC) is illustrated.

4. Radiobiological modeling

Accurate, detailed absorbed dose calculations are useful only to the extent that they are biologically relevant and easily interpretable. The uniformity (or lack thereof) of absorbed dose distributions and their biological implications has been examined intensively, primarily in animal studies, however (73–81). To address the question of how to best represent the large amount of data in 3-D distributions of absorbed dose, one may look to the radiotherapy field and use dose-volume histograms to represent dose distributions in targeted radionuclide therapy (39).

Equivalent Uniform Dose

The Equivalent Uniform Dose (EUD) model takes this one step farther by introducing the radiobiological parameters, α and β, the sensitivity per unit dose and per unit dose squared in the linear-quadratic dose-response model, to convert the spatially varying absorbed dose distribution into an equivalent uniform absorbed dose value that would yield a biological response similar to the one expected from the original dose distribution. This provides a single value that may be used to compare different dose distributions; the value also reflects the likelihood that the magnitude and spatial distribution of the absorbed dose is sufficient for tumor kill. The concept (and value) of EUD is illustrated by considering a tumor in which one-half of the volume receives a dose of 100 Gy and the other half receives 0 Gy. Such an absorbed dose distribution would lead to treatment failure since the tumor half not exposed to radiation would re-grow. In this case the absorbed dose delivered uniformly throughout the tumor volume (i.e., the EUD) would be close to zero in order to be consistent with the expected biological effect of the dose distribution described above. The illustration should also make it clear that EUD is not valid for normal organs since normal organs have a structural organization (i.e., 100 Gy to even a small portion of the spine can lead to paralysis; in contrast, 100 Gy to a large portion of the liver may be inconsequential since the liver can regenerate). Calculation of EUD requires knowledge of the radiosensitivity of the tumor and the assumption that all elements of the tumor are clonogenic. As is well-recognized, the radiosensitivity is likely to vary in different tumor regions (e.g., hypoxic vs. normoxic). Clonogenicity, likewise will be variable throughout the tumor (i.e., dormant vs rapidly proliferating regions). Nevertheless, EUD is still potentially useful in comparing different tumor absorbed dose distributions in a patient trial population.

Biologically Effective Dose (BED)

That dose rate influences response has been known for several decades (82). The BED formalism (83, 84), initially termed Extrapolated Response Dose (ERD), was developed to compare different fractionation protocols for external radiotherapy. BED may be thought of as the actual physical dose adjusted to reflect the expected biological effect if it were delivered at a reference dose rate. As in the case of EUD, by relating effects to a reference value, this makes it possible to compare doses delivered under different conditions. In the case of EUD the reference value relates to spatial distribution and is chosen to be a uniform distribution. In the case of BED the reference value relates to dose rate and is chosen to approach zero (total dose delivered in an infinite number of infinitesimally small fractions). In radionuclide therapy the dose rate varies temporally and a number of investigators have examined the implications of this on tumor control and normal tissue toxicity (85–92). Motivated by the desire to incorporate internal emitter dosimetry in conjunction with external beam radiotherapy the group at the Royal Marsden first implemented voxel-based BED calculations to account for the difference in dose-rate between radionuclide therapy and external beam radiotherapy and to present BED maps (93, 94). The rationale for incorporating BED into imaging-based dosimetry software such as 3D-RD is also driven, in part, by the use of engineered, lower molecular weight targeting agents (peptides and single-chain constructs), by multi-step targeting approaches (95–100) and by bone-seeking agents (101–103). The targeting and excretion kinetics of these agents differ substantially and, as suggested by pre-clinical and clinical evidence (92, 104–107), the dose rate at which a total dose is delivered may become an important parameter in understanding normal organ toxicity and tumor response. To date, almost all clinical studies have considered only total absorbed dose, the majority of which is delivered at an exponentially decreasing dose rate. In contrast, the benchmark for projecting potential toxicity and justifying initial phase I activity and absorbed dose levels has been the experience with normal organ tolerance in external beam radiotherapy. However, in external beam therapy, the absorbed dose is typically delivered at high dose-rate in daily 2-Gy fractions over a period of 30 to 40 days. In the simplest and more generally applied BED model knowledge of three tissue-specific parameters: α, β, and μ, an estimate of the repair rate (assuming exponential repair) following tissue damage is required.

5. Imaging-based 3-D dosimetry

3-D Imaging-based dosimetry entails the following steps: 1. Input a series of longitudinal 3-D SPECT/CT or PET/CT images. 2. Register the images across time by using both the SPECT or PET data set and the corresponding CT set. 3. Obtain the cumulated activity for each voxel either by fitting an exponential function to each voxel and integrating analytically over time or by performing a numerical integration over time for each voxel (40). 4. Use the CT image voxel values to assign density and composition (i.e., water, air and bone) (6, 108). 5. Use the 3-D cumulated activity image and the matched density and composition image to perform a Monte Carlo calculation to estimate the absorbed dose by tallying energy deposition in each voxel (6). 6. Present the absorbed dose distribution as a set of images, isodose contour plots, or as dose volume histograms for user-identified tumor or normal organ volumes.

6. Imaging-based 3-D radiobiological modeling

To introduce radiobiological modeling, the steps described in the previous section are modified so that absorbed dose-rate images are calculated for each time-point rather than for a cumulated activity map. To obtain the total absorbed dose the individual dose-rate images are integrated over time to yield images of absorbed dose. The individual absorbed dose rate images may also be interpreted as absorbed dose images reflecting the absorbed dose delivered over the imaging time-period. By fitting these images voxel by voxel to an exponential function, an image of absorbed dose rate may be obtained. This information, coupled with assignment of the radiobiological parameters, α, β, μ, the radiosensitivity per unit dose, radiosensitivity per unit dose squared and the repair rate assuming an exponential repair process, respectively (109, 110), can be used to generate a BED value for each voxel, and subsequently an EUD value for a particular user-defined volume.

In external radiotherapy, the expression for BED is:

$$\mathit{\text{BED}}=Nd\left(1+\frac{d}{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.}\right)$$ (1)

.

In this equation, N is the number of fractions given of absorbed dose, d, delivered over a time interval that is negligible relative to the repair time for radiation damage (i.e., at high dose rate) where the interval between fractions is long enough to allow for complete repair of repairable damage induced by the dose d; repopulation of cells is not considered in this formulation. The parameters, α and β are the coefficients for radiation damage proportional to dose (single event is lethal) and dose squared (two events required for lethal damage), respectively. A more general formulation of equation 1 is:

$$\mathit{\text{BED}}(T)=D_T(T)·\mathit{\text{RE}}(T)$$ (111)

, where BED(T) is the biologically effective dose delivered over a time T, D_T(T) is the total dose delivered over this time, and RE(T) is the relative effectiveness per unit dose at time T. The general expression for RE(T) assuming a time-dependent dose rate described by D^&(t) is given by:

$$\mathit{\text{RE}}(T)=1+\frac{2}{D_T(T)\left(\frac{\alpha }{\beta }\right)}\times {\displaystyle \underset{0}{\overset{T}{\int }}dt·D^{\&}(t){\displaystyle \underset{0}{\overset{t}{\int }}dw·D^{\&}(w)e^{-\mu (t-w)}}}$$ (3)

.

The second integration over the time-parameter, w, represents the repair of potentially lethal damage occurring while the dose is delivered, i.e., assuming an incomplete repair model (112). If we assume that the dose rate for radionuclide therapy, D^&(t), at a given time, t, can be expressed as an exponential expression:

$$D^{\&}(t)=D_0^{\&}{e}^{-\lambda t}$$ (4)

, where $D_0^{\&}$ is the initial dose rate and λ is the rate at which the absorbed dose decreases (= ln(2)/t_e; t_e= the half-life associated with the absorbed dose decrease), then, in the limit, as T approaches infinity, the integral in equation 3 reduces to:

$$\frac{{D_0^{\&}}^2}{2\lambda \left(\mu -\lambda \right)}$$ (5)

.

Substituting this expression and replacing D_T(T) with D, the total dose delivered, and using $D_0^{\&}=\lambda D$, which may be derived from equation 4, we get:

$$\mathit{\text{BED}}=D+\frac{\beta D^2}{\alpha }\left(\frac{\text{ln}(2)}{\mu ·t_e+\text{ln}(2)}\right)$$ (6)

.

In this expression, the dose rate parameter, λ, is represented by ln(2)/t_e. The derivation follows closely that described by Dale et. al, (109).

In cases where the absorbed dose rate in a particular voxel is not well fitted by a single decreasing exponential, alternative formalisms have been developed that account for an increase in the dose rate followed by exponential reduction. Since the number of imaging time-points typically collected in dosimetry studies would not resolve a dual parameter model (.i.e., uptake and clearance related dose-rate changes) the current methodology assumes that the total dose contributed by the rising portion of a tissue or tumor time-activity curve is a small fraction of the total absorbed dose delivered.

Equation 6 depends upon the tissue-specific intrinsic parameters α, β, and μ. These three parameters are set constant throughout a user-defined organ or tumor volume. The voxel specific parameters are the total dose in a given voxel and the dose-rate assigned to the voxel (represented by the corresponding half-time). Given a voxel at coordinates (i,j,k), D^ijk and t_e^ijk are the dose and half-time associated with the reduction in absorbed dose over time for the voxel. The imaging-based formulation of expression 6 that is incorporated into a 3-D radiobiological dosimetry is then:

$${\mathit{\text{BED}}}^{ijk}=D^{ijk}+\frac{\beta {D^{ijk}}^2}{\alpha }\left(\frac{\text{ln}(2)}{\mu ·{t_e}^{ijk}+\text{ln}(2)}\right)$$ (7)

.

The user inputs values of α, β, and μ for a particular volume and D^ijk and t_e^ijk are obtained directly from the 3-D dose calculation and dose rate image, respectively. This approach requires organ or tumor segmentation that corresponds to the different α, β, and μ values. The dose values are obtained by Monte Carlo calculation as described previously (6), and the effective clearance half-lives are obtained by fitting the data to a single exponential function, as has been previously described (10). Once a spatial distribution of BED values has been obtained a dose-volume histogram of these values can be generated. Normalizing so that the total area under the BED (differential) DVH curve is one, one converts the BED DVH to a probability distribution of BED values denoted, P(ψ), where ψ takes on all possible values of BED. Then, following the derivation for EUD from reference (74), the EUD is obtained as:

$$\mathit{\text{EUD}}=-\frac{1}{\alpha }\text{ln}\left({\displaystyle \underset{0}{\overset{\infty }{\int }}P(\psi )e^{-\alpha \psi }d\psi }\right)$$ (8)

.

The EUD of the absorbed dose distribution, as opposed to the BED distribution, can also be obtained using equation 8, but using a normalized DVH of absorbed dose values rather than BED values. Expression 8 may be derived by determining the absorbed dose required to yield a surviving fraction equal to that arising from the probability distribution of dose values (absorbed dose or BED) given by the normalized DVH.

The voxel-based methodology outlined above has also been applied at the organ level and formulated to be consistent with the MIRD organ-level S-value dosimetry schema (113).

7. Implementation of 3-D imaging based radiobiological modeling

Results from a 3-D imaging–based radiobiological modeling analysis obtained using an early version of the software package, 3D-RD (3D-Radiobiological Dosimetry) (114), in which activity kinetics were used in place of absorbed dose kinetics for the radiobiological modeling are illustrated below.

The 3D-RD dosimetry methodology was applied to the case of an 11 year old female thyroid cancer patient who has been previously described in a publication on MCNP-based 3D-ID dosimetry.

SPECT/CT images were obtained at 27, 74, and 147 hours post injection of a 37MBq (1.0mCi) tracer ¹³¹I dose. All three SPECT/CT images focused on the chest of the patient and close attention was directed at aligning the patient identically for each image. The images were acquired with a GE Millennium VG Hawkeye system with a 1.59 cm thick crystal.

An OSEM based reconstruction scheme was used to improve quantization of the activity map (115). A total of 10 iterations with 24 subsets per iteration was used. This reconstruction accounts for effects including attenuation, patient scatter, and collimator response. Collimator response includes septal penetration and scatter. The SPECT image counts were converted to units of activity by accounting for the detector efficiency and acquisition time. This quantification procedure, combined with image alignment, made it possible to follow the kinetics of each voxel. Using the CTs, which were acquired with each SPECT, each subsequent SPECT and CT image was aligned to the 27 hour 3-D image set. A voxel by voxel fit to an exponential expression was then applied to the aligned data set (40) to obtain the clearance half-time for each voxel.

To obtain mean absorbed dose, mean BED and EUD, as well as absorbed dose and BED-volume-histograms, voxels were assigned to either tumor or normal lung parenchyma using an activity threshold of 21% of highest activity value; this approach is the same as that used in reference (114).

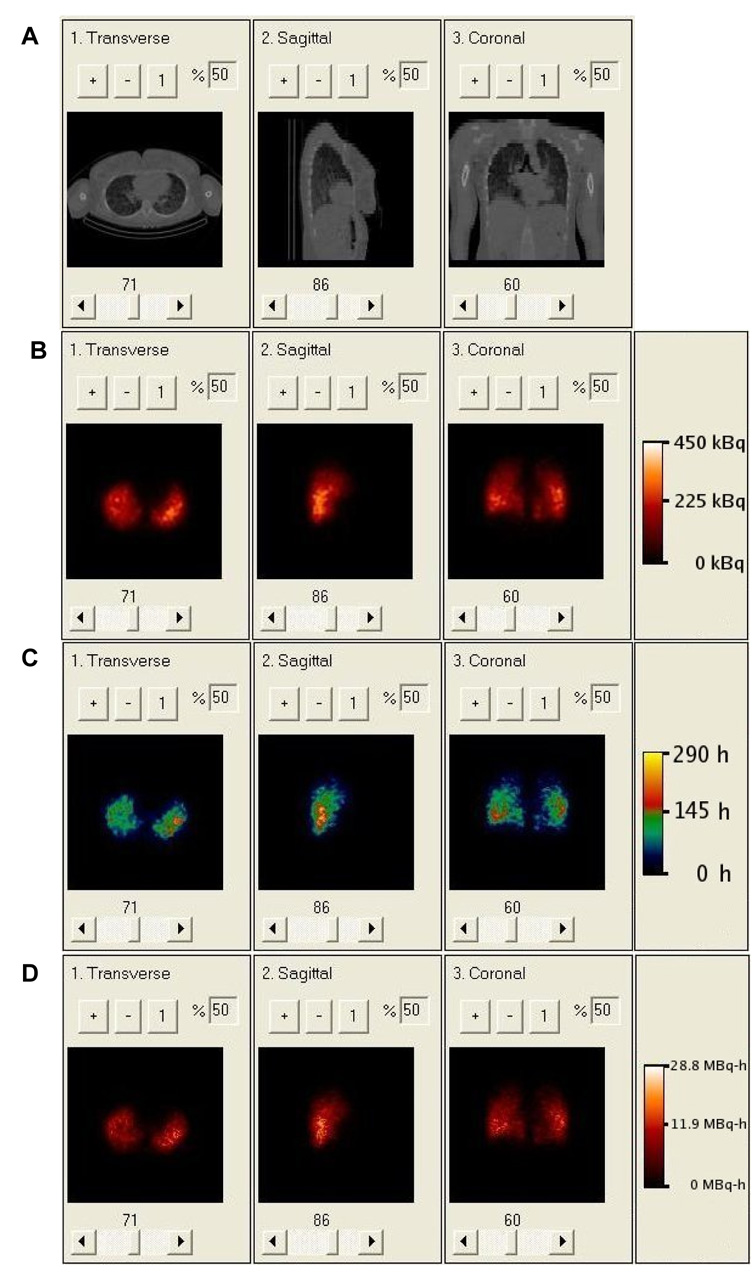
The clinical example illustrates all of the elements that have an influence on absorbed dose at the voxel level. As shown on the CT scan (Fig. 5a), there is a highly variable density distribution in the lungs due to the tumor infiltration of normal lung parenchyma. Coupled with the low lung density, this gives a density and tissue composition that includes air, lung parenchyma and tumor (which was modeled as soft tissue). As shown on figures 5b and 5c, the activity and clearance kinetics of ¹³¹I are also variable over the lung volume. These two data sets were used to calculate the cumulated activity images shown in figure 5d.

Figure 5.

A. Clinical CT of patient showing non-uniform density distribution in lungs. B. Clinical SPECT of patient showing non-uniform activity distribution. C. Rate map generated from 3 longitudinally aligned SPECT images; regions with effective half-life greater than the physical half-life of ¹³¹I reflect tumor uptake. D. Cumulative activity image generated from rate map and SPECT.

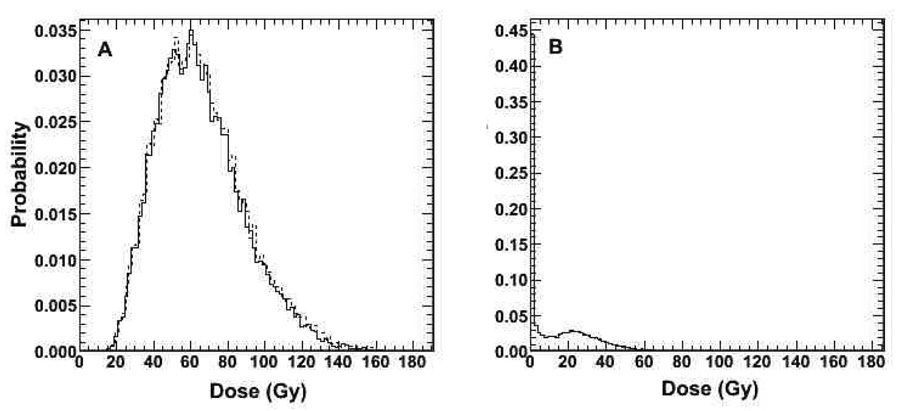
Figure 6 and Figure 7 depict the results obtained with the radiobiological modeling capabilities of 3D-RD. Figure 6 depicts a parametric image of BED values. Within this image the spotty areas of highest dose are areas where high activity and low density overlap. In Figure 7a, normalized (so that the area under the curve is equal to 1) DVH and BED DVH (BVH) are shown for tumor voxels. The near superimposition of DVH and BVH suggests that dose rate will have a minimal impact on tumor response in this case. Figure 7b depicts the normalized BVH for normal lung parenchyma. The DVH and BVH are given in Gy and reflect the predicted doses resulting from the administered therapeutic activity of 1.32 GBq (35.6 mCi) of ¹³¹I. These plots may be used to derive EUD values. Mean absorbed dose, mean BED, and EUD are summarized in table 4. The EUD value for tumor, which accounts for the effect of a non-uniform dose distribution, was approximately 43% of the mean absorbed dose. This reduction brings the absorbed dose to a range that is not likely to lead to a complete response using a single administration of activity. The analysis demonstrates the impact of dose non-uniformity on the potential efficacy of a treatment.

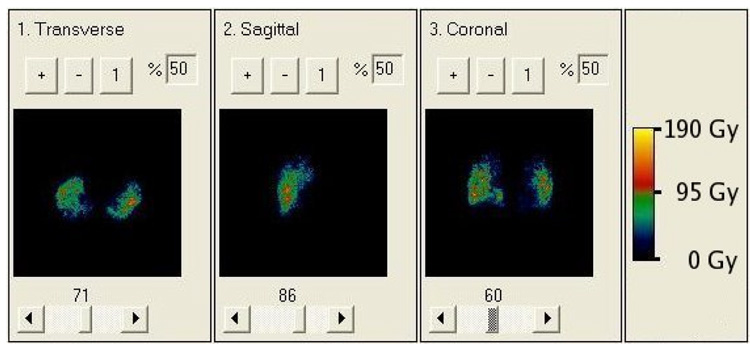
Figure 6.

BED map resulting from 3D-RD using full patient specific data. While the values of absorbed dose and BED are different, their relative changes from voxel to voxel are so similar that it is nearly impossible to visually differentiate the two.

Figure 7.

A. Differential absorbed dose (solid line) and BED-volume-histogram (dashed line) for tumor. B. differential BED-volume-histogram of lung. Both figures show results from full patient specific 3D-RD calculation.

Table 4.

Summary of results from the clinical 3D-RD calculation.

	Tumor (Gy)	Lungs (Gy)
Mean Absorbed Dose	57.7	9.5
Mean BED	58.5	9.8
EUD	25.0	8.3

Future Implementations

The ability to translate parametric absorbed dose images from radionuclide therapy into BED images that can be compared with or added to BED images from external radiotherapy will make it possible to combine these two treatment modalities so that external radiotherapy planning can account for the dose-distribution arising from targeted radionuclide therapy.

Advances in biological imaging may be expected to provide information regarding the spatial variability of radiosensitivity within a tumor and such information could then be incorporated into the radiobiological modeling scheme described above by replacing the assumption of single-valued α, β and μ parameters with voxel specific or sub-region specific values.

Routine implementation of the internal dosimetry methodology outlined in this work will require additional imaging and patient time. Given the attendant logistical and financial costs, a demonstrated improvement in patient care should be a prerequisite for the adoption of such highly-patient specific internal dosimetry.