Aberrant spatiotemporal activation profiles associated with math difficulties in children: A magnetic source imaging study

Abstract

There is ample evidence that parietal cortices serve as key components of the mechanism responsible for number processing. The goal of the present study was to investigate the relative degree and timing of cortical activation in parietal, temporal, and frontal regions during simple arithmetic tasks in children who experience math difficulties. Real-time brain activity was measured with magnetoencephalography during simple addition and numerosity judgments in students with math difficulties and average or above average reading skills (MD group, N = 14), students with below average scores on both math and basic reading tests (MD/RD group, N=16) and students with above average scores on standardized math tests (Control group, N=25). Children with MD showed increased degree of neurophysiological activity in inferior and superior parietal regions in the right hemisphere compared to both controls and MD/RD students. Left hemisphere inferior parietal regions did not show the expected task-related changes and showed activity at a significant temporal delay. MD students also showed increased early engagement of prefrontal cortices. Taken together, these findings may indicate increased reliance on a network of right hemisphere parietal (and possibly frontal areas as well) for simple math calculations in students who experience math difficulties but perform within normal range in reading.

Introduction

Investigating the nature and acquisition of mathematical competence is of importance because of the incidence and persistence of developmental math difficulties (MD). Problems with math occur in about 6% of children (Shalev, Auerbach, Manor, & Gross-Tsur, 2000). As with reading difficulties (RD), MD is persistent over time, with one study reporting that 95% of children with MD in grade 5 continuing to show evidence of MD in Grade 11 (Shalev, Manor, & Gross-Tsur, 2005). Although incidence rates parallel those for reading difficulties, MD is less frequently studied than reading difficulties (Fletcher, Lyon, Fuchs, & Barnes, 2007). Many children with RD and/or attention problems have comorbid MD; in RD, this comorbidity is commonly estimated at 40% (Lewis, Hitch, & Waller, 1994). Regardless of comorbidity, poor math skills significantly impact everyday life and employment, predicting wages, and productivity (Rivera-Batiz, 1992) as well as level of independence in populations like spina bifida, where math problems are common (Dennis & Barnes, 2002).

Mathematical competencies

Cognitive studies suggest that mathematical competence reflects both procedural and conceptual knowledge (Rittle-Johnson, Siegler, & Alibali, 2001). Procedural knowledge includes the understanding of algorithms or step by step procedures needed to perform calculations (Geary, 2004). As procedures become more familiar and developed, they may be represented by explicit knowledge of overlearned arithmetic facts retrieved from long-term memory (e.g., 3 + 2 = 5). Conceptual knowledge refers to an understanding of more basic principles in a domain; examples within math may include counting (e.g., the concept of cardinality) and numerosity (Butterworth, 2005). These types of knowledge are likely to have bidirectional influences on the development of math competency, although they may be supported by different cognitive and neural systems. Indeed, most authors agree that students with MD have difficulty with both types of knowledge. Procedural difficulties include the ability to learn and efficiently retrieve basic arithmetic facts (Jordan, Kaplan, & Hanich, 2002; 2003; Jordan & Montani, 1997; Kirby & Becker, 1988) and the ability to learn and implement efficiently calculation procedures and algorithms (Geary, 1993). Conceptual difficulties include counting principles (Geary, Bow-Thomas, & Yao, 1992; Geary, Hamson, & Hoard, 2000) as well as estimation and number sense (Hanich, Jordan, Kaplan, & Dick, 2001; Jordan & Hanich, 2003). Several investigations have explored differences among subgroups of children with MD alone versus MD comorbid with RD (e.g., Cirino et al., 2007; Geary et al., 2001; Hanich et al., 2001; Fuchs & Fuchs, 2002), with one of the most salient differences being performance on word problem or other problem solving measures, consistent with significant language difficulties in the comorbid group not present in students with MD only (Fuchs et al., in press).

Neural correlates of mathematical competencies

Attempts to outline the brain mechanisms responsible for mathematical knowledge have only recently become the focus of systematic exploration. In these functional brain imaging studies, inferior and superior parietal cortices show robust activation during performance of a variety of arithmetic tasks. In adults, Dehaene, Spelke, Pinel, Stanescu, and Tsiukin (1999) found that different brain areas were preferentially engaged in tasks that involve exact answers versus approximate estimations. Exact calculations engaged the inferior prefrontal cortex in the left hemisphere, as well as the left angular gyrus, whereas estimation tasks activated the inferior parietal lobes bilaterally. Activation was also observed during performance of both of these tasks, in additional frontal cortical areas including inferior and middle frontal cortices (Venkatraman, Ansari, & Chee, 2005), and (primarily) the left precentral gyrus (Chochon et al., 1999) and premotor/supplementary motor cortex (Kawashima et al., 2004; Zhou et al., 2007). Although most brain activation studies were conducted with adults, hemodynamic brain activation profiles associated with performance of arithmetic tasks in school-age children have been investigated in two recent studies. Kawashima et al. (2004) studied eight children who never experienced math difficulties on single-digit addition, subtraction, and multiplication using fMRI (blocked design). Regions that showed significantly higher BOLD signal compared to fixation across tasks included middle frontal (primarily in the left hemisphere), and bilateral inferior temporal and lateral occipital cortices. Additional activity in the supplementary motor area was noted for the addition task, and in the vicinity of the right intraparietal sulcus during performance of the subtraction task.

In a more recent study, Kucian et al. (2006) tested 20 typically achieving 9–12 year old children and 18 age-matched students with a clinical diagnosis of math disability (developmental dyscalculia). Activation tasks included exact and approximate single-digit addition (task-specific activation contrasted with a brightness discrimination task), and a non-symbolic numerocity task involving comparison of arrays of small objects varying in number (a visual fixation task was used as baseline). The two groups did not differ significantly on performance of any of the three tasks which required manual responses. During performance of the exact addition task by the control group, increased activation was observed in ventral and lateral occipitotemporal cortices, inferior, middle, and superior frontal gyri, cortex along the banks of the intraparietal sulcus (bilaterally), and the left precentral gyrus. Children with MD showed a similar pattern of activity, with the exception of left ventral occipitotemporal regions. Activation associated with the numerosity task in the control group included ventral occipitotemporal and intraparietal regions bilaterally. Children in the MD group did not show significant change in activity in the intraparietal region but showed, instead, activity in the right superior parietal lobe. A similar findings has been reported by Price, Holloway, Räsänen, Vesterinen, & Ansari (2007) who found reduced right intraparietal activity in MD children. It should be noted, however, that direct group comparisons did not yield significant differences in activation in any of the ROIs for the exact addition task. It is possible that stronger underlying group differences may have been masked by the lack of adequate temporal resolution of the BOLD method, given that neurophysiological activity associated with the performance of simple arithmetic tasks is expected to take place within the first few hundred milliseconds following the presentation of a stimulus leading up to the point when a verbal or manual response is produced by the participant. If group differences in regional neurophysiological activity are time-limited it is possible that they do not lead to sufficient increases in metabolic demands and subsequent elevation of the BOLD signal.

Altogether, preliterate (Cantlon et al., 2006; Rivera, Reiss, Eckert, & Menon, 2005) and school-age children with typical development of math skills (Kucian et al., 2006) show reliable parietal activity, like adults, predominantly in portions of the inferior and superior parietal lobule surrounding the intraparietal sulcus (IPS). There are some indications that whereas IPS activity in children is bilaterally symmetric in degree and may even show a slight right hemisphere predominance (Cantlon et al., 2006), activity in this region may show left hemisphere predominance at least in some adult participants and under certain testing conditions (Chochon et al., 1999; Rivera, Reiss, Eckert, & Menon, 2005).

The present study approaches the issue of the temporal course of brain activation using magnetoencephalography, a method that possesses adequate spatial and temporal resolution and accuracy. Moreover, while the majority of studies reviewed previously focus on adult participants who never experienced unusual difficulties in learning math (Chochon et al., 1999; Dehaene, Spelke, Pinel, Stanescu, & Tsiukin, 1999; Kawashima et al., 2004; Venkatraman, Ansari, & Chee, 2005; Zhou et al., 2007), the present study investigates math-related brain activity in children that vary in their educational histories with respect to math and reading ability. Brain activity was measured during two tasks: one requiring addition of Arabic numerals (single digit numbers to ensure that all children would perform at above chance levels). The use of this task is consistent with similar tasks used in previous investigations, which focus on arithmetic tasks tapping procedural knowledge. The second task was designed to tap more fundamental numerosity judgments that may be more closely related to conceptual knowledge, and do not involve the processing of visual numeric symbols or calculation. Three groups of children were evaluated: children with below-average general math abilities and average or above average reading skills assessed at the word level (math difficulties or MD group), students with below average scores on both math and basic reading tests (math and reading difficulties or MD/RD group), and students with above average scores on standardized math tests (control group). The key comparison aimed by the study was between the non-impaired students and those in the MD group (presenting with a math-specific learning difficulty not accounted for by concomitant difficulty in the written language domain). We hypothesized that the spatiotemporal brain activation profiles of children in the MD group would involve unique features that distinguish this group from the profiles of activity observed in students who were non-math impaired. These differences were expected to be more prominent in brain areas which previous studies with non-impaired children have shown to host neurophysiological processes involved in the maintenance of conceptual numerosity knowledge, math fact storage and retrieval, or both, depending on which of the two tasks aberrant features of brain activity are to be found. These areas may include inferior and superior parietal regions and possibly also dorsolateral prefrontal regions.

The rationale for including a group of students with combined math and reading difficulties is that comparisons of activation data between this group and each of the other two groups of the study may help establish the specificity of the potentially aberrant profile of activity associated with math difficulties. There is little evidence regarding the neurophysiological deficits associated with comorbid math and reading difficulties, with psychoeducational data pointing to the presence of prominent language deficits contributing to math difficulties (Fuchs et al., in press). These findings raise the possibility that the aberrant brain activation profiles in MD/RD children may feature reduced activity in language-related areas even during the performance of arithmetic calculations. In order to proclaim a particular feature of the brain activation profile observed in the MD as specific to math difficulties, this feature must be clearly different from both the non-impaired and the children with combined math and reading difficulties.

Methods

Participants

The primary target group was 14 children with severe math difficulties (MD group) as indicated by scores at or below the 30th percentile (standard score of 92) on the Arithmetic subtest of the Wide Range Achievement Test-III (range 70–92; Wilkinson, 1993). The 30^th percentile cutoff was employed based on commonly adopted definitions of math difficulties (Jordan, Kaplan, & Hanich, 2002). All children in the group with MD scored in the average range (above the 30th percentile) on the WRAT-III Reading subtest (standard score range 92–120) and all but one were right-handed. Table 1 displays demographic and psychoeducational information for each of the three groups of participants.

Table 1.

Demographic data, educational history, and performance on standardized tests for the three groups of participants (range, mean and SD in parentheses).

	Control1	MD	MD/RD
Gender (boys/girls)	16/9	8/6	7/9
Age (years)	8.2–14.8 (10.4±1.5)	8.8–11.7 (9.7±.9)	8.9–12.2 (10.2±1.4)
Ethnicity (Caucasian, H, A-AM2)	6/10/9	4/3/8	4/3/11
# Retained	0	3	8
Special Education (# attended / years)	1 (RD) / 2	4 / 2–3	8 / 2–6
WASI Vocabulary (T score)	39–64@§ (52.4±7.3)	30–57@ (44.2±8.2)	37–61§ (42.7±6.4)
WASI Matrices SS (T score)	41–65§ (53.0±7.2)	31–62@ (48.8±11.9)	33–54@§ (39.4±10.1)
FSIQ	89–133*@ (106.2±11.7)	79–117* (94.4±12.0)	78–118@ (86.4±11.9)
WRAT Math SS	92–120@† (107.5±6.8)	70–92† (86.6±5.9)	45–92@ (79.0±13.1)
WRAT Reading SS	83–115§ (99.1±8.5)	92–120† (106.0±8.6)	60–92§† (81.2±9.5)

¹Non math-impaired children included six who experienced reading difficulties (age range: 8.9–11.4 years, mean: 10 years, 3 boys, 1 left handed). Their performance on standardized tests was as follows: WRAT Math: 100.8±9.6, WRAT Reading: 88±4.3, WASI Vocabulary: 52.8±9.9, WASI Matrices: 55.2±8.7, FSIQ: 103.8±14). Pairwise group differences

^*p < .05

^@p < .01

^{§ †}p < .0001.

²H: Hispanic, A-AM: African-American.

A second group of 25 children who had never experienced difficulties in math (NI group) served as the primary control group. All 25 children obtained standard scores > 92 on standardized math assessments and all but one was right-handed. The NI group included 6 children who scored below the 30^th percentile on reading tests. This subgroup failed to show any significant difference (at a less conservative criterion of α = .1) with the other members of the NI group on measures of brain activity (see below), and was subsequently incorporated into the NI group.

The third group consisted of 16 students with difficulties in both reading and math (MD/RD group as indicated by scores at or below 92 on reading and math; four were left-handed). All participants were also required to have a score of at least 70 on either the Vocabulary or Matrices subtests of the Wechsler Abbreviated Scales of Intelligence (Wechsler, 2005; corresponding to a T score of 30 as listed in Table 1). We did not require discrepancies of IQ and math achievement because of the absence of evidence suggesting that such definitions identify different subgroups of MD (see Fletcher et al., 2007, Chapter 8). All children spoke English as their primary language.

Statistical comparisons for age, gender, and ethnicity were not significant, but the samples were small. Significant group main effects were found on all five measures listed in Table 1 (p< .0001 in all cases). Bonferroni-corrected pairwise comparisons revealed significant differences between the MD and MD/RD groups which were restricted to WRAT reading, and WASI Matrices subtests (in both cases MD>MD/RD). The Control and MD groups differed on WRAT Math, WASI Vocabulary, and FSIQ. Finally, the Control group performed better than the MD/RD group an all five measures of achievement and cognition. As expected the group with MD/RD was more severely impaired in cognitive and academic skills.

Procedures

Tasks

In the addition task the children were instructed to mentally add two single-digit numbers (excluding ties), presented one above the other, and verbally provide the answer immediately after the stimuli disappeared from the screen to avoid contamination of the MEG data segments by movement-related magnetic artifacts. Stimulus size was 1° (horizontal) × 2.5° degrees (vertical visual angle). Stimuli for the dot estimation task consisted of random dot arrays containing 5 to 25 black dots (each subtending .2°). A total of 100 different arrays were constructed by varying overall size (3° to 4° in diameter) and density in a manner independent of dot number in order to promote estimation based on numerosity rather than density or size. Participants were asked to verbally produce their estimate of the number of dots in each array after the stimulus disappeared from the screen. Stimuli for both tasks were arranged randomly into four blocks of 25 items. The stimuli for each activation task were chosen in order to ensure relatively high performance level for all participants and prevent floor effects by children with math difficulties. The visual stimuli were projected centrally for 1500 ms, one at a time (with a randomly varied interstimulus interval of 3–4 sec) through an LCD projector (Sharp Model XG-E690U) on a back-projection screen located approximately 60 cm in front of the participant. Task order was counterbalanced across participants.

Imaging procedures

Magnetoencephalography or magnetic source imaging (MSI) recordings were obtained with a whole-head neuromagnetometer array (4-D Neuroimaging, Magnes WH3600), that consisted of 248 first-order axial gradiometer coils, housed in a magnetically shielded chamber and arranged to cover the entire head surface. The magnetic flux measurements were digitized at 250 Hz, filtered with a bandpass filter between 0.1 and 20 Hz and subjected to a noise reduction algorithm that is part of the 4D-Neuroimaging software. The single-trial event-related field segments (ERFs) in response to 60–80 stimulus presentations (out of a total of 100 recorded), were averaged after excluding those containing eye movement or other myogenic or mechanical artifacts.

To identify the intracranial origin of ERFs the magnetic flux distribution recorded simultaneously over the entire head surface at successive points (4 ms apart) was analyzed using a minimum norm model to obtain estimates of the time-varying strength of intracranial currents (MNE Software, v. 2.5, Hämäläinen, 2006). This method affords greater spatial resolution and allows detection of simultaneous magnetic sources distributed along the entire cortical surface. The model assumes a continuous distribution of current along the cortical surface which has some minimum norm (Hämäläinen & Ilmoniemi, 1994). Estimated current sources were anatomically constrained by an MRI-derived surface model of each participant’s brain. This surface model was generated by a fully-automated cortical surface reconstruction procedure using FreeSurfer software (Dale, Fischl & Sereno, 1999) for producing a detailed geometric description (regular tessellation of the cortical surface consisting of equilateral triangles known as vertices) of the gray-white matter boundary of the neocortical mantle and the mesial temporal lobe. Each hemisphere consisted of approximately 150,000 vertices (depending on each subject’s cortical surface area). For estimating current sources, the MNE software requires the Freesurfer-derived cortical surface reconstruction for defining the boundaries of a solution source space. A grid-spacing of 7 mm was used to construct icosahedrons to decimate the number of vertices from 150,000 to approximately 3,000 per hemisphere. Additionally, the MNE software was used to construct a single compartment boundary element model using triangular tessellations to model each vertex as a potential current dipole perpendicular to the cortical surface during the forward calculations. The inverse solution was subsequently reduced to obtaining an estimate of the scalar distribution of dipole strength across current sources within orientation-specific cortical patches of vertices (Dale & Sereno, 1993). Co-registration of each MEG dataset with its corresponding MRI dataset was performed using an automated co-registration routine within MNE which aligns digitization points in the MEG headshape file with the fiducial points demarcated on the outer skin surface reconstruction of the MRI.

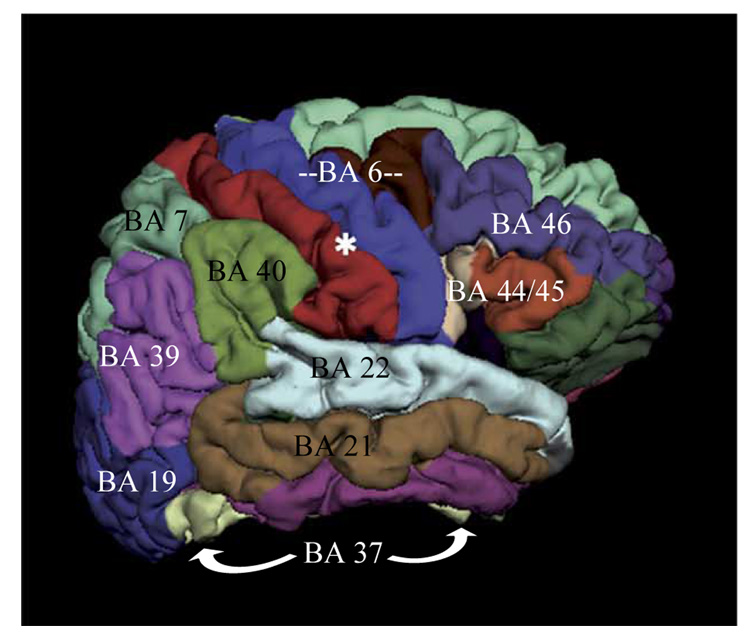
Preliminary Equivalent Current Dipole modeling of magnetic activity using procedures described in detail elsewhere (Simos et al., 2007) indicated that the vast majority (96%) of activity sources were found in the following areas in both hemispheres: posterior portion of the superior temporal gyrus (BA 22), supramarginal gyrus (BA 40), angular gyrus (BA 39), inferior (BA 44/45) and middle frontal cortex (BA 46), motor/premotor cortex (BA 4/6), ventral occipito-temporal cortex (BA 37), lateral occipito-temporal cortex (BA 19), middle temporal gyrus (BA 21), the superior parietal lobule (BA 7), and mesial temporal cortex (hippocampus and parahippocampal gyrus-MTL). The anatomical outline of these data-derived ROIs is shown on a lateral view of the right hemisphere of a model brain in Figure 1. Current estimates derived by MNE were averaged across all voxels defining each of the ROIs listed above. For each ROI averaging was also performed in the time domain, across all of the 3 ms time points comprising 15 successive 50 ms time bins (50–100, 100–150, 150–200 ms, etc up to 800 ms). This approach aimed at (a) establishing the temporal progression of regional activity in each group of participants, (b) determining if group differences in the degree of regional activity were time-dependent (i.e., more systematic for particular time windows), and (c) estimating the peak latency of activity in each ROI and searching for potential group differences in this measure.

Figure 1.

Outline of ROIs used in the MNE analyses.

The first set of analyses established the outline of the spatiotemporal profiles of activity associated with the performance of each task by each group of participants—essentially the temporal progression of regional activity for each group. The dependent variable in these analyses was the median time point of the 50-ms time bin when average MNE current reached peak value. ROIs from both hemispheres were ranked according to peak latency and a series of dependent-sample t-tests were computed between ROIs (earliest peaking ROI with each subsequent ROI, second earliest ROI with each subsequent ROI, etc), in order to test the hypothesis that regional onset latency differences were statistically significant. In order to control for Type I error for multiple comparisons, all tests were evaluated at alpha = .001. This procedure was performed separately for each task and each group of participants. Results were used to identify sets of ROIs that peaked at approximately the same latency after stimulus onset. When activity did not peak at exactly the same time, statistical tests indicated that peak latencies were not systematically different across regions that formed each set. Activity in the majority of ROIs belonging to a particular set of ROIs peaked significantly earlier than activity in the majority of ROIs in the set of subsequently active regions. Across groups two or three sets of successively active ROIs were identified for each task.

The second set of analyses focused on group differences in the degree of activity per hemisphere, task, and time bin. The dependent measure in these analyses, which were performed separately for each ROI, was the average current for each 50 ms time bin. This measure was used as an index for the magnitude of neurophysiological activity that took place during stimulus processing and prior to the initiation of an overt behavioral response (pronunciation of a numeric answer). Significant main effects of Group were further evaluated using planned pairwise comparisons (applying the Bonferroni correction). Significant three-way interactions involving Group were further evaluated by examining lower-order interactions (Group by Hemisphere at each time bin, Group by Time at each hemisphere) whereas significant two-way interactions were followed up by examining simple main effects of Group at each time bin or hemisphere, accordingly. Follow-up tests for interactions involving both Group and Hemisphere, also included Hemisphere simple main effects for each Group. Significant hemisphere asymmetries in the degree of regional activity will be mentioned, even in the absence of group-specific Hemisphere effects, in order to facilitate comparisons between the present and findings from previous studies using similar tasks.

The third set of analyses assessed group differences in peak latency of activity (in milliseconds after stimulus onset). Peak latency data for each ROI were separately submitted to ANOVAs with Group as the between and hemisphere as the within subjects factor.

The fourth set of analyses, were guided by previous findings regarding the brain regions which are presumably involved in the brain mechanisms responsible for math functions (inferior and superior parietal cortices, and inferior and middle frontal cortices). The average MNE current in each of five ROIs (across all time bins) were submitted to an ANOVA with ROI, hemisphere, and task as the within subjects factors. Analyses were performed separately for each group. All ANOVA results were evaluated using the Huynh-Feldt method as a precaution against inhomogeneity of variance problems.

The final set of analyses consisted of zero-order correlations between in-scanner performance (percent correct additions and dot number estimations) and degree of activity in ROIs were significant group differences were revealed by previous analyses. Partial correlation coefficients, controlling for the covariation between performance and activity in all other ROIs were also computed.

Results

In-scanner task performance

Significant group main effects (controlling for age) were found for performance on both tasks (Dot Number Estimation: F[1,51] = 4.90, p < . 01, Addition: F[1,51] = 21.19, p < .0001). As shown in Table 2, performance on the Addition task was significantly higher for the Control group as compared to both the MD and MD/RD groups. Superior performance was also noted for the MD as compared to the MD/RD group. Controls and children in the MD group did not differ significantly on dot number estimation accuracy, although both groups performed better than the MD/RD group. Interestingly, more than half of the variance in the Control vs. MD/RD group difference appears to be common variance with WASI Vocabulary score (indicated by a drop from η² = .52 (when correcting for age only) to η² = .26 (when WASI vocabulary performance was added as a covariate). On the other hand, differences in in-scanner performance between the Control and MD groups did not appear to be due to differences in IQ measures: effect size of the Group effect was minimally reduced from η² = .26 to η² = .25 when WASI vocabulary was added as a covariate and η² = .24 when FSIQ was used as a covariate in addition to age.

Table 2.

In scanner performance (Mean ± SD of percent correct responses in each task¹) for the three groups of participants.

	Control	MD	MD/RD
Addition	88.3±9.5*§	74.4±14.5*@	53.0±24.5§@
Dot Number Estimation	49.7±7.2@	49.7±10.5‡	42.2±8.1‡@

¹Corrected for age. Pairwise tests

^*‡p < .05

^@p < .01

^§†p < .0001

MEG data

Preliminary analyses on MNE current data did not reveal significant differences in the degree of regional activity between the group of students without math or reading difficulties and the group of students who only showed reading difficulties. These analyses failed to show main effects of Group (NI, RD), or interactions involving Group and ROI, or Hemisphere even when evaluated against a less conservative alpha level (p> .1 in all cases). Accordingly, data were collapsed across these two groups in all subsequent analyses.

Temporal progression of regional activity

Addition

Controls

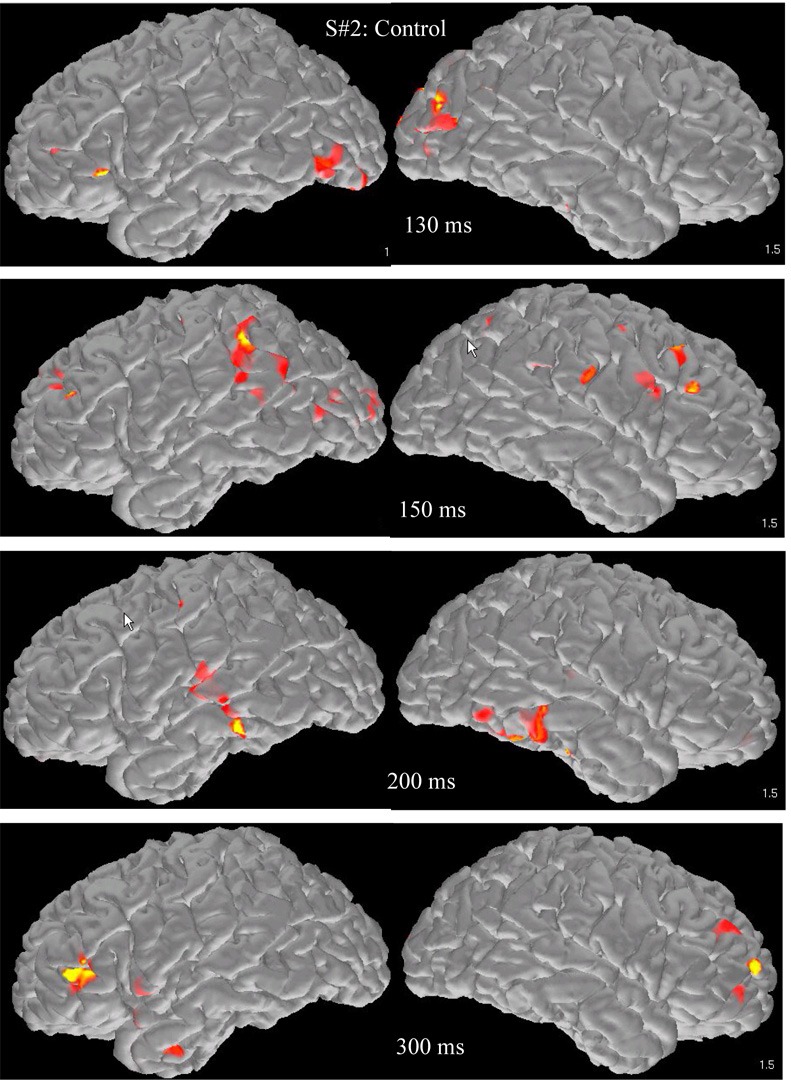
A representative series of snapshots from the activation profile of a student from the Control group is shown in Figure 2. The average spatiotemporal brain activation profile in this group involved early activity in the following ROIs: Bilateral, ventral and lateral occipitotemporal areas (peaking between 215–244 ms after stimulus onset), bilateral precentral/premotor regions (243–255 ms), and also in the supramarginal (260 ms), middle (263 ms), and superior temporal gyri (268 ms) in the right hemisphere (see Figure 3). There were no systematic differences in onset latency among ROIs in this set.

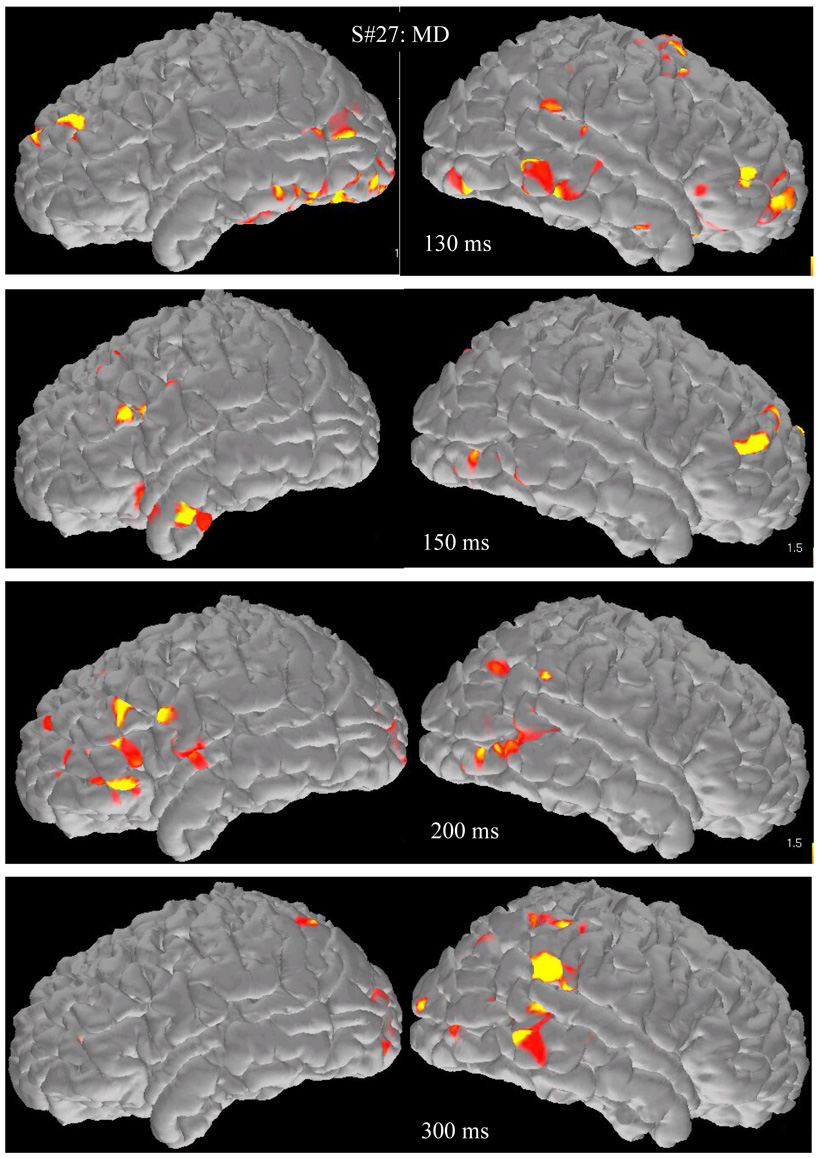
Figure 2.

Brain activation map snapshots during addition from two representative participants (a student from the control group (upper four rows) and a student with math difficulties and average reading performance (MD group, lower set of four rows). Images from the surface of the left hemisphere are in the left hand column and images from the right hemisphere in the right hand column.

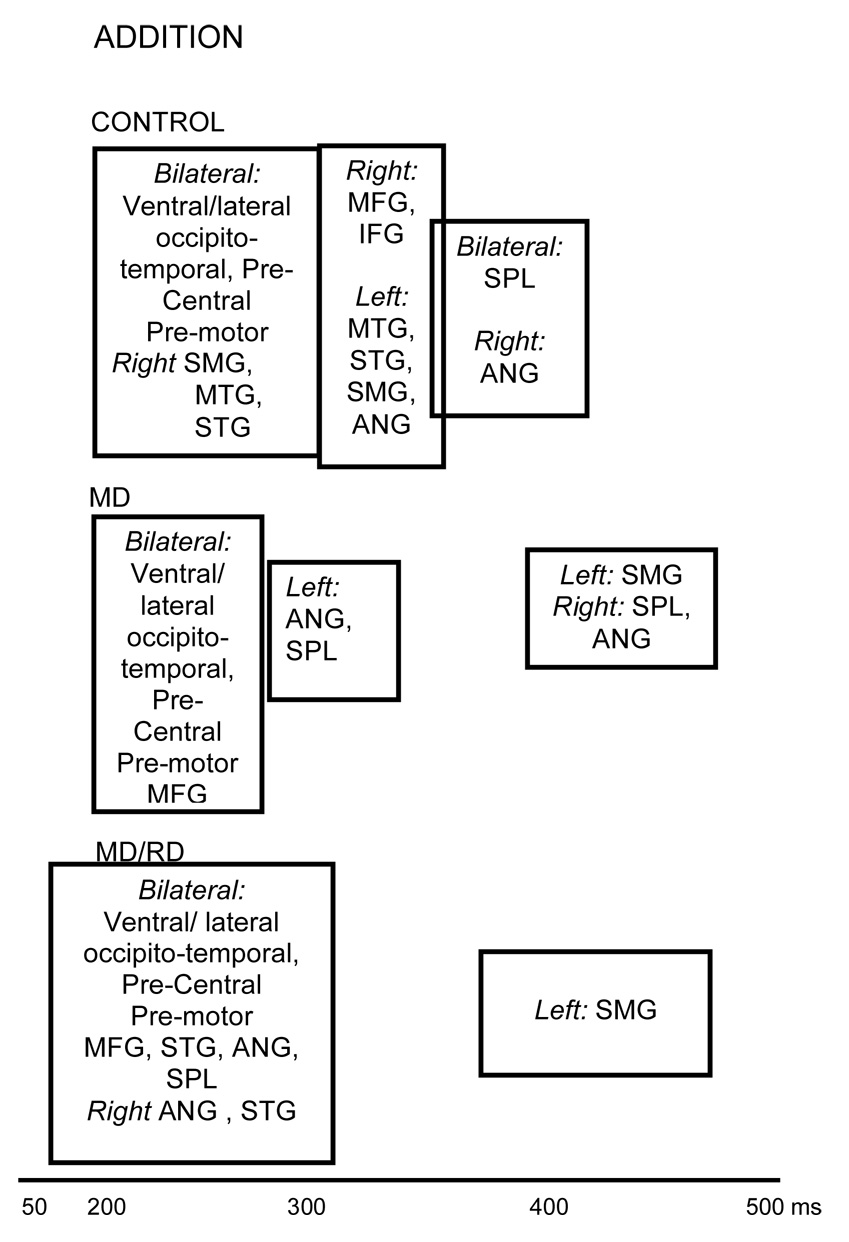
Figure 3.

Temporal progression of activity based on peak latency for each ROI after stimulus onset during Addition. ROIs which are grouped together peak at latencies which are not significantly different from each other. Significant differences in peak latency were found between the majority of ROIs grouped separately. Boxes containing sets of ROIs are aligned on the time axis based on mean peak latency.

Activity subsequently peaked in a second set of ROIs: the left middle temporal (304 ms), inferior frontal (294 ms), supramarginal (318 ms), angular (333 ms), superior (324 ms) and middle frontal gyri, and also in the right mesial temporal cortex, and the right inferior and middle frontal gyri. The third set of ROIs included the right angular gyrus (355 ms), the left mesial temporal cortex (352 ms), and the superior parietal lobule bilaterally (342 ms).

MD group

The lower row of images in Figure 2 displays active voxels projected on the surface of a representative participant’s brain at different time points. As shown in Figure 3, magnetic activity for children in the MD group was initially detected in some of the same ROIs where early activity was detected in the Control group (bilateral precentral/premotor [166–223 ms], ventral [187–222 ms] and lateral [198–227 ms] occipitotemporal regions, and the right superior temporal gyrus [222 ms]). Activity in the remaining ROIs was significantly delayed compared to activity in the majority of areas in the first set of ROIs with latencies that did not differ significantly from each other. The only exception was the left supramarginal gyrus (440 ms), the last ROI in the temporal sequence of regions, which peaked significantly later than activity in two ROIs from the second set, namely the left angular gyrus (282 ms) and the right superior parietal lobule (276 ms).

MD/RD group

As shown in the lower portion of Figure 3, the spatiotemporal profile for addition in the MD/RD group involved early activity in a larger set of temporally undifferentiated regions (with peak latencies ranging between 211 and 300 ms). This set included bilateral ventral and lateral occipitotemporal and precentral/premotor areas and the right superior temporal gyrus (which were part of the earliest set of ROIs in the other two groups of participants), and also middle/inferior frontal regions, bilaterally, and the right angular gyrus. Activity in the left supramarginal gyrus peaked last (413 ms) as in the case of the MD group.

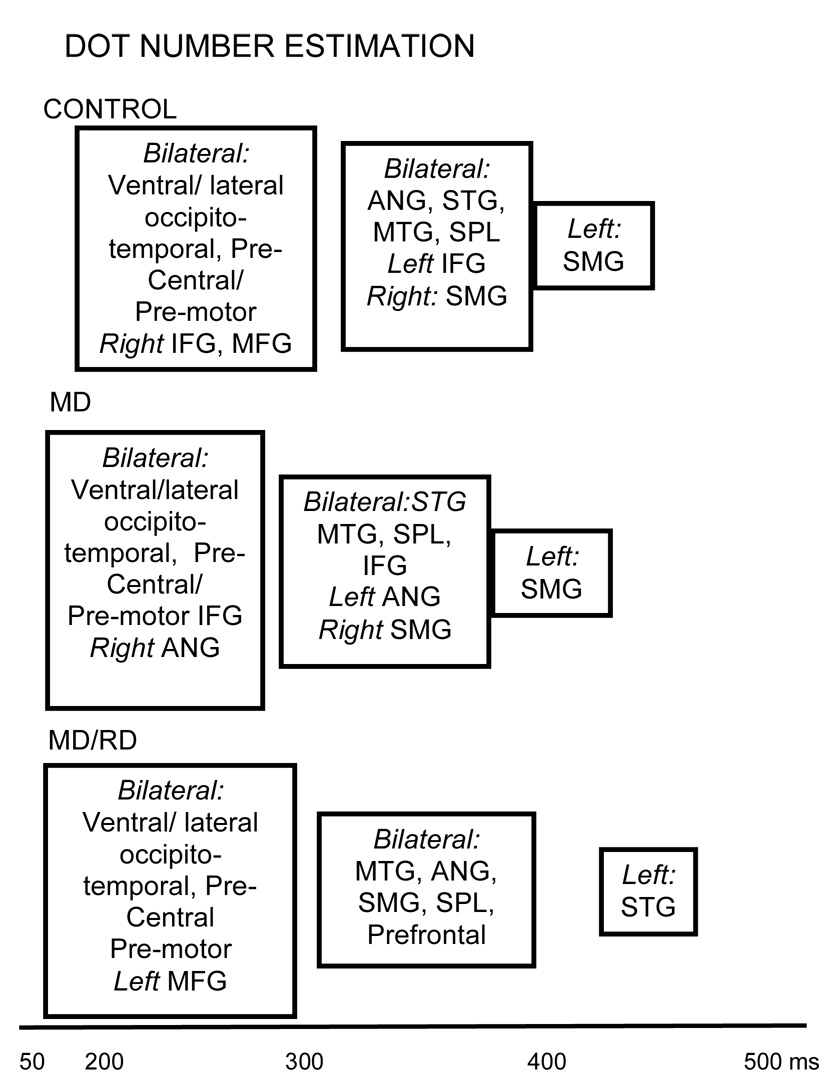
Dot number estimation

Controls

As shown in the upper portion of Figure 4, the spatiotemporal activation profile during performance of the Dot Number Estimation task for Controls involved near simultaneous activity in bilateral lateral (225 ms), ventral occipitotemporal (237 ms), and precentral regions (254 ms), and also in middle (263 ms) and inferior frontal regions (275 ms) in the right hemisphere. Then activity peaked in a second set of ROIs that included the angular gyrus [287–298 ms], the superior parietal lobule [385–390 ms], the superior [380–395 ms] and middle temporal gyri [399–410 ms], bilaterally, and also the left inferior frontal gyrus (299 ms), and the right supramarginal gyrus (364 ms). Activity in the left supramarginal gyrus peaked last (420 ms).

Figure 4.

Temporal progression of activity based on peak latency for each ROI after stimulus onset during performance of the Dot Number Estimation task. Addition. ROIs which are grouped together peak at latencies which are not significantly different from each other. Significant differences in peak latency were found between the majority of ROIs grouped separately. Boxes containing sets of ROIs are aligned on the time axis based on mean peak latency.

MD group

Figure 4 (middle portion) shows the spatiotemporal profile of activity for the MD group. Early, temporally undifferentiated activity was noted in the following ROIs: bilateral ventral occipitotemporal (179–226 ms), precentral/premotor (199–234 ms), lateral occipitotemporal cortex (220–250 ms), and inferior frontal areas (215–270 ms), and also in the right angular gyrus (275 ms). The second set of areas where activity peaked next included bilateral middle/superior temporal gyri, the superior parietal lobule, and the middle frontal region, and also the left angular and the right supramarginal gyrus. Last, activity peaked in the left supramarginal gyrus (393 ms).

MD/RD group

Figure 4 (lower portion) shows that the earliest set of active ROIs for dot estimation included similar areas as those noted for the Controls and MD children (bilateral ventral/lateral occipitotemporal, precentral/premotor regions) and, in addition, the left middle frontal gyrus (latency range for this set of ROIs: 200–277 ms). Peak latency in the remaining areas (range: 303–423 ms) did not significantly differ from each other with the exception of the area with the latest peak (left superior temporal gyrus [457 ms]).

Group differences in the degree of magnetic activity

Initial analyses revealed significant group differences in the whole-brain average MNE current across all ROIs for both tasks (Addition: F[1,51] = 4,90, p < .01, Dot Number Estimation: F[1,51] = 6,90, p < .002). Pairwise comparisons indicated that global current was significantly lower for the MD/RD group as compared to both the Control (Addition: p < .006, Dot Number Estimation: p < .001) and MD groups (Addition: p < .013, Dot Number Estimation: p < .01). Accordingly, the average MNE current across all ROIs in each task was used as a covariate (along with age) in subsequent analyses performed on average current estimates for each ROI (omnibus ANCOVAs and follow-up tests involving Group). Preliminary analyses on data from all 15 time bins (50–800 ms) did not reveal significant activity in the earliest (50–100 ms) and latest time bin (750–800 ms). Accordingly subsequent analyses included only 13 time bins (100–750 ms post-stimulus onset). Group differences in average current in each ROI separately were assessed with a series of ANCOVAs with Task (Addition, Dot Number Estimation), Hemisphere (left, right), and Time bin (13) as the within subjects factors, and Group (Control, MD, MD/RD) as the between subjects factor. In this manner, potential group differences in the strength of regional activity which may be specific to a particular task and time window could be assessed. Analyses also permitted assessment of potential group differences in the degree and/or direction of hemisphere asymmetries in the strength of activity in each region.

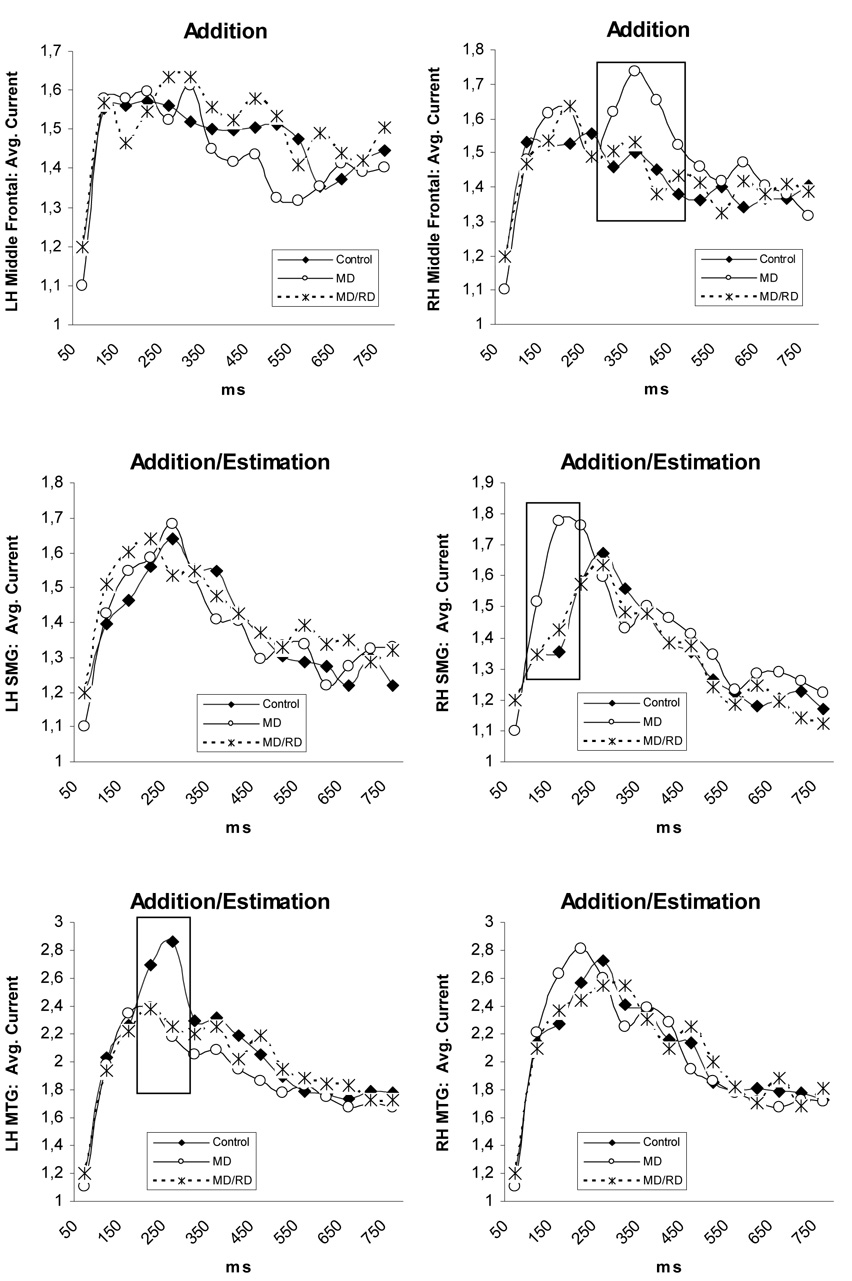
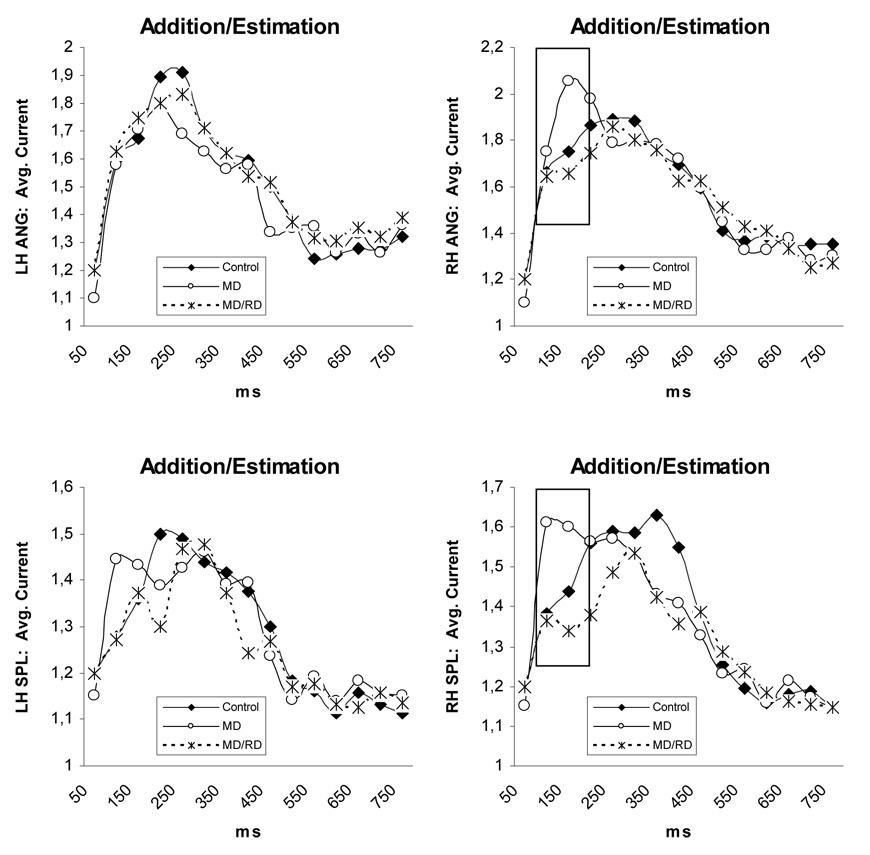
Three-way (Time by Hemisphere by Group) interactions were found in the supramarginal, angular, superior parietal, and middle temporal ROIs (p < .05 in all cases). Time by Group interactions were found for activity in the right supramarginal gyrus, F (26,650) = 1.64, p < .03, right angular gyrus, F (26,650) = 1.68, p < .02, and the right superior parietal region, F (26,650) = 1.96, p < .005, across both tasks (see Figure 5). In each of the three areas, significant Group simple main effects were restricted to between 100 and 200 ms (right supramarginal: F [1, 50] = 7.22, p < .002, right angular: F [1, 50] = 4.60, p < .017, and right superior parietal: F [1, 50] = 4.43, p < .018). Pairwise comparisons indicated that children in the MD group displayed greater magnetic activity as compared to both Controls (supramarginal: p < .001, angular: p < .017, superior parietal: p < .03) and children in the MD/RD group (p < .007, p < .008, & p < .007, respectively; see Figure 5).

Figure 5.

Time course of brain activity (average current in each ROI) illustrating group differences. Values were corrected for the global brain activity and age. Significant differences between groups are indicated by squares. Abbreviations; MTG: middle temporal gyrus, SMG: supramarginal gyrus, ANG: angular gyrus, SPL: superior parietal lobule.

Increased degree of activity in the MD group was also found in the right middle frontal region, as indicated by a Time by Hemisphere by Group by Task interaction, F (24,588) = 3.45, p < .005. The Group simple main effect in this case was significant only for the Addition task between 300 and 500 ms, F (1, 50) = 4, 50, p < .016. Pairwise contrasts indicated that the level of activity was higher in the MD group than the Control group (p < .005) and marginally higher than the MD/RD group (p < .05).

A Time by Group effect was found for activity in the left middle temporal gyrus, F (26,650) = 2.28, p < .003. In this ROI the Group simple main effect was significant only between 200 and 300 ms, F (1, 50) = 5.49, p < .007, and pairwise comparisons showed significantly greater activity for the Control group as compared to both the MD (p < .006) and MD/RD groups (p < .01).

Finally, stronger activity for the Control group was found in the right lateral occipito-temporal region as indicated by a Hemisphere by Task by Group interaction, F (2,650) = 3, 35, p < .04. A significant Group simple main effect was only found for the Dot Number Estimation task F (2, 50) = 4.54, p < .015: activity was stronger for the Control group than either the MD (p < .013) or the MD/RD groups (p < .023). This effect was more pronounced during the early time window (100–350 ms), when most of the activity in this ROI took place.

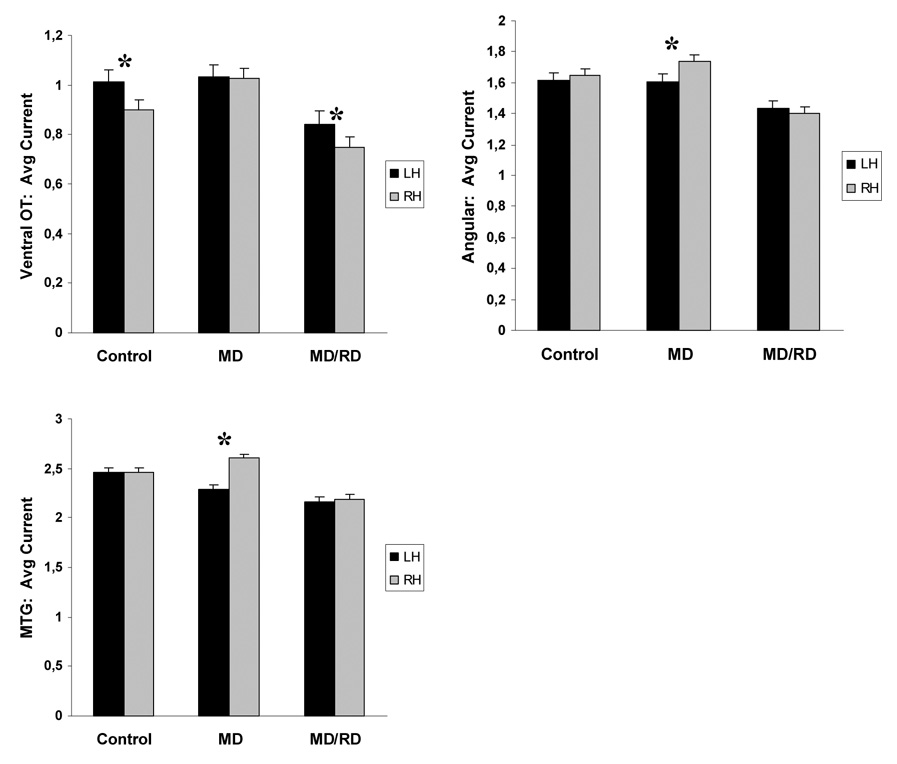
Given that group differences in the degree of activity were noted in only one hemisphere for each ROI, further analyses explored potential group-specific hemisphere differences in these ROIs. As indicated previously, a Time by Hemisphere by Group interaction was found in the angular gyrus, which was accounted for in part by a Hemisphere by Group effect, F (2, 52) = 4.45, p < .02. Separate Hemisphere contrasts computed for each group, showed that activity was significantly higher in the right compared to the left hemisphere only for the MD group, across tasks, F(1,24) = 13.18, p < .003 (the degree of activity was bilaterally symmetric in the other two groups as shown in Figure 6). A Hemisphere by Time by Group interaction was also found for activity in the middle temporal gyrus, and follow-up time-limited hemisphere contrasts computed separately for each group showed that activity was bilaterally symmetric for controls (p > .9) and MD/RD children (p > .1) but greater in the right hemisphere for the MD group, F(1,24) = 24.55, p < .0001, between 100 and 500 ms after stimulus onset. No other group-specific effects involving Hemisphere were found.

Figure 6.

Average degree of activity (mean current for each ROI across all time points). Significant hemisphere differences are indicated by asterisks. Vertical bars represent standard error of the mean. Abbreviations; Ventral OT: ventral occipitotemporal region, MTG: middle temporal gyrus.

Across groups the degree of activity during performance of the addition task was symmetric between hemispheres with two notable exceptions. A Hemisphere by Time interaction, F(12,624) = 2.74, p < .003, was noted for activity in the supramarginal gyrus, and time-specific hemisphere contrasts indicated that greater activity in the left hemisphere was restricted to two time periods, 300–400 ms and 550–750 ms, F(2,52) = 14.45, p < .0001. Main Hemisphere effects revealed greater activity in the right as compared to the left superior parietal, F(1,24) = 7.74, p < .008, and superior temporal ROIs, F(1,24) = 7.16, p < .01, across groups and time bins.

Hemisphere main effects during performance of the Dot Number Estimation task were found, across groups, in the ventral occipitotemporal ROI (L>R, F[1,648] =12.66, p < .001), and the angular gyrus (L<R, F[1,648] =11.77, p < .001). Additionally, Hemisphere by Time effects were found in a number of regions and follow up hemisphere simple main effects computed at each time bin were significant in the superior parietal region (L<R, F[1,648] =10.62, p < .002, between 100 and 500 ms), the superior temporal gyrus (L<R, F[1,648] =7.65, p < .008, between 100 and 450 ms), the middle temporal gyrus (L<R, F[1,648] =4.58, p < .03, between 100 and 450 ms), and the motor/premotor area (L<R, F[1,648] =17.72, p < .0001, between 250 and 450 ms).

Group differences in the peak latency of magnetic activity

Group by task by hemisphere effects were found for peak latency in the superior temporal, precentral/premotor, and ventral occipitotemporal regions (p < .05). Follow-up simple main Group effects were found for the Addition task in the left superior temporal, F (2, 52) = 4.05, p < .023, and right precentral/premotor areas, F (2, 52) = 4, 96, p < .011. Activity in both areas peaked significantly earlier for the MD as compared to the Control (p < .03 & p < .027, respectively) and MD/RD groups (p < .008 & p < .003, respectively). A group main effect was also found for activity in the right ventral occipitotemporal region during performance of the Dot Number Estimation task, F (2, 52) = 3, 55, p < .036. Earlier peak latency was again noted for the MD group as compared to the Control (p < .012) and MD/RD groups (p < .05; see Table 3).

Table 3.

Average peak latency of activity in three ROIs where group differences were observed.

		Control	MD	MD/RD
Addition	Superior Temporal Gyrus (LH)	324 (160)	211 (73)	363 (180)
	Precentral/Premotor (LH)	255 (85)	166 (59)	299 (183)
Dot Number Estimation	Ventral occipitotemporal (RH)	244 (101)	168 (57)	233 (88)

Task differences in the degree of regional activity

Planned analyses assessing task-related differences in the degree of activity in parietal and frontal regions were performed in order to confirm previous reports regarding the role of these areas in the brain mechanisms that support math functions. The average degree of MNE current estimated across all time bins served as the dependent variable in an ANOVA with Area (inferior frontal, middle frontal, angular, supramarginal, and superior parietal ROIs), hemisphere, and task as the within subjects factors. The analysis was initially performed separately for each group.

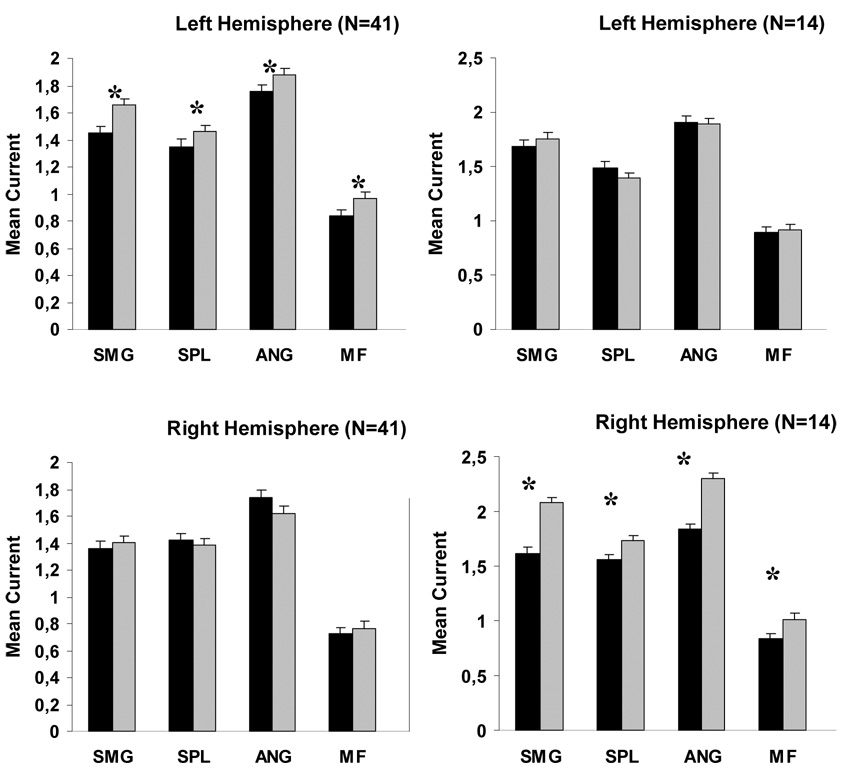
A task by hemisphere interaction was found for both the Control and MD/RD groups, and analyses on the collapsed data (n=41) confirmed the presence of a simple main effect of Task, F (1, 40) = 5.07, p < .03 in the left but not in the right hemisphere (p < .5), indicating greater activity for addition than dot number estimation in all five frontal and parietal ROIs in the left hemisphere (see Figure 7). Analysis of data for the MD group revealed a Task simple main effect (greater activity for the Addition task) across frontal and parietal ROIs in the right hemisphere, F (1, 13) = 12.08, p < .004. Task differences were not significant for the corresponding left hemisphere ROIs (p < .2).

Figure 7.

Average degree of activity across all time points in three parietal and two frontal ROIs for the combined Control-MD/RD groups (left hand column) and the MD group (right hand column). Significant task differences are indicated by asterisks. Vertical bars represent standard error of the mean. Abbreviations; SMG: supramarginal gyrus, ANG: angular gyrus, SPL: superior parietal lobule, MF: middle frontal gyrus.

Correlations between degree of activity and in-scanner performance

Partial correlation coefficients were computed between indices of average current in each of the five ROIs (were significant group differences were found: supramarginal, angular, superior parietal, middle temporal, middle frontal) and in-scanner performance, separately for each task. As shown in Table 4 results of correlational analyses were generally consistent with the conclusions of the findings on group differences in the degree of activity. For Addition, the average degree of activity in left hemisphere parietal regions was a positive (albeit weak) predictor of performance in the Control group, a finding supporting a prominent role of these areas in the brain mechanism responsible for simple math computations during normal development of these functions. For the MD group the only regions that made a moderate positive contribution to calculation accuracy were the right superior parietal and middle temporal ROIs. The left superior parietal and left middle temporal region bore a moderate correlation with addition performance in the MD/RD group. With respect to the Dot Number Estimation task, moderate positive correlations with performance were found for activity in the left superior parietal ROI (Controls), the right angular and superior parietal ROIs (MD group), and the right supramarginal and superior parietal ROIs (MD/RD group).

Table 4.

Zero order/partial correlation coefficients between average MNE current and in-scanner performance (percent correct responses), controlling for activity in the remaining ROIs.

		Addition			Dot Number Estimation
		Controls	MD	MD/RD	Controls	MD	MD/RD
Middle Frontal		.20/.11	.15/.10	.11/.13	−.02/.02	−.20/−.14	−.20/−.13
Angular		.41/.15	−.10/−.00	−.24/−.41	−.02/−.33	−.24/−.13	−.20/−.19
Supramarginal	LH	.08/.16	−.13/−.01	.06/.19	.02/−.25	−.06/−.15	.00/.03
Superior parietal		.35/.21	−.12/−.22	−.13/.25	.25/.45	−.54/−.37	−.04/−.07
Middle temporal		−.14/−.08	−.28/−.30	.22/.38	.10/.23	−.15/.−22	−.28/−.33
Middle Frontal		.07/−.06	.08/−.12	.08/.11	−.02/−.06	−.19/−.24	−.20/−.15
Angular		−.06/−.07	−.16/−.05	−.42/−.10	.06/.11	.16/.39	.02/.11
Supramarginal	RH	.09/−.16	−.12/−.11	.00/.01	.12/.09	−.25/.−.18	.35/.40
Superior parietal		−.24/−.30	−.13/.31	−.39/−.22	.06/−.10	.33/.28	.21/.45
Middle temporal		−.10/.05	−.16/.28	−.33/−.14	−.13/−.16	.34/.30	−.11/.09

Discussion

This study showed differences in brain activation profiles among children with no math impairment, only impairment in math, and both math and reading impairment. At the behavioral level, there were clear differences in performance on tasks associated with addition. However, the controls and MD group did not differ in performance on a numerosity task. Nonetheless, differences in brain activation were apparent on both tasks in areas known to play a key role in the brain mechanism for math for the group with MD versus controls. These findings suggest the presence of an aberrant brain circuit for processing numbers, symbolic or not, which characterizes children with MD. In contrast, children with MD/RD showed behavioral impairment on both tasks and a more generalized tendency for globally suppressed neural activity during performance of both tasks.

The features of the aberrant activation profile of students with MD and typical reading achievement can be summarized as follows. First, as a group, children with MD showed increased degree of neurophysiological activity in inferior parietal regions lying on the banks of the intraparietal sulcus (which includes parts of the supramarginal and angular gyri) and also in superior parietal regions, all in the right hemisphere. Group differences in the corresponding left hemisphere areas were either absent or represented by an opposite trend which, however, did not reach statistical significance, as in the case of the left angular gyrus. These three parietal regions are widely believed to serve as key components of the mechanism responsible for number processing (Dehaene, Molko, Cohen, & Wilson, 2004; Geary, 2004; Menon, Rivera, White, Glover, & Reiss, 2000). However, whereas control children demonstrated consistent increases in the degree of activity in these regions during the addition as compared to the (non-symbolic, non-computational) estimation task in the left hemisphere, children with MD showed this increase in corresponding right hemisphere areas. An associated finding was the increased rightward asymmetry in the degree of activity in the angular gyrus during the addition task for the MD as compared to the other two groups. Increased early engagement of prefrontal cortex in the MD group was probably not associated with increased task difficulty for this group compared to controls (see for instance, Menon et al., 2000), given that students who were at least as severely impaired in math (MD/RD group) did not show this finding. Correlational analyses are generally consistent with these results.

Taken together, these findings may indicate increased reliance on a network of right hemisphere parietal (and perhaps also frontal) areas for simple math calculations in students who experience math difficulties but perform within normal range in reading. Interestingly, there was a significant temporal uncoupling between the group and task differences described above. Increased activity in right hemisphere parietal areas in the MD as compared to the control group was restricted to early stages of stimulus processing (100–200 ms poststimulus onset), immediately before the time window when consistent task differences were observed, in the form of increased activity during performance of the addition compared to the estimation task (250–300 ms). Given the short temporal delay between the two effects, replication of this finding is required before it can be properly interpreted. Increased activity in the left middle temporal gyrus during performance of both tasks in Controls as compared to both groups of children who experience math difficulties, has not been reported before and is more difficult to interpret given the scarcity of evidence regarding a possible role of this region in math functions. In view of the fact that this effect was not specific to a particular task or math impairment subgroup, increased activity in this region may simply reflect the higher rate of verbal responses by children in the control group.

The second set of features of the aberrant activation profile associated with addition in the MD group concerns the temporal progression of regional activity. First, reduced latency of neurophysiological activity was found in two areas which, based on previous studies using hemodynamic measures do not appear to operate in a function-specific manner in number processing (Chochon et al., 1999; Rivera et al., 2005; Venkatraman, Ansari, & Chee, 2005): namely the superior temporal gyrus and precentral/premotor cortex (in the left hemisphere). In addition, there were notable differences in the temporal order of regional activity between groups. For the Control group, the supramarginal gyri, bilaterally, were the earliest parietal ROIs to show activity peaks, with the right angular and superior parietal regions peaking last, and at a significant delay following supramarginal activity. In contrast, the activation profile characteristic of students with MD without concomitant reading difficulties during addition featured, first, activity in the right superior parietal lobule, whereas activity in the left supramarginal gyrus peaked last, after a significant delay. Left superior parietal activity reached maximum amplitude first, during addition for the MD/RD group, followed by the remaining parietal regions (left supramarginal activity peaked, again, last). These findings are consistent with the notion that cortical patches in at least a portion of the parietal network of areas believed to be involved in number processing become active in an aberrant temporal sequence in children with math difficulties.

The only other imaging study that studied students with math difficulties (Kucian et al., 2006) reported only slight differences between students with MD and typically achieving students which were seen primarily during an approximate calculation task. The two studies differed in several important features. First, students in the math difficulties group in Kucian et al.’s study were defined on the basis of a discrepancy between IQ and achievement, a procedure that may have biased sample selection toward less severely impaired children. Moreover, the severity of math difficulties and potential comorbitity with reading problems of students in the MD group was not clearly specified. Second, the exact calculation task used in Kucian et al.’s study was probably easier for their (older) students with MD relative to the task used in the present study (performance was nearly identical between groups of impaired and non-impaired students). Third, a block design fMRI procedure was used in the earlier study, and group-specific brain activation profiles consisted merely of statistical parametric maps reflecting contrasts between math-related and control tasks. This procedure is known to yield significant discrepancies with MEG data obtained from the same subjects and on the same task (Billingsley-Marshall et al., 2007). Taken together, a number of features of the earlier imaging study on math difficulties may have affected the sensitivity of the procedures used to uncover group-specific differences in regional brain activation.

A potential confound in the present study concerns the possibility that children with math difficulties may have been using different cognitive strategies to perform the addition task than children who never experienced math difficulties. With respect to regional strength of activation, the data do not indicate that MD children (with or without concomitant reading problems) relied on language areas to a greater extent than controls, although there was evidence that they may have attempted to engage cortex in the left superior temporal gyrus earlier than the other two groups. Future studies should query children about strategies used to perform tasks during imaging studies.

To conclude, the spatiotemporal profile of neurophysiological activity observed as students with difficulties in math and average reading ability engage in simple math calculations (single-digit addition) appears to be distinct from the profile of activity in students who either never experienced difficulties in math or have shown such difficulties in the context of a more generalized learning disability. This profile involves increased activity in right hemisphere inferior and superior parietal regions and possibly reduced reliance on left hemisphere parietal areas. This should not be taken as direct evidence that students with combined math and reading difficulties have typical brain activation profiles, especially in view of a generalized tendency toward suppressed activity in several brain areas was found in students with MD/RD during both tasks (hence regardless of the symbolic nature of the stimuli). Our findings raise the possibility, however, that children with specific math difficulties form a distinct population at least with respect to the neurophysiological “phenotype” when they perform tasks that involve numbers (in either symbolic or non-symbolic form). Cognitive and neuropsychological studies support this finding (Geary, 1993; 2004; Rourke, 1993). However, more recent studies focusing on different aspects of mathematical knowledge have not found major differences in procedural knowledge on several different tasks between MD and MD/RD groups (Barnes et al., 2006; Jordan et al., 2003). Other recent studies have found evidence supporting a specific MD group defined by a computational disorder characterized by strengths in language and weaknesses in attention and processing speed, contrasting this group with those impaired in mathematical competencies involving problem solving skills (word problems). This latter group was impaired in language, reading, and other cognitive skills and was generally more impaired in cognitive performance and math ability. In the present study, problem solving skills were not assessed, but it is apparent that just because of their reading problems, children with MD/RD have more significant language difficulties involving phonological processing and vocabulary. The general suppression of brain activity seen in this study in the MD/RD group may be related to their overall greater severity of math and language ability.

Given the relatively small size of the two groups of children with math difficulties, the present findings (and especially those concerning timing of activation) should be considered initial results, requiring replication in future studies. Rather than drawing firm conclusions regarding the neurophysiological substrate of specific math disability, we consider these findings as simply highlighting the complexity of the neurobiological substrate of math disability which, in turn, is expected to reflect significant phenotypical variation in the expression of this form of learning disability. Some of the factors contributing to this variation have been described, mostly concerning cognitive component skills (Geary, 1993; 2004; Rourke, 2004), while others, including socio-emotional characteristics, have received less attention (see Fletcher et al., 2007). Future larger scale studies are needed in order to assess the impact of these sources of individual variability on brain activation profiles in the context of both correlational (like the one described here) and intervention studies where systematic changes in the level of potential contributors to math skill are implemented, assessing systematic changes in both the outline of the brain mechanism responsible for arithmetic ability, as well as psychoeducational outcome.