Representation of the spectral dominance region of pitch in the steady-state temporal discharge patterns of cochlear nucleus units

Abstract

Single-unit responses to infinitely iterated rippled noise and wideband noise were recorded from the cochlear nucleus of anesthetized chinchillas. Rippled noises had a fixed delay of 4 ms, and spectral depth was varied by attenuating the delayed version of the noise. Temporal discharge patterns were analyzed using neural autocorrelograms, and responses to rippled noises were compared to wideband noise responses. Chopper units with best frequencies in the range of the first to second harmonics of the rippled noise showed large differences in discharge patterns between rippled noise and wideband noise responses, but chopper units with best frequencies centered at higher harmonics did not show large differences. Consequently, the Chopper group of units showed no evidence of a neural representation of the dominance region. Primarylike units did show a neural representation of dominance that is related to behavioral performance. For Primarylike units with best frequencies around the third to fifth harmonics of the rippled noise, large differences in discharge patterns between rippled noise and wideband noise responses were observed. The results suggest that bushy cells play an important role in processing pitch-related information and should be included as important elements in neural models of periodicity processing.

INTRODUCTION

Pitch is a fundamental perception associated with a variety of complex periodic sounds. In music perception, changes in pitch form the basis of melody recognition. In speech perception, changes in pitch form the basis of prosody in languages such as English, but for tonal languages like Mandarin, changes in pitch of a monosyllabic word result in a change in the meaning of the word. Pitch also plays a role in the ability of human listeners to segregate sounds from many simultaneous sources (i.e., auditory scene analysis).

A variety of psychological attributes of pitch have been described in human listeners [see Plack et al. (2005)], and a principal attribute is the existence of a spectral dominance region of pitch. In general, for a sound comprised of successive harmonic tones, the frequencies most effective in evoking the pitch perception are found in the region of the third to fifth harmonics (Plomp, 1967; Ritsma, 1967). The existence of the dominance region of pitch is not limited to harmonic complex tones but has also been demonstrated in human listeners using pitch discrimination tasks with bandpass filtered rippled noises (Bilsen and Ritsma, 1970; Yost and Hill, 1978; Yost, 1982; Leek and Summers, 2001). In addition, the existence of a spectral dominance region does not appear to be a perceptual attribute that is the result of a uniquely human neural mechanism. Behavioral studies using operant conditioning in chinchillas have shown the existence of a dominance region for the discrimination of rippled noise from flat-spectrum wideband noise (WBN) (Shofner and Yost, 1997). The discrimination of rippled noise from WBN is known as coloration discrimination, and the location of dominance in the chinchilla for coloration discrimination also corresponds to the spectral region around the third to fifth harmonics.

Physiological correlates of spectral dominance for tone complexes have been described for the frequency following response (FFR) recorded from humans (Greenberg et al., 1987). The FFR is a scalp-recorded, auditory evoked potential that represents the synchronous or phase-locked activity of auditory brainstem neurons to periodic sounds (Marsh et al., 1972). The amplitude of the FFR recorded in response to two successive harmonics of a fundamental frequency was largest when the third and fourth harmonics were presented (Greenberg et al., 1987). Further evidence of the role of neural synchrony in the representation of the dominance region can be found from the responses of single auditory nerve fibers (Cariani and Delgutte, 1996). Interspike intervals (ISIs) of auditory nerve fibers were measured in response to two different harmonic tone complexes presented simultaneously. One complex was made of the third to fifth harmonics of a fundamental frequency, whereas the other complex was made of the 6th–12th harmonics of a different fundamental frequency. For fundamental frequencies of 160 Hz and above, the predominant ISI corresponded to the period of the fundamental frequency associated with third to fifth harmonics (Cariani and Delgutte, 1996). The findings of these two studies suggest that dominance is related to neural synchrony and is encoded as early as the auditory nerve. Thus, a neural representation of dominance would be expected to exist in the cochlear nucleus, but do all cochlear nucleus unit types show a representation of dominance in their temporal discharge patterns?

The cochlear nucleus receives its ascending input from the auditory nerve and is the first nucleus along the central auditory pathway where neural processing can occur. The nucleus is divided into three major subdivisions: anteroventral cochlear nucleus, posteroventral cochlear nucleus, and dorsal cochlear nucleus (Osen, 1969; Morest et al., 1990). Each of these subdivisions contains several distinct principal cell subsystems that differ in their neuronal morphologies, innervation, and physiological response properties. The principal cells of the anteroventral division are the bushy cells and the stellate or multipolar cells; primarylike responses are associated with bushy cells (Rhode et al., 1983; Rouiller and Ryugo, 1984; Smith and Rhode, 1987; Smith et al., 1991, 1993; Ostapoff et al., 1994), whereas chopper responses are associated with stellate or multipolar cells (Rhode et al., 1983; Rouiller and Ryugo, 1984; Smith and Rhode, 1989; Ostapoff et al., 1994). Multipolar cells receive auditory nerve input in the form of small bouton terminals (Redd et al., 2002), whereas bushy cells receive large end bulb or calyx synaptic terminals from auditory nerve fibers (Cant and Morest, 1979; Lorente de No, 1981; Ryugo and Fekete, 1982; Sento and Ryugo, 1989; Ryugo and Sento, 1991). The depolarization that occurs in end bulb synapses can be recorded extracellularly as prepotentials (Pfeiffer, 1966; Guinan and Li, 1990). Although both unit types can give synchronous responses to rippled noise stimuli that are correlated with the pitch perceived in human listeners (Shofner, 1991, 1999; Wiegrebe and Winter, 2001; Winter et al., 2001; Verhey and Winter, 2006; Sayles and Winter, 2007), the specific functional roles that primarylike and chopper units play in periodicity processing as related to pitch remain unclear. Chopper units show stronger phase-locked responses than primarylike units to sinusoidal-amplitude modulated tones (Frisina et al., 1990; Rhode and Greenberg, 1994; Shofner et al., 1996) as well as to the fundamental frequency of synthetic vowels (Wang and Sachs, 1994). Consequently, chopper units have been thought to play an important role in periodicity processing, and most attempts to model periodicity processing utilize either chopper units exclusively (Meddis and O’Mard, 2006) or as one component of the neural circuit (Borst et al., 2004; Dicke et al., 2007). Although none of these models includes contributions from primarylike units, Nelson and Carney (2004) developed an alternative model based exclusively on the contributions of primarylike units rather than chopper units.

The present study seeks to extend the previously reported physiological findings into the cochlear nucleus of chinchillas using rippled noise stimuli. The approach of the present experiment is not to study the responses of a single unit to a variety of pitch-evoking stimuli but rather to examine the neural representation across a population of units to a limited set of stimuli. This approach is similar to that previously taken to study the encoding of steady-state vowels [e.g., see Blackburn and Sachs (1990) and Winter and Palmer (1990b)]. Stimuli were chosen to allow comparisons between single-unit responses and behavioral performance obtained previously in the chinchilla (Shofner and Yost, 1997). The present report describes a neural correlate of the dominance region in the temporal discharge of primarylike units but not of chopper units. The results argue that in addition to chopper units (stellate cells), primarylike units (bushy cells) play an important role in processing pitch-related information and should also be included in neural models of periodicity processing.

Properties of iterated rippled noises

Rippled noises have been used to study a wide range of auditory phenomena, including masking and frequency selectivity (Houtgast, 1977; Pick, 1980; Niemiec et al., 1992) and echo processing (Bassett and Eastmond, 1964), and as a general stimulus for complex sound processing (Schreiner and Calhoun, 1994; Shamma et al., 1995; Amagai et al., 1999). Moreover, rippled noises have become an important class of stimuli for studying the perception of pitch and are important stimuli for testing models of pitch perception (Meddis and Hewitt, 1991; Cohen et al., 1995; Yost et al., 1996).

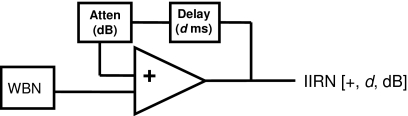
Rippled noises are generated when a WBN is delayed [d (ms)] and the delayed noise is added to the undelayed version of the noise. If the rippled noise is delayed again and added to the original WBN, the output is an iterated rippled noise of two iterations (i.e., two iterations of delay and add). An infinitely iterated rippled noise (IIRN) can be achieved using a positive feedback loop in the delay and add process (Fig. 1). For convenience, IIRNs will be referred to using the following notation: IIRN [+, d, dB], where + indicates that the delayed noise is added, d is the delay in ms, and dB is the attenuation of the delayed noise relative to the original undelayed noise (see Fig. 1). Unlike complex tones, which are characterized by line spectra, rippled noises are characterized by continuous spectra, and sample spectra based on the WBN input [Fig. 2A] to the positive feedback network described in Fig. 1 are shown in Figs. 2B, 2C for a 4 ms delay. When the delayed noise is added to the original noise, the spectrum of IIRN has peaks at integer multiples of 1∕d; this is the harmonic condition of IIRN. When the delayed noise attenuation is decreased from −3 to −1 dB, there is an increase in the peak-to-valley ratio of the spectral peaks.

Figure 1.

Schematic diagram shows the positive feedback circuit used for generating infinitely iterated rippled noise (IIRN [+, d, dB]) from a wideband noise (WBN) input, where + indicates positive gain (i.e., added), d is the delay, and dB is the delayed noise attenuation.

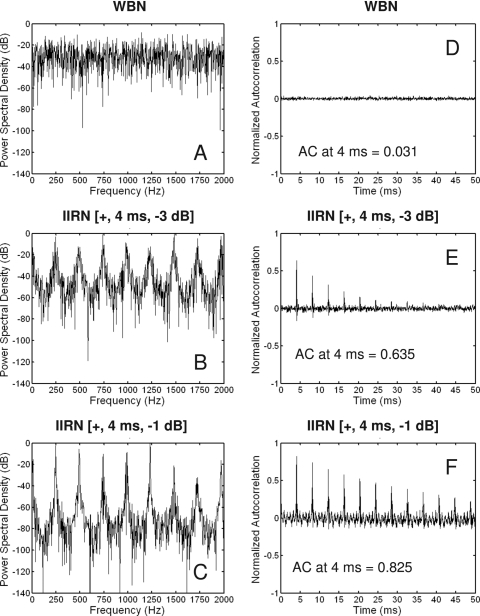
Figure 2.

[(A)–(C)] Sample spectra are shown for samples of the WBN input (A) and IIRNs with a fixed delay (d) of 4 ms and delayed noise attenuations of −3 dB (B) and −1 dB (C). The bandwidths of the noises were 10 kHz, but for purposes of clarity, only frequencies up to 2000 Hz are shown. Note for the IIRN spectra, the peaks occur at integer multiples of 250 Hz, i.e., 1∕d. The spectral depth of the ripple increases as the amount of delayed noise attenuation decreases. [(D)–(F)] Sample autocorrelation functions of the waveform are shown for the same samples of WBN and IIRNs. The height of the autocorrelation at 4 ms (AC at 4 ms) is given for each stimulus. Note that both the height and number of the peaks increase as the delayed noise attenuation decreases.

The temporal properties of rippled noises are best described by autocorrelation functions, and sample autocorrelation functions based on a WBN noise input [Fig. 2D] to the positive feedback network described above are also shown in Figs. 2E, 2F. When the delayed noise is added to the original noise, the waveform autocorrelation functions of IIRN stimuli show positive correlations at time lags corresponding to integer multiples of d. The heights of these peaks increase as the amount of delayed noise attenuation decreases from −3 to −1 dB. Unlike complex tones, which are periodic, rippled noises possess a regularity in their temporal structure but are not truly periodic. Rather, the correlations in the IIRN autocorrelation functions reflect a part of the waveform that repeats itself throughout the stimulus waveform but does not repeat itself in a periodic manner. Thus, rippled noises have been described as pseudoperiodic or quasiperiodic waveforms, and the height of the first peak in the autocorrelation function can be taken as a measure of the strength of the regularity [Figs. 2E, 2F].

Rippled noises evoke pitches in human listeners that are the same as the pitches evoked by the many other classes of stimuli that produce complex pitches. For iterated rippled noise stimuli, the pitch is determined by d. In general, the pitch of iterated rippled noise with positive gain (i.e., added) is at a frequency corresponding to 1∕d and corresponds to the time lag of the first positive correlation in the waveform autocorrelation function (Yost, 1996a). The pitch strength of rippled noises can be made to vary along a continuum from a flat-spectrum noise (having no real pitch) to a periodic pulse train (having a very strong pitch). The pitch strength increases as either the number of iterations increases (Yost, 1996b) or the amount of delayed noise attenuation decreases (Shofner and Selas, 2002).

METHODS

General procedures

The experiments were carried out at Loyola University Chicago and Indiana University, and the procedures have been reviewed and approved by the Institutional Animal Care and Use Committees of both Loyola University Chicago and Indiana University. Adult chinchillas weighing 500–800 g were anesthetized with intraperitoneal injections of sodium pentobarbital. For recordings obtained at Loyola University, animals were initially injected with a dose of 70 mg∕kg; for recordings obtained at Indiana University, animals were initially injected with a dose of 60 mg∕kg and given a subcutaneous injection of Rimadyl (4 mg∕kg) as additional analgesic. Supplemental injections of pentobarbital were given to maintain areflexia. Body temperature was maintained at around 38 °C with a dc heating pad.

A tracheotomy was performed, and the external auditory canals were exposed and transected. Animals were placed in a modified headholder (Kopf Model 900), and the left bulla was exposed and opened in order to expose the cerebellum as originally described by Frisina et al. (1982) for the gerbil. An opening was made in the temporal bone to expose the cerebellum, and electrodes were advanced through the cerebellum into the underlying cochlear nucleus using a hydraulic microdrive system (Kopf 650). The advantage of this transbullar approach to the cochlear nucleus is that the recording of a single-unit activity can be very stable; it is not uncommon to hold units for 1–2 h. Any effect opening the bulla may have on the middle ear transfer function [e.g., see Ruggero et al. (1990)], and thus on neural thresholds, should be equal across all unit types in the cochlear nucleus.

Neurophysiological recording and stimuli

Animals were placed in a double-walled sound attenuating chamber during neurophysiological recording of single-unit responses. Commercially purchased tungsten microelectrodes were used to record single-unit activities. Data acquisition and stimulus presentation were under the control of a Gateway computer system and Tucker-Davis Technologies System II modules. Extracellular action potentials were amplified, filtered, and passed through a spike discriminator. The times of occurrences of the pulses were determined online relative to the onset of the stimulus with 1 μs resolution. Data from the neural activity was only recorded from clearly isolated single-units as determined by monitoring the triggered spike waveform online. Single-units were not isolated from multiunit clusters of spikes. Acoustic stimuli were presented to the left ear through a Sennheiser HD 414 SL earphone enclosed in a brass housing that also held a calibration microphone. Search stimuli were 100 ms bursts of either WBN or tones at the best frequency (BF) of the background neural activity.

When a unit was isolated, its BF was first determined using audiovisual cues, and data were collected for unit classification. The classification of unit types was based on poststimulus time (PST) histograms, ISI histograms, regularity histograms (Young et al., 1988), and the presence or absence of a prepotential. At least 1000 amplified spikes were digitized through an analog-digital (A∕D) channel and were averaged online in order to determine if prepotentials were present in the averaged spike waveform. BF tones were generated by the computer and presented through a 16 bit digital-analog (A∕D) converter. The sampling rate of the A∕D and the conversion rate of the D∕A were 50 kHz. BF tones of 200 ms duration presented once every 1000 ms with rise∕fall times of 10 ms were used to generate rate-level functions over a 100 dB range in 1 dB steps. One stimulus was presented at each level, and the rate-level function was smoothed using a five-bin triangular moving window average. The lowest stimulus level presented was well below the audiovisual threshold, and the smoothed firing rate produced at the ten lowest levels was used to estimate the mean and standard deviation of the spontaneous discharge rate. The threshold was then defined as the level that first evoked an increase in discharge rate greater than 2 standard deviations above the spontaneous discharge rate, provided that the next three levels were also greater than 2 standard deviations above the spontaneous rate. PST histograms were then generated for 250 presentations of a 50 ms BF tone with 2 ms rise∕fall times presented once every 250 ms at levels of 20–40 dB above the threshold. If a PST histogram showed strong phase-locking such that a characteristic discharge pattern was obscured, then BF tones were also presented with random starting phases in an attempt to ascertain a characteristic discharge pattern. Spike times were also used to generate ISI histograms and regularity histograms. Spikes that occurred during the initial 20 ms were not used for generating ISI histograms in order to ensure that ISI histograms characterized the steady-state portion of the response. The mean ISI and standard deviation were determined from pairs of spikes in which the times of occurrence were 20–50 ms. The coefficient of variation (CV) was computed as the ratio of the standard deviation to the mean.

After the data were collected for unit classification, the responses to WBN and IIRN were studied. Sets of WBN and IIRN stimuli were generated using the same equipment and parameter settings that were previously used to measure discrimination performance in chinchillas (Shofner and Yost, 1997). For WBN and each IIRN, 5 s of the waveform was sampled at 50 kHz; the waveform amplitudes were then adjusted so that all WBN and IIRN stimuli had equal root-mean-squared amplitudes. The 5 s samples of each noise were stored on a disk as stimulus files. For a stimulus presentation, WBN and IIRN signals were presented through a 16 bit D∕A converter (TDT DA3-2 module) at a conversion rate of 50 kHz. During a stimulus presentation for a particular noise signal, a separate 500 ms sequence was randomly obtained from the 5 s sample for each stimulus presentation. Consequently, the waveform of the noise was not the same for each presentation.

Rate-level functions were first generated over a 100 dB range in 1 dB steps for 500 ms WBN bursts with rise∕fall times of 10 ms presented once every 1500 ms. One noise burst was presented at each level, and the rate-level function was smoothed using a five-bin triangular moving window average. The threshold for the WBN was estimated as defined above for BF tone rate-level functions. After the WBN rate-level function had been obtained, the responses of the isolated unit were studied for WBN and IIRN stimuli. A total of 100 separate samples of WBN or IIRN were presented, having durations of 500 ms and rise∕fall times of 10 ms; bursts were presented once every 1000 ms. These were the same stimulus parameters used to measure behavioral performance (Shofner and Yost, 1997). Typically, data were first obtained for WBN and then for a series of IIRN stimuli with a fixed delay of 4 ms and delayed noise attenuations of −1 to −4 dB. The overall levels of the WBN and IIRN stimuli were presented at 20 dB above the threshold as determined from the WBN rate-level function.

Because multiple electrode tracks were made in a typical experiment, the histological location of units was not determined. However, recovered lesions and electrode tracks that were verified histologically from past experiments (Shofner, 1991; Shofner et al., 1996) using the same surgical approach and angle of penetration were limited to ventral cochlear nucleus (VCN). In addition, the large proportion of units with prepotentials in the present sample strongly suggests many electrode penetrations passed through the anteroventral cochlear nucleus (AVCN).

Data analysis

Temporal responses of units to WBN and IIRN were analyzed as autocorrelograms (i.e., all-order ISI histograms). The autocorrelogram displays the average discharge pattern following a given action potential. Autocorrelograms were generated for action potentials occurring between 20 and 500 ms of the stimulus; spikes that occurred during the initial 20 ms were not used in order to ensure that autocorrelograms characterized the steady-state portion of the response. The ordinates of the autocorrelograms were first scaled in terms of firing rate as described by Abeles (1982), and were then scaled in terms of normalized firing rate (λ_τ) as

$${\lambda }_{\tau }=\frac{R_{\tau }-R_{\mathrm{ave}}}{R_{\mathrm{ave}}},$$ (1)

where R_τ is the firing rate at a time lag of τ ms and R_ave is the average firing rate. Normalized rate is a unitless measure, and a normalized rate of 0 represents the average firing rate. The difference in temporal response patterns between responses to IIRNs and WBN was quantified by using the fourth moment of the normalized autocorrelogram (see Sec. 4). The fourth moment can be used as a measure of the instantaneous fluctuations in power in a waveform (Hartmann, 1998), and the normalized autocorrelogram is treated as a waveform. The average fourth moment of the normalized autocorrelogram was computed as

$$\overline{{\lambda }^4}=\frac{\Sigma {({\lambda }_{\tau }-{\lambda }_{\mathrm{ave}})}^4}{N},$$ (2)

where N corresponds to a 50 ms window (i.e., 500 bins that are each 100 μs wide). Because λ_ave is equal to 0 in the normalized autocorrelogram, the average fourth moment becomes

$$\overline{{\lambda }^4}=\frac{\Sigma {\left({\lambda }_{\tau }\right)}^4}{N}.$$ (3)

The ratio of the averaged fourth moments for IIRN and WBN responses (i.e., relative fourth moment) was expressed in decibel and given as

$$\mathrm{dB}=10\log \frac{{\overline{{\lambda }^4}}_{\mathrm{IIRN}}}{{\overline{{\lambda }^4}}_{\mathrm{WBN}}}.$$ (4)

A large decibel indicates greater deviations from a normalized rate of 0 in the IIRN response relative to the deviations around 0 in the WBN response.

RESULTS

Unit classification

The results of the present study are based on the responses of 118 single-units recorded from the cochlear nucleus of adult chinchillas. Units were classified on the basis of their discharge characteristics generated for BF tone bursts at 20–40 dB above the threshold, as described in Sec. 2. For purposes of clarity, the use of the word “Primarylike” will be used to refer specifically to the group of prepotential and primarylike units obtained in the present study, whereas the word “Chopper” will be used specifically in reference to the sample of chopper and regular units obtained in this study.

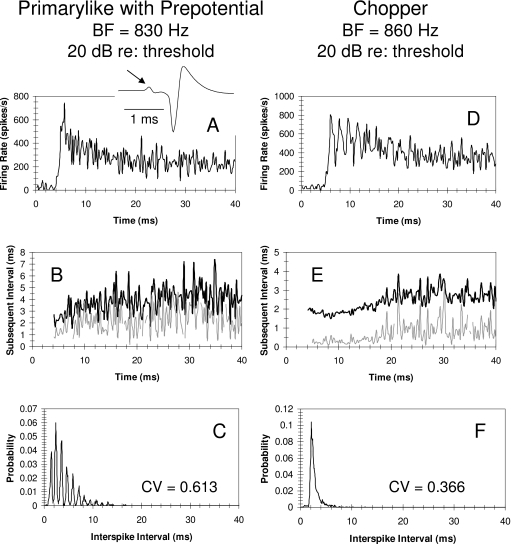
A total of 48 units were classified as Primarylike; in response to BF tones, these units show an initial increase in firing rate that adapts to a relatively constant steady-state discharge [Fig. 3A]. Of the units classified as Primarylike, 26 units were observed to have a prepotential in the averaged spike waveform (see the inset in Fig. 3). The analysis of the discharge pattern of this primarylike with a prepotential unit based on regularity histograms (Young et al., 1988) and ISI histograms indicates an irregular discharge of spikes during the tone [Figs. 3B, 3C]. The CV calculated from the ISI histogram shown in Fig. 3C is 0.613, and for BF tones at 20–40 dB above the threshold for the sample of prepotenital units, the CVs ranged from 0.5–0.8 with a mean of 0.67.

Figure 3.

Discharge properties of a primarylike unit and a chopper unit with similar best frequencies (BFs) are illustrated. Responses were obtained from BF tones at 20 dB above the threshold. The primarylike unit in this example exhibited a prepotential in the averaged spike waveform (see arrow in the inset). (A) PST histogram obtained from the primarylike unit. (B) Regularity histogram obtained for the primarylike unit shows mean subsequent ISI (black line) as a function of time through the PST histogram and the standard deviation of the subsequent interval (gray line). (C) ISI histogram obtained from the primarylike unit. The CV calculated from ISI histogram was 0.613. The interval analysis shown in (B) and C indicates an irregular discharge pattern. (D) PST histogram obtained from a chopper unit. Note the peaks and valleys in the onset portion of the histogram. (E) Regularity histogram obtained for the chopper unit. Black and gray lines same as in (B). (F) ISI histogram obtained from the chopper unit. The CV calculated from the ISI histogram was 0.366. The interval analysis shown in (E) and (F) indicates a more regular discharge pattern for the chopper unit than for the primarylike unit.

A total of 64 units were classified as Chopper units. In this sample, 34 units showed a series of peaks in the PST histogram; this observed chopping pattern is the result of a precisely timed onset spike followed by a regular discharge of spikes [Fig. 3D]. The regularity histogram [Fig. 3E] and ISI histogram [Fig. 3F] indicate a regular discharge pattern; the CV calculated from the ISI histogram in Fig. 3F is 0.366. The mean CV calculated from the ISI histograms in response to BF tones at 20–40 dB above the threshold for the sample of units with chopper PST histograms was 0.41. The remaining 30 units in this group did not show the characteristic chopping discharge pattern in the PST histograms but had CVs of ISI histograms that were smaller than those of prepotential units, indicating a more regular discharge that is characteristic of chopper units. The mean CV calculated from the ISI histograms in response to BF tones at 20–40 dB above the threshold for the sample of regular units was 0.43.

A single-factor analysis of variance (ANOVA) was carried out on the CV calculated from the ISI histograms for the prepotential units, regular units, and chopper units. Because primarylike PST histograms can be recorded from cell types other than bushy cells, while the presence of a prepotential is a signature characteristic of a bushy cell, the ANOVA only included prepotential units as a quantitative estimate of the irregular discharge of bushy cells. A significant effect across groups was found for the mean CVs (F=78.43, P<0.0005). Paired comparisons were made using Tukey’s test. At α=0.001, there was a significant difference between the mean CVs of the prepotential and regular units and between the mean CVs of the prepotential and chopper units. The difference between mean CVs of the chopper units and regular units was not significant (P>0.05). Consequently, regular and chopper units were combined to form the Chopper group. These regular units are considered to be Chopper units that do not have a precisely timed onset spike and thus do not show the characteristic chopping in the PST histogram [see Winter and Palmer (1990a); and Shofner (1999)].

Units having low BFs (<500 Hz) typically show strong phase-locking to BF tones, thus making it difficult to distinguish a characteristic discharge pattern. Low BF units were classified as Primarylike if the CV was greater than 0.6 and were classified as regular if the CV was less than 0.5. These low BF regular units were included in the Chopper category. A total of six units had CVs that were 0.5-0.6. Thus, it was difficult to determine on this basis if they were primarylike or regular. These six units were classified as phase locked.

Responses to infinitely iterated rippled noise

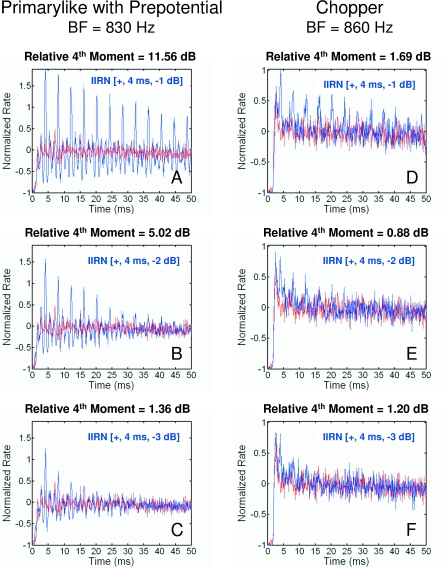
The temporal discharge patterns obtained in response to WBN and to IIRNs with a fixed delay of 4 ms and delayed noise attenuations of −1, −2, and −3 dB are shown in Figs. 4A, 4B, 4C for the primarylike unit with a prepotential illustrated in Fig. 3. Discharge patterns are displayed as normalized neural autocorrelograms, which show the average firing pattern of the unit following an action potential that occurs at a time lag of 0. A normalized firing rate of 0 is equal to the average firing rate of the unit (see Sec. 2). For comparison, the temporal discharge patterns in response to WBN are also shown. The normalized autocorrelogram obtained in response to WBN is relatively flat, indicating a random nonperiodic discharge pattern. In contrast, the normalized autocorrelograms obtained in response to IIRNs show a series of peaks and nulls. The peaks occur at 4 ms and integer multiples of 4 ms, indicating that there is a periodicity to the discharge pattern of the unit that is related to the IIRN delay. Notice that the number of peaks and the heights of the peaks both decrease as the delayed noise attenuation increases from −1 to −3 dB [blue lines in Figs. 4A, 4B, 4C]. That is, as the amount of delayed noise attenuation increases, the periodicity of the discharge pattern decreases, becoming more like that of WBN (see the red lines in Fig. 4). Thus, for the autocorrelograms illustrated in Figs. 4A, 4B, 4C, the deviations around a normalized firing rate of 0 are small for WBN, but are large for IIRNs. These deviations are a reflection of the periodic discharge of the unit in response to IIRN with larger deviations, indicating a stronger periodicity of discharge or a more synchronous discharge.

Figure 4.

Normalized neural autocorrelograms for the primarylike unit [(A)–(C)] and chopper unit [(D)–(F)] characterized in Fig. 3 are illustrated. Blue lines show the autocorrelograms obtained in response to IIRNs; red lines show the autocorrelograms obtained in response to WBN. The delayed noise attenuation are −1 dB [(A) and (D)], −2 dB [(B) and (E)], and −3 dB [(C) and (F)]. The relative fourth moment as defined in the text is given for each panel.

The normalized autocorrelogram can be treated as a waveform, and for any waveform, the fourth moment can be used as a measure of the instantaneous fluctuations in power (Hartmann, 1998). The difference in discharge patterns between WBN and IIRN responses was quantified by computing the average fourth moment of the normalized autocorrelogram over a 50 ms time window (see Sec. 2). The relative fourth moment expressed as a decibel was then computed (see Sec. 2) in order to compare the response to an IIRN to the WBN response. Because chinchillas discriminated IIRN from WBN in the behavioral task (Shofner and Yost, 1997), it would be expected that the underlying neural processing would involve a comparison of responses between IIRN and WBN. For the autocorrelograms of the primarylike unit shown in Fig. 4, the relative fourth moments are 11.56, 5.02, and 1.36 dB for IIRNs with delayed noise attenuations of −1, −2, and −3 dB, respectively. Larger relative fourth moments indicate a greater difference in the discharge patterns between IIRN and WBN responses. For comparison, Figs. 4D, 4E, 4F also show the autocorrelograms obtained in response to WBN and IIRNs for a chopper unit having a similar BF. Note that in this example, the deviations around a normalized rate of 0 are not as pronounced as those for the primarylike unit, and consequently, the values of the relative fourth moments are smaller. For the autocorrelograms of the chopper unit shown in Figs. 4D, 4E, 4F, the relative fourth moments are 1.69, 0.88, and 1.20 dB for IIRNs with delayed noise attenuations of −1, −2, and −3 dB, respectively. These smaller values of the relative fourth moment reflect less of a difference between the discharge patterns for IIRN and WBN responses for this chopper unit. Note also that in response to the IIRN with the larger delayed noise attenuation of −3 dB, there is a clear periodicity to the discharge pattern for the primarylike unit but not for the chopper unit [Figs. 4C, 4F].

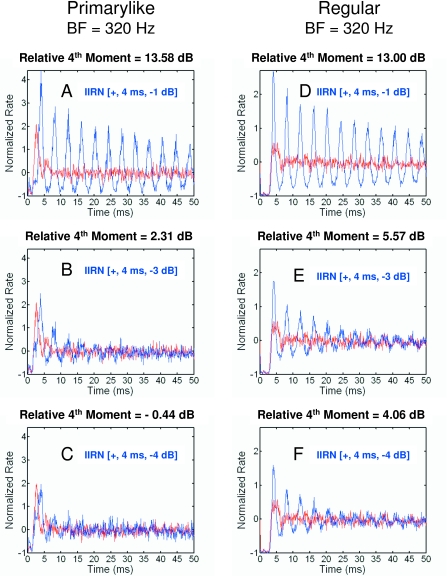
Neural autocorrelograms for a low BF primarylike unit [Figs. 5A, 5B, 5C] and a low BF regular unit [Fig. 5D, 5E, 5F] are similar to the responses previously shown in Fig. 4 for primarylike and chopper units in that large differences in discharge patterns are observed between IIRN [+, 4 ms, −1 dB] and WBN. That is, a comparison of the responses in Figs. 4A, 4D, 5A, 5D shows periodicities in the responses for all units related to the 4 ms delay. Also, for both the low BF primarylike and regular units, the differences in discharge patterns between IIRN and WBN decrease as the delayed noise attenuation increases, as shown by the decreases in the relative fourth moments (Fig. 5). Also note that the difference in discharge patterns between IIRN [+, 4 ms, −4 dB] and WBN is larger for the regular unit [Fig. 5F] than for the primarylike unit [Fig. 5C]. This example contrasts with the previous example shown in Fig. 4 in which the response to the IIRN was larger for the primarylike unit [Fig. 4C] than for the chopper unit [Fig. 4F] at the larger delayed noise attenuation of −3 dB.

Figure 5.

Normalized neural autocorrelograms for a primarylike unit [(A)–(C)] and a regular unit [(D)–(F)] having BFs of 320 Hz are illustrated. Blue lines show the autocorrelograms obtained in response to IIRNs; red lines show the autocorrelograms obtained in response to WBN. The delayed noise attenuation is −1 dB [(A) and (D)], −3 dB [(B) and (E)], and −4 dB [(C) and (F)]. The relative fourth moment as defined in the text is given for each panel.

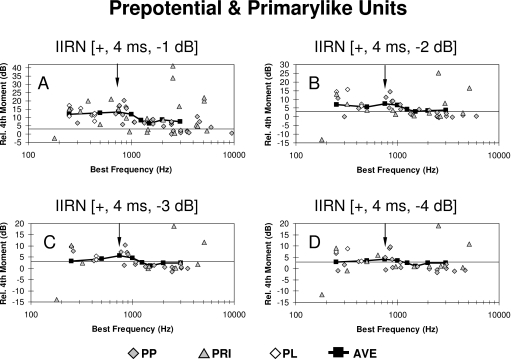
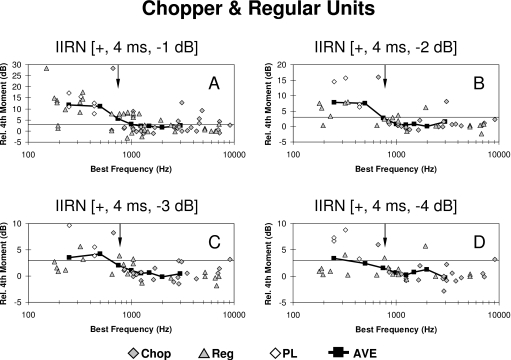
Scatter plots of the relative fourth moment as a function of BF are shown in Fig. 6 for individual Primarylike units in response to 4 ms delayed IIRN having delayed noise attenuations of −1, −2, −3, and −4 dB. The neural profiles of the relative fourth moment across BFs are shown by the black squares and heavy solid lines. These profiles are the relative fourth moment averaged in one-octave widebands that are centered at the harmonic frequencies of the IIRN (i.e., at 250, 500, 750, 1000 Hz, etc.) and are estimates of the population responses across BFs. Note that these are moving window averages, and this averaging within one-octave bands is similar to the one-octave bandpass filtering used to collect behavioral data from chinchillas (Shofner and Yost, 1997). A single-factor ANOVA was carried out on the relative fourth moment for Primarylike units having BFs less than or equal to 1250 Hz (i.e., less than or equal to the fifth harmonic of the IIRN), with the four delayed noise attenuations as the factor. A significant effect of delayed noise attenuation was found on the mean relative fourth moment for the Primarylike group (F=10.52; P<0.0005). Scatter plots of the relative fourth moment as a function of BF for individual Chopper units are shown in Fig. 7. A single-factor ANOVA was carried out on the relative fourth moment for Chopper units having BFs less than or equal to 1250 Hz for the four delayed noise attenuations. A significant effect of delayed noise attenuation was found on the mean relative fourth moment for the Chopper group (F=7.67; P<0.0005).

Figure 6.

Scatter plots illustrating the relative fourth moment as a function of BF for the Primarylike group for delayed noise attenuations of −1 dB (A), −2 dB (B), −3 dB (C), and −4 dB (D). Gray diamonds show units having a prepotential (PP); gray triangles show units with primarylike PST histograms but without a prepotential (PRI). The open diamonds illustrate the relative fourth moments obtained from low BF phase-locked (PL) units that could not be characterized as either Primarylike or Chopper. The black squares and solid black line show the relative fourth moment averaged in one-octave bands (ave), centered at harmonic frequencies of the rippled noise (i.e., 250, 500, 750, 1000 Hz, etc). The one-octave bandpass averaging is similar to the one-octave bandpass filtering used to collect behavioral data (Shofner and Yost, 1997). For reference, the downward pointing arrow indicates the frequency of the third harmonic. Note that the ordinate changes scales in (A)–(D).

Figure 7.

Scatter plots illustrating the relative fourth moment as a function of BF for the Chopper group for delayed noise attenuations of −1 dB (A), −2 dB (B), −3 dB (C), and −4 dB (D). Gray diamonds show units with chopper PST histograms (Chop); gray triangles show units characterized as regular (Reg). The open diamonds illustrate the relative fourth moments obtained from low BF phase-locked (PL) units that could not be characterized as either primarylike or chopper. The black squares and solid black line show the relative fourth moment averaged in one-octave bands (ave), centered at harmonic frequencies of the rippled noise (i.e., 250, 500, 750, 1000 Hz, etc). The downward pointing arrow indicates the frequency of the third harmonic. Note that the ordinate changes scales in (A)–(D).

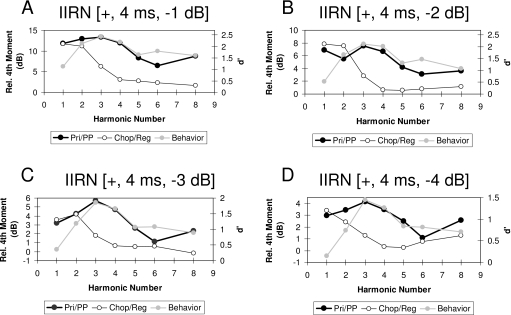
The neural profiles of the relative fourth moment averaged in one-octave widebands centered at the harmonic frequencies of the IIRN are shown by the black squares and heavy solid lines in Figs. 67. Although it is not clear from the scale used in these figures, the shape of the neural profiles appears to be different for the Primarylike and Chopper groups. Figure 8 compares the neural profiles for the two groups of units on the same ordinate scale in order to highlight differences in the shapes of the neural profiles. The harmonic number in Fig. 8 indicates the locations of the spectral peaks for the 4 ms IIRN. The profiles obtained for the Primarylike group appear to have more of a lowpass shape for delayed noise attenuations of −1 and −2 dB but more of a bandpass shape for delayed noise attenuations of −3 and −4 dB. In contrast, the profiles obtained for the Chopper group have a definite lowpass shape at all delayed noise attenuations, and the cutoff frequency appears to occur at a lower harmonic than the cutoff frequency for the Primarylike group (Fig. 8). The averaged relative fourth moments for the first and second harmonics are similar for Primarylike and Chopper groups, but are larger at the third to fifth harmonics for Primarylike units than for Chopper units (Fig. 8). The neural profiles shown in Fig. 8 are moving window averages, and as such, there is some overlap in the relative fourth moments between successive harmonics. Consequently, the averages for each harmonic number cannot be treated as independent groups, thus making the use of a statistical analysis such as ANOVA across harmonics invalid. In order to compare neural profiles for the Primarylike and Chopper groups, the following correlational analysis was carried out.

Figure 8.

Comparison of the relative fourth moment averaged in one-octave bands as a function of the harmonic number of the IIRN fundamental frequency (i.e., 250 Hz) for delayed noise attenuations of −1 dB (A), −2 dB (B), −3 dB (C), and −4 dB (D). These are the same functions illustrated in Figs. 67 by the solid black squares and lines. For comparison, behavioral data measured as d^′ from Shofner and Yost (1997) are shown by the gray circles and gray lines. The profiles of the averaged relative fourth moment for Primarylike units (black circles and black heavy lines) show more of a bandpass profile with a peak around the third harmonic and have a similar shape to the profile of the behavioral data. The profiles of the averaged relative fourth moment for Chopper units (open circles and thin black lines) have a lowpass profile and do not have a similar shape to the profile of the behavioral data. Note the change in the ordinate scale across the panels.

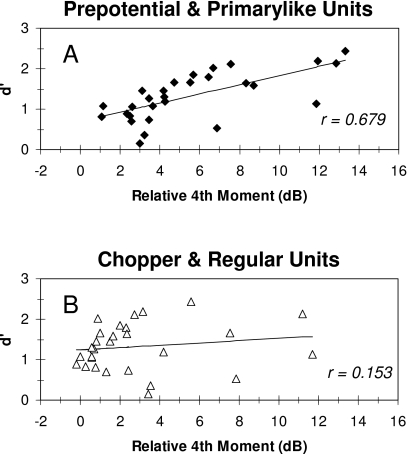
Figure 8 also shows the behavioral performance for discrimination of bandpass filtered IIRN from bandpass filtered WBN averaged from five chinchillas (Shofner and Yost, 1997). Behavioral performance was measured as d^′, and the ordinate for the behavioral performance has been adjusted arbitrarily to align the behavioral data with the Primarylike data in each panel. In general, there appears to be a correlation between the shape of the averaged profile for the Primarylike group and the shape of the profile for the behavioral performance for all IIRNs illustrated. On the other hand, the neural profile for Chopper units and the profile for behavioral performance do not appear to be similar in shape at any delayed noise attenuation. These comparisons suggest that the shapes of the neural profiles for the Primarylike group are correlated with behavioral performance, whereas the profiles for the Chopper group are not correlated with behavioral performance. These relationships are quantified in Fig. 9, which shows scatter plots of d^′ as a function of the relative fourth moments averaged in the one-octave bands. For the Primarylike units, there is a significant correlation between d^′ and the averaged relative fourth moment (r=0.679; p=0.000036, one-tailed t-test). In contrast, there is not a significant correlation between d^′ and the relative fourth moment for the Chopper group of units (r=0.153; p=0.218, one-tailed t-test).

Figure 9.

Scatter plots showing the relationship between the relative fourth moment averaged in the one-octave bands, with d^′ obtained behaviorally for IIRN filtered by one-octave bandpass filters. Correlation is high for Primarylike units (A) but not for Chopper units (C). Correlation coefficients (r) are indicated in each panel.

DISCUSSION

General comments

A spectral dominance region has been described for pitch discrimination of rippled noises in human listeners (Bilsen and Ritsma, 1970; Yost and Hill, 1978; Yost, 1982; Leek and Summers, 2001) as well as for the discrimination of IIRN from WBN in chinchillas (Shofner and Yost, 1997). These studies indicate that the region most effective in generating the pitch percept is generally around the third to fifth harmonic peaks of the rippled noise. The present results show that a neural correlate of the spectral dominance region exists in the temporal discharge of single units at the level of the cochlear nucleus for 4 ms delayed IIRNs.

The present study measured the temporal discharge patterns of cochlear nucleus units to IIRN and WBN using neural autocorrelograms. Presumably, a difference in the neuronal firing patterns evoked by IIRN and WBN underlies the behavioral discrimination in chinchillas (Shofner and Yost, 1997). Although IIRNs do not have periodic waveforms, they do possess temporal regularities that do not repeat in a periodic manner. Thus, rippled noises have been termed pseudoperiodic or quasiperiodic. The discharge patterns of Primarylike and Chopper units can reflect this temporal regularity as observed in the neural autocorrelograms. For both Primarylike and Chopper groups of units, there can be large differences in the temporal regularity for autocorrelograms obtained in response to IIRNs and WBN. That is, there is a regularity in the temporal discharge related to the delay that can be observed in response to the IIRNs. WBN does not possess any temporal regularity, and thus, there is no regularity in the temporal discharge of cochlear nucleus units. The difference in discharge patterns obtained in response to IIRNs and to WBN is reflected in the relative fourth moment, and presumably, this difference in discharge patterns is important in coloration discrimination (see below).

The results of the present study indicate that the spectral dominance region described for coloration discrimination in chinchillas (Shofner and Yost, 1997) is not found for units that are characterized by chopper and regular discharge patterns. The Chopper group of units show large differences in temporal discharge patterns between IIRN and WBN responses if the BFs correspond to the first and second harmonics of the IIRN. However, the shape of the profile of the relative fourth moment averaged in one-octave bands for these Chopper units is not correlated with the shape of the profile of behavioral performance. In contrast, the dominance region is better represented across BFs in the temporal discharge of cochlear nucleus units characterized by prepotentials in the spike waveforms and primarylike PST histograms. For this Primarylike group of units, the shape of the neural profile and the shape of behavioral performance are significantly correlated.

The approach of the present study was to examine the neural profile of the phase-locked activity across BFs for Primarylike and Chopper units in response to a fixed stimulus. The fixed stimuli were 4 ms delayed IIRN having four different delayed noise attenuations; these stimuli evoke a fixed pitch percept of 250 Hz that differ in pitch strength as delayed noise attenuation varies. Similar to the approach described for the representation of steady-state vowels in the cochlear nucleus (Blackburn and Sachs, 1990;Winter and Palmer, 1990b), data for the present study were pooled across animals to give an estimate of the population response. Unlike the vowel studies in which stimuli were presented at fixed sound levels, the present study presented stimuli at fixed levels above the threshold. In order to generate a meaningful estimate of the temporal discharge pattern through the autocorrelogram, it is important to evoke a high enough firing rate to collect a sufficient number of intervals over the 100 stimulus presentations. However, synchrony to the modulation frequency of sinusoidal-amplitude modulated tones decreases as sound level increases above the threshold for single-units in the cochlear nucleus (Rhode and Greenberg, 1994). Thus, at sound levels where the average firing rate is high, synchrony is reduced. A presentation level of 20 dB above the threshold was chosen to evoke a strong synchronous response and at the same time to ensure that a sufficient number of spike intervals for the autocorrelogram analysis were generated. Since the neural profile for Chopper units was not correlated with the behavioral profile of performance under these “optimal” stimulus conditions, it strongly suggests that dominance is not encoded in the temporal discharge of stellate cells.

Previous studies investigating physiological correlates of the dominance region have been carried out using complex tones. Greenberg et al. (1987) recorded the FFR from human listeners to two-tone complexes of successive harmonics of a fundamental frequency and showed that the largest responses were obtained for the third and fourth paired harmonics. The FFR is an auditory evoked potential based on the synchronous discharge of brainstem auditory neurons (Marsh et al., 1972). Cariani and Delgutte (1996) measured ISIs for single auditory nerve fibers in response to harmonic tone complexes comprised of the 3rd–12th harmonics. In this tone complex, the third to fifth harmonics were of one fundamental frequency, whereas the 6th–12th harmonics were of another fundamental frequency. The predominant ISI corresponded to the fundamental frequency of harmonics 3–5 when the fundamental was 160 Hz or higher and thus showed a neural correlate of the dominance region. In response to iterated rippled noise with negative gain, Sayles and Winter (2007) found examples of both primarylike and chopper units in guinea pigs that showed synchronous responses related to the ambiguous pitches perceived by human listeners for units having BFs corresponding to 4∕d, where d ranged from 4 to 16 ms. These BFs corresponded to the dominance region. For the negative gain iterated rippled noises used in the above guinea pig study, the pitch that is evoked in human listeners would not be ambiguous but would be one octave lower than 1∕d, because a large number of iterations was used (i.e., 16 iterations) [see Yost (1996a)]. It is unknown whether the guinea pig perceives the pitch to be ambiguous or at the lower octave for these particular rippled noises. Moreover, for chopper units, the most prominent interspike interval did not necessarily correspond to the ambiguous pitch but rather could correspond to the natural chopping frequency of the unit [see Fig. 3 in Sayles and Winter (2007)]. Thus, these findings suggest that there may be differences in the representation of the dominance region between chopper units and primarylike units.

The results of the present study further extend these findings into the cochlear nucleus for rippled noise stimuli. The delay used in the present study was fixed at 4 ms, and direct comparisons can be made between the observed physiological responses and behavioral performance obtained from the same species with the same stimuli (Shofner and Yost, 1997). The findings of the present and previous physiological studies (Greenberg et al., 1987; Cariani and Delgutte, 1996; Sayles and Winter, 2007) argue that the neural representation of the dominance region of pitch is established early on in auditory processing and is not the result of higher level processing mechanisms. It is interesting to note that all of these physiological studies show the existence of the spectral dominance region based on the temporal discharge patterns of auditory neurons.

Use of the fourth moment

In the present study, the responses of cochlear nucleus units were analyzed in the context of the behavioral data previously obtained (Shofner and Yost, 1997). In that behavioral task, chinchillas discriminated an IIRN from WBN, and presumably, this discrimination is based on a difference between neuronal firing patterns in response to IIRN and those in response to WBN. It is the difference in discharge patterns obtained in response to 4 ms IIRNs and WBN that the present study attempts to quantify. One approach to this problem might be to generate period histograms and compute synchronization index or vector strength. However, as previously described, IIRNs are not truly periodic stimuli, but rather their waveforms have regularities that are not repeated in a periodic manner. Thus, since WBN and IIRN are not periodic stimuli, period histograms cannot be utilized.

Alternatively, differences in temporal discharge patterns could be assessed using ISI statistics. For example, the normalized rate at a time lag of 4 ms is related to the total number of 4 ms ISIs and could potentially be used to quantify the difference in discharge patterns between IIRN responses and WBN responses. However, any measure based exclusively on the number of 4 ms ISIs makes the assumption that in the behavioral discrimination, the decision maker knows beforehand to analyze 4 ms ISIs. This assumption may or may not be true. More importantly, however, units can show a difference in discharge patterns between 4 ms IIRN and WBN without showing a change in the number of 4 ms ISIs.

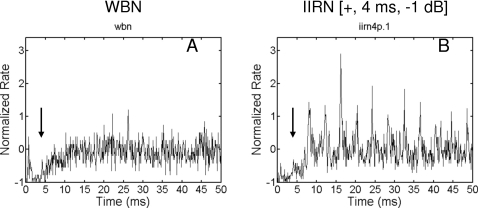
Figure 10 illustrates normalized autocorrelograms obtained in response to WBN and IIRN [+, 4 ms, −1 dB] for a 770 Hz BF unit classified as a Chopper. Note that the normalized rate at a time lag of 4 ms is small for both responses (arrows in Fig. 10, and there is no clear difference between the normalized rate at 4 ms for the WBN and IIRN responses. The normalized rate at 4 ms is −0.304 for the WBN response and −0.316 for the IIRN response. Thus, it is unlikely that this unit can encode the difference between 4 ms IIRN and WBN based only on the number of 4 ms ISIs. Nevertheless, there is a clear difference in the temporal discharge patterns between the responses to the IIRN and WBN. That is, this unit clearly responds differently to the IIRN than it does to the WBN even though there is no apparent difference in the number of 4 ms ISIs.

Figure 10.

Normalized autocorrelograms obtained from a unit in the Chopper group with a BF of 770 Hz in response to WBN (A) and IIRN [+, 4 ms, −1 dB) (B). Arrows indicate the location of the 4 ms ISI.

The fourth moment of a waveform is related to the fluctuations in instantaneous power (Hartmann, 1998), and it is clear in the example illustrated in Fig. 10 that the fluctuations in the response to IIRN are greater than those for the WBN. Strictly speaking, the fourth moment does not require the response to be synchronous, and large fourth moments could be obtained if the neural discharge pattern to IIRN showed deviations that were unrelated to the delay. However, the fact that the neural discharge patterns obtained in response to IIRNs often show periodicities related to the delay does not preclude the use of the fourth moment as an analytical tool. The use of the fourth moment was chosen because it captures the difference in the discharge patterns between IIRNs and WBN, and it makes no a priori assumptions that the decision maker must specifically analyze 4 ms ISIs.

Correlates of pitch strength

Iterated rippled noise evokes the perception of two simultaneous sound sources in human listeners: (1) the perception of a noise source and (2) the perception of a tonal source (Patterson et al., 1996). The relative amounts of these two perceptions are determined by the number of iterations or the delayed noise attenuation. As the number of iterations increases (Yost, 1996b) or as the amount of delayed noise attenuation decreases (Shofner and Selas, 2002), there is a progressive decrease in the noise percept and a progressive increase in the tonal percept. That is, the saliency of the pitch percept (i.e., pitch strength) increases. Thus, the pitch strength of iterated rippled noise can be made to vary from that of a flat-spectrum noise to that of a pulse train. Chinchillas trained to discriminate IIRN [+, d, −1 dB] from WBN and tested in a stimulus generalization paradigm with IIRNs having the same delays but varying delayed noise attenuations show increases in behavioral responses as delayed noise attenuation decreases (Shofner et al., 2005). These generalization gradients obtained from chinchillas presumably reflect a psychological dimension related to the delayed noise attenuation (i.e., pitch strength).

Physiological correlates of pitch strength have been described by Griffiths et al. (2001). As the number of iterations of the rippled noise increases, there is an increase in blood flow in each of the central auditory nuclei, including the cochlear nucleus, as measured by functional magnetic resonance imaging in the human auditory system. This finding suggests that there is an increase in neural activity as the number of iterations increases and is a correlate of the increase pitch strength. Similarly, the results of the present study show that there is an increase in the periodicity in the discharge patterns of Primarylike and Chopper units as the delayed noise attenuation decreases (e.g., see Figs. 45). The ANOVA indicated significant effects of delayed noise attenuation for both Primarylike and Chopper groups for units with BFs less than or equal to 1250 Hz (i.e., less than or equal to the fifth harmonic of the IIRN). Thus, the increase in pitch strength observed with the decrease in delayed noise attenuation appears to be related to an increase in the strength of periodicity in the temporal discharge pattern of cochlear nucleus units.

Roles of primarylike and chopper units

Several studies have shown that the phase-locked responses to amplitude modulation are larger for chopper units than for primarylike units (Frisina et al., 1990; Rhode and Greenberg, 1994; Wang and Sachs, 1994; Shofner et al., 1996). Morphologically, chopper units correspond to stellate (multipolar) cells (Rhode et al., 1983; Rouiller and Ryugo, 1984; Smith and Rhode, 1989; Ostapoff et al., 1994), which send an axonal projection directly to the inferior colliculus (Adams, 1979; Cant, 1982). The enhanced ability of chopper units to encode amplitude modulation has suggested the importance of these units in processing information related to pitch. Indeed, neural models of periodicity processing have been based heavily on contributions from chopper units (Borst et al., 2004; Meddis and O’Mard, 2006; Dicke et al., 2007).

Although, both primarylike and chopper units with low BFs can encode temporally the difference in pitch of iterated rippled noises generated with positive and negative gains (Shofner, 1999; Verhey and Winter, 2006; Sayles and Winter, 2007), chopper units can also show bandpass tuning to iterated rippled noise delay as estimated from first-order ISI historgrams that is independent of the stimulus level (Wiegrebe and Winter, 2001). This latter finding has also been used to argue for the importance of chopper units in processing pitch-related information. The above discussion suggests that chopper units have an important role in periodicity processing.

The results of the present study show that a representation of the dominance region of pitch for 4 ms delayed IIRN does not appear to exist in the temporal discharge of the Chopper group of units. This finding should not be interpreted to imply that Chopper units are unimportant for periodicity processing. On the contrary, the present results show that these units give large averaged relative fourth moments if the BFs are around the first and second harmonics. For the 4 ms delayed IIRNs used in the present study, these harmonics would correspond to units having BFs below 500 Hz. In other words, low BF Chopper units show large differences in discharge patterns between 4 ms IIRN and WBN. Higher BF Chopper units, however, do not show as large of a difference in discharge patterns between IIRN and WBN, as evidenced by their smaller averaged relative fourth moments at harmonics above 2. Consequently, the dominance region is not well represented in these units.

The lack of a neural representation of the dominance region for the Chopper group presumably reflects the poor phase-locking ability of chopper units to BF tones. At 1000 Hz the synchronization index is approximately 0.2 for chopper units but is around 0.6 for primarylike units in the guinea pig (Winter and Palmer, 1990a). In a cat for 1000 Hz tones, the synchronization indices for chopper and primarylike units are approximately 0.4 and 0.8, respectively (Blackburn and Sachs, 1989). Thus, there is a decreased ability of chopper units to encode the frequency corresponding to the fourth harmonic of the 4 ms delayed IIRNs used in the present study. As a consequence, Chopper units with BFs corresponding to the third to fifth harmonics are unable to encode the 4 ms delay of the IIRNs as well as Primarylike units. Although chopper units can show enhanced phase-locking to envelope modulation, they show poorer phase-locking to the fine structure. IIRN is not highly modulated, but rather the delay information is predominately found in the fine structure [see Fig. 1 of Shofner and Selas (2002), for example]. Thus, the encoded neural information used by the animal for discriminating the 4 ms IIRNs from WBN is likely to be dominated by the discharge patterns of primarylike units rather than chopper units.

Although chopper units provide a synchronous neural discharge to the inferior colliculus, which is important for periodicity processing, the present findings of a neural correlate of the dominance region in the temporal discharge of primarylike units suggest that periodicity processing related to pitch perception is not exclusive to chopper units. In this regard, it is interesting to note that an alternative neural model based exclusively on the information encoded in primarylike units can also account for many aspects of periodicity processing (Nelson and Carney, 2004). Each of the neural models previously cited in this paper has attempted to account for aspects of periodicity processing through the exclusive use of either chopper units or primarylike units. As previously mentioned, chopper units correspond to stellate cells, which send a direct axonal projection to the inferior colliculus. Primarylike units correspond morphologically to bushy cells, and the information encoded in the discharge patterns of bushy cells will arrive at the inferior colliculus indirectly through projections from the superior olive [e.g., Oliver et al. (1995)]. Thus, the information encoded in the discharge patterns of primarylike and chopper units will ultimately converge at the level of the inferior colliculus.

In order to address how this convergence of neural information might affect the dominance region, the information for Primarylike and Chopper units having BFs within each of one-octave bands was evaluated using a signal detection theory approach. The d^′ for each one-octave band was computed as

$$d^{\prime }{}_e=\frac{{\mu }_{\mathrm{Pr}i}-{\mu }_{\mathrm{Chop}}}{0.5({\sigma }_{\mathrm{Pr}i}+{\sigma }_{\mathrm{Chop}})},$$ (5)

where μ_{Pr i} and μ_Chop are the averaged relative fourth moments in each one-octave band for the Primarylike and Chopper groups and σ_{Pr i} and σ_Chop are the standard deviations of the samples within each one-octave band. Note that Kim et al. (1990) showed that Eq. 5 is equivalent to d^′_e as defined by Green and Swets (1988) (p. 98). This analysis treats the information in the Primarylike group as the signal and the information in the Chopper group as the noise.

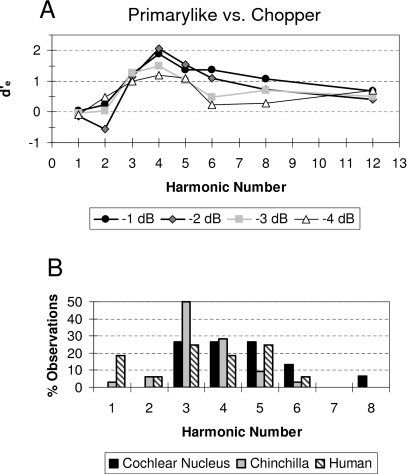
The d^′_e in each one-octave band is illustrated in Fig. 11A where the octave bands are shown as harmonic numbers. Note that across the four delayed noise attenuations (i.e., −1, −2, −3, and −4 dB), the third to fifth harmonics consistently have d^′_e values greater than or equal to 1. The harmonics that showed a d^′_e greater than or equal to 1 were determined for each of the delayed noise attenuations [Fig. 11B]. For comparison, Fig. 11B shows similar data obtained from chinchillas discriminating 4 ms IIRN from WBN (Shofner and Yost, 1997) and normal hearing human listeners discriminating a 4 ms iterated rippled noise standard from another rippled noise having a 12% pitch change (Leek and Summers, 2001). This analysis suggests that the neural profile of the dominance region becomes well defined when the information in the discharge patterns of both bushy cells and stellate cells is combined.

Figure 11.

(A) Profile of the dominance region expressed as d^′_e as a function of harmonic number. d^′_e represents the difference between Primarylike and Chopper groups (see text for details). (B) Black-filled bars show the distribution of harmonics, which resulted in a d^′_e⩾1 from the functions in (A). Gray-filled bars and striped bars show the distributions obtained from a similar analysis for chinchillas (data from Shofner and Yost, 1997) and normal hearing human listeners [data from Leek and Summers (2001)], respectively.

In summary, the results of the present study argue for the importance of cochlear nucleus bushy cells in processing periodicity information related to pitch. It should be emphasized that this is not meant to imply that this is the exclusive pitch pathway. While it is likely that other cochlear nucleus cell types also contribute to the overall pitch perception, the contributions of bushy cells to processing pitch-related information should not be ignored.