Abstract
There is a need for an imaging sequence that can provide high-resolution diffusion tensor images at 3T near air/tissue interfaces. By employing a radial fast spinecho (FSE) collection in conjunction with magnitude filtered back-projection reconstruction, high-resolution diffusion-weighted images can be produced without susceptibility artifacts. However, violation of the CPMG condition of diffusion prepared magnetization is a prominent problem for FSE trains that is magnified at higher fields. The unique aspect of violating the CPMG condition in trajectories that over sample the center of k-space and the implications for choosing the solution are examined. For collecting diffusion-weighted radial-FSE data at 3T we propose mixed-CPMG phase cycling of RF refocusing pulses combined with a 300% wider refocusing than excitation slice. It is shown that this approach produces accurate diffusion values in a phantom, and can be used to collect undistorted, high-resolution diffusion tensor images of the human brain.
Introduction
Diffusion-weighted MRI (DWI) is a prevalent clinical tool used for many applications, from monitoring tumor response to chemotherapy to mapping white matter fiber trajectories in the brain (1,2). The majority of clinical studies employ single-shot echo planar imaging (SSEPI) sequences due to their insensitivity to bulk motion. SSEPI is, however, inherently limited in image resolution and prone to susceptibility artifacts. For quantitative applications of DWI, in particular for diffusion tensor imaging (DTI) (3), higher resolutions are sought and, consequently, the 3T environment is desired to compensate for smaller voxels with an inherent gain in signal-to-noise ratio (SNR). However, imaging at higher fields has well known drawbacks such as the increase in susceptibility at air/tissue interfaces. Although, parallel imaging methods, like SENSE and GRAPPA, have greatly reduced the effects of susceptibility in diffusion-weighted SSEPI images (4,5), when pushed to high resolution at 3T SSEPI images still contain areas with prohibitive susceptibility gradient effects. Use of a spin-echo readout in the sequence almost entirely eliminates the resulting susceptibility artifacts, but this procedure requires a multi-shot acquisition to collect the necessary data. Multi-shot acquisitions may increase image resolution, but when combined with diffusion weighting are prone to ghosting artifacts due to inconsistent phase from shot to shot. A solution to this dilemma is to use a multi-shot acquisition that contains a radial readout and is reconstructed with magnitude filtered back-projection (6). Previously, work has been published on a diffusion-weighted radial fast spin-echo (FSE) sequence implemented on a 1.5T scanner that can produce high-resolution images that are insensitive to both magnetic field inhomogeneity and bulk motion (7,8). Therefore, the goal of this work is to produce high-resolution diffusion-weighted images with a radial sequence at 3T that are suitable for clinical DTI mapping in areas of high susceptibility. To our knowledge this is the first paper to present in vivo diffusion tensor images at 3T using a radial acquisition sequence.
Several strategies can be pursued to achieve this goal, each with advantages and drawbacks. For example, the increase in image resolution due to a multi-shot acquisition comes at a cost of increased scan time; this problem can be mitigated by expanding to an FSE readout. Another drawback at higher field strength that is particularly problematic for spin-echo sequences is the decline in B1 homogeneity due to the lack of RF penetration, which is inversely linked to increases in the main magnetic field strength (9). To counteract the issue of B1-inhomogeneity in FSE trains, the well-known Carr-Purcell- Meiboom-Gill (CPMG) method was developed (10). For this method to be successful the CPMG condition has to be met, i.e., the initial phase of the transverse magnetization and the phase of the RF refocusing pulse must be the same. However, when a diffusion-weighted preparation is played out, the large amplitude diffusion gradients can produce eddy-currents that may add a spatially varying phase to the transverse magnetization so that it no longer meets the CPMG condition, which may result in severe echo attenuation within the echo train.
Addressing the violation of the CPMG condition at higher fields is not a trivial task, illustrated by the striking lack of publications on DWI at 3T using an FSE based sequence. However, several schemes have been published to combat the violation of the CPMG condition with FSE sequences at 1.5T (11-14). The method proposed by Norris et. al., further developed by Alsop, removes some components of the net magnetization that destructively interfere, thereby producing a stable echo magnitude throughout the echo train. Although this method circumvents the violation of the CPMG condition, it also results in half the signal intensity for imaging. As the resolution in an image is limited by SNR, this solution is undesirable when the goal is higher resolutions. Le Roux has proposed a non-CPMG method that uses a quadratic phase modulation of the refocusing RF pulses and can produce a stable echo magnitude throughout the echo train after a suitable preparation period of RF pulses. The additional RF pulses are feasible for single-shot FSE sequences as scan time increases modestly. However, for multi-shot FSE acquisitions, with an echo train length (ETL) between 4 and 16, the increase in scan time is great, as the quadratic phase preparation period of RF pulses must be executed every TR period. In the mixed-CPMG phase cycling method proposed by Pipe et. al., the phase of the RF refocusing pulses alternates between the x' and y' axes producing a fairly stable echo train for up to 32 echoes, when used with a refocusing flip angle near 180°. The mixed-CPMG phase cycling method brings the magnetization back into the transverse plane after four RF refocusing pulses, regardless of the initial phase. This is similar to the CPMG sequence, which brings the magnetization back into the transverse plane after two RF refocusing pulses. However, due to this four RF pulse periodicity, oscillation is induced in the echo magnitude along the echo train. The pattern and amplitude of oscillation depends on the initial phase of the magnetization and the flip angle of the refocusing pulses: in general, the farther away from the CPMG condition and the lower the flip angle, the greater the oscillation amplitude. For a more detailed description of initial staring phase and flip angle dependency on the oscillation pattern in the echo decay see Pipe et. al. (14). It is important to note that the received signal, being the net magnetization, is a sum of spins that may not all have the same starting phase. Therefore, the pattern of oscillation may not be as well defined in real data.
An alternative approach to addressing the violation of the CPMG condition would be to improve the B1-homogeneity and exactness of the 180° RF refocusing pulses at 3T. If the RF pulse is strictly 180° then the transverse magnetization will be refocused regardless of the initial phase. For 3T imaging, Pell et. al. have proposed the incisive technique of utilizing a refocusing slice that is wider than the excitation slice to improve the B1-homogeneity of the RF refocusing pulse for more accurate and precise measurements of T2 (15).
Because B1-homogeneity is affected by both slice profile and RF penetration, in this work, both the mixed-CPMG phase cycling method and using a refocusing slice that is wider than the excitation slice were investigated for use in the diffusion-weighted radial-FSE sequence for high resolution DTI in areas of increased susceptibility at 3T.
Methods
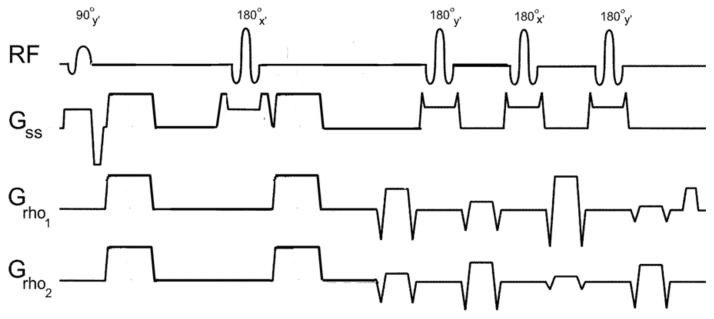
The diffusion-weighted radial-FSE sequence developed for DTI at 3T contains a standard Stetjskal-Tanner diffusion preparation period followed by a train of 180° refocusing pulses. A single radial line of k-space is read out at each spin-echo point with all read gradients balanced before successive RF refocusing pulses. The phase of the 90° RF excitation pulse is set to y', the 180° RF pulse phase in the diffusion preparation period is set to x', and the phase of the 180° RF refocusing pulses in the echo train alternates between the y' and x' axes, as shown in FIG. 1. The crushers surrounding the 180° RF pulse in the diffusion preparation period have about five times the area of the crushers in the echo train to remove subtle banding artifacts present in the b-value = 0 s/mm2 image near susceptibility gradients. Consequently, when diffusion gradients are applied in the Z direction, there is a slight increase in the b-value of 33.4 s/mm2(16). In addition, a refocusing slice that is wider than the excitation slice was incorporated into the 3T diffusion-weighted radial-FSE sequence by introducing a user-controlled variable for the refocusing slice gradient. Note that the RF refocusing pulses were coded to have a flip angle of 180°, which is not the default flip angle at 3T in the product FSE sequence.
FIG1.
Diagram of the diffusion-weighted radial-FSE pulse sequence with mixed-CPMG phase cycling. Diffusion weighting is shown in the XYZ direction with an ETL = 4 readout. The phase of the 180° RF refocusing pulses alternates between the x' and y' axes.
All data were collected on a GE Signa 3T scanner with maximum gradient strength of 40 mT/m and slew rate of 150 T/m/s. To test the accuracy of diffusion measures, including the possible occurrence of artificial directional bias in the diffusion-weighted signal, an isotropic diffusion phantom was scanned. This phantom consisted of a 50 mL plastic tube filled with a 1% agarose and saline gel doped with 0.025% by volume of ProHance gadoteridol, by Bracco Diagnotics. Data of a single slice were acquired on this phantom with three different DWI sequences: 1) radial-FSE, 2) conventional SSEPI, and 3) Cartesian spin-echo. Data acquired with 2) and 3) are considered to be gold standards for comparison because these sequences do not suffer from CPMG violation effects; moreover, in the phantom, susceptibility is not a relevant problem at the center of the object, and there is no motion.
The phantom data were acquired with a standard head coil. Careful attention was given to the manual adjustment of receiver gains, transmit gain, and transmit frequency to achieve the most accurate flip angle for phantom testing. Data collected with the radial-FSE sequence had 1 mm2 in-plane resolution and the following scan parameters: TE/TR = 62/2000 ms, ETL = 8, BW= ±16 KHz, FOV = 24 cm, 256 points, views = 256, and 3mm slice thickness. Images with diffusion sensitization in the X, Y, and Z directions with b-value = 500 s/mm2 were acquired along with DTI data at b-value =1000 s/mm2 in six gradient directions according to the scheme presented in (17). The data were collected with a sequential view order to examine the behavior of the echo decay within the echo train (18). Six direction DWI data were collected at the same resolution with SSEPI, provided by the manufacturer, with the following scan parameters: TE/TR = 100/3000 ms, FOV = 24 cm, 256 × 256, NEX = 4, 5 repetitions, and b-value = 1000 s/mm2. For the diffusion-weighted spin-echo sequence the following parameters were used: 2 × 2 mm in-plane resolution, TE/TR = 50/1000 ms, BW = ±16 KHz, FOV = 24 cm, 128 × 128, and 3 mm slice thickness,. The lower in-plane resolution and shorter TR were used to reduce the total scan time needed to collect spin-echo DTI data.
To verify that radial-FSE can be used for high quality in vivo brain imaging a healthy 42-year-old male volunteer was scanned. In particular, high-resolution DTI data obtained with the radial-FSE sequence was compared to that obtained with the state-of-the-art SSEPI sequence available from the manufacturer. Six direction DWI data sets, with b-value = 1000 s/mm2, were acquired with an 8-channel phased-array coil at the highest resolution achievable with the SSEPI sequence (1mm2 in-plane resolution and 1.5 mm slice thickness; a slice thickness of 1 mm was attempted but at that resolution the available SSEPI sequence produced artifacts in the image). The radial-FSE data were collected with peripheral gating to minimize effects of cardiac pulsation. The scan parameters were TE = 62, ETL = 4, BW = ±16 KHz, FOV = 25 cm, 256 points, views = 384, and the subjects heart rate was ∼50 BPM, yielding a TR∼1.2 sec and total scan time of 13:46 min for the single repetition. Data were collected over 1 R×R interval with a trigger delay of 250 ms allowing 2 slices to be collected with a prescribed gap of 6 mm. A bit-reversed view ordering was used to minimize streaking artifacts (18). For a sensible comparison, the total scan time of the SSEPI acquisition was set to be similar to that of the radial-FSE (15 minutes). Moreover, the time was used to increase SNR by collecting multiple repetitions of a limited number of slices, rather than to increase coverage. The SSEPI data were collected with TE/TR = 82/3000ms, BW= ±250 KHz, FOV = 25 cm, 256 × 256, NEX = 4,10 repetitions, and 7 slices with a gap of 6 mm. To reduce the sensitivity of the SSEPI acquisition to susceptibility artifacts a SENSE factor of 2 was employed.
From the diffusion-weighted data, the diffusion tensor was computed by non-linear least squares fitting using IDL code developed in-house (19). The orientationally-averaged apparent diffusion coefficient (ADC), which is equal to 1/3 of the Trace of the diffusion tensor, and the fractional anisotropy (FA) (20), were calculated on a voxel by voxel basis, as well as directionally encoded color (DEC) maps (21).
Results
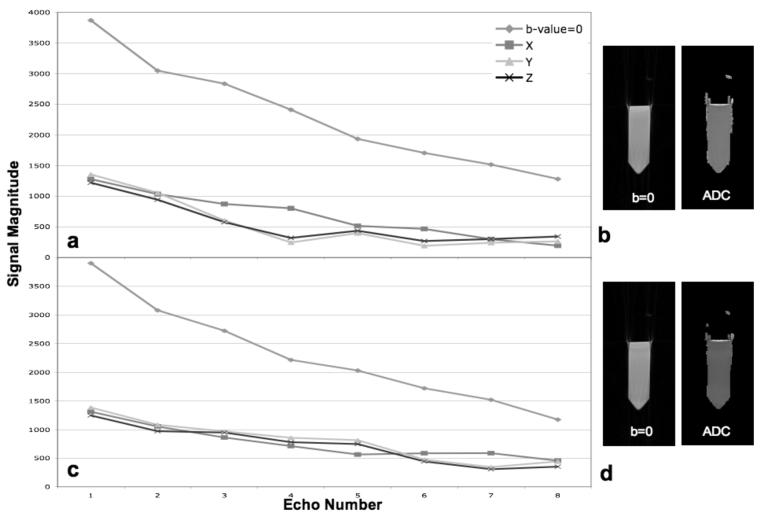
A plot of the average center point magnitude at each echo time in the echo train is shown in FIG. 2a for data collected with a diffusion-weighted radial-FSE sequence using the conventional CPMG method. Although the flip angle was carefully calibrated and the object was small and homogeneous, the echo magnitude decays more quickly for diffusion-weighted data than for the data with b-value = 0 s/mm2. In this case the decay is most pronounced for diffusion weighting in the Z direction. In general, the severity of this effect depends on residual eddy-currents and may affect diffusion directions other than Z more strongly depending on the eddy current compensation of the scanner. Exaggerated echo decay causes the computed ADC to be too high; the variation in echo decay per diffusion direction causes the calculated diffusion anisotropy, e.g. FA, also to be too high. An ROI selected in the center of the calculated average diffusivity image, shown in FIG. 2b, yields an ADC = 2.66×10−3 mm2/s. For comparison, the ADC of the phantom when collected with SSEPI is 2.07×10−3 mm2/s, which is consistent with that expected for free water at room temperature (20° C).
FIG 2.
Plots of the average echo magnitude of diffusion-weighted radial-FSE data sets, with b-value = 0 s/mm2 and 500 s/mm2 with weighting in the X, Y, and Z directions, collected with the conventional CPMG phase cycling, a, and mixed-CPMG phase cycling, c. Corresponding b-value = 0 s/mm2 images and ADC maps are shown in b and dfor the conventional CPMG and mixed-CPMG phase cycling, respectively.
When the mixed-CPMG phase cycling method is introduced into the echo train, the echo magnitude of the diffusion-weighted signals decays less rapidly, but an oscillation pattern can be observed, as seen in FIG 2c. The amplitude of oscillation varies for the different diffusion directions, consistent with what was described in the introduction. In addition, the b-value = 0 data also oscillates. An ROI selected in the center of the calculated average diffusivity image, shown in FIG. 2d, yields an ADC = 2.12×10−3 mm2/s. This is a considerable improvement over the CPMG method, but some bias is still present; the remaining variance in echo attenuation for different directions is still problematic for anisotropy calculations.
FIG. 3 shows the effect of varying the thickness of the refocusing slice on the oscillation amplitude of the echo decay. Echo magnitude plots are shown for a b-value = 500 s/mm2 data set with diffusion weighting in the Z direction. The refocusing slice width was systematically increased in 50% increments from 100% to 500% of the excitation slice width. The oscillation amplitude steadily diminishes as the refocusing slice widens. In addition, SNR increases substantially, by a factor of 1.7 from the 100% to ≥300% data, as more magnetization experiences a 180° flip angle. Similarly to what was reported by Pell et. al., great improvement is seen when the refocusing slice is about 300% of the excitation slice width, but little is gained after this point. Incidentally, the default refocusing slice width set by the manufacturer for FSE acquisition (150%) appears suboptimal based on our results. The use of a refocusing slice that is 300% wider than the excitation slice was tested with the conventional CPMG echo train to investigate if this technique alone could eliminate the issue of the violation of the CPMG condition at 3T. Although the severity of the echo decay was reduced, it was still greater than that seen with the mixed-CPMG phase cycling. In addition, the difference in echo decay between diffusion directions was still substantial (data not shown).
FIG 3.
Plots of the average echo magnitude from data collected with the mixed-CPMG phase cycled radial-FSE and b-value = 500 s/mm2 in the Z diffusion direction. The ratio of the refocusing to excitation slice thickness was varied from 100 to 500%. As the ratio increases, the amplitude of oscillation along the echo train decreases, leveling off at 300%.
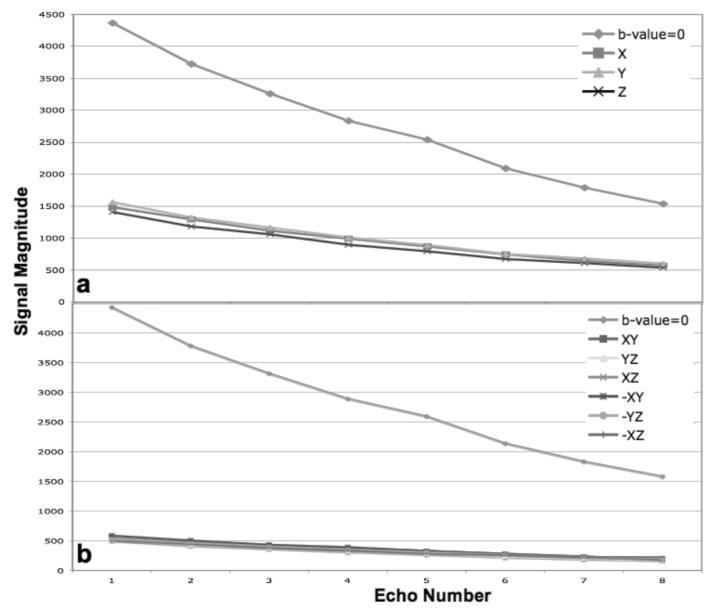
Therefore, an optimal strategy should include both the mixed-CPMG phase cycling and a 300% wider refocusing slice. FIG. 4a shows plots of the echo decay obtained with this strategy for diffusion weighting in the X, Y, Z and b-value = 0 s/mm2 in the phantom. FIG. 4b shows similar results obtained with six diffusion directions. The decay along the echo train is smooth, without oscillation, regardless of diffusion weighting or direction.
FIG 4.
Plots of the average echo magnitude data collected from the gel phantom with the modified radial-FSE sequence containing mixed-CPMG phase cycling and using a refocusing slice 300% wider than the excitation slice. The individual diffusion gradients with b-value = 500 s/mm2 is shown in a. Six DTI directions with b-value = 1000 s/mm2 are shown in b. Notice the smooth, non-oscillatory, decay along the echo train for all diffusion directions.
FIG. 5 shows a comparison of diffusion tensor parameter maps (b-value = 0 s/mm2 image, ADC and FA) computed from data shown in FIG. 4b, and from data collected using diffusion-weighted spin-echo and SSEPI. The ADC and FA calculated from diffusion-weighted spin-echo data were 2.00×10−3 mm2/s and 0.03 respectively. The very low FA value shows the great consistency between the different diffusion directions. The corresponding SSEPI data set, however, contains some susceptibility artifacts. Taking an ROI in the upper-center of the gel where FA is lowest to avoid these artifacts, calculated ADC and FA values were 2.07×10−3 mm2/s and 0.07, respectively. For the data collected with the modified radial-FSE sequence, the calculated ADC and FA were 2.03×10−3 mm2/s and 0.05. The radial-FSE images do not contain distortions due to susceptibility and have an FA value even lower than that of the EPI, indicating greater consistency between diffusion directions or better SNR (22). When both the mixed-CPMG phase cycling method and the widened refocusing slice are used to improve B1-homogeneity, both the ADC and FA values of the radial-FSE data are comparable to those of the diffusion-weighted spin-echo and SSEPI data.
FIG 5.
Images from six direction DTI data sets from the gel phantom collected with a spin-echo sequence, a, single-shot EPI, b, and the modified radial-FSE sequence, c. Images with b-value = 0 s/mm2, the calculated ADC and FA maps are shown from each data set.
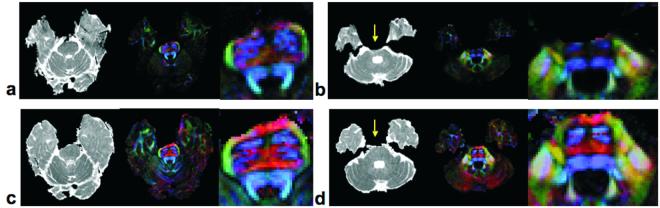
FIG. 6 shows average diffusivity and DEC maps in two slices collected at the level of the Pons in the healthy volunteer. In a) and b) maps from data collected with SSEPI are shown, while those from data collected with the radial-FSE sequence are shown in c) and d). As a point of reference the SNR, defined here as the signal mean divided by the signal standard deviation, of an ROI taken in the undistorted part of the cerebellum (b and d) were 22 and 18 for the non-diffusion-weighted radial-FSE and averaged SSEPI images, respectively. The ADC images computed from the SSEPI data show marked susceptibility artifacts and geometric distortions both in the Pons (yellow arrow) and in the temporal lobes. The corresponding DEC maps appear blurred in these regions. Geometric distortion and susceptibility artifacts are virtually absent in the diffusion-weighted radial-FSE images. DEC maps of the Pons at 4× magnification, shown on the right side of each panel, highlight the anatomical information lost in the SSEPI images. For example, in data acquired with the radial-FSE sequence (FIG. 6d) bundles of descending motor fibers (blue), and a group of transverse pontine fibers positioned anteriorly to them (red) in the ventral portion of the Pons are all visible. In the corresponding data acquired with the SSEPI sequence (FIG. 6b) the red ventral transverse fibers are completely absent and there is a significant loss of the adjacent descending motor fibers.
FIG 6.
DTI data sets of a normal volunteer were collected of two slices with single-shot EPI, a and b, and the modified radial-FSE sequence, c and, d. Both the ADC and directionally encoded color anisotropy maps are shown, along with a 4x magnified image of the brainstem region.
Discussion
Despite the many advances in diffusion-weighted SSEPI sequences, including SENSE phase encoding with phased-array coils, when pushed to 1mm2 in-plane resolution at 3T, SSEPI still has severe artifacts in areas of high susceptibility, effectively precluding the investigation of several anatomic regions of the brain. Conversely, the modified radial-FSE sequence presented in this work allows structures near air/tissue interfaces, like those in the orbito-frontal and inferior temporal lobes along with the brainstem, to be studied with DTI at high-resolution. Images are presented at 1 mm2 in-plane resolution with 1.5 mm slice thickness for comparison to SSEPI, but less than 1 mm3 voxels are easily achievable with the presented radial-FSE sequence (23). In addition, because radial-FSE images do not have geometric distortions, ROIs drawn on structural images can be directly overlaid on diffusion-weighted radial-FSE images without the need for unwarping.
However, there are drawbacks to the radial-FSE sequence presented in this work for DTI at 3T. Currently, the most robust method to combat the effects of cardiac pulsation in multi-shot DWI, cardiac gating, is not ideal for several reasons: increased imaging time, limited number of slices that can be collected in a single acquisition, and possible variations in TR if the heart rate varies and/or heart beats are skipped. In addition, because radial-FSE is a multi-shot sequence, long imaging time—longer than for SSEPI—is prohibitive for radial-FSE to be used for full brain coverage DTI. The sequence is better suited for applications of limited coverage in areas of high susceptibility, e.g., the brainstem, optic nerve, and hippocampus. There are different approaches to high-resolution DTI of limited coverage, such as the use of a diffusion-weighted driven equilibrium type of preparation with a data collection strategy that is insensitive to susceptibility effects (24,25). However, a drawback of these techniques is the ability to accurately calculate the b-value and diffusion coefficient due to T1-contamination.
Advantages of diffusion-weighted radial-FSE vis-à-vis Cartesian based FSE acquisitions used for DWI (like PROPELLER and single-shot FSE) with the mixed-CPMG phase cycling method are: 1) due to the magnitude filtered back-projection reconstruction, even and odd echoes can be treated identically and combined directly in reconstruction; and 2) data can be collected on a multi-channel phased array coil and reconstructed in the standard way without extra post-processing to account for possible phase differences between receiver coils (26).
The mixed-CPMG phase cycling method is robust to initial phase, but induces an oscillation in the echo magnitude along the echo train that is dependant on the initial starting phase of the magnetization and the flip angle of the refocusing pulses. Because eddy currents may be different for different diffusion directions, the initial starting phase will also be different and, accordingly, the oscillation pattern will differ. This variation can be circumvented when data are collected on a Cartesian grid by noting the order in which lines of data are collected and putting the most stable echo points near the center of k-space (14). In radial trajectories, each line of data passes through the center of k-space and contributes more or less equally to the intensity in the image. Consequently, any variation in the echo magnitude along the echo train between diffusion directions will be present in the reconstructed images and bias calculated diffusion parameters, like ADC and FA. Thus, the mixed-CPMG phase cycling method alone cannot overcome the violation of the CPMG condition in diffusion-weighted radial-FSE acquisitions at 3T. Nevertheless, when combined with a refocusing slice that is 300% wider then the excitation slice, which improves B1-homogeneity, the oscillation is nearly eliminated. The implementation of the widened refocusing slice does require additional attentiveness to the spacing of slices whose data are collected within the same TR. Comparing the signal in the central slice of a three slice acquisition with a slice gap of 0 mm to four times the slice thickness with that of a single slice acquisition of the phantom, it was found that a slice gap of two times the prescribed slice thickness results in negligible effects on neighboring slices.
Conclusion
A modified diffusion-weighted radial-FSE sequence has been presented for imaging at 3T that employs both mixed-CPMG phase cycling and use of a refocusing slice that is 300% wider than the excitation slice. With these modifications, high resolution DTI of less than 1mm3 voxels may be obtained of structures near air/tissue interfaces that are currently impossible to image accurately with SSEPI.
Acknowledgements
The authors would like to thank Dr. Alan Barnett for insightful discussions. The Intramural Research Program of the National Institute of Child Health and Human Development supported this research.
References
- 1.Charles-Edwards EM, deSouza NM. Diffusion-weighted magnetic resonance imaging and its application to cancer. Cancer imaging : the official publication of the International Cancer Imaging Society. 2006;6:135–143. doi: 10.1102/1470-7330.2006.0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Mori S, Zhang J. Principles of Diffusion Tensor Imaging and Its Applications to Basic Neuroscience Research. Neuron. 2006;51(5):527–539. doi: 10.1016/j.neuron.2006.08.012. [DOI] [PubMed] [Google Scholar]
- 3.Basser PJ, Mattiello J, LeBihan D. Mr Diffusion Tenser Spectroscopy and Imaging. Biophysical Journal. 1994;66(1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bammer R, Auer M, Keeling SL, Augustin M, Stables LA, Prokesch RW, Stollberger R, Moseley ME, Fazekas F. Diffusion tensor imaging using single-shot SENSE-EPI. Magnetic Resonance in Medicine. 2002;48(1):128–136. doi: 10.1002/mrm.10184. [DOI] [PubMed] [Google Scholar]
- 5.Skare S, Newbould RD, Clayton DB, Albers GW, Nagle S, Bammer R. Clinical multishot DW-EPI through parallel imaging with considerations of susceptibility, motion, and noise. Magnetic Resonance in Medicine. 2007;57(5):881–890. doi: 10.1002/mrm.21176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Trouard TP, Sabharwal Y, Altbach MI, Gmitro AF. Analysis and comparison of motion-correction techniques in Diffusion-Weighted Imaging. Journal of Magnetic Resonance Imaging. 1996;6(6):925–935. doi: 10.1002/jmri.1880060614. [DOI] [PubMed] [Google Scholar]
- 7.Trouard TP, Theilmann RJ, Altbach MI, Gmitro AF. High-resolution diffusion imaging with DIFRAD-FSE (diffusion-weighted radial acquisition of data with fast spin-echo) MRI. Magn Reson Med. 1999;42(1):11–18. doi: 10.1002/(sici)1522-2594(199907)42:1<11::aid-mrm3>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- 8.Sarlls JE, Newbould RD, Altbach MI, Gmitro AF, Seeger J, Trouard TP. Isotropic diffusion weighting in radial fast spin-echo magnetic resonance imaging. Magn Reson Med. 2005;53(6):1347–1354. doi: 10.1002/mrm.20493. [DOI] [PubMed] [Google Scholar]
- 9.Yang QX, Wang J, Zhang X, Collins CM, Smith MB, Liu H, Zhu XH, Vaughan JT, Ugurbil K, Chen W. Analysis of wave behavior in lossy dielectric samples at high field. Magnetic Resonance in Medicine. 2002;47(5):982–989. doi: 10.1002/mrm.10137. [DOI] [PubMed] [Google Scholar]
- 10.Meiboom S, Gill D. Modified spin-echo method for measuring nuclear relaxation times. The Review of Scientific Instruments. 1958;29(8):688–691. [Google Scholar]
- 11.Alsop DC. Phase insensitive preparation of single-shot RARE: application to diffusion imaging in humans. Magn Reson Med. 1997;38(4):527–533. doi: 10.1002/mrm.1910380404. [DOI] [PubMed] [Google Scholar]
- 12.Le Roux P. Non-CPMG Fast Spin Echo with full signal. J Magn Reson. 2002;155(2):278–292. doi: 10.1006/jmre.2002.2523. [DOI] [PubMed] [Google Scholar]
- 13.Norris DG, Bornert P, Reese T, Leibfritz D. On the application of ultra-fast RARE experiments. Magn Reson Med. 1992;27(1):142–164. doi: 10.1002/mrm.1910270114. [DOI] [PubMed] [Google Scholar]
- 14.Pipe JG, Farthing VG, Forbes KP. Multishot diffusion-weighted FSE using PROPELLER MRI. Magnetic Resonance in Medicine. 2002;47(1):42–52. doi: 10.1002/mrm.10014. [DOI] [PubMed] [Google Scholar]
- 15.Pell GS, Briellmann RS, Waites AB, Abbott DF, Lewis DP, Jackson GD. Optimized clinical T2 relaxometry with a standard CPMG sequence. J Magn Reson Imaging. 2006;23(2):248–252. doi: 10.1002/jmri.20490. [DOI] [PubMed] [Google Scholar]
- 16.Mattiello J, Basser PJ, Le Bihan D. The b matrix in diffusion tensor echo-planar imaging. Magnetic Resonance in Medicine. 1997;37(2):292–300. doi: 10.1002/mrm.1910370226. [DOI] [PubMed] [Google Scholar]
- 17.Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G. Diffusion tensor MR imaging of the human brain. Radiology. 1996;201(3):637–648. doi: 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- 18.Theilmann RJ, Gmitro AF, Altbach MI, Trouard TP. View-ordering in radial fast spin-echo imaging. Magnetic Resonance in Medicine. 2004;51(4):768–774. doi: 10.1002/mrm.20031. [DOI] [PubMed] [Google Scholar]
- 19.Basser PJ, Mattiello J, LeBihan D. Estimation of the Effective Self-Diffusion Tensor from the Nmr Spin-Echo. Journal of Magnetic Resonance Series B. 1994;103(3):247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- 20.Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. Journal of Magnetic Resonance Series B. 1996;111(3):209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- 21.Pajevic S, Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: Application to white matter fiber tract mapping in the human brain. Magnetic Resonance in Medicine. 1999;42(3):526–540. [PubMed] [Google Scholar]
- 22.Pierpaoli C, Basser PJ. Toward a quantitative assessment of diffusion anisotropy. Magnetic Resonance in Medicine. 1996;36(6):893–906. doi: 10.1002/mrm.1910360612. [DOI] [PubMed] [Google Scholar]
- 23.Sarlls JE, Marenco S, Pierpaoli C. DTI of the Human Brain with Sub-millimeter Voxel Size: Clear Depiction of the Fiber Decussation in the Optic Chiasm; Proceedings of the XVI ISMRM; Toronto. 2008. [Google Scholar]
- 24.Jeong EK, Kim SE, Kholmovski EG, Parker DL. High-resolution DTI of a localized volume using 3D single-shot diffusion-weighted STimulated echo-planar imaging (3D ss-DWSTEPI) Magn Reson Med. 2006;56(6):1173–1181. doi: 10.1002/mrm.21088. [DOI] [PubMed] [Google Scholar]
- 25.Numano T, Homma K, Hirose T. Diffusion-weighted three-dimensional MP-RAGE MR imaging. Magn Reson Imaging. 2005;23(3):463–468. doi: 10.1016/j.mri.2004.12.002. [DOI] [PubMed] [Google Scholar]
- 26.Pipe JG. Whole Blade method for Robust PROPELLER DWI. Proceedings of the Joint ISMRM-ESMRMB. 2007:1486. [Google Scholar]