Cell Spreading Analysis with Directed Edge Profile-Guided Level Set Active Contours

Abstract

Cell adhesion and spreading within the extracellular matrix (ECM) plays an important role in cell motility, cell growth and tissue organization. Measuring cell spreading dynamics enables the investigation of cell mechanosensitivity to external mechanical stimuli, such as substrate rigidity. A common approach to measure cell spreading dynamics is to take time lapse images and quantify cell size and perimeter as a function of time. In our experiments, differences in cell characteristics between different treatments are subtle and require accurate measurements of cell parameters across a large population of cells to ensure an adequate sample size for statistical hypothesis testing. This paper presents a new approach to estimate accurate cell boundaries with complex shapes by applying a modified geodesic active contour level set method that directly utilizes the halo effect typically seen in phase contrast microscopy. Contour evolution is guided by edge profiles in a perpendicular direction to ensure convergence to the correct cell boundary. The proposed approach is tested on bovine aortic endothelial cell images under different treatments, and demonstrates accurate segmentation for a wide range of cell sizes and shapes compared to manual ground truth.

1 Introduction

Endothelial cells (ECs) reside in the innermost layer of blood vessels, and constantly experience mechanical stimulation such as shear stress and cyclic stretching. Increasing evidence shows the direct effects of these mechanical signals on endothelial structure and functions [1]. One particular example is that atherosclerotic lesions usually locate at the bifurcations and curvatures in the arterial tree, areas that are characterized by disturbed flow with low shear stress magnitudes [2]. This indicates that EC mechanosensitivity plays a critical role in atherosclerosis development. Atherosclerosis development is a complex, multiple stage process with various causing factors, among which high level of cholesterol is one of the most important. The corresponding biological study is to investigate cholesterol effects on EC mechanosensitivity by studying cell spreading dynamics (e.g. cell spreading area as a function time) on substrates of different rigidity. This is of particular importance for ECs because mechanics of the endothelium changes during the development of atherosclerosis. Cell cholesterol level may be either elevated or decreased using chemical drugs (e.g. methyl-beta-cyclodextran) [3] and cell spreading is recorded for further cell area analysis. Under some conditions, cells show subtle difference between different cholesterol modulations (e.g. cholesterol enrichment and cholesterol depletion). To get good statistics, accurate cell area measurement and large sample size are needed. This requires automatic and accurate methods, especially when large volume of data are collected to obtain better statistics. In recent years, active contours have become increasingly popular for cell segmentation [4]. Geometric model of active contours [5] provides advantages such as eliminating the need to reparameterize the curve and automatic handling of topology changes via level set implementation [6]. The major drawbacks of the classical edge-based active contours are the leakage due to weak edges and stopping at local maximums in noisy images. While the region-based active contours [7, 8, 9] overcome these drawbacks, they require a bimodal image model to discern background and foreground which is not applicable in some high resolution cell images. Figure 1 shows typical phase contrast images of cells. The white regions surrounding the cells are the typical phase halo. A straight-forward implementation of [7] converges to the boundaries between phase halo and the rest of the image. Using various features in Chan and Vese formulation such as variance to discern cells from background gives satisfactory results [10] but the sharp phase halos contribute to the variance and cause early stopping of curve evolution. Similarly, edge stopping functions used in regular geodesic active contours, if initialized outside of the cells, respond to the outer edges of phase halos and cause early stopping which produces an inaccurate segmentation. When the curve is initialized inside the cells, the texture inside the cell also causes premature stopping. Often phase halo is compensated by normalizing the image but this weakens the cell boundaries further, especially in the areas where cells are flattened, and leads to leakage of the curve. One remedy is to enforce a shape model, but it fails for cells with highly irregular shapes. Nucleus-based initialization and segmentation [11] is also not applicable to images such as in figure 1. To obtain an accurate segmentation, we propose an approach that exploits the phase halo effect instead of compensating it. The intensity profile perpendicular to the local cell boundary is similar along the whole boundary of a cell; it passes from the brighter phase halo to the darker cell boundary. We propose to initialize the curve outside the cell and phase halo, and guide the active contour evolution based on the desired edge profiles which effectively lets the curve evolve through the halos and stop at the actual boundaries. We also use a spatially adaptive force to slow the curve evolution at boundaries to prevent leakage.

Fig. 1.

Phase contrast cell images. Left to right: sample cell, intensity profile at the marked direction, derivative of the directed profile. The actual cell boundary point is marked on the graphs.

2 Methods

2.1 Ridge-Based Cell Detection

An initial curve close to the actual cell boundary needs to be detected to capture the desired characteristic of the local directional derivative as shown in figure 1. Shape-based properties of the intensity surface are utilized to produce the initial coarse cell detection. These properties are chosen because of their robustness to image contrast and intensity variations. In phase contrast microscopy images, the cell membrane boundaries and phase halos around the cells produce crest lines (ridges and valleys), and subcellular structures produce blob- or ridge-like patterns so the use of ridge detection methods are ideal for the initial detection. In curvature based detection, ridges can be defined as local extrema of principal curvatures [12]. Principal curvatures and directions of a hypersurface L correspond to the eigenvalues κ₁ ≥ ...≥ κ_n—1 and eigenvectors ξ₁ ≥ ... ≥ ξ_n—1 of the shape operator matrix on the tangent space W . In 2D case, W is given by:

$$W={\mathrm{I}}^{-1}\mathrm{II}={\left[\begin{array}{cc}\hfill L_x\cdot L_x\hfill & \hfill L_x\cdot L_y\hfill \\ \hfill L_x\cdot L_y\hfill & \hfill L_y\cdot L_y\hfill \end{array}\right]}^{-1}\left[\begin{array}{cc}\hfill L_{\text{xx}}\cdot c\hfill & \hfill L_{\text{xy}}\cdot c\hfill \\ \hfill L_{\text{xy}}\cdot c\hfill & \hfill L_{\text{yy}}\cdot c\hfill \end{array}\right]$$ (1)

where I and II are the first and second fundamental forms and $c=\frac{L_x\times L_y}{\mid L_x\times L_y\mid }$ [12]. Since computation of principal curvatures is expensive, mean curvature $H=\frac{1}{2}({\kappa }_1+{\kappa }_2)=\frac{1}{2}\text{trace}\left(W\right)$ is often used [13,14] to classify surface patches (H < 0 : peak, ridge, or saddle ridge; H = 0 : flat or minimal surface; H > 0 : pit, valley, or saddle valley). In generalization of local extrema for real-valued functions of a vector variable [12], a point x₀ is classified as maximum if ▽L(x₀) = 0 (critical point) and $\mathcal{H}\left(L\left(x_0\right)\right)$ is negative definite (all eigenvalues λ_i < 0) where $\mathcal{H}$ is the Hessian matrix:

$$\mathcal{H}=\left[\begin{array}{cc}\hfill L_{\text{xx}}\hfill & \hfill L_{\text{xy}}\hfill \\ \hfill L_{\text{xy}}\hfill & \hfill L_{\text{yy}}\hfill \end{array}\right]$$ (2)

For critical points (▽L(x₀) = 0), according to the Taylor series expansion and curvature definitions eigenvalues λ_i and eigenvectors v_i of the Hessian matrix correspond to principal curvatures к_i and principal directions ξ_i respectively [15]. Eigenvalues and eigenvectors of the Hessian matrix have been used in many medical image processing applications as a ridgeness measure [16, 17]. Since we want to detect membrane boundaries, phase halos, and subcellular structures associated with cells (dark ridges, bright ridges and dark blobs respectively ), we use $\mid {\lambda }_1\left(\mathcal{H}\right)\mid$. Initial cell detection is done by thresholding $\mid {\lambda }_1\left(\mathcal{H}\right)\mid$. Threshold value T_r is selected based on mean and standard deviation (σ) of ${\lambda }_1\left(\mathcal{H}\right)$. Regions where $\mid {\lambda }_1\left(\mathcal{H}\right)\mid >T_r$ are classified as cells. The obtained mask is further refined using morphological closing to make cell masks more compact, and morphological opening and area opening to remove spurious detections and to refine cell contours.

2.2 Directed Edge Profile-Guided Level Set Active Contours

Initial detection of cells produce cell masks that have discontinuities and spurious results and they are larger than the actual cells, particularly where the phase halos are thick. To refine the initial cell detection, we propose a novel geodesic active contour evolution with spatially adaptive force and guided by edge profiles. In level set based active contour methods, a curve $\mathcal{C}$ is represented implicitly via a Lipschitz function ϕ by $\mathcal{C}=\{(x,y)\mid \varphi (x,y)=0\}$, and the evolution of the curve is given by the zero-level curve of the function ϕ(t, x, y) [7]. We propose use of a modified version of the geodesic active contours [5]. In regular geodesic active contours [5] the level set function ϕ is evolved using the speed function,

$$\frac{\partial \varphi }{\partial t}=g(\nabla \mathbf{I})(F_c+\mathcal{K}\left(\varphi \right))\mid \nabla \varphi \mid +\nabla \varphi \cdot \nabla g(\nabla \mathbf{I})$$ (3)

where F_c is a constant, $\mathcal{K}$ is the curvature term (Eq.4) and g(▽I) is the edge stopping function, a decreasing function of the image gradient which can be defined as in Eq.5.

$$\mathcal{K}=\mathrm{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)=\frac{{\varphi }_{\text{xx}}{\varphi }_y^2-2{\varphi }_x{\varphi }_y{\varphi }_{\text{xy}}+{\varphi }_{\text{yy}}{\varphi }_x^2}{{({\varphi }_x^2+{\varphi }_y^2)}^{\frac{3}{2}}}$$ (4)

$$g(\nabla \mathrm{I})=\exp (-\mid \nabla G_{\sigma }(x,y)\ast \mathrm{I}(x,y)\mid )$$ (5)

The constant balloon force F_c pushes the curve inwards or outwards depending on its sign. The regularization term $\mathcal{K}$ ensures boundary smoothness and g(I)is used to stop the curve evolution at cell boundaries. The term ▽g . ▽ϕ is used to increase the basin of attraction for evolving the curve to the boundaries of the objects. The geodesic active contours are more suitable for our application where intensity inside the cell boundaries is highly heterogeneous, and there is no clear difference between inside and outside intensity profiles so intensity thresholding or Chan-Vese type minimal variance models are not applicable. However, since they are designed to stop at edges, they suffer from: (1) early stopping on background or foreground edges, (2) contour leaking across weak boundaries, and (3) for our particular application, early stopping at outer edges of phase halos. To overcome the first problem, we use the ridge-based initialization to start the contour from outside, close to the actual boundary. To reduce the effects of the second problem, we propose replacing the constant balloon force F_c in Eq. 3 with an intensity adaptive force F_A:

$$F_A(x,y)=c\mathrm{I}(x,y)$$ (6)

This intensity adaptive force increases the speed of contraction on bright phase halos and reduces it on thin dark extensions and prevents leaking across weak edges. To handle the third problem, we propose a modified edge stopping function. The existence of phase halo increases the edge strength at cell boundaries. We propose the edge stopping function g_d (Eq. 9) guided by the directed edge profile, that lets the curve evolve through the outer halo edge and stop at the actual boundary edge. As shown in figure 1, if initialized close to the actual boundary, the first light-to-dark edge encountered in the local perpendicular direction corresponds to the actual boundary. By choosing this profile as the stopping criterion we avoid the outer edge of phase halo. This stopping function is obtained as follows. Normal vector N to the evolving contour/surface can be determined directly from the level set function:

$$N=-\frac{\nabla \varphi }{\mid \nabla \varphi \mid }$$ (7)

Edge profile is obtained as the intensity derivative in opposite direction to the normal:

$${\mathrm{I}}_{-N}=\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\cdot \nabla \mathrm{I}$$ (8)

Dark-to-light transitions produce positive response in I_—N. We define the edge profile-guided edge stopping function g_d as:

$$g_d(\nabla \text{I})=1-\mathrm{H}(-{\mathrm{I}}_{-N})(1-g(\nabla \mathrm{I}))$$ (9)

where H is the heaviside step function:

$$\mathrm{H}\left(x\right)=\{\begin{array}{cc}1\hfill & \text{if}x>0\hfill \\ 0\hfill & \text{elsewhere}\hfill \end{array}\phantom{\}}$$

This sets g_d to 1 at regions where there is a dark-to-light (background-to-halo) transition perpendicular to boundary, and keeps regular edge stopping function everywhere else. Thus it lets the active contour evolve through the edges with a dark-to-light profile and stop at edges with light-to-dark profile. Eq.10 shows the speed function of the proposed curve evolution.

$$\frac{\partial \varphi }{\partial t}=(1-\mathrm{H}(-{\mathrm{I}}_{-N})(1-g(\nabla \mathrm{I})))(c\mathrm{I}+\mathcal{K}\left(\varphi \right))\mid \nabla \varphi \mid +\nabla \varphi \cdot \nabla (1-\mathrm{H}(-{\mathrm{I}}_{-N})(1-g(\nabla \mathrm{I})))$$ (10)

3 Experiments and Results

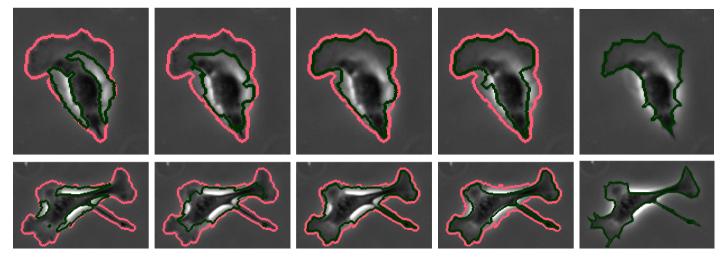
Bovine aortic endothelial cells (BAECs; Cambrex East Rutherford, NJ) between passages 12 and 16 were grown in DMEM (Invitrogen, Carlsbad, CA) containing 10% fetal bovine serum (FBS; Sigma-Aldrich, St. Louis, MO), 10 g/ml penicillin, streptomycin and kanamycin sulfate (Invitrogen, Carlsbad, CA). Cell cultures were maintained in a humidified incubator at 37C, with 5% CO₂. Cells were split every 3-4 days. Rat-tail collage I (BD Biosciences, Bedford, MA) at 0.3 mg/ml in acidic acid was absorbed onto the glass coverslip for 24 hours. Then the coverslip was rinsed in PBS to remove unbound collagen. A glass coverslip in a 35 mm Petri dish with 1 ml cell culture medium is placed on an Olympus IX70 inverted microscope. 2Χ10⁴ cells from cell suspension were added to the Petri dish. Images of spreading cells were recorded in phase contrast mode with a CoolSNAPfx digital video camera (Photometrics, Tucson, AZ), using a 10Χ objective. The proposed method was tested on a data set of BAECs obtained as described above. Each image in the data set is 1300 Χ 1030 pixels in size and contains about 30–50 BAECs. Figure 2 shows segmentation results of four methods and the manually drawn ground truth on magnified sample cells. Light red contours represent the ridge-based initialization as described in previous section. Dark green contours represent the final segmentation results, all methods have been initialized with the red contours. Chan and Vese method, as expected, converges to phase halos. Geodesic active contour with fixed force and regular edge stopping function (regular GAC) leaks through weak edges and is stopped by the strong phase halo edges. If the spatially adaptive force is applied, the contour tends to stop at weak edges most of the time as well as on strong halo edges. The proposed edge profile-guided stopping function with spatially adaptive force assures the desired result, it is stopped by weak halo-to-boundary edges, but evolves through the strong outer halo edges and converges to the desired boundary, producing a very tight cell segmentation. To obtain a quantitative validation of the proposed method, a small set of images have been selected and cells not in direct contact have been manually segmented by an expert in the art. Majority of cells have been successfully segmented by the proposed method except a few cells that were merged or separated. Table 1 shows error analysis with respect to this ground truth. The same parameters are used for all images, 0.5σ is chosen as the threshold at the ridge-based initial detection phase. Fourth and fifth columns of the table show the average cell area and average percentage error for each image respectively, regular GAC has a big error due to leakage through the actual boundaries whereas the proposed method gives good results. In total (36 cells) the average error of regular GAC is -28.6%, that of proposed method is 2.3%. Sixth column shows the RMS error, again the proposed method results in better performance as opposed to regular GAC. Figure 3 compares regular GAC and proposed method with respect to the manual ground truth in terms of percentage deviation from the actual cell area for each of the 36 cells.

Fig. 2.

Magnified results on sample cells from BAEC data set. light red: ridge-based initialization, dark green: final segmentation. From left to right: Chan and Vese, GAC, GAC with adaptive force, proposed method, manual ground truth.

Table 1.

Error analysis with respect to manual ground truth

Image	Cells	Method	Avg. Area (pixels)	Avg. Error (%)	RMS
1	9	Regular GAC	1872	-51.9%	2038
		Proposed	3947	1.4%	243
2	6	Regular GAC	2259	-21.1%	838
		Proposed	3137	7.2%	213
3	12	Regular GAC	2797	-14.9%	692
		Proposed	3327	0.4%	130
4	9	Regular GAC	2367	-28.7%	1216
		Proposed	3476	2.5%	262
####
Total	36	Regular GAC	2368	-28.6%	1298
		Proposed	3488	2.3%	212

Fig. 3.

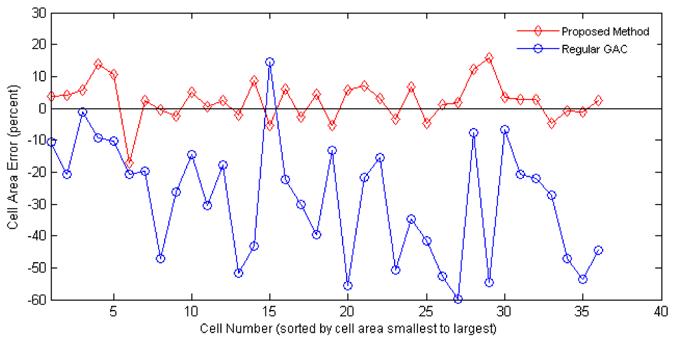
Percentage error of cell area with respect to ground truth: proposed method vs. regular GAC

4 Discussion and Conclusion

A new approach to obtain accurate cell boundaries in phase contrast microscopy is presented in this paper. The use of ridge and blob measures provides a robust initial detection. The active contour is implemented with level set and its evolution is guided by edge profiles to stop it at the desired boundaries. This enables the active contour to pass through phase halo edges and stop at the actual cell boundary. Also, the use of spatially adaptive force prevents leakage at the boundaries. The proposed method is tested on time lapse images of bovine aortic endothelial cells with highly complex structure, it provides very robust performance compared to other methods and ground truth. Methods that cannot successfully exclude phase halos skew the statistics because at different times and substrates, the amount of halo around a cell is variable. The proposed method provides an automatic estimate of cell area that is of suffcient accuracy to test various biological hypotheses.