Feasibility of a Multigroup Deterministic Solution Method for 3D Radiotherapy Dose Calculations

Abstract

Purpose

To investigate the potential of a novel deterministic solver, Attila, for external photon beam radiotherapy dose calculations.

Methods and Materials

Two hypothetical cases for prostate and head and neck cancer photon beam treatment plans were calculated using Attila and EGSnrc Monte Carlo simulations. Open beams were modeled as isotropic photon point sources collimated to specified field sizes (100 cm SSD). The sources had a realistic energy spectrum calculated by Monte Carlo for a Varian Clinac 2100 operated in a 6MV photon mode. The Attila computational grids consisted of 106,000 elements, or 424,000 spatial degrees of freedom, for the prostate case, and 123,000 tetrahedral elements, or 492,000 spatial degrees of freedom, for the head and neck cases.

Results

For both cases, results demonstrate excellent agreement between Attila and EGSnrc in all areas, including the build-up regions, near heterogeneities, and at the beam penumbra. Dose agreement for 99% of the voxels was within 3% (relative point-wise difference) or 3mm distance-to-agreement criterion. Localized differences between the Attila and EGSnrc results were observed at bone and soft tissue interfaces, and are attributable to the effect of voxel material homogenization in calculating dose-to-medium in EGSnrc. For both cases, Attila calculation times were under 20 CPU minutes on a single 2.2 GHz AMD Opteron processor.

Conclusions

The methods in Attila have the potential to be the basis for an efficient dose engine for patient specific treatment planning, providing accuracy similar to that obtained by Monte Carlo.

INTRODUCTION

Dose calculations are a critical step in radiotherapy treatment planning. The physics governing radiation transport through the human anatomy is highly complex, and most dose calculation methods in clinical use today employ approximations and simplifications that may limit their accuracy or range of applicability. In cases where heterogeneities such as air, lung, bone and prostheses exist, dosimetric differences as large as 10 to 20% (percentage of the maximum dose) or more can exist between predictions and measurements (1-4). Even more advanced methods such as superposition convolution can substantially overestimate interface doses near low density heterogeneities (air passages or lungs) and may not be able to predict sharp dose peaks due to electron disequilibrium around bones or other high density materials such as implants (1, 4-6). These differences can be substantial considering that variations of five percent in the delivered dose can result in a dramatic change in the local response of the tissue (1).

To improve the accuracy of dose calculations during treatment planning, Monte Carlo (MC) methods of radiation transport are being introduced to the clinic. MC stochastically predicts particle transport through media by simulating particle trajectories using random number based probabilities. If enough particles are simulated, MC can approach the true physical solution within the limits of the particle interaction data and uncertainties regarding the geometry and composition of the field being modeled. However, traditional MC solutions can be time consuming, which limits their effectiveness for clinical treatment planning. A substantial amount of research in the radiotherapy community has been dedicated to acceleration of Monte Carlo simulations, through techniques such as condensed history algorithms and statistical de-noising. Examples of this include VMC (7, 8) and DPM (9) codes, both of which are substantially faster than general-purpose codes such as EGS4 (10), EGSnrc (11), GEANT 4 (GEometry ANd Tracking 4) (12), and MCNPX (13).

An alternative to Monte Carlo is to deterministically solve the linear Boltzmann transport equation. A common approach for solving this equation is known as discrete-ordinates. Although the name specifically refers to the angular differencing, it is frequently used to describe a class of solvers that discretize in space (finite-difference or finite-element), angle (discrete-ordinates) and energy (multigroup cross sections). The differential form of the transport equation is then iteratively solved (14). Discrete-ordinates methods solve for the phase-space solution everywhere in the computational domain. While relatively unknown in the radiotherapy community, discrete-ordinates methods have been shown to be useful for neutral particle applications such as neutron-capture therapy (15, 16) and brachytherapy (17). They have also been used in a variety of shielding applications, where large attenuations considerably lengthen Monte Carlo computational times. Traditional discrete ordinates solvers have only been applicable for neutral particle transport.

We present here the application of the novel deterministic solution method towards radiotherapy dose calculations. In this context, ‘deterministic’ refers to methods which deterministically solve the Boltzmann transport equation, rather than empirical methods which rely on pre-calculated dose kernals. The prototype for this technology is the Attila^® solver (18, 19), the original prototype of which was developed at Los Alamos National Laboratory (LANL) by the cofounders of Transpire, Inc. Transpire has since significantly expanded Attila, to improve performance, capabilities, and ease-of-use. The impetus for Attila was to create an efficient, generalized geometry alternative to Monte Carlo for neutral and charged particle simulations. Attila solves the differential form of the linear Boltzmann transport equation and is generalized for neutral, charged and coupled particle simulations.

Attila has been previously validated against Monte Carlo for radiotherapy applications (20). However, no studies to date have verified the accuracy of Attila’s methods on arbitrary heterogeneous patient data derived from CT. Thus, the objective of this study is to investigate the clinical efficacy of Attila’s methods, by evaluating its performance on arbitrary heterogeneous patient datasets.

METHODS AND MATERIALS

A. Finite Element Discrete Ordinate Methods (The Attila Solver)

Attila solves the differential form of the linear Boltzmann transport equation and is generalized for neutral, charged and coupled particle simulations (14). Attila’s methods are briefly described here; a detailed description can be found in (18-20). Angular discretization is performed using the discrete-ordinates method. The scattering source is expanded in spherical harmonics and the multigroup method is used in energy. An accurate and robust linear discontinuous finite-element method (DFEM) is used for spatial discretization, which was adapted for use with arbitrary tetrahedral elements. For charged particle simulations, the linear Boltzmann-Fokker-Planck transport equation is solved. This equation includes all terms of the linear Boltzmann transport equation, including Boltzmann scattering for the nuclear interactions, with the addition of the continuous slowing down operator and continuous scattering operator, which account for Coulomb interactions. The discretized equation is solved using an algorithm known as source iteration. Source iteration can converge slowly for problems where scattering is dominant, a known problem for deterministic methods. Additionally, scattering dominated media can also lengthen calculation times in Monte Carlo. Attila incorporates an efficient diffusion synthetic acceleration (DSA) algorithm (18, 19) which can greatly reduce the number of iterations required for convergence and hence, can significantly reduce the CPU time. Through the use of linear discontinuous finite element spatial differencing, Attila solves for 4 spatial unknowns in each tetrahedral element, with a linear variation between each spatial unknown. At each spatial unknown, Attila calculates the angular and energy dependent flux (fluence) for each particle type solved. Dose is calculated as a post processing operation by multiplying the angle integrated, energy dependent fluence by the corresponding energy deposition cross section for the desired material (water or medium) and dividing by the density of the medium. Since Attila calculates a spatially variable solution within each element, dose can be calculated at multiple locations within each element.

To obtain an accurate solution, sufficient resolution in the discretized variables; space, angle, and energy, must be employed. Notably, if the angular differencing is not sufficient, numerical artifacts may arise. Commonly referred to as ‘ray-effects’, these are nonphysical buildups in the particle flux along discrete angles, and are most pronounced for localized sources in low density media. In external beam radiotherapy, a large amount of angles may be required to resolve highly collimated beams, which in turn, can greatly increase the required computational time. To improve the angular resolution, Attila incorporates an analytic ray tracing method to calculate the first scattered photon and electron sources inside the patient anatomy. This process is briefly summarized here, but described in detail by Gifford, et al. (20). Ray tracing from source points is tracked to multiple Gaussian spatial integration points in each tetrahedral element. From this, the electron and photon sources produced by the un-collided photons are rigorously computed using finite element integration rules on each element. This produces an accurate linear representation of the first collided sources within each element, from which the full scattering calculation is performed. Ray tracing time is largely independent of the source spectrum.

Attila directly solves the transport equation without employing numerical fix-ups or empirical corrections which may reduce accuracy. Since both Attila and Monte Carlo directly account for the same particle interactions in photon beam radiotherapy, the achievable accuracy of both methods is equivalent.

B. Monte Carlo Simulations

Monte Carlo calculations were performed using the DOSXYZnrc program (21). The program is based on the EGSnrc general purpose Monte Carlo code. It calculates three-dimensional dose distributions in rectilinear coordinates. A utility program CTCREATE was used to convert CT data from Digital Imaging and Communications in Medicine (DICOM) format to the format of DOSXYZnrc input files. In the input file 3D geometry of the computational domain is represented by a voxelized rectangular phantom surrounded by a homogeneous medium, air in this study. Radiation transport in the accelerator was not modeled since the focus of this study was on radiation transport in the patient. Open beams were modeled as point isotropic photon sources collimated to the specified field size. Each source was located at a distance 100 cm from the isocenter. The source had a realistic energy spectrum calculated by Monte Carlo and corresponding to a Varian Clinac 2100 series (Varian Medical Systems, Palo Alto, CA) operated in a 6 MV photon mode. The electron transport cut-off kinetic energy was 189 keV. Details of the Monte Carlo model used in the spectrum calculations are described elsewhere (22).

C. Simulated Patient Cases

From our clinical patient database, we retrospectively selected two DICOM patient datasets, one for a prostate case and one for a head and neck case. Both cases had 6 MV IMRT plans already developed and delivered. The calculations were performed with exactly the same beam set up as the actual treatment except beam modulation with a multi-leaf collimator was not modeled, i.e. all the fields were open. The rationale for these two different cases is to investigate the performance of Attila under both large field (prostate case) and small field (head and neck case) conditions. The CT slices, the contoured structures, and beam setting were exported in DICOM format from the Pinnacle3 treatment planning system (v6.2b, Philips Medical Systems, Andover, MA). The Attila and EGSnrc codes start by processing the parameters exported from the Pinnacle system for each plan. Both Attila and DOSXYZnrc convert the CT image into a 3D matrix with information on the density and chemical composition of materials throughout the computational domain. In this study four materials with fixed densities were used: air, adipose tissue, soft tissue and bone, where each material corresponded to a specific CT Hounsfield number range (21). Hounsfield numbers greater than 125 corresponded to bone and less than -350 to air (21). Intervals -350 to 0 and 0 to 125 corresponded to adipose and soft tissues, respectively. The choice of interval boundaries was verified by visual examination of patient anatomy in CT images. The material properties in each EGSnrc voxel are homogeneous. Since the EGSnrc voxels are larger than the spatial resolution of the CT data, a homogenization process was performed. The material properties in each EGSnrc voxel were obtained by first calculating an average CT number in each voxel. Then, from a user defined look-up table, the voxel material and its density are determined. In Attila, homogenized material properties were created in each tetrahedral element by first looking up the material and density associated with each image pixel located within a given element. Material homogenization is then performed to calculate a single, homogenized material in each element which is used for the fluence calculation.

Absorbed dose estimates (dose-to-medium: D_M) calculated by Attila and EGSnrc were compared at voxel resolutions of 0.98×0.98×2.5 mm³ for the prostate case, and 0.98×0.98×3.0 mm³ for the head and neck case, both of which were equivalent to the resolution of the acquired CT data. Evaluating the results at a fine spatial resolution enabled a rigorous comparison accuracy comparison between both approaches. The Attila dose (D_M) at each CT voxel was computed by first extracting the local energy dependent, angle integrated, and electron fluence at that voxel centroid, as determined by the linearly varying finite element representation within the element containing that CT voxel centroid. The local electron fluence is then multiplied by the energy dependent energy deposition cross section for the material of that image voxel, divided by the CT voxel material density and integrated over all energy. EGSnrc calculated a single D_M in each 2.5 mm³ voxel, for which material properties were averaged based on the approximately 6 CT voxels contained in each EGSnrc dose grid voxel.

The prostate case consisted of a treatment plan with eight coplanar beams ranging from 9.3 × 8.2 to 11.3 × 8.2 cm² in size. The gantry angles were 30, 65, 100, 135, 225, 260, 295 and 330 degrees. The Attila computational grid consisted of approximately 106,000 tetrahedral elements, encompassing a patient volume of approximately 8,400 cm³. Since Attila solves for four spatial unknowns per element, this equates to 424,000 spatial degrees of freedom being solved. Thus, on average, the volume associated with each spatial degree of freedom in Attila was 0.02 cm³. 2.5×2.5×2.5 mm³ voxels were used in the EGSnrc calculation, equating to a per-voxel volume of 0.016 cm³.

A head and neck case was selected to evaluate the performance of Attila in the presence of narrow fields in combination with significant air and bone heterogeneities. For this case, eight coplanar beams were used with field sizes of 1.5×1.5 cm². The small field size was selected to assess calculation accuracy in the presence of substantial lateral electron scattering. The gantry angles of the eight fields were 20, 60, 100, 140, 220, 260, 300, and 340 degrees. The Attila computational grid consisted of approximately 123,000 tetrahedral elements, encompassing a patient volume of approximately 2,700 cm³. This equates to 492,000 spatial degrees of freedom being solved. On average, the volume associated with each spatial degree of freedom in Attila was 0.0055 cm³. 2.5×2.5×3.0 mm³ voxels were used in the EGSnrc calculation, equating to a per-voxel volume of 0.019 cm³.

For the two cases presented in this paper, multiple Attila calculations were performed to assess the sensitivity of the solution accuracy to various deterministic transport parameters such as the element size, angular quadrature (S_N) order, spherical harmonics polynomial expansion order (P_N), energy cutoff for spatial electron transport, and spatial density of the ray tracing for transport of the primary beam. For both cases, a 300 keV cutoff in spatial electron transport was employed (reducing this cutoff to 1 keV resulted in a negligible difference in both cases). A spherical harmonics expansion order of P₃ was used to represent the scattering source anisotropy in the prostate case. A spherical harmonics expansion order of P₄ was used for the head and neck case. In both cases diagonal transport correction and Galerkin scattering treatment were employed, which have the effect of providing similar accuracy to a degree higher spherical harmonics expansion order for within group scattering. In both cases, particle dependent variable S_N orders were employed using a Triangular Chebychev Legendre Quadrature set having N*(2+N) angles per unit sphere. S_N orders were varied between S₈ and S₄, corresponding to 80 and 24 angles, respectively. S₈ was applied for the photons, which have larger mean free paths and thus require a higher angular resolution than the electrons, for which S₄ was applied.

In this manner, the photon transport was performed using a higher angular quadrature order than what was employed for the electron transport. Compared with electrons at similar energies, photon mean free paths are substantially larger, requiring a higher angular quadrature order. Additionally, it was found that only a single DSA accelerated inner iteration was required for each photon energy group. Without DSA acceleration, a single inner iteration would correspond to a single photon collision.

The Attila calculations were performed using multi-group cross sections generated by the CEPXS cross section processing code (23). CEPXS generates multi-group coupled electron-photon cross sections, and accounts for a large number of photon interactions including Compton incoherent scattering, photoelectric absorption, pair production, and electron interactions including elastic scattering from nuclei, inelastic scattering from collisions with atomic electrons, and radiative scattering from nuclei. CEPXS has been benchmarked against TIGER, TIGERP, EGS4 and measurements (24). The cross sections used in the Attila calculations included 12 photon energy groups and 31 electron groups.

RESULTS

Figure 1a shows a partial section of the Attila mesh for the prostate case, overlaid on an axial slice of the CT material map through isocenter. Figure 1b displays the isodose contours calculated by Attila on an axial plane passing through isocenter. An absorbed dose of two Gy was prescribed to the isocenter point. Figures 2 and 3 compare the Attila and EGSnrc calculated dose fields for the prostate case at a resolution of 0.98× 0.98 mm² on the axial plane through isocenter. Pixels where the dose difference between Attila and EGSnrc exceeded the ±3%/±3mm (agreement within ±3% pointwise differences or ±3mm distance-to-agreement) criterion are colored black in Figure 2. As shown, excellent agreement exists between both codes in all areas, including build-up regions and beam perimeters, where the effects of lateral electron scatter are significant. The majority of pixels that exceed this criterion are at the perimeters of bone heterogeneities, and are likely due to differences between Attila and EGS in calculating D_M. This is illustrated in Figure 3a and 3b, showing the absorbed dose along lines L1 and L2 drawn in Fig 2, respectively. Since Attila calculates D_M at each 0.98×0.98×2.5 mm³ pixel using the material properties of that pixel, the peaks tend to be sharper in Attila than for EGSnrc, which calculates D_M based on the homogenized material properties in each 2.5×2.5×2.5mm³ voxel.

Figure 1.

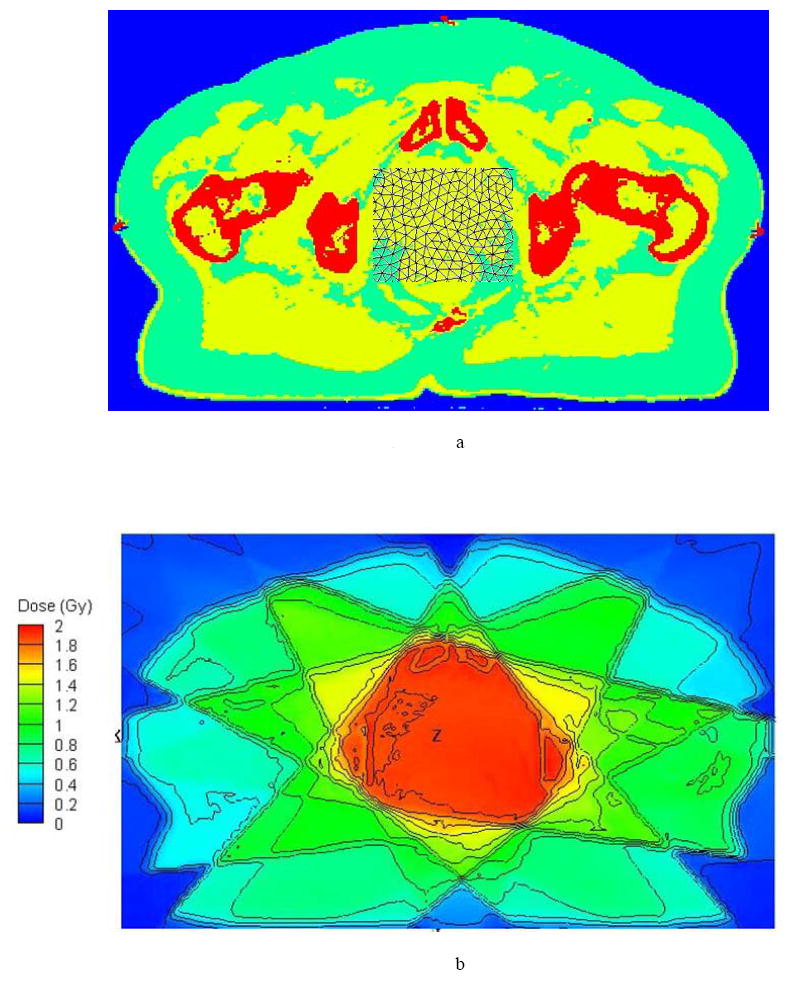
Prostate case (a) Attila mesh partially overlaid to the CT material map through an axial slice through the isocenter (b) the isodose contours calculated by Attila on an axial plane passing through isocenter prescribed for a dose of 2 Gy at the isocenter point.

Figure 2.

Dose field calculated by Attila on the axial plane through isocenter, with dose output at 0.98 × 0.98 mm resolution. Pixels where difference between Attila and EGSnrc is greater than ±3%/±3mm are shown in black. 98.1% of pixels on this plane (where dose ≥ 10% of D_MAX) satisfied the ±3%/±3mm criterion.

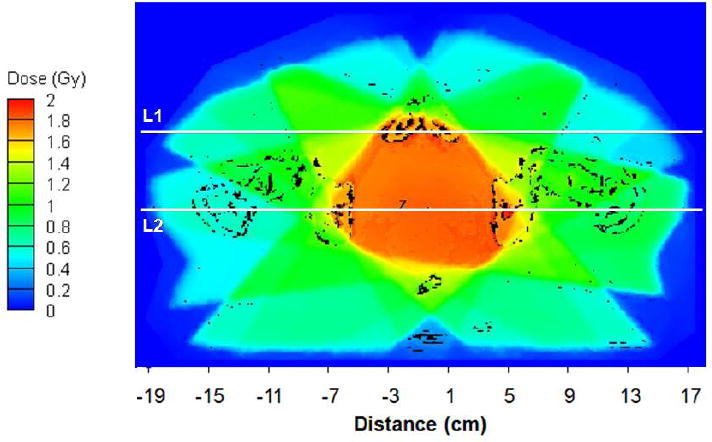
Figure 3.

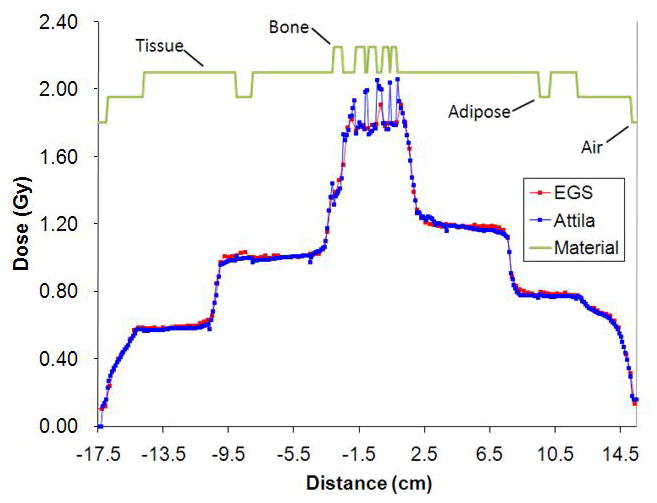
Dose line plot comparisons between EGSnrc (red) and Attila (blue) along line L1 (a) and L2 (b) in Figure 2 (prostate case). Sharp peaks and dips in Attila solution correspond to material heterogeneities, which are resolved at the CT image pixel level by Attila.

Figure 4(a) shows the head and neck Attila mesh partially overlaid to the CT material map through an axial slice through the isocenter and Figure 4(b) shows the isodose contours calculated by Attila on an axial plane passing through isocenter prescribed for a dose of 2 Gy at the isocenter point. Figure 5(a) depicts the dose field calculated by Attila for the head-and-neck case on the axial plane through isocenter, with dose output at the 0.94 mm × 0.94 mm dose grid resolution. Pixels where the dose difference between Attila and EGS exceeds ±3%/±3mm are black on (a) and (b). 98.5% of evaluated pixels (where dose > 5% of D_MAX) on this plane satisfied the ±3%/±3mm criterion. Fig 5(b) indicates that most of the pixels which exceed this criterion are at the perimeters of bone heterogeneities (red). As discussed previously for the prostate case, these are due to differences between Attila and EGSnrc in calculating D_M. As shown, excellent agreement exists between both codes in all areas, including build-up regions, beam perimeters, and bone/air heterogeneities, where the effects of lateral electron scatter are significant.

Figure 4.

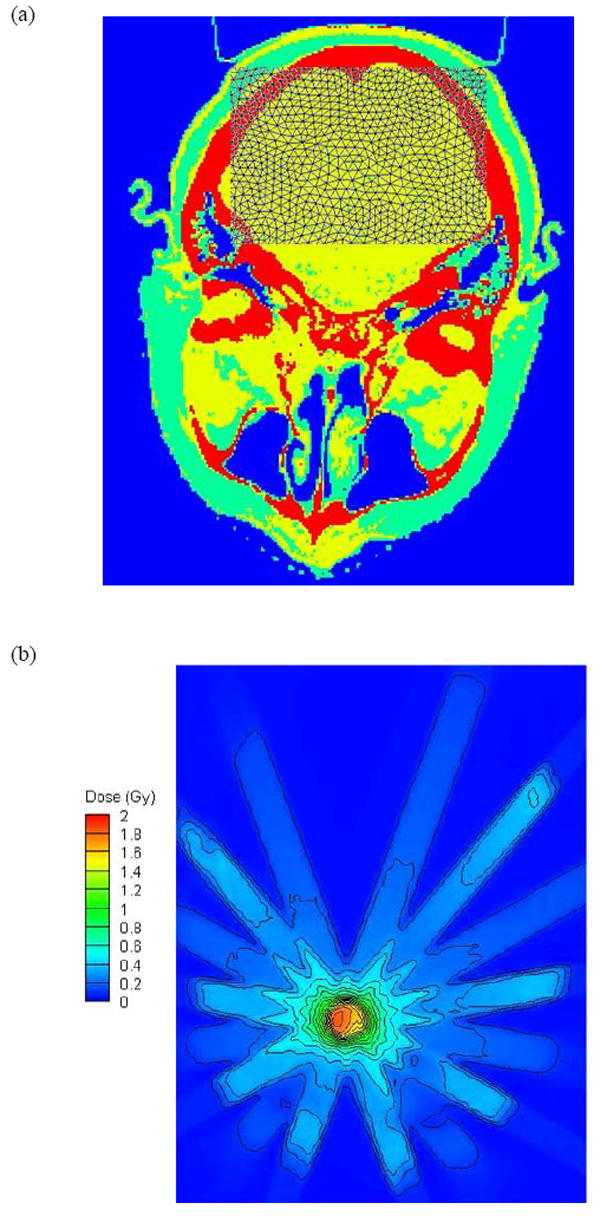
Head and neck case (a) Attila mesh partially overlaid to the CT material map through an axial slice through the isocenter (b) the isodose contours calculated by Attila on an axial plane passing through isocenter for a dose of 2 Gy prescribed at the isocenter point.

Figure 5.

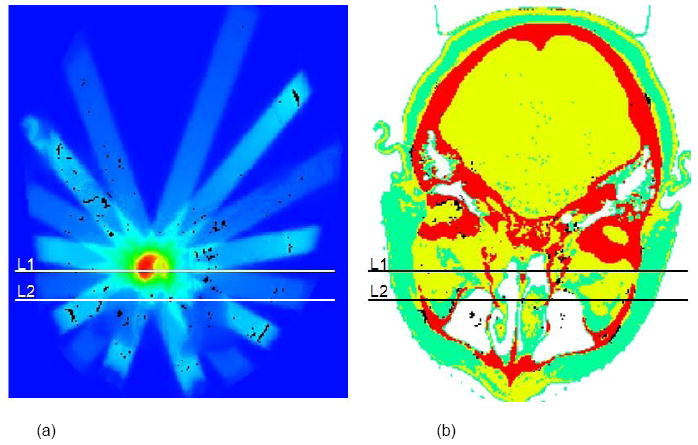
(a) Dose field calculated by Attila for the head-and-neck case on the axial plane through isocenter, with dose output at the 0.94 × 0.94 mm image resolution. Pixels where the dose difference between Attila and EGS exceeds ±3%/±3mm are black on (a) and (b).98.5% of evaluated pixels (where dose > 5% of D_MAX) on this plane satisfied the±3%/±3mm criterion.

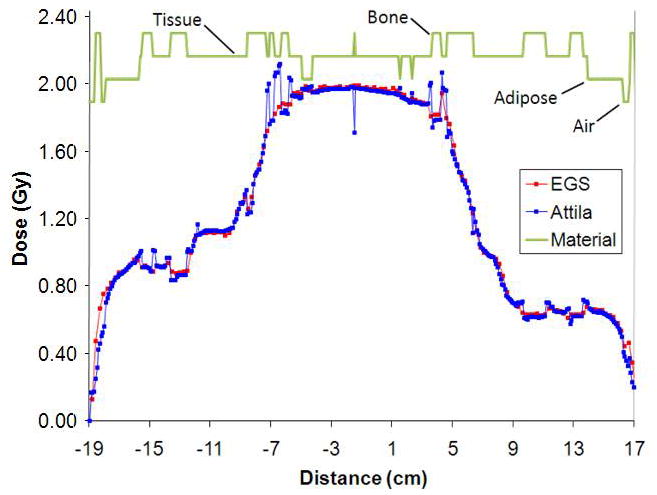
Lines L1 and L2 correspond to plots in Figure 6, where the error bars on the EGSnrc solutions represent the min/max values in the two neighboring voxels (2.5 mm away) on either side of lines L1 and L2 on the axial plane. Values in the neighboring EGSnrc voxels in the axial direction were not included. The agreement is excellent, even along line L2, Fig 5(b), which passes through multiple narrow beams and air and bone heterogeneities.

Figure 6.

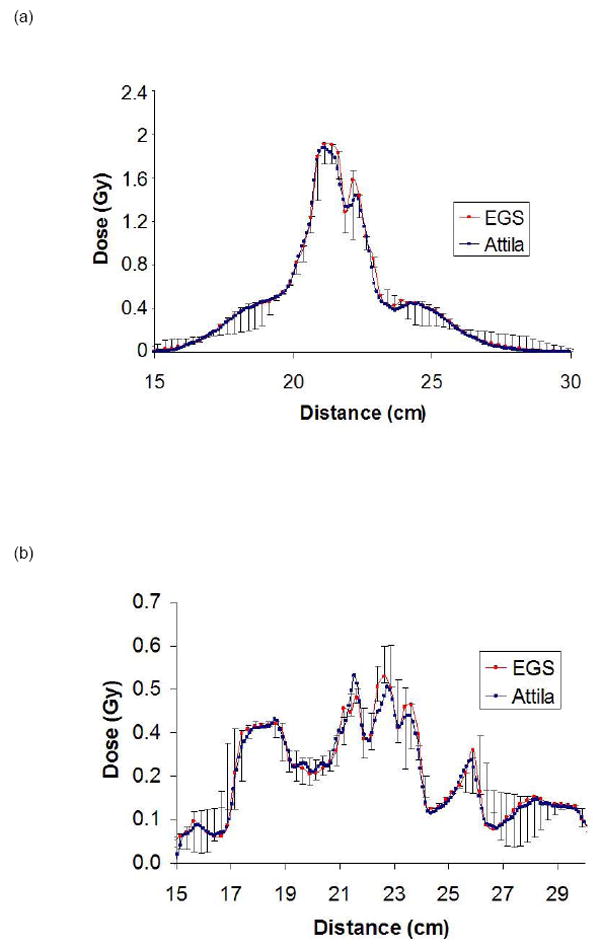
Dose line plot comparisons between EGSnrc (red) and Attila (blue) along line L1 (a) and L2 (b) in Figure 5 (head and neck case). Sharp peaks and dips in Attila solution correspond to material heterogeneities, which are resolved at the CT image pixel level by Attila.

Table 1 presents the CPU times in minutes as reported by Attila for each calculation step (ray tracing, photon transport, and electron transport). The Attila calculations were performed on a single core 2.2 GHz AMD Opteron processor with a 64 bit Linux operating system. The EGSnrc calculations were performed on a 3.0 GHz Pentium IV processor, for which EGSnrc calculation times were 3,180 and 14,880 CPU minutes for the head-and-neck and prostate cases respectively. These times would be roughly equivalent to 2,900 and 13,500 CPU minutes on the 2.2 GHZ AMD Opteron processor used by Attila. However, it should be noted that the EGSnrc calculations were performed using conservative settings and a tight statistical uncertainty, so as to provide an accurate reference solution. Thus, a considerably faster EGSnrc calculation time could be expected under more realistic clinical conditions.

Table 1.

Calculation times (minutes) for the prostate and head-and-neck calculations for both the full and high dose region cases. Results presented in CPU minutes on a single 2.2 GHz AMD Opteron processor. ‘High Dose’ refers to the CPU time required to calculate the dose within regions having a dose of 25% of D_max or greater.

	Prostate (Full Volume)	Prostate (High Dose)	Head-and-Neck (Full Volume)	Head-and-Neck (High Dose)
Ray Tracing	5.5	5.5	3.8	3.8
Photon Transport	2.2	2.2	2.5	2.5
Electron Transport	8.4	1.7	13.3	2.4
Total (Minutes):	16.1	9.4	19.6	8.7

DISCUSSION

Collectively, the results for both cases show an excellent agreement between Attila and EGSnrc in all areas, including the build-up regions and near beam perimeters, even in the presence of significant heterogeneities and narrow fields. As has previously been demonstrated on a heterogeneous slab phantom (20), the proposed approach can provide equivalent accuracy to Monte Carlo, and is free of statistical noise. However, random heterogeneities and arbitrary structures in CT derived patient data provide challenges not present in simple phantom geometries. Thus, the primary objective of this work was to quantify performance of Attila’s methods, in terms of both accuracy and speed, on arbitrary heterogeneous patient data.

For the prostate case, we observed minor differences at the 20% isodose line in the build up regions at the bottom left and bottom right of Figure 2. This is likely attributed to differences in the computational domain extents used by Attila and EGSnrc. The EGSnrc calculation included the couch in the voxel grid, which caused a small degree of attenuation not modeled by Attila, where the computational grid included only the patient anatomy and air in the immediate vicinity, and thus the table geometry was not represented.

As shown in Figures 2 and 3, the regions where minor differences occur are primarily at the immediate boundaries of bone heterogeneities, where D_M calculated by EGSnrc is on homogenized voxels, which contain both bone and tissue. This is evident in Figure 2, where the discrepancies clearly follow the bone perimeters. Since Attila outputs the dose directly based on the material in each CT image voxel, it has more accurately calculated D_M in these regions than EGSnrc, which computes a single D_M in each homogenized voxel. This argument is supported through the line plots in Figures 3, which compares Attila (blue) and EGS (red) solutions for lines L1 (a) and L2 (b) in Figure 2. Figure 3 shows both codes in excellent agreement in both the build-up regions and at the beam perimeters, which are marked by the steep slopes. In both graphs, differences only exist where the lines pass through bone/tissue interfaces, where Attila calculates D_M with a finer spatial precision, which is evidenced by more pronounced peaks in the Attila solution. Over the 3D volume, dose was compared at 444,279 voxels where the dose is greater than 10% of D_max. Out of these, 6,291 voxels exceeded the ±3%/±3mm criterion (98.6% passed).

For the H&N case, 99% of voxels satisfied the ±3%/±3mm criterion (94,251 out of 95,183 voxels evaluated where the dose is greater than 10% of D_max). As shown in Figure 5, a majority of pixels exceeding these criteria were located at the perimeters of bone heterogeneities, and resulted from differences in how EGSnrc and Attila calculated D_M. Again, EGSnrc calculates D_M based on homogenized voxel properties, and Attila calculates D_M based on material in each CT image voxel.

As shown in Table 1, the Attila calculations were approximately 840 and 148 times faster than EGSnrc for the prostate and head-and-neck cases, respectively. It should be noted that since the EGSnrc calculations were used as the reference calculation, tight statistical uncertainties (±0.4% average in voxels having doses greater than D_max/2), and a low energy cutoff was used. Assuming a clinically relevant Monte Carlo statistical uncertainty of ±1.0% (7), the EGSnrc calculation time for each case will reduce by about a factor of 6.25. Additional substantial speed-ups in the EGSnrc calculations can be achieved through a higher energy cutoff and the use of variance reduction techniques. Since neither Attila nor EGSnrc are optimized for radiotherapy, it is not the objective of this paper to provide an absolute speed comparison between Attila’s methods and Monte Carlo. However, the comparably favorable calculation speed of Attila is an indication that Attila’s methods could successfully be adapted for radiotherapy dose calculations.

Similar to Monte Carlo, the photon and electron transport times in Attila are expected to increase by approximately 20%-30% for an 18 MV spectrum. The calculation times are independent of the poly-energetic nature of the spectrum.

CONCLUSIONS

Deterministic methods, such as those of Attila, directly solve for the phase-space solution everywhere in the computational domain. Due to absence of statistical noise, they are well suited for evaluating the effects of small perturbations. Both Monte Carlo and Attila’s methods use cross-section data from the same evaluated libraries and with sufficient refinement both will converge on the same solution. In this context, the achievable accuracy of Attila’s methods, like Monte Carlo, is limited only by that of the particle interaction data and uncertainties regarding the geometry and composition of the field being modeled. The close agreement between EGSnrc and Attila for the two cases presented support this conclusion.

The efficacy of Attila’s methods for use in clinical radiotherapy treatment planning is highly dependent on the computational speed. The favorable computational speed of Attila with respect to EGSnrc, both of which are general purpose codes, is a promising indicator that deterministic methods may provide a viable alternative to Monte Carlo in the clinic.