Design and analysis of ChIP-seq experiments for DNA-binding proteins

Abstract

Recent progress in massively parallel sequencing platforms has allowed for genome-wide measurements of DNA-associated proteins using a combination of chromatin immunoprecipitation and sequencing (ChIP-seq). While a variety of methods exist for analysis of the established microarray alternative (ChIP-chip), few approaches have been described for processing ChIP-seq data. To fill this gap, we propose an analysis pipeline specifically designed to detect protein binding positions with high accuracy. Using three separate datasets, we illustrate new methods for improving tag alignment and correcting for background signals. We also compare sensitivity and spatial precision of several novel and previously described binding detection algorithms. Finally, we analyze the relationship between the depth of sequencing and characteristics of the detected binding positions, and provide a method for estimating the sequencing depth necessary for a desired coverage of protein binding sites.

A combination of chromatin immunoprecipitation and microarray hybridization (ChIP-chip) has been used extensively to determine chromosome binding patterns of DNA-associated proteins¹. Several recent studies have demonstrated that newly developed high-throughput sequencing methods can be used to provide marked improvements over the microarray measurements². While sequencing techniques have been previously used in combination with both chromatin immunoprecipitation (ChIP-seq) and sequence tagging methods^3–6, the new generation of sequencing platforms provides orders of magnitude increase in the number of generated sequences⁷, allowing cost-effective genome-wide mapping for many proteins of interest.

Processing of ChIP-chip has focused on compensating for array limitations, such as probe-specific behavior, dye bias and tiling resolution^8–10. The ChIP-seq approach avoids such biases and can provide greater sensitivity and specificity while requiring a much smaller amount of starting material^{2, 11}. The ChIP-seq data, however, poses a number of different challenges. Given that the rate of sequencing errors varies between and within the sequenced reads, what range of sequence tag quality should be tolerated when aligning tags to the reference genome?¹². What background tag distribution is appropriate for assessing the significance of observed binding positions? What is the required depth of sequencing? Finally, how can this information be utilized to accurately determine protein binding positions?

Here we describe a data processing pipeline optimized for detection of localized protein binding positions from unpaired sequence reads (Figure 1a). We illustrate the proposed pipeline on datasets for genome-wide binding of NRSF², CTCF¹³ and STAT1¹¹, produced using the Solexa platform. The alignment procedure is enhanced to maximize the number of informative tags, based on the strand-specific pattern of tag distribution expected around a binding position. Filtering and background corrections steps are used to lower false-positive rates. We compare performance of several novel and previously described computational methods for calling specific binding positions, and show that some methods provide higher specificity and position accuracy. The final step of the proposed pipeline examines the saturation level of detected binding positions to determine the amount of additional sequencing that may be necessary.

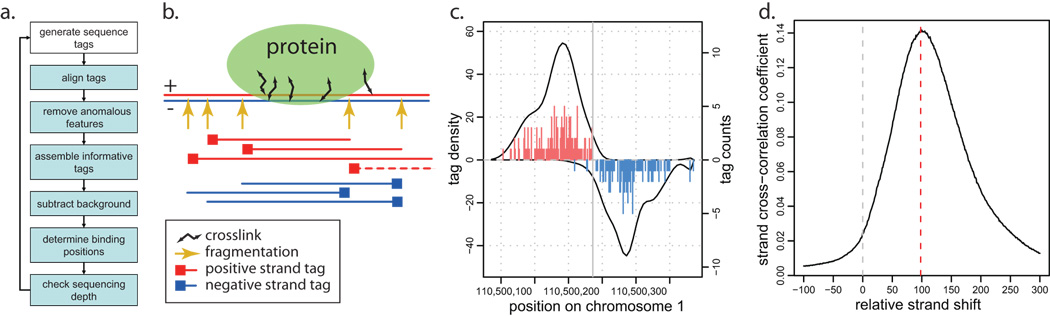
Figure 1.

a. Main steps of the proposed ChIP-seq processing pipeline. b. A schematic illustration of ChIP-seq measurements. DNA is fragmented or digested, and fragments cross-linked to the protein of interest are selected with IP. The 5’ ends (squares) of the selected fragments are sequenced, typically forming groups of positive and negative strand tags on the two sides of the protected region. The dashed red line illustrates a fragment generated from a long cross-link that may account for the tag patterns observed in CTCF and STAT1 datasets. c. Tag distribution around a stable NRSF binding position. Vertical lines show the number of tags (right axis) whose 5’ position maps to a given location on positive (red) or negative (blue) strands. Positive and negative values on the y-axis are used to illustrate tags mapping to positive and negative strands respectively. The solid curves show tag density for each strand (left axis, based on Gaussian kernel with σ =15bp). d. Strand cross-correlation for the NRSF data. The y-axis shows Pearson linear correlation coefficient between genome-wide profiles of tag density of positive and negative strands, shifted relative to each-other by a distance specified on the x-axis. The peak position (red vertical line) indicates a typical distance separating positive- and negative-strand peaks associated with the stable binding positions.

Results

Tag distribution around protein binding positions

In general, immunoprecipitation selects a set of overlapping DNA fragments around bound positions. High-throughput sequencing identifies short (~35bp for Solexa or SOLiD) tags on the 5’ ends of fragments from either DNA strand. The positions of the tags are then determined by aligning them to the genome assembly, with ambiguous alignments typically being discarded. The resulting spatial distribution of tag occurrences around a stable binding position will therefore show separate peaks of tag density on positive and negative strands (Figure 1b,c). The distance between the peaks should reflect the size of the protected region, although it may also be influenced by the size distribution of the DNA fragments. This distance does not exhibit strong dependency on the number of tags within the peaks (Supplementary Table 1).

A genome-wide signature of such tag pattern can be assessed by calculating cross-correlation of positive and negative strand tag densities, shifting the strand coordinates relative to each other by increasing distance (see Methods). All of the examined datasets exhibit a clear peak in the strand cross-correlation profile, corresponding to the predominant size of the protected region (Figure 1c, Supplementary Figure 1). The magnitude of the peak reflects the fraction of tags in the dataset that appear in accordance with the expected binding tag pattern (Figure 1c). In an ideal case, when all of the sequenced tags participate in such binding patterns, the correlation magnitude would reach a maximum value. Conversely, the magnitude decreases as tag positions are randomized (Supplementary Figure 2).

Using variable-quality tag alignments

While some tags align perfectly to the reference genome, others align only partially, with gaps or mismatches. Poorly aligned tags may result from experimental problems such as sample contamination, correspond to polymorphic or unassembled regions of the genome, or reflect sequencing errors. For the Solexa platform, the sequencing errors are more abundant towards the 3' ends of the sequenced fragments, frequently resulting in partial alignments that include only the beginning portion of the tag. From the growth of mismatch frequencies with nucleotide position, we estimate that such sequencing errors account for 41–75% of observed mismatches in the examined datasets (Supplementary Figure 3). Since it is not unusual to have more than 50% of the total tags result only in partial alignment, inclusion of tags that are partially aligned but still informative is important for making optimal use of the dataset^{11, 12}. We therefore chose to classify the quality of tag alignment using the length of the match and the number of nucleotides covered by mismatches and gaps (Table 1, Supplementary Table 2).

Table 1. Classification of tag alignments based on the length of the match and the number of mismatches.

The table gives the number of NRSF dataset tags whose best alignment falls within each class, as defined by the length of alignment (columns) and the number of mismatches (rows). The tags from the NRSF dataset were aligned using BLAT. The number of mismatches includes the number of nucleotides covered by gaps.

length of tag alignment
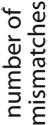		16	17	18	19	20	21	22	23	24	25
	0	63388	50613	34707	21230	16775	14453	11068	6556	54455	1234829
	1			16625	25991	24715	23431	17540	12705	31416	192975
	2					295	3436	7939	6042	6379	16495

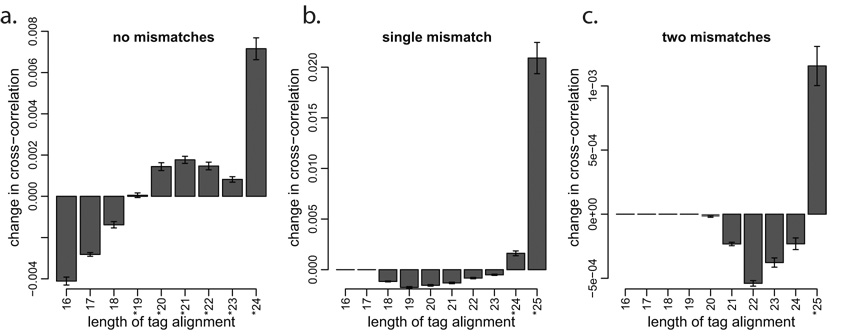
Given a classification of tags by quality of alignment, we propose to use strand cross-correlation profile to determine if a particular class of tags should be included in further analysis. A set of tags that is informative about the binding positions would increase cross-correlation magnitude, whereas a randomly mapped set of tags would decrease it (Supplementary Figure 2). Using this approach for the NRSF dataset (Figure 2), we find that alignments with matches greater than 18bp and zero mismatches improve cross-correlation profile. However, only full-length (25bp) matches should be considered for tags with two mismatches. Accepting tags using such a criterion increases their number over the set of perfectly aligned tags by 27% for NRSF dataset, 30% for CTCF and 36% for STAT1 (Supplementary Figure 4). The incorporation of these tags improves sensitivity and accuracy of the identified binding positions (Supplementary Figure 5).

Figure 2. Selecting informative tag classes based on the change in strand cross-correlation magnitude.

For each class of tag alignment quality listed in Table 1, the plots show the change in strand mean cross-correlation profile when this class of tags is considered together with the base class of perfectly aligned tags (25bp, no mismatches). Three plots correspond to tag classes (a) without mismatches, (b) with a single mismatch, and (c) with two mismatches. Informative tag classes improve cross-correlation (marked by *), and are incorporated into the final tag set. The y-axis gives the mean change in cross-correlation profile within 40bp around the cross-correlation peak (Figure 1d).

Controlling for background tag distribution

The statistical significance of the tag clustering observed for a putative protein binding position depends on the expected background pattern. A simplest model would assume that the background tag density is distributed uniformly along the genome and independent between the strands¹¹. In addition to the NRSF ChIP sample, Johnson et al¹⁴ have sequenced a control input sample, providing an experimental assessment of the background tag distribution. We find that the background tag distribution exhibits a degree of clustering that is significantly greater than expected from a homogeneous Poisson process suggested by the aforementioned simple model (P<10⁻⁶, Supplementary Figure 6).

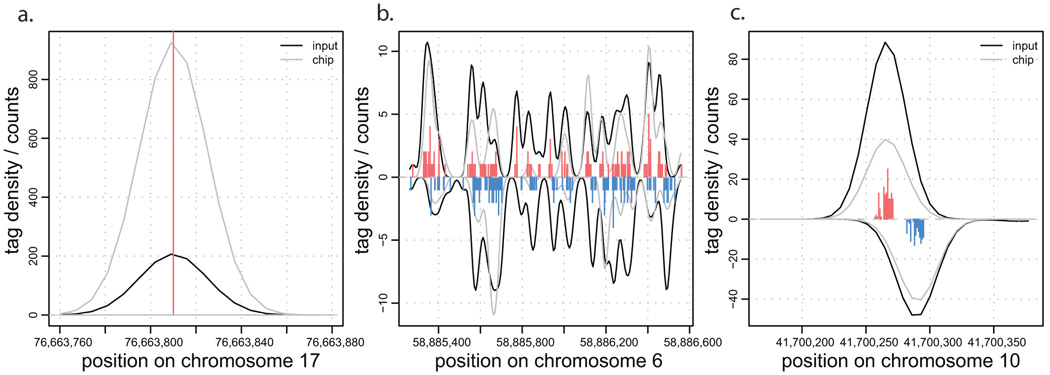
Examining the input tag density, we find three major types of background anomalies. The first type results in singular peaks of tag density at a single chromosome position many orders of magnitude higher than the surrounding density (Figure 3a). Such peaks commonly occur at the same position on both chromosome strands. The second type of anomaly results in non-uniform, wide (>1000bp) clusters of increased tag density appearing on one or both strands (Figure 3b). The third type exhibits small clusters of strand-specific tag density resembling the pattern expected from a stable protein binding position, although it typically shows smaller separation between strand peaks (Figure 3c). A similar set of anomalies can be observed in the input sequencing of other organisms (data not shown).

Figure 3. Examples of anomalies in background tag distributions.

a. Singular positions with extremely high tag count. b. Larger, non-uniform regions of increased background tag density. c. Background tag density patterns resembling true protein binding positions. Each plot shows density of tags from ChIP and input samples. The tag histograms give combined tag counts.

The first type of anomaly can be easily detected and eliminated due to its extreme deviation from the surrounding tag density (see Methods). However, the other types of anomalies, in particular the third one, are hard to distinguish within the ChIP data. This indicates that sequencing of input material is essential to properly account for the background tag distribution. Sequencing of a mock control experiment (non-specific antibody or no antibody) may also be necessary.

To control for the uneven background distribution, the binding methods proposed below subtract rescaled background tag density prior to determining binding positions, if such data are available (see Methods). In addition, only binding positions within regions of acceptable ChIP to input tag ratio are accepted². The effect of such background corrections will be characterized in the subsequent sections.

Binding detection methods and relative coverage of binding sites

We have examined five different methods of calling binding positions, including two previously published algorithms (CSP², XSET¹¹), and three novel ones. Briefly, the ChIPSeq Peak locator (CSP) method identifies regions of significant enrichment compared to the input profile and determines binding positions as those with the highest number of tags within such regions. The extended set (XSET) method extends positive- and negative-strand tags by the expected length of the DNA fragment, and determines binding positions as those with the highest number of overlapping fragments.

The newly proposed methods take advantage of the strand-specific tag pattern observed at binding positions (Figure 1c). The first such method, Window Tag Density (WTD), is similar to XSET but scores positions based on the strand-specific tag counts upstream and downstream of the examined position (Figure 4a). The second method, Matching Strand Peaks (MSP), determines local peaks of strand-specific tag density and identifies positions surrounded by positive- and negative-strand peaks of a comparable magnitude at the expected distance (Figure 4b). Finally, the third method, Mirror Tag Correlation (MTC), scans the genome to identify positions exhibiting pronounced positive and negative-strand tag patterns that mirror each other (Figure 4c). See Methods for details.

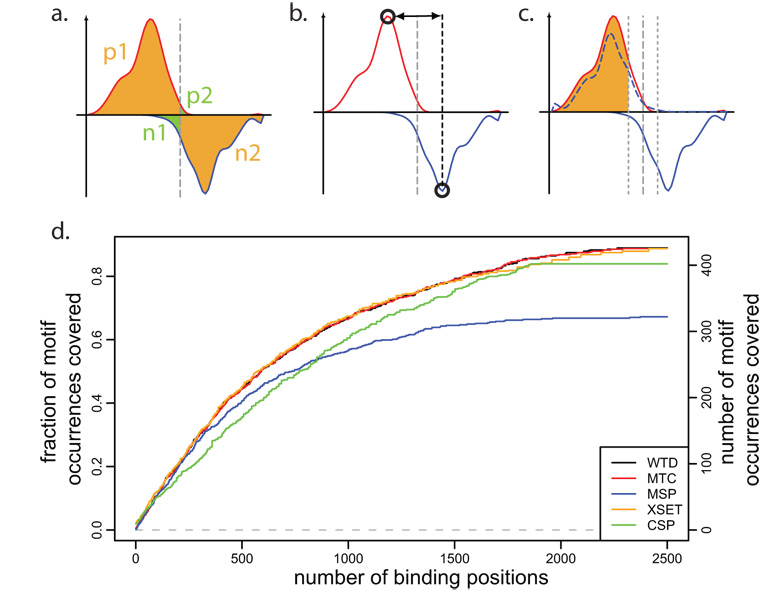
Figure 4. Binding position detection methods and their relative sensitivity.

a. Schematic illustration of the Window Tag Density (WTD) method. To identify positions with a tag pattern expected from a strong binding, the method calculates the difference between geometric average of the tag counts within the regions marked by orange color (p1 and n2), and the average tag count within the regions marked by green color (n1 and p2). b. The Matching Strand Peaks (MSP) method first identifies local maxima on positive and negative strands (open circles) and then determines positions where such two peaks are present in the right order, with the expected separation and comparable magnitude. c. The Mirror Tag Correlation (MTC) method is based on the mirror correlation of positive and negative-strand tag densities. The mirror image of negative-strand tag density is shown by dashed blue line. The tags within 15bp of the center position are omitted. d. Coverage of high-confidence NRSF motif matches by top peaks. The plot shows the fraction of motif instances that coincide (with 50bp) with identified binding positions, as a function of increasing number of top binding positions identified by different methods. Most methods, except for MSP and CSP are able to achieve similarly high coverage.

A complete list of true binding sites is not known for any of the examined datasets, however all three proteins exhibit known binding sequence specificities. While the binding detection methods described in this work do not rely on sequence information, we will utilize high-scoring sequence motif instances to assess relative performance of different binding detection methods. In doing so we only assume that the high-scoring motif instances contain a representative subset of true binding positions, and do not require for all high-scoring motifs to be bound, or all true binding sites to exhibit a motif signature. We evaluated performance using canonical sequence motifs for the NRSF and CTCF binding^{15, 16}, and using GAS motif as a predictor of STAT1 binding^{5, 11} (see Methods). The binding detection methods provide peak magnitude scores associated with the identified binding positions, thus allowing prioritization of binding positions determined by each method.

To compare sensitivity of different methods, we selected increasing numbers of top binding positions returned by each method, and examined the fraction of motif occurrences for which a binding position was identified (Figure 4d). We find that 89% of the selected highest-scoring NRSF motif matches coincide with the detected binding positions. The motif coverage rate is clearly above the random expectation, allowing for comparison of relative performance of different binding detection methods. All of the methods except for the MSP and CSP achieve similarly high motif coverage. The CSP method performs worse for the more prominent binding positions (top 500), while the MSP method exhibits poor performance throughout the entire range. Analyses of the STAT1 and CTCF binding show analogous results in terms of relative performance of different methods (Supplementary Figure 7). These results are also confirmed by analysis of PCR-validated binding loci from the literature^2,16,11 (Supplementary Figures 8,9). We note that the motif and PCR-validated test sets represent only a fraction of true binding sites. As this fraction is smaller for CTCF and STAT1 larger sets of top binding positions are used to illustrate test set coverage by different methods.

The background subtraction methods outlined in the previous section improve the NRSF motif coverage, reaching the same level of coverage at up to 11% fewer top binding positions (Supplementary Figure 10). The corrections have little effect on the top 1500 binding positions, which are associated with higher tag counts than any false positive peaks arising from uneven background. The background-driven false positive positions are generally smaller in magnitude and begin to influence predictions as more binding positions are considered.

Precision of binding positions

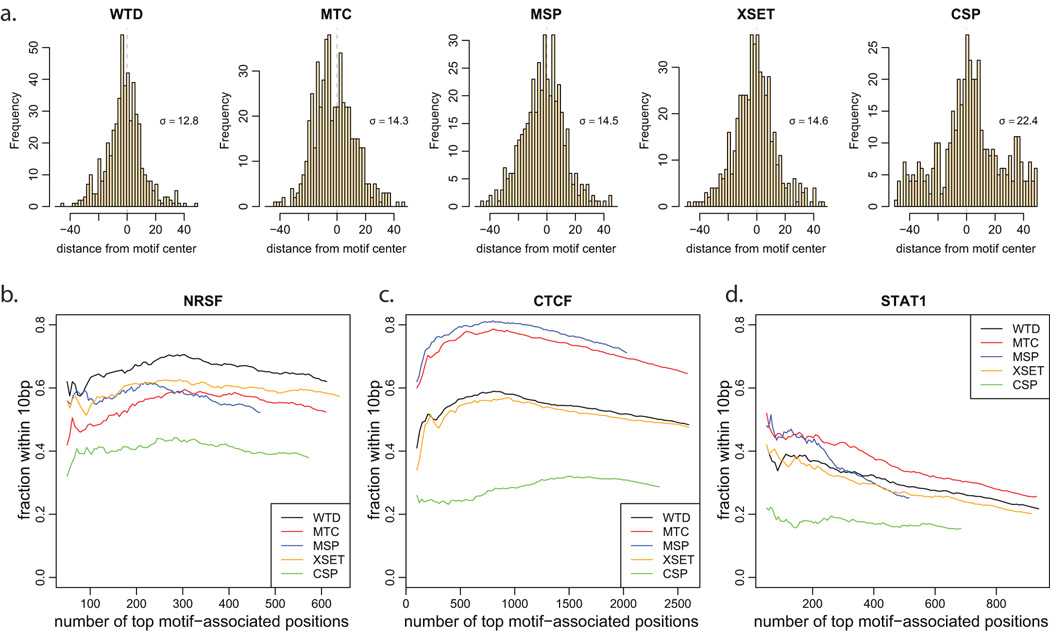
To evaluate the spatial precision with which protein binding positions are identified by different methods, we have analyzed the distances between predicted positions and locations of high-scoring motif hits (Figure 5a). For the NRSF dataset, the WTD method predicts most precise binding positions, with over 60% of predicted peaks located within 10bp of the motif center (Figure 5b, Supplementary Figure 11a). It is followed by XSET and MTC and MSP methods, with CSP calling approximately 40% of peaks within 10bp of the motifs. Background corrections have limited effect on the precision of the predicted positions, with only WTD method showing 3% improvement for strong binding positions (data not shown).

Figure 5. Accuracy of determined binding positions.

a. Distribution of distances between high-confidence NRSF motif instances and locations of binding positions identified by different methods. The standard deviation of the resulting distribution (σ) is shown for each method. Only motifs containing a binding position within 100bp were considered. b–d. The fraction of the identified binding positions within the 10bp of the motif position is shown for an increasing numbers of top binding positions identified by different methods. Only binding positions occurring within 300bp of a sequence motif instance are included in the analysis. Median distance to motif center was subtracted for each method to account for non-central position of sequence motif relative to the center of the protected binding region (see Methods). The MTC method achieves highest accuracy for CTCF and STAT1; however, WTD gives more accurate positions for the NRSF binding.

For the CTCF and STAT1 predictions, however, the MTC method achieves better precision than WTD (Figure 5c,d, Supplementary Figure 11b,c). The difference can be explained by the properties of the tag distribution immediately near the center of the protected region. Unlike WTD and XSET, the MTC method does not take into account tags within the central region (30bp) when scoring binding positions. Altering the MTC method to take such positions into account reduces the precision of the determined binding positions to the level similar to the WTD predictions. Examining the overall distribution of tag positions relative to high-scoring motif hits, we find that CTCF and STAT1 show unexpected peaks of tag density immediately adjacent (10–15bp) to the motif position (Supplementary Figure 12). Such pattern, in which small sets of negative strand tags appear immediately upstream of the protected region and are mirrored by the positive strand tags immediately downstream, may result from cross-linking interactions occurring beyond the central protected region (Figure 1b, dashed line). As a result, peak detection methods that take into account the tags near the central region tend to call positions 15–20bp upstream or downstream of the true binding site.

Statistically significant positions

The binding detection methods should limit the resulting binding positions to those that are not likely to have occurred by chance. The desired level of statistical significance is commonly given in terms of a false discovery rate (FDR) or the number of expected false positive positions (E-value). The detection methods can then use background tag distribution to determine the minimal binding position score satisfying the specified level of significance. Many false positive calls originate from large anomalous regions described earlier. Such systematic errors can be filtered prior to determination of significance thresholds (see Methods). Based on the input sample data for the NRSF, we find a total of 2755 binding positions for the FDR threshold of 0.01 using WTD method. We note that this closely corresponds to the number of top peaks that was required to achieve maximal coverage of high-scoring motif positions that were utilized in the previous sections (Figure 4d).

In the absence of an empirical estimate of the background tag distribution, it may be possible to rely on an analytical model. The simplest such model is a spatial Poisson process where the tags are uniformly distributed across the accessible regions of the genome¹¹. However, because the true background tag distributions exhibit significant degree of tag clustering, such Poisson-based threshold is significantly lower than the one obtained from empirical background measurement, resulting in overestimation of the number of significant binding positions (9206 vs. 2755 for FDR 0.01). Comparing with the input-based FDR calculations, we find that the Poisson-based model underestimates FDR by 8–20 times depending on the target FDR (see Supplementary Table 3).

A closer estimate of statistical thresholds may be obtained by accounting for the degree of clustering present in the background tag distribution. A simple approach is to utilize a randomization that maintains tags occurring at the same or nearby positions together, instead of assigning them independent positions as it is done under Poisson model. The number of significant positions determined using such randomization models with different bin sizes are shown in Supplementary Table 3. For the FDR of 0.01 a randomization model that maintains together tags occurring at the exactly the same position in the genome results in a comparable number of NRSF binding positions (2985). We used such randomization to determine the number of statistically significant binding positions for the CTCF (23981 positions at FDR of 0.01) and STAT1 (44921 positions) datasets. Matching the number of binding positions for more stringent FDR values requires larger tag randomization blocks (Supplementary Table 3), indicating that simple randomization strategies cannot properly account for the background clustering properties.

Testing for sufficient sequencing depth

To assess whether the sequencing depth has reached a saturation point beyond which no additional binding sites are detected, we have analyzed how the set of the predicted binding sites changes when only a subset of tag data is utilized for prediction. Sampling increasing fractions of the tag data, we determined binding positions and compared these predictions with the set of reference binding sites identified from the complete data (Figure 6a, Supplementary Figure 13).

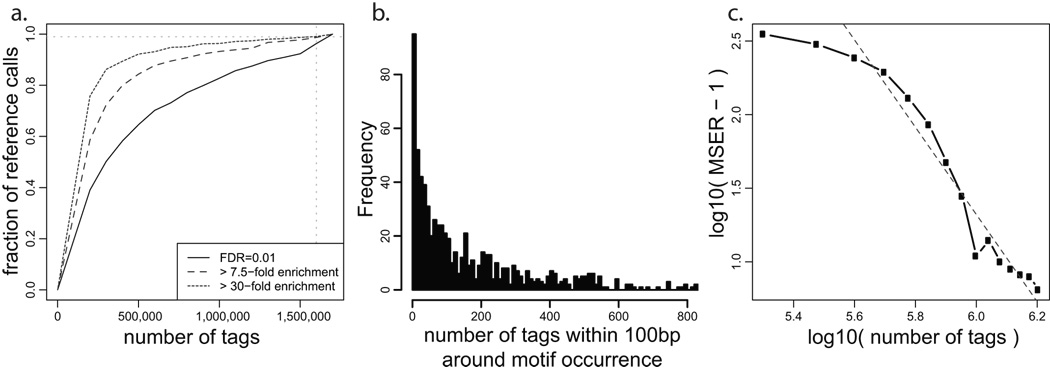
Figure 6. Analysis of sequencing depth.

a. Given the NRSF binding positions determined using complete dataset (y-axis), the black curve shows the fraction of positions that can be predicted (within 50bp) using smaller portions of the tag data (x-axis). All of the binding predictions are generated using FDR of 0.01 using the WTD method. The curve does not reach a horizontal asymptote, indicating that the set of detected NRSF binding sites has not stabilized at the current sequencing depth. The additional curves limit the analysis to binding positions whose fold enrichment ratio over the background is significantly (P<0.05) higher than 7.5 (MSER: Minimal Saturated Enrichment Ratio, dashed line) and 30 (dotted line). The observed enrichment ratios are evaluated independently for each tag subsample (x-axis). b. Distribution of tag counts around high-confidence NRSF motif positions. Positions with zero tags were not included. c. The relationship between MSER of the detected binding positions and sequencing depth (expressed as a fraction of the complete dataset). The dashed gray line shows a log-log model that can be used to estimate the sequencing depth required to saturate detection of binding positions with lower fold-enrichment ratio. By that estimate, 1.2×10⁶ more sequence tags would be necessary to saturate detection of binding positions that are two-fold enriched over background (MSER=2 corresponds to y=0, at which the red line crosses x-axis: x=2.8×10⁶).

If the sequencing depth has moved beyond the saturation point, it would be possible to arrive at the reference set using only a subset of the tag data. We find, however, that none of the three datasets have reached such a saturation point (horizontal asymptote), and that the fraction of the concordant binding positions decreases when even a small fraction of tag data is omitted. This indicates that additional binding sites are being continuously identified with increasing sequencing depth. The observed trend holds for a range of FDR thresholds (Supplementary Figure 13): although the slope of the saturation curve can be reduced by setting a considerably more stringent FDR threshold that results in a significantly smaller number of binding sites.

To understand the properties of the binding site coverage, we have examined tag counts associated with high-scoring sequence motifs (Figure 6b, Supplementary Figure 14). In all three datasets, the distribution of tag counts shows a very wide dynamic range. While some positions have hundreds of tags, others barely rise above the expected background counts. Moreover, these distributions appear to be continuous in that they do not show distinct sub-populations of binding positions. This suggests that increasing sequencing depth may allow distinguishing an increasing number of weakly pronounced binding positions without a qualitative threshold that would define a complete set of binding sites.

Since more pronounced binding positions are identified using smaller sequencing depth, an experiment of given depth may saturate detection of the binding positions that exceed a certain tag enrichment ratio relative to the background. We will refer to such enrichment ratio as Minimal Saturated Enrichment Ratio (MSER). The saturation criteria that define the maximal acceptable slope of the saturation curve (Figure 6a) can be formulated as a requirement for stability of the set of predicted binding sites. For instance, we will require 99% agreement in the set of binding positions when dataset is reduced by 10⁵ tags. Using NRSF input tag data to determine the confidence intervals for the enrichment ratio of each binding position, we find that current sequencing depth is sufficient to saturate detection of binding positions with tag enrichment ratios significantly above 7.5 (P-value <0.05, see Methods, Fig. 6a, Supplementary Figure 17). Of the 2755 NRSF binding positions detected at FDR 0.01, 1879 (68%) are above MSER 7.5 (Supplementary Figure 13). We note that a particular MSER value does not imply that all of the true binding positions of that enrichment fold have been discovered; instead, it attests that new binding positions with enrichment significantly higher than the MSER value are being detected at a sufficiently slow rate. A potential range of true enrichment ratios can be assessed from the enrichment confidence intervals calculated for each binding position (Supplementary Figure 15). Since estimation of the enrichment ratio confidence intervals also depends on the amount of information available about the background tag distribution, input datasets of similar genomic coverage should be used when comparing different MSER values.

For practical purposes, it is important to be able to predict the number of tags required to saturate detection of peaks above a given target enrichment ratio. The relationship between the number of tags and the MSER settles into a dependency that can be extrapolated using a log-log model (Figure 6c). We predict, for instance, that 1.2×10⁶ more tags would be required to reach saturation in detecting NRSF binding positions with enrichment over the background significantly higher than two-fold (P-value < 0.05). The MSER values and extrapolations depend on the saturation criteria and on methods used to calculate enrichment confidence intervals (see Methods, Supplementary Figure 18).

Increasing the sequencing depth is also likely to lead to increased accuracy of the determined binding positions. Using the NRSF dataset, we analyzed how the mean distance between the detected binding positions and sequence motifs depends on the number of tags used for predictions. Our results show that accuracy indeed improves with the increasing number of tags (Supplementary Figure 16). The improvement, however, is minor: the accuracy decreases by only several base-pairs even when number of tags is halved.

Discussion

Analysis of protein-DNA interactions using high-throughput short sequencing poses a number of novel computational challenges. We show that many aspects of the processing pipeline can be specifically tailored to improve detection of binding positions.

The protein binding positions exhibit a strand-specific pattern of tag occurrences. We illustrate that a genome-wide signature of such a pattern can be obtained with strand cross-correlation of tag density, providing a quick assessment of dataset quality and binding characteristics. The proposed alignment procedure also relies on this signature to determine the range of alignment quality that is informative about the binding positions. In our implementation, we have used a simple classification of tag alignment quality, based on the number of nucleotide mismatches. The same procedure can be applied to more elaborate measures of alignment quality, such as those incorporating confidence in specific base calls¹².

The examination of the input sequencing clearly indicates that experimental assessment of the background tag distribution is necessary for accurate evaluation of the ChIP-seq data. The background distribution is far from uniform and, in some cases, shows tag density patterns similar to those expected from true binding positions. We demonstrate that the knowledge of such distribution is instrumental for accurately assessing and reducing rates of false positive predictions. As additional datasets become available, it will be important to analyze the degree to which tag profiles of input or no-antibody measurements differ between independent experiments.

Comparison of different binding prediction algorithms shows that even though several methods can reach optimal sensitivity, there is a considerable variation in the accuracy of the identified binding positions. While the MTC method provides more accurate positions for CTCF and STAT1 binding, the WTD method is better at identifying precise positions of NRSF binding. The difference can be attributed to the consideration of tag patterns immediately near the center of the binding pattern, which show qualitative differences between NRSF and CTCF/STAT1 datasets (Supplementary Figure 12). Since the NRSF binding tag pattern is more consistent with the basic expectations, we recommend using WTD method in the cases when the tag pattern cannot be examined beforehand on a set of expected binding positions. It remains to be seen, however, which tag pattern will be typical of other experiments and whether both patterns can be efficiently handled by a single method.

The ability to evaluate and predict the sequencing depth requirement is an important aspect of ChIP-seq studies. Our analyses demonstrate that none of the three examined datasets definitively reach a point of saturation at which the set of determined binding positions stabilizes. The binding positions exhibit very wide range of enrichment ratios so that additional sequencing reveals increasing number of weaker binding sites. This bears some resemblance to other genomics studies. In genome-wide association studies, for instance, increasing the sample size allows one to find more and more loci with smaller LOD scores; in gene expression studies, it leads one to find more and more genes with a statistically significant but smaller fold-change. In practical terms, this lack of saturation point has profound implications in study design. It suggests that it would be difficult to define a “sufficient” depth of sequencing and that other criteria must be specified.

We therefore propose that the sequencing depth requirements should be evaluated with respect to a specific target enrichment ratio of the binding positions. Towards that end, we provide a method to determine the minimal fold enrichment ratio above which the detection of binding positions has been saturated (i.e. stabilized) at a current sequencing depth. We also show that the relationship between saturated fold enrichment and the number of sequenced tags may be extrapolated to estimate the sequencing depth that would be required to reach saturation for lower fold enrichment ratio. It will be important to examine how well such extrapolations describe saturation properties of much larger datasets that are likely to be come available in the near future.

The fold enrichment ratio of a particular binding position may depend on diverse factors, such as binding affinity or efficiency of chromatin extraction. Since its relationship to the functional importance of binding positions is uncertain, the desired fold enrichment ratio target would clearly vary for different experiments. When some functional binding positions are already known for a particular protein, the target enrichment ratio can be chosen based on examination of these positions in the initial sequencing data or with quantitative PCR. If a target enrichment ratio cannot be estimated from other sources, it can be specified relative to the maximum or median enrichment observed in the dataset (e.g. detect binding positions with enrichment 5-fold below the maximum observed enrichment).

As more ChIP-seq datasets are generated, it will be important to analyze additional factors, such as sequencing biases associated with individual sequencing platforms, or stability of ChIP and input tag distributions between replicate experiments. Such data will likely lead to improvements in the binding prediction methods and allow better interpretation of the functional relevance of observed variability in fold enrichment ratios of different binding positions. Finally, it will be important to see whether the described techniques can be adapted for analysis of histone modifications or other widely-distributed chromatin marks that do not fit the models of point binding patterns.

Methods

Datasets

The analysis of the NRSF binding were performed using tag data from Johnson et al². Raw tag information necessary for the analysis was only available for experiment #2. CTCF data was taken from Barski et al¹³. The STAT1 binding was analyzed using INF-γ stimulated dataset from Robertson et al¹¹.

Cross-correlation profiles

For each chromosome c, the tag count vector $n_c^s(x)$ was calculated to give the number of tags whose 5’ end maps to the position x on the strand s . Strand cross-correlation for a strand shift δ was then calculated as $\mathrm{X}(\mathit{\delta })={\displaystyle \sum _{c\in C}\frac{N_c}{N}P\left[n_c^{+}\left(x+\raisebox{1ex}{$\mathit{\delta }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right),n_c^{-}\left(x-\raisebox{1ex}{$\mathit{\delta }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\right]}$, where P[a, b] is the Pearson linear correlation coefficient between vectors a and b, C is the set of all chromosomes, N_c is the number of tags mapped to a chromosome c, and N is the total number of tags.

Tag alignment and selection of informative tags

Sequence tags were aligned to human genome assembly (NCBI build 36, hg18) using BLAT¹⁷, with min score threshold of 16, max gap of 4 and step size of 3. Tags aligning to multiple locations in the genome were discarded in this analysis.

Anomalous tag positions were identified as those with the number of mapped sequence tags (5’ ends) above the significance threshold defined by Z-score of 10. All of the tags mapping to such anomalous position (on either strand) were omitted prior to further analysis.

The resulting tag alignments were classified based on 1) the length of the alignment and 2) the number of nucleotide differences (number of mismatches + total gap length). A given class of tags was accepted if adding these tags to the reference set significantly (Z-score > 6) increased the cross-correlation profile within the region ±20bp around the cross-correlation peak. The set of perfectly aligned tags (maximum length, no mismatches) was used as a reference set.

Detection of binding positions

WTD

A binding score was calculated for all positions i in the genome as $S_{\mathit{\text{wtd}}}(i)=2\sqrt{p_U{n}_D}-(p_D+n_U)$, where p_D and p_U are the number of 5’-end tag positions mapping to a positive strand within a distance of w upstream and downstream of a position i respectively. Similarly, n_D and n_U correspond to the number of upstream and downstream tags mapping to the negative strand. Window size w = 200bp was used for CTCF and NRSF, and w = 400bp was used for STAT1. The window sizes were chosen to encompass the size of the average binding tag pattern (i.e. Supplementary Figure 12). We find that this size can be estimated from the cross-correlation profiles (Figure 1d, Supplementary Figure 1) as the width of the cross-correlation peak at 1/3 of the peak height. Positions on the chromosome corresponding to non-unique tag alignment and mirror positions with respect to point i were excluded from score calculation. Binding peaks were determined as local maxima of S_wtd(i).

MSP

Tag density profiles along each chromosome strand were calculated using Gaussian smoothing kernel with bandwidth corresponding to the 0.45*σ_scc where σ_scc is the width of the strand cross-correlation peak (Figure 1d) at half height. The kernel bandwidth was selected for optimal coverage and accuracy of the method (Supplementary Figure 20). A binding position was accepted when local maxima (peaks) of positive and negative strand density were found the distance of µ±20bp, where µ is the size of the protected region for that protein (estimated from cross-correlation analysis). The peaks were required to be comparable in magnitude (based on likelihood ratio test with a Z-score cutoff of 8).

MTC

Similar to WTD, the binding score was calculated as $S_{\mathit{\text{mtc}}}(i)=\rho \sqrt{S_{\mathit{\text{wtd}}}(i)}+S_{\mathit{\text{wtd}}}(i)$, where ρ is the Pearson linear correlation coefficient between tag vectors v⁺ and v⁻, such that v⁺ (k) is the number of 5’-end tag positions mapping to positive strand in position i + k, and v⁻ (k) is the number of 5’-end tag positions mapping to negative at i − k . The correlation is evaluated for $k\in \left\{-w,\dots ,-w_0\right\}\cup \left\{w_0,\dots ,w\right\}$, where w₀ = 15bp, and the values of w are the same as in the WTD method.

When using the methods described above, peaks within distance w of a larger peak were omitted ( w = 200bp for CTCF and NRSF, 400bp for STAT1). The CSP method implementation provided by Johnson et al² was used, and the XSET method was implemented as described in Robertson et al¹¹.

Background tag density corrections

To normalize for background tag density in the analysis of NRSF binding, the window tag counts described in the WTD and MTC methods were adjusted by subtracting the weighted number of background (input) tags occurring within that window. To account for differences between ChIP and background dataset sizes, the background tags were multiplied by N_c / N_b, where N_c and N_b are non-specific sizes of ChIP and background datasets. The non-specific size of the dataset was determined as a number of dataset tags outside of highly-enriched regions: regions of 1Kbp with the number of tags exceeding uniform (Poisson) density with P-value < 10⁻⁵. This type of weighting allows for proper estimation of the background density ratios when a large fraction ChIP dataset tags is concentrated within localized bound regions (which for NRSF is 23%).

To reduce the impact of false positives from large regions of systematically high background, subsequent calculation excluded regions of size 10⁴bp or larger where input tag counts are significantly larger (Z − score ≥ 5) than ChIP counts.

Statistical significance of detected positions

For a predicted binding position with score s , the false discovery rate (FDR) was estimated as $\frac{N_r(s)+0.5}{N_c(s)+0.5}$, where N_r(s) is the number of binding positions with score s or higher found in the real dataset, and N_c (s) is the number found in a control dataset. The FDR estimates of positions with scores above maximal score found in the control dataset (i.e. N_c(s) = 0) were assigned minimal FDR found in the set of detected positions. Two types of control models were used: randomized models, and a model based on the background (input) tag data.

Under a completely randomized model, control data was generated by randomly reassigning positions of the real (ChIP) dataset tags. More restrictive randomization models maintained together tags that occurred within a distance d in the original data. Supplementary Table 3 shows results based values of d ranging from 1 to 7. A total of 10 randomized permutations of the complete dataset were employed for FDR calculations.

Under a background-based model, the control predictions were generated in the same way as predictions on real data, interchanging background (input) and ChIP data.

Sequence motifs position accuracy

Motif occurrence positions within human genome were calculated using MAST¹⁸. High-scoring NRSF motif occurrences were determined using position-specific matrix (PSSM) from Mortazavi et al¹⁵. Positions with P value < 4×10⁻⁹ were chosen, to match the number of motifs obtained in Johnson et al². For STAT1, GAS motif occurrences were determined using the PSSM from the TRANSFAC database¹⁹, with maximum P value of 10⁻⁵. High-confidence CTCF motif positions were determined using the PSSM from Kim et al¹⁶, with the P value threshold of 4×10⁻⁸.

The accuracy of the predicted protein binding positions was analyzed based on the distances between identified positions and centers of high-scoring motif hits. Only binding positions occurring within 300bp of a sequence motif instance were included in the analysis. The sign of the distance was adjusted according to the strand on which the motif hit occurred. Since the center of the motif hit may not represent a true center of binding (e.g. protected region), the distances to the motif were centered by subtracting the median distances. The centered distances were used in Figures 5b–d, and Supplementary Figure 11.

Sequencing depth analysis

To evaluate stability of the identified set of binding positions on the set of tags, binding positions were predicted on randomly sampled subsets of the original tag data. Sampling was performed without replacement. WTD method with FDR of 0.01 was used to generate the predictions. A chain of subsampled datasets was generated by 15 successive random reduction of a dataset by 10⁵ tags. A total of 100 such random chains were generated. The convergence of the MSER and depth predictions with the increasing number of chains is shown in Supplementary Figure 17.

We will use fractional agreement F(s_i, s_j), to refer to an average fraction of binding positions determined using randomly sampled fraction of tags of size s_j that is also present (within 50bp) in a set of binding positions determined using tag subsample of size s_i . The basic saturation curves (Figure 6a) show the values F(s_t, x), where x is the number of tags sampled (x-axis), and s_t is the total size of the original dataset.

To estimate the minimal fold enrichment ratio of the identified binding positions over the background, we calculated the number of ChIP (n_c) and input (n_b) tags within 100bp surrounding the identified position. The counts were used to estimate 95% confidence interval of the fold enrichment ratio based on a Poisson model with non-informative Bayesian prior ²⁰. As the background tag density is lower than the ChIP tag density, we also tested using larger window sizes in counting background tags (see Supplementary Figure 18). While such approach should provide tighter enrichment confidence intervals, it appears to result in over-estimation of enrichment folds relative to qPCR data.

We will use F_e(s_i, s_j) to refer to the fractional agreement after filtering both predictions to include only those binding positions with lower bound of enrichment ratios above e. The minimal saturated enrichment ratio (MSER) for a dataset x was calculated as the minimal value of e such that F_e(s_x, s_x − 10⁵) ≥ 0.99. The relationship between log₁₀(MSER − 1) and the size of the dataset (x) was approximated using a linear model based on a least squares fit.

Availability

An implementation of the described methods is available as an R package and can be downloaded at http://compbio.med.harvard.edu/Supplements/ChIP-seq

Supplementary information is available on the Nature Biotechnology website.