Modeling individual differences in working memory performance: a source activation account

Abstract

Working memory resources are needed for processing and maintenance of information during cognitive tasks. Many models have been developed to capture the effects of limited working memory resources on performance. However, most of these models do not account for the finding that different individuals show different sensitivities to working memory demands, and none of the models predicts individual subjects' patterns of performance. We propose a computational model that accounts for differences in working memory capacity in terms of a quantity called source activation, which is used to maintain goal-relevant information in an available state. We apply this model to capture the working memory effects of individual subjects at a fine level of detail across two experiments. This, we argue, strengthens the interpretation of source activation as working memory capacity.

1. Introduction

Working memory provides the resources needed to retrieve and maintain information during cognitive processing (Baddeley, 1986, 1990; Miyake & Shah, 1999). For example, during mental arithmetic one must hold the original problem and any intermediate results in memory while working toward the final answer. Working memory resources have been implicated in the performance of such diverse tasks as verbal reasoning (Baddeley & Hitch, 1974), prose comprehension (Baddeley & Hitch, 1974), sentence processing (Just & Carpenter, 1992), memory span (Baddeley, Thompson & Buchanan, 1975), free recall learning (Baddeley & Hitch, 1977), and prospective memory (Marsh & Hicks, 1998). Given its ubiquitous influence, the study of working memory is critical to understanding how people perform cognitive tasks.

Working memory resources are limited, and these limits govern performance on tasks that require those resources. Prior research has demonstrated that as the working memory demands of a task increase, people's performance on the task decreases (e.g., Anderson & Jeffries, 1985; Anderson, Reder & Lebiere, 1996; Baddeley & Hitch, 1974; Engle, 1994; Just & Carpenter, 1992; Salthouse, 1992). Salthouse, for instance, had subjects perform four different tasks at 3 levels of complexity. He found that as task complexity increased, performance decreased. Moreover, this decrease was greater for older adults. This last finding, that people differ in their sensitivity to the working memory demands of a task, is an important feature of working memory results: some individuals are less affected by increases in working memory demands than others. Just and Carpenter (1992), for example, demonstrated that differences in working memory capacity account for differential sensitivity to working memory load during several language comprehension tasks. Further, Engle (1994) reported that differences in working memory capacity predict performance on a variety of tasks including reading, following directions, learning vocabulary and spelling, notetaking, and writing. Working memory resources, it seems, (a) are drawn upon in the performance of cognitive tasks, (b) are inherently limited, and (c) differ across individuals.

Several computational models of working memory have been proposed. Each makes very different assumptions about the structure of working memory and the nature of working memory limitations. Broadly speaking, the models are of two types: connectionist networks and production systems. Burgess and Hitch (1992) developed a connectionist model of Baddeley's (Baddeley, 1986, 1990) articulatory loop, a component of working memory hypothesized to hold verbal stimuli for a limited amount of time. In their model, item-item and item-context associations are learned via connection weights that propagate activation between memory items and enable sequential rehearsal through a list. Because these weights decay with time, more demanding tasks (e.g., remembering longer lists or lists of longer words) tend to propagate less activation to the memory items, leading to more errors. Page and Norris (1998a; 1998b) have also developed a connectionist model of the articulatory loop. Their model, which uses a localist representation of the list items, focuses on the activation of the nodes representing the list items; the strength of activation for successive list items decreases as a function of list position creating what Page and Norris term a primacy gradient. Activation is assumed to decay during the input process if rehearsal is prevented and during output. Recall is achieved by a noisy choice of the most active item; this item is then suppressed to prevent its retrieval on successive recall attempts. In contrast, O'Reilly, Braver and Cohen (1999) have proposed a biologically inspired, connectionist model in which working memory functions are distributed across several brain systems. In particular, their model relies on the interaction between a prefrontal cortex system, which maintains information about the current context by recurrently activating the relevant items, and a hippocampal system, which rapidly learns arbitrary associations (e.g., to represent stimulus ensembles). Both systems' excitatory activation processes, however, are countered by inhibition and interference processes such that only a limited number of items can be simultaneously maintained. This limitation leads to decreased performance in complex tasks. Similarly, Schneider's CAP2 (Schneider, 1999) model also assumes that working memory functions are distributed across multiple systems. In CAP2, memory and processing occur in a system of modular processors arranged in a multilayered hierarchy. A single executive module regulates the activity of the system. Working memory limits arise due to cross-talk in the communication between modules, storage limitations in specific regions of the system, and severe limits on the executive module.

Another approach to working memory is taken by production-system architectures. One such architecture is EPIC (Kieras, Meyer, Mueller & Seymour, 1999; Meyer & Kieras, 1997a, 1997b). Here, an articulatory loop is implemented via the combined performance of an auditory store, a vocal motor processor, a production-rule interpreter, and various other information stores. Performance of the model is governed by production rules which implement strategies for rehearsal and recall and which, in turn, draw on the capabilities of the other components. Working memory limitations stem from the all-or-none decay of items from the auditory store (with time until decay being a stochastic function of the similarity among items) and from the articulation rate attributed to the vocal motor processor. As the vocal motor processor takes the prescribed amount of time to rehearse a given item (reading that item to the auditory store), other items have a chance to decay (disappearing from the auditory store), thereby producing subsequent recall errors. In contrast, SOAR (Newell, 1990; Young & Lewis, 1999) proposes that working memory functions are distributed across its long-term production memory, which stores permanent knowledge, and its dynamic memory, which stores information relevant to the current task. Unlike many other models of working memory, SOAR assumes no limit on its dynamic memory (the component most commonly identified with working memory). Limitations in SOAR are primarily due to functional constraints; the assumption is that individuals differ in terms of past experience and, therefore, they also differ in terms of the acquired knowledge that can be drawn upon to perform a task. Young and Lewis also suggest that SOAR's dynamic memory may only be able to hold two items with the same type of coding (e.g., phonological, syntactic). This constraint allows SOAR to capture some limitations (e.g., similarity-based interference) not possible with functional constraints alone.

An important advantage common to these computational approaches is that each presents a theory of working memory in a rigorous enough form to enable quantitative comparisons with human data. Indeed, despite the wide variety of approaches, all of these models have successfully accounted for assorted working memory effects at the group level (i.e., aggregated across subjects). As noted above, however, working memory capacity differs from person to person, and these differences can result in very different patterns of performance. Thus, a complete model of working memory should be able to capture not only aggregate working memory effects but also individual subjects' different sensitivities to working memory demands. Just and Carpenter (1992) modeled different patterns of performance in groups of subjects with low, medium, or high capacity by assuming different caps on the total amount of activation in the system. This was an important step in the computational modeling of individual differences in working memory capacity.

We build upon this approach and explore a fully individualized computational modeling account of working memory capacity differences that shares some similarities with other activation accounts of working memory (e.g., Burgess & Hitch, 1992; Just & Carpenter, 1992; Page & Norris, 1998a, 1998b; O'Reilly et al., 1999). Our main goal is to show that a single model—with an adjustable individual differences component—can capture the performance of individual subjects and that the model's predictions relate to other measures of subjects' working memory capacity. Several new features distinguish our approach. First, we are modeling performance at the individual subject level. This is necessary if one wants to show that a model is able to capture individuals' actual patterns of performance and not just a mixture of several individuals' differing patterns. Thus, our approach is qualitatively different from aggregate or subgroup analyses, which suffer in varying degrees from the perils of averaging over subjects (cf. Siegler 1987). Second, we attempt to capture individual subjects' performance at a detailed level, modeling several performance measures collected under varying task demands. Third, we collect data within a paradigm where we try to reduce the impact of other differences between subjects such as prior knowledge, strategic approaches, and self-pacing of activities. In this way, the observed variations in performance are more likely attributable to differences between subjects in their cognitive processing resources, for example, working memory resources. Fourth, we develop our individual-differences model of working memory within an existing cognitive architecture, ACT-R (Anderson & Lebiere, 1998). This architecture offers both a set of basic mechanisms which constrain how working memory can be modeled and a set of prior results suggesting that these mechanisms provide an adequate account of people's cognitive processing across a variety of tasks. More specifically, a variant of the working memory model we explore in this paper has already been tested in its ability to simulate aggregate performance in a different working-memory-demanding task (Anderson et al., 1996). Thus, the current paper focuses not on how the model accounts for various working memory effects per se but rather on how this single model of working memory can capture the variation among subjects in their working memory performance, while maintaining its basic structure.

1.1. Modeling working memory in ACT-R

ACT-R combines a procedural and declarative memory in a single framework capable of modeling a wide variety of cognitive tasks. Procedural knowledge in ACT-R is represented as a set of independent productions, where each production is of the form “IF <condition>, THEN <action>.” The firing of productions is governed by the current goal, which acts as a filter to select only those productions relevant to the current task. Among the relevant productions, only the one deemed most useful is fired. Declarative knowledge, in contrast, is represented as a network of interconnected nodes or chunks. Each node has an activation level that governs its accessibility: the higher a node's activation, the more likely and more quickly it is accessed. Node activation is increased when a node is accessed and decreases as time passes without further stimulation. This kind of activation is called base-level activation and it reflects practice and forgetting effects. The activation of a node is also increased if it is relevant to the current goal, a special declarative node that represents the person's focus of attention. There is a certain amount of activation called source activation that flows from the current goal to related nodes to maintain them in a more active state relative to the rest of declarative memory. Only one goal is active at any given time; if a subgoal is set, it becomes the new current goal and hence the focus of attention.

Take the example of a person whose current goal is to find the sum of 3 and 4. In this case, 3 and 4 are items in the focus of attention and source activation flows from these nodes to other related nodes in declarative memory. This makes those related nodes more active relative to the rest of declarative memory, making them more likely to be retrieved. Because the node encoding the fact that 3+4=7 is related to both 3 and 4, it will receive source activation from both items in the focus of attention, leading it to be most likely to be retrieved. Thus, source activation plays the role of producing context effects: the fact 3+4=7 is more activated when 3 and 4 are in the focus of attention. If the task being performed is complex (e.g., many pieces of information are relevant to the goal), the source activation must be spread thinly, and each relevant node will receive less source activation. This makes the relevant information less distinct and less easily accessed. As a result, performance suffers.

Cantor and Engle (1993) suggested that working memory limits could be modeled in ACT* (an ACT-R predecessor) as a limit on the number of items that could be maintained in an active state relative to the rest of declarative memory. This is precisely the function of source activation in ACT-R: it increases, to a limited degree, the activation of context-related items. Anderson et al. (1996) formally implemented and tested this conceptualization of working memory with a working ACT-R simulation. In their study, subjects were required to hold a digit span for later recall while solving an algebraic equation. Both the size of the span and the complexity of the equations were manipulated. Also, in some cases, digits from the memory span had to be substituted for symbols in the equation. Results showed that, as either of the subtasks became more difficult, performance on both decreased. In particular, for both the accuracy and latency of equation solving, the effects of span size were greater when subjects had to perform a substitution.

In the Anderson et al. (1996) model, a fixed amount of source activation was shared between the two components of their task—maintaining the items of the memory span and solving the equations. As either of the subtasks became more complex, source activation was more thinly spread among a greater number of relevant nodes, decreasing performance. Quantitative predictions of the model provided a good fit to many performance measures (e.g., accuracy on both subtasks and latency on problem solving) across two experiments. Thus, an ACT-R model with a limit on source activation reproduced two of the three key features of working memory resources: (a) they are drawn upon in the performance of cognitive tasks, and (b) they are inherently limited. The third feature, that working memory resources differ in amount across individuals, was not addressed. To account for the third feature, Lovett, Reder, and Lebiere (1999) hypothesized that the limit on source activation may differ among individuals and that this difference accounts for individual differences in working memory capacity. According to this view, a larger working memory capacity is represented by a larger amount of source activation which, in turn, can activate more goal-relevant information, thereby facilitating performance.

1.2. Modeling individual differences in ACT-R

To describe how working memory differences can be incorporated in ACT-R, it is helpful to have a more detailed, quantitative specification of the theory. As previously described, the ACT-R architecture (Anderson & Lebiere, 1998) is a production system that acts on a declarative memory. The knowledge in declarative memory is represented as schema-like structures called chunks. A single chunk consists of a node of a particular type and some number of slots that encode the chunk's contents. Fig. 1, for instance, depicts a chunk that encodes a memory of the digit 7 appearing in the first position of a list presented on the current trial. This chunk has three slots: one to store the identity of the to-be-remembered item, one to store the item's position within the list, and one to store some tag that identifies the trial on which that list occurred. Retrieval of a chunk is based on its total activation level. This level is the sum of the chunk's base-level activation (i.e., activation level based on its history of being accessed) and the total amount of source activation it receives from elements currently in the goal, or focus of attention. Total chunk activation is given by:

Fig. 1.

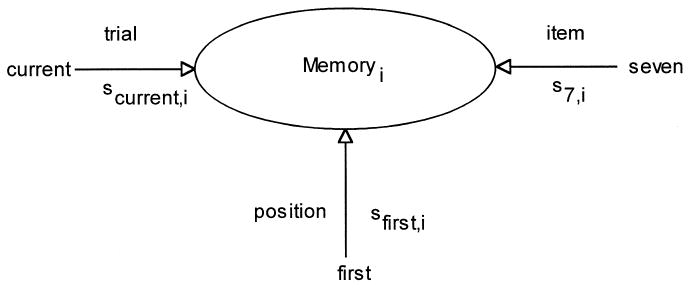
The structure of a declarative chunk encoding the fact 7 is the first item of the current list.

$$A_i=B_i+\sum _{j=1}^n\frac{W}{n}{S}_{ji}$$ (1)

where A_i is the total activation of chunk i and B_i is the base-level activation of chunk i. W, of course, is source activation and it is divided equally among the n filled slots in the goal chunk. The S_jis are the strengths of association between chunks j and i. For example, when the current goal is to recall the item in the first position of the current trial's list, the chunk in Fig. 1 receives source activation from “first” and “current” in the goal making this chunk more activate than if it were not related to the current goal.

The total activation of a chunk determines the probability of its retrieval as given by the following:

$$\text{Probability of retrieving chunk i}=\frac{1}{1+e^{-\left(A_i-\tau \right)/s}}$$ (2)

where A_i is, as before, the total activation of chunk i, τ is the retrieval threshold, and s is a measure of the noise level affecting chunk activations.

If a chunk's total activation (with noise) is above the threshold τ, its latency of retrieval as given by the following:

$$\text{Latency to retrieve chunk i}=F{e}^{-\text{fAi}}$$ (3)

where F and f are constants mapping A_i onto latency. If the total activation falls below threshold, the model commits an error of omission. Errors of commission are produced by a partial matching mechanism that will be discussed later.

To review, the critical insight offered by Anderson et al. (1996) is that the performance of this model is limited by a fixed amount of source activation, W. A default value of 1.0 for W was adopted by Anderson et al. as a scale assumption. As discussed above, however, this model does not account for individual differences in working memory capacity. Extending this framework, Lovett et al. (1999) hypothesized that individual differences in working memory capacity could be represented by different values for W. To capture individual differences, W is not fixed at 1.0 (as in Anderson et al.) but rather varies to represent the particular amount of source activation for each individual. The distribution of these W values across a population would be expected to follow a normal distribution centered at 1.0.

Putting these equations together, one can see how performance is influenced by the value of a particular individual's W. The higher W, the higher a chunk's total activation (Equation 1), especially relative to chunks not related to the goal (S_ji's = 0). This activation in turn impacts the probability and speed of a successful retrieval of goal-relevant information (Equations 2 and 3). Hence, the model predicts that an individual with a larger value of W will be able to retrieve goal-relevant information more accurately and more quickly than will an individual with a smaller value of W. Indeed, such accuracy and speed advantages not only affect the subject's final overt performance but can produce additional, indirect benefits as well. For example, when W is larger, the rehearsal of each item in a memory list will more likely succeed (i.e., strengthen the correct item) and will complete in a shorter period of time. This means that in speeded tasks requiring rehearsal, more rehearsals can be accomplished in the limited time when W is larger, producing even greater subsequent recall.

It should be emphasized that differences in W reflect differences in a particular kind of attentional activation, spreading from the filled slots in the goal, not in total activation per se. Although individual differences in the amount of source activation, W, can result in differences in total activation of the system, the important influence of W is on the ability to differentially activate goal-relevant information relative to nongoal-relevant information. Thus, the larger W, the better this ability, and the more likely goal-relevant chunks will be correctly retrieved. Moreover, this relationship between W and performance is complex (e.g., W influences not only performance effects but also various indirect learning effects such as the rehearsal effect just mentioned) and nonlinear (e.g., a small change in W in Equation 1 affects A_i which, in turn, has an exponential effect on latency in Equation 3). Nevertheless, with computational modeling techniques it is possible to estimate an individual's W from measures of performance, provided the measures meet the criteria discussed in the next section.

1.3. Challenges of this approach

There are some practical difficulties that must be addressed before applying a computational modeling approach to estimate individuals' working memory capacities. The main challenge is finding a task that emphasizes individual differences in working memory and reduces the impact of other individual differences on performance. Performance on cognitive tasks is affected by a number of factors besides working memory capacity. These include prior knowledge of relevant procedures and strategies and possession of related facts. Traditionally, working memory capacity has been measured using simple span tasks in which subjects attempt to recall ever-lengthening strings of simple stimuli (e.g., letters or digits) until recall fails. The use of compensatory strategies, however, has been shown to contaminate measures of working memory capacity derived from simple span tasks (Turner & Engle, 1989). A further concern in estimating working memory capacity is the influence of different individuals' task-specific knowledge on their performance. To cite an extreme case, Chase and Ericsson (1982) described a subject with a digit span of more than 80 digits (compared to a normal span of approximately 7 items). This feat was accomplished in part because the subject, a runner, was able after extensive practice to recode the digits into groups based on personally meaningful running times. Thus, knowledge of relevant procedures and related facts enabled Chase and Ericsson's subject to overcome normal working memory limitations. To obtain valid measures of working memory capacity, then, requires a task that can be completed in only one way and is equally unfamiliar to all the subjects.

To avoid the difficulties of traditional span tasks, Lovett et al. (1999) developed a modified digit span (MODS) task. The task is a variant of the task developed by Oakhill and her colleagues (e.g., Yuill, Oakhill & Parkin, 1989). In each trial of the MODS task, subjects are presented strings of digits to be read aloud in synchrony with a metronome beat and are required to remember the final digit from each string for later recall. Specifically, a set of boxes appears on the screen indicating the length of the digit strings for the current trial. Each digit appears one at a time on the screen, in the box corresponding to its position in the string. Thus, subjects know to store and maintain the current digit when it appears in the rightmost box. After a certain number of digit strings are thus presented, a recall prompt cues the subject to report the memory digits in the order they were presented.

This task is similar to the reading span task (Daneman & Carpenter, 1980), in which subjects read a set of sentences and maintain the sentence-final words for later recall, and the operation span task (Turner & Engle, 1989), in which subjects solve arithmetic expressions paired with words and maintain the words for later recall. For current purposes, however, the MODS task has several advantages. First, it reduces knowledge-based individual differences because the procedures required for this task are equally familiar to subjects in our sample (potentially more so than reading complex sentences or solving arithmetic expressions). Second, it carefully directs the pacing of subjects' processing so as to reduce variability among subjects in choosing their own articulation rates. And third, by virtue of the speed of its pacing, the MODS task requires virtually continual articulation, which serves to restrict subvocal rehearsal (Baddeley, 1986, 1990) or at least minimize the use of different rehearsal strategies. Finally, the inclusion of filler items increases the delay before recall, adding to the working memory demands of the task.

1.4. Lovett et al.'s model fitting

To facilitate measurement of individual subjects' sensitivity to varying working memory load, Lovett et al. (1999) manipulated the difficulty of the task in several ways. First, they varied the number of digits (3,4,5, or 6) to be recalled on each trial. They also varied the number of digits to be read per string (4 or 6) and the interdigit presentation rate (0.5 s or 0.7 s). Each subject completed 4 trials in each of the 16 possible combinations of these conditions for a total of 64 trials.

Lovett et al. (1999) developed an ACT-R model of this task and found that the model's aggregate predictions, based on the default values for W and other parameters, compared quite favorably with subjects' actual recall accuracy. It should be emphasized that the initial fit they obtained was not based on optimized parameters, yet it nicely captured the main trends in the data. This basic model did not, however, match the exact quantitative results for each condition. In addition, the standard error bars for the model's predictions were consistently smaller than the error bars for the subject data. To address these deficiencies they then incorporated individual differences into their model as discussed above.

Because the hypothesis is that W varies across individuals, they allowed W to vary randomly across the 22 simulation runs (each run represented one subject) but left all other parameters at their previous values. This addition of variability to the parameter W, intended to simulate the variability among subjects, resulted in a much better fit between predicted and actual recall performance. Specifically, when the model was adjusted to include individual differences in W, its aggregate predictions were closer to the actual data points and its error bars more closely approximated those of the subjects. It should be emphasized that this improved fit was achieved without making any changes to the basic model; rather, it was the addition of variability to one of the model's parameters that improved both the overall prediction (goodness of fit) and the variability of prediction (relative error bar size). Further, by selecting a specific value of W for each individual, Lovett et al. obtained excellent fits to the data of individual subjects who completed multiple sessions.

In the remainder of this paper, we report the results of two experiments designed to replicate and extend the work of Lovett et al. (1999). More important than these empirical results, per se, we demonstrate that our model—by varying only the amount of source activation W—can successfully account for the systematic differences among individuals in their performance of a working memory task. Furthermore, we show that the model captures these individual subjects' performance at a finer level of detail than has been achieved previously.

2. Experiment 1

The primary motivation for Experiment 1 was to test the limits of our model of the MODS task. Lovett et al. (1999) were successful in modeling subjects' overall performance, but we wished to determine whether the model could capture more of the details of individual subjects' performance, again with only a single parameter to capture individual differences. One aspect of performance that is often examined in memory tasks is accuracy of recall as a function of serial position within the memory set. Serial position functions are typically bowed, with better recall for items at the beginning of the list (the primacy effect) and for items at the end of the list (the recency effect). We hoped that accurate predictions of individual subjects' serial position curves would follow from the functioning of the model.

A secondary motivation for Experiment 1 was to further refine the Lovett et al. (1999) version of the MODS task. In their study, all the stimuli, both filler and to-be-remembered items, were digits. While this version of the MODS task addresses several concerns about traditional span tasks (e.g., variable strategy use, opportunities to rehearse), the use of all digits may have led subjects to experience interference effects from the filler items that were not captured by the model. To minimize such interference and hence maximize the similarity of the task representation by the subjects and the model, the current studies used letters for filler items and digits for to-be-remembered items.

2.1. Method

2.1.1. Subjects

The 22 subjects in Experiment 1 were recruited from the Psychology Department Subject Pool at Carnegie Mellon University. Subjects received credit for their participation that partially fulfilled a class requirement.

2.1.2. Materials and design

On each trial subjects were required to read aloud 3, 4, 5, or 6 strings consisting of letters in all positions except the last position, which contained a digit. The task was, therefore, to recall memory sets of 3, 4, 5, or 6 digits. In addition to this memory set size variable, there were 2 values of string length; strings were either short (2 or 3 letters per string) or long (4 or 5 letters per string) ¹. These variables were crossed yielding 8 separate within-subjects treatment conditions. Subjects completed 8 trials in each condition for a total of 64 experimental trials. Three practice trials preceded the experimental trials for a total of 67 trials per subject. Strings were constructed of the letters a through j and the digits 0 through 9. No letter repeated within a string and no digit repeated within a trial. A single random ordering of the stimuli and conditions was generated and used for all subjects to minimize differences among subjects induced by stimulus order.

2.1.3. Procedure

Subjects were first presented computerized task instructions that included practice at the reading task. The experimenter then reiterated those instructions and emphasized both speed and accuracy in responding. A trial began with a READY prompt displayed in the center of the computer screen. When ready, subjects pressed a key to initiate presentation of the stimuli. The strings were presented at a rate of 1 every 0.9² s and 0.91 s for the digits. Subjects were required to name each character aloud as it appeared. To help pace subjects' articulation, a click sounded after the presentation of each character and subjects were instructed to name each character aloud in time with the click. As shown in Fig. 2, all of the characters in a given string appeared in a single location on the screen with each new character replacing the one before it. Characters in the first string appeared in the leftmost position and display of the following strings each moved one position toward the right. Recall that the digit at the end of each string (position) was to be stored in the memory set. After presentation of the final string, a recall prompt appeared on the screen along with one underscore for each digit in the memory set. The underscores appeared in the same locations as their respective strings. Subjects recalled by typing in digits on the computer keyboard and were required to recall the digits in order, with no backtracking allowed. Subjects could, though, skip digits that they could not remember. Following recall, subjects were given feedback about the accuracy of their response: “perfect” if they recalled all the digits correctly, “very good” for recall of more than 3 of the digits, “good” for recall of 3, and “OK” if they recalled fewer than 3 of the digits. Following the feedback, the ready prompt for the next trial appeared.

Fig. 2.

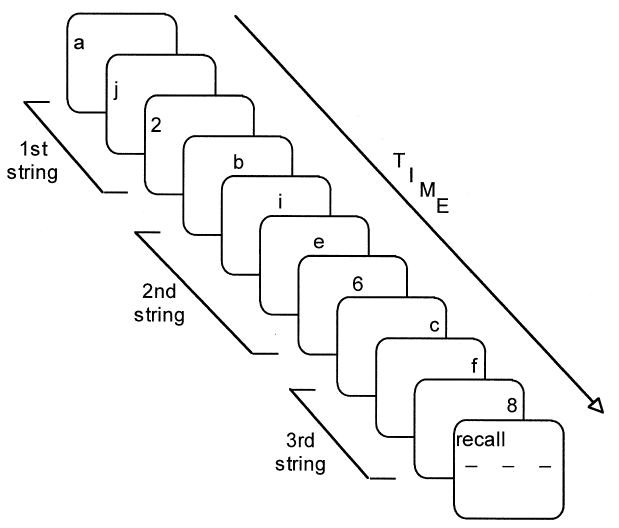
Graphic illustration of a trial with a memory set of size 3. The differences in the positions of the characters on-screen have been exaggerated for clarity; in actuality the final string would appear in the middle of the screen instead of the right side.

2.2. Results

2.2.1. Empirical results

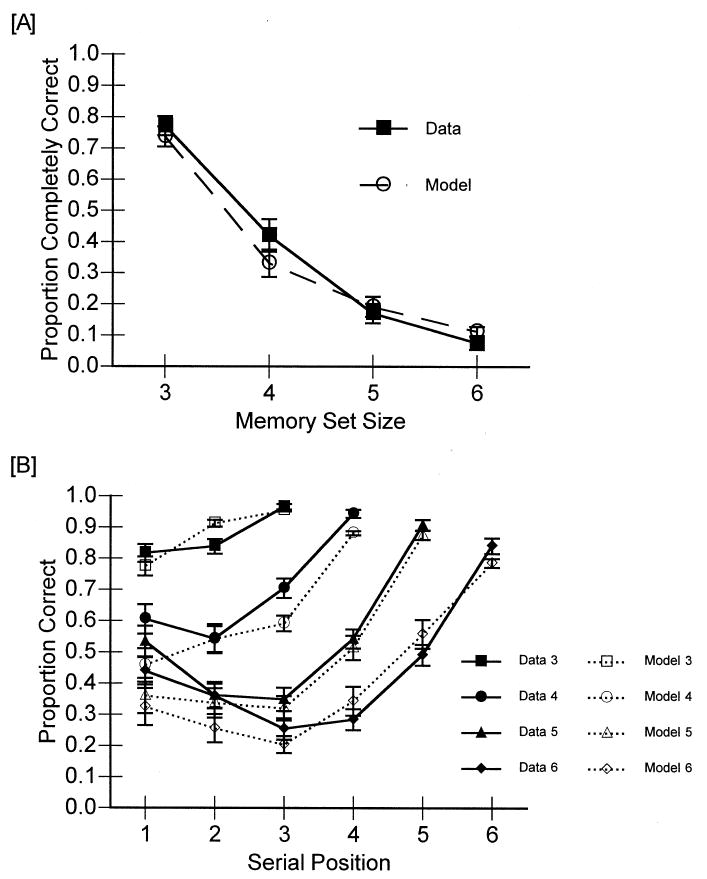
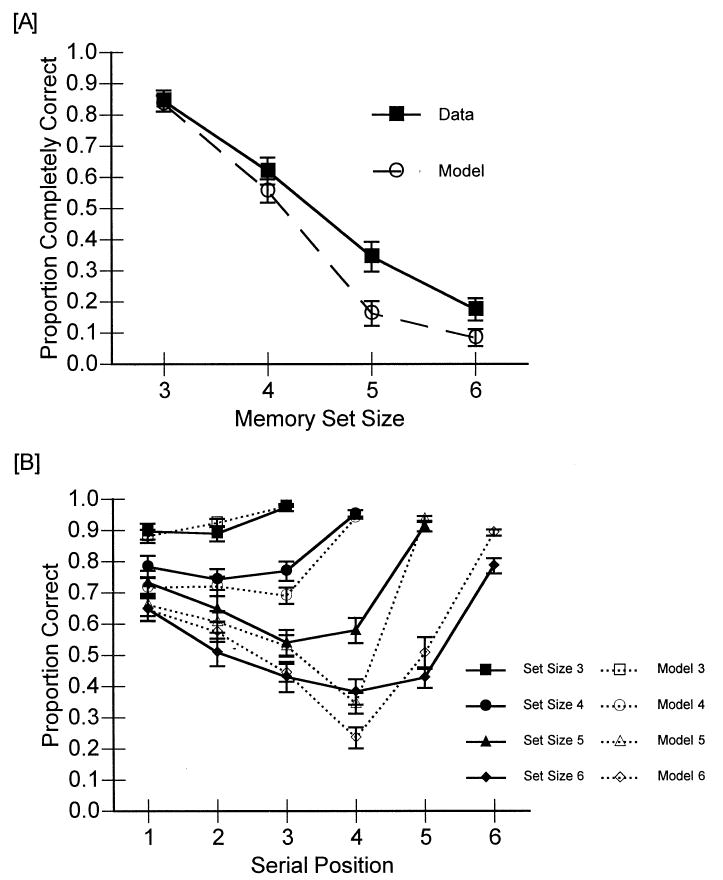
For our overall measure of subject performance, we used a strict scoring criterion: For an answer to be correct, all of the digits in the memory set had to be recalled in their correct serial position. Using proportion of memory sets completely correct as the dependent measure, subject performance as a function of memory set size is shown in panel A of Fig. 3. For all inferential tests reported in this paper, α was set at 0.05. The effect of memory set size was significant, F (3, 63) = 90.80, p = .0001, MSE = 0.0260. Subjects recalled fewer sets completely correct as the size of the memory set increased. The effect of string length was also statistically significant, F (1, 21) = 4.84, p = .0391, MSE = 0.0124. Subjects tended to recall the digits better when they read short sequences of letters than when they read longer sequences of letters. Because the effect of string length was small (0.72 for short strings and 0.69 for long strings), we elected to collapse over that factor in our modeling and presentation of figures. The interaction of memory set size and string length was not significant, F (3, 63) = 2.15, p = .1032, MSE = 0.0133. These effects are consistent with the view that we manipulated working memory load.

Fig. 3.

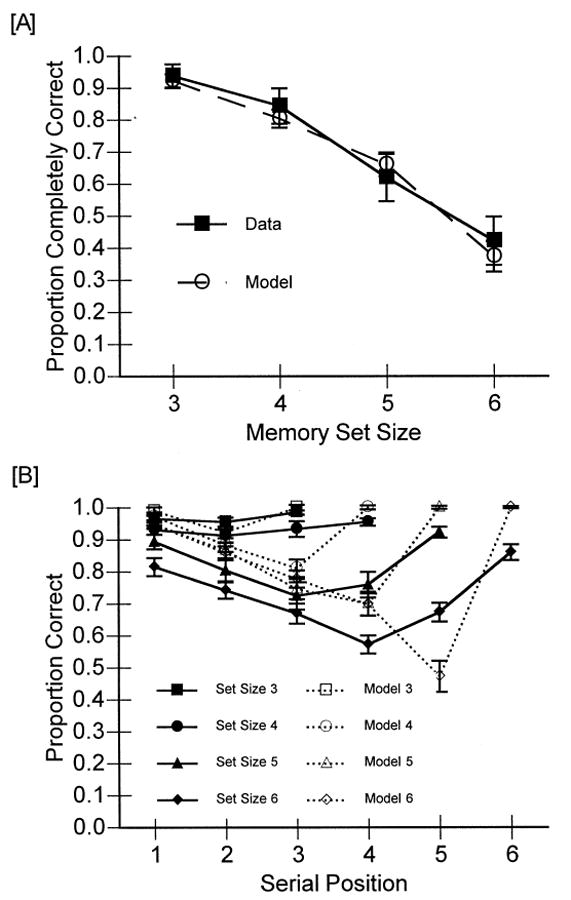
The model's fit to the overall accuracy data from Experiment 1 is shown in panel A. We collapsed over the string length variable for these fits. Panel B shows the model's fits to the serial position data.

We also examined subjects' performance by memory set size and serial position within the memory set. These data are shown in panel B of Fig. 3. There are several interesting points about these data. First, performance on the smaller set sizes is near ceiling. Further, the serial position curves for the larger set sizes, where performance is not on the ceiling, show a pronounced primacy effect. This finding can be taken as evidence that subjects were rehearsing; typically a lack of rehearsal eliminates the primacy effect (e.g., Glanzer & Cunitz, 1966, Glenberg et al., 1980). Finally, the serial position functions for the larger set sizes also show the expected recency effect.

2.2.2. Model fits

Our model of the MODS task is a slight variation of the one developed by Lovett et al. (1999)³. The critical productions are shown in Table 1. Corresponding to the two parts of the MODS task, there are two goals in this model: a goal to articulate each character as it appears and a goal to recall the digits from the current trial. The articulate goal contains slots to hold the character currently in vision, an index to the current trial, the position of an item within the list, and a status flag. The recall goal has slots indexing the current trial, the list position to recall, and the identity of the character to recall. We now show the sequence of production firings that occur as a single character, the final to-be-remembered digit of a list, is presented. As we will show below, the items in each slot of the current goal are the sources of source activation that flows to related chunks in memory.

Table 1.

Productions for the modified digit span task model

READ-ALOUD

IF the goal is to articulate

and a character is in vision

and the character has not been articulated

THEN say the name of the character

and note that it has been articulated

CREATE-MEMORY

IF the goal is to articulate

and the current character is a digit (i.e., the last character of the string)

and it has already been articulated

THEN create a memory of that character in the current position of the current trial

and increment to the next position

and set a flag to rehearse the first position

REHEARSE-MEMORY

IF the goal is to articulate

and the current character in vision has been articulated

and the rehearsal flag is set to rehearse the memory item in a certain position

and there is a memory of an item in that position

THEN rehearse the item

and increment the rehearsal flag to the next position

PARSE-SCREEN

IF the goal is to articulate on the current trial

and there are recall instructions on the screen

THEN change the goal to recall the first position of the current trial

RECALL-SPAN

IF the goal is to recall a position on the current trial

and there is a memory of an item in that position on this trial

and the item has not been recalled already

THEN recall the item

and increment the recall position to the next position

NO-RECALL

IF the goal is to recall

and there's no memory of an item in the current position

THEN recall blank

and increment the recall position to the next position

At the beginning of a trial, the goal is set to articulate. The trial slot is filled with the current trial number and the vision slot with the character to be presented. At this point, these two components of the goal each possess half the total amount of source activation (or W). Source activation will spread from each of these items to any related chunks in declarative memory. The amount of source activation spread to each related chunk is governed by the strength of association between the two chunks (the s_ji's in Equation 1). The read-aloud production fires to read the character in vision. Because this production requires only a single retrieval (the chunk for the number to be read) and source activation is only shared among two goal slots, articulation occurs quickly and seldom, if ever, fails regardless of the value of W. The production then sets the status flag to indicate that articulation has been completed.

Because this character is a digit (as opposed to a letter, which would not need to be stored), the create-memory production fires next to create a memory chunk representing that digit in the appropriate position within the current trial (see Fig. 1). At this point in the sequence 4 goal slots are filled: the trial number, the character in vision, the position of the item in the list, and the status flag. Source activation is divided evenly among these 4 slots and spreads to chunks related to those items. The last action of this production is to alter the status flag to indicate that rehearsal can now occur.

If sufficient time remains before the next character appears, then the rehearse-memory production fires in order to begin rehearsing the list (note that this only occurs at the end of a string). It attempts to rehearse each stored memory chunk individually, starting from the first position. The effects of W here are important. Three goal slots are filled, including the trial and position slots. Two retrievals are required: the position chunk and the memory chunk for the item in the current position on the current list. Source activation spreads from the trial and position slots in the goal to any memory chunks that have the same values in their trial and position slots. Because the correct chunk matches on both of those values, it receives a larger activation boost than other chunks, making it more likely to be retrieved. Moreover, this boost relative to the rest of declarative memory is larger the larger W. The governing factors for the success of the rehearsal process are the activations of the memory chunks and the time remaining after the digit has been articulated and stored. If the total activation of the correct item does not reach threshold (which could occur if the base-level activation has decayed significantly or if W is spread to many items) or if the time available for rehearsal is exceeded, rehearsal will fail.

Because this item is the last digit of the last string, after rehearsal the focus of attention is shifted to recall. The trial slot is filled with the current trial number; the other two slots are nil. Under these conditions, the parse-screen production fires to simulate subjects encoding this change in task and sets the position slot to first.

The recall goal now has two slots filled: the trial and position slots. Each receives half of the source activation and spreads it to related chunks (e.g., any memory chunk with the correct value in either its trial or position slot). This production requires retrieval of a chunk on the current trial in the correct position. If this retrieval is successful, the item slot is filled with the identity of the to-be-recall digit and the read-item production “types” the recalled item. Otherwise the no-recall production fires and “recalls” a blank. The model then attempts to recall the next position in the list.

We fit this model to the aggregate data shown in Fig. 3. Thus, there were 22 data points to be fit; 4 for the accuracy data shown in panel A and 18 serial position points (i.e., 3 for memory set size 3, 4 for memory set size 4, etc.) from panel B. For our model fitting, most of ACT-R's global parameters were left at their default values (see Anderson & Lebiere, 1998). Activation noise (the s in Equation 2), which has no default value in ACT-R, was set at the arbitrary value of 0.04. The action time for the parse-screen production was set at 1.57 s.⁴ Both the retrieval threshold (τ in Equation 2) and the mismatch penalty (described below) were estimated to optimize the fit to the data. The values of these parameters were 0.93 and 3.08, respectively.

The mismatch penalty parameter is part of ACT-R's partial matching mechanism. This mechanism allows the retrieval of a chunk that only partially matches the current production pattern, thus producing errors of commission. The higher the mismatch penalty, the less likely a partially matching chunk will be retrieved instead of the target chunk. Specifically, each chunk i that partially matches the current retrieval specifications, or production pattern, p competes for retrieval not based on its total activation A_i but rather based on an adjusted activation value called the match score M_ip. That is, when the partial matching mechanism is enabled, M_ip substitutes for A_i in Equations 2 and 3, influencing probability and latency of retrieving chunks that do not exactly match the target chunk pattern. M_ip is computed as:

$$M_{ip}=A_i-MP\left(1-si{m}_{ip}\right)$$ (4)

where A_i is the activation of chunk i, MP is the mismatch penalty parameter (which we estimate), and sim_ip is the similarity between the chunk i to be retrieved and the production pattern p. Thus, Equation 4 implies that the more similar a given chunk is to the target chunk (with similarity of 1 signaling an exact match), the higher its match score and hence, all else being equal, the more likely it is to be retrieved. This bias toward retrieving closely matching chunks is especially strong when the mismatch penalty is large, because MP accentuates any lack of similarity to the target chunk. However, if a partially matching chunk happens to have a high level of total activation A_i or if noise in the system makes it appear so, it is possible for that chunk to be retrieved in place of one that matches exactly.

Given the positional representation of memory chunks in the current model, we define these chunks as more or less similar based on their relative positions. Chunks for adjacent positions (e.g., first and second) are more similar than chunks for distant positions (e.g., first and fifth) with the degree of similarity, sim_ip, falling off exponentially as positions are more remote from one another. This similarity metric was adopted from prior work within the ACT-R framework (see Anderson & Lebiere, 1998).

Panel A of Fig. 3 shows the model's fit to the strict accuracy measure. The model's predictions are averaged over 30 simulation runs. Each run had a different value of W randomly drawn from a normal distribution with mean 1.0 and variance 0.0625. Thus we have incorporated variation in this fit of the model, but that variation is not tailored to the individual differences among subjects. The serial position data and the model's fit to those data are shown in panel B of Fig. 3. These fits are certainly acceptable given that the model was not specifically designed to produce them. Examination of panel B of Fig. 3 shows that the model tends to overpredict the magnitude of the primacy effect. This may be due, in part, to the parameters of the model attempting to compensate for the subjects' use of rehearsal strategies that the model did not have. We will come back to this issue of rehearsal in the Discussion section.

The real question, though, is whether we can model data from individual subjects using W as the only free parameter. Overall accuracy for four typical subjects is shown as a function of memory set size, along with the corresponding model fits, in Fig. 4. To obtain these fits, we held all of the model's parameters constant at the values described above except for W, which we varied to capture each individual subject's data. There were, therefore, 24 parameters (2 global parameters and 22 individual W's) used to fit 88 data points (4 data points for each of the 22 subjects). As expected, the fits are quite good and strongly support our claim that variations in W can model variations in subjects' performance of a working memory task. Across all the subjects, the best fitting line was observed = 0.97·predicted + 0.04, R² = 0.88. This value indicates a good fit, but there is still a certain amount of variance not predicted by the model. As a comparison, leaving W at the ACT-R default of 1.0 for each subject decreased the quality of the fit; the best-fitting line in this case was observed = 0.93·predicted + 0.06, R² = 0.57.

Fig. 4.

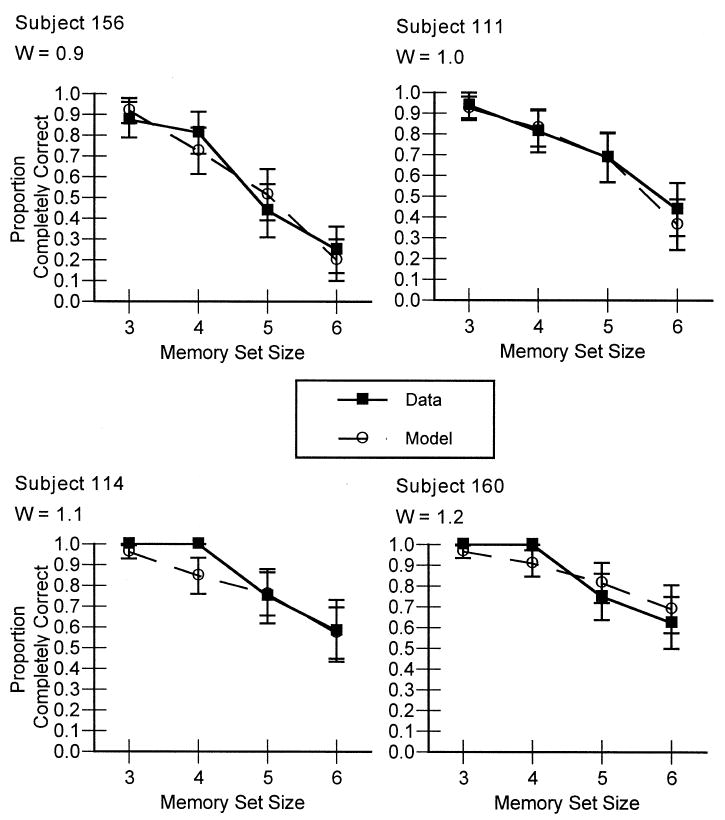
Proportion of strings correctly recalled as a function of memory set size for four representative subjects in Experiment 1. Also shown are the model's predictions for each subject, varying only the W parameter.

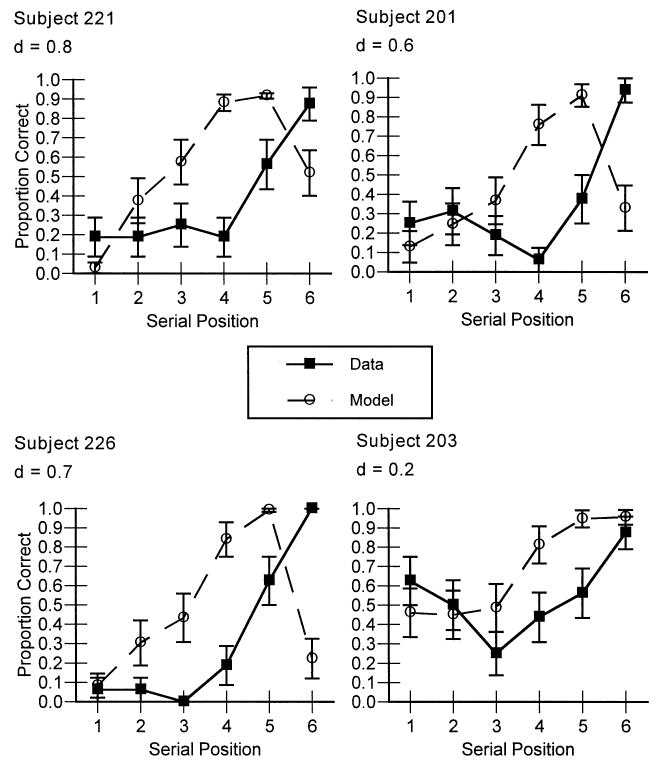
We were also interested in the model's ability to predict individual subjects' serial position curves. Serial position data for the same four subjects are shown in Fig. 5. For simplicity, only data for the largest memory set size is shown. This analysis used no new parameters; these fits used the W's estimated in the prior analysis. The best fitting line across all subjects' serial position curves (22 subjects with 18 positions for each or 396 data points) is observed = 0.68 predicted + 0.25, R² = 0.51. These fits are good, but not as good as we initially expected. This is a point taken up in the Discussion section. As in the case of overall accuracy for each set size, assuming a W of 1.0 for each subject reduced the quality of the fit. The best-fitting line with the default W for each subject was observed = 0.64·predicted + 0.28, R² = 0.30.

Fig. 5.

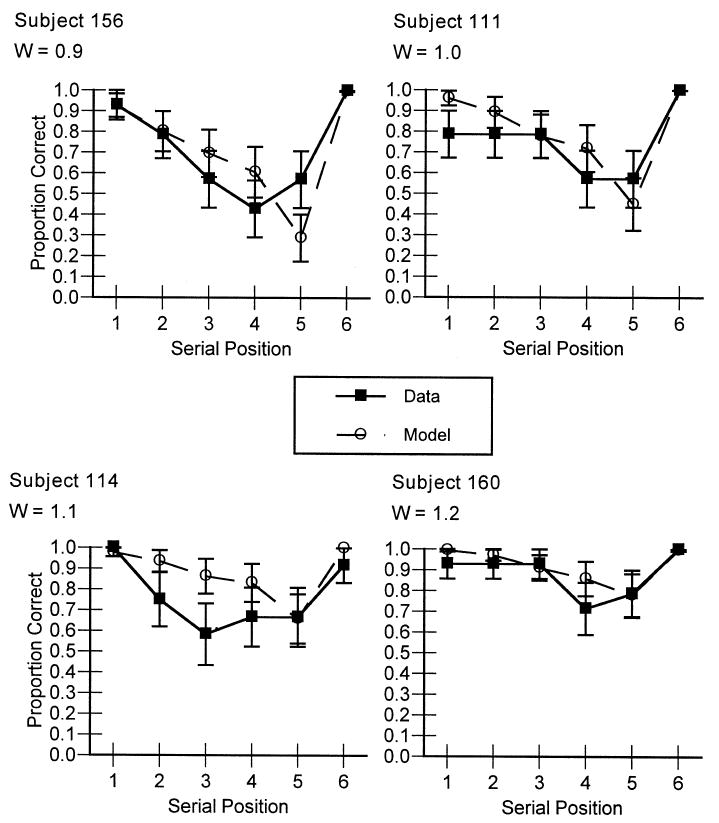
Proportion correct as a function of serial position and the corresponding model predictions for the largest memory set size only for four representative subjects in Experiment 1, varying only the W parameter.

2.3. Discussion

We had several goals in Experiment 1. We wanted to test our conceptualization of working memory capacity in a refined version of the MODS task. In particular we asked: Would varying source activation in our model enable it to match not only the aggregate results but the performance of individual subjects as well? We also wanted to extend earlier work within this framework by modeling performance at a more detailed level than had been done previously (i.e., fitting serial position curve data).

We found that our model was able to capture the aggregate performance data from the MODS task quite well. With its limitation to source activation, the model—like subjects—showed worse performance as memory load increased. Further, the model was able to capture the primacy and recency effects observed in the aggregate serial position curves, although not perfectly. More important than these aggregate fits, however, we found that varying a single parameter W allowed the model to capture individual differences in subjects' performance of the MODS task. It should be noted that the model's fit to individual subject's accuracy data were quite good in that it captured subjects' different shapes of the performance curve as a function of memory set size. Thus our model captures one of the principle findings in the working memory literature: people are differentially sensitive to increases in memory load.

The model's fit to the individual subjects' serial position functions, however, was not quite as good as we had anticipated. As we stated earlier, fitting a model to individual subject data at this level of detail (i.e., 18 data points per subject) requires a strong alignment between the model's processing and each subject's. Thus, finding subpar fits for the individuals' serial position curves led us to re-evaluate how well we had achieved this alignment. One of the empirical results from this experiment is relevant: A quite pronounced primacy effect in the serial position curves (especially for large memory sets) indicated that subjects were able to do substantial rehearsing. Moreover, by referring to subjects' postexperimental reports, we found that many subjects in this experiment used quite sophisticated rehearsal strategies (e.g., relating pairs of digits to friends' ages, relating digit triplets to area codes or local phone exchanges, etc.). The prevalence of these sophisticated strategies did not match our expectations and, more importantly, it does not match the model's processing. While our model included rehearsal, it only used a simple “run-through” of the individual memory elements at the end of each string; it was not endowed with a capability for storing digits in terms of familiar groups or generating elaborations. Thus, with subjects developing sophisticated rehearsal strategies relative to the model's, it is not surprising that there was some discrepancy between the subjects' performance and the model's predictions—different types of processing were being used. But, why did this difference arise? Our goal had been to minimize subjects' ability to involve prior knowledge.

After checking the experimental protocol and equipment, we determined that subjects' ability to develop and use such elaborate strategies was most likely due to the fact that the computers used in the current experiment produced an unintendedly long interitem delay. Specifically, we found that the computers were slow in loading and playing the sound file used to pace subjects' articulation. As a result, our nominal 0.5 s interstimulus interval was inadvertently lengthened to 0.9 s. Thus, subjects had sufficient time to execute their rehearsal strategies and probably benefited greatly from it. In contrast, the model was constrained to use this same (long) interstimulus interval to execute a much simpler (and probably less effective) rehearsal strategy. When we fit the model to the data, however, the global parameters MP and τ were allowed to vary to get our model's aggregate predictions close to the subjects' data. It is quite possible that these parameters' values helped the model compensate for its simpler rehearsal strategy so it would predict performance at a level commensurate with subjects'. It also helps explain why the model tended to overpredict the magnitude of the primacy effect in subjects' serial position curves.

This is not to say, however, that modeling sophisticated rehearsal strategies is impossible in the current framework (cf. Anderson & Matessa, 1997). Rather, given that our focus is on individual differences in working memory capacity, rather than in strategies, we took a different tack: simply correct the timing issue and verify that when subjects are only able to use a simple rehearsal strategy (consistent with the model's), the fits to the serial position data will be better. This was one of the main goals for Experiment 2.

3. Experiment 2

Experiment 2 was designed to control the ability of subjects to engage in idiosyncratic rehearsal strategies by holding the presentation rate at the desired value of 1 character every 0.5 s. This should reduce the use of rehearsal and thereby improve the predictive power of our model, which assumes only a simplified rehearsal routine.

3.1. Method

3.1.1. Subjects

For Experiment 2 we recruited 29 subjects from the Psychology Department Subject Pool at Carnegie Mellon University. Because we expected, based on prior work (Reder & Schunn, 1999; Schunn & Reder, 1998) that W would be correlated with scores on the CAM inductive reasoning subtest (Kyllonen, 1993, 1994, 1995) and because we wanted a wide range of W values, we recruited individuals based on their CAM scores. Specifically, we tried to recruit individuals with both high and low scores ⁵. All subjects received a large candy bar and credit for their participation that partially fulfilled a class requirement.

3.1.2. Procedure

The MODS task used in Experiment 2 was an exact replication of the Experiment 1 design, except that the interstimulus interval was corrected to 0.5 s.

3.2. Results and discussion

3.2.1. Empirical results

As in Experiment 1, we used a strict scoring criterion for our overall measure of subject performance. All of the digits in the memory set had to be recalled in their correct serial position for an answer to be correct. Using proportion of memory sets completely correct as the dependent measure, subject performance as a function of memory set size (collapsed across string length) is shown in panel A of Fig. 6. The main effect of memory set size was significant, F (3, 72) = 189.89, p = .0001, MSE = 0.0261. Subjects recalled fewer sets completely correct as the size of the memory set increased. The effect of string length, however, was not statistically significant, F (1, 24) = 1.07, p = .3114, MSE = 0.0164. We take this finding as further justification for averaging over this factor in our modeling efforts, as we did in Experiment 1. As in Experiment 1, the interaction of memory set size and string length was not significant, F (3, 72) = 1.74, p = .1661, MSE = 0.0149. In general, the recall levels in Experiment 2 are lower than those in Experiment 1, suggesting that we were successful in reducing subjects' use of rehearsal.

Fig. 6.

Panel A shows the model's fit to the overall accuracy data from Experiment 2. We collapsed over the string length variable for these fits. Panel B shows the model's fits to the serial position data.

The serial position curves for Experiment 2 are shown in panel B of Fig. 6. Several differences between these curves and those shown in Fig. 2 are readily apparent. First, performance on the smaller set sizes is pulled away from the ceiling, reflecting the fact that subjects in Experiment 2 were unable to rehearse as effectively as in Experiment 1. Second, the primacy effects in Experiment 2 are much smaller than those in Experiment 1. This further supports the notion that subjects' rehearsal was reduced in Experiment 2. Moreover, subjects in Experiment 2 reported being unable to engage in anything other than simple rehearsal, a strategy just like the model's. Together, these findings suggest that we were successful in eliminating or reducing the use of rehearsal in Experiment 2.

3.2.2. Model fits

The data from Experiment 2 were fit using the same model used in Experiment 1. As before, most of ACT-R's global parameters were left at their default values. Activation noise was maintained at the arbitrary value of 0.04 used in our modeling from Experiment 1. Three parameters were estimated to optimize the fit to the data. The retrieval threshold and the mismatch penalty were estimated to be 0.19 and 1.87, respectively. The action time for the parse-screen production was estimated at 1.57 s, and this value was also used in Experiment 1.

Panel A of Fig. 6 shows the model's fit to the data, collapsed across the string length variable. The model's fit to the serial position data are shown in panel B of Fig. 6. These fits are somewhat better than the corresponding fits in Experiment 1, most likely due to the greater control over rehearsal in Experiment 2. As before, though, our main interest is in the individual subject fits.

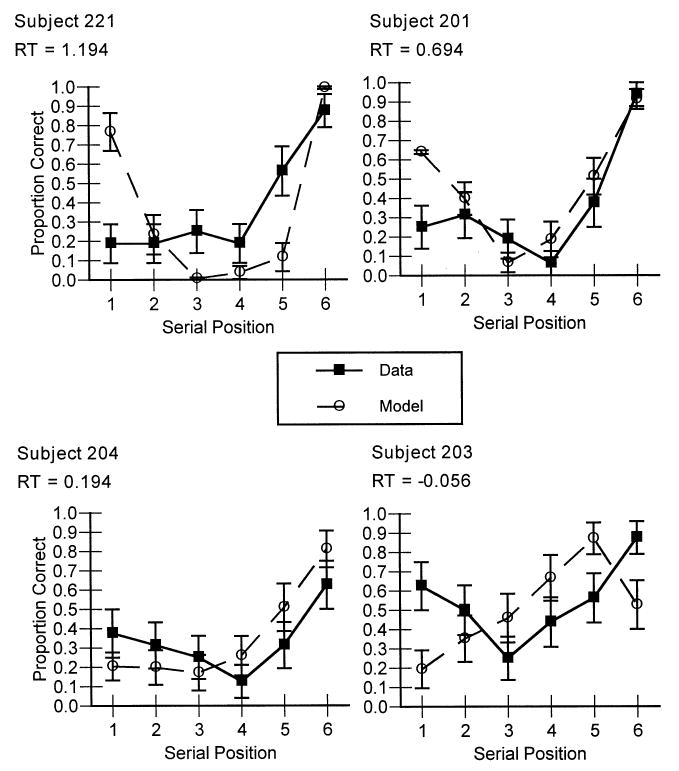
Accuracy as a function of memory set size for 4 representative subjects is shown in Fig. 7. Also shown are the model's predictions for those subjects. These predictions were obtained using 32 parameters (3 global parameters and 29 individual W's) to fit 116 data points (4 data points for each of the 29 subjects). The best-fitting line over all subjects is observed = 1.12·predicted + -0.07, R² = 0.92. As with the aggregate data, greater control over strategy use has improved the fits somewhat; the corresponding R² from Experiment 1 was 0.88. In comparison, if W is set to 1.0 for every subject the best-fitting line is observed = 1.10·predicted + -0.02, R² = 0.66. The improvement in R² is even more dramatic in the fits to individual subjects' serial position functions. Examples of the fits to the largest set size data for the same 4 subjects as in Fig. 7 are shown in Fig. 8. These fits required no new parameters; we simply used the W's estimated in the prior analysis. Over all subjects and all set sizes the best-fitting line is observed = 0.87·predicted + 0.08, R² = 0.72. In Experiment 1, the corresponding R² was only 0.51. It appears, then, that we were successful in controlling the use of strategies by our subjects and that this greater control has improved the predictive power of our model. Again, assuming a W of 1.0 for every subject reduces the quality of the fits compared to adopting individual W's; the best-fitting line is observed = 0.92·predicted + 0.09, R² = 0.57.

Fig. 7.

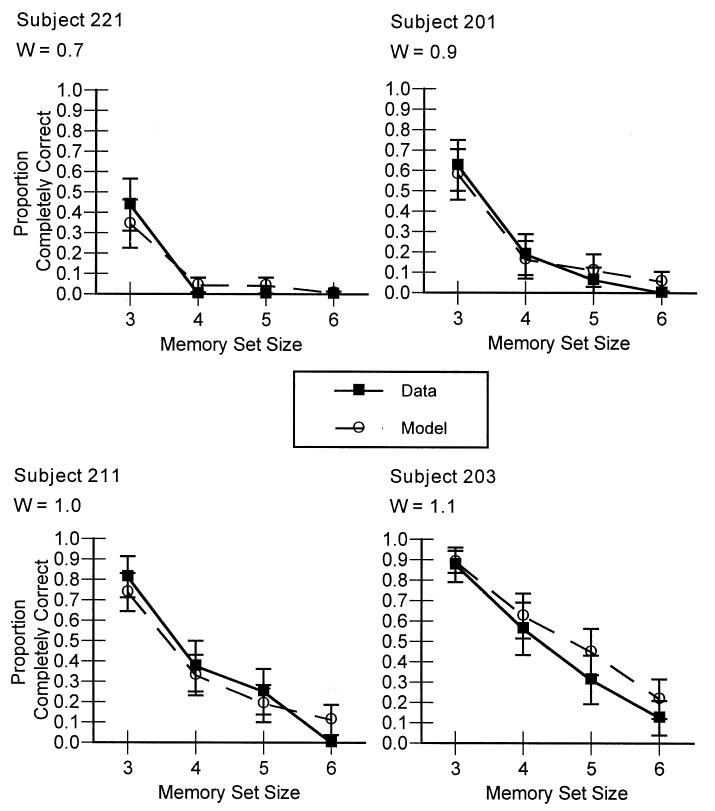
Proportion of strings correctly recalled as a function of memory set size and the model's predictions for four representative subjects in Experiment 2, varying only the W parameter.

Fig. 8.

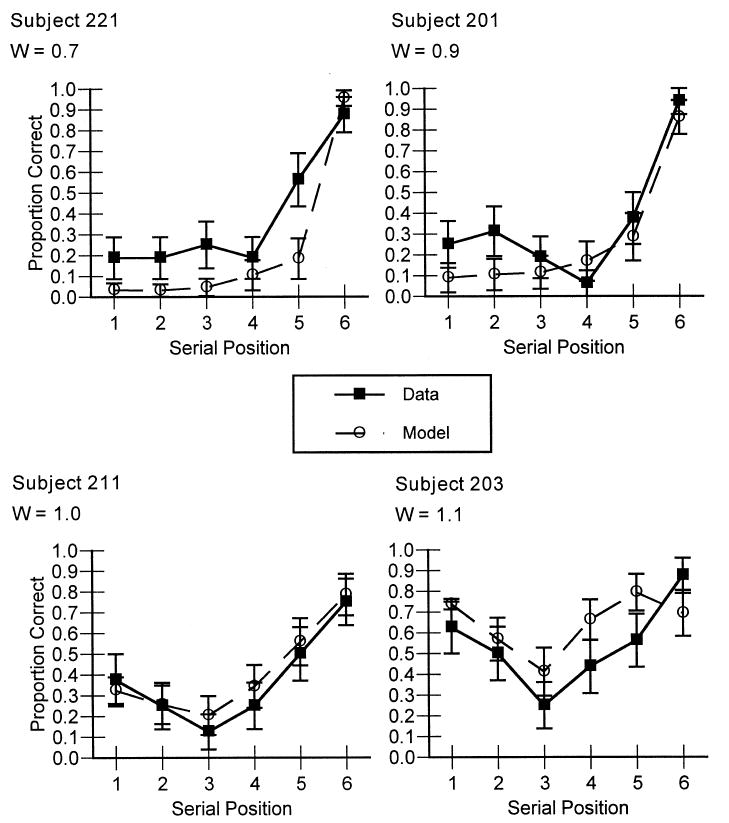
Proportion correct as a function of serial position and the corresponding model predictions for the largest memory set size only for four representative subjects in Experiment 2, again varying only the W parameter.

3.3. Alternative accounts of working memory

While we have presented evidence that supports our conceptualization of working memory as source activation, there are other accounts of working memory that could be devised within the ACT-R framework. That is, there are other continuously valued parameters in ACT-R that modulate performance and that, conceivably, could capture individual differences in working memory capacity. In this subsection we explore two plausible candidates.

One possibility is that subjects differ, not in their amount of source activation, but in the rate at which the activation of individual chunks decays. This view is consistent with Baddeley's (Baddeley, 1986) working memory model in which the capacity of the articulatory loop is limited by the rate of decay. Because the probability and latency of retrieval are dependent on activation (Equations 2 and 3), if two individuals differ in how quickly activation decays, they will also differ in the speed and accuracy of their retrieval after similar retention intervals (as in the MODS task). Items with fast-decaying activations can be maintained via rehearsal, but if an individual's decay rate is fast enough, it is possible that activation levels will decay below threshold before the opportunity to rehearse occurs. When this is the case, performance will be seriously degraded.

In ACT-R, the decay rate affects activation through a chunk's base-level activation. Recall from Equation 1 that base-level activation is added to source activation to determine a chunk's total activation. The base-level activation of chunk i, the B_i in Equation 1, is given here in more detail by:

$$B_i=\text{ln}\left(\sum _{j=1}^n{t}_j^{-d}\right)+\beta$$ (5)

where β is the chunk's initial base-level activation. In most ACT-R simulations, including ours, β is set to 0. The t_j's measure the time lag between the present and each of the n past encounters with the chunk. Thus, base-level activation depends on the sum of these individually decaying activation bursts, with each burst occurring with a single access of the chunk. The parameter d is the decay rate. It is usually set at 0.5 in ACT-R simulations, but it is conceivable that individuals could differ in their decay rates. That is the hypothesis we wish to test as an alternative to our source activation hypothesis.

To test whether differences in decay rate could predict individual subjects' performance on the MODS task, we adopted a method analogous to that by which we tested W. We held all global parameters except d constant at the optimal values obtained by fitting the aggregate data and allowed d to vary around the default value of 0.5. We then estimated the best-fitting value of d for each subject. Across all subjects and all memory set sizes, the best-fitting line for the proportion of strings correctly recalled was observed = 1.23·predicted + -0.07, R² = 0.85. The R² value for our W-varying model was 0.92. Though the difference in R² is in favor of the W-varying model, the difference is small and not very compelling. However, Fig. 9, which presents serial position data from the largest set size for 4 subjects⁶, shows that the d-varying model cannot capture the individual subjects' serial position functions well. The best-fitting line is observed = 0.56·predicted + 0.23, R² = 0.23. The corresponding value for our W-varying model is 0.72. The difference in the fits is largely due to the fact that the serial position curves with d varying tend to be the wrong shape. For values of d below the default value of 0.5, recall performance is near ceiling: The activations of chunks simply do not drop below threshold. As d increases from the default, the model predicts worse recall for the items at the beginning and end of the list. The first items are poorly recalled because they must endure the longest retention interval (i.e., they are stored first and must be maintained while the remaining strings are presented). With this long time lag until recall, a high decay rate causes the first items' activations to drop below threshold, and the model fails to retrieve these items. The final list item, however, has the shortest retention interval and hence a very high level of activation at recall. If all retrievals identified the exact chunk being sought (i.e., the fifth memory item for the fifth recall position), this would imply a large recency effect. However, the model's partial matching mechanism allows it to incorrectly retrieve a memory item from the wrong position in the list when the item's adjusted activation is high enough (see Equation 4). Because this is true for the final item, it tends to be erroneously recalled in place of earlier items. Once the final item is recalled for an earlier position in the list, it is “ineligible” for recall again in its proper position making correct recall of the final digit extremely low. Because this pattern of retrieval across positions does not match the data, we conclude that individual differences in decay rate do not account for differences in performance on the MODS task.

Fig. 9.

Comparison of behavioral data to a model of performance that varies decay rate rather than source activation, W. These are the model predictions for the largest memory set size only for four representative subjects in Experiment 2.

Another plausible account of performance differences is that different subjects could adopt different retrieval thresholds. A conservative subject with a high threshold would display lower overall accuracy than would a subject with a more lenient, lower retrieval threshold. To test this account within the ACT-R framework, we again varied only the parameter of interest, the retrieval threshold, around the value of 0.19, which was obtained from fitting the model to the aggregate data. All other parameters were fixed at the optimal values. For the proportion of strings correctly recalled as a function of memory set size, the best-fitting line is observed = 1.13·predicted + -0.0002, R² = 0.90. This value is only slightly less than the R² of 0.92 for W, and the difference is again not very convincing. For a more discriminating test of the model's ability to fit individual subjects by varying its retrieval threshold, we look to the serial position data. Fig. 10 presents the serial position data for 4 representative subjects. The best-fitting line for these data are observed = 0.64·predicted + 0.21, R² = 0.35. The corresponding R² for the W-varying model is 0.72, indicating that the W-varying model captures much more of the variability in the data. As was the case when the decay rate was varied, changing the retrieval threshold results in behavior that does not match the pattern of subjects' behavior. Lowering the threshold allows for more retrievals, but many of these are retrievals of incorrect chunks, resulting in a serial position curve that is low on the ends and high in the middle. In contrast, raising the threshold results in recall of only highly activated items. These tend to be the first and last items, the first because its activation likely received a boost from rehearsal and the last because its activation has not yet decayed. It seems reasonable, therefore, to conclude that, among the alternatives considered, conceiving of working memory capacity as the amount of source activation (the W parameter) provides the best account of the data.

Fig. 10.

Comparison of behavioral data to a model of performance that varies retrieval threshold rather than source activation, W. These are the model predictions for the largest memory set size only for four representative subjects in Experiment 2.

4. General discussion

We have presented a view of working memory capacity in terms of a limitation to source activation, a specific kind of activation used to maintain goal-relevant information in an available state. This limit to source activation produces the observed degradation in performance as the working memory demands of a task increase. More importantly, we have proposed that, holding prior knowledge and strategic approaches relatively constant, differences among individuals in the performance of working memory tasks can be largely attributed to differences in their amount of source activation. Based on this theory, we presented a computational model of individual differences in working memory. The model's basic structure is built within the ACT-R cognitive architecture (Anderson & Lebiere, 1998). However, we used and tested the model according to a new, individual differences approach: Besides testing the model's fit to aggregate working memory effects, we focused on whether the model's performance could be parametrically modulated to capture the different patterns of working memory effects exhibited by different individual subjects. In two experiments, we demonstrated that, by varying only the source activation parameter W, the model was able to account for individual differences in performance of a working memory task. In particular, different values of W enabled the model to successfully capture individual subjects' serial position curves, a feat that it was not specifically designed to accomplish. Based on these results, we find the model sufficient to account for (a) aggregate performance effects taken from our sample as a whole, (b) the range of performance differences found across our sample, and (c) individual patterns of performance exhibited by the different subjects in our sample.

In the subsections below, we discuss several modeling issues raised by this work and set our individual differences approach in the context of related approaches in the field.

4.1. Parameter estimates and model fidelity

We feel that the data and model fits we have presented above support our conceptualization of working memory, but some readers may be concerned by the fact that the parameter estimates in Experiments 1 and 2 were different. Note that we are not referring to the source activation parameter W here but rather to the two global parameters (retrieval threshold and mismatch penalty) we used to fit the model to the aggregate data in both experiments. We believe the difference in these parameter estimates between Experiments 1 and 2 is well explained by the (unintentional) difference in the interitem intervals in the two experiments, namely, 0.9 s in Experiment 1 and 0.5 s in Experiment 2. With much longer interitem intervals in Experiment 1, subjects were able to devise and deploy various sophisticated rehearsal strategies. In contrast, in Experiment 2, the shorter interitem intervals constrained subjects to the simplest rehearsal strategy (i.e., repetition at the end of each string) and did not even allow much time for its application. Given that subjects were engaging different rehearsal strategies across the two experiments, it makes sense that the activation levels of memory chunks would be different and thus require different values for the parameters retrieval threshold and mismatch penalty. For example, memory chunks could be rehearsed more and better in Experiment 1 than in Experiment 2, producing higher activation levels in the former. Higher levels of activation would, in turn, lead Experiment 1 subjects to adopt a more conservative retrieval threshold to avoid retrieving incorrect but highly active items. Further, with greater opportunities to rehearse, subjects might be less willing to accept an item that only partially matched the target. Thus, higher values for retrieval threshold and mismatch penalty would be expected in Experiment 1, and this is what our model fitting produced.

Although these differences in parameter values can be explained, there is a sense in which the values from Experiment 2 are more meaningful. This is analogous to the “interpretability” of parameters in statistical modeling. Take, for example, a set of data being fit to a regression line. The tighter the linear trend in the data, the better the estimated slope parameter describes those data, that is, the more meaningfully that parameter value can be interpreted as a slope. Similarly, in our computational modeling, we found that our model fit the data of Experiment 2 better than it fit the data of Experiment 1. Thus, we can take the parameter values estimated in Experiment 2 as more meaningful. However, in the computational modeling case, we can use more than the relative R² (a quantitative measure) to support this preference. We have qualitative evidence that the model's rehearsal strategy mirrored that of Experiment 2 subjects better than Experiment 1 subjects. This evidence includes subjects' postexperimental reports and certain telltale features of their performance (e.g., the size of the primacy effect). Thus, we have multiple types of evidence supporting somewhat greater fidelity between the model's processing and the processing of subjects in Experiment 2.

The issue of model fidelity is important when using computational models to study individual differences: The greater the overlap in the model's processing and subjects' processing, the more easily parameters—even individual difference parameters—can be interpreted. We strove to achieve high fidelity between subjects' cognitive processing and the model's processing in both experiments by (a) refining the experimental paradigm to reduce the influence of prior knowledge and strategy differences among subjects and (b) explicitly developing our model to perform all aspects of the task just as subjects would. Other individual difference approaches do not always emphasize these points. For example, some working memory tests do not constrain the timing and randomization of trials, and some computational models do not aim to include the same set of cognitive processes engaged by subjects. The experiments reported in this paper illustrate the importance of these issues: A mere 0.4 s difference in the timing of Experiment 1 versus Experiment 2 produced qualitative differences in subjects' rehearsal strategies. In paradigms where timing is not constrained, there is the danger that different subjects could pace themselves at very different rates in order to execute specific strategies for task performance. To the degree that this is the case in other studies, individual differences in performance should be attributed more to strategic differences between subjects and less to cognitive processing differences such as working memory capacity. By attending to these issues of model fidelity, especially in Experiment 2, we have been able to show that our individual difference parameter not only explains the variability among subjects in our main task but also relates meaningfully to other measures of working memory.

Before leaving the issue of model fidelity, we wish to address several concerns. One reviewer of this paper questioned whether ours was the only possible ACT-R model of the MODS task and wondered whether our results were due to the specific set of productions we used. There are undoubtedly many sets of productions that could be written within the ACT-R architecture to perform the MODS task. It is possible that some of those models would not depend in any critical way on W. What, then, leads us to conclude that ours is the a reasonable model? First, as noted above, we carefully matched our productions to the verbal protocols of our subjects. Second, our model and the role it confers on W would receive a great deal of support if estimates of W obtained from this model predicted the performance of individual subjects on a second working memory task. Lovett, Daily, and Reder (in press) provide such a demonstration. They had subjects perform both the MODS task and a separate working memory task called the n-back task. They found that individual W's, estimated from the MODS model presented here and simply plugged into the n-back model, accurately predicted individual performance of the n-back task. Both of these points, we argue, suggest that our model of the MODS task is, in some sense, the correct one within the ACT-R framework.

4.2. Refitting the Lovett et al. data

In the Introduction we described a study by Lovett et al. (1999) that, in part, motivated the current studies. Because our model uses a slightly different rehearsal strategy (see footnote 3), one designed to match what our subjects were doing, and because we wished to determine whether our model could fit the individual subject serial position curves from yet another experiment, we attempted to fit the Lovett et al. data with our model. In this section, we show that our model can be fit to those data—both in aggregate and at the individual subject level—without any new global parameter estimates. Thus, this demonstration offers a 0-parameter fit of our model to data. Further, it tests whether our model can capture individual differences in yet another variant of the MODS task. This version of the task differed from that used in Experiments 1 and 2 in that all of the characters were digits and the trials were presented at either a fast (0.5 s) or slow (0.7 s) interdigit pace.

4.2.1. Model fits

To fit these data, we used a combination of our model fits from Experiments 1 and 2. For the slower trials, we used the parameters from Experiment 1 (the slower of our two experiments) and for the faster trials we used the parameters from Experiment 2. Because we had found differences in subjects' strategies across our two experiments, we expected similar differences might have arisen across trials in the Lovett et al. study. Indeed, in that study the pacing of each trial was apparent before subjects had to begin memorizing digits, so they would have been able to shift their rehearsal strategies to suit. Since the global mismatch penalty and retrieval threshold parameters accounted for this shift in our modeling above, we used the same values here. All other parameter values were set at their default values. Thus, no parameters were allowed to vary freely to optimize this fit. The only varying parameter was W, because it represents individual differences in source activation.

Panel A of Fig. 11 shows the model's fit to the aggregate data from Lovett et al., collapsed across both the string length variable and the timing variable (as was done by Lovett et al.). Here, for each individual simulation, W was drawn at random from a normal distribution (mean = 1.0, variance = 0.625) and the different simulations were averaged together. The same model predictions are plotted according to serial position accuracy in panel B of Fig. 11. These predictions match the shape of the observed curves very well. While these fits demonstrate some of the predictive power of our model, again our main question is how well the model can be fit to individual subjects' data.

Fig. 11.

The model's fits to the Lovett et al. (1999) data. Panel A shows the overall accuracy and panel B the serial position data.

Accuracy as a function of memory set size for 4 representative subjects is shown in Fig. 12. Also shown are the model's predictions for those subjects, obtained by varying W to individually fit each subject. The best-fitting line over all 26 subjects' individual accuracy data are observed = 0.98·predicted + 0.01, R² = 0.90. This fit was obtained using 26 parameters (the 26 individual W's) to fit 104 data points (4 data points for each of the 26 subjects). If, instead of adopting a different W for each subject, we set W to the default value of 1.0, the best-fitting line is observed = 0.83·predicted + 0.15, R² = 0.78. Examples of the serial position fits to the largest set size data for the same 4 subjects are shown in Fig. 13, using no new parameter estimates. Over all subjects and all set sizes the best-fitting line is observed = 0.91·predicted + 0.03, R² = 0.65. This is in line with the corresponding R² values from Experiment 1 (0.51) and Experiment 2 (0.72). Although there is residual variance not accounted for by the model, these fits offer some additional support for our model's ability to capture the variation among subjects, especially considering the fact that these predictions were based on fixed values for all the global parameters. Once again, when we leave W at the default value of 1.0, the quality of the fit decreases. The best-fitting line in this case is observed = 0.81·predicted + 0.15, R² = 0.47.

Fig. 12.

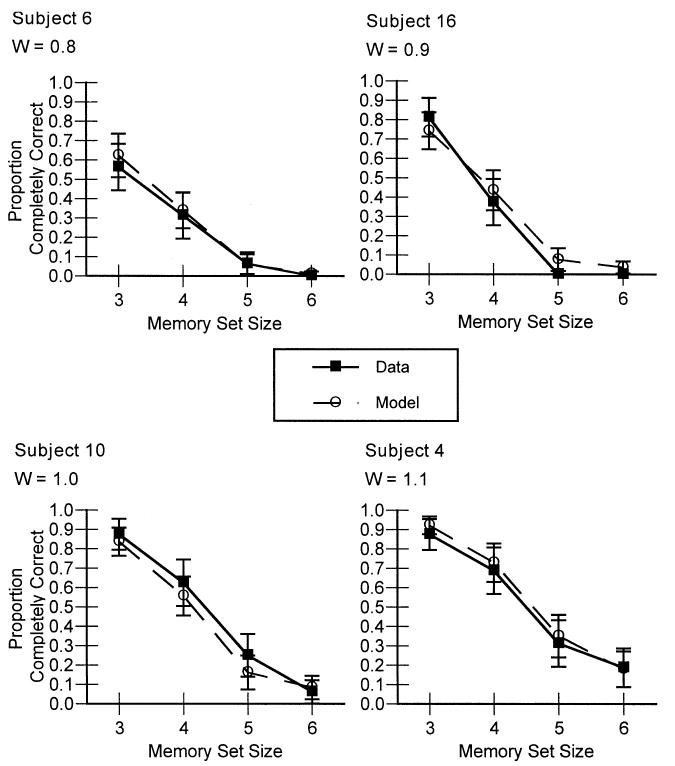
Fits to the proportion of strings correctly recalled as a function of memory set size for four of Lovett et al.'s (1999) subjects.

Fig. 13.

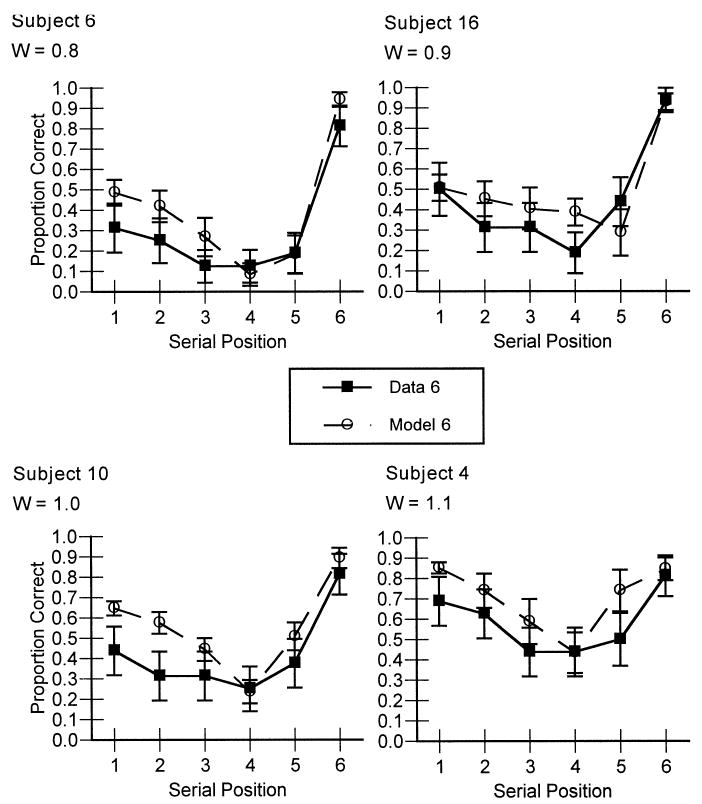
Fits to the serial position data, largest set size only, for four of Lovett et al.'s (1999) subjects.

4.3. Comparison to other working memory models

We have explored the notion that working memory capacity can be modeled in terms of ACT-R's source activation parameter W, where source activation is used to maintain goal-relevant information in an available state. According to this conception, working memory capacity is a limited resource that must be shared among the components of the current goal that are being processed. The more complex the current task, either in terms of its greater memory demands or its requirement of dual-task performance, the smaller each share of this limited resource, and hence the poorer performance. Moreover, we have shown how differences in the overall size of this resource (i.e., how much source activation there is to be shared) impact how much the sharing will degrade performance.

This conception is closely related to other resource-based views of working memory capacity (e.g., Engle, Kane & Tuholski, 1999; Just & Carpenter, 1992; Shah & Miyake, 1996). There are some differences, however, among the various resource-based views. For example, our model posits a limit to ACT-R's source activation, a specific kind of dynamically changing activation linked to the current goal, whereas Just and Carpenter's (1992) model posits a limit on the total activation in the system. Byrne and Bovair (1997) have interpreted such individual differences in total activation as essentially producing differences in the rate of decay of activation in the system. As we have shown above, varying decay rate versus source activation in our model can have quite different consequences for performance. Another difference among these resource views involves the degree to which working memory capacity is considered a general resource (e.g., Engle, 1994; Engle et al., 1999) or a set of separate modality-based or representation-based resources (as in a separate resource for maintaining spatial vs. verbal materials, Shah & Miyake, 1996). Regarding this issue, our model takes source activation to be a limited resource that is drawn upon in the performance of all cognitive tasks; therefore, it is a general resource. However, we do allow for modality-based or representation-based differences to explain other individual differences. For instance, people will differ in the relative amounts of experience they have with verbal and spatial items. Because of this, there will be differences in total activation for verbal and spatial chunks and these differences will impact performance of tasks involving these items (e.g., performing better at spatial tasks because of more highly activated spatial knowledge). Note that in ACT-R such effects of differential experience are carried, not in source activation, but in changes in the base-level activation of particular chunks in declarative memory (see Eqs. (1) and (5)).

Our view of working memory capacity also has an interesting relationship to working memory models that largely attribute working memory limitations to the decay of information from memory (e.g., Baddeley, 1986; Burgess & Hitch, 1992; Kieras, Meyer, Mueller & Seymour, 1999). While our explanation of individual differences does not involve differences in decay rate per se, it is the case that, when our model's source activation parameter W is varied, the overall rate of information processing changes. That is, a larger W implies faster memory retrievals which enable faster task completion, all else being equal (see Equation (3)). Thus, when the amount of source activation is larger, information relevant to task completion tends to be more available because it has decayed less in the shorter elapsed time. According to this logic, then, our source activation account of working memory differences is also quite compatible with processing-speed accounts of individual differences (e.g., Salthouse, 1994; Byrne, 1998). In our model, however, differences in source activation are the underlying cause of differences in processing speed.

Although we do not see a one-to-one mapping between aspects of our model and components of the working memory model by O'Reilly et al. (1999), there are several conceptual similarities. First, O'Reilly et al. emphasize the role that the current goal plays in modulating the propagation of activation. In our model, source activation is the very means by which the current goal differentially activates goal-related items; it enables goal-relevant items to be more easily processed than nongoal-relevant items. Second, O'Reilly et al. interpret working memory limitations in terms of attentional limitations. The same interpretation is natural within our model: Source activation is a limited kind of activation that is directed from the goal; in ACT-R, the goal represents the system's current focus of attention. So, whatever is currently in the focus of attention must share this limited quantity of source activation, that is, attentional activation is limited. Third, O'Reilly et al. allow for the possibility of both domain-general and domain–specific sources of variability among individuals, as do we.

Finally, Engle and his colleagues (Conway & Engle, 1994; Engle et al., 1999) have shown that working memory limits only affect performance of tasks requiring controlled processing. Differences in working memory capacity do not predict differences in how people perform on tasks using automatic processing. Our model is consistent with these findings because an individual's W value will only affect processing that requires goal-directed retrieval of information. Consider a simple example: that of an individual learning that 3+4=7. At first the individual must compute the answer, perhaps using a count-up strategy (Siegler, 1991; Siegler & Shrager, 1984). This is a controlled process and requires retrieval of applicable declarative chunks for counting. It is, therefore, dependent on W. After practice, the person may acquire a chunk encoding the fact that 3+4=7. Performance is now faster, but still dependent on W as a retrieval from declarative memory is still required. With even more practice, giving the sum of 3 and 4 may become proceduralized: the person will learn a new production of the form IF the goal is to provide the sum of 3 and 4 THEN say 7. This constitutes automatic processing and, as no declarative retrievals are required, W will not play a role.

4.4. Other sources of individual differences

It should be emphasized that our arguments regarding individual differences do not claim that source activation, W, is the only thing that explains differences in people's performance on laboratory tasks or on everyday tasks. As noted above, individual differences in prior knowledge and strategies can significantly influence task performance (Chase & Ericsson, 1982; Ericsson & Kintsch, 1995). However, we have argued that when those other sources of variability in task performance are reduced, differences in source activation (our model's representation of working memory capacity) can largely explain differences in an individual's task performance. In the current studies, we used a fast-paced, unfamiliar task to try to reduce sources of variation other than source activation. This is especially evident in Experiment 2, in which the interstimulus interval was 0.5 s. Subjects in that study did not report using sophisticated rehearsal strategies. In fact, they appeared to use a common, simple approach to the task, one that our model was designed to simulate. These results provide converging evidence that we managed to reduce other sources of variation, thereby highlighting the effects of individual differences in working memory capacity.

4.5. Other approaches to studying individual differences

As Reder and Schunn (1999; Schunn & Reder, 1998) have noted, two distinct approaches to studying individual differences have been employed in the field. One approach focuses on differences in knowledge and strategies. Expert-novice studies (e.g., Chi, Glaser, & Rees, 1982; Ericsson & Kintsch, 1995; Larkin, 1981) and strategy choice studies (e.g., Lovett & Anderson, 1996; Lovett & Schunn, 1999; Reder, 1982, 1987; Siegler, 1988) fall into this camp. The other, more psychometrically oriented approach focuses on how differences in the functioning of basic cognitive processes influence performance (e.g., Just & Carpenter, 1992; Salthouse, 1994). Our work is an example of this second approach with the additional feature that we used a computational model to predict and explain the differences in working memory performance among individual subjects. It is interesting to note the similarities and differences between our approach and that developed within psychophysics. For example Nosofsky and Palmeri (1997) have done an excellent job modeling 3 individual subjects' data in a perceptual classification task. They too fit individual subjects with a computational model. However, their approach differed in that they were not interested in holding any parameters constant across subjects, but rather allowed all six parameters to vary for each subject. Moreover, they do not interpret their estimated parameter values beyond the scope of the specific task they were modeling.

In contrast our parameter W is intended to represent a stable characteristic of the subjects that applies across tasks. Our goal was to limit ourselves to this single subject-specific parameter to capture individual differences. Thus, our work also demonstrates that computational models can be especially helpful in testing the “individual differences component” of working memory models. We believe that studying and modeling systematic individual differences in performance are just as important as studying and modeling aggregate effects. For example, looking at individual subjects can reveal new patterns of performance that may only be seen as a mixture when results are aggregated. A computational model that can reproduce the mixture results but not the results of any given individual cannot be said to have fully captured the phenomenon under study. Moreover, as we have shown, employing an individual level of analysis in combination with computational modeling techniques offers a new way of correlating individuals' working memory performance across tasks.

In the Introduction we summarized three important characteristics of working memory resources: (a) they are drawn upon in the performance of cognitive tasks; (b) they are inherently limited; and (c) they differ in capacity across individuals. Because our model possesses all of these characteristics and captures working memory effects at the aggregate and individual levels, we believe that it provides a promising account of individual differences in working memory capacity. Though previous research has highlighted that individual differences exist, these differences have not been modeled at the level of the individual subject. That we were able to do so speaks to the power of our approach and to the generality of the ACT-R theory.