Abstract
We investigate the fitting of response curves in the presence of a continuous covariate. A model is presented in which the expected random response curves, viewed as functions of time and conditional on the covariate, are products of a smooth mean function of time and a smooth function of the covariate. We propose a simple and straightforward estimation scheme for the component functions of the product, and provide basic consistency results for the estimates of the model components. This functional multiplicative effects model for longitudinal data is compared with an unrestricted nonparametric smooth surface model. In an application to the egg-laying behavior of 936 female medflies, the shape of the egg-laying curves is related to the total number of eggs laid by an individual fly. This sheds light on how reproduction intensity is regulated at the individual level. The proposed multiplicative effects model is compared with an unrestricted multivariate smoothing approach.
Keywords: Fecundity, functional regression, longitudinal data, response curves, smoothing
1. Introduction
Studies on aging, longevity and reproduction are often longitudinal with data being recorded repeatedly for an individual over a period of time. If longitudinal measurements are made on a suitably dense grid, such data can be regarded as a sample of curves or as functional data. This is frequently the case in experimental aging research, where fruit flies (Müller, Wang, Capra, Liedo and Carey (1997)) or nematodes (Wang, Müller, Capra and Carey (1994)) are commonly used as experimental subjects due to their relatively short lifespans and the feasibility of mass rearing.
The analysis of a sample of curves is often referred to as “Functional Data Analysis (FDA)”. While in many instances, longitudinal data may be viewed as curve data, the FDA approach differs from traditional longitudinal data analysis. Standard methods for longitudinal data are typically parametric, as exemplified by the popular GEE approach in Diggle, Heagerty, Liang and Zeger (2002) or the nonlinear modeling approach in Davidian and Giltinan (1995). The FDA approach, in contrast, is intrinsically nonparametric and often involves smoothing methods.
Such nonparametric approaches have recently emerged as promising and flexible tools for the analysis of longitudinal data. For instance, Brumback and Rice (1998) apply spline smoothing methods to a set of hormone data in a functional analysis of variance setting, and Rice and Wu (2001) and Shi, Weiss and Taylor (1994) use B-splines for sparsely sampled longitudinal AIDS data in a mixed effects model. The attractiveness of the nonparametric approach has been well documented in the analysis of the Zürich longitudinal growth study, where a midgrowth spurt around age seven was detected in Gasser, Müller, Köhler, Molinari and Prader (1984). An insightful introduction to the various nonparametric approaches for longitudinal or functional data is provided in the monograph by Ramsay and Silverman (1997).
We consider a parsimonious nonparametric model for fitting longitudinal response curve data with multiplicative covariate effects. While product-type models were also investigated by Breiman (1991) and especially by Staniswalis and Lee (1998) in a very interesting analysis of variance type setting, we propose a particularly simple implementation and the application to functional data. Our approach is demonstrated and motivated by a sample of egg-laying curves representing the entire reproductive history of 936 female Mediterranean fruit flies (medflies for short).
The data for our analysis originated from experiments in biodemographic research, where daily fecundity, quantified for individual flies by the number of eggs laid per day, was recorded for a large sample of 1,000 female medflies. Among these, 64 flies did not lay any eggs and were excluded from the analysis, thus resulting in a sample of 936 curves. This seems to be the first extensive experiment where the entire reproductive history of daily fecundity was examined for a large sample. Details of the data and experimental background are described in Carey, Liedo, Müller, Wang and Chiou (1998), where one can also find a preliminary analysis of the daily egg-laying data and the relation between lifetime and reproductive success as measured by the total number of eggs produced during the lifetime of a medfly (also called lifetime reproduction).
Our paper is motivated by recent increased interest in the assessment of reproductive patterns and their implications. Reproduction essentially serves as a proxy for evolutionary fitness. It has been conjectured that an increase in reproductive activity has a negative effect on longevity, due to a trade-off of resources between maintenance and reproduction, and this has led to the notion of a “cost of reproduction” (Partridge and Harvey (1985)). However detailed longitudinal data on reproductive activity, as measured by daily egg laying, were hardly ever recorded. Previous biological studies that looked at much rougher measures of egg-laying in different age groups include Aigaki and Ohba (1984) and Partridge (1988). These and other studies showed that egg-laying activity declines as insects grow older. This finding was also discussed in Carey et al.(1998), where this phenomenon was termed “reproductive senescence”, and its connections to the “cost of reproduction” hypothesis were explored.
Since the total number of eggs produced by a fly is a measure of reproductive success, it is of biological interest to study the relationship between the dynamics of egg-laying, in the form of a fecundity curve, and lifetime reproduction, in terms of total number of eggs produced. Pertinent biological questions which we address in this paper are the following. How is egg-laying distributed over lifetime in dependence on lifetime reproduction? Can one find a relatively simple and interpretable relationship between the shape of the egg-laying curve and the total number of eggs laid?
The paper is organized as follows. The multiplicative effects model is described in Section 2, and a more general class of smooth surface models is the theme of Section 3. Issues regarding smoothing and estimation of the components of the multiplicative effects model are discussed in Section 4, which also contains basic consistency results for the proposed estimates. Section 5 is devoted to the application to the medfly egg-laying data, and concluding remarks are in Section 6.
2. The Multiplicative Effects Model
We now describe a multiplicative model which provides a framework for the study of these questions and, in particular, leads to a simple and easily interpretable class of functional regression models. Assume that one has a sample of n individuals and, for the ith individual, one observes (Zi, Yi(t)) where Zi is a vector of covariates and Yi is a response curve observed on a time interval I, i.e., is an infinite-dimensional dependent variable. The following Multiplicative Effects Model implements the idea that in many situations the covariates may have a multiplicative effect on the response curve,
Here, the ei(t) are i.i.d. random error processes, independent of the covariate Z, satisfying
| (1) |
Both μ and φ are smooth functions that are twice continuously differentiable; we require 0 < ∫ μ(t) dt < ∞ and
| (2) |
to assure identifiability of the components of model (M1). The assumptions imply EY (t) = μ(t), the population mean curve.
Since the shapes of functions μ and φ are arbitrary, and the distribution of the random error e(t) is also unrestricted, model (M1) is nonparametric. In Section 5 we illustrate the use of this model for the egg-laying data. In this application, Y(t) is the fecundity curve for a fly. The covariate is one-dimensional in this case, Z stands for the lifetime reproduction of eggs, and μ(t) is the population average number of eggs laid at age t, the baseline fecundity curve.
Under model (M1), the conditional fecundity curves E[Y (t)|Z] of female medflies are proportional to the baseline fecundity curve μ(t), where the multiplying factor depends on Z. In our data analysis in Section 5, the covariate effects function, φ(z), is seen to be an increasing function of z, as expected for biological reasons. Our model then implies that flies with higher lifetime reproduction simply lay proportionally more eggs daily. The Multiplicative Effects Model (M1), if applicable, then provides a simple and biologically appealing way to summarize the variation of the complicated individual reproductive histories of female medflies across the population.
We note that for model (M1),
| (3) |
and, owing to (2),
| (4) |
| (5) |
These relations prove useful for the construction of estimators for μ and φ in Section 4.
3. The Smooth Functional Surface Model
Our main model is the Multiplicative Effects Model (M1), which incorporates the covariate Z by allowing it to have a smooth multiplicative influence on the mean response function μ(t). A smooth influence of a covariate effect on the regression function can be modeled in various alternative ways. One approach fits a mean surface which is smooth in both time and covariate. The resulting Smooth Functional Surface Model is
As above, the error process e(t) is required to satisfy (1) and m(·, ·) is a smooth (say twice differentiable) function in both arguments. In this model, the regression function is
| (6) |
which allows for arbitrarily complex interactions between time and covariate.
Since the form of m(·, ·) is completely unspecified, model (M2) contains the Multiplicative Effects Model (M1) as a special case. Model (M2) has the drawback of a slower (higher-dimensional) rate of convergence and increased computational effort as compared to model (M1). In addition, it is less readily interpretable.
We note that the covariance of the errors Cov (e(t), e(s)) needs to decline fast enough as |t - s| → ∞ so as to enable consistent smoothing of e(t) if sampling occurs at a regular grid; for details on sufficient conditions we refer to Hart and Wehrly (1986). For simplicity of presentation, and because our data application involves a one-dimensional covariate, we assume without loss of generality that the covariate Z is in ℝ.
For higher dimensional Z, various options exist: the product model can be extended to allow for a one-dimensional factor in each covariate; a second option is projection to one dimension, or a fully nonparametric smooth analysis, with the associated well known computational and rate of convergence cost of employing higher dimensional smoothers, owing to the “curse of dimensionality”. Model (M1) and its higher dimensional versions implement dimension reduction since these models contain only one-dimensional nonparametric components, as compared to higher dimensional nonparametric components such as the two-dimensional nonparametric component m(·, ·) that appears in model (M2). A class of more general models is given by m(t,Z) = H(γ1(t), γ2(Z)), where H is a known link function and γ1, γ2 are smooth univariate functions. In model (M1), we chose m(t,Z) = γ1(t)γ2(Z), selecting H(x1, x2) = x1x2. Another possibility would be an additive mean surface structure with H(x1, x2) = x1 + x2. The latter was exploited in Zeger and Diggle (1994).
4. Estimation of the Smooth Components
4.1. Smoothing
Both (M1) and (M2) are nonparametric models, hence smoothing methods are applied to estimate the various components of the mean surfaces. We first describe the smoothing procedures involved. Let (Ui, Vi), i = 1,…, n, be generic data in ℝ2 with underlying regression function g(u) = E (V|U = u). We define the nonparametric regression function estimate by ĝ(u) = S(u, b, (Ui, Vi)i=1,…,n), where n is the number of data in the scatterplot and b is the bandwidth or smoothing parameter of the smoother S.
Generally a smoother will satisfy, for a sequence τn → 0, that
| (7) |
The rate of convergence τn depends on the particular choice of smoothing method and bandwidth sequence. Common smoothing techniques include kernel estimators, splines or local polynomial fitting.
For our application, we choose the locally linear smoother, denoted by SL, which is obtained by fitting weighted least squares lines to the data in local windows. This smoother has a number of nice features such as automatic adjustment to estimation near endpoints, compare Fan (1992, 1993). A formal definition is to denote the minimizers of the weighted sum of squares
by and , and to set
| (8) |
Here the kernel weights K((u − Ui)/b) are determined by a nonnegative kernel function K and bandwidth b. We use the Bartlett-Parzen-Epanechnikov kernel K(x) = (1 − x2)1{|x|≤1}, which is the optimal weight function for local weighted least squares fitting (Müller (1987)). The value of the smoother SL, fitting local lines at the argument u, is the estimated intercept of a line fitted by weighted least squares locally to only those data which fall into the window [u − b, u + b].
The above smoother (8) is for one-dimensional covariates U only. If the covariates are multi-dimensional, as is the case in model (M2), then multivariate smoothing methods are needed. We consider a two-dimensional smoother as required for fitting the fecundity data to model (M2), aiming at the regression function h(x1, x2) = E(Y |X1 = x1, X2 = x2). In analogy to the one-dimensional case, we choose as smoother the local weighted least squares fitting of planes, noting as above that other smoothers such as two-dimensional kernel estimators or thin plate smoothing splines could be used alternatively.
Given scatterplot data with bivariate covariates (Xi1,Xi2, Yi), i = 1,…, n, the locally fitted plane is then obtained by employing the smoother SL,
| (9) |
where are the minimizers of the local weighted sum of squares
Here, K(·, ·) ≥ 0 is a real-valued kernel function, for example a two-dimensional analogue of the Epanechnikov weight function, K(u, v) = [1 − (u2 + v2)1/2]1 {u2+v2≤1}, and (b1, b2) is a pair of bandwidths, aligned with the coordinate axes. This corresponds to the local fitting of a weighted least squares plane in the window and evaluating it at the midpoint of this window.
4.2. Estimation
In practice, functional data Yi(t) are typically available in discretized form, i.e., the actual measurements are Yi(tij), j = 1, …, ni, i = 1, …, n, tij denoting the time of the jth measurement on the ith-subject. For the fecundity data, the measurements (which correspond to the number of eggs laid per day) were taken daily and ni thus corresponds to the number of days during which the ith medfly is alive. In this data application, the measurement times are equally spaced by day and thus tij = tj.
When applying smoother (9) for the Smooth Functional Surface Model (M2), it is natural to proceed with estimates
| (10) |
Then we obtain a fit for the process Yi(t) by means of the estimate of E[Y (t)|Z = Zi] given by
| (11) |
Useful for model checking and diagnostics are the leave-one-curve-out predictors
| (12) |
where is the above estimate (10) of m, constructed from a reduced sample, in which the data Zi and (Yi(tj), j = 1,…, ni) are omitted. The difference measured in a suitable function norm, then provides a more reliable prediction error than
Estimation in the Multiplicative Effects Model (M1) requires additional considerations. From (3),∫ E[Y (t)|Z]dt = φ(Z) ∫ μ(t)dt = φ(Z)c*−1 for some constant c*, 0 < c* < ∞. It follows that φ(Z) = c* ∫ E[Y (t)|Z]dt. Plugging this into (3) and following (4), we obtain
| (13) |
Accordingly, the problem of estimating m can be reduced to the problem of estimating the two functions μ(t) = E[Y (t)], and ψ(z) = ∫ E[Y (t)|Z = z]dt = E[∫Y(t)dt|Z = z].
Natural smoothed estimates are obtained by replacing the expectation in μ with an averaged smoothed curve, and the conditional expectation in ψ with a nonparametric regression smoother, substituting the integral with a Riemann sum. These ideas lead to the estimates
| (14) |
where, thus averaging over those smoothed curves which have actual measurements in the neighborhood of t, and
| (15) |
where qi is an estimate of the integral with ti0 = 0. Consistency will require that for irregular designs, we have an asymptotic design density which is bounded away from 0 on the common range of the individual curves.
We note that in the construction of these estimates, we apply one-dimensional smoothers to either independent data as in (15) or, in the equidistant case at least, to data with covariance of the order n−1 as in (14). In either case, nonparametric rates of convergence for estimating one-dimensional functions apply, so that (conditional) mean squared errors are of the order n−4/5 for twice continuously differentiable functions μ and ψ. To estimate the regression function m(t, z) = E[Y (t)|Z = z] = c* μ(t)ψ(z) we also require an estimate of the constant c* which appears in (13). Note that since m(t,Z) = E[Y (t)|Z] provides the best linear predictor for Y (t) given Z. This motivates the estimator
| (16) |
substituting μ̂ in (14) and ψ̂ in (15) for μ and ψ. Then (14)–(16) lead to our proposed estimate for the product surface,
| (17) |
In analogy to (11), the prediction for process Yi(·) is
| (18) |
and the leave-one-curve-out predictors are found to be
| (19) |
We note that these estimates are conceptually simple and straightforward to compute.
4.3. Consistency
To establish basic consistency results for the estimates μ̂(·) (14) and ψ̂(·) (15), the following assumptions are made.
(A1) The response curves Y(t) are Lipschitz continuous of order α, 0 ≤ α ≤ 1, with bounded first derivatives on a compact support I.
(A2) For each subject i, the times of measurements {ti1, …, tini} form a sequence of designs generated by a design density fT which is Lipschitz continuous on a compact support I and is twice continuously differentiable, satisfying ∫ fT (t)dt = 1, 0 < inf fT(·) < sup fT (·) < ∞ and for all ni.
Theorem 1
Assume (A1) holds and that the smoother satisfies the basic consistency requirement in (7) with some sequence τn → 0. If the observed covariates Z are sampled from distributions that have the same mean and variance, then the proposed estimator μ̂(·) (14) of μ(·) satisfies |μ̂ (t) − μ(t)| = Op(τn) + op(1).
Theorem 2
If (A1) and (A2) hold and the smoother satisfies the basic consistency requirement in (7) with the sequence τn → 0 replaced by a (possibly different) sequence γn → 0, the proposed estimator ψ̂ (·) (15) of ψ (·) is consistent such that, given where n0 = min1≤i≤n{ni}.
We note that if the observed covariates Z are independently and identically distributed, then the op(1) in Theorem 1 may be strengthened to leading to a root-n′ rate of convergence, where n′ is defined after (14). The above consistency results can easily be extended to uniform consistency over the respective supports, if the underlying smoothers are uniformly consistent. The consistency of the surface estimator (17) follows from Theorem 1 and Theorem 2, observing the consistency of the least squares estimator of c* under mild regularity conditions.
Proof of Theorem 1
We can express the estimate of μ(t) in (14) via a linear smoother with weight functions Gj(·) as , where . The result follows from the Law of Large Numbers.
Proof of Theorem 2
Condition (A2) implies max1≤j≤ni|tij − ti(j−1)| = O(1/ni). In addition, with (A1), Y (t) is Riemann integrable and . Using a linear smoother with weight functions Gi(·) for the estimator ψ of ψ, we find
.
5. Modeling A Sample Of Egg-Laying Curves
In this section, we discuss an application of the proposed methods to data from an experiment on medfly fecundity which was briefly described in the introduction. This experiment was carried out in 1992–1995 at the medfly mass rearing and sterilization facility (Moscamed) at Metapa, Chiapas, Mexico, and consisted of 1,000 female medflies for which daily egg production was recorded. The daily egg laying data form the basis of the curve data analysis to be described in the following. The goal of our analysis is a biologically meaningful model that provides a parsimonious and interpretable description of the association between changes in total number of eggs produced and the shape changes in the egg-laying curve for individual flies.
It was reported in Carey et al. (1998) that lifetime reproduction increases linearly with lifetime, but only up to day 51. There was no reproductive gain due to added longevity past day 50. Thus, there is a marked change-point at day 51 for the total number of eggs as a function of lifetime. Because of this and the fact that random variation of fecundity curves is quite large after day 51, we restrict the fecundity curves to a support up to day 50. For flies that live less than or equal to 50 days, their entire reproductive history was retained and recorded as Yi(tj), tj = 1,…, Ti, where Ti is the lifetime of the ith fly. Note that here tij = tj as we have a regular design. For the 150 flies that live longer than day 50, the truncated trajectories Yi(tj), tj = 1,…, 50, were used as curve data, but lifetime reproduction still refers to the total number of eggs laid by a fly in the entire lifetime. We also deleted the 64 flies that never laid any eggs from the analysis. Therefore, the sample consists of 936 egg-laying curves.
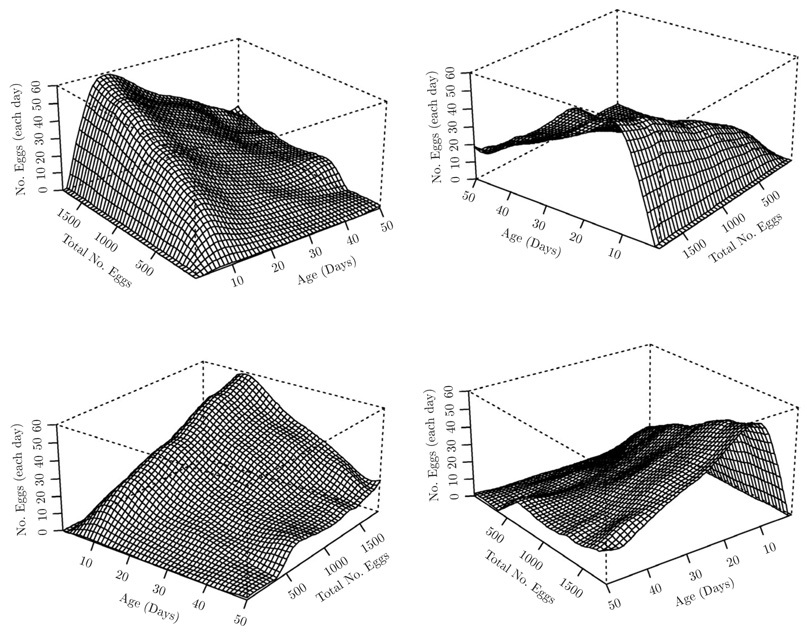
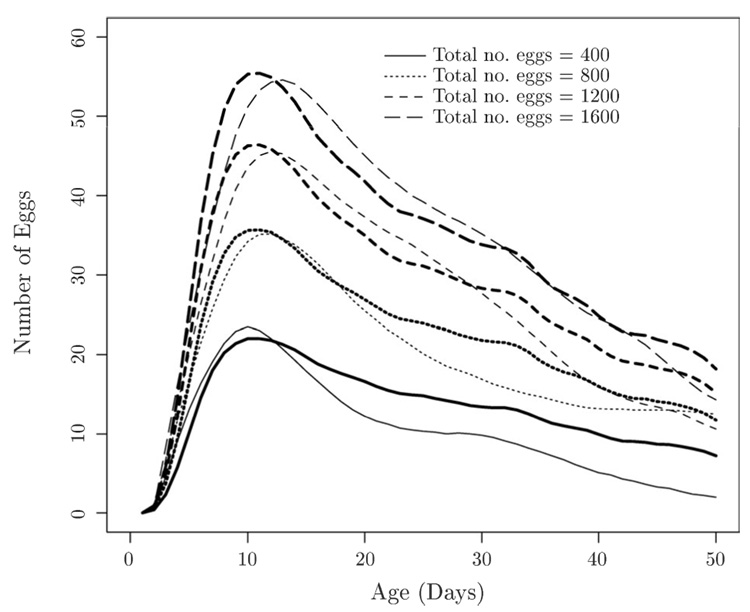
As a first analysis, serving as a reference, the fitted surface for the general Smooth Functional Surface Model (M2) was obtained as in Figure 1, with total number of eggs as covariate. Here the surface estimate m̂(2)(t, z) results from an application of the two-dimensional smoother as described in (10). Cross-sections through the estimated surface at several fixed values of the covariate are presented in Figure 3 (thinner lines). We observe a “ridge” in the smooth functional surface estimated for (M2), with a steep initial slope, followed by a less steep decline towards the right. Consideration of the smooth functional Multiplicative Effects Model (M1) is particularly motivated by the cross-sections through the fitted surface of the model (M2) in Figure 3 (thinner lines). The shape of the egg-laying curve remains remarkably stable throughout the various cross sections. These shapes appear to differ mainly in terms of a factor which depends on the level of total number of eggs and by which the entire curves are multiplied.
Figure 1.
Fitted mean surface (t, z) (11) with total number of eggs as covariate, for the Smooth Functional Surface Model (M2), in different perspectives. Bandwidths in the direction of age and total number of eggs are chosen as 6 days and 180, respectively.
Figure 3.
Cross-sections through the fitted surface (t, z) of Figure 1 (thinner lines) and the fitted multiplicative model (t, z) (thicker lines), for total number of eggs fixed at 400, 800, 1200 and 1600.
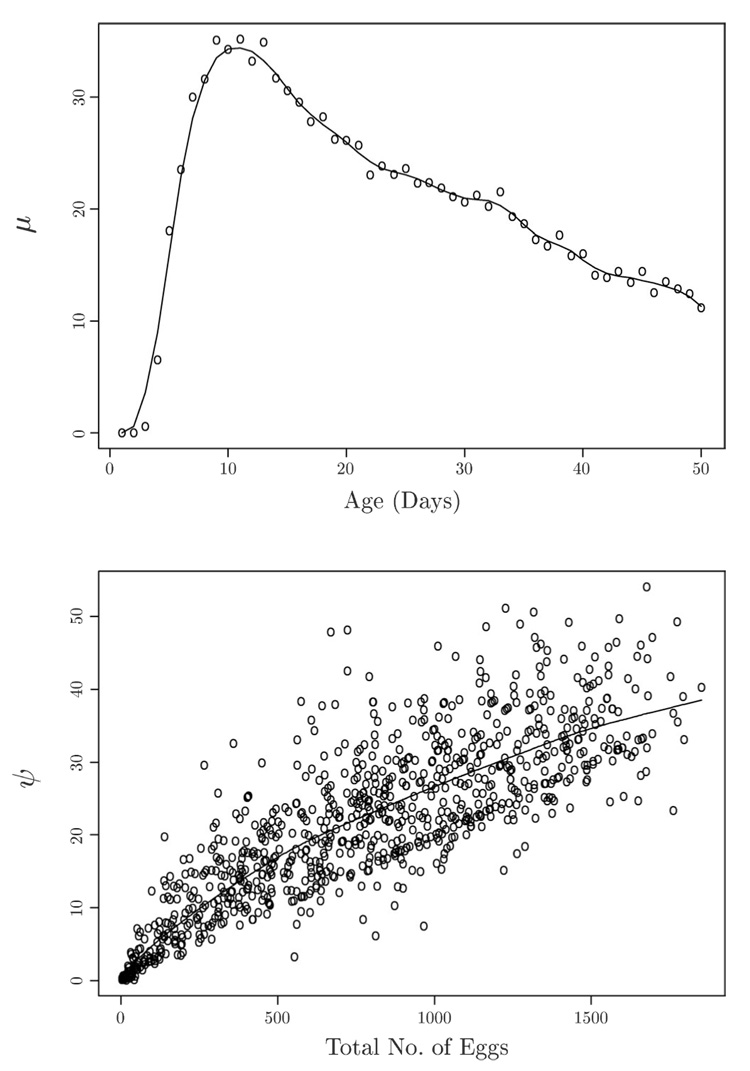
This feature indicates that these data may be well fitted by the dimension-reduced model (M1) with its product surface, m(t, z) = c*μ(t)ψ(z). Here the function μ describes the basic shape function of age-dependency on the number of eggs laid, and the function ψ provides the necessary factor by which this basic shape function has to be multiplied to obtain the profile for a given value for total number of eggs. The basic unimodal egg-laying shape function μ̂ (14) and the monotone increasing and concave function ψ̂ (15), constructed with leave-one-point-out bandwidths, can be viewed in Figure 2. The fitted product surface (t, z) (18), resulting from the minimization step (16), is qualitatively quite similar to the surface in Figure 1, but is constructed from the simpler and more restricted product structure corresponding to the Multiplicative Effects Model (M1). The surface is not displayed here as it is similar to Figure 1.
Figure 2.
Scatterplots and function estimates μ̂ (14) (above) for function μ and ψ̂ (15) (below) for function ψ, for the components of the Multiplicative Effects Model (M1), with total number of eggs as covariate. Cross-validated bandwidths are 2.5 days for μ̂ and 502 for ψ̂.
The comparison between the surface with only the smoothness constraint in Figure 1 and the one with the product structure constraint is seen in the corresponding cross-sections in Figure 3 (thinner vs. thicker lines). This comparison shows how the product model forces the location of all peaks to be the same, i.e., the ridge in the Multiplicative Effects Model (M1) runs parallel to the total number of eggs-axis, while the ridge in the nonparametric surface of Figure 3 is slightly tilted as compared to this axis. Indeed, model (M1) requires that the cross-sections be parallel as can be seen in Figure 3 (thick lines), while the cross-sections from the unrestricted model fit in Figure 3 (thin lines) are not necessarily parallel.
We find that the Multiplicative Effects Model (M1) is a serious contender in situations like this. Apart from visual comparisons of model fits, the leave-one-curve-out prediction error is a useful quantification of the quality of a model. These predictors are for the Smooth Functional Surface Model (M2) and for the Multiplicative Effects Model (M1). Here,are estimates (14)–(16), obtained by excluding the ith sample process.
Prediction errors
can be compared for the various models. We find PE = 320.53 for the Smooth Functional Surface Model (M2) and PE = 319.68 for the Multiplicative Effects Model (M1). Since the latter only contains one-dimensional nonparametric functions, it is of lower dimension and, since it also achieves a lower prediction error, it is the preferred model for this application. We note that prediction errors are also useful for bandwidth choice. The optimal prediction-based bandwidth choice is , and this criterion produced days for model (M1).
6. Concluding Remarks
We have studied a multiplicative effects model for longitudinal studies that easily lends itself to both exploratory data analysis as well as interpretation. The model is conceptually straightforward and easy to implement. The proposed algorithm is fast and effective. Extensions of the method to higher dimensional covariates, for example in combination with single index models, would be a natural extension.
Alternative approaches that are somewhat similar in scope but do not provide the simplicity and interpretability in modeling and estimation that the proposed functional multiplicative effects model does would be log-additive modeling and generalized additive modeling. In log-additive modeling, we would fit an additive model to log(Y (t)). This transformation model assumes that the errors are also multiplicative and when we implemented this model it did not work well for the egg-laying data, yielding prediction errors between 486 for a smoothing spline and 511 for a loess implementation, in contrast to a prediction error of around 320 for the functional multiplicative model. Similarly, the generalized additive model (Hastie and Tibshirani (1990)) with log link could be used, yielding prediction errors between 339 and 357 under different implementations.
We demonstrated the usefulness of the multiplicative effects model for the analysis of how the reproductive trajectory of medflies is regulated in relation to the total number of eggs produced. Our analysis suggests a fairly simple interplay between the dynamics of egg-laying and total number of eggs laid, that serves as a proxy for reproductive success. The regulation of total output is seen to occur by simply up- or down-regulating the entire egg-laying trajectory. This observation characterizes reproduction as a dynamic process whose intensity is a random characteristic of an individual fly, while its shape is relatively invariant and is a population characteristic. The population reproductive trajectory is characterized by an early rise to a peak, followed by a protracted decline.
We conclude that the functional multiplicative effects model provides a useful tool for analyzing and interpreting a sample of curves.
Acknowledgements
This research was supported in part by NHRI Grant BS-091-PP07, NSC Grant 88-2118-M-194-004, NSF Grants DMS-98-03627, DMS-99-71602 and DMS-02-04896, and NIH Grant 99-SC-NIH-1028. We wish to thank the reviewers for helpful remarks.
References
- Aigaki T, Ohba S. Individual analysis of age-associated changes in reproductive activity and life span of Drosophila virilis. Experimental Gerontology. 1984;19:13–23. doi: 10.1016/0531-5565(84)90027-5. [DOI] [PubMed] [Google Scholar]
- Breiman L. The pi method for estimating multivariate functions from noisy data. Technometrics. 1991;33:125–143. [Google Scholar]
- Brumback B, Rice J. Smoothing spline models for the analysis of nested and crossed samples of curves. J. Amer. Statist. Assoc. 1998;93:961–994. [Google Scholar]
- Carey J, Liedo P, Müller HG, Wang JL, Chiou JM. Relationship of age patterns of fecundity to mortality, longevity and lifetime reproduction in a large cohort of Mediterranean fruit fly females. J. Gerontology, Biological Sci. 1998;53A:B245–B251. doi: 10.1093/gerona/53a.4.b245. [DOI] [PubMed] [Google Scholar]
- Davidian M, Giltinan DM. Nonlinear Models for Repeated Measurement Data. London: Chapman and Hall; 1995. [Google Scholar]
- Diggle PJ, Heagerty PJ, Liang KY, Zeger SL. Analysis of Longitudinal Data. 2nd edition. Oxford, England: Oxford University Press; 2002. [Google Scholar]
- Fan J. Design-adaptive nonparametric regression. J. Amer. Statist. Assoc. 1992;87:998–1004. [Google Scholar]
- Fan J. Local linear regression smoothers and their minimax efficiencies. Ann. Statist. 1993;21:196–216. [Google Scholar]
- Gasser T, Müller HG, Köhler W, Molinari L, Prader A. Nonparametric regression analysis of growth curves. Ann. Statist. 1984;12:210–229. [Google Scholar]
- Hart JP, Wehrly TE. Kernel regression estimation using repeated measurements data. J. Amer. Statist. Assoc. 1986;81:1080–1088. [Google Scholar]
- Hastie T, Tibshirani R. Generalized Additive Models. London: Chapman and Hall; 1990. [DOI] [PubMed] [Google Scholar]
- Müller HG. Weighted local regression and kernel methods for nonparametric curve fitting. J Amer. Statist. Assoc. 1987;82:231–238. [Google Scholar]
- Müller HG, Wang JL, Capra WB, Liedo P, Carey JR. Early mortality surge in protein-deprived females causes reversal of sex differential of life expectancy in Mediterranean fruit flies. Proc. National Academy of Sciences of the USA. 1997;94:2762–2765. doi: 10.1073/pnas.94.6.2762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Partridge L. Lifetime reproductive success in Drosophila. In: Clutton-Brock TH, editor. Reproductive Success. Chicago: University of Chicago Press; 1988. pp. 11–23. [Google Scholar]
- Partridge L, Harvey PH. Costs of reproduction. Nature. 1985;316:20–21. [Google Scholar]
- Ramsay JO, Silverman BW. The Analysis of Functional Data. New York: Springer; 1997. [Google Scholar]
- Rice JA, Wu CO. Nonparametric mixed effects models for unequally sampled noisy curves. Biometrics. 2001;57:253–259. doi: 10.1111/j.0006-341x.2001.00253.x. [DOI] [PubMed] [Google Scholar]
- Shi MG, Weiss RE, Taylor JMG. An analysis of paediatric CD4 counts for acquired immune deficiency syndrome using flexible random curves. Appl. Statist. 1994;45:151–163. [Google Scholar]
- Staniswalis JG, Lee JJ. Nonparametric regression analysis of longitudinal data. J. Amer. Statist. Assoc. 1998;93:1403–1418. [Google Scholar]
- Wang J-L, Müller H-G, Capra WB, Carey JR. Rates of mortality in population of Caenorhabbditis elegans. Science. 1994;200:827–828. doi: 10.1126/science.7973642. [DOI] [PubMed] [Google Scholar]
- Zeger SL, Diggle PJ. Semiparametric models for longitudinal data with application to CD4 cell numbers in HIV seroconverters. Biometrics. 1994;50:689–699. [PubMed] [Google Scholar]