Abstract
Researchers and clinicians routinely rely on interference electromyograms (EMGs) to estimate muscle forces and command signals in the neuromuscular system (e.g., amplitude, timing, and frequency content). The amplitude cancellation intrinsic to interference EMG, however, raises important questions about how to optimize these estimates. For example, what should the length of the epoch (time window) be to average an EMG signal to reliably estimate muscle forces and command signals? Shorter epochs are most practical, and significant reductions in epoch have been reported with high-pass filtering and whitening. Given that this processing attenuates power at frequencies of interest (< 250 Hz), however, it is unclear how it improves the extraction of physiologically-relevant information. We examined the influence of amplitude cancellation and high-pass filtering on the epoch necessary to accurately estimate the “true” average EMG amplitude calculated from a 28 s EMG trace (EMGref) during simulated constant isometric conditions. Monte Carlo iterations of a motor-unit model simulating 28 s of surface EMG produced 245 simulations under 2 conditions: with and without amplitude cancellation. For each simulation, we calculated the epoch necessary to generate average full-wave rectified EMG amplitudes that settled within 5% of EMGref. For the no-cancellation EMG, the necessary epochs were short (e.g., < 100 ms). For the more realistic interference EMG (i.e., cancellation condition), epochs shortened dramatically after using high-pass filter cutoffs above 250 Hz, producing epochs short enough to be practical (i.e., < 500 ms). We conclude that the need to use long epochs to accurately estimate EMG amplitude is likely the result of unavoidable amplitude cancellation, which helps to clarify why high-pass filtering (> 250 Hz) improves EMG estimates.
The electromyogram (EMG) is the spatial and temporal interference pattern of the potentials of many motor units recorded by electrodes. Although EMG amplitude is the most common experimental means to estimate muscle forces (Inman et al., 1952; Milner-Brown and Stein, 1975) and the neural drive to a muscle (Schieber, 1995; Valero-Cuevas et al., 1998), amplitude cancellation in the interference EMG limits information extraction from this signal (Farina et al., 2004a). Amplitude cancellation can limit not only measures of EMG amplitude (Moore, 1967; Day and Hulliger, 2001; Keenan et al., 2005), but also in other measures derived from the EMG including: evoked potentials (Rösler et al., 2002; Keenan et al., 2006a), spike-triggered averages (Botteron and Cheney, 1989; Fortier, 1994; Keenan et al., 2006b), and motor unit decomposition (Gazzoni et al., 2004).
Developing methods to improve information extraction from the interference EMG are critical and urgent because, in the absence of other means, measures derived from the EMG are critical to improve our understanding of neuromuscular function. For example, the length of the epoch (time window) over which to average an EMG signal to reliably estimate muscle force and command signals is a key question in EMG analysis, especially during maximal voluntary contractions (MVC). A standard procedure is to first identify the peak force magnitude over several repetitions of a task (Gandevia, 2001), and then average EMG over an epoch centered on that peak to estimate the maximal EMG amplitude. Epochs commonly used include: > 1 s (Fuglevand et al., 1993b), 1 s (Hakkinen and Komi, 1983; Farina et al., 2002b), 750 ms (Valero-Cuevas et al., 1998), 500 ms (Rudroff et al., 2007), and < 500 ms (Cannon and Cafarelli, 1987; Laidlaw et al., 2002; Kuo et al., 2006). Although shorter epochs are most practical, random fluctuations in EMG amplitude estimates are diminished with longer epochs (Farina and Merletti, 2000; Clancy et al., 2002). This tradeoff between selecting a long duration epoch to reduce amplitude variance error versus selecting a short duration epoch to reduce amplitude bias error is critical during MVCs as peak forces can only be maintained for a very brief time.
Although significant reductions in epoch have been reported with high-pass filtering and whitening the interference EMG (Clancy et al., 2002; Potvin and Brown, 2004; Staudenmann et al., 2007), this processing attenuates power at frequencies generally considered of greatest interest (< 250 Hz). Thus, it is unclear whether and how these processing methods improve the extraction of physiologically-relevant information. Signal whitening reduces the variance of amplitude estimates by removing the temporal correlation present among neighboring EMG samples, with this structure arising from the limited signal bandwidth in the EMG produced by the recording electrodes, volume conductor, and generation of action potentials (Clancy and Hogan, 1994; Clancy et al., 2001). In addition, it has been suggested that a high-pass filter (> 250 Hz) may improve EMG amplitude estimation by increasing the pick-up area of the recording electrodes (Staudenmann et al., 2007), and provides a better balance between deep and superficial motor unit contributions to the EMG signal. We investigated another possibility, that amplitude cancellation dominates at frequencies < 250 Hz, and that high-pass filtering and whitening improve EMG amplitude estimates by attenuating the influence of amplitude cancellation.
We used a motor-unit model of surface EMG to examine the influence of amplitude cancellation and high-pass filtering on the necessary epoch to accurately estimate the average EMG amplitude. Structure-based EMG models (reviewed in Stegeman et al., 2000; McGill, 2004), in contrast to phenomenological models (Clancy and Hogan, 1994; Farina and Merletti, 2000), simulate the interference EMG as the sum of the constituent motor unit potentials. One advantage of structure-based EMG models is that it is possible to generate two different signals for each set of parameter values and excitation level to compare the influence of amplitude cancellation on EMG processing (Keenan et al., 2005). The first signal, the interference EMG, is the sum of the positive and negative phases of motor unit potentials, as occurs naturally. The second signal, the no-cancellation EMG, is identical to the interference EMG except that each motor unit potential is first rectified before being summed, which is an idealized signal where cancellation is prevented. This no-cancellation EMG is not seen experimentally because it would require the identification and rectification of each potential contributed to the EMG. Many previous studies have used comparisons between the physiologic “cancellation EMG” and the no-cancellation EMG as the only method to improve our understanding of this important feature of EMG (Moore, 1967; Person and Libkind, 1970; Day and Hulliger, 2001; Keenan et al., 2005). We now extend this approach to examine the influence of amplitude cancellation on the epoch necessary to accurately estimate EMG amplitude. Because model predictions are sensitive to the parameter values (Keenan and Valero-Cuevas, 2007), we used a Monte Carlo approach to improve the experimental validity of the EMG simulations and establish the sensitivity of our results to motor unit parameter variability and uncertainty.
METHODS
To quantify the influence of amplitude cancellation and high-pass filtering on the epoch to estimate EMG amplitude, we nested a motor unit model of EMG and force (Keenan et al., 2005; Keenan et al., 2006b) inside a Monte Carlo simulation (Valero-Cuevas et al., 2003; Santos and Valero-Cuevas, 2006). The computational model is based on a model of recruitment of a population of motor units and muscle force (Fuglevand et al., 1993a) with the addition of an EMG model (Farina and Merletti, 2001) to simulate surface EMG with a planar volume conductor with muscle, fat, and skin tissues. The model and all data analyses were implemented in Matlab version 7.0 (The Mathworks, Natick, MA). Motor-unit potentials and the EMG signal are computed at 4096 samples/s and muscle force at 500 samples/s.
One test of the experimental validity of the model is the degree to which its EMG simulations can replicate well-established experimental relations. In a previous study (Keenan and Valero-Cuevas, 2007) we used Monte Carlo simulations to test the ability of the most popular motor unit model available (Fuglevand et al., 1993a) to robustly predict the well-established scaling of EMG amplitude and force variability with mean force (Milner-Brown and Stein, 1975; Bigland-Ritchie, 1981; Jones et al., 2002; Enoka et al., 2003). In that study, we varied the numerical values for 9 motor neuron and muscle parameters within experimentally-identified ranges (Table 1) by randomly sampling from uniform distributions. Although we found that the model was not robust to parameter variability, we identified a parameter set (i.e., numerical values for the 9 motor unit parameters) that best replicated the well-established scaling of EMG amplitude and force variability.
Table 1.
Model parameters, previous ranges over which parameters varied, and the parameter set used in the current study that best reproduced the experimentally-reported scaling of EMG and force variability with mean force level.
| Parameters | Ranges | Fixed parameters |
|---|---|---|
|
| ||
| 1) Number of motor neurons | 150 –500 | 381 |
| 2) Range in innervation numbers | 1–100x | 50x |
| 3) Recruitment range | Up to 30 – 80% maximal excitation | 79% |
| 4) and 5) Peak discharge rate: | ||
| First & last recruited neuron | 25 – 50 pulses per second | 28 & 30 pps |
| 6) Number of fibers | 50,000 – 250,000 | 71,487 |
| 7) Fiber length | 4 – 16 cm | 6 cm |
| 8) Mean conduction velocity | 3 – 4 m/s | 3.5 m/s |
| 9) Conduction velocity spread | 0 – 0.5 m/s (SD) | 0.1 m/s (SD) |
In this study, our Monte Carlo simulations held all motor unit parameters fixed except: i) the distribution of motor unit territories, and ii) interspike intervals. The rationale for only changing these two parameters values is that, first, all models of motor unit populations show that EMG is influenced by the assumed distribution of motor unit territories within the muscle. Published simulations that study this phenomenon have used an arbitrary number (e.g., 20) of random motor unit locations (Farina et al., 2002a; Lowery et al., 2003), while holding all other parameters fixed (e.g., conduction velocities, number of motor units, and number of fibers for each motor unit). In contrast, in this Monte Carlo study we varied the number of random locations to convergence (see below). Second, prior studies take into consideration the stochastic nature of motor neuron discharge by using a Gaussian probability distribution to simulate interspike intervals for each motor-unit discharge train at each activation level. In contrast, our Monte Carlo simulations investigated how changing interspike intervals influenced epoch to estimate EMG amplitude, while keeping the number of motor units recruited and mean discharge rates for each motor unit unchanged. For each Monte Carlo iteration, the distribution of motor unit territories within the muscle and interspike intervals were selected at random from uniform and Gaussian distributions, respectively. Then, the motor unit potentials and forces were simulated for each motor unit. EMG and muscle force were simulated at each of six excitation levels by summing all trains of motor unit potentials and forces, respectively. Convergence was declared when there was < 2% change in the running mean and coefficient of variation of EMG amplitude and mean force for the last 20+% of the simulations at each excitation level (Valero-Cuevas et al., 2003; Santos and Valero-Cuevas, 2006).
Only those simulations that met the same two fitness criteria as in our previous study (Keenan and Valero-Cuevas, 2007) were used for subsequent analysis (i.e., approximated a match between simulated and experimental EMG/force and force/force-variability relations). First, force variability is known to scale with mean force (Enoka et al., 1999; Slifkin and Newell, 2000), and Jones and Wolpert (2002) reported that the mean slope of the log-log regression line between SD and mean force was 1.05. We chose a slope > 0.75 and < 1.25 (Keenan and Valero-Cuevas, 2007) to indicate a log-log linear (slope = 1) scaling consistent with Signal Dependent Noise (Harris and Wolpert, 1998). And second, EMG amplitude is known to scale with force (Inman et al., 1952; Milner-Brown and Stein, 1975; Bigland-Ritchie, 1981), with the EMG/force relation described as either linear or nonlinear - with EMG increasing less rapidly than force at low-to-moderate contraction levels. We chose a slope in the regression line between EMG and force of < 1.05 (Keenan and Valero-Cuevas, 2007) as a liberal estimate of a match with experimental observations so as to not over-constrain the model output a priori.
The flow chart of our simulations and analysis is as follows (Figure 1):
Figure 1.
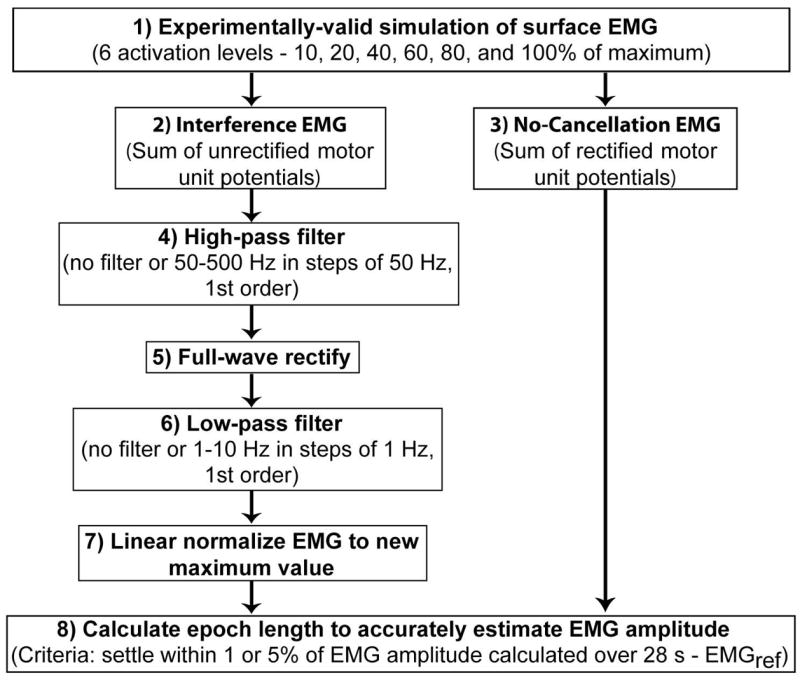
Flow chart of EMG simulation and data analysis steps.
The distribution of motor unit territories within the muscle and interspike intervals were selected at random from uniform and Gaussian distributions, respectively.
The interference EMG was simulated as the sum of motor unit potentials and all data analysis was performed on the middle 28 s during the 30 s constant level of excitation. Activation of the motor-unit pool is modeled as a ramp-and-hold function, with a 1-s ramp increase in excitation to a constant level for 30 s.
The no-cancellation EMG was simulated as the sum of rectified motor unit potentials.
The interference EMG signal was high-pass filtered with a cutoff that varied from 50–500 Hz using a 1st order Butterworth filter.
The interference EMG was full-wave rectified.
The full-wave rectified EMG signal was low-pass filtered with a cutoff that varied from 1–10 Hz using a 1st order Butterworth filter.
The filtered and rectified EMG signal was then linearly normalized as a percentage of the maximum EMG amplitude for each filtering step. The maximum EMG amplitude was calculated over 28 s.
Epochs to accurately estimate EMG amplitude were calculated at 6 levels of excitation from the no-cancellation EMG and from the interference EMG after the different processing steps (4–7). A progressively increasing window (in steps of 0.24 ms because the signal was simulated at 4096 samples/s) was used to determine the epoch when EMG amplitude settled within either 1 or 5% of the EMG calculated from the entire 28 s trial, which served as reference (EMGref).
Epochs from the interference EMG were calculated for all high-pass (n = 11, step 4) and low-pass cutoff frequencies (n = 11, step 6). From the 121 possible combinations, we identified the epoch from the unfiltered interference EMG signal and also the shortest epoch for all combinations of high- and low-pass filters for each excitation level. Also, to calculate the influence of interference in the EMG, epochs were calculated from the no-cancellation EMG and compared with those from the interference EMG. The no-cancellation EMG signal was not filtered. Note that high-pass filtering was applied to the interference EMG signal (step 4) and low-pass filtering (step 6) was applied after rectifying the interference EMG signal (step 5). 1st order Butterworth filters (steps 4 and 6) with zero phase shift were used as suggested in previous studies (Potvin and Brown, 2004; Staudenmann et al., 2007). Also, to compare our results with previous studies, signals that had white noise with identical variance to the interference EMG signals were generated and epochs were determined using the same procedures used on the unfiltered interference EMG.
Because the original equations (Fuglevand et al., 1993a; Farina et al., 2004b) and our implementation (Keenan et al., 2005; Keenan et al., 2006a, b) of the model have been published, the following section will only review key components of the model.
Motor neuron pool model
The distributions of properties across the motor-unit pool were based on the Size Principle (Henneman, 1957), and these included innervation number, twitch force, recruitment threshold, motor-unit territory, and conduction velocity of motor-unit potentials. The distribution of recruitment thresholds for the 381 motor neurons (Table 1) is represented as an exponential function with many low-threshold neurons and progressively fewer high-threshold neurons. The range over which recruitment occurs varied up to 79% of maximal excitation (Table 1), consistent with the wide range found experimentally (Thomas et al., 1986). Each motor unit began discharging at 8 pulses per second (pps) once excitation exceeded the assigned recruitment threshold for that unit, and discharge rates increase linearly with increases in excitation. The interspike interval for motor unit discharge is modeled as a random process with a Gaussian probability distribution function, with the coefficient of variation (CV = 100 × (SD/mean) %) of the interspike intervals fixed for all motor units at 20%. Peak discharge rates were assigned for the first- and last-recruited motor neuron as 28 and 30 pulses per second (pps), respectively (Table 1).
Muscle force generation model
Muscle force is modeled as the impulse response of a critically damped, second-order system (Milner-Brown et al., 1973). A large number of units produce small forces, whereas relatively few units generated large forces. Twitch force is modeled as directly proportional to the number of fibers assigned to each motor neuron (innervation number), and the range in innervation numbers, calculated by dividing the innervation number of the last-recruited motor unit by the first-recruited motor unit, was set at 50x (Table 1). Innervation numbers increase exponentially from the smallest to the largest motor unit. There is an inverse relation between twitch force and twitch contraction time. The first- and last-recruited units are assigned a twitch contraction time to peak of 90 and 30 ms, respectively. All motor units follow the established sigmoidal relation between motor unit force and motor unit discharge rate (Bigland and Lippold, 1954; Kernell et al., 1983; Fuglevand et al., 1993a). Total force of the muscle is calculated as the linear summation of all the individual motor unit forces.
Surface EMG simulations
The planar volume conductor consists of an isotropic fat (3-mm thick) and skin layer (1-mm thick), and an anisotropic muscle layer. Each tissue layer is homogeneous and the conductivity properties of each layer are similar to those reported by Farina et al (2004b). There were 71,487 simulated muscle fibers (Table 1). Average fiber length was 6 cm (Table 1), and the center of the innervation zones was located at 50% of the length of the fibers and in the same transverse location within the volume conductor. The end-plate and insertion of each fiber into the tendons varies randomly (uniform distribution) over a range of 5 mm. The electrodes are simulated as circular (4-mm diameter) and arranged in bipolar pairs (10-mm inter-electrode distance) along the direction of the muscle fibers. The electrodes are located halfway between the innervation zone and the distal tendon and are placed directly over the center of the muscle in the radial direction. The simulation of the intracellular action potential is based on the analytical description of Rosenfalk (1969). Motor units have mean muscle fiber conduction velocities of 3.5 m/s and a spread (SD) of 0.1 m/s (Table 1), with the smallest motor units assigned the slowest conduction velocities (Andreassen and Arendt-Nielsen, 1987). The motor unit potential comprises the sum of the action potentials of the muscle fibers belonging to the motor unit and the surface EMG is simulated by summing the trains of motor unit potentials.
The distribution of the motor units within the muscle (Johnson et al., 1973; Milner-Brown and Stein, 1975) is determined by randomly selecting the x-y coordinates corresponding to the center of each motor unit territory within the circular cross-section of the muscle. The fibers of a motor unit are randomly scattered in the motor unit territory (Stålberg and Antoni, 1980) with a density of 20 fibers/mm2 (Armstrong et al., 1988), and interdigitated with fibers belonging to many other units. The territories of the largest motor units, therefore, are greater than those of the smallest motor units (Bodine et al., 1988). To restrict the distribution of the fibers of a motor unit (Stålberg and Antoni, 1980; Bodine et al., 1988), motor unit territories are modeled as circular (Buchthal et al., 1959). The radius of the motor unit territory is based on the density of 20 fibers/mm2 and the assigned innervation number of the motor unit. However, when a portion of the motor unit territory is constrained by the muscle boundary, the radius of the territory of the unit is augmented to accommodate the required number of motor unit fibers within the new territory while maintaining fiber density.
RESULTS
The Monte Carlo simulations converged after 500 iterations, with 245 simulations that met our criteria to approximate both experimental relations for EMG/force and force/force-variability. Figure 2 shows those 500 Monte Carlo iterations plotted against the required experimental relations. Horizontal and vertical dashed lines indicate boundaries for the fitness criteria representing an approximate match with experimental data (Figure 2), with quadrant IV containing those iterations that match both relations. Figure 3 depicts EMG/force (A) and force/force-variability relations (B) for those 245 valid iterations.
Figure 2.
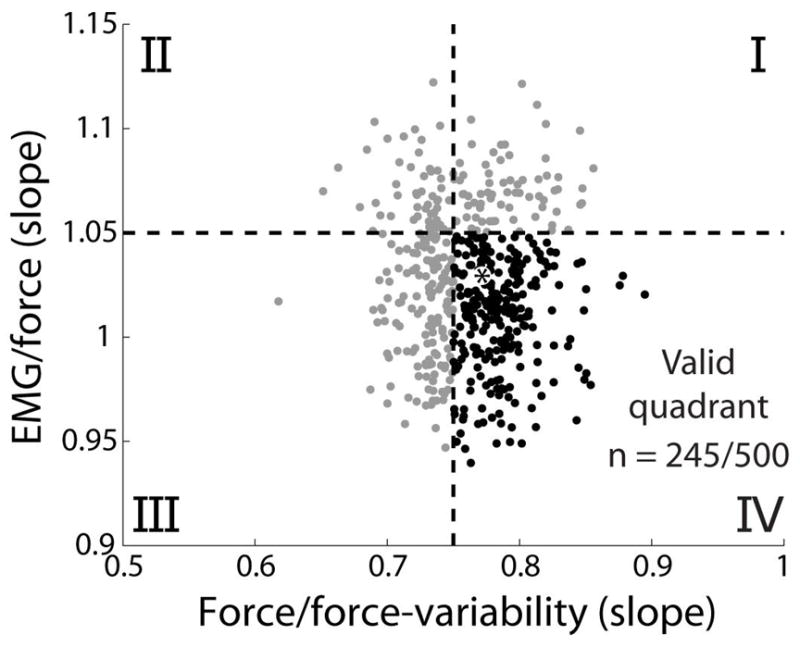
The motor unit model replicated well-established experimental EMG/force and force/force-variability relations for 245 of 500 Monte Carlo iterations. 2 criteria (dashed lines) were used to compare the model results with experimental findings: a near linear increase in force variability with mean force (regression line slope > 0.75), and a near linear or less than linear EMG/force relation (regression line slope < 1.05). Of 500 Monte Carlo iterations, 245 satisfied both criteria (quadrant IV, black). The best parameter set (i.e., that most closely approximated the linear scaling of EMG and force variability with force from our previous study) is shown with a black asterisk and parameter values are reported in Table 1.
Figure 3.
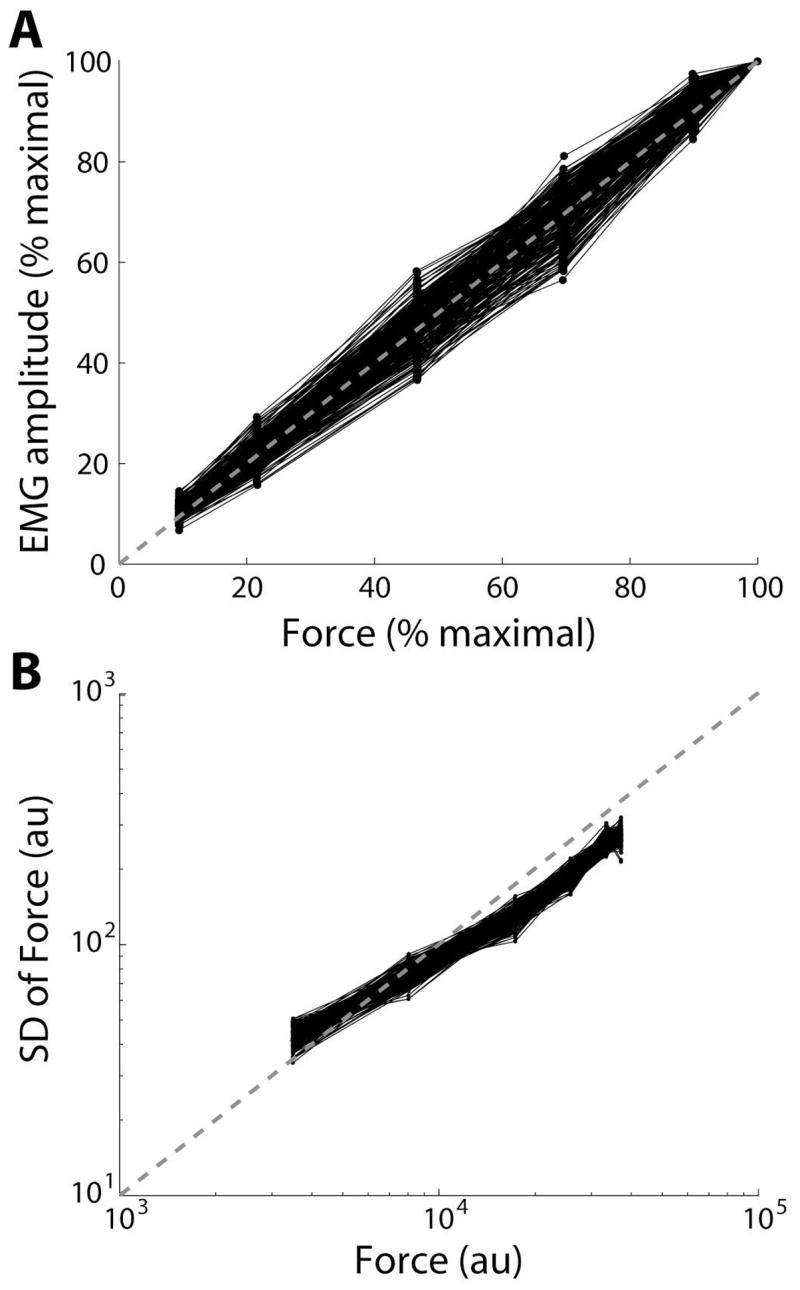
The ability of the motor unit model to match experimental EMG/force and force/force-variability relations is shown. The motor unit model replicated EMG/force and force/force-variability relations for 245 of 500 Monte Carlo iterations. Note the near linear scaling of EMG (A) and force variability (B) with mean force. au = arbitrary units.
High- and low-pass filtering and removal of interference from the EMG led to reductions in the epoch necessary to estimate EMGref. In Figure 4A, representative EMGs are rectified and a 20 ms moving average (bidirectional) was applied (moving average used only for this figure, the influence of moving averages was not addressed in this study). The unfiltered interference EMG (red), filtered (500 Hz high-pass, 1 Hz low-pass) interference EMG (black), no-cancellation EMG (blue), and muscle force (green) were simulated at 100% maximal excitation and normalized to the average EMG amplitude calculated over 28 s (between vertical dashed lines). In Figure 4B, the influence of increasing epochs (one sample [0.24 ms] at a time) is shown for the unfiltered and filtered EMG signals, in addition to the no-cancellation EMG. Values in Figure 4B show the epoch necessary for EMG amplitude estimates to decrease within 1% of EMGref. Epochs decreased from 14.1 to 4.3 s with filtering, and decreased to 0.1 s when amplitude cancellation was prevented. Note that no additional filtering was applied to the no-cancellation EMG to calculate epochs (Figure 1).
Figure 4.
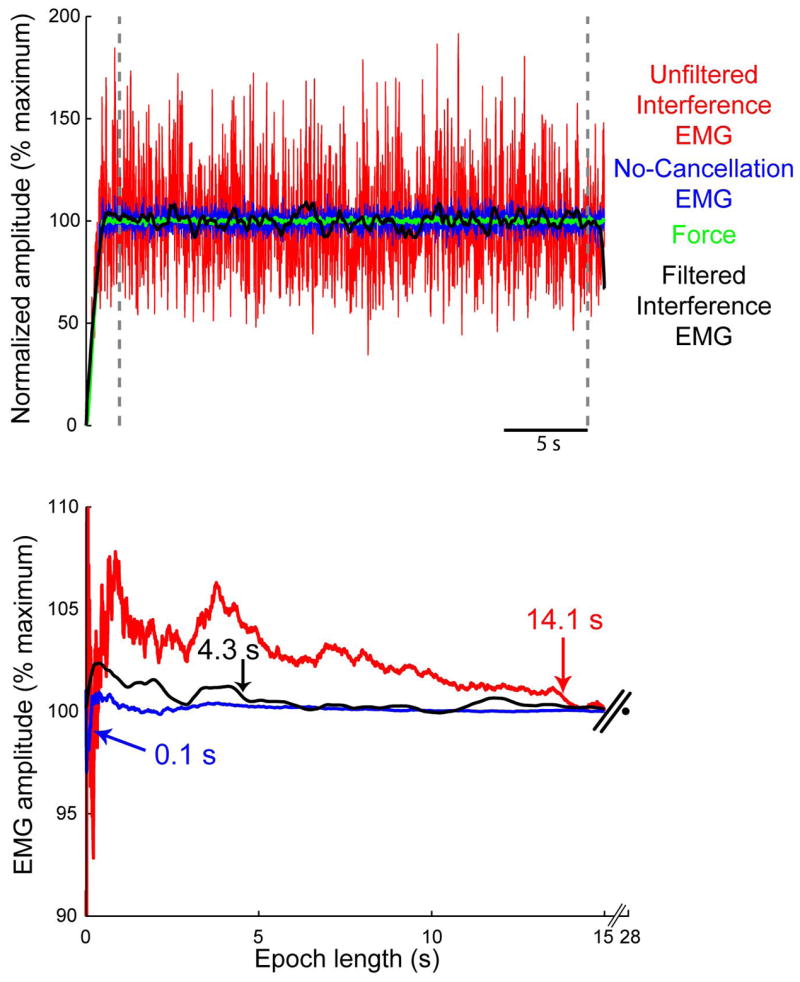
Representative data showing the influence of amplitude cancellation and high-pass filtering on EMG amplitude estimates. Top) Representative EMGs were simulated at 100% maximal excitation and normalized to the average EMG calculated between the vertical dashed lines (28 s). EMGs were rectified and a 20 ms moving average (bidirectional) was applied. The unfiltered interference EMG (red), filtered interference EMG (black), no-cancellation EMG (blue), and muscle force (green) are all shown for the same Monte Carlo iteration. Bottom) Relative to the unfiltered interference EMG, the epoch to estimate EMG amplitude declined from 14.1 to 4.3 s after applying a 500 Hz high-pass filter to the interference EMG and 1 Hz low-pass filter to the rectified EMG. Epochs were substantially shorter when amplitude cancellation was prevented (in blue).
The reduction in epochs to estimate EMG amplitude by high- and low-pass filtering is shown across all 245 trials (mean ± SE) at 6 excitation levels (Figure 5). Results are shown for both criteria used to analyze epochs – a decrease to within 1% (A and C) or 5% (B and D) of EMGref. As there was no systematic effect of excitation level on epoch, we collapsed the data across excitation levels to find that increasing high-pass filter cutoff frequency to 500 Hz, relative to the unfiltered interference EMG, reduced epochs (mean ± SD) from 13.2 ± 5.0 s to 7.8 ± 4.1 s (Figure 5A, within 1% EMGref) and from 1.3 ± 1.0 s to 0.4 ± 0.4 s (Figure 5B, within 5% EMGref). In addition, decreasing low-pass filter cutoff frequency to 1 Hz, while maintaining a 500 Hz high-pass filter cutoff, reduced epochs further to 6.4 ± 4.3 s (Figure 5C, within 1% EMGref) and to 0.1 ± 0.3 s (Figure 5D, within 5% EMGref). Figure 6 shows the histograms with counts for epochs across all excitation levels for the unfiltered EMG (A and B) and filtered EMG signals (C and D). Numbers in Figure 5 correspond with the case presented by the same numbers in Figure 6. When the criterion was epochs within 5% of EMGref (Figure 6B and D), ~85% of all epochs were shorter than 160 ms after applying a 500 Hz high-pass and 1 Hz low-pass filter.
Figure 5.
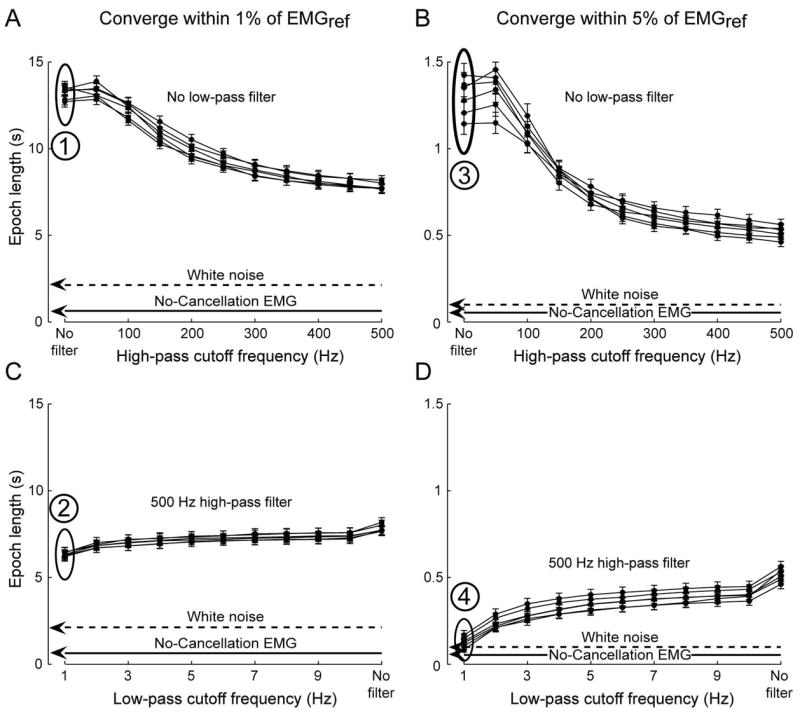
Combinations of high- and low-pass filtering decrease epochs to estimate EMG amplitude, and approach those from the no-cancellation EMG. Results are shown across all 245 Monte Carlo iterations (mean ± SE) at 6 excitation levels for both criteria used to analyze epochs – a decrease to within 1% (A and C) or 5% (B and D) of EMG amplitude calculated over 28 s, which we used as reference (EMGref.). High-pass filtering with cutoffs > 250 Hz resulted in substantial decreases in epoch lengths (A and B), with low pass filters (C and D) contributing to a lesser extent. Numbers and associated ovals in Figure 5 correspond with the case presented by the same numbers as histograms in Figure 6. Performance of the no-cancellation and white noise signals are shown by lines (means across conditions) for clarity, although filtering was not applied to either signal.
Figure 6.
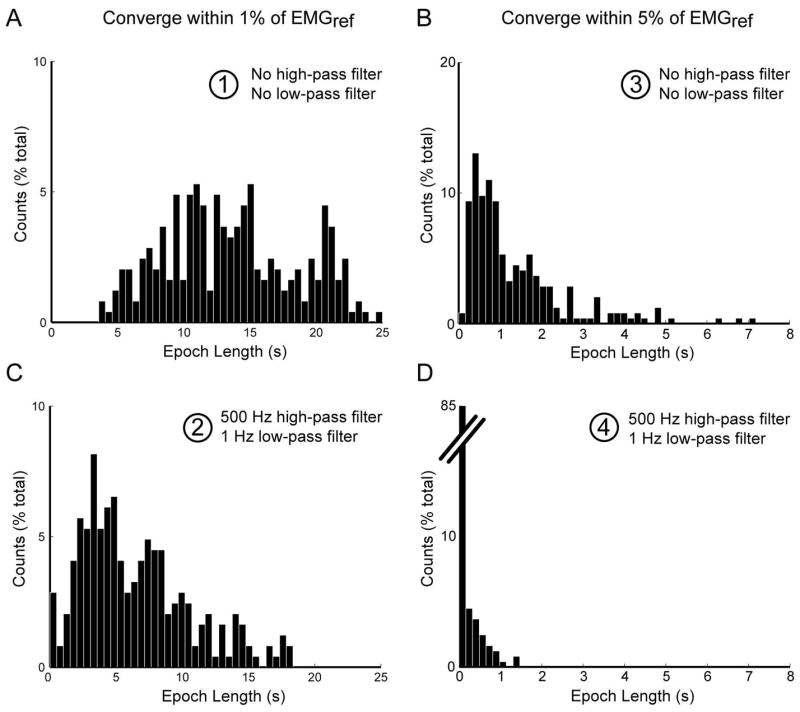
Histograms show the influence of high- and low-pass filtering on epochs to estimate EMG amplitude. Each histogram is generated for the conditions identified in Figure 5 by numbers (1–4) and associated ovals. Counts are shown for epochs derived from the unfiltered EMG (A and B) and filtered EMG (C and D). ~85% of all epochs (within 5% of EMGref, B and D) were shorter than 160 ms after applying a 500 Hz high-pass and 1 Hz low-pass filter.
Epochs were also calculated from the no-cancellation EMG and white noise signals (mean values for each condition in Figure 5) and are shown as lines for clarity, although filtering was not applied to either signal. For the criteria within 1% and 5% EMGref, epochs for the no-cancellation EMG (mean ± SD across 6 excitation levels and 245 trials) were 0.64 ± 0.38 s (Figure 5A and C) and 0.05 ± 0.03 s (Figure 5B and D), respectively. Also, epochs for the white noise signal (mean ± SD across 245 trials and 6 levels of variance matching the interference EMG from each trial) were 2.45 ± 1.82 s (Figure 5A and C) and 0.11 ± 0.09 s (Figure 5B and D), respectively. Thus, epochs were substantially shorter for the no-cancellation EMG and white noise signals, relative to epochs from the interference EMG. Also, epochs derived from the filtered interference EMG approached the length of epochs derived from the no-cancellation EMG and white noise signals with high-pass filter cutoffs > 250 Hz and low-pass filter cutoffs < 2 Hz, specifically when using the 5% EMGref criterion (Figure 5D).
DISCUSSION
We used a motor-unit model of surface EMG to evaluate the influence of high-pass filtering and amplitude cancellation on the necessary epoch to accurately estimate average EMG amplitude. Developing methods to improve information extraction from measures commonly derived from the interference EMG (e.g., amplitude, timing, and frequency content) are critical to improve our understanding of neuromuscular function. As an alternative to the common use of phenomenological models to examine the epoch necessary to estimate EMG amplitude, we used a state-of-the-art motor-unit model of EMG, and carefully evaluated whether the EMG signals simulated by that model were experimentally realistic. We used a Monte Carlo approach to certify that our results are robust to the inherent variability in motor unit locations and interspike intervals, and are consistent with the well-established scaling of EMG amplitude and force variability with force magnitude. Thus, running additional simulations will not change our results substantially. Our results find that high-pass filtering (> 250 Hz) the interference EMG signal results in substantially shorter epochs necessary to reliably and accurately estimate EMG amplitudes. Moreover, after carefully evaluating alternative explanations, we conclude that that the need to use long epochs to accurately estimate EMG amplitude is likely the result of unavoidable amplitude cancellation. These results continue to clarify why high-pass filtering (> 250 Hz) improves EMG estimates and the extraction of physiologically relevant information. We begin by discussing limitations and finish by indicating how our results suggest strategies to improve information extraction from EMG.
The results of the current study should be interpreted with respect to the limitations of the modeling approach, which we do not believe affect the validity of our conclusions. Due to previously identified limitations in the current model structure, we fixed most parameters to generate experimentally realistic data (Figures 2 and 3). This approach does not address all the sources of variability in estimates of EMG amplitude. However, even when fixing most parameters in the model, a large degree of variability is still introduced in our output measures (Figure 2 and 6), solely by varying interspike intervals and random motor unit locations in the muscle. Also, we did not directly address the influence of whitening the interference EMG because high-pass filtering with a low-order filter has been reported to approximate whitening with equal power at all frequencies in the filtered EMG signal (Potvin and Brown, 2004; Staudenmann et al., 2007). Although we did not directly assess the ability of these processing methods to remove the correlation structure present in the EMG (Clancy et al., 2002), or to improve the pick-up area of the recording electrodes (Staudenmann et al., 2007), the predominant determinate of the epoch to accurately estimate EMG amplitude was amplitude cancellation. Also, the 1% and 5% settling time metric in this study was used to provide two examples of the advantage of high-pass filtering, not to replace more common standard error metrics (Farina and Merletti, 2000; Clancy et al., 2002). Lastly, we did not simulate the influence of all the different sources of noise in the EMG, or techniques to attenuate the influence of this noise (reviewed in Clancy et al., 2002), which may pose additional limitations on any techniques to extract information from the EMG.
High-pass filtering with cutoff frequencies > 250 Hz results in substantial decreases in epochs to reliably and accurately estimate EMG amplitude. This result is consistent with a growing number of reports that suggest that attenuating power in the interference EMG at low-frequencies improves estimates of EMG amplitude (Clancy and Hogan, 1994; Farina and Merletti, 2000; Clancy et al., 2002; Potvin and Brown, 2004; Staudenmann et al., 2007). However, using high-pass filters > 250 Hz is in direct contrast to the high-pass filter cutoffs (< 30 Hz) commonly used (Fuglevand et al., 1993b; Valero-Cuevas et al., 1998; Thoroughman and Shadmehr, 1999; Kilner et al., 2000; Laidlaw et al., 2002). Nevertheless, Figure 6B and D show a clear example of the benefit of high-pass filtering at frequencies > 250 Hz: for a same level of accuracy in estimating EMG amplitude (i.e. within 5% of EMGref), epoch declined more than 10x when applying a 500 Hz high-pass and 1 Hz low-pass filter. Thus, appropriate combinations of high- and low-pass filter settings can lead to significant reductions in the epoch necessary to estimate EMG amplitude. This result is likely of greatest importance when the epoch over which to average the EMG is limited (e.g., during brief MVCs or following changes in EMG amplitude during time-varying contractions).
We find that the necessity to use long epochs to accurately estimate EMG amplitude is likely the result of unavoidable amplitude cancellation, which further clarifies why high-pass filtering (> 250 Hz) improves EMG amplitude estimates and the extraction of physiologically relevant information. Amplitude cancellation dominates measures of epoch length, as is evident by comparing epochs derived from the interference EMG with those from the no-cancellation EMG (Figure 5). The mechanisms by which amplitude cancellation influences epoch length to estimate EMG amplitude are not fully known. Certainly, high-pass filtering performs like signal whitening (Potvin & Brown 2004) to reduce the variance of amplitude estimates by removing the temporal correlation present among neighboring EMG samples (Clancy and Hogan, 1994; Clancy et al., 2001). We propose two additional advantages of high-pass filtering. First, it is possible that high-pass filtering of the signal preferentially magnifies the contribution of the high-frequency, monophasic end-fiber effects (Dimitrova et al., 2002) in the EMG and leads to a more faithful representation and a better balance between deep and superficial motor unit contributions to the EMG signal, as previously suggested by Staudenmann et al. (2007). However, this is an unlikely contributor to the current results as bipolar electrodes were simulated and they were not positioned at the ends of the muscle, where the influence of end-fiber effects is greatest (Dimitrova et al., 2002). We believe it is more likely that a phenomenon like beating observed in superimposed waves (defined as the interference between two waves at different frequencies) may artificially introduce low-frequency oscillations, and therefore artifactually increase power at those frequencies (Halliday et al., 2003). Uncovering the underlying mechanisms of amplitude cancellation, and their influence on epoch to estimate EMG amplitude, requires further investigation.
Acknowledgments
Work supported by US National Science Foundation (NSF) Grant 0237258 and US National Institutes of Health (NIH) grants R21-HD048566, R01-AR050520, R01-AR052345. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institute of Arthritis and Musculoskeletal and Skin Diseases (NIAMS), the National Institute of Childhood and Human Development (NICHD), the NIH, or the NSF.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andreassen S, Arendt-Nielsen L. Muscle fibre conduction velocity in motor units of the human anterior tibial muscle: a new size principle parameter. J Physiol. 1987;391:561–571. doi: 10.1113/jphysiol.1987.sp016756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong JB, Rose PK, Vanner S, Bakker GJ, Richmond FJ. Compartmentalization of motor units in the cat neck muscle, biventer cervicis. J Neurophysiol. 1988;60:30–45. doi: 10.1152/jn.1988.60.1.30. [DOI] [PubMed] [Google Scholar]
- Bigland B, Lippold OCJ. The relation between force, velocity and integrated electrical activity in human muscles. J Physiol. 1954;123:214–224. doi: 10.1113/jphysiol.1954.sp005044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bigland-Ritchie B. EMG/force relations and fatigue of human voluntary contractions. Exerc Sport Sci Rev. 1981;9:75–117. [PubMed] [Google Scholar]
- Bodine SC, Garfinkel A, Roy RR, Edgerton VR. Spatial distribution of motor unit fibers in the cat soleus and tibialis anterior muscles: local interactions. J Neurosci. 1988;8:2142–2152. doi: 10.1523/JNEUROSCI.08-06-02142.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botteron GW, Cheney PD. Corticomotoneuronal postspike effects in averages of unrectified EMG activity. J Neurophysiol. 1989;62:1127–1139. doi: 10.1152/jn.1989.62.5.1127. [DOI] [PubMed] [Google Scholar]
- Buchthal F, Erminio F, Rosenfalck P. Motor unit territory in different human muscles. Acta Physiol Scand. 1959;45:72–87. doi: 10.1111/j.1748-1716.1959.tb01678.x. [DOI] [PubMed] [Google Scholar]
- Cannon RJ, Cafarelli E. Neuromuscular adaptations to training. J Appl Physiol. 1987;63:2396–2402. doi: 10.1152/jappl.1987.63.6.2396. [DOI] [PubMed] [Google Scholar]
- Clancy EA, Hogan N. Single site electromyograph amplitude estimation. IEEE Trans Biomed Eng. 1994;41:159–167. doi: 10.1109/10.284927. [DOI] [PubMed] [Google Scholar]
- Clancy EA, Bouchard S, Rancourt D. Estimation and application of EMG amplitude during dynamic contractions. IEEE Eng Med Biol Mag. 2001;20:47–54. doi: 10.1109/51.982275. [DOI] [PubMed] [Google Scholar]
- Clancy EA, Morin EL, Merletti R. Sampling, noise-reduction and amplitude estimation issues in surface electromyography. J Electromyogr Kinesiol. 2002;12:1–16. doi: 10.1016/s1050-6411(01)00033-5. [DOI] [PubMed] [Google Scholar]
- Day SJ, Hulliger M. Experimental simulation of cat electromyogram: evidence for algebraic summation of motor-unit action-potential trains. J Neurophysiol. 2001;86:2144–2158. doi: 10.1152/jn.2001.86.5.2144. [DOI] [PubMed] [Google Scholar]
- Dimitrova NA, Dimitrov GV, Nikitin OA. Neither high-pass filtering nor mathematical differentiation of the EMG signals can considerably reduce crosstalk. J Electromyogr Kinesiol. 2002;12:235–246. doi: 10.1016/s1050-6411(02)00008-1. [DOI] [PubMed] [Google Scholar]
- Enoka RM, Burnett RA, Graves AE, Kornatz KW, Laidlaw DH. Task- and age-dependent variations in steadiness. Prog Brain Res. 1999;123:389–395. doi: 10.1016/s0079-6123(08)62873-3. [DOI] [PubMed] [Google Scholar]
- Enoka RM, Christou EA, Hunter SK, Kornatz KW, Semmler JG, Taylor AM, Tracy BL. Mechanisms that contribute to differences in motor performance between young and old adults. J Electromyogr Kinesiol. 2003;13:1–12. doi: 10.1016/s1050-6411(02)00084-6. [DOI] [PubMed] [Google Scholar]
- Farina D, Merletti R. Comparison of algorithms for estimation of EMG variables during voluntary isometric contractions. J Electromyogr Kinesiol. 2000;10:337–349. doi: 10.1016/s1050-6411(00)00025-0. [DOI] [PubMed] [Google Scholar]
- Farina D, Merletti R. A novel approach for precise simulation of the EMG signal detected by surface electrodes. IEEE Trans Biomed Engin. 2001;48:637–646. doi: 10.1109/10.923782. [DOI] [PubMed] [Google Scholar]
- Farina D, Fosci M, Merletti R. Motor unit recruitment strategies investigated by surface EMG variables. J Appl Physiol. 2002a;92:235–247. doi: 10.1152/jappl.2002.92.1.235. [DOI] [PubMed] [Google Scholar]
- Farina D, Merletti R, Enoka RM. The extraction of neural strategies from the surface EMG. J Appl Physiol. 2004a;96:1486–1495. doi: 10.1152/japplphysiol.01070.2003. [DOI] [PubMed] [Google Scholar]
- Farina D, Mesin L, Martina S, Merletti R. A surface EMG generation model with multilayer cylindrical description of the volume conductor. IEEE Trans Biomed Eng. 2004b;51:415–426. doi: 10.1109/TBME.2003.820998. [DOI] [PubMed] [Google Scholar]
- Farina D, Madeleine P, Graven-Nielsen T, Merletti R, Arendt-Nielsen L. Standardising surface electromyogram recordings for assessment of activity and fatigue in the human upper trapezius muscle. Eur J Appl Physiol. 2002b;86:469–478. doi: 10.1007/s00421-001-0574-0. [DOI] [PubMed] [Google Scholar]
- Fortier PA. Use of spike triggered averaging of muscle activity to quantify inputs to motoneuron pools. J Neurophysiol. 1994;72:248–265. doi: 10.1152/jn.1994.72.1.248. [DOI] [PubMed] [Google Scholar]
- Fuglevand AJ, Winter DA, Patla AE. Models of recruitment and rate coding organization in motor-unit pools. J Neurophysiol. 1993a;70:2470–2488. doi: 10.1152/jn.1993.70.6.2470. [DOI] [PubMed] [Google Scholar]
- Fuglevand AJ, Zackowski KM, Huey KA, Enoka RM. Impairment of neuromuscular propagation during human fatiguing contractions at submaximal forces. J Physiol. 1993b;460:549–572. doi: 10.1113/jphysiol.1993.sp019486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gandevia SC. Spinal and supraspinal factors in human muscle fatigue. Physiol Rev. 2001;81:1725–1789. doi: 10.1152/physrev.2001.81.4.1725. [DOI] [PubMed] [Google Scholar]
- Gazzoni M, Farina D, Merletti R. A new method for the extraction and classification of single motor unit action potentials from surface EMG signals. J Neurosci Meth. 2004;136:165–177. doi: 10.1016/j.jneumeth.2004.01.002. [DOI] [PubMed] [Google Scholar]
- Hakkinen K, Komi PV. Electromyographic changes during strength training and detraining. Med Sci Sports Exerc. 1983;15:455–460. [PubMed] [Google Scholar]
- Halliday D, Resnick R, Walker J. Fundamentals of physics. 6. New York: Wiley; 2003. [Google Scholar]
- Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394:780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
- Henneman E. Relation between size of neurons and their susceptibility to discharge. Science. 1957;126:1345–1347. doi: 10.1126/science.126.3287.1345. [DOI] [PubMed] [Google Scholar]
- Inman VT, Ralston HJ, Saunders JB, Feinstein B, Wright EW. Relation of human electromyogram to muscular tension. Electroencephalogr Clin Neurophysiol. 1952;4:187–194. doi: 10.1016/0013-4694(52)90008-4. [DOI] [PubMed] [Google Scholar]
- Johnson MA, Polgar J, Weightman D, Appleton D. Data on the distribution of fibre types in thirty-six human muscles. An autopsy study. J Neurol Sci. 1973;18:111–129. doi: 10.1016/0022-510x(73)90023-3. [DOI] [PubMed] [Google Scholar]
- Jones KE, Hamilton A, Wolpert DM. The sources of signal dependent noise during isometric force production. J Neurophysiol. 2002;88:1533–1544. doi: 10.1152/jn.2002.88.3.1533. [DOI] [PubMed] [Google Scholar]
- Keenan KG, Valero-Cuevas FJ. Identification of parameter sets for experimentally valid simulation of motor units. 17th Annual Meeting of the Neural Control of Movement Meeting; Seville, Spain. 2007. [Google Scholar]
- Keenan KG, Farina D, Merletti R, Enoka RM. Influence of motor unit properties on the size of the simulated evoked surface EMG potential. Exp Brain Res. 2006a;169:3749. doi: 10.1007/s00221-005-0126-7. [DOI] [PubMed] [Google Scholar]
- Keenan KG, Farina D, Merletti R, Enoka RM. Amplitude cancellation reduces the size of motor unit potentials averaged from the surface EMG. J Appl Physiol. 2006b;100:1928–1937. doi: 10.1152/japplphysiol.01282.2005. [DOI] [PubMed] [Google Scholar]
- Keenan KG, Farina D, Maluf KS, Merletti R, Enoka RM. Influence of amplitude cancellation on the simulated electromyogram. J Appl Physiol. 2005;98:120–131. doi: 10.1152/japplphysiol.00894.2004. [DOI] [PubMed] [Google Scholar]
- Kernell D, Eerbeek O, Verhey BA. Motor unit categorization on basis of contractile properties: an experimental analysis of the composition of the cat’s m. peroneus longus. Exp Brain Res. 1983;50:211–219. doi: 10.1007/BF00239185. [DOI] [PubMed] [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Hari R, Lemon RN. Human cortical muscle coherence is directly related to specific motor parameters. J Neurosci. 2000;20:8838–8845. doi: 10.1523/JNEUROSCI.20-23-08838.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo PL, Lee DL, Jindrich DL, Dennerlein JT. Finger joint coordination during tapping. J Biomech. 2006;39:2934–2942. doi: 10.1016/j.jbiomech.2005.10.028. [DOI] [PubMed] [Google Scholar]
- Laidlaw DH, Hunter SK, Enoka RM. Nonuniform activation of the agonist muscle does not covary with index finger acceleration in old adults. J Appl Physiol. 2002;93:1400–1410. doi: 10.1152/japplphysiol.00391.2002. [DOI] [PubMed] [Google Scholar]
- Lowery MM, Stoykov NS, Kuiken TA. A simulation study to examine the use of cross-correlation as an estimate of surface EMG cross talk. J Appl Physiol. 2003;94:1324–1334. doi: 10.1152/japplphysiol.00698.2002. [DOI] [PubMed] [Google Scholar]
- McGill KC. Surface electromyogram signal modelling. Med Biol Eng Comput. 2004;42:446–454. doi: 10.1007/BF02350985. [DOI] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB. The relation between the surface electromyogram and muscular force. J Physiol. 1975;246:549–569. doi: 10.1113/jphysiol.1975.sp010904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milner-Brown HS, Stein RB, Yemm R. Changes in firing rate of human motor units during linearly changing voluntary contractions. J Physiol. 1973;230:371–390. doi: 10.1113/jphysiol.1973.sp010193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore AD. Synthesized EMG waves and their implications. Am J Phys Med. 1967;46:1302–1316. [PubMed] [Google Scholar]
- Person RS, Libkind MS. Simulation of electromyograms showing interference patterns. Electroencephalogr Clin Neurophysiol. 1970;28:625–632. doi: 10.1016/0013-4694(70)90205-1. [DOI] [PubMed] [Google Scholar]
- Potvin JR, Brown SH. Less is more: high pass filtering, to remove up to 99% of the surface EMG signal power, improves EMG-based biceps brachii muscle force estimates. J Electromyogr Kinesiol. 2004;14:389–399. doi: 10.1016/j.jelekin.2003.10.005. [DOI] [PubMed] [Google Scholar]
- Rosenfalck P. Intra- and extracellular potential fields of active nerve and muscle fibers. Acta Physiol Scand. 1969;(Suppl 47):239–246. [PubMed] [Google Scholar]
- Rösler KM, Petrow E, Mathis J, Arányi Z, Hess CW, Magistris MR. Effect of discharge desynchronization on the size of motor evoked potentials: an analysis. Clin Neurophysiol. 2002;113:1680–1687. doi: 10.1016/s1388-2457(02)00263-8. [DOI] [PubMed] [Google Scholar]
- Rudroff T, Barry BK, Stone AL, Barry CJ, Enoka RM. Accessory muscle activity contributes to the variation in time to task failure for different arm postures and loads. J Appl Physiol. 2007;102:1000–1006. doi: 10.1152/japplphysiol.00564.2006. [DOI] [PubMed] [Google Scholar]
- Santos VJ, Valero-Cuevas FJ. Reported anatomical variability naturally leads to multimodal distributions of Denavit-Hartenberg parameters for the human thumb. IEEE Trans Biomed Eng. 2006;53:155–163. doi: 10.1109/TBME.2005.862537. [DOI] [PubMed] [Google Scholar]
- Schieber MH. Muscular production of individuated finger movements: the roles of extrinsic finger muscles. J Neurosci. 1995;15:284–297. doi: 10.1523/JNEUROSCI.15-01-00284.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slifkin AB, Newell KM. Variability and noise in continuous force production. J Mot Behav. 2000;32:141–150. doi: 10.1080/00222890009601366. [DOI] [PubMed] [Google Scholar]
- Stålberg E, Antoni L. Electrophysiological cross section of the motor unit. J Neurol Neurosurg Psychiatry. 1980;43:469–474. doi: 10.1136/jnnp.43.6.469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Staudenmann D, Potvin JR, Kingma I, Stegeman DF, van Dieen JH. Effects of EMG processing on biomechanical models of muscle joint systems: sensitivity of trunk muscle moments, spinal forces, and stability. J Biomech. 2007;40:900–909. doi: 10.1016/j.jbiomech.2006.03.021. [DOI] [PubMed] [Google Scholar]
- Stegeman DF, Blok JH, Hermens HJ, Roeleveld K. Surface EMG models: properties and applications. J Electromyogr Kinesiol. 2000;10:313–326. doi: 10.1016/s1050-6411(00)00023-7. [DOI] [PubMed] [Google Scholar]
- Thomas CK, Ross BH, Stein RB. Motor-unit recruitment in human first dorsal interosseous muscle for static contractions in three different directions. J Neurophysiol. 1986;55:1017–1029. doi: 10.1152/jn.1986.55.5.1017. [DOI] [PubMed] [Google Scholar]
- Thoroughman KA, Shadmehr R. Electromyographic correlates of learning an internal model of reaching movements. J Neurosci. 1999;19:8573–8588. doi: 10.1523/JNEUROSCI.19-19-08573.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Zajac FE, Burgar CG. Large index-fingertip forces are produced by subject-independent patterns of muscle excitation. J Biomech. 1998;31:693–703. doi: 10.1016/s0021-9290(98)00082-7. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ, Johanson ME, Towles JD. Towards a realistic biomechanical model of the thumb: the choice of kinematic description may be more critical than the solution method or the variability/uncertainty of musculoskeletal parameters. J Biomech. 2003;36:1019–1030. doi: 10.1016/s0021-9290(03)00061-7. [DOI] [PubMed] [Google Scholar]


