Deconvolving an Estimate of Breath Measured Blood Alcohol Concentration from Biosensor Collected Transdermal Ethanol Data

Abstract

Biosensor measurement of transdermal alcohol oncentration in perspiration exhibits significant variance from subject to subject and device to device. Short duration data collected in a controlled clinical setting is used to calibrate a forward model for ethanol transport from the blood to the sensor. The calibrated model is then used to invert transdermal signals collected in the field (short or long duration) to obtain an estimate for breath measured blood alcohol concentration. A distributed parameter model for the forward transport of ethanol from the blood through the skin and its processing by the sensor is developed. Model calibration is formulated as a nonlinear least squares fit to data. The fit model is then used as part of a spline based scheme in the form of a regularized, non-negatively constrained linear deconvolution. Fully discrete, steepest descent based schemes for solving the resulting optimization problems are developed. The adjoint method is used to accurately and efficiently compute requisite gradients. Efficacy is demonstrated on subject field data.

1. Introduction

The idea of using transdermal alcohol to measure blood alcohol concentration (BAC)originated in the 1930’s, when it was determined that ingested ethanol can be measured in perspiration in concentrations that are approximately equal to its concentration in the blood [17].The appeal of a skin surface based sensor is that it is noninvasive, passive, and relatively simple to use. Giner, Inc. of Newton, Massachusetts, has developed the Transdermal Alcohol Sensor/Recorder (TAS) named WrisTAS™,(see Figure 1.1 below), a wearable electrochemical detector. It measures transdermal alcohol continuously, samples the alcohol, skin temperature and skin resistance signals every 10–30 seconds and stores average values at predetermined intervals ranging from 0.5 to 10 minutes for later retrieval. Placed on the skin surface, the sensor oxidizes ethanol in a continuous manner, generating a current that is linearly related to the local alcohol concentration. It responds to 10–200 mg/dl BAC with a lag time of ~30 minutes to plateau. The electrochemical sensor is specific for ethanol; it does not respond to oxygen, CO or acetone at their maximum physiological levels. Detailed descriptions of the development and performance of the Giner transdermal alcohol sensors can be found in [24], [25], [26] and [27]. In addition, other researchers have studied and utilized other devices that measure alcohol content in perspiration (see, for example, [1]).

FIGURE 1.1.

The Giner WrisTAS V.

The Giner WrisTAS V was developed primarily to monitor alcohol abstinence, rather than to provide quantitative measurements of BAC. However, the accurate and reliable determination of BAC over both short and long time periods is important for treatment, research and forensic applications. Adapting the Giner device to the more challenging task of providing a quantitative estimate of BAC from TAS field data, requires the development of a sophisticated data analysis system that is capable of teasing the BAC signal out of the observed transdermal alcohol concentration (TAC) signal. Ultimately, for the system to be truly commercially viable, extracting BAC from the transdermal signal will have to be at best, only minimally, or superficially, and statistically quantifiably, subject and device dependent. Currently BAC is estimated by measuring breath alcohol concentration (BrAC). Breath analyzers, at least as they are currently used in practice, are not calibrated to each individual subject. These instruments estimate BAC via an idealized linear stoichiometric calculation based on Henry’s law. (In fact, the relationship between BAC and BrAC is not so simple and actually may vary from instrument to instrument and individual to individual. More about this later.)

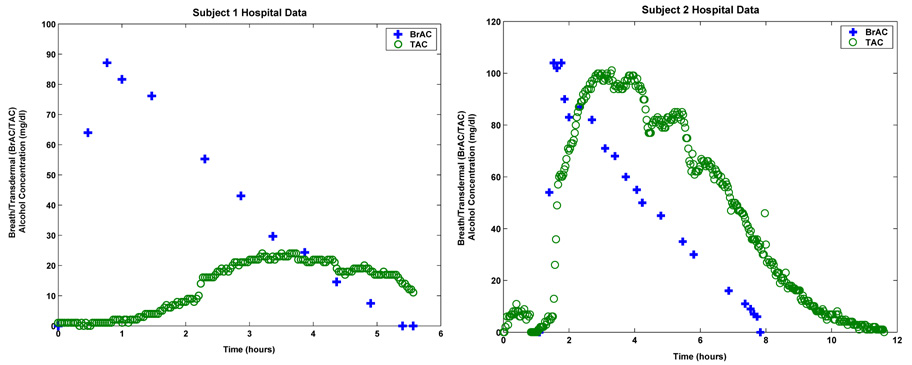
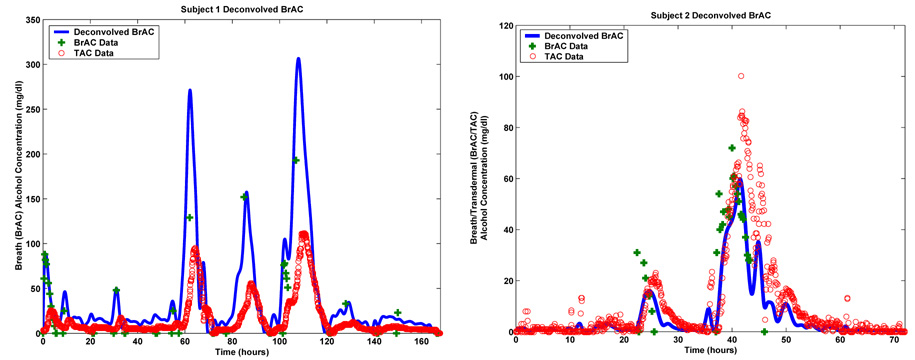
Unfortunately, at least at this point, a similar patient and device independent calibration involving a single linear gain, simply will not work in the case of transdermal measurements. Indeed, this is immediately clear from the two plots shown in Figure 1.2. These plots show the resulting BrAC measurements and TAC measurements yielded by two different Giner sensors worn by two different but equivalently dosed subjects. Assuming the breath measurements to be ground truth, one readily observes significant differences in decay rates and attenuation, not to mention many other less obvious quantitative and qualitative variations between the two subjects. Consequently, it becomes clear that obtaining any kind of meaningful estimate of BAC from the TAC data provided by the TAS device will require some sort of subject and device dependent calibration. At this point, the best one could envision in the case of the Giner device, would be a data analysis system that is calibrated to the individual subject but only based on readily observable covariates (e.g. height, weight, sex, age, etc.) statistically determined via population analysis.

FIGURE 1.2.

Breath and transdermal data for Subject 1 (left) and Subject 2 (right).

The current protocol for using the Giner sensor in either a research or clinical setting allows for the obtaining of breath based calibration data in a controlled clinical setting before the subject is sent out into the field wearing the device. We develop and test an approach that uses the data obtained in the clinic to first calibrate a model for ethanol transport and analysis to both the individual subject and the sensor unit employed, and then, based on this calibration, provides an estimate of BrAC from the transdermal alcohol signal measured by the TAS sensor in the field.

Central to our approach is a mathematical model for the forward transport of ethanol from the blood through the skin to the TAS sensor (forward model). We require a model that on the one hand is sophisticated enough to capture the dynamics of the underlying physical and physiological processes, and on the other is simple enough to allow for 1) the estimation of the individual subject and device dependent parameters appearing in the model during a calibration phase and 2) the use of the model to estimate BrAC from the TAC signal. Since our interest here is the transport of ethanol from the blood through the device to the skin, BAC can be thought of as an exogenous input and our model need not capture the typically nonlinear Michaelis-Menten kinetics associated with the enzymatic metabolism of alcohol in the liver. Some studies (see, for example, [5]) have shown that there is some enzymatic metabolism of ethanol in the skin, and our general approach should allow for the inclusion of this effect if so desired.

We formulate the TAC inversion as a two phase process. First a calibration phase is formulated as a nonlinear least squares fit to data in which a particular subject’s and device’s parameters in the model are estimated based on simultaneous short duration breath and transdermal measurements collected in a clinical or hospital setting. A second inversion phase in which the resulting fit model is used to obtain an estimate of BrAC from transdermal measurements made by the sensor in the field (short or long duration) then follows. This second estimation problem is in general, formulated as a non-negatively constrained nonlinear least squares fit. However, if the underlying model is in fact linear, the second phase takes the form of a non-negatively constrained deconvolution problem which can be formulated and solved as a quadratic program. In any case, solving the two optimization problems that are at the heart of the calibration and inversion phases of the process require the accurate and efficient computation of gradients. To accomplish this we employ a highly efficient adjoint based method that provides exact or analytic (i.e. zero truncation error) gradients.

Although the general approach and framework we develop here can be used with any one of a number of models for the forward transport of ethanol from the blood to the sensor (for example, ARMA, neural network, response surface, etc.), we have chosen to illustrate our approach using a quai-first principles, quasi-physiologically based model consisting of a coupled system of ordinary (ODE) and partial (PDE) differential equations. The use of a model that has at least some physiological basis as opposed to a completely non-physical input-output model, may tend to increase the level of mathematical complexity. But on the other hand, such a model has the potential to capture more of the essential dynamics of the process while reducing the number of parameters that have to be estimated in the calibration phase. We looked at a number of different models of this general form with varying degrees of complexity (see [6]) and did not observe significant variations in accuracy and performance. Our primary focus here is the general formulation of our approach in terms of input/output modeling, calibration and inversion, and consequently we illustrate it with one particular transport model with the implicit understanding that a variety of models could be used in its place to obtain similar results. It is also worth noting that in [1], a PDE based model for transdermal transport of alcohol is developed and validated via simulation studies. This modeling effort involved using data provided by a somewhat different, but similar transdermal sensor. Its primary intent was the development of sophisticated and validated models for the forward transport of ethanol through the skin and not the active inversion of the transdermal signal to produce an estimate of BAC as is done here. Ranges of values for the numerous physiological parameters that appear in the model developed in [1] are obtained from the experimental literature and the results of simulation studies are then compared to patient data. It would be straight forward to use the model developed and the device described in [1] in the context of our inversion framework. Although, as is the case for the model we employ in this effort, it is likely that a great many of the numerous parameters appearing in the model in [1] would ultimately prove to be unidentifiable from TAC data. However, we reiterate that while the injectivity of the parameters to data map would be welcome, its absence does not appear to have serious consequences for what we are attempting here. Finally, we note that since PDE based models are both infinite dimensional and continuous in time, the computational algorithms for solving the resulting nonlinear least squares problems in both phases of our inversion scheme will require discretization in both time and space. Because discretization of PDEs typically results in high dimensional approximating systems of difference equations that will necessarily have to be solved numerous times in each iteration of any gradient based optimization scheme, the use of the adjoint method to efficiently produce accurate gradients becomes highly desirable if not absolutely essential.

In Section 2, we develop an abstract framework for a two phase inversion process. We describe the calibration and inversion phases and their formulation as nonlinear least squares estimation problems. When the model is linear, we show how the inversion takes the form of a non-negatively constrained regularized deconvolution problem that can be formulated as a quadratic program. In Section 3 we develop a PDE based model for the forward transport of ethanol through the skin and show how it can be used in the context of the abstract framework developed in Section 2. In the fourth section we discuss some issues relating to the convergence of the approximations used in the discretization of the infinite dimensional continuous time model developed in Section 3. We also discuss the actual implementation of the adjoint method for computing gradients that was introduced in Section 2. In Section 5, we present the results of our numerical studies involving actual patient data, while Section 6 contains some discussion of our results and a few concluding remarks.

2. A Two Phase Abstract Inversion Process for Estimating BrAC from TAC Measurements

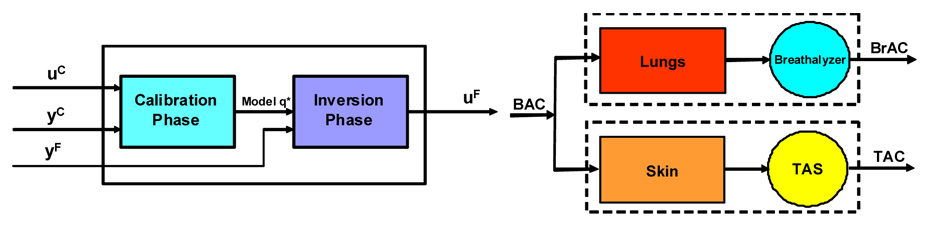
We formulate our inversion scheme as an input/output process with two phases; a calibration phase in which a controlled dose of alcohol is administered and simultaneous breath and transdermal data is collected in a hospital or clinical setting, and an inversion phase in which, in general much longer duration, field measurements of transdermal alcohol is provided by the sensor. The first set of data, which we refer to as the calibration data consists of two time series, BrAC measurements $u^C={\left\{u_k^C\right\}}_{k=1}^{L_1}$ obtained by having the subject periodically blow into a breath analyzer, and TAC measurements $y^C={\left\{y_k^C\right\}}_{k=1}^{L_2}$ obtained by the sensor. This data set is used to fit a forward model for the transport of ethanol from the blood through the skin and the processing and measurement of the ethanol by the sensor. The second set of data, which we shall refer to as the field data consists of a single relatively long time series of TAC measurements $y^F={\left\{y_k^F\right\}}_{k=1}^M$ provided by the TAS sensor. Our over all goal is to obtain an estimate for the breath estimated blood alcohol concentration in the field, i.e., the BrAC, ${\widehat{u}}^F={\left\{{\widehat{u}}_k^F\right\}}_{k=1}^M$. The system we will develop here can be viewed schematically as shown in the left panel of Figure 2.1

FIGURE 2.1.

Two phase design of the data analysis system (left) and the Blood/Lung/Breath analyzer and Blood/Skin/TAS systems (right).

2.1 The Calibration Phase

The clinical protocol for obtaining the calibration data is as follows. Eligible participants were fitted with a WrisTAS V sensor. They then received an oral dose of 95% ethanol in fruit juice. The ethanol dose was calculated to produce a peak blood alcohol concentration (BAC) of approximately 0.080 g/l using a formula based on body water content. Breath alcohol concentration (BrAC) was determined at 10–30 minute intervals with an Intoximeter Alco-Sensor IV. The raw transdermal data (in the form of current) typically measured at a rate of one every two minutes is transformed into TAC using pre-established bench calibration parameters for the particular WrisTAS V Transdermal Alcohol Sensor being worn by the subject. Thus the calibration data set consists of a relatively small number L₁ of BrAC measurements and a larger number L₂ of corresponding TAC measurements. An interpolation scheme is used to yield an equal number L of BrAC and TAC measurements $u^C={\left\{u_k^C\right\}}_{k=1}^L\text{and}{y}^C={\left\{y_k^C\right\}}_{k=1}^L$, respectively, at equally spaced intervals of time with interval length τ.

Our approach is based on a forward model for the transport and possible metabolism of ethanol through and by the skin and ethanol’s processing and measurement by the TAS sensor. The model is a parameter dependent, finite dimensional, discrete time, semilinear evolution equation of the form

$$x_{k+1}=A(q)x_k+F\left(x_k,{\tilde{u}}_k,q\right),y_k=C(q)x_k,$$

where the states and outputs of the system at time kτ are given by vectors x_kand y_k, respectively, ${\tilde{u}}_k$ denotes the BAC at time kτ, and q denotes a vector of parameters from a feasible set of parameters Q. We note that in what is to follow, it would be straight forward to also allow the linear operators A(q) and C(q) and the nonlinearity F to depend explicitly on time.

We formulate the calibration problem as a nonlinear least squares fit of the model parameters q ε Q to the TAC data $y^C={\left\{y_k^C\right\}}_{k=1}^L$. However, since the input model, ũ, is BAC, but the calibration data set provides BrAC, $u^C={\left\{u_k^C\right\}}_{k=1}^L$, some care must be taken in the formulation of the parameter estimation problem. The situation is illustrated in the block diagram shown in the right panel of Figure 2.1.

Since the primary role of the TAS sensor and the associated data analysis system, at least at this point, is to serve as a passive and unobtrusive replacement for the breath analyzer and because of the relatively simple relationship between BrAC and BAC used in practice, it is in fact sufficient to simply consider BrAC as the input to our model. Indeed, BrAC, as measured by a typical breath analyzer, is an indirect estimate of BAC based upon assumptions of ideality and a simple linear model. The model that is typically used for the exchange of blood alcohol and breath alcohol and its measurement is based on Henry’s Law which expresses the relationship between the concentration of a volatile substance dissolved in a liquid (e.g. blood) and its partial pressure in the vapor above the solution (e.g. air). The instrument which may employ any one of a number of technologies (e.g. infrared spectrophotometer technology, electro-chemical fuel cell based analysis) essentially counts the number of moles present in the sample from which it is then able (for example, via the ideal gas law), to estimate the partial pressure of the ethanol vapor in the sample. By assuming a highly simplified and idealized model for the human lung, Henry’s Law which states that the partial pressure of a gaseous solute above a solution is proportional to its concentration in the solution, can be applied to obtain an estimate for BAC in the form of BrAC. The constant of proportionality in Henry’s Law is referred to as the partition coefficient or ratio or more simply, as the Henry’s Law constant. The value of this constant depends on both the solvent and, more significantly, on temperature. The value that is typically used when the solvent is human blood and the solute is ethanol is 2100:1; blood will contain 2100 parts ethanol for each part ethanol measured in the breath at 34°C [15]. Because of the obvious legal ramifications for DUI prosecutions, the soundness of this model and what the appropriate value for the partition ratio should be are constantly coming under scrutiny. In fact, BrAC measurements can very by as much as ±20% when correlated with actual direct measurements of blood alcohol concentration. This high degree of variability is a result of a number of uncontrolled or uncontrollable factors including variation in the solubility of ethanol in blood and water [11], the temperature and humidity content of the inspired air [9], pretest breathing behavior (e.g. hyper- or hypo- ventilating, for example) [10], the cooperation of the test subject [12], and the lung capacity of the test subject [13].

These largely unresolved issues related to breath-based estimates of BAC are beyond the scope of this effort. Indeed, our aim here is to provide the researcher or clinician with an estimate of the field BrAC (i.e. the breath based estimate of BAC) that is based on the TAS measurements of field TAC and that is consistent with the subject’s calibration data. It would then be up to those professionals to relate the estimate we provide for BrAC to BAC. This could be achieved in any one of a number of ways including, for example, via an analog of the modeling, calibration and inversion approach we develop here for relating TAC to BrAC. This of course would involve the development of an appropriate model for pulmonary gas exchange. One could also use the readily invertible, generally accepted linear relationship between BAC and BrAC based on Henry’s law. Indeed, in this case, so long as the blood/TAS model is such that there is a gain λ̃ in front of the BAC input term in equation (2.2) below, ${\tilde{u}}_k$, that is to be estimated when the model is calibrated, we may simply replace the BAC input signal, ũ, with the BrAC input signal, u= κũ with the understanding that when we calibrate the model we will now be estimating the value of the gain $\lambda =\tilde{\lambda }{\kappa }^{-1}$ rather than the value of λ̃. Moreover, when we subsequently use the fit model to invert the TAC signal, we will actually be obtaining an estimate of BrAC, u=κũ, the breath analyzer’s estimate of BAC, rather than ũ the BAC signal itself.

We then formulate the estimation problem as a nonlinear least squares minimization problem. That is we seek a vector q^* ε Q which minimizes the functional

$$J(q)={\displaystyle \sum _{i=1}^L{\left|y_i(q)-y_i^C\right|}^2}$$ (2.1)

where ${\left\{y_i\left(q\right)\right\}}_{i=1}^L$ given by

$$x_{i+1}=A\left(q\right)x_i+F\left(x_i,u_i^C,q\right),x_0=0,y_i\left(q\right)=C\left(q\right)x_i,$$ (2.2)

are the values of the modeled TAS sensor signal corresponding to the choice of parameter values q ε Q. We have assume that when the calibration data is collected, the subject has abstained from drinking for a period long enough for all alcohol to have cleared from his system (i.e. x₀ = 0).This is a nonlinear least squares problem since in general, y depends on q in a highly nonlinear fashion.

Solving the minimization problem posed in (2.1) and (2.2) is typically achieved via a steepest descent or quasi-Newton method to search for local minima. All of these approaches typically require the calculation of the gradient of J, ∇J. This can be achieved via finite differences, but this is likely to be computationally expensive (requiring p + 1 forward integrations of the model, where p is the number of unknown parameters being identified) and, more seriously, it is likely to yield inaccurate gradients. The latter is of concern since it can cause the search method to either converge extremely slowly or not at all. Consequently, we use an adjoint method [20] to compute exact (up to numerical round off) gradients.

We begin by substituting (2.2) into (2.1) and then differentiating (2.1) and (2.2) with respect to q to obtain $\nabla J\left(q\right)=\frac{\partial J}{\partial q}\left(q\right)=2{\displaystyle \sum _{i=1}^L{\left[C\left(q\right)x_i\left(q\right)-y_i^C\right]}^T}\left[C\left(q\right)\frac{\partial x_i\left(q\right)}{\partial q}+\frac{\partial C\left(q\right)}{\partial q}{x}_i\left(q\right)\right]$ and

$$\frac{\partial x_{i+1}\left(q\right)}{\partial q}=A\left(q\right)\frac{\partial x_i\left(q\right)}{\partial q}+\frac{\partial A\left(q\right)}{\partial q}{x}_i\left(q\right)+\frac{\partial F\left(x_i\left(q\right),u_i;q\right)}{\partial x_i}\frac{\partial x_i\left(q\right)}{\partial q}+\frac{\partial F\left(x_i\left(q\right),u_i;q\right)}{\partial q}$$

Then define the co-states z_i(q), and the co-state or adjoint equation by the discrete time terminal value problem

$$z_{i-1}\left(q\right)=\left\{A^T\left(q\right)+\frac{\partial F^T\left(x_i\left(q\right),u_i;q\right)}{\partial x_i}\right\}{z}_i\left(q\right)+v_i\left(q\right),z_L\left(q\right)=0,$$ (2.3)

where $v_i\left(q\right)=2C^T\left(q\right)e_i\left(q\right)\text{with}{e}_i\left(q\right)=\left[C\left(q\right)x_i\left(q\right)-y_i^C\right]$. It then follow that

$$\begin{array}{c}\hfill \nabla J\left(q\right)=\frac{\partial J}{\partial q}\left(q\right)={\displaystyle \sum _{i=1}^L{v}_i^T\left(q\right)\frac{\partial x_i\left(q\right)}{\partial q}+2{\displaystyle \sum _{i=1}^L{e}_i^T\left(q\right)\frac{\partial C\left(q\right)}{\partial q}{x}_i\left(q\right)}}\hfill \\ ={\displaystyle \sum _{i=1}^L{\left[z_{i-1}\left(q\right)-\{A_{M,N}^T\left(q\right)+\frac{\partial F^T\left(x_i\left(q\right),u_i;q\right)}{\partial x_i}\}{z}_i\left(q\right)\right]}^T\frac{\partial x_i\left(q\right)}{\partial q}+2{\displaystyle \sum _{i=1}^L{e}_i^T\left(q\right)\frac{\partial C\left(q\right)}{\partial q}{x}_i\left(q\right)}}\hfill \\ ={\displaystyle \sum _{i=1}^L{z}_{i-1}^T\left(q\right)\frac{\partial x_i\left(q\right)}{\partial q}-{\displaystyle \sum _{i=1}^L{z}_i^T\left(q\right)\left\{A\left(q\right)+\frac{\partial F(x_i\left(q\right),u_i;q)}{\partial x_i}\right\}\frac{\partial x_i\left(q\right)}{\partial q}}+2{\displaystyle \sum _{i=1}^L{e}_i^T\left(q\right)\frac{\partial C\left(q\right)}{\partial q}{x}_i\left(q\right)}}\hfill \\ ={\displaystyle \sum _{i=0}^{L-1}{z}_i^T\left(q\right)\left\{\frac{\partial x_{i+1}\left(q\right)}{\partial q}-\left\{A\left(q\right)+\frac{\partial F\left(x_i\left(q\right),u_i;q\right)}{\partial x_i}\right\}\frac{\partial x_i\left(q\right)}{\partial q}\right\}}\hfill \\ \hfill +z_0^T\left(q\right)\left\{A\left(q\right)+\frac{\partial F\left(x_0\left(q\right),u_i;q\right)}{\partial x_0}\right\}\frac{\partial x_{0,N}\left(q\right)}{\partial q}+2{\displaystyle \sum _{i=1}^L{e}_i^T\left(q\right)\frac{\partial C\left(q\right)}{\partial q}}{x}_i\left(q\right)\hfill \\ ={\displaystyle \sum _{i=0}^{L-1}{z}_i^T\left(q\right)w_i\left(q\right)+2{\displaystyle \sum _{i=1}^L{e}_i^T\left(q\right)\frac{\partial C\left(q\right)}{\partial q}+x_i\left(q\right),}}\hfill \end{array}$$ (2.4)

, where $w_k\left(q\right)=\left[\frac{\partial A\left(q\right)}{\partial q}\right]x_i\left(q\right)+\frac{\partial F\left(x_i\left(q\right),u_i;q\right)}{\partial q}$. It follows, therefore, that to compute the gradient ∇J(q) at a given value of q ∈ Q, the following calculation is done: the forward model (2.2) is integrated once and the state x_i, i = 0, 1, 2,…., ML is saved. Then the co-state or adjoint system, (2.3), is integrated backwards once. Note that even if the original system, (2.2) is nonlinear, the adjoint system is always linear! Then from (2.4), as the adjoint system is being integrated backwards, the gradient is computed using the saved states via

$$\nabla J\left(q\right)=\frac{\partial J\left(q\right)}{\partial q}={\displaystyle \sum _{i=0}^{L-1}{z}_i^T}\left(q\right)w_i\left(q\right)+2{\displaystyle \sum _{i=1}^L{e}_i^T\left(q\right)\frac{\partial C\left(q\right)}{\partial q}}{x}_i\left(q\right),$$ (2.5)

with

$$w_k\left(q\right)=\left[\frac{\partial A\left(q\right)}{\partial q}\right]x_i\left(q\right)+\frac{\partial F\left(x_i\left(q\right),u_i;q\right)}{\partial q}\text{and}{e}_i\left(q\right)=\left[C\left(q\right)x_i\left(q\right)-y_i^C\right].$$

Note that this calculation yields the exact value of the gradient without the introduction of any truncation error and that it requires essentially only two integrations regardless of the number of unknown parameters being estimated. Note also that if, as is commonly the case, one wants to add a Tychonov regularization term to the least squares performance index, J, to enhance the stability of the minimization, this can be readily done and will have no effect on the adjoint method. The regularization term depends explicitly on the unknown parameters q, and consequently its derivative can simply be added to the formula for the gradient given by (2.5). Finally, it is worth noting that at leat in the linear case, the costate equation will inherit the same stability properties as the state equation. This is especially relevant as it is in our case, when the state equation (2.2) resulted from the finite dimensional approximation or discretization of an infinite dimensional or distributed parameter model involving partial differential equations

2.2 The Inversion Phase

In this section we describe how we use the fit model to produce an estimate of field BrAC, ${\widehat{u}}^F={\left\{{\widehat{u}}_k^F\right\}}_{k=1}^M$, from the TAC field data, $y^F={\left\{y_k^F\right\}}_{k=1}^M$. Our general approach once again involves using the model to formulate the TAC inversion problem as a non-negatively constrained nonlinear least squares fit to data. That is we seek a vector ${\widehat{u}}^F={\left\{{\widehat{u}}_k^F\right\}}_{k=1}^M$ with nonnegative entries ${\widehat{u}}_k^F\ge 0$ which minimizes the functional

$$J\left(u^F\right)={{\displaystyle \sum _{i=1}^M\left|y_i\left(u^F\right)-y_i^F\right|}}^2,$$ (2.6)

where $\{y_i{\left(u^F\right)\}}_{i=1}^M$ given by

$$x_{i+1}=A\left(q^{*}\right)x_i+F\left(x_i,u_i^F,q^{*}\right),x_0=0,y_i\left(u^F\right)=C\left(q^{*}\right)x_i.$$ (2.7)

Once again, we assume that initially there is no alcohol in the subject’s system when the field data is collected. In this case the optimization problem given in (2.6) and (2.7) can be solved using a gradient based iteration for constrained optimization problems. In this case, the adjoint equations for the gradient are given by

$$x_{i+1}=A\left(q^{*}\right)x_i+F\left(x_i,u_i^F,q^{*}\right),x_0=0,$$

$$z_{i-1}=\left\{A{\left(q^{*}\right)}^T+\frac{\partial F{\left(x_i,u_i^F,q^{*}\right)}^T}{\partial x_i}\right\}{z}_i+2C{\left(q^{*}\right)}^T\left\{C\left(q^{*}\right)x_i-y_i^F\right\},z_M=0,$$

$$\nabla J\left(u^F\right)={\displaystyle \sum _{i=0}^{M-1}{z}_i^T\frac{\partial F\left(x_i,u_i^F,q^{*}\right)}{\partial u_i^F}.}$$

When the state equation is linear in both the state x and the BrAC input u, the inversion becomes a deconvolution problem with non-negativity constraints which can be formulated as a nonnegative linear least squares problem and solved via standard quadratic programming techniques. The approach can be described as follows. The assumption of linearity in the state and input dictates that F(x_i,u_i,q^*)=B(q^*)u_i, where B(q^*) is a linear map from R¹ into the finite dimensional state space, and q^* denotes the optimal set of parameters as determined in the calibration phase. In this case the modeled field TAC measurements, ${\left\{y_i\left(u^F\right)\right\}}_{i=1}^M$, are given by the discrete convolution

$$y_i\left(u^F\right)={\displaystyle \sum _{j=0}^{i-1}C\left(q^{*}\right)A{\left(q^{*}\right)}^{i-1-j}B\left(q^{*}\right)u_j^F={\displaystyle \sum _{j=0}^{i-1}h\left(i-1-j,q^{*}\right)u_j^F,}}$$

where the convolution kernel h, is given by h(k,q^*) = C(q^*)A(q^*)^kB(q^*), and the BrAC input signal u^F has been zero order hold sampled as $u_i^F=u^F\left(i\tau \right)$. In this way, recovering BrAC from the TAC data is a linear deconvolution problem with the added constraint that the recovered BrAC signal be nonnegative; $u_i^F\ge 0,$ i = 0,1,2…

To solve the, in general, ill-posed deconvolution problem, we approximate the BrAC signal on the compact interval [0,T] by a linear combination of linear splines, $u_m^F\left(t\right)={\displaystyle \sum _{k=0}^m{\alpha }_k{\phi }_k^M\left(t\right),}$ where the ${\left\{{\phi }_k^m\right\}}_{k=0}^m$, are the linear spline functions on [0,T] corresponding to the uniform mesh ${\left\{kT/m\right\}}_{k=0}^m$. It then follows that

$$\begin{array}{cc}{y}_i\left(u_m^F\right)\hfill & ={\displaystyle \sum _{j=0}^{i-1}C\left(q^{*}\right)A{\left(q^{*}\right)}^{i-1-j}B\left(q^{*}\right){\displaystyle \sum _{k=0}^m{\alpha }_k{\phi }_k^m\left(j\tau /m\right)}}\hfill \\ \hfill & ={\displaystyle \sum _{k=0}^m{\alpha }_k{\displaystyle \sum _{j=0}^{i-1}h\left(i-1-j,q^{*}\right){\phi }_k^m\left(j\tau /m\right)={\displaystyle \sum _{k=0}^m{H}_{i,k}^m\left(q^{*}\right){\alpha }_k}}}\hfill \end{array}$$

where $H_{i,k}^m\left(q^{*}\right)={\displaystyle \sum _{j=0}^{i-1}h\left(i-1-j,q^{*}\right){\phi }_k^m\left(j\tau /m\right)}$, for i = 1,2,…, M and k=0,1,2,…m.

We formulate the deconvolution problem as a regularized nonnegative linear least squares fit to data. We then seek ${\widehat{u}}_m^F\left(t\right)={\displaystyle \sum _{k=0}^m{\widehat{\alpha }}_k{\phi }_k^m\left(t\right)}$, our optimal estimate of the field BrAC, as the solution to the following nonnegative least squares minimization problem:

$$\begin{array}{c}{\text{min}}_{\alpha >0}\left\{{\Vert y^F-H^m\left(q^{*}\right)\alpha \Vert }^2+{\beta }^2{\displaystyle \underset{0}{\overset{T}{\int }}{\left\{D{u}_m^F\left(s\right)\right\}}^{2}ds}\right\}={\text{min}}_{\alpha >0}\left\{{\Vert y^F-H_m\left(q^{*}\right)\alpha \Vert }^2+{\beta }^2{\alpha }^T{\mathrm{\Omega }}_m\alpha \right\}\hfill \\ \hfill ={\text{min}}_{\alpha >0}{\Vert \left[\begin{array}{c}\hfill y^F\hfill \\ \hfill 0\hfill \end{array}\right]-\left[\begin{array}{c}\hfill H_m\left(q^{*}\right)\hfill \\ \hfill -\beta {\mathrm{\Omega }}_m^{\frac{1}{2}}\hfill \end{array}\right]\alpha \Vert }^2,\hfill \end{array}$$

where Ω_m is the nonnegative definite symmetric tri-diagonal matrix whose (i, j)-th entry is given by${\left[{\mathrm{\Omega }}_m\right]}_{i,j}={\displaystyle \underset{0}{\overset{T}{\int }}D{\phi }_i^m\left(s\right)}D{\phi }_j^m\left(s\right)ds$and β≥0 is the regularization parameter. Choosing the value of the regularization parameter to tune the scheme to yield optimal results is part art and part science. The value of the regularization parameter does not depend directly on the individual test subject or the TAS device used. But rather its value is determined by the general nature (number and steepness of peaks, frequency content, etc.) of the TAC data sets being inverted and the number of spline elements used to approximate the BrAC signal.

3. Modeling the Transdermal Transport and Processing of Ethanol

The abstract framework outlined in the previous section requires a discrete time parametric family of state space models for ethanol transport from the blood through the skin and processing by the sensor. ARMA, neural networks, frequency domain techniques, and response surface modeling are examples of viable approaches that could be used to produce a reasonable model. In this treatment we have opted to construct a physiologically based distributed parameter model involving a coupled system of ordinary and partial differential equations. Our decision to employ such a model is motivated by the fact that our general approach dictates that the model will have to first be fit to calibration data before it can be used to invert the field data. Our scheme determines parameter values yielding local minima and consequently they may not be physically meaningful. Nevertheless, a model which respects the physics and physiology of the process offers the potential to significantly reduce the overall number of parameters required to capture the underlying dynamics. On the other hand, in the present context it makes little sense to employ a highly detailed multi-phase first principles model since it would almost certainly be impossible to estimate physically meaningful values for the numerous parameters that would appear in such a model from the very limited calibration data available to us.

It is believed that the primary driver of alcohol transport in the skin is diffusion [2]. Ethanol is a highly water soluble molecule which, when ingested into the human body via the consumption of alcoholic beverages and absorbed into the blood stream through the small intestine, eventually winds up distributed throughout the body water which comprises anywhere from 50% to 80% of the body by weight depending upon gender, body type, age, etc. [2]. We are interested in modeling the movement of the ethanol molecules from their dissolved state in the water component of the blood, through the walls of the blood vessels into the interstitial fluid through the various layers of the skin and finally into the TAS device. We assume that ethanol molecules undergo Fickian transport through the porous, tortuous medium that is the skin [29].The skin is considered to consist of two distinct layers, the dermis and the epidermis. Below these layers lies the hypodermis, a layer of subcutaneous fat between the skin and the bone and muscle tissue below through which larger blood vessels wend their way. The epidermis has sub-layers with non-homogeneous mechanical properties [8], one of which, the outer stratum corneum, consists of just a few layers of dead cells that are continually being keritanized and sloughed off at the top and replenished from below by the death of the cells in the upper region of the epidermal layer. We assume that the dermal layer intimately surrounds a web of capillaries from which ethanol can move from the blood to the skin. The epidermal layer does not have direct contact with the blood supply receiving nutrients, oxygen and ethanol via diffusion from the dermal layer [29]. In our model, the skin is composed of three layers, the dermis, the epidermis (without the stratum corneum) and the stratum corneum.

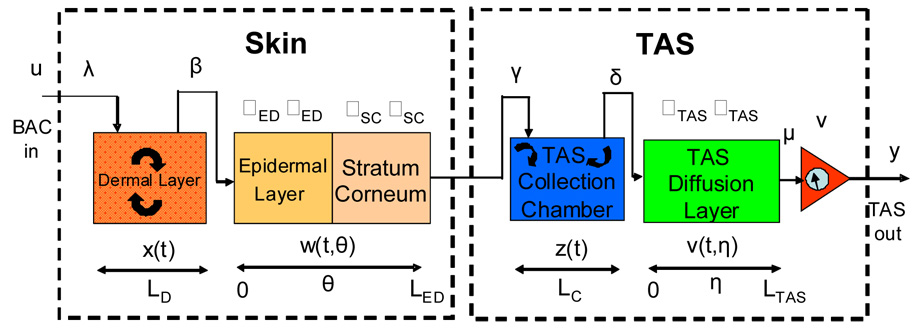
The model consists of a linear diffusion equation for two layers of the skin (the epidermal and stratum corneum layers) coupled to a detailed model of the TAS device itself. The model for the TAS device consists of the space between the skin surface and a barrier membrane that impedes moisture from escaping (the device requires a certain amount of water present to function properly). The skin is assumed to be L_S cm thick, the stratum corneum is assumed to be L_SC cm thick, the epidermal layer is assumed to be L_ED − L_SC cm thick, and the dermal layer is assumed to be L_S − L_ED cm thick. We refer to the volume between the skin and the moisture barrier as the TAS collection chamber and it is assumed to have thickness L_C (in cm). The barrier membrane is assumed to be of thickness L_TAS (in cm). The dermal layer is modeled as a well-mixed compartment and coupled to the lower boundary of a two layer one dimensional diffusion model describing the epidermis and stratum corneum. The skin and TAS models are also coupled at the boundary. That is, the ethanol leaving through the top surface of the stratum corneum enters the TAS collection chamber. A representation of the model is shown in Figure 3.1.

FIGURE 3.1.

A schematic diagram the Skin and TAS model.

The model equations are as follows. The dynamics in the dermal layer is given by

$$L_D\dot{x}\left(t\right)=-\beta \left\{\left[x\left(t\right)-w\left(t,0\right)\right]\right\}+\tilde{\lambda }\tilde{u}\left(t\right),t>0,$$ (3.1)

where L_D is the thickness of the dermal layer in cm, x(t) is the concentration of ethanol in the dermal layer in units of mg/cm, w(t,0) is the concentration of ethanol at the boundary between the epidermal and dermal layers in units of mg/cm, ũ(t) is the concentration of alcohol in the blood in units mg/dl, and the rate constants β and λ̃ have units cm/hr and dl/hr, respectively. The model assumes that the ethanol will be transported down the concentration gradient between the dermal layer and the lower boundary of the epidermal layer.

The diffusion of the ethanol molecules in the epidermal and stratum corneum layers of the skin is governed by the simple one dimensional linear diffusion equation

$$\phi \left(\theta \right)\frac{\partial w}{\partial t}\left(t,\theta \right)=\frac{\partial }{\partial \theta }\left\{\alpha \left(\theta \right)\frac{\partial w}{\partial \theta }\left(t,\theta \right)\right\},0<\theta <L_{ED},t>0,$$ (3.2)

where w(t,θ) is the concentration of ethanol at depth L_ED-θ in the skin in units of mg/cm, and where the piecewise constant diffusivity α in units of cm²/hr and dimensionless porosity φ are given by

$$\alpha \left(x\right)=\{\begin{array}{c}{\alpha }_{ED}0\le x\le L_{ED}-L_{SC}\hfill \\ {\alpha }_{SC}{L}_{ED}-L_{SC}<x\le L_{ED}\hfill \end{array}\text{and}\phi \left(x\right)=\{\begin{array}{c}{\phi }_{ED}0\le x\le L_{ED}-L_{SC}\hfill \\ {\phi }_{SC}{L}_{ED}-L_{SC}<x\le L_{ED}\hfill \end{array},$$

respectively. The associated gradient driven boundary conditions are given by

$$-{\alpha }_{ED}\frac{\partial w}{\partial \theta }\left(t,0\right)=\beta \left\{x\left(t\right)-w\left(t,0\right)\right\},-{\alpha }_{SC}\frac{\partial w}{\partial \theta }\left(t,L_{ED}\right)=\gamma \{w\left(t,L_{ED}\right)-z\left(t\right)\}t>0,$$

where z(t) is the concentration of ethanol in the TAS collection chamber in units of mg/cm, and the rate constant γ has units cm/hr. The TAS collection chamber is also modeled as a well-mixed compartment. Equity of fluxes defines the boundary conditions between layers as described by the equation

$$L_C\dot{z}\left(t\right)=\gamma \left\{w\left(t,L_{ED}\right)-z\left(t\right)\right\}-\delta \left\{z\left(t\right)-v\left(t,0\right)\right\}t>0,$$

where L_C is the thickness of the TAS vapor collection chamber in cm, v(t,η) is the concentration of ethanol in the TAS barrier membrane at time t > 0 and depth L_TAS−η in units of mg/cm, and δ is the exchange rate constant between the collection chamber and the barrier membrane in units of cm/hr.

Transport in the barrier membrane is assumed to be one dimensional diffusion and is described by the equation

$${\phi }_{\mathit{\text{TAS}}}\frac{\partial v}{\partial t}\left(t,\eta \right)={\alpha }_{\mathit{\text{TAS}}}\frac{{\partial }^{2}v}{\partial {\eta }^2}\left(t,\eta \right)0<\eta <L_{\mathit{\text{TAS}}}t>0,$$

where φ_TAS is the non-dimensional porosity and α_TAS is the diffusivity in units of cm²/hr, together with the boundary conditions

$$-{\alpha }_{\mathit{\text{TAS}}}\frac{\partial v}{\partial \eta }\left(t,0\right)=\delta \left\{z\left(t\right)-v\left(t,0\right)\right\},-{\alpha }_{\mathit{\text{TAS}}}\frac{\partial v}{\partial \eta }\left(t,L_{\mathit{\text{TAS}}}\right)=\mu v\left(t,L_{LAS}\right)t>0$$

where µ is in units of cm/hr. Finally, we assume that the observed TAS measurement y(t) in units of either mg/dl is proportional to the concentration of ethanol on the upper surface of the barrier membrane, y(t)=vν(t,L_TAS), t >0, where ν has units cm/ml.

We note that we also considered a similar model in which the exchange between the various compartments is uni-directional. In this case the dynamics in the dermal and TAS collection chambers and corresponding boundary conditions become

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=-\frac{\beta }{V_D}x\left(t\right)+\tilde{\lambda }\tilde{u}\left(t\right),\dot{z}\left(t\right)=-\delta z\left(t\right)+\gamma w\left(t,L_{ED}\right),-{\alpha }_{ED}\frac{\partial w}{\partial \theta }\left(t,0\right)=\frac{\beta }{V_D}x\left(t\right),\hfill \\ \hfill -{\alpha }_{SC}\frac{\partial w}{\partial \theta }\left(t,L_{ED}\right)=\gamma w\left(t,L_{ED}\right),-{\alpha }_{\mathit{\text{TAS}}}\frac{\partial v}{\partial \eta }\left(t,0\right)=\delta z\left(t\right),t>0,\hfill \end{array}$$

where V_D is the volume of the dermal layer in units of cm³, x(t) is the amount of alcohol in the dermal layer at time t in units of mg, β is in units of cm³/hr, λ̃ is in the units of dl/hr, z(t) is the amount of alcohol in the TAS collection chamber in units of mg, δ is in units of hr^-1 and γ is in units cm/hr.

We note that there is some evidence (see, for example, [5] and [14]) of enzymatic metabolism of ethanol by, for example, the observed presence of trace amounts of alcohol dehydrogenase (ADH) in the skin. If one chose to include this in the model, nonlinear Michaelis-Menten reaction terms of the form −σ_Dx(t)/(ρ_D + x(t)) and −σ_EDw(t,θ)/(ρ_ED + w(t,θ)) would be included in equation (3.1) and equation (3.2), respectively.

During the calibration phase, the vector of parameters that must be estimated is given by

$$q=\left[{\alpha }_{SC},{\alpha }_{ED,}{\phi }_{SC,}{\phi }_{ED},{\alpha }_{\mathit{\text{TAS}}},{\phi }_{\mathit{\text{TAS}},}{\sigma }_D,{\rho }_D,{\sigma }_{ED},{\rho }_{ED},\tilde{\lambda },\beta ,\gamma ,\delta ,\mu ,\nu \right].$$

4. Finite Dimensional Approximation, Time Discretization and Convergence

In this section we describe and discuss the mathematical formulation and convergence of the finite dimensional and discrete time approximations we employed in adapting the continuous time, infinite dimensional model developed in the previous section to the abstract calibration and inversion framework outlined in Section 2. We begin by defining an abstract infinite dimensional continuous time parameter estimation problem and indicate how we approximate it with a sequence of finite dimensional discrete time parameter estimation problems. We also describe in some detail how we solve the approximating problems and the relationship (in particular, convergence issues) between the solutions to the approximating estimation problems and the original infinite dimensional identification problem.

Let H be a Hilbert space with inner product <·, ·> and norm | · | let V be a reflexive Banach space with norm ∥ · ∥ which is densely and continuously embedded in H, and let Q be a closed and bounded subset of R^p, where p is the number of parameters. We consider the following abstract parameter identification problem, Problem (PID).(PID) Minimize over all q ∈ Q the least squares functional J: Q → R given by

$$J\left(q\right)={\displaystyle \sum _{i=1}^L{\left|y\left(i\tau ;q\right)-{\widehat{y}}_i\right|}^2}$$

subject to the, in general, semi-linear abstract evolution system given by

$$\dot{x}\left(t\right)=A\left(q\right)x\left(t\right)+F\left(x\left(t\right),u\left(t\right),q\right),x\left(0\right)=x_0\left(q\right),y\left(t;q\right)=C\left(q\right)x\left(t\right),t>0,$$

where τ > 0 is the sampling time, the ${\widehat{y}}_i\in {\mathrm{R}}^{\mathrm{r}}$ are given experimental observations at time iτ, i = 1, 2, …, L (where L is the number of samples taken), for each q ∈ Q the linear operator A(q): Dom(A(q)) $\subseteq \mathrm{H}\to \mathrm{H}$ is possibly unbounded, the function F(·, ·,q): H × R^s → H is in general nonlinear, s is the dimensionality of the system input u(t), C(q) is a bounded linear operator from V into R^r, r the dimensionality of the experimental data y(t:q), x₀(q) ∈ H is the initial data, and u is a given input signal with values in R^s.

We require basic assumptions on the operators A(q) and nonlinearity F(·, ·,q) to insure that the abstract evolution system is, in some sense, well posed (see, for example, [19]). In particular we will assume that for each q ∈ Q the operator A(q) is the infinitesimal generator of a C₀ semigroup, {T(t ; q) : t ≥ 0}, of bounded linear operators on H and that the nonlinearity, F(·, ·,q), satisfies appropriate Lipschitzian and boundedness conditions (see, for example, [19]) so as to insure the existence of a mild solution given by

$$x\left(t\right)=T\left(t;q\right)x_0\left(q\right)+{\displaystyle \underset{0}{\overset{t}{\int }}T\left(t-s;q\right)F\left(x\left(s\right),u\left(s\right),q\right)}ds,t>0,$$

for t ∈ [0, Lτ]. The reason we introduced the Banach space V in our abstract formulation is two fold. First, all of the models of interest to us are either abstract parabolic or hyperbolic. More precisely, they may be formulated in weak or variational form in terms of a bounded coercive linear operator, Â(q), from V into V*, the dual of V. In this way we find (see, for example [22] or [28]) that by identifying H with its dual, that H will be densely and continuously embedded in V*, and the operator A(q) : Dom(A(q)) $\subseteq \mathrm{H}\to \mathrm{H}$ defined by Dom(A(q)) = {φ ∈ V : Â(q)φ ∈ H} with Â(q)φ will have the requisite properties. Second, by requiring that C(q) be only bounded as an operator on V rather than on H, we allow for the case frequently encountered in applications when the observational data are either pointwise in the spatial variable or on the boundary of the spatial domain. It is frequently the case that this type of observation operator will not be bounded on H, the underlying state space in which the problem is formulated but is bounded when restricted to subspace of H endowed with a stronger norm. Finally, we will also require assumptions on how A(q), F(·, ·, ·;q), C(q) and x₀(q) depend on q ∈ Q so as to be able to guarantee that the problem (PID) has a solution, q^* ∈ Q, and that we will be able to find at least local minima of J via gradient based descent methods (see [4])

In order to solve the, in general, infinite dimensional optimization problem given by Problem (PID), we must fully discretize; that is discretize in both time and space, the abstract evolution system. Toward that end, we first consider the discretization in the space variable in the form of abstract Galerkin approximations. In the context of a concrete partial differential equation, this can be thought of as a generalization of semi-discrete approximation by ordinary differential equations via either finite elements or finite differencing. For each N = 1, 2, …, let H_N be a finite dimensional subspace of H and let P_N : H → H_N denote the orthogonal projection of H onto H_N. For each q ∈ Q let A_N(q) : H_N → H_N be a bounded linear operator on H_N. We then approximate the abstract evolution equation given in problem (PID) above by the finite dimensional ordinary differential equation initial value problem given by

$${\dot{x}}_N\left(t\right)=A_N\left(q\right)x_N\left(t\right)+P_{N}F\left(x_N\left(t\right),u\left(t\right),q\right),t>0,x_N\left(0\right)=P_N{x}_0\left(q\right).$$ (4.1)

.

A fully discrete approximation in both time and space is then achieved by imposing a backwards Euler scheme on the linear part on the system (4.1), and a standard explicit Euler approximation on the non-linearity. If M is a positive integer, discretize the time domain with time step τ/M and obtain

$$x_N\left(\left(i+1\right)\tau /M\right)-x_N\left(\left(i\tau /M\right)\right)/\left(\tau /M\right)\approx A_N\left(q\right)x_N\left(\left(i+1\right)\tau /M\right)+P_{N}F\left(x_N\left(i\tau /M\right),u\left(i\tau /M\right),q\right)$$

Our choice of temporal approximation scheme is driven by a desire for both computational ease and efficiency and the ability to theoretically demonstrate convergence for a broad class of systems and spatial discretization schemes (see the discussion on convergence issues below).

We then consider the following doubly indexed sequence of approximating finite dimensional discrete time parameter estimation problems.(PID_M,N) Minimize over all q ∈ Q the least squares functional J_M,N : Q→R given by

$$J_{M,N}\left(q\right)={\displaystyle \sum _{i=1}^{ML}{I}_i^M{\left|y_i\left(q\right)-{\widehat{y}}_{\left[\frac{i}{M}\right]}\right|}^2,}$$

where $I_i^M$ is the sequence that is 1 if i is a multiple of M and 0 otherwise and [·] is the floor function, subject to the abstract nonlinear difference equation given by

$$x_{i+1}=A_{M,N}\left(q\right)x_i+F_{M,N}\left(x_i,u_i,q\right),x_0=x_{0,N}\left(q\right),y_i\left(q\right)=C\left(q\right)x_i,$$

where u_i = u(iτ/M), for each q ∈ Q the linear operator A_M,N(q) ∈ H_N → H_N is given by

$$A_{M,N}\left(q\right)={\left(I-\left(\tau /M\right)A_N\left(q\right)\right)}^{-1},$$ (4.2)

the nonlinearity, F_M,N(·, ·, q) : H_N × R^s → H_N, is given by

$$F_{M,N}\left(x_i,u_i,q\right)=\left(\tau /M\right){\left(I-\left(\tau /M\right)A_N\left(q\right)\right)}^{-1}{P}_{N}F\left(x_i,u_i,q\right),$$

and x_0,N = P_Nx₀. We note that the operator inverse required in (4.2) is guaranteed to exist for all τ sufficiently small or all M sufficiently large by the well known theorem on Neumann Series (see [18]).

Before we turn our attention to describing how we went about carrying out the computations necessary to solve the estimation problems, (PID_M,N), we make a few remarks concerning the convergence of solutions, $q_{M,N}^{*}$, of the problems (PID_M,N) to a solution, q^* to problem (PID). We assume that the dependence of the operators A_N, and C and the function F and the initial data x₀ on the unknown parameters q ∈ Q is such that the functional J_M,N ∈ C¹(Q); that is, that the gradient of J_M,N, ∇J_M,N, exists and is continuous for all q ∈ Q. In this way, it follows that the problems (PID_M,N) involve the minimization of a continuous function over a closed and bounded, and therefore compact, subset of R^p. Consequently, it follows that each of the problems (PID_M,N) admit a solution, $q_{M,N}^{*}\in Q$. Now, Q being compact implies that there exists a subsequence, $\left\{q_{M_j,N_i}^{*}\right\}\subseteq \left\{q_{M,N}^{*}\right\}\text{with}{q}_{M_j,N_j}^{*}\to q^{*}$, as j → ∞ for some q^* ∈ Q. By arguing that

$${\text{lim}}_{j\to \infty }\Vert x_{k{M}_j}\left(q_{M_j,N_j}^{*}\right)-x\left(k\tau ;q^{*}\right)\Vert =0$$ (4.3)

for k=1,2,… L, it follows that q^* is a solution to (PID). Banks and Ito [3] were able to argue the analog of (4.3) for the case of semi-discrete approximations, $\underset{j\to \infty }{\text{lim}}\Vert x_{N_j}\left(k\tau ;q_{N_j}^{*}\right)-x\left(k\tau ;q^{*}\right)\Vert =0$ for a wide class of abstract parabolic and hyperbolic systems by showing that $e^{A_{N_j}\left(q_{N_j}^{*}\right)k\tau }\to T\left(k\tau ;q^{*}\right)$ strongly in V as j → ∞. We have been able obtain (4.3) for the fully discrete case, by arguing that

$${\left(I-\left(\tau /M_j\right)A_{N_j}\left(q_{M_j,N_j}^{*}\right)\right)}^{{-kM}_j}\to T\left(k\tau ;q^{*}\right),$$

strongly in V as j → ∞ for k = 0, 1, 2, …, L (see [22]).

In order to actually carry out the requisite computations, matrix/vector representations for the operators A_M,N(q) and functions F_M,N have to be computed. To do this, we first determine the matrix representation for the semi-discrete Galerkin approximations A_N(q) to the operator A(q). This is most easily achieved by rewriting the original infinite dimensional system in weak or variational form as

$${\langle \dot{x}\left(t\right),\phi \rangle }_q=\sigma \left(q;x\left(t\right),\phi \right)+{\langle F\left(x\left(t\right),u\left(t\right),q\right),\phi \rangle }_q,\phi \in V,t>0,$$

where 〈·,·〉_q is the parameter dependent inner product on H, and the sesquilinear form σ(q;·,·):V×V → R is given by $\sigma \left(q;\phi ,\psi \right)=={\langle \widehat{A}\left(q\right)\phi ,\psi \rangle }_{V\times V}$, with 〈·,·〉_V×V^* denoting the duality pairing between the space V and its dual V* induced by the dense and continuous embedding of H in V (see, for example, [23] or [28]). Then, for i = 1, 2, …, K_N, let ${\phi }_i^N$ be linearly independent elements in V and set $H_N=\text{span}{\left\{{\phi }_i^N\right\}}_{i=1}^{K_N}$. The Galerkin approximation is then defined by

$${\langle {\dot{x}}_N\left(t\right),{\phi }_i^N\rangle }_q=\sigma \left(q;x_N\left(t\right),{\phi }_i^N\right)+\langle F(x_N\left(t\right),u\left(t\right),q),{\phi }_i^N{\rangle }_q,i=1,2,\dots ,K_N,t>0.$$ (4.4)

.

For the model we developed in Section 3, the appropriate choices for the state and energy spaces, H and V, respectively, are H = R × L₂(0,L_ED) × R × L₂(0,L_TAS) together with the inner product

$${\langle \left(x_1,w_1,z_1,v_1\right),\left(x_2,w_2,z_2,v_2\right)\rangle }_q=L_D{x}_1{x}_2+{\displaystyle \underset{0}{\overset{L_{ED}}{\int }}\phi \left(\theta \right)w_1\left(\theta \right)w_2}\left(\theta \right)d\theta +L_C{z}_1{z}_2+{\phi }_{\mathit{\text{TAS}}}{\displaystyle \underset{0}{\overset{L_{\mathit{\text{TAS}}}}{\int }}{v}_1\left(\eta \right)}{v}_2\left(\eta \right)d\eta$$

and V = R × H₁(0,L_ED) × R × H₁(0,L_TAS) together with the norm

$$\Vert \left(x,w,z,v\right)\Vert ={\left\{x^2+{\displaystyle \underset{0}{\overset{L_{ED}}{\int }}w{\left(\theta \right)}^{2}d\theta +z^2+{\displaystyle \underset{0}{\overset{L_{\mathit{\text{TAS}}}}{\int }}v{\left(\eta \right)}^{2}d\eta }}\right\}}^{\frac{1}{2}}.$$

In the case of the gradient driven exchange model, the sesquilinear form σ(q;·,·):V×V → R is

$$\begin{array}{c}\hfill \sigma \left(q;\left(x_1,w_1,z_1,v_1\right),\left(x_2,w_2,z_2,v_2\right)\right)=-\beta \left\{x_1-w_1\left(0\right)\right\}\left\{x_2-w_2\left(0\right)\right\}-\gamma \left\{w_1\left(L_{ED}\right)-z_1\right\}\left\{w_2\left(L_{ED}\right)-z_2\right\}\hfill \\ \hfill -\delta \left\{z_1-v_1\left(0\right)\right\}\left\{z_2{v}_2\left(0\right)\right\}-{\displaystyle \underset{0}{\overset{L_{ED}-L_{SC}}{\int }}\alpha \left(\theta \right)w_1^{\prime }\left(\theta \right)w_2^{\prime }\left(\theta \right)d\theta -{\alpha }_{\mathit{\text{TAS}}}{\displaystyle \underset{0}{\overset{L_{\mathit{\text{TAS}}}}{\int }}{v}_1^{\prime }\left(\eta \right)v_2^{\prime }\left(\eta \right)d\eta ,}}\hfill \end{array}$$

while in the case of the uni-directional exchange model, it is given by$\begin{array}{c}\hfill \sigma \left(q;\left(x_1,w_1,z_1,v_1\right),\left(x_2,w_2,z_2,v_2\right)\right)=-\frac{\beta }{V}{x}_1\left\{x_2-w_2\left(0\right)\right\}-\gamma w_1\left(L_{ED}\right)\left\{w_2\left(L_{ED}\right)-z_2\right\}\hfill \\ \hfill -\delta z_1\left\{z_2-v_2\left(0\right)\right\}-{\displaystyle \underset{0}{\overset{L_{ED}-L_{SC}}{\int }}\alpha }\left(\theta \right)w_1^{\prime }\left(\theta \right)w_2^{\prime }\left(\theta \right)d\theta -{\alpha }_{\mathit{\text{TAS}}}{\displaystyle \underset{0}{\overset{L_{\mathit{\text{TAS}}}}{\int }}{v}_1^{\prime }\left(\eta \right)v_2^{\prime }\left(\eta \right)d\eta .}\hfill \end{array}$ For both models, the input or forcing function F(·,·,q) : H × R × R^p → H is given by

$$F(\left(x,w,z,v\right),u\left(t\right);q)=\left(-{\sigma }_{D}x/\left({\rho }_D+x\right)+\lambda u\left(t\right),-{\sigma }_{ED}w/\left({\rho }_{ED}+w\right),0,0\right),$$

where we have included the nonlinear Michaelis-Menten terms describing the enzymatic metabolism of alcohol in the skin by ADH. The finite element Galerkin approximations used to discretize and finite dimensionalize the partial differential equation or distributed parameter component of the model were constructed using linear spline bases for the approximating subspaces H_N.

By setting $x_N\left(t\right)={\displaystyle \sum _{i=1}^{K_N}{X}_i^N\left(t\right){\phi }_i^N}$ in equation (4.4), the matrix representation for the operators A_N(q), which we will again denote by A_N(q) are readily determined to be given by A_N(q)=G_N(q)⁻¹E_N(q) where the non-singular generalized mass matrix G_N(q) is given by ${\left[G_N\left(q\right)\right]}_{i,j}={\langle {\phi }_i^N,{\phi }_i^N\rangle }_q$, and the generalized stiffness matrix E_N(q) by $[E_N{\left(q\right)]}_{i,j}=\sigma \left(q;{\phi }_j^N,{\phi }_i^N\right)$ The matrix representation for the operators A_M,N(q) are then immediately seen to be given by $A_{M,N}\left(q\right)={\left[G_N\left(q\right)-\frac{\tau }{M}{E}_N\left(q\right)\right]}^{-1}{G}_N\left(q\right)$ and the vector representations for the nonlinearity F_M,N by

$$F_{M,N}\left({\phi }_N,u_i,q\right)={\left(\frac{M}{\tau }{G}_N\left(q\right)-E_N\left(q\right)\right)}^{-1}{F}_N\left({\phi }_N,u_i,q\right)$$

with the K_N dimensional vector ${\left[F_N\right]}_j\left({\phi }_N,u_i,q\right)={\langle F\left({\phi }_N,u_i,q\right),{\phi }_j^N\rangle }_q$, j = 1,2,…, K_N.

Finally, it is worth noting that the partial derivative with respect to q of the backward Euler state transition operator, A_M,N(q), that is required by the adjoint method described in Section 2 is readily calculated from the formula $\frac{\partial A_{M,N}\left(q\right)}{\partial q}=\frac{\tau }{M}{A}_{M,N}\left(q\right)\frac{\partial A_N\left(q\right)}{\partial q}{A}_{M,N}\left(q\right)$ in terms of the partial derivatives of the semi-discrete approximation, A_N(q). It follows that

$$\frac{\partial A_N\left(q\right)}{\partial q}=G_N{\left(q\right)}^{-1}\left\{\frac{\partial E_N\left(q\right)}{\partial q}-\frac{\partial G_N\left(q\right)}{\partial q}{A}_N\left(q\right)\right\},$$

and therefore that

$$\frac{\partial A_{M,N}\left(q\right)}{\partial q}=\frac{\tau }{M}{\left[G_N\left(q\right)-\frac{\tau }{M}{E}_N\left(q\right)\right]}^{-1}\left\{\frac{\partial E_N\left(q\right)}{\partial q}-\frac{\partial G_N\left(q\right)}{\partial q}{G}_N{\left(q\right)}^{-1}{E}_N\left(q\right)\right\}{\left[G_N\left(q\right)-\frac{\tau }{M}{E}_N\left(q\right)\right]}^{-1}{G}_N\left(q\right).$$

Obtaining the requisite finite dimensional discrete-time state space representation for this infinite dimensional (involving functional or distributed states and partial differential operators) and continuous time model requires finite dimensional approximation and time sampling. We employ finite differencing and finite dimensional linear spline based Galerkin approximation to produce matrices A_M,N(q) and functions F_M,N where M and N denote the levels of time sampling and finite dimensional approximation, respectively, and an approximating discrete time state space model of the form

$$x_{i+1}=A_{M,N}\left(q\right)x_i+F_{M,N}\left(x_i,u_i;q\right),x_0=x_{0,N}\left(q\right),y_i\left(q\right)=C\left(q\right)x_i$$ (4.5)

A more detailed description of how these systems are actually obtained and discussion of convergence issues are given in an appendix. Using the approximating systems (4.5), in the abstract framework developed in the previous section is the basis for our data analysis system.

5. Numerical Results

The Calibration Data Set we use to calibrate the model to a particular subject and a particular WrisTAS V Transdermal Alcohol Sensor is collected in a clinic or hospital under controlled conditions (i.e. known dosage with breath alcohol measurements taken at regular intervals). This data was obtained at the Brown Medical School according to the following protocol. Alcohol was administered to the subjects in accordance with Recommended Council Guidelines for Alcohol Administration to Human Subjects (NIAAA, 1989) and the study was approved by the Brown University Internal Review Board (IRB). Non-alcoholic, alcohol drinkers were screened by personal interview, laboratory testing and physical examination to exclude those with medical or substance abuse problems.

The plots shown in Figure 1.2 are the calibration data sets for two subjects whom we shall refer to as Subject 1 (the plot on the left) and Subject 2 (the plot on the right). In these plots, the blue plus signs represent the subject supplied BrAC measurements and the green circles represent the TAC data as supplied by the TAS sensor. Once again we point out the significant qualitative and quantitative differences between the two data sets. The differences may be a result of physiological variation from subject to subject or manufacturing differences from device to device. Subject 1 was wearing WrisTAS unit no. 4 and Subject 2 was wearing WrisTAS unit no. 7. Unit no. 7 produced transdermal alcohol measurements that are roughly the same magnitude as the breath measured blood alcohol concentrations. However, the transdermal alcohol levels yielded by unit no. 4 were significantly attenuated when compared to the breath alcohol measurements.

5.1 Calibrating the Model

All of the computations we describe here were carried out on either desktop or laptop personal computers using MATLAB. The calibration phase parameter estimation problems were solved as constrained optimization problems using a sequential quadratic programming (SQP) method where an estimate of the Hessian of the Lagrangian is updated at each iteration using the BFGS formula (routine FMINCON from the MATLAB Optimization Toolbox). We set N = 4 (i.e. our Galerkin approximations used 13 linear splines). The requisite gradients were computed using the adjoint method as described in the above and supplied to FMINCON. Once the parameters were estimated, the resulting forward models were implemented and all forward simulations were carried out in SIMULINK. In the numerical studies presented here, we chose to ignore the effects of ethanol metabolism in the skin and consequently the resulting model is linear.

Fairley and Rasmussen ([7]) reported the postmortem measurements of the abdominal stratum corneum of 10 adults ages 17 to 46. Using ultrasonic imaging to measure the thickness of the skin, a linear relationship can be used to describe the total thickness of the skin in the volar forearm [21]. The dermis remains relatively constant in the volar forearm between the ages of 20 and 70 while the epidermis increases in thickness. And while this linear model may be appropriate for future versions of the model with a larger range of ages, it shall suffice to model the skin as 20% epidermis and 80% dermis for the age group of our subjects. The total thickness of the skin in the volar forearm for the age group between 21 and 25 is 9.2 × 10⁻² cm, from which we derive the thickness of the epidermal and dermal layers of the skin.

The lengths of the stratum corneum, epidermal and dermal layers are assumed to be 3.54 × 10⁻³ cm, 1.77 × 10⁻² cm, 7.08 × 10⁻² cm, respectively. The estimated lengths for the WrisTAS V collection chamber and barrier membrane are assumed to be 1.20 × 10⁻² cm, 6.35 × 10⁻⁴ cm, respectively. We find that L_S = 9.20 × 10⁻²cm, L_SC = 3.54 × 10⁻³ cm, L_ED = 2.12 × 10⁻² cm, L_D = 7.08 × 10⁻² cm, L_C = 1.2 × 10⁻² cm, and L_TAS = 6.35 × 10⁻⁴ cm. The values for the skin layers are consistent with those used in [1].

One of the models developed in Section 3 requires a value for V_D, the total volume of the dermal layer. To compute this we used the Mosteller Formula

$$\mathit{\text{BSA}}\left(c{m}^2\right)={10}^4\sqrt{Ht\left(cm\right)·Wt\left(Kg\right)/3600}$$

for Body Surface Area (BSA) [16] and multiplied that by the thickness of the dermal layer, L_D. In this way we obtain V_D= 1269.10 cm³.

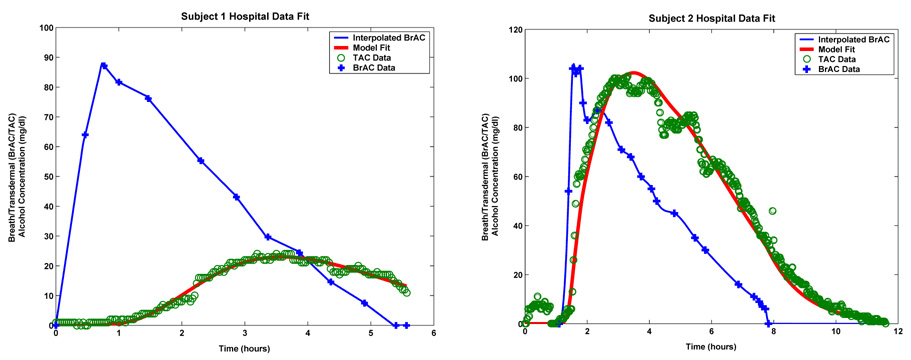
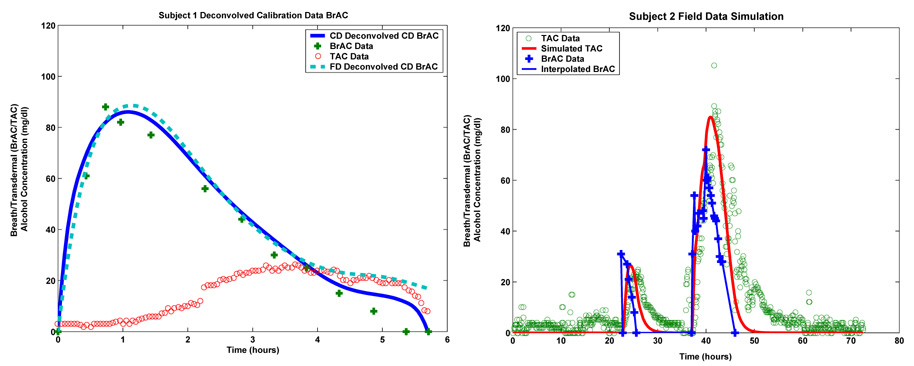
The results of calibrating the model to Subject 1’s and Subject 2’s calibration data sets are shown in Table 5.1 and Table 5.2 and Figure 5.1. Table 5.1 gives the calibrated values of the model parameters for Subject 1 while Table 5.2 gives the values for Subject 2. The plot on the left in Figure 5.1 is for Subject 1 while the one on the right is for Subject 2.

Table 5.1.

Values of the parameters for the uni-directional model for Subject 1.

λ	7.44×10−1 dl/hr	µ	1.42×100 cm/hr	φTAS	45.42×101
β	31.05×10−2 cm3/hr	ν	7.44×10−1 cm/dl	αED	2.60×10−3 cm2/hr
γ	1.44×100 cm/hr	φED	7.69×100	αSC	2.26×10−2 cm2/hr
δ	2.48 ×100 hr−1	φSC	99.93×100	αTAS	2.29×10−4 cm2/hr

Table 5.2.

Values of the parameters for the gradient driven model for Subject 2.

λ	2.44×100 dl/hr	µ	7.22×100 cm/hr	φTAS	13.33×103
β	76.48×101 cm/hr	ν	30.64×100 cm/dl	αED	1.44×102 cm2/hr
γ	14.10×102 cm/hr	φED	11.60×10−7	αSC	11.24×100 cm2/hr
φ	19.69×102 cm/hr	φSC	28.60×10−5	αTAS	4.62×10−1 cm2/hr

FIGURE 5.1.

The fit of the model to Subject 1’s hospital data (left) and the fit of the model to Subject 2’s hospital data (right).

The values for the diffusion parameters of the epidermis and the stratum corneum layers shown in Table 5.1 for Subject 1 are relatively close to those obtained from the literature used in [1] for simulation purposes when the porosity values are taken into account. However, those shown in Table 5.2 for Subject 2 on the other hand are not. The fit model parameter values are the result of a nonlinear least squares procedure and hence represent local minima of the total error functional. The difference between the parameter values for both subjects is robably due to the fact that the TAS signal for Subject 2 exhibits completely different behavior than that of Subject 1. Nevertheless, our primarily interest here is in the inversion of the TAC signal to obtain an estimate of the BrAC. We are not necessarily interested in being able to forward simulate the TAC signal as is the case in [1]. However, the TAC simulations displayed in Figure 5.2 do in fact exhibit the same shapes those shown in Figure 8 of [1].

FIGURE 5.2.

BrAC recovery for Subject 1 (left) and BrAC recovery for Subject 2 (right).

In the plots shown in Figure 5.1 the blue curves show the BrAC data and the cubic spline interpolated BrAC signal which serves as the input to the model. The green circles are the TAC data supplied by the TAS sensor and the red curve is simulated TAC signal produced by the model after the parameters have been fit to the data. In the case of Subject 1, the relative L₂ error (the quotient of the square root of the sum of squares of the difference between the TAC data and the forward simulated TAC signal produced by the fit model, and the square root of the sum of squares of the TAC data) is 7.50%. For Subject 2, the relative L₂ error was 9.63%.

5.2 The Inversion Phase

Subject 1 and Subject 2 also supplied a second data set that was collected in the field. The subject wearing the sensor was sent into the field for an extended period of time (either days or weeks) and told to continue normal activities. In some cases they were supplied with pre-measured doses of alcohol and told to ingest them at particular times. They were provided with a breath alcohol device and asked to take and record some relatively small number of breath alcohol measurements during the periods when they were drinking. They were also asked to keep a diary in which they were to record what they drank and when they drank it. These data sets will be referred to as Field Data Sets. For Subject 1 we were provided with two weeks (336 hours) of field data and for Subject 2 we were provided with 72 hours of field data. In the case of Subject 1 we inverted both the entire two week data set and only the first week of data. Here we show the results of the one week inversion. Our results for the two weeks of data were similar.

The nonnegative least squares minimization problems were solved using an algorithm for solving least squares problems based on the maximum component of the dual basis vector (MATLAB routine LSQNONNEG) with various choices for the number of spline basis elements (i.e. the parameter L) and the value of the Tychonov regularization parameter β. In the case of Subject 1, the first drinking epoch (approximately 6 hours) in the field data is the calibration data. This explains the relatively high density of BrAC measurements in the first 6 hours. We did some pre-processing of the TAC data before it was inverted. This included re-sampling to make the entire data set evenly spaced (the calibration data is collected every 2 minutes, while the rest of the field data is collected every 5 minutes), and the removal of a nonzero baseline from the data (typically about 7 mg/dl).

The results of the deconvolution for Subject 1 and Subject 2 are shown on the left and right of Figure 5.2. The plots show the results of the BrAC recovery along with the limited number of BrAC measurements that were supplied by the subject. We have also plotted the TAC data from which the estimate of BrAC was deconvolved. In the case of Subject 1 the deconvolution was carried out using L = 336 splines and with a regularization parameter β = 0.003. In the case of Subject 2, we used L = 128 splines and a regularization parameter of β = 0.1. The plots in Figures 5.2 appear to indicate that for both subjects, the scheme does a reasonably good job in recovering the temporal location of drinking events. For Subject 2 the scheme is also able to identify the level and decay of the peaks in the BrAC signal. For Subject 2, for whom we have a reasonable number of closely spaced field BrAC measurements we computed a relative BrAC L₂ error of 38.10%. In general, the method appears to have done somewhat less well in recovering peak BrAC levels. In the case of underestimates, the BrAC readings could be residual mouth alcohol, while in the case of over estimates, the BrAC reading may have been taken past the peak. A more careful assessment of how well the inversion scheme actually performed is presented in the next section.

6. Discussion and Concluding Remarks

An engineering solution to the problem of estimating (breath measured) blood alcohol concentration from measurements of transdermal alcohol produced by a transdermal alcohol sensor was developed. Our approach involved 1) the mathematical modeling of the transport of ethanol from the blood through the skin to the sensor, 2) a procedure by which the model is calibrated to the subject wearing the sensor and the particular sensor being worn, and 3) the deconvolution of the blood alcohol concentration from the transdermal signal. The model we developed is based on a spatially distributed description of the transport of alcohol from the bloodstream throughout the skin and toward the skin surface. The model contains a number of unknown subject and device specific physical and physiological parameters, the values of which must be estimated before the model can be used for forward simulation, prediction and inversion. The input to the model is the breath alcohol concentration (BrAC) and the output is the measured transdermal alcohol signal (TAC). The parameters in the model are estimated using a least squares procedure that minimizes the square error between the measured TAC signal provided by the biosensor in the hospital test and the simulated skin vapor alcohol concentration at the skin surface as predicted by the model.

In order to assess the performance of our inversion scheme, we looked at Subject 1’s inverted BrAC for the calibration data. We looked at the calibration data because it is the only part of the field data set for which we have a reasonable number of BrAC measurements to compare to the inverted BrAC signal. We looked at two inversions. We first inverted just the calibration data. That is, we used the first 6 hours of TAC data to obtain an estimate of the BrAC during this same period. More significantly, we also compared the first 6 hours of the estimated BrAC signal obtained by inverting the entire first week of Subject 1’s TAC data. The results are plotted in the left hand panel of Figure 6.1. The calibration data was inverted using 32 splines and a regularization parameter of β = 0.01. The full week of field data was inverted using 336 splines and β = 0.003. For the calibration data based inversion, the relative L₂ error in the first 6 hours of BrAC was 11.41% and for the full field data based inversion it was 19.18%. Of course it is not surprising that the inversion based solely on the calibration TAC data would do somewhat better than the inversion based on the entire first week of field data.

FIGURE 6.1.

Deconvolution of Subject 1’s calibration data (left) and forward simulation of Subject 2’s field test using fit model (right).

On the right in Figure 6.1 we plot the result of using the calibrated model to forward simulate Subject 2’s field data. We note it is not really meaningful to look at a similar plot for Subject 1 since Subject 1 did not provide us with field BrAC measurements at a sufficiently high enough resolution for us to be able to reconstruct a reasonable continuous time signal to serve as input to the model for a forward simulation. In the plot shown on the right in Figure 6.1, the blue plus signs are the subject supplied BrAC measurements, the blue curve is our continuous time reconstruction (via cubic spline interpolation) of the BrAC signal, the red curve is the model simulated TAC signal and the green circles are the TAC data supplied by the TAS sensor. The right plot in Figure 6.1 clearly shows that the model was able to capture not only the temporal location of the two peaks in the WrisTAS sensor data but also their magnitudes. However, it is also clear that the vapor alcohol predictions decay more rapidly than does the data. This may be related to the presence of ethanol trapped in the sensor chamber. It can also be observed that during the first thirty hours the sensor measured a non-zero level of alcohol on the skin surface but the values predicted by the model were zero. This difference may be due to the fact that the data collected for Subject 2 was intended to be for a period of one week (and indeed the transdermal device recorded measurements for this period of time). Subject 2, however, failed to keep a record of the quantities of alcohol ingested and to carefully record regular breath alcohol measurements during a period of four days prior to the period we have used here to test the simulation capability of our model. Consequently, the level of alcohol detected by the transdermal device in the first thirty hours of the data we have used may be a result of residual alcohol in the skin from the drinking he did prior to this period. On the other hand, the non-zero level of skin alcohol may also be the result of the device registering a non-zero baseline. We have no way of determining which if either of these possible explanations is correct. We note that the use of a truncated data set, did not appear to significantly degrade the ability of the model to predict skin surface alcohol levels. This demonstrates that our approach as implemented appears to be reasonably robust with respect to data loss and a non-zero set-point in the hardware.

The possibility of residual alcohol remaining in the skin suggests considering trying to capture the result of metabolic effects. For example, other researchers have considered models for the metabolic effects of the ethanol specific enzymes ADH and ALDH typically found in the liver, but also known to be present in trace amounts in the skin [5], [14]. It might be of some interest to combine these metabolic reactions, typically modeled via a Michaelis-Menten approach, with our transport model and to then attempt to estimate the relevant parameters that appear in the models.

The model yielded essentially the same level of accuracy in estimating the transdermal alcohol vapor signal over short and long periods. The value of the least squares performance index was less than 5% of the L₂ norm of the transdermal signal. We consider this to be quite acceptable given the level of precision in what are essentially hand manufactured WrisTAS devices. This is especially relevant, if it is in fact the case that the transdermal device used has a systematic tendency to return to a non-zero base line when all alcohol has been removed from the bloodstream. The presence of alcohol trapped in the device chamber may be the cause of this anomaly when the device is in operation over long periods of time.

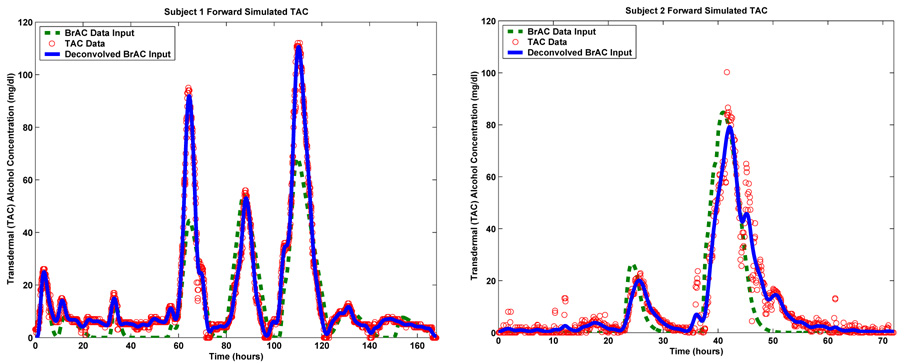
The plots in Figure 6.2 show the result of forward simulating the model using both the recovered (i.e. deconvolved) BrAC and an appropriate interpolation of the limited subject supplied BrAC measurements as input. The plot on the left is for Subject 1, while the plot on the right is for Subject 2. For comparison, on the same set of axes, we have also plotted the TAC field data from which the estimates of BrAC were deconvolved. For both subjects, the recovered BrAC signal is completely consistent with the TAC data from which it was deconvolved and the TAC and BrAC hospital data that was used to calibrate the model. This conclusion is supported by the plots shown in Figure 6.2 where it can be seen that when the recovered BrAC signal is fed back into the forward model as input, the resulting simulated TAC signal is in good agreement with the TAC field data upon which the BrAC recovery or deconvolution was based. Quantitatively, for Subject 1’s field data, the relative L₂ error when the deconvolved BrAC signal was used as input to the model was 6.05% When the interpolated BrAC data was used as input the relative L₂ error was 40.38%. In the case of Subject 2, the relative L₂ error when the deconvolved BrAC signal was used was 17.61% and for the interpolated BrAC data it was 45.07%

FIGURE 6.2.

Forward simulation of Subject 1’s (left) and Subject 2’s (right) field test using recovered and interpolated subject supplied measurements of BrAC.