A new FFT-based algorithm to compute Born radii in the generalized Born theory of biomolecule solvation

Abstract

In this paper, a new method for calculating effective atomic radii within the generalized Born (GB) model of implicit solvation is proposed, for use in computer simulations of bio-molecules. First, a new formulation for the GB radii is developed, in which smooth kernels are used to eliminate the divergence in volume integrals intrinsic in the model. Next, the Fast Fourier Transform (FFT) algorithm is applied to integrate smoothed functions, taking advantage of the rapid spectral decay provided by the smoothing. The total cost of the proposed algorithm scales as O(N³logN + M) where M is the number of atoms comprised in a molecule, and N is the number of FFT grid points in one dimension, which depends only on the geometry of the molecule and the spectral decay of the smooth kernel but not on M. To validate our algorithm, numerical tests are performed for three solute models: one spherical object for which exact solutions exist and two protein molecules of differing size. The tests show that our algorithm is able to reach the accuracy of other existing GB implementations, while offering much lower computational cost.

1 Introduction

Accuracy and speed are two primary objectives in developing computational techniques for modeling biomolecular systems [1] in aqueous environments where electrostatic interactions play an important role. Explicit solvent methods adopt microscopic representations of both solute and solvent molecules and offer an accurate description of the molecular system. However, these methods usually entail high computational cost. In contrast, implicit solvent simulations characterize the solvent in terms of macroscopic physical quantities such as dielectric constants and Debye lengths, and provide a higher speed in practical calculations while still providing a realistic description of the solvent environment.

In implicit solvent models [2], the degrees of freedom pertaining to water are integrated out and replaced by an effective potential energy term, ΔG, acting on the degrees of freedom of the solvated molecule only. From the thermodynamics point of view, this effective energy term corresponds to the free energy associated with the transfer of a solute molecule from vacuum to solvent, and is therefore referred to as solvation free energy. In practical calculations, ΔG, is most conveniently decomposed into two parts, ΔG_pol and ΔG_np, which are referred to as polar and nonpolar solvation energy, respectively [3]. The nonpolar part, ΔG_np, is associated with the first step of the insertion process, at which empty space is created inside solvent and filled with solute atoms whose charges were canceled. The polar solvation energy, ΔG_pol, corresponds to the free energy associated with charging the atoms of the neutral solute immersed in solvent, to their actual values.

The polar solvation energy is the more computationally expensive part in ΔG and it represents the bottleneck in computer simulations of biomolecules. In principle, ΔG_pol can be found exactly in the framework of continuous electrostatics in inhomogeneous media. Depending on whether free ions are present in aqueous solution or not, ΔG_pol is given by the solution of the Poisson or Poisson-Boltzmann (PB) equations, respectively, in which solute is treated as a medium of low dielectric constant, typically ε=1−10, while the solvent is assigned a high dielectric constant ε=80 [4]. As exact analytical solutions of the PB equation exist only for a few solute geometries, in the general case of arbitrarily shaped solutes, this equation has to be solved numerically. Apart from the more fundamental issues concerning applicability of continuous solvent representation at molecular length scales, the necessity to find a numerical solution severely limits the range of problems to which PB model can be applied. Although much progress has been made recently [5, 6] in developing efficient algorithms for solving PB equation, such as finite difference and boundary element methods, overall these methods are still considered too slow to be applied directly in molecular dynamic simulations of macromolecular systems. More commonly, numerical solutions of the PB equation are used as benchmarks in developing other, faster models of electrostatic solvation.

The generalized Born (GB) theory [7, 8], is one of the most successful fast though approximate approaches to electrostatic solvation in biomolecular systems. The solvation energy ΔG_pol in GB model is represented as a pairwise summation over all atoms comprising a solute molecule, and is therefore relatively cheap to compute, compared to solving PB equation numerically. A critical ingredient of this model is effective atomic radius, so-called Born radius, whose physical meaning is based on the Born solvation model of spherical ions. The accuracy of the GB model was critically tested in relation to the PB theory, which it was designed to approximate. Remarkably, very good agreement between the PB and GB results were reported for model solutes of various shapes [9] as well as a large number of biomolecules of practical interest, proteins [10–12].

Although the generalized Born formula for electrostatic solvation is not computationally expensive per se, provided that the effective Born radii are given, evaluating these radii presents a major computational challenge. The calculation of the Born radii, which requires an exterior domain integration or an integration over the molecular volume for each atom, remains the most expensive part in the GB theory. There are several methods including analytical and non-analytical approaches to obtain the Born radii. The analytical pairwise GB models [13–17] approximate the volume integral by a sum of spherical integrals centered at each atom, in which the overlap region is compensated through an empirical correction. The spherical integrals can then be computed analytically. Nonetheless, the non-analytical approaches usually give more accurate results due to the deficiencies in the empirical corrections of analytical models. In one of the earliest and most widely accepted studies on GB model by Still et al. [18], the Born radii were obtained by constructing a set of concentric spherical shells and summing the fractional area of the shells inside the volume. In other papers, the Born radii were calculated by grid-based numerical methods, such as, using volume integration of the molecule based on a cubic grid [19], or applying the Green's function to convert the volume integral into a surface integral [20], or the approach of numerical quadrature techniques used in the density functional theory [21, 22].

Despite much recent improvement, most grid-based calculations of Born radii available today are not sufficiently fast to be applied in large macromolecular simulation [8]. As these methods usually need to compute integrals individually for each atom, for a grid of O(N³) points in the computational domain containing the molecule, a direct calculation of the volume integral has a computational complexity of O(MN³), where M is the total number of the atoms within the molecular volume. Even with the volume integrals reduced to surface integrals for a complexity of O(MN²), the computational cost remains too high for large atom number M in practical simulations. In this paper, we propose a new method to compute Born radii using the fast Fourier transform (FFT) algorithm. Our method relies on a new formulation of the Born radius where the singularity of the kernel function inside the exclusion sphere for each charge is removed by a smoothing function, resulting in high efficiency and accuracy of the FFT calculations. The Born radii for atoms located off grid sites are obtained by interpolations from nearby grid points. The overall complexity of our algorithm is linear (apart from a logarithmic factor) in the number of atoms comprised in a molecule, M, and the number of grid points N³ one uses to perform FFT, O(N³ log N + M). The grid parameter N is independent of M and is chosen such that sufficient accuracy in volume integrals over the biomolecules of interest is achieved. By changing the smoothness of the kernel function, one can control the rate of its spectral decay, and therefore keep the number of the grid points to a minimum. Comparing the complexity of our algorithm to other grid-based methods, it is clear that our FFT-based method has an advantage. As we will demonstrate later in the text in direct comparisons, this advantage becomes more pronounced for systems with large number of atoms.

The remainder of the paper is organized as follows. In Section 2, we review the approximate generalized Born theory. Section 3 contains a new formulation of the generalized Born radius with smooth kernels. Then, a new FFT based fast algorithm is proposed in Section 4 while Section 5 contains numerical validation of the proposed algorithm for one model molecule and two protein molecules. Finally, Section 6 summarizes this paper with conclusions.

2 Generalized Born theory

In the implicit description of bio-molecules in solvent environments, we approximate solvent as a uniform dielectric medium and the solute molecule with a lower dielectric constant and partial charges at atomic centers. The electrostatic potential therefore satisfies the Poisson equation

$$\nabla [∊\left(\mathbf{r}\right)\nabla \varphi \left(\mathbf{r}\right)]=-4\pi \rho \left(\mathbf{r}\right),$$ (2.1)

where ε(r) is the dielectric constant taking value ε_in (ε_in = 1 in most cases) inside the molecule and ε_ex outside the solute molecule (ε_ex = 80 for water), and ρ(r) is the charge distribution

$$\rho \left(\mathbf{r}\right)=\sum _i{q}_i\delta (\mathbf{r}-{\mathbf{r}}_i),$$ (2.2)

with r_i being the atomic position of the ith point charge of strength q_i of both signs for $i=1,\cdots ,M$. If ionic salt effects are to be considered, the linearized Poisson-Boltzmann (PB) equation will be used in (2.1) instead (with the right hand side as a linear function of ϕ(r) for the exterior region outside the molecule). Numerical methods for the Poisson equation for molecules of arbitrary shape include finite difference methods [23], finite element methods [24] and boundary element methods [25, 26]. Among these methods the boundary element method has been known as one of the most effective PB solvers, when used with fast multipole methods [27]. To compute the electrostatic solvation energy, we calculate the potential inside the molecule for two exterior dielectric environments ε_ex = 1 and ε_ex = 80 for water solvent, denote the corresponding potentials as ϕ_vac, ϕ_sol, respectively. Then, the difference of these two potentials gives a reaction field, ϕ_re = ϕ_sol - ϕ_vac, based on which we define the electrostatic solvation energy [7]

$$\Delta G_{pol}=\frac{1}{2}\int {\varphi }_{re}\left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)d\mathbf{r}=\frac{1}{2}\sum _i{q}_i{\varphi }_{re}\left({\mathbf{r}}_i\right).$$ (2.3)

Because of the high computational cost of solving the PB equation directly, much effort has been made in finding equivalent models with a reduced cost. The generalized Born (GB) theory is accepted as the most popular substitution of the Poisson equation, which provides an approximation to the solution of the Poisson equation with a relatively simple formula. The starting point is the well-known Born formula [28] for the solvation energy of a single ion q of radius R immersed in a solvent with the dielectric constant ε,

$$\Delta G_{pol}=-\frac{q^2}{2R}\left(1-\frac{1}{∊}\right),$$ (2.4)

which can be obtained analytically from the Poisson equation. The concept of the atomic radius R in the Born model is extended to polyatomic molecules, in which, for computational efficiency, it is assumed that the solvation energy is represented as a sum over the pairs of all atoms [18, 29, 30]

$$\Delta G_{pol}=-\frac{1}{2}\left(1-\frac{1}{∊}\right)\sum _{i,j}\frac{q_i{q}_j}{f_{GB}}.$$ (2.5)

Here f_GB is a function of the distance r_ij between atoms i and j and their ‘effective Born radii’ R_i and R_j. To be consistent with the Born result for one particle and for two particles at a large separation, f_GB has to interpolate between R_i and r_ij as the interparticle distance tends to zero and infinity respectively. In this paper, we use the expression of Still et al. [18] $f_{GB}=\sqrt{r_{ij}^2+R_i{R}_j\exp (-r_{ij}^2∕4R_i{R}_j)}$, which clearly satisfies these two conditions. The resulting solvation energy

$$\Delta G_{pol}=-\frac{1}{2}\left(1-\frac{1}{∊}\right)\sum _{i,j}\frac{q_i{q}_j}{\sqrt{r_{ij}^2+R_i{R}_j\exp (-r_{ij}^2∕4R_i{R}_j)}}$$ (2.6)

contains atomic positions, atomic charges and effective Born radii as input. The Still's formula for GB solvation energy was shown to be very accurate in test calculations of a large number of model solutes [9,10]. While positions and charges are readily available for a given configuration of the solute molecule to evaluate its solvation energy, the Born radii have to be calculated separately. The physical meaning of the effective Born radius R_i of atom i in a solute molecule, is that it corresponds to the radius of the sphere centered at this atom, whose solvation energy is equal to the solvation energy this molecule would have if all its charges were canceled except for the charge on the target atom. Using this definition allows Born radii to be computed directly by solving the PB equation numerically for a solute of arbitrary shape. As we noted earlier, however, numerical solutions entail significant computational cost, which makes the direct evaluation of R_i impractical.

Much effort has been invested recently in developing approximate analytical formulations for Born radii, which avoid solving the PB equation directly [10, 18, 21, 31]. Historically, the first such formulation approximated electric displacement created by charge i inside a solute molecule of arbitrary shape as coming from a point charge in homogeneous medium, that is being Coulombic in form [7, 15]. Termed accordingly as the Coulomb-field approximation (CFA), this GB formulation provides a simple expression for the Born radii as a volume integral

$$\frac{1}{R_i}=\frac{1}{4\pi }{\int }_{{\Omega }_{ex}}\frac{1}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^4}d\mathbf{r},$$ (2.7)

where Ω_ex denotes the exterior domain outside the molecule, and r_i is the location of the atom i within the molecule. The CFA is known to overestimate the Born radii of atoms, especially those located near the surface of the solute [9, 21], and much better models have been introduced recently [9, 10]. Nevertheless, we use this approximation in the present work as it is most widely accepted in the literature and available in software packages [8]. The main purpose of this paper is to prove that an algorithm based on the FFT can be adapted for use in the GB theory of solvation. Once the methodology is available to compute Born radii within the CFA, it will be a matter of technicality to extend it to more accurate approximations. Therefore, our starting point here is Eq. (2.7).

Typically, the integral over the exterior of a macromolecule in Eq. (2.7) is rewritten as an integral over the interior domain Ω_in excluding a small sphere S_i with a radius a_i centered at the position of the charge (see Bashford and Case [7]),

$$\frac{1}{R_i}=\frac{1}{a_i}-\frac{1}{4\pi }{\int }_{{\Omega }_{in}\backslash S_i}\frac{1}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^4}d\mathbf{r},$$ (2.8)

where the value of the integration outside $S_i{\int }_{{\mathbb{R}}^3\backslash S_i}\frac{1}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^4}d\mathbf{r}=4\pi ∕a_i$ is used. Due to the arbitrary shapes of the molecule, there is no analytical formula for R_i, and therefore, a numerical integration or approximate analytical formula is required.

3 A new formulation for the generalized Born radius with smooth kernels

In this section, we introduce a new method to calculate the generalized Born radius where the singularity of the kernel around the atom site in (2.8) is replaced by a smoothing function, which will be called “a smoother”. We rewrite Eq.(2.7) in the following form

$$\frac{1}{R_i}=\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}-\frac{1}{4\pi }{\int }_{{\Omega }_{in}}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r},$$ (3.1)

where we assume the excluded sphere S_i, embedded inside the molecule (Fig. 1(a)), has a common radius a_i = a for every atom i. G is a smoothed version of the function 1/r⁴ inside the excluded sphere S_i, i.e.

$$G\left(\mathbf{r}\right)=\{\begin{array}{cc}{W}_a^n\left(r\right)\hfill & \text{when}r\le a,\hfill \\ \frac{1}{r^4}\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (3.2)

where the smoother $W_a^n\left(r\right)$ produces a n-th order continuity of G(r) at r = a. For example,

$$W_a^1\left(r\right)=-\frac{2}{a^6}{r}^2+\frac{3}{a^4},$$ (3.3)

$$W_a^2\left(r\right)=\frac{3}{a^8}{r}^4-\frac{8}{a^6}{r}^2+\frac{6}{a^4},$$ (3.4)

$$W_a^3\left(r\right)=-\frac{4}{a^{10}}{r}^6+\frac{15}{a^8}{r}^4-\frac{20}{a^6}{r}^2+\frac{10}{a^4}.$$ (3.5)

Fig. 1.

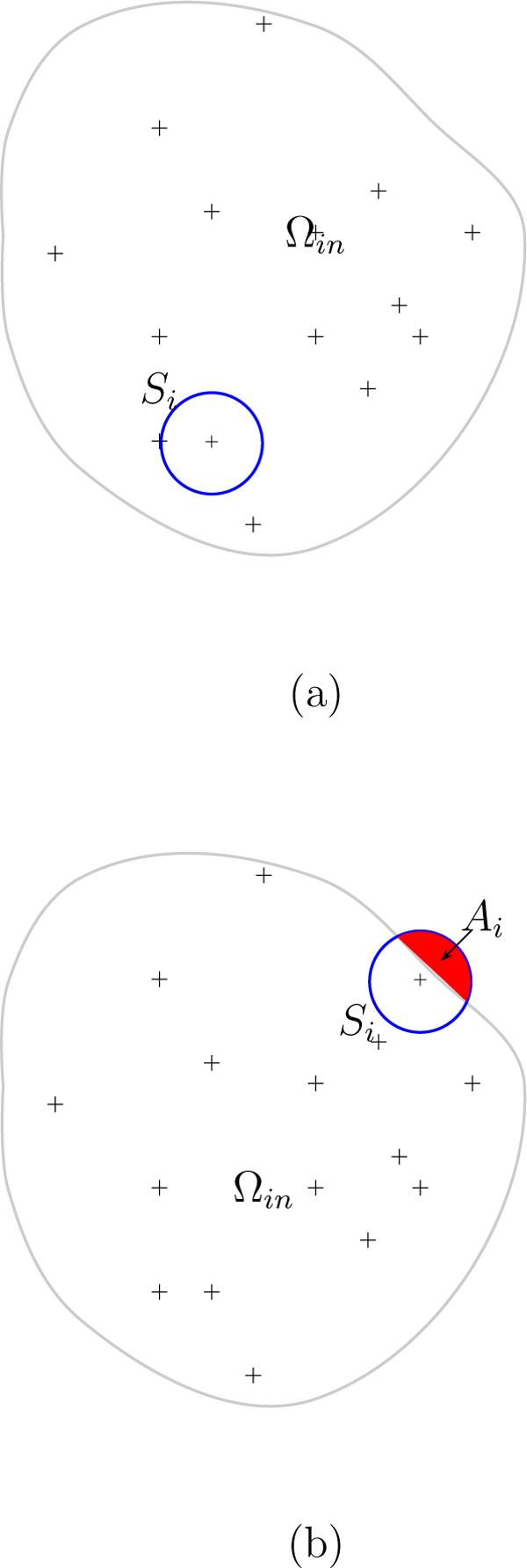
An illustration of how integration in eqs.( 2.7) and ( 3.7) is carried out for atoms at grid points in the interior of a solute and near its surface. A small sphere S_i is drawn around each grid point that is: (a) fully inside the molecule and (b) partially outside of the molecule where A_i is the outlying part of S_i

Note that a larger n will lead to a faster decay in the spectral of G(r) in the Fourier frequency domain, such a fast decay will be an important factor in the efficiency of the proposed method for calculating the Born radius with the FFT. The first integration on the right hand side of (3.1) can be calculated analytically as

$$\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}=\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3\backslash S_i}\frac{1}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^4}d\mathbf{r}+\frac{1}{4\pi }{\int }_{S_i}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}.$$ (3.6)

In Eq. (3.6), the first integral on the right equals to $\frac{1}{a}$ while the second term is the integral of the smoother $W_a^n\left(r\right)$ inside $S_i,\frac{1}{4\pi }{\int }_{S_i}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}=\frac{1}{4\pi }{\int }_{S_i}{W}_a^n\left(r\right)d\mathbf{r}=\frac{3}{5a},\frac{29}{35a}$, and $\frac{65}{63a}$ when n = 1, 2 and 3, respectively.

If the smoother radius a here is taken as the atomic radii, for instance, the van der Waals radius in literature, then, the sphere S_i is completely inside Ω_in. In fact the radius a can be chosen arbitrarily. If the sphere S_i is not completely inside Ω_in, as illustrated in Fig. 1(b). Eq. (2.7) will be rewritten as

$$\frac{1}{R_i}=\frac{1}{4\pi }{\int }_{{\mathbb{R}}^3}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}-\frac{1}{4\pi }{\int }_{{\Omega }_{in}}G(\mathbf{r}-{\mathbf{r}}_i)d\mathbf{r}+\frac{1}{4\pi }{\int }_{A_i}\left[\frac{1}{{\mid \mathbf{r}-{\mathbf{r}}_i\mid }^4}-G(\mathbf{r}-{\mathbf{r}}_i)\right]d\mathbf{r},$$ (3.7)

in which A_i is the portion of S_i outside Ω_in. Since the center of S_i is inside Ω_in, the integration over the region A_i is not singular, and can be calculated by a numerical quadrature or by an approximate analytical formula to be discussed below.

3.1 Analytical formula for the integration over A_i

We consider the integral in A_i for Eq. (3.7), which can be written in the form of a local spherical coordinate system with the origin located at r_i as

$${\int }_{A_i}\left[\frac{1}{{\mid \mathbf{r}\mid }^4}-G\left(\mathbf{r}\right)\right]d\mathbf{r}={\int }_0^{\pi }{\int }_0^{2\pi }{\int }_0^{a}H\left(\mathbf{r}\right)r^2\text{sin}\psi drd\theta d\psi ,$$ (3.8)

where $H\left(\mathbf{r}\right)=\frac{1}{{\mid \mathbf{r}\mid }^4}-G\left(\mathbf{r}\right)$ when r is in A_i and zero elsewhere. If we assume that the sphere S_i is much less than the volume of the molecule and the portion of the molecular surface can be approximated by a plane, then, A_i is a spherical cap of the sphere S_i. This assumption reduces the three dimensional integral to an one dimensional one

$$4\pi {\int }_s^a(r^2-sr)\tilde{H}\left(r\right)dr,$$ (3.9)

where s (s < a) is the shortest distance from r_i to the plane approximating the portion of the molecular surface inside A_i and $\tilde{H}\left(r\right)=\frac{1}{r^4}-W_a^n\left(r\right)$. We have

$${\int }_s^a(r^2-sr)\frac{1}{r^4}dr=\frac{{(a-s)}^2}{2a^{2}s},$$ (3.10)

and

$${\int }_s^a(r^2-sr)W_a^1\left(r\right)dr=\frac{6a^5-10a^{4}s+5a^2{s}^3-s^5}{10a^6},$$ (3.11)

$${\int }_s^a(r^2-sr)W_a^2\left(r\right)dr=\frac{58a^7-105a^{6}s+70a^4{s}^3-28a^2{s}^5+5s^7}{70a^8},$$ (3.12)

$${\int }_s^a(r^2-sr)W_a^3\left(r\right)dr=\frac{130a^9-252a^{8}s+210a^6{s}^3-126a^4{s}^5+45a^2{s}^7-7s^9}{126a^{10}}.$$ (3.13)

4 A FFT-based Algorithm for the Born Radii

In this section, we present a new FFT-based algorithm to calculate the GB radii. The main tool will be the FFT for the evaluation of the second integral on right hand sides of Eqs. (3.1) and (3.7), which takes on the form,

$$\Phi \left(\mathbf{r}\right)={\int }_{{\Omega }_{in}}G(\mathbf{r}-{\mathbf{r}}^{\prime })d{\mathbf{r}}^{\prime }.$$ (4.1)

Once Φ(r) is calculated on grid lattice points, the value Φ(r_i) corresponding to the ith off grid lattice atom can be obtained by a simple interpolation from the nearby data on the lattice sites surrounding the atom. In order to use the FFT, we define an indicator function for the molecular volume domain Ω_in

$$f\left(\mathbf{r}\right)=\{\begin{array}{cc}1\hfill & \mathbf{r}\in {\Omega }_{in},\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}$$ (4.2)

then, the integral in (4.1) can be extended to the full space as

$$\Phi \left(\mathbf{r}\right)={\int }_{{\mathbb{R}}^3}G(\mathbf{r}-{\mathbf{r}}^{\prime })f\left({\mathbf{r}}^{\prime }\right)d{\mathbf{r}}^{\prime }=G\ast f\left(\mathbf{r}\right),$$ (4.3)

which is a convolution fit for evaluation by the Fourier transform $\widehat{f}\left(\xi \right)=\frac{1}{{\left(2\pi \right)}^{3∕2}}{\int }_{{\mathbb{R}}^3}f\left(\mathbf{r}\right)e^{-i\mathbf{r}\cdot \xi }d\mathbf{r}$. We will show later how the transform can be implemented by the discrete fast Fourier transform (FFT) in 1D case (3D case will be done dimension by dimension).

The FFT-based method to be proposed will give Φ(r_ijk) on the grid lattice sites r_ijk = (x_i, y_j, z_k), 0 ≤ i, j, k ≤ N at a cost of O(N³ log N). Then, Φ(r_α) for the α-th off grid lattice site atom can be obtained by an interpolation from Φ(r_ijk) at a cost of O(M) = 8M, for instance, with a linear interpolation for M atom sites. In this paper, we use a weighted average of surrounding eight grid points by taking the inverse of the square of the distance as weights, which gives a better accuracy than the linear interpolation, namely

$$\Phi \left({\mathbf{r}}_{\alpha }\right)=\sum _{\xi =0}^1\sum _{\eta =0}^1\sum _{\zeta =0}^1{W}_{\xi \eta \zeta }\Phi \left({\mathbf{r}}_{i+\xi ,j+\eta ,k+\zeta }\right),$$ (4.4)

where

$$W_{\xi \eta \zeta }=\frac{w_{\xi \eta \zeta }}{\sum _{\xi =0}^1\sum _{\eta =0}^1\sum _{\zeta =0}^1{w}_{\xi \eta \zeta }},\text{and},w_{\xi \eta \zeta }=\frac{1}{({\mid {\mathbf{r}}_{\alpha }-{\mathbf{r}}_{i+\xi ,j+\eta ,k+\zeta }\mid }^2+\delta )},$$ (4.5)

and δ is a small positive number to avoid a division by zero. Here, N is independent of M and only depends on the shape of the molecule Ω_in, i.e., the lattice should be fine enough to resolve the boundary of the molecule within a prescribed accuracy. Therefore, the total complexity is O(N³ log N + M).

4.1 Decay conditions for the smoother's spectral - $\widehat{G}\left(\xi \right)$

The decay conditions of the smoother G and indicator function f in the Fourier frequency space will affect the cost of calculating the convolution (4.3) by the Fast Fourier transforms. Let us consider the 1D analog of (4.1) for the evaluation of

$$\Phi \left(x\right)={\int }_{-b}^{b}G(x-x^{\prime })d{x}^{\prime }$$ (4.6)

for x ∈ V = (−b, b) and

$$G(x-x^{\prime })=\{\begin{array}{cc}{W}_a^n\left(\mid x-x^{\prime }\mid \right),\mid x-x^{\prime }\mid \le a,\hfill & \hfill \\ \frac{1}{{\mid x-x^{\prime }\mid }^4},\text{otherwise}.\hfill & \hfill \end{array}\phantom{\}}$$ (4.7)

Let f(x) be the indicator function for domain V defined in (4.2), then, the one-dimensional convolution corresponding to (4.1) is

$$\Phi \left(x\right)={\int }_{-\infty }^{+\infty }G(x-x^{\prime })f\left(x^{\prime }\right)d{x}^{\prime }=G\ast f\left(x\right).$$ (4.8)

Applying the Fourier transform, we have

$$\widehat{\Phi }\left(\xi \right)=\widehat{G}\left(\xi \right)\widehat{f}\left(\xi \right)$$ (4.9)

with

$$\widehat{G}\left(\xi \right)=\mathcal{F}\left\{G\left(x\right)\right\}=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }G\left(x\right)e^{-i\xi x}dx,$$ (4.10)

$$\widehat{f}\left(\xi \right)=\mathcal{F}\left\{f\left(x\right)\right\}=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f\left(x\right)e^{-i\xi x}dx,$$ (4.11)

and, then, using the inverse Fourier transform, we have

$$\Phi \left(x\right)={\mathcal{F}}^{-1}\left\{\widehat{G}\left(\xi \right)\widehat{f}\left(\xi \right)\right\}=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\widehat{G}\left(\xi \right)\widehat{f}\left(\xi \right)e^{+i\xi x}d\xi .$$ (4.12)

Due to the fact that f(x) is discontinuous at x = ±b and G(x) is Cⁿ-continuous at x = ±a with the smoother $W_a^n$, the decay conditions of $\widehat{f}\left(\xi \right)$ and $\widehat{G}\left(\xi \right)$ are

$$\widehat{f}\left(\xi \right)=O\left(\frac{1}{\xi }\right),\mid \xi \mid \to +\infty ,$$ (4.13)

$$\widehat{G}\left(\xi \right)=O\left(\frac{1}{{\xi }^{n+1}}\right),\mid \xi \mid \to +\infty .$$ (4.14)

If we further smooth the indicator function f(x), for example in the vicinity of x = b, using $f\left(x\right)\approx -\frac{1}{\pi }$ arctan $\lambda (x-b)+\frac{1}{2}$ with λ a large real number, higher order of decay for $\widehat{f}\left(\xi \right)$ can also be obtained.

4.2 Calculation of Φ(x_j) in one dimensional case

We will follow two steps in the calculation of (4.8).

• Step 1: Using the decay condition of the Fourier transform of the smoother $\widehat{G}\left(\xi \right)$, integral in (4.12) can be truncated to a finite interval [−Ωπ, Ωπ], and the resulting integral will be approximated by a N point quadrature rule using $\widehat{f}\left({\xi }_k\right)\widehat{G}\left({\xi }_k\right),{\xi }_k=k\frac{2\pi \Omega }{N}$.

• Step 2: Each $\widehat{G}\left({\xi }_k\right)$, $\widehat{f}\left({\xi }_k\right)$, defined by (4.10) (4.11), only involves integral over a finite interval due to the compact support of f(x) and rapid decay of G(x), and will be approximated by another N point quadrature.

Both steps can be implemented by the FFT, which has an O(NlogN) complexity of evaluating the following two transforms between data $\{f\left(x_j\right),-\frac{N}{2}\le j\le \frac{N}{2}-1\}$ and discrete Fourier coefficients $\{{\widehat{f}}_k,-\frac{N}{2}\le k\le \frac{N}{2}-1\}$

$$f\left(x_j\right)=\sum _{k=-N∕2}^{N∕2-1}{\widehat{f}}_k{e}^{ik{x}_j},\text{for}{x}_j=j\frac{2\pi }{N},-\frac{N}{2}\le j\le \frac{N}{2}-1,$$ (4.15)

$${\widehat{f}}_k=\frac{1}{N}\sum _{j=-\frac{N}{2}}^{\frac{N}{2}-1}f\left(x_j\right)e^{-ik{x}_j},-\frac{N}{2}\le k\le \frac{N}{2}-1.$$ (4.16)

Let ε be an error tolerance of the whole algorithm, against which we truncate the integral over ξ ∈ (−∞, +∞), i.e.,

$$\Phi \left(x\right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{+\infty }{e}^{i\xi x}\widehat{f}\left(\xi \right)\widehat{G}\left(\xi \right)d\xi \approx \frac{1}{\sqrt{2\pi }}{\int }_{-\Omega \pi }^{\Omega \pi }{e}^{i\xi x}\widehat{f}\left(\xi \right)\widehat{G}\left(\xi \right)d\xi ,$$ (4.17)

with the truncation parameter Ω defined as follows based on the decay condition (4.13)(4.14)

$$\frac{1}{{\left(\pi \Omega \right)}^{n+1}}=\epsilon .$$ (4.18)

An N-point rectangle quadrature rule to the integral in (4.17) yields

$$\Phi \left(x\right)\approx \frac{\sqrt{2\pi \Omega }}{N}\sum _{k=-N∕2}^{N∕2-1}{e}^{i{\xi }_{k}x}\widehat{f}\left({\xi }_k\right)\widehat{G}\left({\xi }_k\right),$$ (4.19)

where ${\xi }_k=k\frac{2\pi \Omega }{N}$ and N will be selected based on the Shannon sampling rate of $T=\frac{\pi }{L}\text{for}{e}^{i\xi L}$ in the ξ variable

$$N=\frac{2\pi \Omega }{T}=2\Omega L.$$ (4.20)

Remark 1 In principle, the selection of N should also depend on the oscillatory behavior of the spectral function $\widehat{f}\left(\xi \right),\widehat{G}\left(\xi \right)$. In case a larger N is needed to resolve the oscillations in $\widehat{f}\left(\xi \right),\widehat{G}\left(\xi \right)$, we can achieve that by increasing the size of L.

4.2.1 Computing $\Phi \left(x_j\right),x_j=j\frac{2L}{N}\in [-L,L],-\frac{N}{2}\le j\le \frac{N}{2}-1$

Next, we will calculate the value of Φ(x_j) at N points inside the interval [−L, L]. Again, the size of N will be based on the Shannon sampling rate $T=\frac{1}{\Omega }$ for function e^±iΩπx in the x-variable, which gives again

$$N=\frac{2L}{T}=2\Omega L.$$ (4.21)

Let

$$x_j=j\frac{2L}{N}\in [-L,L],-\frac{N}{2}\le j\le \frac{N}{2}-1,$$ (4.22)

then

$$\Phi \left(x_j\right)\approx \frac{\sqrt{2\pi }\Omega }{N}\sum _{k=-N∕2}^{N∕2-1}\widehat{f}\left({\xi }_k\right)\widehat{G}\left({\xi }_k\right)e^{ik\frac{2\pi \Omega }{N}j\frac{2L}{N}}=\frac{\sqrt{2\pi }\Omega }{N}\sum _{k=-N∕2}^{N∕2-1}\widehat{f}\left({\xi }_k\right)\widehat{G}\left({\xi }_k\right)e^{ikj\frac{2\pi }{N}},$$ (4.23)

which can be evaluated by one FFT at a cost of O(N log N).

4.2.2 Calculation of $\widehat{f}\left({\xi }_k\right),{\xi }_k=k\frac{2\pi \Omega }{N},\mid k\mid \le \frac{N}{2}$

As sup(f) ⊂ [−L, L], we have

$$\widehat{f}\left(\xi \right)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }f\left(x\right)e^{-i\xi x}dx=\frac{1}{\sqrt{2\pi }}{\int }_{-L}^{L}f\left(x\right)e^{-i\xi x}dx,$$ (4.24)

which will also be approximated by an N−point rectangle quadrature rule

$$\widehat{f}\left(\xi \right)\approx \frac{2L}{N\sqrt{2\pi }}\sum _{j=-N∕2}^{N∕2-1}f\left(x_j\right)e^{-i\xi x_j},$$ (4.25)

where $x_j=j\frac{2L}{N}$.

As N = 2ΩL, we have for $-\frac{N}{2}\le k\le \frac{N}{2}$

$$\widehat{f}\left({\xi }_k\right)=\frac{2L}{N\sqrt{2\pi }}\sum _{j=-N∕2}^{N∕2-1}f\left(x_j\right)e^{-ik\frac{2\pi \Omega }{N}j\frac{2L}{N}}=\frac{2L}{N\sqrt{2\pi }}\sum _{j=-N∕2}^{N∕2-1}f\left(x_j\right)e^{-ikj\frac{2\pi }{N}},$$ (4.26)

which can be evaluated by one FFT at a cost of O(N log N).

The values for $\widehat{G}\left({\xi }_k\right)$ can be obtained by analytical formulae as to be shown later.

4.2.3 Algorithm I - 1D case

The following steps form the flow of the algorithm in the 1-D case.

• Step 1. For an n-th order smoother $W_a^n\left(r\right)$ in (3.2) and an error tolerance ε > 0, choose the truncation parameter Ω by

  $$\Omega =\frac{1}{\pi {\epsilon }^{1∕(n+1)}}$$ (4.27)

  and set

  $$N=2\Omega L.$$ (4.28)

• Step 2. Compute $\widehat{f}\left({\xi }_k\right),{\xi }_k=k\frac{2\pi \Omega }{N},\mid k\mid \le \frac{N}{2}$ using the FFT according to (4.26).

• Step 3: Compute $\Phi \left(x_j\right),x_j=j\frac{2L}{N}\in [-L,L],-\frac{N}{2}\le j\le \frac{N}{2}-1$ using one FFT according to (4.23).

4.3 Calculation of Φ(x_m, y_n, z_l) in three dimensional case

4.3.1 Analytical expression for $\widehat{G}\left(\xi \right)$

The 3-D Fourier transform $\widehat{G}\left(\xi \right)$ can be found analytically. We consider the three-dimensional Fourier transform of G(r) defined by

$$\widehat{G}\left(\xi \right)=\frac{1}{{\left(2\pi \right)}^{3∕2}}{\int }_{{\mathbb{R}}^3}G\left(\mathbf{r}\right)e^{i\xi \cdot \mathbf{r}}d\mathbf{r},$$ (4.29)

which is a spherical symmetric function of ξ due to the spherical symmetry of G(r) in the spatial domain. Therefore, the Fourier transform at a radial distance ρ (by letting ξ = (0, 0, ρ)) is

$$\widehat{G}\left(\xi \right)=\frac{1}{{\left(2\pi \right)}^{3∕2}}{\int }_0^{2\pi }{\int }_0^{\pi }{\int }_0^{\infty }G\left(r\right)e^{ir\rho \text{cos}\psi }{r}^2\text{sin}\psi drd\psi d\theta ,$$ (4.30)

where ρ = |ξ|, and (r, θ, ψ) is the spatial spherical coordinate system with x = r cos θ sin ψ, y = r sin θ sin ψ and z = r cos ψ. Integration in ψ and substitution of the piecewise definition of G(r) yields

$$\begin{array}{cc}\hfill & \widehat{G}\left(\xi \right)=\frac{\sqrt{2}}{\pi }{\int }_0^{\infty }G\left(r\right)r\frac{\text{sin}\left(r\rho \right)}{\rho }dr\hfill \\ \hfill & =\frac{\sqrt{2}}{\pi }[{\int }_0^a{W}_a^n\left(r\right)r\frac{\text{sin}\left(r\rho \right)}{\rho }dr+{\int }_a^{\infty }\frac{\text{sin}\left(r\rho \right)}{r^3\rho }dr]\hfill \\ \hfill & =\frac{\sqrt{2}}{\pi }(I_n+II).\hfill \end{array}$$ (4.31)

The second term II can be integrated to give

$${\int }_a^{\infty }\frac{\text{sin}\left(r\rho \right)}{r^3\rho }dr=\frac{1}{a}\left[-\frac{\pi \mu }{4}{+}_1{F}_2(-\frac{1}{2};\frac{1}{2},\frac{3}{2};-\frac{1}{4}{\mu }^2)\right],$$ (4.32)

where μ = aρ, and ₁F₂(α; β, γ; x) is the hypergeometric function

$${}_{1}F_2(\alpha ;\beta ,\gamma ;x)=\sum _{m=0}^{\infty }\frac{{\left(\alpha \right)}_m}{{\left(\beta \right)}_m{\left(\gamma \right)}_m}\frac{x^m}{m!},$$

with ${\left(\alpha \right)}_m=\alpha (\alpha +1)\cdots (\alpha +m-1)$ as the rising factorial.

For the first integral in (4.31), we have, for n = 1, 2 and 3,

$$I_1=-\frac{1}{a{\mu }^5}[\mu ({\mu }^2+12)\text{cos}\mu +3({\mu }^2-4)\text{sin}\mu ],$$ (4.33)

$$I_2=-\frac{1}{a{\mu }^7}[\mu ({\mu }^4-12{\mu }^2+360)\text{cos}\mu +3({\mu }^4+44{\mu }^2-120)\text{sin}\mu ],$$ (4.34)

$$\begin{array}{cc}\hfill I_3& =-\frac{1}{a{\mu }^9}[\mu ({\mu }^6-12{\mu }^4-1560{\mu }^2+20160)\text{cos}\mu +\hfill \\ \hfill & 3({\mu }^6-20{\mu }^4+2760{\mu }^2-6720)\text{sin}\mu ].\hfill \end{array}$$ (4.35)

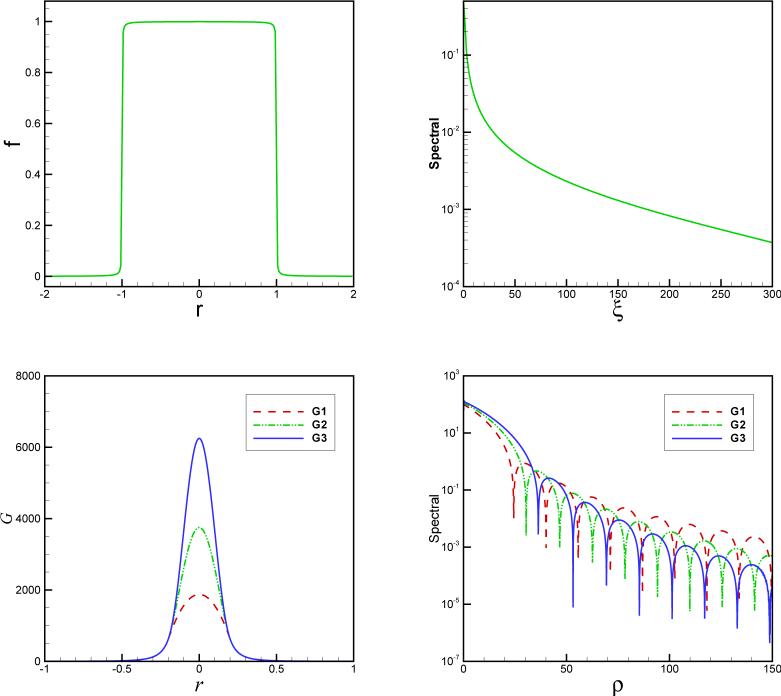
In Fig. 2, the spectral $\widehat{f}$ and $\widehat{G}$ with different choices of smoother are plotted where Gn denotes a Cⁿ continuity. We remark that I_n is not convergent at μ = 0 due to higher order infinitesimal of the denominator than the numerator in I_n. Therefore, I_n(0) should be calculated by an extrapolation, for example for a first order accurate extrapolation, we can use $I_n\left(0\right)=2I_n\left(\frac{a}{2}\right)-I_n\left(a\right)$.

Fig. 2.

Smoothed f(x) (top left), smoothed kernel G(r) (bottom left) and their Fourier transforms (right). Gn refers to a smoothed kernel using the smoother $W_a^n\left(r\right)$, a = 0.2

4.3.2 Algorithm II - 3D case

Let the molecule be contained in a rectangular box of size [−L_x, L_x]×[−L_y, L_y]×[−L_z, L_z]. If the smallest box that contains the molecule is [−a, a] × [−b, b] × [−c, c], then, due to the periodicity of the FFT, the computational box [−L_x, L_x]×[−L_y, L_y] × [−L_z, L_z] should be chosen such that L_x ≥ 2a, L_y ≥ 2b, and L_z ≥ 2c to avoid the overlap of the images of f and G.

The following steps form the flow of the algorithm in the 3-D case.

• Step 1. For an n-th order smoother $W_a^n\left(r\right)$ in (3.2) and an error tolerance ε > 0, choose the truncation parameter Ω by

  $$\Omega =\frac{1}{\pi {\epsilon }^{1∕(n+1)}}$$ (4.36)

  and set

  $$N_x=2\Omega L_x,N_y=2\Omega L_y,N_z=2\Omega L_z.$$ (4.37)
• Step 2. compute $\widehat{f}({\xi }_i,{\eta }_j,{\chi }_k),({\xi }_i,{\eta }_j,{\chi }_k)=(i\frac{2\pi \Omega }{N_x},j\frac{2\pi \Omega }{N_y},k\frac{2\pi \Omega }{N_z}),-\frac{N_x}{2}\le i\le \frac{N_x}{2}-1,-\frac{N_y}{2}\le j\le \frac{N_y}{2}-1,-\frac{N_z}{2}\le k\le \frac{N_z}{2}-1$, using one 3-D FFT for the following sums at a cost of O(N_xN_yN_z log(N_xN_yN_z)).

  $$\widehat{f}({\xi }_i,{\eta }_j,{\chi }_k)=\frac{8L_x{L}_y{L}_z}{{\left(2\pi \right)}^{3∕2}{N}_x{N}_y{N}_z}\sum _{m=-N_x∕2}^{N_x∕2-1}\sum _{n=-N_y∕2}^{N_y∕2-1}\sum _{l=-N_x∕2}^{N_x∕2-1}f(x_m,y_n,z_l)e^{-\mathbf{i}2\pi (\frac{mi}{N_x}+\frac{nj}{N_y}+\frac{lk}{N_z})},$$ (4.38)

  where $\mathbf{i}=\sqrt{-1}$.
• Step 3: Compute $\Phi (x_m,y_n,z_l),(x_m,y_n,z_l)=(m\frac{2L_x}{N_x},n\frac{2L_y}{N_y},l\frac{2L_z}{N_z})\in [-L_x,L_x]\times [-L_y,L_y]\times [-L_z,L_z]-\frac{N_x}{2}\le m\le \frac{N_x}{2}-1,-\frac{N_y}{2}\le n\le \frac{N_y}{2}-1,-\frac{N_z}{2}\le l\le \frac{N_z}{2}-1$, using one 3-D FFT for the following sums at a cost of O(N_xN_yN_z log(N_xN_yN_z)).

  $$\Phi (x_m,y_n,z_l)=\frac{{\left(2\pi \right)}^{3∕2}{\Omega }^3}{N_x{N}_y{N}_z}\sum _{i=-N_x∕2}^{N_x∕2-1}\sum _{j=-N_y∕2}^{N_y∕2-1}\sum _{k=-N_x∕2}^{N_x∕2-1}\widehat{f}({\xi }_i,{\eta }_j,{\chi }_k)\widehat{G}({\xi }_i,{\eta }_j,{\chi }_k)e^{\mathbf{i}2\pi (\frac{mi}{N_x}+\frac{nj}{N_y}+\frac{lk}{N_z})}.$$ (4.39)

Remark 2 In the 3-D case, the function f(x, y, z) is the indicator function of the solute molecule, therefore, N_x, N_y, N_z should be large enough so the boundary of the solute molecule is well resolved on the N_xN_yN_z–lattice grid to ensure a prescribed accuracy in the Fourier transform (4.38).

Remark 3 In (4.38)(4.39), only the simplest rectangle quadrature rules are used. In fact, higher order equally spaced Newton-Cotes formula could be used and the FFT could still be applicable.

5 Validation of the FFT-based Algorithm

5.1 A model molecule - numerical accuracy

To test the accuracy and speed of the proposed method, we first implement a test example by taking a dimensionless unit sphere

$${\Omega }_{in}=\{(x,y,z):x^2+y^2+z^2\le 1\},$$

as the interior region of a molecule. A window function $W_a^2$ is used as the smoother in (4.7). For the spherical geometry, the 3D exterior integral (2.7) can be computed exactly due to the radial symmetry of the sphere, i.e.

$$\frac{1}{R_i}=\frac{1}{2}{\int }_0^{\pi }{\int }_1^{\infty }\frac{r^2\text{sin}\psi }{{(r^2-2r{r}_i\text{cos}\psi +r_i^2)}^2}drd\psi =\frac{2r_i+(1-r_i^2)\text{log}\frac{1+r_i}{1-r_i}}{4r_i(1-r_i^2)},$$ (5.1)

where r_i (r_i < 1) is the distance between the ith atom and the origin.

We test the accuracy of the FFT-based algorithms by computing the relative error in R_i for a uniformly distributed 100 charges along a radial direction. In cases where part of the sphere S_i for a charge is outside the molecule, we can obtain the height of the spherical cap A_i in (3.7) and the distance between the charge and the molecular surface analytically. In practical calculations, this can be done by defining a level set function C(r) [32, 33] as in the next section, which is a signed distance function (being greater or less than 0 when r is inside or outside the molecule, respectively). The distance function C(r) on a 3-D grid can be evaluated by a fast sweeping algorithm [34] with a complexity O(N_xN_yN_z) with N_xN_yN_z grid points. As the interior region in this test model molecule can be parameterized, the exact normal direction to the surface is known and, therefore, it is straightforward to compute the distance along that direction for the charges close to the boundary.

We summarize our results in Tab 1, which shows the maximum and average errors for different window sizes and grids in a spatial region [−L, L]³ with L = 2. We remark that there are several sources for errors in the calculations of Born radius R_i. The first source is the error in numerical quadrature involved in (4.23) (Step 3 in the FFT-based Algorithms). The second source comes from the interpolation of Born radii for atoms at off-lattice sites using the neighboring grid points. And the last source results from the treatment of atoms whose small sphere has a portion A_i outside the molecule and an approximation for the shape of A_i is used in (3.7). These three different sources of error depend on the parameters of our algorithm in a non-trivial way. In what follows we investigate their effect in detail. For the sake of comparison, we also implement the solution of the grid-based GB method [21] with a Cartesian grid [−1, 1]³, which directly sums the data at the centers of grid boxes for the numerical integration. This method is well known for its high accuracy, especially for solutes with complicated surface geometry.

Table 1.

The maximum and average relative errors of the FFT radii compared to the exact solution for a spherical solute of radius 1.

Grid Size h	a = 0.25		a = 0.2		a = 0.15		a = 0.1
	max.	ave.	max.	ave.	max.	ave.	max.	ave.
0.125	7.16%	1.95%	9.15%	2.16%	11.1%	2.50%	12.8%	3.19%
0.0625	4.18%	0.86%	3.77%	0.82%	4.20%	0.95%	6.15%	1.34%
0.03125	4.00%	0.76%	3.53%	0.56%	2.98%	0.49%	2.32%	0.77%

Tables 1 and 2 contain the numerical errors for our FFT-based method and the original grid-based method, respectively. It is seen that at the largest grid spacing h=0.125, the error is large for all sizes of the smoothing window radius a considered. Both FFT and grid-based integration yield errors well over 1%. For increasing values of a, the error is seen to decrease gradually. In the FFT-based calculations, this decrease is due to the faster decay in the spectral of the window function at larger a. In the grid-based integration, small size of the window function a can not be efficiently resolved in a volume integration using a grid of comparable spacing h ∼ a. Note that for the smallest a=0.1, the FFT calculation yields a ∼ 3% error which is a significant improvement over the grid-based calculation generating a 68% error. Comparing the results of FFT and grid-based calculations for h=0.125 it is clear that the main source of error is space integral discretization and that the error is unacceptably large.

Table 2.

Same as Tab. 1 but for the grid-based calculations

Grid Size h	a = 0.25		a = 0.2		a = 0.15		a = 0.1
	max.	ave.	max.	ave.	max.	ave.	max.	ave.
0.125	3.66%	1.13%	5.11%	1.76%	35.9%	11.4%	125.3%	68.03%
0.0625	3.82%	0.61%	3.22%	0.63%	2.57%	0.74%	10.37%	3.31%
0.03125	3.96%	0.38%	3.35%	0.28%	2.66%	0.19%	1.88%	0.30%

As the grid spacing h is reduced, the Born radii computed using our algorithms become more accurate. At h=0.0625, both FFT and grid-based errors show a tendency to decrease with increasing a, echoing the results observed for a larger h=0.125. On a grid of higher resolution, h=0.03125, that tendency is reversed for the largest a considered. In the FFT calculation, the error jumps from 0.56% at a=0.2 to 0.76% at a=0.25. In the grid-based calculation, a similar increase is from 0.28% to 0.38%. That a non-linear behavior with a is observed signals that the dominant error in Born radii present at larger h due to the numerical quadrature, has become comparable to the error resulting from the treatment of surface atoms at the smaller h=0.0315. For the surface atoms, the approximation involved in calculating the volume of spheres overlapping with the solute becomes worse for larger a. Consequently, the total error in R_i grows. Analyzing the last rows in Tabs. 1 and 2 we conclude that for a sufficiently fine grid network, it is possible to find a size of the window function a such that the cumulative error in R_i reaches a minimum. For both FFT and grid-based algorithms the minimum error is well below 1%. The error is slightly higher, 0.49%, in the FFT algorithm than in its grid-based counterpart, 0.19%, highlighting the importance of the intrinsic numerical errors present in the former algorithm that go beyond space discretization. Nevertheless, Tabs. 1 and 2 clearly show that the new algorithm proposed in this paper is sufficiently accurate to yield reliable Born radii for a spherical solute.

To evaluate the cost-efficiency of our FFT algorithm, time-performance tests were carried out in comparison to the grid-based method. The results of these tests are summarized in Fig. 3, which shows the CPU times for both methods implemented on a notebook PC with AMD 1.90 GHz double CPUs and 2G memory. As expected, the FFT-based algorithm incurs a much less computational cost. It is seen in Fig. 3 that for the grid size h = 0.0625, where the average error in R_i is below 1% (See Tab. 1), the FFT algorithm becomes faster than the grid-based method when the number of atoms in a solute molecule reaches 600. Typically, proteins of moderate sizes contain more than 600 atoms. It is clear, therefore, that for such proteins the new method proposed here becomes advantageous. For a system composed of about 4000 atoms, the speed improvement of our algorithm reaches one order of magnitude. For larger systems, the improvement is even more dramatic. For instance, starting at approximately 5000 atoms, FFT calculations on a finer mesh h = 0.03125 with much improved accuracy, become faster than the grid-based calculations on a coarser mesh of h=0.0625. We conclude from this analysis, that the FFT algorithm offers a much better performance over the grid-based methods, and should therefore become the method of choice in GB calculations of large solute molecules.

Fig. 3.

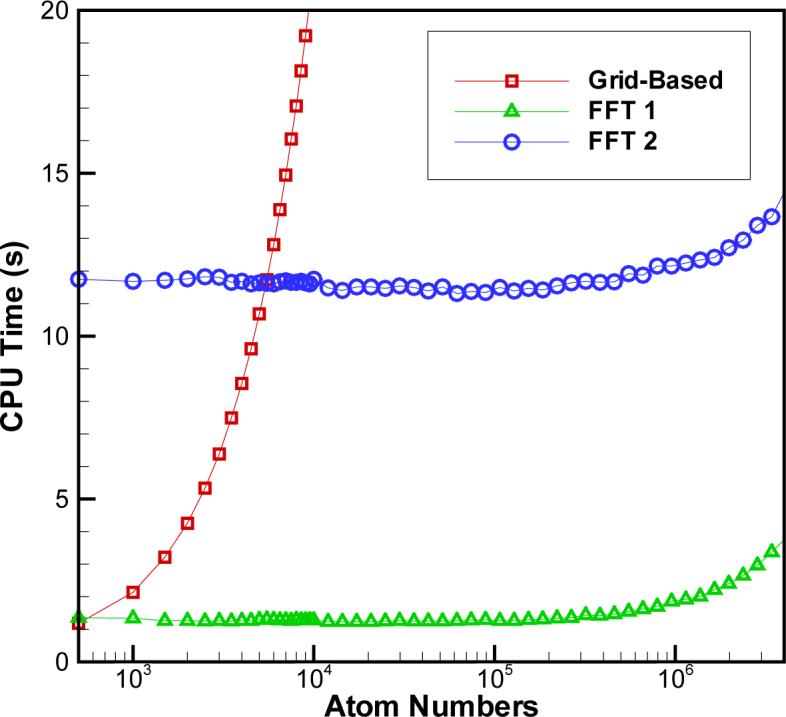
CPU time vs. number of atoms for three settings of our new FFT-based algorithm with a smoother $W_a^2\left(r\right)$, a = 0.2 and the average relative error less than 1.0%. Grid-based: h = 0.0625; FFT 1: h = 0.0625; FFT 2: h = 0.03125. All tests were done for a model spherical solute of radius 1.

In the example of a spherical solute, the Born radii are known exactly, and, in principle, there is no need to evaluate R_i using grid-based approach; FFT calculations could be compared to the known solutions directly. For an arbitrarily shaped solute, however, the exact solution is not known and it is the grid-based solutions that serve as the reference point for comparison with the FFT algorithm. In view of this, it makes sense to compare FFT and grid-based solutions for a spherical solute, to estimate the level of agreement one can expect between the two methods for an arbitrarily shaped solute. Figure 4 presents such analysis for the radius of the smoothing function a=0.2. It is visually apparent from the Born radii plotted in this figure, that the results of the FFT algorithm agree well with those of the direct grid summation. The smaller the grid spacing h the better the agreement is observed. To characterize the agreement between the two data sets quantitatively, we use the standard correlation coefficient, defined as

$$\rho =\frac{E\left(XY\right)-E\left(X\right)E\left(Y\right)}{\sqrt{E\left(X^2\right)-E^2\left(X\right)}\sqrt{E\left(Y^2\right)-E^2\left(Y\right)}},$$ (5.2)

where E is the mathematical expectation, X and Y are FFT radii and grid-based radii, respectively. The correlation coefficients we observe are very high, ρ=0.9936, 0.9994 and 0.9999 for h = 0.125, 0.0625 and 0.03125, respectively.

Fig. 4.

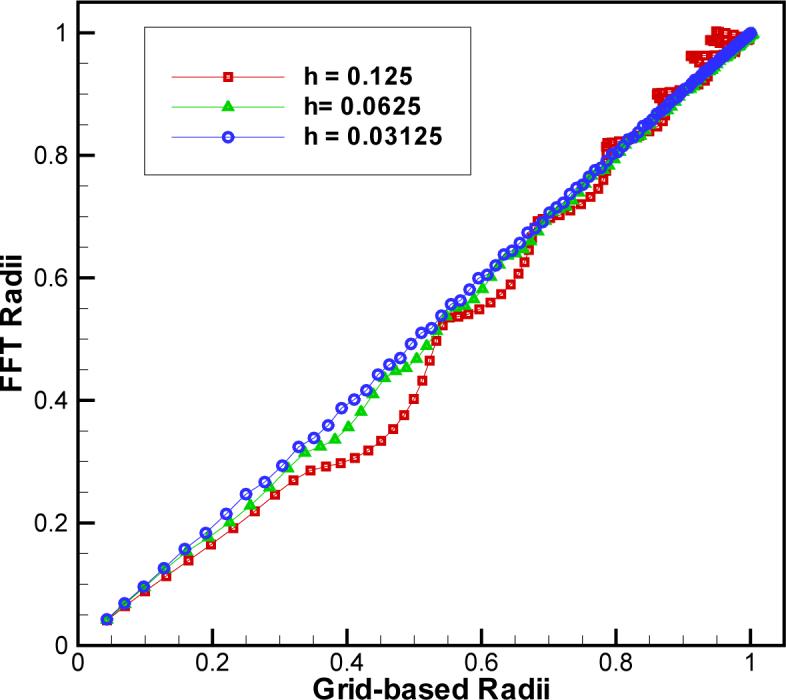
Born radii derived using our new FFT-based algorithm vs. grid-based radii computed for a model spherical solute of radius 1 using the smoother $W_a^2\left(r\right)$, a = 0.2. The correlation coefficients are 0.9936, 0.9994 and 0.9999 for h = 0.125, 0.0625 and 0.03125, respectively.

5.2 Effective Born Radii for Proteins

A thorough investigation on the performance of the new FFT-based algorithm proposed in this work to large set of proteins is underway and its results will be reported in a separate publication. Here in this paper we present our results for two proteins, immunoglobulin binding protein [35]( PDB access code 3GB1 ) and human cyclophilin A [36] ( PDB access code 1OCA ). These two proteins differ in size significantly, containing 56 amino acids, 855 atoms and 165 amino acids, 2503 atoms, respectively, and thus serve well the aim of critically testing the performance of our algorithm. The indicator function which defines the molecular domain is generated by the solvent accessible surface with a probe radius of 1.5 Å. The fast sweeping method [34] with 8N³ operations is used to obtain the distance function from grid points to the surface. In order to smooth the step-like discontinuity of the indicator function across the surface, a smoothing procedure based on a time dependent heat equation [37] is employed with the indicator function as the initial condition so that there are 2−4 grid points across the molecule boundary. We remark that smoothing treatment is also often used in generalized Born models [22] and for the purpose of avoiding numerical instability in finite difference Poisson-Boltzmann solvers [38]. In our FFT implementation, a cubic box of dimension L=32 Å was used for protein 3GB1 and a box of dimension L=40 Å for protein 1OCA. In Figs. 5 and 6, we plot the FFT results for different window size a, in comparison with the reference calculations of the effective Born radii using the macromolecular modeling package CHARMM [39]. In the reference computations, the grid-based version of the molecular volume GB formulation (GB/MV) of Brooks and colleagues [21] was used, with the grid spacing set at 0.2 Å. Atomic charges and radii were adopted from the PARAM22 version of the CHARMM force field [40] and all calculations were done in the Coulomb-field approximation.

Fig. 5.

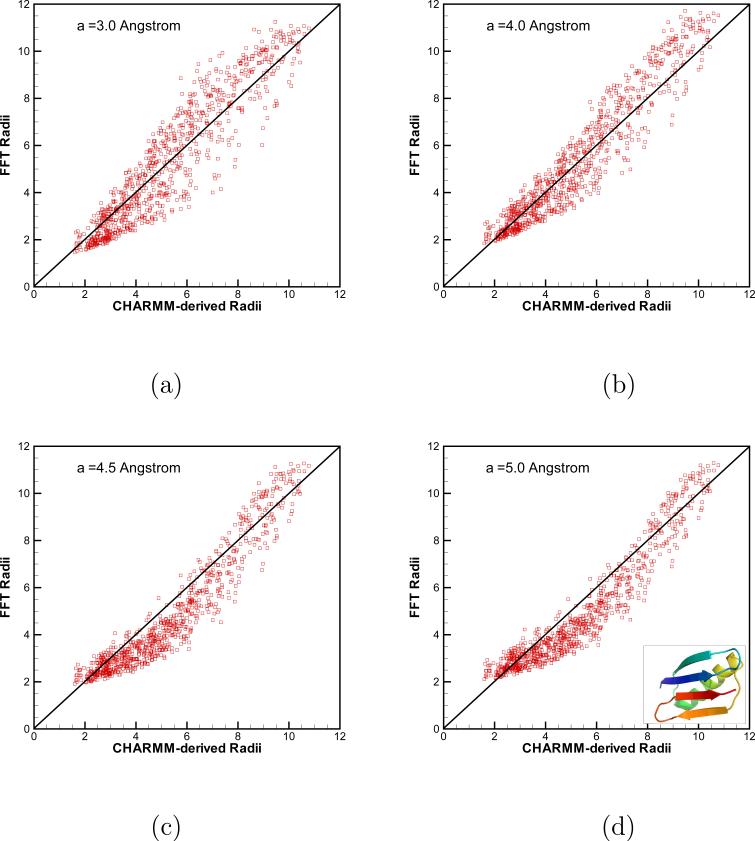
Born radii computed using our new FFT-based algorithm vs. grid-based radii obtained in CHARMM [39] for immunoglobulin binding protein (PDB access code 3GB1 ). In FFT calculations, 128³ grid points in domain [−32 Å, 32 Å]³ were used. Results for different smoothers $W_a^2\left(r\right)$ are shown in (a) a = 3.0 Å; (b) a = 4.0 Å; (c) a = 4.5 Å; (d) a = 5.0 Å

Fig. 6.

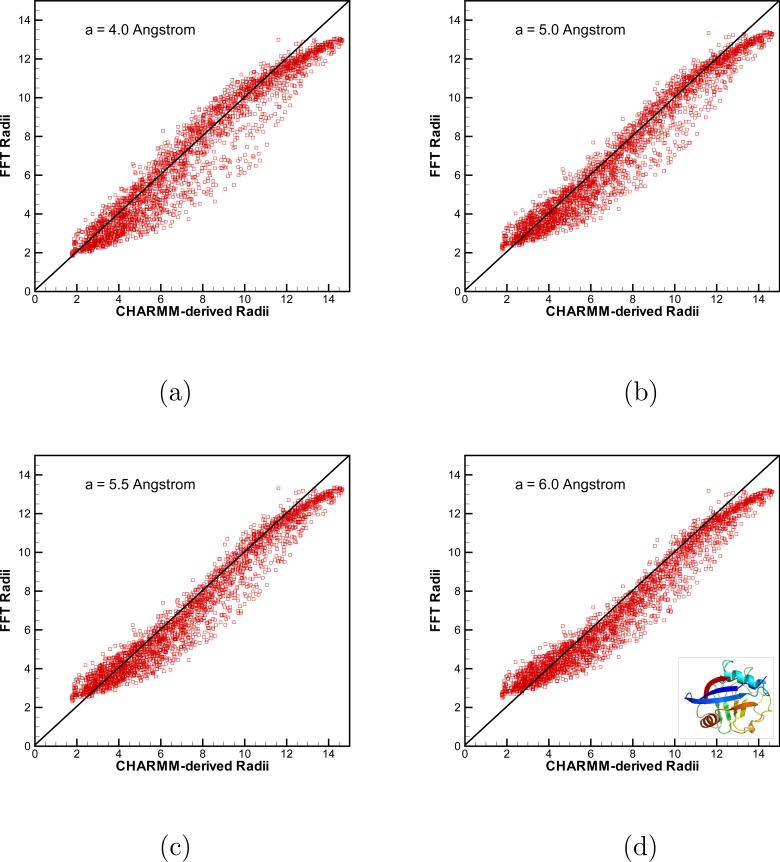
Same as Fig. 5 but for the human cyclophilin A (PDB access code 1OCA). In the FFT calculations, 128³ grid points in domain [−40 Å, 40 Å]³ were used. Results for different smoothers $W_a^2\left(r\right)$ are shown in (a) a = 4.0 Å; (b) a = 5.0 Å; (c) a = 5.5 Å; (d) a = 6.0 Å

Overall, the agreement between the Born radii obtained by our FFT-based algorithm and those derived in CHARMM is good. Some scatter is seen in Fig. 5 and 6 but in general, it is clear that the two methods produce well correlated data. As mentioned previously, there are several factors contributing to the numerical error in R_i, with one of them being how atoms close to molecular surface are treated. A direct consequence of this approximation is that large window radii a should lead to large errors for surface atoms. This is exactly the trend we observe for both proteins in Figs. 5 and 6. As the window radius a is increased, the atoms with small R_i, that is those close to the surface, deviate more from the diagonal than do the atoms buried inside the protein and whose Born radii are large. The surface atoms place an upper limit on how large a one is allowed to adopt and still obtain accurate values for R_i. Much will depend on the geometry of a solute of interest, in deciding on what radius a is optimal. The extent of correlation observed between FFT results and those obtained in CHARMM are summarized in Tab. 3 for protein 3GB1 and in Tab. 4 for protein 1OCA. For the smaller protein 3GB1, it is seen that for all but the smallest value of a considered, 3 Å, and a fine integration mesh h=0.5Å, the correlation coefficient ρ > 0.95 is comparable to the values reported in the literature for other GB implementations [21]. The correlation is even better for the larger protein 1OCA, where for all values of a tested, ρ > 0.96. It is not clear at the moment, what causes this improvement. Importantly, Tabs 3 and 4 show that ρ is not very sensitive to a as long as this parameter is larger than 4 Å. This observation gives hope that a value of a between 4 and 6 Å would be acceptable for a large data set of proteins in our planned forthcoming systematic study of the FFT-algorithm for more proteins.

Table 3.

The correlation coefficients between Born radii computed for protein 3GB1 using the new FFT-based algorithm proposed in this work and those obtained using grid-based integration within CHARMM [39]. CPU time for both types of calculations is also shown.

	Corr. Coef.		CPU time (s)
	h=1 Å	h=0.5 Å	h=1 Å	h=0.5 Å
FFT, a = 3.0 Å	0.945	0.931	4.64	38.78
FFT, a = 4.0 Å	0.950	0.953	4.59	39.79
FFT, a = 4.5 Å	0.949	0.956	4.67	38.82
FFT, a = 5.0 Å	0.948	0.957	4.68	40.01
Grid-based			22.11	191.04

Table 4.

Same as Tab. 3 but for the protein 1OCA

	Corr. Coef.		CPU time (s)
	h=1.25 Å	h=0.625 Å	h=1.25 Å	h=0.625 Å
FFT, a = 4.0 Å	0.969	0.962	4.59	39.99
FFT, a = 5.0 Å	0.974	0.973	4.57	40.04
FFT, a = 5.5 Å	0.974	0.975	4.57	40.00
FFT, a = 6.0 Å	0.973	0.975	4.61	40.09
Grid-based			64.13	529.73

Finally, to evaluate the time performance of our FFT-based algorithm, for comparison, we carried out grid-based calculations using the same set of grid parameters (comparison with CHARMM would not be appropriate here as CHARMM does more than just calculation of R_i). The results of this comparison, presented in Tab. 4, show that the FFT approach is 5 times faster than the grid-based approach for protein 3GB1, and 14 times faster for protein 1OCA. These speed improvements are in line with what we observed for the spherical solute and they clearly demonstrate the advantage of using the FFT-based algorithm for Born radii proposed in this work when computing GB solvation energy of large proteins.

6 Conclusions

In this paper, we have proposed a fast FFT-based algorithm to calculate the effective Born radii in the generalized Born model of implicit solvation. The algorithm relies on a new formulation for the GB radii using a smooth kernel in the definition of the GB radii via a convolution integral. Using the fast spectral decay of the smooth kernel in the Fourier space and the FFT to calculate the convolution integral on a grid, the GB radii at grid lattice sites are obtained at a cost of O(N³ log N) with N independent of the number of atoms M inside the molecule, only dependent on the geometry of the bio-molecule and the spectral decay of the kernel through (4.37) (see also Remark 2). The GB radii for off grid lattice sites are obtained by a simple interpolation at a cost O(M). Thus, the total cost for finding the GB radius using the FFT-based method for M atoms using a N³ grid is O(N³ log N + M), thus yielding significant speed improvement over traditional grid based methods, as demonstrated by numerical tests of model spherical and protein solute molecules.