Socioeconomic Status and School Grades: Placing their Association in Broader Context in a Sample of Biological and Adoptive Families

Abstract

SES has long interested researchers investigating school achievement. Its effects are often addressed by studying predictors of achievement in economically disadvantaged samples living primarily in biological families, confounding genetic and environmental influences. Little is known about SES’s purely environmental effects. We measured them in 617 adoptive and biological families, adjusting for sample restriction of SES range. Controlling for gender, parenting, parental expectations for educational attainment (PEEA), IQ, engagement in school, and genetic and shared environmental influences on sibling pairs, SES still made a small but significant nonshared environmental contribution to school grades. IQ, PEEA, and SES had collinear associations with school grades, as did engagement and parenting. The associations of IQ and engagement with school grades were largely independent of each other. The link between PEEA and IQ was stronger in adoptive than biological offspring. We discuss the implications of these findings.

Over 20 years ago, White (1982) published a meta-analysis documenting the fact that, measured at the level of the individual, the correlation between socioeconomic status (SES) and academic achievement is rather modest, averaging about .22. At the same time, when measured at the level of some aggregated unit of analysis such as the school or the neighborhood, the correlation is much higher, ranging as high as .80. Though SES is a variable that applies to the individual or family, its much higher aggregate than single-family correlation with academic achievement implies that people of similar SES tend to cluster together. To the extent this is true, children receive similar SES influences from both their families and their surrounding communities. If the community influences are strong, SES has the potential to be a powerful environmental variable exerting broad-based effects at a population level, despite its relatively modest effects at the level of the individual. It is probably for this reason that SES continues to be so interesting to researchers investigating educational outcomes.

Measured properly at the level of the individual, SES reflects the occupations and thus the underlying levels of education and resulting incomes of the adult members of a household (Jeynes, 2002; White, 1982). It is thus generally considered to be an indication of economic and educational opportunity or privilege. In reality, however, SES reflects a much wider range of human qualities that contribute to the ability to attain and maintain any given occupation, including diligence, intelligence, determination, interpersonal skills, materialism, ambition, and passion for life (Jeynes, 2002). In short, it reflects an aspect of culture, an as pect that, because of the importance of educational attainment to occupational status, has some natural associations with academic achievement that transcend mere economic and educational opportunity. This aspect of culture is reflected at the level of the community in which the individual resides as well.

Though SES and culture are both commonly considered environmental variables, there is substantial evidence that the individual personal characteristics contributing to SES and the aspect of culture it reflects are under genetic as well as environmental influence (Bouchard & McGue, 2003). This means that, in the most readily available and commonly used samples of students mostly from biological families, the genetic and environmental effects of SES are confounded. That is, it is unclear to what degree to attribute the association between SES and achievement to the economic and educational opportunities environmentally afforded by SES, to the genetic transmission from parent to offspring of the personal characteristics associated with SES, or to correlation between the two. This is particularly the case because it is uncommon in studies of academic achievement to measure a range of associated individual student and environmental characteristics in such a way that their relative effects can be compared.

A logical approach to quantifying the extent of the environmental effects of SES on achievement is to measure a range of characteristics in a sample of substantial numbers of adoptive offspring that also includes biological offspring that can be used as a basis of comparison. There is, however, one problem with this approach. As Stoolmiller (1999) has pointed out, samples of adoptive families are subject to substantial restriction of range in SES due to the parental circumstances leading them to select themselves into the adoption process in the first place, the adoption agency selection processes that see them through to acquisition of a child, and the parental characteristics associated with willingness to participate in a study of child development. Restriction of range has the well-known effect of reducing the correlation of the range-restricted variable with others. Stoolmiller maintained that the degree of restriction of range in SES can be as high as 70%, rendering it an issue of considerable potential consequence even if his estimate was high. With some understanding of the nature of the range restriction, it is possible to quantify it and to adjust for its effects. Such adjustment is obviously important because it makes possible estimates of the strength of the association in the full population without range restriction. The ranges of other variables in adoption samples could be restricted as well.

The purpose of this study was to make use of the Sibling Interaction and Behavior Study (SIBS), a sample of adoptive and biological Minnesota families, to quantify the environmental roles of SES and associated parenting variables in predicting academic achievement. In doing so, we placed SES in the context of several parental environment and individual student characteristics and explicitly adjusted for the restriction of range of SES in the sample. We thus addressed four questions. First, to what degree was the range of SES restricted in this sample and were other variables restricted as well? Second, when placed in context with other variables, how was SES related to achievement? What about the other parenting variables? Third, how much difference did adjustment for the effects of range restriction make in the estimates of the associations? Fourth, to what degree did the relations among the variables we considered differ in adoptive and biological families?¹ The parental environment and individual student characteristics we considered in context with SES included gender, parenting practices, parental expectations for educational attainment (PEEA), IQ, and student engagement in school. All have well-established associations with academic achievement in their own rights (e.g., Mau & Lynn, 2001, for gender; Steinberg, Lamborn, Darling, Mounts, & Dornbusch, 1994, for parenting practices; Butler, Marsh, Sheppard, & Sheppard, 1985, for IQ; Gottfried & Gottfried, 1996, for engagement in school; and Kaplan, Liu, & Kaplan, 2001, for PEEA).

Method

Sample

SIBS consists of a community-based sample of pairs of adoptive and biological siblings and their parents living in the Minneapolis-St. Paul area. Recruitment was initiated in 1998. The SIBS adoptive sample was recruited in collaboration with three large metropolitan area adoption agencies. These agencies minimally screen prospective parents, in a manner typical of current agency practices, for commitment to raising a child, a modest minimum level of income, and willingness to undergo a criminal record check. Some criminal record does not preclude a placement. The parents participating in SIBS were representative of those accepting infant placements from these agencies. They spanned a broad cross-section of the population, with educational attainment ranging from high school drop-out to PhD, and single parents, gay couples, divorced couples, and stably married couples all represented.

The adoptive families participating in SIBS included an adolescent between the ages of 10 and 22 who was adopted by the family within the first 2 years of life, and a second adolescent not biologically related to the first but within five years of his/her age. In most cases, the second sibling was also adopted by the parents in infancy, but there were some cases in which the second offspring was the biological offspring of the parents. A majority of the adoptees were internationally placed (most from Korea). Thus race is confounded with adoption status, as most of the biological families were Caucasian. Race, however, was not independently associated with the variables used in this study. The biological sample was recruited using birth records for the same geographic area. Each biological family included an adolescent between the ages of 11 and 19 and born to both parents, and a second full biological sibling within five years of the age of the first. The majority of participants were in the mid-teenage years. Table 1 shows the age distribution in both adoptive and biological families. There was no attempt to match adoptive and biological families. This should optimize the potential to generalize from the findings in this sample to other samples.

Table 1.

Distribution of sibling ages in adoptive and biological families

	Frequencies in
Age	Adoptive Families	Biological Families
10	6	0
11	72	13
12	77	43
13	121	62
14	139	88
15	196	88
16	90	73
17	57	21
18	33	21
19	16	7
20	8	0
21	0	0
22	1	0
Total	816	416

Among eligible families, participation rates were 63% for adoptive and 57% for biological families. The difference in participation rates was not significant (χ²(1 df) = 3.42, p=.064). Some comparison between participating and non-participating families is possible, because 73% of mothers in eligible but non-participating families completed a brief telephone interview providing demographic and child mental health information. These mothers reported that their primary reasons for not participating were the time demands of the study and privacy concerns. Importantly, there were few differences between participating and non-participating families. Participating and non-participating adoptive families did not differ in reported child behavioral disorders (learning disabilities, substance abuse, attention deficit disorder, depression), percent of original parents remaining married, maternal or paternal education, or maternal or paternal occupational status. Participating and nonparticipating biological families differed on only one of these variables: participating mothers were more likely to have a college degree (43.8%) than were nonparticipating mothers (28.6%; χ²(1 df) = 10.0, p=.002). Thus, although there was evidence for a small amount of positive selection in our sample of biological families, analysis of the nonparticipating families indicated that our samples of adoptive and biological families were generally representative of the populations of eligible families from which they were drawn.

We made use of the integrated public use microdata series (IPUMS) 1% random sample (Ruggles et al., 2004) from Census 2000 to explore the representativeness of the sample of biological families further (McGue, et. al, 2005). To form a census-level sample comparable in family composition and geographical location to our sample of biological families, we examined IPUMS Census 2000 individuals age 35–55 living in the broader Minneapolis/St. Paul metropolitan area with two or more of their own children. Individuals who live with two or more of their own children have higher rates of college graduation than the general population of adults (and thus likely higher SES). This is probably associated with the relationship and financial stability necessary to maintain a family situation through the births of two children over a period of several years. In the IPUMS Census 2000-based sample, 47% of men and 39% of women had at least a college degree. This was similar to the 44% of dads and 44% of moms who had college degrees in our biological families. The data suggested a small amount of positive selection in biological moms, in a manner similar to our analysis of non-participating families. We found little evidence from either source, however, that SIBS biological families differed substantially from families consisting of parents living with two or more of their own children in the Minneapolis/St Paul metropolitan region. This did not preclude the possibility that their higher level of education than the general population reflected somewhat higher SES.

The sample providing data for the current study included 409 adoptive and 208 biological families, made up of 558 boys and 678 girls, though two adoptive families of girls provided data on only one sibling. One sibling’s data in one family were eliminated because we learned after the assessment that the two siblings were biologically related. In the other family, one sibling’s data were eliminated because her IQ score suggested mental retardation. Among the complete adoptive families, there were 96 pairs of boys, 148 pairs of girls, 104 opposite-gender pairs with an older boy, and 59 opposite-gender pairs with an older girl. Among the biological families, there were 62 pairs of boys, 68 pairs of girls, 40 opposite-gender pairs with an older boy, and 38 opposite-gender pairs with an older girl. All participating families completed a 5-hour in-person lab assessment, and completed a battery of self-report measures prior to the lab assessment.

Measures

Academic achievement

SIBS collected much of the same data in the same manner as does the Minnesota Twin Family Study (MTFS). The overall procedure used in that study is described in greater detail in Iacono, Carlson, Taylor, Elkins, & McGue (1999). The siblings and their parents and teachers provided data. We assessed siblings and parents with structured in-person interviews in our laboratories, structured telephone interviews, and self-report questionnaires in our laboratories and at home. To obtain teacher reports, siblings nominated as many as three different teachers and we asked these teachers to complete an extensive questionnaire of student behavior and achievement. Because the teachers saw the individual siblings frequently in a normative, structured setting away from their immediate families and had no a priori emotional ties to them, teachers provided an important perspective on student behaviors. They were also in a position to put the individual siblings’ school behavior in a broader and less biased context than were the parents. In addition, the teachers assigned some of the grades on which they reported.

We measured academic achievement using reports of grades. SIBS did not collect data on actual grades, however, because the participants came from school systems located throughout the metropolitan area that had large disparities in grading formats, procedures, and standards. Instead, parents, siblings, and teachers reported separately on student grades in language arts, math, social studies, science classes, and overall by indicating that the grades were much better than average (A’s=4), better than average (B’s=3), average (C’s=2), below average (D’s=1), or much below average (failing=0). The estimated internal consistency reliability for the grade reports of teachers was .86, and estimated inter-teacher agreement reliability was .75. We computed average teacher grade reports based on the number of teacher reports obtained for each sibling. Overall, the correlations among the grade reports for the three categories of reporters were high, with an average correlation of .72. We made use of the same form of composite reported grades for this study as we did in Johnson, McGue, & Iacono (2004b). That is, we averaged the reported grades in each subject by reporter, and then averaged across reporters to generate a straightforward continuous measure most directly analogous to grade point average. Thus, possible scores ranged from 0 to 4. In a random sample, the correlation between this composite and available actual grade reports from school records for the data in Johnson, McGue, and Iacono (2004b) was .89. Table 2 shows mean Grades, standard deviations, and effect sizes of differences for girls and boys and biological and adoptive siblings. Girls had higher Grades than boys by about one-half standard deviation. Biological siblings had higher Grades than adoptive siblings by about .14 standard deviation.

Table 2.

Descriptive statistics and effect sizes of mean differences and their significance for girls and boys and biological and adoptive offspring

	Mean	SD	Mean	SD	Differences
Measure	Girls		Boys		Effect size	p-value
SES	6.5	1.4	6.5	1.4	.00	.946
Parenting	.1	1.0	−.1	.9	−.14	.025
IQ	105.1	13.3	109.3	13.8	.31	<.001
Engagement	3.2	.4	3.0	.4	−.53	<.001
PEEA	5.0	.8	4.7	1.0	−.33	<.001
Grades	3.4	.6	3.0	.8	−.49	<.001
	Biological Offspring		Adoptive Offspring
SES	6.2	1.5	6.7	1.3	.35	<.001
Parenting	.1	.9	−.1	1.0	−.20	.001
IQ	107.8	13.2	106.3	14.0	−.11	ns
Engagement	3.1	.4	3.1	.4	−.08	ns
PEEA	4.9	.8	4.9	1.0	.01	ns
Grades	3.3	.7	3.2	.7	−.14	.010

Note: Effect size is the mean difference divided by pooled standard deviation, stated so that boys higher is positive, and adoptive offspring higher is positive. PEEA is parental expecatations of educational attainment. SES is socioeconomic status, measured by Hollingshead codes, reversed so that higher code numbers reflect higher SES and a code of 8 refers to professional status.

SES

We measured SES using the two-factor index of social position developed by Hollingshead (1957). The index results in the assignment of an occupational code ranging from 1 to 8 based on job held, education, and income. In this coding, 1 represents major professionals and higher executives in large business organizations, 7 represents unskilled employees, and 8 represents lack of employment, but we reversed the coding so that 8 represented professional status and 1 represented unemployment. Like most attempts to rate occupation, homemakers are not rated on this scale. We collected data to assign occupational codes for both mothers and fathers, and assigned family SES based on the highest status code received by either parent, a well-established method (Krieger, Chen, & Selby, 1999; Krieger, Williams, & Moss, 1997) that recognizes that SES likely follows the dominant member of the household, whether male or female. Families received a code of 1 (unemployed) only if both spouses were listed as unemployed, and families that included a homemaking parent were rated based on the occupation of the other parent. Table 2 shows the descriptive statistics. Consistent with the somewhat higher level of education in the sample relative to the general population described above, average SES was quite high (6.7 for adoptive families and 6.2 for biological families). These values fell between semi-professionals such as dental hygienists and lesser professionals such as pharmacists, with the adoptive families closer to the lesser professional level and the biological families closer to the semi-professional level on average. As discussed in greater detail below, restriction of range appeared to be an issue particularly for the adoptive families, which had higher SES than did biological families by about a third of a standard deviation. Not surprisingly, there was no difference in SES between girls and boys.

Parenting practices

Parents and siblings completed the Parental Environment Questionnaire (PEQ; Elkins, McGue, & Iacono, 1997). This is a 42-item, factor-analytically derived inventory designed to assess the relationship of each parent-child dyad in the family, and it was completed by each sibling about his/her own relationship with each parent. There are 5 scales: Structure (e.g., “My parent makes it clear what she or he wants me to do or not to do.”), Parent’s Regard for Child (e.g., “My parent does not seem to think highly of me [reversed].”), Child’s Regard for Parent (e.g., “I often get good advice from my parent.”), Parental Involvement (e.g., “My parent tries to keep up with how well I do in school.”), and Conflict (e.g., “My parent and I often get into arguments.”). These five scales have a single dominant component in principal component analyses. In this sample, the first two eigenvalues were 3.31 and .79, and the first principal component accounted for 66% of the variance.² As did Johnson et al. (2004b) and Walden et al. (2004), we used as our measure of parenting practices a composite across parents of the first principal component scores from these sibling reports. Again, Table 2 shows descriptive statistics. Girls reported slightly more positive relationships with parents than did boys, by .14 standard deviation. This was primarily because girls perceived greater involvement with their mothers than did boys. Biological siblings reported slightly more positive relationships with parents than did adoptive siblings, by .20 standard deviation. This was primarily due to greater conflict with parents in adoptive families.

Parental Expectations for Educational Attainment (PEEA)

One parent (usually the mother) completed a single item indicating expected eventual educational attainment for each sibling as part of a larger questionnaire. Item options included 1) not completing high school, 2) high school only, 3) high school plus some trade school, 4) some college, 5) complete college, and 6) college plus professional degree. As shown in Table 2, overall parental expectations for educational attainment were high. Most parents expected their offspring to attend at least some college. Still, parents had higher expectations for girls than for boys, by about one-third standard deviation. There was no significant difference in expectations for biological and adoptive siblings.

IQ

Sibling IQ was assessed using abbreviated versions of either the WISC-R for participants under age 16 or the WAIS -R for participants 16 and older. The abbreviated versions of these tests consisted of 2 verbal (Vocabulary and Information) and 2 performance (Block Design and Picture Arrangement) subtests. We selected these subtests for their high correlation (.90) with total IQ based on all subtests. As Table 2 shows, boys had higher IQ’s than did girls, by about one-third standard deviation. There was no significant difference between the IQ’s of adoptive and biological siblings.

Engagement in school

As in Johnson, McGue, & Iacono (2004a) and Johnson et al. (2004b), we assessed student engagement in school using questions from a self-report questionnaire on school behaviors. Items included studying without being reminded, interest in school work, turning in homework, wanting good grades, and enjoying attending school, rated on a 4-point scale ranging from “1. definitely true of me” to “4. definitely false of me.” We scored these items so that high scores reflected high engagement and summed them. This brief scale thus tapped a variety of personal characteristics involving interest, personal responsibility, ambition, and enjoyment of life that are probably related both to school Grades and to later occupational status and thus SES. Possible scores ranged from 5 to 20. Estimated internal consistency reliabilities for the scale was .74. Table 2 shows that girls had higher engagement in school than did boys, by about one-half standard deviation. There was no significant difference in engagement between adoptive and biological siblings.

Analytical Approach

Though we established that SIBS biological families were generally representative of families in the Minneapolis area living with two or more of their own children, there was also some evidence that these relatively stable biological families tended to have higher levels of education, and thus likely higher SES than the population of adolescents as a whole, and the variances in the samples of adoptive and biological families were quite similar. The presence of the sibling pairs in our sample provides a wealth of information not otherwise available about the nature of family influences, but the greater family stability necessary for such pairs to reach adolescence together may entail some costs in the form of restriction of range of SES relative to the more general population as well. Because we wished to examine the effects of SES on academic achievement in the general population, we believed that it was important to recognize the maximum possible restriction of SES range we could reasonably quantify, and another basis of comparison was available in the form of the intake sample from the 11-year-old cohort of the Minnesota Twin Family Study (MTFS).

MTFS is an ongoing longitudinal study of a population-based sample of like-sex Minnesota-born twins and their parents. The current status and location of more than 90% of these twin pairs born in the targeted years from 1977 to 1991 was determined starting from birth records and using various publicly available databases. Eligible located twins were invited to complete a day -long, in-person assessment at our labs; about 20% declined to do so. More than 80% of the families who did not participate completed a brief mail or telephone survey, however, which enabled some comparison of participants and non-participants. Parents in participating families were significantly, though only modestly, better educated than those in non-participating families, with a mean difference of less than .3 years of education (less than .1 sd). The two groups of families did not differ significantly in self-reported mental health. The MTFS intake sample is thus generally representative of families with twins born in Minnesota and it appears to be generally representative of the relevant population as a whole (Holdcraft & Iacono, 2002). It can serve as a basis of comparison to the SIBS sample in the sense that it is drawn from the same regional area and highly overlapping offspring birth years. In addition, the MTFS parents are slightly less educated (39.5% of fathers and 35.5% of mothers are college graduates) than those in SIBS, making them more broadly representative, and twin births require only a single pregnancy. Thus, there is no need in the twin families for the greater relationship and financial stability associated with maintaining a stable family situation through the births of at least two children over several years that may be associat ed with higher levels of education and SES in the biological families in SIBS. A complete description of the ascertainment procedures used in MTFS as well as an analysis of non-participants is given in Iacono et al. (1999).

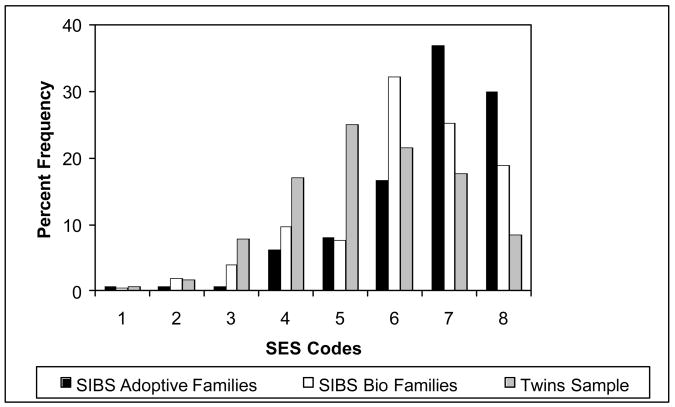
In the SIBS sample, SES was the variable primarily affected by restriction of range in comparison to MTFS, though PEEA also showed some probably associated restriction. Figure 1 shows a comparison of the two SES distributions. In MTFS, the mean (reversed) Hollingshead code was about 5.8 (sd=1.6), corresponding to a level between semi-professional and clerical and sales workers and technicians, such as bookkeepers. This was about .6 standard deviation lower than the mean level for the adoptive families and .3 standard devi ation lower than the mean level for the biological families in the SIBS sample. In addition, the variance of SES in the adoptive families was about 66% of that in MTFS, and the variance in the biological families was about 88% of that in MTFS.

Figure 1.

Illustration of restriction of SES range in SIBS sample.

In a sample in which selection effects have operated on one of the variables measured, the mean of the affected variable is increased by some amount h, and the means of the unaffected variables are increased by r_ih, where r_i represents the appropriate original covariances between the affected variable and the unaffected variables. The variance of the affected variable and its covariances with other variables are also decreased. When only one variable is affected by the range restriction, the decreases in the covariances between this variable and the others are proportional to the decrease in variance of the affected variable. Covariances between variables not explicitly affected by the restriction of range are reduced somewhat as well; the amounts of the reductions are proportional to the amounts by which the variances of the affected variables are reduced. The formulas articulating the relations between the variances and covariances before and after restriction of range due to selection effects are specified in Aitken (1934). We applied these formulas to re-construct an estimated unrestricted variance-covariance matrix, using the variance in SES in MTFS and the covariances between SES and the other variables in MTFS as the original variances and covariances that would have been observed in the SIBS sample had the SES range not been restricted. We also used this variance-covariance matrix to rescale the variables to have the indicated relations. SES was reasonably normally distributed in MTFS, but was negatively skewed in SIBS in a manner consistent with the restriction of range.

Because participant ages in the sample ranged from 10 to 22 and there were substantial effects of age on Grades (r=−.08) and engagement (r=−.13), we regressed the effects of age and age² from these variables, stating the residuals in standardized form. Age effects were not significant for Parenting, PEEA, SES or IQ, but we stated these variables as residuals in standardized form as well. We made use of LISREL 8.53 (Joreskog & Sorbom, 2002) to specify a series of hierarchical linear regressions relating gender, SES, parenting, PEEA, IQ, and engagement to Grades. The sample consisted of sibling pairs; thus the variables for members of the sibling pairs were correlated. We therefore made use of family as the unit of analysis in our regression model, allowing sibling variation around the family average with random effects in a hierarchical linear model (HLM; Bryk & Raudenbush, 1992). Because some participants were missing data for some variables, we read the raw data into the LISREL program, using maximum likelihood estimation to estimate the model parameters allowing for the absence of small amounts of data. The raw data procedure relies on the assumptions that the variables are normally distributed and that the data not present are missing at random (Little & Rubin, 1987). These assumptions were reasonable for these variables (no data were missing for gender or SES). In addition to the main effects of the variables, we considered the possibility of interactive effects between all of the possible pairs among gender, SES, parenting, PEEA, IQ, and engagement in the model. None was significant, however, so we discuss them no further.

HLM makes specific provision for data that are clustered in systematic ways. It was originally developed to study the effects of educational programs on students clustered in classrooms, schools, districts, and so forth. In SIBS, students are clustered in families as pairs of individual adoptive and biological siblings. Given this structure, there are two ways in which the independent variables we are considering, SES, gender, Parenting, PEEA, IQ, and Engagement, might affect the dependent variable, reported Grades. First, they may exert fixed effects across the family level of the data, and/or, second, they may exert effects that vary at the individual level of the data. When they exert effects that vary at the individual level of the data, the independent variables are associated with the variance in Grades within families in a way that is independent of their fixed family-level effects.

The information about biological relatedness contained in the SIBS data, along with its hierarchical structure, make it possible to do more than just estimate the effects of our independent variables on reported Grades. They also make it possible to assess the degree to which the independent variables exert their effects independently of genetic influences on Grades and SES and to distinguish environmental effects acting to make members of the same family similar from those that act to make members of the same family different. Environmental effects that act to make members of the same family similar are typically termed shared environmental effects. Common examples usually reflect childhood experiences such as parental SES. Environmental effects that act to make members of the same family different are commonly known as nonshared environmental effects. Examples might be having different teachers or participating in different activities. The distinction between shared and nonshared environmental effects can be subtle. For example, two children growing up in the same family may experience the same event (e.g., parental divorce), but that event is only a shared environmental influence to the extent that it makes the children similar, and they may react to it very differently.

The fixed effects can occur as a result of any combination of genetic, shared, and nonshared environmental influenc es, but we can control for the presence of genetic and shared environmental effects. This can be accomplished by including with the fixed effects a set of terms defined by DeFries and Fulker (1985) and known as D-F regression terms. As long as an independent variable can be measured separately for each sibling in a pair, the effect of that independent variable remaining after inclusion of the D-F regression terms can be considered a nonshared environmental effect (Turkheimer, et al., 2005). When, as for SES, the independent variable cannot be measured separately for each sibling in a pair, the effect can be considered to result from environmental influences only to the extent that it is reasonable to assume that there are no genetic influences common to the independent variable and to Grades. It would be tenuous to assume this to be true in samples consisting of individual members of biological families because of the possibility that genetically influenced parental characteristics contributing to SES also contribute to the Grades of their offspring. In this case, however, we can use the adoptive offspring in the SIBS sample, who share no genetic relationship with their parents, to evaluate the nature of the environmental role played by SES.

The effects that vary at the level of the individual within families occur as a result of some combination of genetic and nonshared environmental influences because they distinguish only within families. We can also use the D-F regression terms to distinguish the within-family genetic effects from the within-family nonshared environmental effects. Clearly, this can only be accomplished for variables that differ for members of sibling pairs in the same family.

The primary purposes of the series of HLM’s we specified were to examine the effects of SES on reported Grades and to assess the degree to which those effects were independent of the other family and individual characteristics. SES was thus the first independent variable we entered into the regression model. Secondarily, we wanted to assess the associations of Parenting and PEEA with reported Grades in the same way. We therefore entered these variables into the regression model next. We then entered the individual characteristics IQ and Engagement, making it possible to address the individual characteristics through which the family environmental variables were associated with reported Grades. As we brought each independent variable into the model, we entered it as a fixed effect and as a variable effect at the individual level of the model. We retained variable effects in the model, however, only to the extent that they significantly improved model fit. We entered the D-F regression coefficients last in order to assess the degree to which the independent variables were operating independently of genetic effects on both Grades and on SES, and to distinguish shared from nonshared environmental effects. To assess the effects of restriction of range in SES, we specified the HLM regressions using the data both adjusted and unadjusted for restriction of range in SES.

For the data adjusted for restriction of range in SES, we used path analysis (Wright, 1934) to develop a model that more fully expressed the associations among the variables associated with Grades, and tested this model by comparing its fit with those of others with different arrangements of paths. The primary purpose in developing this model was to specify it separately for adoptive and biological offspring in order to compare effects in the two groups, but it allowed for greater clarification of some of the effects of the independent variables as well. To make the group comparison, we first allowed all paths to vary freely from group to group. We then constrained paths equal across groups if that could be accomplished without significant increase in the chi-square associated with the overall model fit. We tested the model fits for each path so constrained both singly and overall.

Results

Descriptive statistics

Table 3 shows the zero-order correlations among the variables we used, separately for girls and boys, and for adoptive and biological siblings. The patterns of correlations were generally similar for girls vs. boys and for adoptive vs. biological siblings. There were, however, some notable except ions involving SES. In girls, the correlations between SES and the other variables were not significant, with the exception of the correlation between SES and PEEA. In boys, these correlations were significant, though not substantial. Except for PEEA, correlations involving SES were not significant in adoptive offspring. They were significant, though of small magnitude, in biological offspring. There was no significant confounding of gender with adoption status in the sample, though there was a trend toward adoptive families being more likely to have girls (p=.09). Besides the correlations involving SES in adoptive families, the only other correlations in either grouping that were not statistically significant were between IQ and parenting. The highest correlations involved Grades and IQ, PEEA, and Engagement. The largest difference in correlations was in the correlation between PEEA and IQ in biological (.24) and adoptive (.40) siblings. This difference was significant (p<.05, uncorrected for potential multiple comparisons).

Table 3.

Correlations among study variables in girls and boys and adoptive and biological offspring

	1	2	3	4	5	6
Girls and boys
1. SES		.04	.04	.05	.12	.06
2. Parenting	.12		.07	.42	.18	.28
3. IQ	.11	.08		.14	.38	.43
4. Engagement	.10	.39	.21		.26	.49
5. PEEA	.23	.27	.39	.31		.48
6. Grades	.15	.34	.44	.54	.53
Adoptive and biological offspring - before adjustment for SES range
1. SES		.22	.16	.14	.20	.17
2. Parenting	−.02		.07	.46	.25	.35
3. IQ	.02	.05		.13	.24	.31
4. Engagement	.02	.37	.15		.32	.57
5. PEEA	.15	.23	.40	.32		.47
6. Grades	.07	.28	.43	.51	.57
Adoptive and biological offspring - after adjustment for SES range
1. SES		.24	.24	.16	.32	.27
2. Parenting	.04		.08	.45	.25	.37
3. IQ	.12	.05		.14	.25	.31
4. Engagement	.08	.37	.15		.32	.59
5. PEEA	.31	.23	.40	.32		.47
6. Grades	.19	.28	.43	.51	.57

Note: PEEA is parental expectations for educational attainment. Girls are above the diagonal in the top panel, boys below. Adoptive offspring are below the diagonal in the bottom panels, biological offspring above. Correlations in excess of about .1 are significant at p<. 01, adjusting for the existence of correlations within sibling pairs.

Estimates from the HLM regressions

Table 4 shows the parameter estimates and their significance in the HLM regressions fitted, after adjustment for restriction in SES range. The significance of each parameter is displayed in the table in two ways. First, we show the associated t-statistic and its significance level and, second, we show the −2*log-likelihood associated with the model as a whole. The difference between the −2*log-likelihoods for two models is distributed approximately chi-square, with degrees of freedom equal to the difference in the numbers of parameters in the two models. When the −2*log-likelihood statistic decreases by a significant amount, the model with the lower −2*log-likelihood statistic can be considered to provide a significantly better fit to the data. It is important to evaluate the significance in this way when considering the possibility of random effects due to the covariance structures associated with them. The table also shows the percentage of the initial effect of SES accounted for by the model as each of the other independent variables was added. The variables after adjustment for restriction in range were stated as if they were standardized in the population, so the b coefficients can be interpreted as standard deviation increments in Grades for a 1 standard deviation increment in the associated variable, conditional on the other variables in the model. Thus, when SES was introduced into the model at Step 2, a 1 standard deviation increase in SES predicted a .19 standard deviation increase in Grades. As would be expected, this effect was essentially independent of the effect of gender, entered at Step 3, but gender had a substantial effect of its own (.38, indicating that girls had higher reported Grades than boys). Parenting also had a substantial effect at Step 4 (.25) and it accounted for 13.5% of the effect of SES, reducing its coefficient from .19 to .17. PEEA had both a fixed effect on reported Grades at the family level and an effect at the individual level. The effect at the individual level indicated genetic and nonshared environmental influences distinguishing siblings. Together, the fixed family-level and individual-level effects of PEEA accounted for an additional 19% of the effects of SES on Grades. The variables describing family characteristics together accounted for 32.6% of the effects of SES, reducing its coefficient from .19 to .13.

Table 4.

Summary of HLMs predicting school grades, adjusting for restriction in range of SES

Variable	b	SE b	t	p	−2LL	χ2	p	%SES
Step 1
Fixed effects - family level
Constant	−.26	.03	−9.22	<.001	3083.67
Step 2
Fixed effects - family level
Constant	−.32	.03	−10.55	<.001	2799.82	283.85 (1 df)	<.001
SES	.19	.03	6.76	<.001
Step 3
Fixed effects - family level
Constant	−.91	.08	−10.94	<.001	2743.32	56.50 (1 df)	<.001	0.1
SES	.19	.03	6.95	<.001
Gender	.38	.05	7.61	<.001
Step 4
Fixed effects - family level
Constant	−.73	.08	−9.06	<.001	2490.68	252.64 (1 df)	<.001	13.5
SES	.17	.03	6.23	<.001
Gender	.35	.05	7.16	<.001
Parenting	.25	.02	10.26	<.001
Step 5
Fixed effects - family level
Constant	−.59	.08	−7.46	<.001	2358.04	132.64 (1 df)	<.001	19.0
SES	.13	.03	5.19	<.001
Gender	.29	.05	6.15	<.001
Parenting	.22	.02	9.37	<.001
PEEA	.15	.06	2.40	.017
Individual level
PEEA	.49	.10	5.05	<.001
Step 6
Fixed effects - family level
Constant	−.58	.07	−7.90	<.001	2188.46	169.58 (1 df)	<.001	30.6
SES	.07	.02	3.02	.003
Gender	.41	.04	9.29	<.001
Parenting	.22	.02	9.92	<.001
PEEA	−.01	.06	−.09	.93
IQ	.32	.02	13.59	<.001
Individual level
PEEA	.50	.09	5.56	<.001
Step 7
Fixed effects - family level
Constant	−.27	.07	−4.03	<.001	1985.27	203.19 (1 df)	<.001	4.0
SES	.06	.02	2.97	.003
Gender	.30	.04	7.51	<.001
Parenting	.09	.02	4.16	<.001
PEEA	−.02	.05	−.44	.66
IQ	.27	.02	12.70	<.001
Engagement	.30	.02	14.99	<.001
Individual level
PEEA	.39	.07	5.37	<.001
Step 8
Fixed effects - family level
Constant	−.30	.07	−4.00	<.001	1939.62	45.65 (7 df)	<.001	0.0
SES	.06	.02	2.18	.029
Gender	.30	.04	7.47	<.001
Parenting	.08	.02	3.83	<.001
PEEA	.02	.05	.29	.77
IQ	.26	.02	12.30	<.001
Engagement	.30	.02	15.04	<.001
Sibling relatedness	.08	.07	1.21	.22
Sibling Grades	.06	.03	2.31	.021
Sibling Grades × relatedness	.10	.06	1.67	.09
Offspring status	.02	.07	.27	.78
SES × offspring status	.01	.04	.31	.76
Individual level
PEEA	.29	.06	4.71	<.001
Sibling Grades × relatedness	.09	.04	2.38	.017

Note: Effects of age were removed from Grades, Parenting, PEEA, and Engagement. SES is socioeconomic status. PEEA is parental expectations for educational attainment. All variables were standardized. %SES is percent of initial effect of SES accounted for by model. Girls were coded 1; boys 0. The constant indicates the amount by which mean Grades are higher in SIBS than in MTFS due to restriction of range in SES. Variables were added at both the family and individual levels, though only those that generated signficant improvement in model fit were retained. At Step 5, we did not include a constant at the individual level.

At Step 6, IQ was another variable that had an important association with reported Grades (.32). It accounted for almost a third of the effect of SES, independent of the variables preceding it in the model, and accounted for effectively all of the fixed effects of PEEA. In addition, it had an interesting effect on the coefficient for gender, increasing it from .27 at Step 5 to .41 at Step 6. This occurred because girls had higher Grades in the sample, but boys had higher IQ’s (see Table 2). Engagement, entered at Step 7, also had substantial effects on Grades. It accounted for an additional 6.5% of the effects of SES on Grades. Though it accounted for relatively little of the effect of SES on reported Grades, Engagement accounted for much of the effect of Parenting on reported Grades, reducing its coefficient from .22 at Step 6 to .09 to Step 7. In total, the addition of the independent variables describing individual characteristics reduced the effect of SES on reported Grades by an additional 35%, from .14 to .06.

Step 8 of the HLM regression showed that small amounts of the effects of each of the independent variables on reported Grades resulted from common genetic and shared environmental influences on Grades and on SES. At the same time, because most of the independent variables could be distinguished for each member of the pairs of siblings, this regression step made clear that most of the effects of these independent variables could be considered nonshared environmental effects. SES, of course, was the same for both members of the sibling pairs, so Step 8 did not establish this clearly for SES, as it remained possible that common genetic influences contributed to parental SES and child reported Grades. We repeated the series of HLM regressions, however, using only the adoptive offspring in our sample. At Step 2, the coefficient for SES was .18, significant at p<.001. At Step 7, the coefficient for SES was .06, significant at p=.038. Once again, IQ accounted for the greatest portion of the effect of SES, reducing the SES coefficient from .13 to .08 when it was added at Step 6. Thus, it is reasonable to consider the effects of SES too to be independent of genetic influences on Grades.

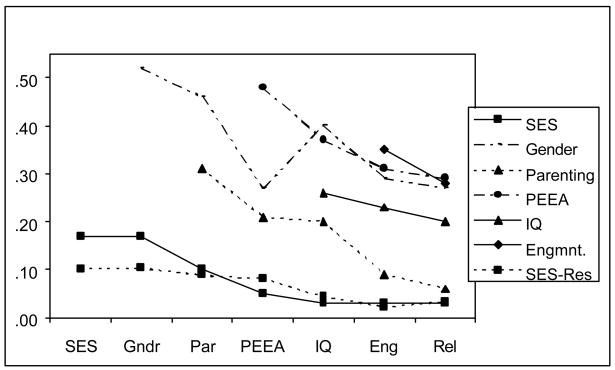
Figure 2 presents the results of the HLM regressions in graphical form, making it possible to assess the results in two ways at a glance. First, it is possible to compare the relative importance of the various fixed regression coefficients in the full model by comparing their heights at the far right of the graph. Individual characteristics were more important than family characteristics. Engagement and gender had the highest regression coefficients, with IQ closely following. The family variables were of relatively similar and lesser importance. Second, it is possible to examine what happened to the relative importance of particular variables as other variables were added to the model, in order to determine which variables shared effects on reported Grades. As noted above, IQ largely accounted for the effects of SES and the fixed effect of PEEA. Engagement largely accounted for the effects of Parenting. Figure 2 includes one more piece of information: the effects of SES before adjustment for restriction in range of SES. We carried out the same HLM regressions based on the actual data in the sample, unadjusted for restriction in SES range. The variables unadjusted for restriction in range were standardized, so the resulting b coefficients should be interpreted as increments against a smaller standard deviation. They are thus smaller increments on a smaller base. Most of the regression coefficients and the relations among them were very similar to those after adjustment for restriction in range, but the overall effect of SES was of course much smaller. The importance of this result is that the effect was only about half as large as it appeared to be after adjustment for restriction of range.

Figure 2.

Standardized regression coefficients predicting school grades as variables are added to the model. SES-Res refers to SES as measured in the original sample with restricted range of SES. Rel refers to the effects of biological relatedness on Grades and SES.

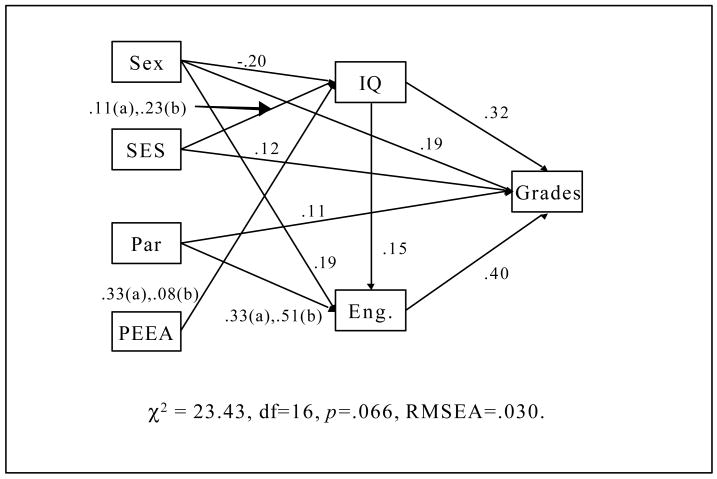
Figure 3 shows the path analysis model we constructed based on the order of entry of the independent variables in the HLM regressions and the results that indicated that IQ accounted for many of the effects of SES and PEEA and Engagement accounted for many of the effects of Parenting. We specified this model separately for adoptive and biological offspring. The model shown in the figure provided the best fit to the data. All of the paths shown were significant, and there were no other significant paths. Thus, for example, SES contributed significantly to Grades both directly and indirectly via IQ, but it did not contribute significantly via Engagement. Working with each path individually as well as in combination with the others, we were able to constrain all paths except three equal between the adoptive and biological offspring groups (Δχ² = 10.28, 8 df, p = .07). With these constraints, the model fit well (χ² = 23.43, 16 df, p = .10; Root Mean Square Error of Approximation = .030). Most of the path coefficients essentially reproduced the results from the HLM regressions. The paths that could not be constrained equal in the adoptive and biological offspring groups, however, provided new information. They ran from Parenting to Engagement, from SES to IQ, and from PEEA to IQ. The association between Parenting and Engagement was much stronger in biological than in adoptive offspring (.33 in adoptive offspring vs. .51 in biological offspring). This was the pattern for the association between SES and IQ (.11 in adoptive offspring vs. .23 in biological offspring). The reverse was true of the association between IQ and PEEA: it was much stronger in adoptive than in biological offspring (.33 in adoptive offspring vs. .08 in biological offspring).

Figure 3.

Structural equation model predicting grades. Coefficients labeled (a) are for the adoptive offspring. Coefficients labeled (b) are for the biological offspring. SES was adjusted for restriction of range. All paths shown were significant.

Discussion

In this study, we used a sample of biological and adoptive families to investigate several questions about the role of SES in predicting academic achievement as measured by reported school Grades. The range of SES was restricted in the sample, and we made an explicit adjustment for this in order to estimate SES’s role in the general population. After adjustment for restriction of range, the association between SES and Grades in SIBS was very similar to the average reported in White’s (1982) meta-analysis (.19 in our model alone vs. an average of .22 reported by White). The adjustment for restriction of range of SES did appear to have a substantial effect on the magnitude of its association with Grades. The effect of SES on Grades appeared to be about twice as strong after adjustment as it did before. The other independent variables we considered (gender, Parenting, PEEA, IQ, and engagement), however, accounted for about two-thirds of the effects of SES. IQ alone accounted for a third of the total effect. Still, it was clear that SES exerted some, albeit small, environmental effects on Grades because the effects were similar whether we examined them in the full sample of biological and adoptive offspring, or in the subsample of adoptive offspring alone.

This study is subject to several methodological limitations that should be considered before discussing the results in greater detail. First, our assessment of school performance is based on child’s, parents’, and teachers’ reports rather than direct observation or actual report cards of grades from a consistently administered system, though, as described earlier, we have substantial reason to believe the reporters to be relatively accurate. Second, Asian vs. Caucasian race is largely confounded with adoptive vs. biological family status in our sample. Race, however, was not independently associated with the variables included in this study. Third, the same reporter (the child) provided the data on parenting practices and engagement in school, and contributed to the grade reports. Fourth and potentially most importantly, we assumed that the degree of restriction of range in SES in our SIBS sample of sibling pairs relative to the general population of individual adolescents could be quantified by comparing its range with that of the MTFS 11-year-old cohort sample of twins. The two samples were drawn from the same geographic region during generally similar time periods, and the range of SES in the MTFS sample seems comparable to that in the relevant population as a whole (Holdcraft & Iacono, 2002), so the assumption appears generally reasonable.

IQ accounted for a substantial portion of the effects of both SES and PEEA on Grades, and Engagement played a similar role on the effects of Parenting. It is tempting to think of IQ and Engagement as playing mediating roles in the associations between SES and Grades, PEEA, and Grades, and Parenting and Grades. This is, however, premature. The formal definition of a mediator includes the requirement that the independent variable (i.e., SES, PEEA, or Parenting) have a causal effect on the mediator (i.e., IQ or Engagement), and that the mediator have no causal effect on the independent variable (Baron & Kenny, 1986). Our contemporaneous measurements did not allow us to establish the directions of the associations in our data. Moreover, there is substantial evidence that IQ plays a causal role in the establishment of parental SES (Jencks, 1979; Waller, 1971), and that parental IQ is transmitted genetically to biological offspring (Bouchard & McGue, 1981), which would suggest some causal role for IQ in the effect of SES on Grades in biological (though not adoptive) families. Still, our results show clearly where the pathways involving common variance lie, thus providing guidance for future research.

The regression coefficient associated with gender increased when IQ was added to the model, indicating that IQ had some suppressing effect on gender. This was a function of the differences in mean and standard deviation in IQ in boys and girls (boys had higher IQ’s but girls had higher Grades), but it appeared to be complicated by the fact that there was a bigger difference between the Grades of girls and boys when IQ was relatively low than when IQ was relatively high. That is, the correlation between IQ and Grades was lower in girls with relatively high IQ’s than in boys with relatively high IQ’s. The reverse was true for girls and boys with relatively low IQ’s: the correlation with Grades was higher in girls than in boys. The difference was significant as measured by the interaction of IQ and gender in a regression predicting Grades based on those two variables alone (t=29.4, p<.001). As girls had higher Grades than boys at all levels of IQ, this suggests that girls tend to earn relatively high Grades in spite of relatively low IQ, while boys tend to earn relatively low Grades in spite of relatively high IQ. Other data have pointed in this direction as well (e.g., Mau & Lynn, 2001). In our full model, introduction of Engagement more than reversed the suppression effect of IQ on gender, suggesting that some aspect of effort, conscientiousness, or cooperativeness at least partly captured by this measure could possibly account for this difference.

Addition of Engagement to our HLM regression acted to reduce the association between IQ and Grades to only a very small degree. This suggested that Engagement acted almost completely independently of IQ in its association with Grades. At the same time, both appeared to have important associations with Grades. Many studies have been carried out under the assumption that the link between engagement or motivation and school performance is independent of academic ability or intelligence (Gottfried & Gottfried, 1996), but the assumption has been tested only relatively rarely. Results have generally indicated that engagement does make some independent contribution to school performance, but its contribution is small in relation to the contribution of intelligence (e.g, Aspinwall & Taylor, 1992; Gagne & St. Pere, 2001; Lloyd & Barenblatt, 1984). Our results suggest that the contribution of Engagement is not small, and that, in fact, in the presence of several variables, Engagement is more closely associated with Grades than is IQ. This warrants further exploration in future research. It is possible that Engagement at any particular point in time is relatively strongly associated with contemporaneous Grades because it reflects students’ responses to particular teachers, classroom situations, and competing life events, while IQ reflects a more stable level of ability. If so, over time IQ may be a better predictor of Grades than Engagement, yet Engagement may be more closely associated with them at any particular point in time.³

The single item assessing PEEA proved to be strongly associated with Grades at the family level. This hints that parents exert their effects on offspring school performance through the culture involving education they establish rather than through the emotional quality of their relationships with their offspring. IQ, however, completely accounted for the fixed effect of PEEA. In addition, the path between PEEA and IQ was one of the three pathways showing significant differences between adoptive and biological offspring in the path analysis model. In all likelihood, parents have some expectations regarding offspring educational attainment that predate the actual arrival of the offspring. These expectations will tend to be based on their financial situation, their own experiences with educational attainment, and their own aspirations regarding education. There is evidence for genetic influences on these circumstances for the parents, and these genetic influences will be transmitted to the offspring (as appropriate to the type of offspring). As well, there is evidence that the environment these parental circumstances creates will affect the offspring. Together, these genetic and environmental influences will lend some degree of realism to these a priori parental expectations for offspring educational attainment. Once the offspring actually arrive, however, parents probably tend to modify their expectations based on the actual behavior of the offspring with respect to school. Thus PEEA probably operate bi-directionally, as they both contribute to the background family culture involving education and are affected by the offspring’s actual degree of assimilation of this culture.

This suggests two further hypotheses for which our data can provide additional evidence. First, it suggests that adoptive parents may make greater modifications to their pre-existing PEEA based on offspring behavior than biological parents because they have less reason to expect their offspring to resemble themselves. In our model, the greater association between IQ and PEEA in adoptive offspring (.33 in Figure 3) than in biological offspring (.08) provided evidence in support of this hypothesis because it hinted that parents might pay more attention to the degree to which their offspring appeared to be “smart” in forming their PEEA in adoptive than in biological families. Of course, it is also possible that adoptive parents with high PEEA were more successful in increasing their offspring’s IQ than were biological parents, but this seems unlikely.

Second, the likely bi-directional operation of PEEA suggests that offspring age should moderate the association between Grades and PEEA. That is, as offspring get older, the Grades they actually earn in school should be increasingly important predictors of PEEA. In fact, this proved to be the case for both adoptive and biological offspring: a moderating term consisting of the product of centered age and Grades was significant in predicting PEEA when added to a model including age of offspring, IQ, Grades, and the product of centered age and IQ (p< .005). The magnitude of the effect was somewhat stronger in adoptive than in biological offspring, and the total variance accounted for by the model was also higher in adoptive than in biological offspring (.37 vs. .24), corroborating the stronger association between IQ and PEEA observed in our path analysis model.

The second pathway that showed differences between adoptive and biological offspring ran from SES to IQ. As with the association between PEEA and IQ, the association was stronger in biological (.23) than in adoptive offspring (.11). The association in adoptive offspring suggests an environmental influence of SES on IQ. Such an association was not found in this sample by McGue et al. (2005), but a wider range of school-related individual characteristic variables was considered here. The greater association in biological offspring probably reflects the genetic transmission from parents to offspring of the association bet ween SES and IQ (Ceci & Williams, 1997).

The final pathway in our path analysis model that showed differences between adoptive and biological offspring ran from Parenting to Engagement. Here, the association was stronger in biological (.51) than in adoptive (.33) families. Our Parenting measure captured Structure, Involvement, Child Regard for Parent, Parent Regard for Child, and Conflict, and some of the items directly addressed school performance (e.g., “My parent tries to keep up with how well I do in school.”). Thus, the measure directly assessed parental engagement in one of their major life roles (that of being a parent), and to some degree also assessed parental engagement in their offspring’s school performance. At the same time, because the child was the reporter for this measure, the measure also assessed to some degree the child’s engagement in one of his/her major life roles (that of being a child in a parental home). The greater association between Parenting and Engagement may reflect greater similarity between biological parents and offspring than between adoptive parents and offspring in level of engagement in major life roles. It may also indicate that the greater conflict between parents and offspring that was observed in adoptive in comparison to biological parent-offspring relationships undermined offspring Engagement in school. Another possibility is that level of Engagement was one of the triggers for greater conflict in adoptive families. This deserves greater attention in future research.

In conclusion, this study shed light on the manner in which SES influences school performance. It also showed the importance of considering the possibility of restriction of range in evaluating the effects of SES on Grades, as the effect of SES was about twice as great after adjustment for the restriction of range that was present in this sample. In addition, the study provided insight into the manner in which the transactions between genetic and environmental influences on school performance are transmitted from parents to offspring. It indicated that PEEA has important associations with school performance at the level of the family, and suggested the manner in which this variable has its effects. Finally, this study has implications for future research in this area because it makes clear that there are many important contributors to school performance, and that we will come to understand this important social outcome best when we study it in a multivariate context using samples in which genetic and environmental influences can be distinguished and their interplay examined.