Slow Stress Propagation in Adherent Cells

Abstract

Mechanical cues influence a wide range of cellular behaviors including motility, differentiation, and tumorigenesis. Although previous studies elucidated the role of specific players such as ion channels and focal adhesions as local mechanosensors, the investigation of how mechanical perturbations propagate across the cell is necessary to understand the spatial coordination of cellular processes. Here we quantify the magnitude and timing of intracellular stress propagation, using atomic force microscopy and particle tracking by defocused fluorescence microscopy. The apical cell surface is locally perturbed by atomic force microscopy cantilever indentation, and distal displacements are measured in three dimensions by tracking integrin-bound fluorescent particles. We observe an immediate response and slower equilibration, occurring over times that increase with distance from perturbation. This distance-dependent equilibration occurs over several seconds and can be eliminated by disruption of the actin cytoskeleton. Our experimental results are not explained by traditional viscoelastic models of cell mechanics, but they are consistent with predictions from poroelastic models that include both cytoskeletal deformation and flow of the cytoplasm. Our combined atomic force microscopy-particle tracking measurements provide direct evidence of slow, distance-dependent dissipative stress propagation in response to external mechanical cues and offer new insights into mechanical models and physiological behaviors of adherent cells.

INTRODUCTION

Treatment of the cell as a material has provided a foundation for understanding mechanical responses of cells and for modeling coordinated cellular behaviors (1). Recent studies investigating the relaxation behavior of cells demonstrated a power-law dependence of material properties on the frequency of perturbation (2,3), suggesting that cells behave as a soft, glassy material (4,5). These cell rheology studies provided insights into localized cellular relaxation, but did not investigate how a cell spatially equilibrates in response to an applied stress. Other studies that investigated the structural organization of cells mechanically perturbed the cell by a variety of techniques and observed displacement of focal adhesions or intracellular fiduciary markers away from the stimulus (6–14). These studies demonstrated elastic coupling to be heterogeneous, propagating applied stresses between specific points within the cell, but they did not systematically address the timescales of the relaxation behavior, which are critical to understanding cell dynamics.

Several mechanisms have been proposed to describe the spatial and temporal aspects of mechanical coupling in cells. Constitutive viscoelastic theory describes the elastic response and viscous relaxation of the whole cell as a single homogeneous material, whereas tensegrity or “action-at-a-distance” models describe the cytoskeleton as a conduit for stress propagation (11). Recent work has proposed that cells behave like a poroelastic material (15–17). Poroelastic models provide a prediction of the spatiotemporal connections within a cell by treating it as a biphasic material with a tightly meshed elastic network infiltrated by a viscous cytosol (16,18). Devised by Biot to predict the settling of porous soil (19), poroelasticity theory has been used to explain the mechanical behavior of biological materials such as bone, soft tissues, and collagen gels (20,21). When a poroelastic material is locally stressed, the elastic phase deforms, creating a localized pressure increase in the interstitial fluid, whose flow is impeded by the dense network. Over time, the pressure equilibrates radially away from the site of perturbation. Charras et al. (16) and Mitchison et al. (17) applied poroelasticity theory to explain various cell behaviors (including motility, morphology, division, and blebbing) and predicted a diffusive response to a local changes in the network, with an equilibration time that increased with distance from perturbation.

To measure the distance-dependent mechanical response of cells to localized stresses and to evaluate specific mechanical models of the cell, a new technique is needed to quantify mechanical responses with high resolution at multiple locations and set distances from the perturbation. Typically, the cellular response at one point, such as displacement of the cell surface, is measured by visually tracking a fiduciary marker in two dimensions (2–5,7,8,22). However, out-of-plane (z) motion often comprises a significant component of the response and cannot be neglected. Recently, several strategies were developed for tracking particles in three dimensions (3D) in a single image plane using defocused epifluorescence microscopy (23–26). These techniques are hindered, however, by long computation times or by the inability to track closely spaced particles, effectively limiting probe density.

Here we present an atomic force microscopy (AFM)-based method to apply local stresses and simultaneously measure the mechanical response away from the perturbation (Fig. 1), and we use it to quantify stress propagation in adherent cells. This method uses AFM as a mechanical input, rather than in its traditional role as an imaging tool or a local material property probe. To quantify cell-surface displacement in response to AFM-induced mechanical perturbation, we track the motion of 500-nm integrin-bound fluorescent particles in 3D, using defocused fluorescence microscopy. This combination of AFM and defocused microscopy enables exploration of distance-dependent cellular responses in 3D to spatially localized external perturbations, an investigative goal that was previously unattainable. Using this technique, we observe a biphasic response of adherent cells to an applied stress: immediate propagation, followed by a distance-dependent equilibration that cannot be explained by traditional viscoelastic models.

FIGURE 1.

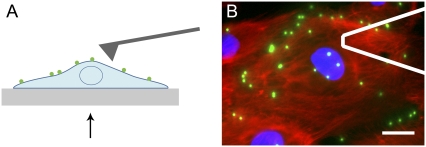
Combined AFM and defocused microscopy. (A) An AFM cantilever is used to locally indent the cell, and displacement of the cell surface is tracked in 3D by defocused epifluorescent microscopy of 500-nm fibronectin-coated fluorescent particles bound to the cell. Stage motion is controlled by a single-axis piezo-electric platform. Arrow in A indicates perspective of the objective. (B) Typical field of view, with AFM cantilever outlined in white. This endothelial cell was fixed and stained to show the nucleus (blue) and actin cytoskeleton (red), in addition to fluorescent particles (green). Scale bar, 15 μm.

MATERIALS AND METHODS

Cell culture and sample preparation

Bovine aortic endothelial cells were cultured in endothelial growth media supplemented with 0.1% human epidermal growth factor, 0.1% hydrocortisone, 0.1% GA-1000, 0.4% bovine brain extract, and 2% fetal bovine serum (Lonza, Basel Switzerland). Cells were plated on acrylic-reinforced glass coverslips coated with fibronectin (BD Biosciences, Franklin Lakes, NJ) and incubated overnight. On the morning of the experiments, sample media were replaced with a 0.009% solids fibronectin-coated particle solution (500 nm YG Fluoresbrite carboxylate microspheres, Polysciences, Warrington, PA) in CO₂-independent media (Gibco, Carlsbad, CA). Cells were incubated in the particle solution for 45 min, and then rinsed thoroughly in CO₂-independent media (Gibco). The sample remained in CO₂-independent media with 3 μL/mL Hoescht stain (to visualize the nucleus) for the remainder of the experiment. Not all cells showed significant particle displacement upon cantilever indentation. For this analysis, only well-spread cells with at least one instance of particle displacement greater than 500 nm were included. Particles that did not show significant displacement, even when the cantilever was a few microns away, were most likely endocytosed by the cell. The dynamics of particle endocytosis were examined using confocal microscopy to determine experimental guidelines to exclude endocytosed particles from analysis (data not shown).

Multipoint 3D particle-tracking

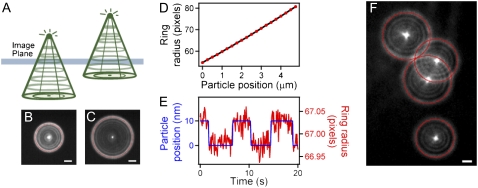
By focusing several microns above or below the particle plane, each particle appears as a set of concentric rings in the image plane, with the image determined by the diffraction pattern of the particle and point spread function of the imaging system (Fig. 2, A–C) (23). The radius of the outer ring is predictably related to the distance from the particle to the image plane, and can be used to determine relative z displacements (Fig. 2 D). For every frame of the acquired image stack, a modified Hough transform was used to determine the (x, y) position and radius of each ring corresponding to the particle of interest. A Hough transform is an image-processing technique used to find arbitrary shapes within an image (27). Using MATLAB 7 (The MathWorks, Natick, MA), the ring image was inserted into the middle of a 3D matrix of zeros. The Fourier transform of this image matrix was convolved with the Fourier transform of a thin-walled cone, with a radius spanning the range of the particle ring radii. The inverse Fourier transform of the convolution yielded a 3D matrix in (x, y, radius) space resembling a point spread function with center coordinates corresponding to the (x, y) position and radius, respectively, of the original ring image. We fit the center of this object to a 3D Gaussian function to determine the position and radius of the ring, which was then translated to the particle position, using a lookup table created after each experiment (Fig. 2).

FIGURE 2.

Defocused multipoint 3D particle tracking in a single image plane. (A) A defocused fluorescent particle appears as concentric rings in the image plane. (B and C) Outer ring radius increases predictably with distance from object plane. (D) A particle is stepped in 250-nm increments away from the object plane, and the outer ring is fit with our modified Hough transform numerical technique. Using this method, we can track the z-position of the particle over a range of at least 5 μm. (E) A particle is subjected to 10-nm steps on a piezo-controlled platform, demonstrating the resolution of our technique. (F) Our modified Hough transform method allows for tracking of multiple, overlapping rings with up to 4-nm and 80-ms resolution. This analysis enables multipoint tracking of particles as close as 1.5 μm to each other in (x, y), which is essential for tracking multiple points on the same cell. Scale bars, 2 μm.

Atomic force microscopy

Indentation of cells was performed with a modified Bioscope AFM (Veeco Metrology, Santa Barbara, CA) atop an epifluorescent microscope (Zeiss Axiovert 25, Carl Zeiss, Thornwood, NY) at 23°C, as described previously (28). A cell was approached with a pyramid-tipped AFM cantilever (3-μm tip height, 35° half-angle, 30 pN/nm stiffness; Microlevers, Veeco Metrology). Cells were indented with a subnanometer-accuracy closed-loop piezo platform (Mad City Labs, Madison, WI), controlled with a software-based data-acquisition system (LabVIEW, National Instruments, Austin, TX).

Stress propagation experiment

We dropped the focus below the sample plane in epifluorescence to form rings from the particles in the image plane. Images of particles were acquired at 80–100 ms/frame, using a 100× 1.3 NA oil immersion objective (NeoFluar, Carl Zeiss) and a Retiga-SRV camera (QImaging, Pleasanton, CA), as the cantilever was stepped vertically in and out of the cell with 2-μm steps of the stage. This step cycle was repeated for several cantilever positions on a single cell, with each particle returning to its original position upon each cantilever retraction. The repeatability of both particle displacement (Fig. 3) and cantilever deflection (data not shown) for a series of step cycles suggests that the indentation did not significantly damage the cell. The average cantilever indentation depth for experiments presented was 1703 ± 182 nm, with 93% ± 3% (mean ± SD, n = 37) of the total indentation occurring in an immediate elastic step (<100 ms). These indentations are larger than those in traditional AFM elasticity experiments, and as such, the displacements are likely to be influenced by substrate elasticity. Stress propagation through cells adhered to compliant substrates would be an interesting subject for future study. To determine if the position on a cell affected the particle response, cells were indented at multiple positions in both the nuclear and lamellar regions. After stress-propagation experiments, the cantilever was removed, and z-positions of particles were calibrated by raising the piezoelectric stage in 1-μm steps and capturing images at each stage height. This created a lookup table for each particle, which was used to convert ring radius into z-position.

FIGURE 3.

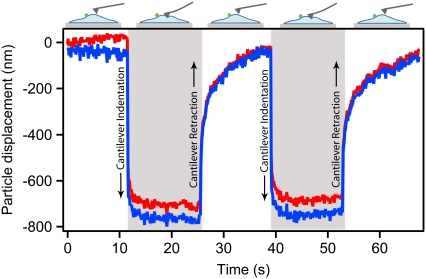
Cantilever indentation-retraction cycles induce particle displacement. Indentation and retraction of the AFM cantilever into the cell is repeated by moving the stage in 2-μm steps toward and away from the cantilever, with stage position held constant for 10–15 s after each step. A particle 2.5 μm away from the cantilever is displaced because of this indentation. The z displacement (red) accounts for the majority of total particle displacement (blue). Upon each cantilever step, an immediate fast response is evident, followed by slower equilibration approaching a final displacement. Upon cantilever retraction, the particle again displaces elastically, and then relaxes toward the original particle position.

To account for drift of the system during experiments, particle position was referenced with respect to a particle fixed to the glass surface in the same field of view as the cell-bound particles. This reference particle was also used to determine relative heights of particles associated with cells, as a precaution against using endocytosed particles. After several experiments, cells were fixed and stained to visualize the actin cytoskeleton (Alexa Fluor 488 phalloidin conjugate, Molecular Probes, Carlsbad, CA), using standard immunofluorescence protocols.

Mechanical modeling

To determine if a traditional viscoelastic model explains the observed cellular response, we modeled the cell as a Voigt-Kelvin viscoelastic material (29,30) undergoing a step compression strain. To account for spatial variation of viscoelastic properties, the model used a series of viscoelastic elements, where the first was simple elastic (modeled as a spring) and the second two were viscoelastic (modeled as a spring and dashpot in parallel) (Fig. S2 A in Supplementary Material, Data S1). To simulate the experiment, a step compression was applied, and the relaxation of points at increasing distances from the compression point was observed. We then varied the viscosity of the viscous elements, and observed the motion within the material to determine if the relaxation response matched the observed experimental behavior (Fig. S2, B–D in Data S1).

We also compared the observed cellular response to predictions of the poroelasticity model, based on the theory in Charras et al. (16). After a deformation, fluid propagates through a cell because of a local pressure increase in a two-dimensional (2D), diffusion-based manner in time t = x²/4D, where x is distance and the diffusion constant, D = kE/φ, where k is the hydraulic permeability, E is Young's modulus of the elastic phase of the material, and φ is the fluid fraction. For a fluid-filled porous material with a small fluid fraction, hydraulic permeability is k ≈ ξ²/(μφ^⅓), where ξ is the pore size, and μ is the cytosolic viscosity. Young's modulus, E, of endothelial cells was measured at 1–9 kPa (31) with AFM, and the fluid fraction was measured at 29–34% by volume change after exposure to hyperosmotic conditions (15,32). Pore size ξ was estimated at 13–26 nm from hindered tracer particle-diffusion experiments, and interstitial cytosolic viscosity μ was measured at between 0.004–0.18 Pa·s based on nanometer-sized particle and actin diffusion experiments (33–35).

RESULTS

Stress propagation observed with combined AFM and multipoint 3D particle tracking

We measured intracellular stress propagation by generating a local mechanical perturbation using AFM and observing the distal surface displacements of the cell by tracking fluorescent particles bound to integrins. We followed the 3D motion of closely spaced particles by acquiring defocused images of the particles (Fig. 2, A–C), which appeared as rings on the image plane. Using a custom-modified Hough transform method, we were able to track 3D particle position with up to 4-nm and 80-ms resolution by determining the (x, y) position of the particle from the (x, y) position of the ring and the z-position from the ring radius (Fig. 2, D–F; see Materials and Methods for details).

We tested our experimental system by indenting a thin polyacrylamide gel with an AFM cantilever at increasing distances from a single 500-nm fluorescent particle bound to the surface. We observed a decay of equilibrium particle displacement with distance from indentation (Fig. S1 in Data S1), which closely followed the expected displacement of an elastic half-space (36,37) or thin film (38).

To characterize stress propagation through adherent cells, we tracked the motion of fibronectin-coated 500-nm fluorescent particles bound to cultured bovine aortic endothelial cells as an AFM cantilever tip was repeatedly stepped into the cell (Fig. 3). Particle displacement occurred primarily in the z direction. When the cantilever was stepped into the cell, the particle was significantly displaced within the first frame (100 ms), which we call the initial fast response. We refer to the particle's subsequent creep toward an equilibrium displacement position as the slow response.

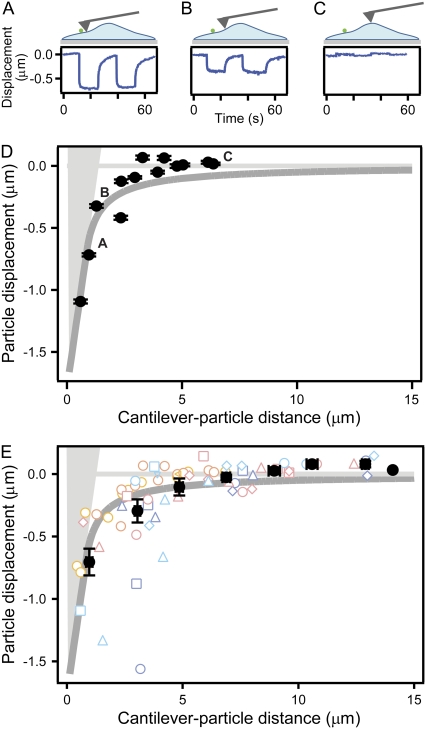
When we indented an endothelial cell at increasing distances from a single particle, a distance-dependent decay in the displacement magnitude was observed (Fig. 4, A–D), similar to results from the polyacrylamide gel control. The binned average of n = 71 coupling instances clearly displayed distance-dependent decay (Fig. 4 E) with particles farther from the indentation point displacing upward, as might be expected for the indentation of a constrained-volume material. Clear heterogeneity was observed, with some particle displacements behaving very differently from the expected response of an elastic material.

FIGURE 4.

Particle displacement magnitude decays in a distance-dependent manner. Displacement of a single particle on a cell was quantified as an AFM tip was stepped into the cell at distances ranging between 0–7 μm from the particle (A–C, taken from D). (D) As distance from the tip increased, particle movement decayed toward zero, sometimes rising up at the farthest distances. Displacement magnitude was measured after particle relaxation. Error bars represent the fitting error of a flat line to equilibrated particle position, as recorded over several seconds. Dark gray curve represents predicted surface for a semi-infinite elastic half-space (37). The light-gray shaded area represents the cantilever tip. (E) When pooled, average displacement from n = 71 coupling instances (16 particles on seven cells) shows similar distance-dependent decay that closely follows the elastic model, although single points clearly exhibit heterogeneity. Error bars represent standard error of the mean. Each color point represents a different cell, and each shape represents a different particle.

Equilibration time increases with distance from perturbation

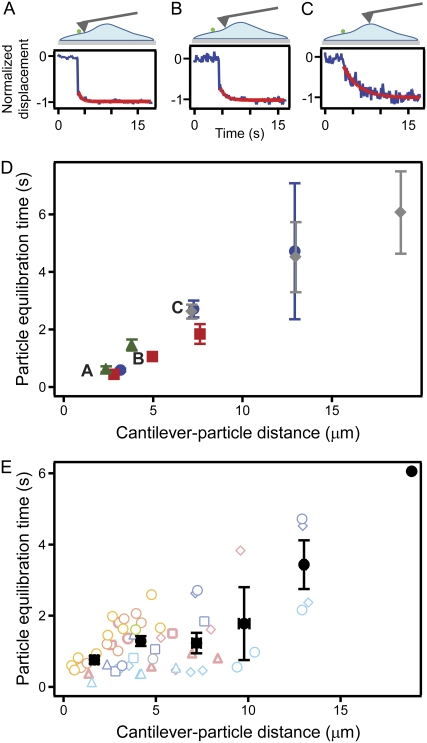
For a better understanding of the equilibration behavior of endothelial cells, we measured the timescale over which stresses propagated through the cells by tracking particle movement immediately after mechanical perturbation by the AFM cantilever. Equilibration time was quantified by fitting a single exponential to the z component of the slow response of the particle, beginning 100 ms after indentation (Fig. 5, A–C). Fig. 5 D shows the response of four particles to indentations at three different points on a single cell. Notably, equilibration time increased with distance for the four particles tracked. This distance-dependent increase in equilibration time was further seen in the population response of n = 57 coupling points (16 particles on seven cells) (Table 1, Fig. 5 E).

FIGURE 5.

Particle equilibration time increases with cantilever-particle distance. (A–C) As distance between the indentation point and a particle increases, the particle takes a longer time to relax to equilibrium. Blue traces represent raw data, and red traces represent exponential fit to the data. (D) Four particles on a single cell showed increasing equilibration time with distance from perturbation when indented at three different positions. Data from each particle are represented by a different color and shape. Error bars represent the fitting error to a single exponential decay function. (E) Equilibration response of n = 57 coupling instances (16 particles on seven cells). Each cell is represented by a different color. Each particle on each cell is represented by a different shape. Average equilibration time is shown by black points, with error bars representing standard error of the mean.

TABLE 1.

Particle equilibration time increases with distance from indentation

Cell	n	r	p
Cell 1	9	0.86	0.003
Cell 2	8	0.93	<0.001
Cell 3	11	0.95	<0.001
Cell 4	13	0.51	0.072
Cell 5	14	0.79	<0.001
All particles	57	0.68	<0.001

For each cell individually and for all observed particles, equilibration time was positively correlated with distance from indentation (each relationship was statistically significant, except for Cell 4). n, number of particles; r, Pearson correlation coefficient.

To quantify the correlation between distance and equilibration time, the Pearson correlation coefficient was used. A coefficient value of 0 indicates no correlation, and a value of 1 or −1 indicates perfect positive or negative correlation, respectively. The Pearson correlation coefficient of all 57 coupling points was r = 0.68 (p < 0.001), indicating that a distance-dependent equilibration response was common and occurred in a majority of cases. This correlation was even higher in four of five cells in an independent analysis of cells with enough coupling points to perform statistics (Table 1). An additional analysis showed that this increase in equilibration time with distance was seen in 93% of particles with equilibration time values for at least two distinct distances (13 of 14 particles).

No significant variations in response were observed when either particle location or cantilever perturbation was above the nuclear or lamellar regions, indicating that the observed trend was not dominated by proximity to the nucleus. As further insurance that the observed trend was not attributable to position on the cell, the depth of cantilever indentation was measured for each indentation. There was no significant correlation between either equilibration time or particle displacement and cantilever indentation depth (r = −0.18, p = 0.39, and r = −0.15, p = 0.51, respectively).

Actin cytoskeleton is required to maintain distance-dependent equilibration

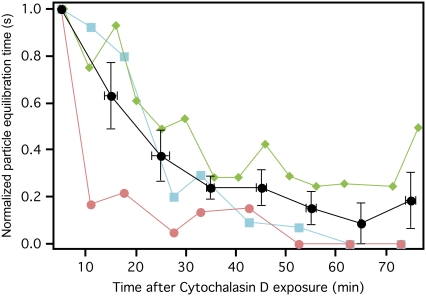
To determine the effect of the actin cytoskeleton on the measured distance-dependent equilibration response, we exposed cells to cytochalasin D, an inhibitor of actin polymerization. We then periodically indented cells at a fixed point over the course of 1 h, and observed the response of particles away from the indentation. Although the fast response was still observed, the equilibration time of particles decreased significantly within the first 30 min after cytochalasin D exposure. After 1 h, equilibration time dropped to a small fraction of the initial equilibration time. This illustrates a clear decrease in equilibration time over the course of cytochalasin D exposure (Fig. 6). The Pearson correlation coefficient for time after exposure to cytochalasin D and equilibration time was −0.66 (p < 0.001). Particles on cells not exposed to cytochalasin D had no observed decrease in equilibration time over the same time period, with no significant correlation of equilibration time to time after exposure to cytochalasin D.

FIGURE 6.

Particle equilibration time decreases after cell exposure to cytochalasin D. In two separate experiments, a cell with at least one particle located several microns from the cantilever tip was exposed to cytochalasin D at time = 0 min. Indentation-retraction experiments were repeated at the same location every 5 min for over 1 h. Equilibration time of all three particles (three particles on two cells) decreased over time after exposure to cytochalasin D. Equilibration time for each particle is normalized by maximum observed equilibration time (first time point in all three cases), and represented by a different color and shape. Average normalized equilibration time is shown by the black points with error bars representing standard error of the mean.

DISCUSSION

We present a method for directly quantifying mechanical coupling in cells, and we observe an unexpectedly slow stress propagation and distance-dependent equilibration. Distance-dependent relaxation behaviors are outside the scope of most existing cell-mechanics models, in part because of a lack of experimental data and techniques to address this phenomenon.

We compared our results to two material models: viscoelasticity and poroelasticity. A single-phase homogeneous viscoelastic material, such as the traditional spring-and-dashpot standard linear solid model, cannot explain the observed behavior, because it assumes that the material will simultaneously relax in response to a local perturbation with a single time-constant. To determine if a heterogeneous viscoelastic model could explain this behavior, we modeled the experiment as a step-strain of a series of parallel spring-dashpot pairs (Voigt-Kelvin material (29,30)), which could account for varying viscoelastic properties within a cell (for details, see Materials and Methods and Fig. S2). By increasing the viscosity of dashpots furthest from the step strain, a distance-dependent increase in equilibration time was observed. However, placing the more viscous elements closer to indentation resulted in a distance-dependent decrease in equilibration time. Because our findings were spatially invariant (wherever the cell was indented, a distance-dependent increase in equilibration time was observed), this model of a series of spring-dashpot pairs cannot explain the observed behavior.

The poroelastic model can account for the observed slow distance-dependent equilibration across the cell. The biphasic nature of a poroelastic material results in both a fast propagation of stress through the solid phase (cytoskeleton), and a much slower diffusive equilibration of hydrostatic pressure of the fluid phase (cytosol), resulting in increasing equilibration time with distance (20). Using cytoplasm viscosity, cell fluid fraction and porosity, and cytoskeletal elasticity measurements from the literature (16,31–35,39), we found that our experimental results were consistent with and on the same scale as the diffusive equilibration predicted by poroelasticity theory (see Materials and Methods for calculation details). Although this suggests poroelastic behavior, such predictions are highly dependent on the values of parameters put into the model, and some parameters, such as cytosolic viscosity, were measured previously to range by an order of magnitude or more.

Poroelasticity theory predicts that equilibration time depends quadratically on distance from perturbation (15–17). When the averaged equilibration data (Fig. 5 E) were fit to a linear (t = C₀ + kx) versus quadratic (t = C₀ + kx²) model, the resulting χ² values were 2.070 and 0.289, respectively. The significantly smaller χ² value for the fit to a quadratic model indicates that the experimental data are more in line with the quadratic trend predicted by the poroelastic model. However, equilibration times of each individual cell exhibited a more linear dependence on distance, indicating that a quadratic poroelastic model does not fully account for all observations, and additional mechanical behaviors may be important (Fig. 5 D). In summary, the observed increase in equilibration time with distance from perturbation cannot be explained by conventional viscoelastic models of cell mechanics, but is in agreement with the poroelastic model.

The observed decrease of equilibration time after exposure to cytochalasin D is also consistent with the poroelastic model. The actin cytoskeleton serves as both the source of elasticity and the barrier to the flow of cytosol. As the actin cytoskeleton begins to depolymerize because of cytochalasin D, pore size increases, resulting in a less impeded flow of cytosol and reduced time to equilibrium. Eventually, the cytoskeleton is disrupted to the point that it no longer serves as an effective barrier to the cytosol, significantly reducing equilibration times across the cell.

As discussed by Mitchison et al. (17), it is not entirely surprising that a cell would not behave like a simple viscoelastic material, because viscoelasticity assumes that the material involves a single homogeneous phase. Because cells contain a dense and crowded cytoplasm consisting of water, soluble and nonsoluble proteins, organelles, cytoskeleton, and a complex lipid bilayer membrane, it seems unlikely that these components would not move relative to each other, as viscoelasticity theory implicitly assumes. Modeling the cell as a two-phase material consisting of fluid and solid portions that can move with respect to one another allows for the investigation of a more dynamic cytoplasm.

Our measurements of stress propagation in single cells, using a combination of AFM and multipoint 3D particle tracking, raise three major points. First, our data show that a distance-dependent equilibration can occur over several seconds, demonstrating temporary storage of mechanical energy by the cell. The potential existence of long-lived pressure gradients has significant implications for cell motility, because localized pressure gradients created by actomyosin contraction of crawling cells could induce a fluid flow that contributes to the coordination of cell protrusions. Second, our results have important implications for mechanical signal transduction. Pressure gradients and cytosolic flow may result in convective biochemical transport, thereby speeding up signaling pathways. Mechanical equilibration takes longer at greater distances from the perturbation, thus serving as a distance-dependent low-pass filter, with only lower-frequency deformations transmitted across the whole cell. Finally, our results suggest that a thorough material model of the cell must go beyond the traditional viscoelastic representation. Experiments explained in the context of soft, glassy rheology showed that a single timescale cannot be applied to cell relaxation (4). We add an additional dimension by showing that the observed timescales of equilibration are also dependent on distance from the perturbation location. Our combined AFM and high-resolution 3D multiparticle tracking method offers a powerful approach to probe these theories further, and to quantify mechanical coupling in cells directly in response to mechanical stimuli and during highly coordinated mechanical processes, including motility, shape change, cytokinesis, and cell-cell and cell-extracellular matrix interactions.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.