Protein Localization by Actin Treadmilling and Molecular Motors Regulates Stereocilia Shape and Treadmilling Rate

Abstract

We present a physical model that describes the active localization of actin-regulating proteins inside stereocilia during steady-state conditions. The mechanism of localization is through the interplay of free diffusion and directed motion, which is driven by coupling to the treadmilling actin filaments and to myosin motors that move along the actin filaments. The resulting localization of both the molecular motors and their cargo is calculated, and is found to have an exponential (or steeper) profile. This localization can be at the base (driven by actin retrograde flow and minus-end myosin motors), or at the stereocilia tip (driven by plus-end myosin motors). The localization of proteins that influence the actin depolymerization and polymerization rates allow us to describe the narrow shape of the stereocilia base, and the observed increase of the actin polymerization rate with the stereocilia height.

INTRODUCTION

Cells produce a variety of actin-based membrane protrusions on their surface, such as microvilli, filopodia, and stereocilia (1). These protrusions contain a core of treadmilling actin filaments, usually in a tightly cross-linked bundle, which push the membrane outwards and drive the growth and shape of the protrusion. The cell controls the final length of these protrusions, depending on their functionality. Some of the previously proposed key physical parameters that control the protrusions' shape are the rate of actin polymerization at the protrusion tip and the number of actin filaments inside the protrusion (2,3). These parameters are regulated by a large number of proteins—e.g., formin (4), ARP2/3 (5,6), Ena/VASP (7,8), myosin-XVa (9,10), and myosin-X (11)—all of which are still being actively investigated and not fully characterized at present. Some of the actin-regulating proteins (AP) are localized at different compartments along the protrusion length, and this localization is important for the correct shape and dynamics of the protrusion (12).

The stereocilia of inner ear hair cells provide us with a well-characterized example of a tightly organized cellular protrusion with distinct compartments, which we will attempt to model here. In this system, the actin core is in the form of a tight straight bundle, with an approximate cylindrical symmetry. This allows us to treat the transport and dynamics in this system as one-dimensional along the stereocilia contour. Furthermore, the actin inside the stereocilia is uniformly polarized (13) and has steady-state actin treadmilling behavior (9,14). For stereocilia, there exists data for many of the parameters needed to verify our model, such as treadmilling rates and myosin distributions (15). Nevertheless, our model demonstrates mechanisms that can be generalized to other parallel actin bundle protrusions.

The main new concept of this article is based on the idea that the average rates of actin polymerization and depolymerization are modulated by the local concentrations of various APs that influence these chemical reactions (16). Controlling the spatial concentrations of these proteins therefore allows the cell to control the local actin reaction rates. In this article, we propose a physical mechanism for this spatial localization, which results from the interplay between passive diffusion and transport by myosin motors and/or by the actin treadmilling. We also explore the conditions that could make such a localization effect significant inside stereocilia.

We next use this model to calculate the possible consequences of such localization of APs on the internal dynamics and shape of the stereocilia (Fig. 1). For this purpose we consider three types of proteins that 1), promote disassembly (severing) of actin filaments (DP); 2), inhibit actin polymerization (IP); and 3), enhance/promote polymerization of the actin barbed ends (PP). Localization of these types of proteins to either the stereocilia base or tip, provides a possible explanation for two observed phenomena: the narrow shape of the stereocilia base, and the dependence of the polymerization rate on the protrusion height in stereocilia. The decaying concentration profile of IP proteins gives rise to an increase in the polymerization rate with the stereocilia height, as observed (9). Note that various possible effects, such as the restoring force of the membrane and the availability of actin monomers, would suggest an inverse relationship between polymerization rates and length (2,3). Furthermore, our prediction of a localized concentration profile of DPs can explain the distinct shape where the narrowing is confined to a short region of the stereocilia base.

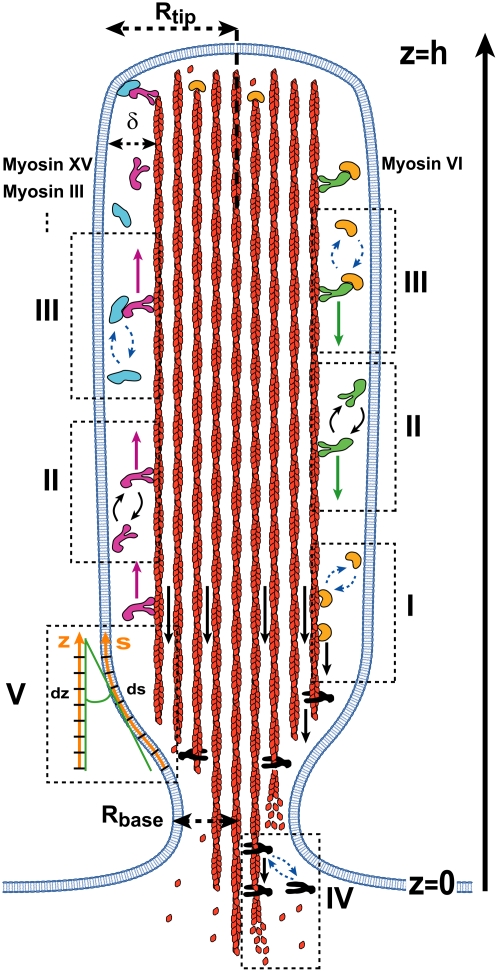
FIGURE 1.

A schematic cross section of a stereocilia, with indication of the transport and actin regulation processes: red filaments represent the treadmilling actin (black arrows show the retrograde flow with velocity v_a), with actin monomers shown diffusing from the depolymerizing ends at the base to the tip. Proteins that regulate the actin dynamics are shown to bind to either the treadmilling of actin filaments (dashed box I), or to the downward moving myosin-VI (green), or to the upward moving myosins (purple; myosin-XV, myosin-III, etc.) (dashed box III). The purple arrows show the constant velocity v_m of the myosin motion up and the green arrows show the constant velocity v_m down along the stereocilia (dashed box II). Proteins that inhibit the actin polymerization (IP) are shown in orange, while proteins that promote the actin polymerization (AP) are shown in light blue. Disassembly factors (black shapes) depolymerize the actin filaments at the stereocilia base and are localized there by the actin treadmilling or by myosin-VI (dashed box IV). The stereocilia has a narrow base of radius R_base, and assumes the shape of a cylinder with radius R_tip higher up. All the transport processes (diffusion and myosin motion) are confined to the narrow space separating between the actin bundle and the membrane (of thickness δ), along the outer contour (coordinate s, dashed box V).

A recent theoretical model of the actin polymerization dynamics and the steady-state shapes of membrane protrusions was presented in Prost et al. (17). This model describes in detail the internal polymerization dynamics in the cross section of the protrusion tip and the base. A similar study of the dynamics at the protrusion tip was given in Atilgan et al. (3). Our model introduces an entirely new effect: the strong compartmentalization of actin capping and disassembling proteins to distinct regions along the protrusion height. Since the models include different physical aspects of this complex system, they are somewhat complementary, and future experiments will be required to pinpoint the key mechanisms that dominate.

In the next section, we describe the localization of proteins due to interactions with the treadmilling F-actin's retrograde motion, and due to translocation by myosin motors. We then use these results to calculate the effect of this localization on the stereocilia shape and the actin treadmilling rate, in the following section.

THEORY: ACTIVE MECHANISMS OF LOCALIZATION INSIDE STEREOCILIA

In this section, we calculate the concentration profile of proteins that both diffuse in the cytoplasm or membrane, and also interact with either or both the retrograde motion of the actin filaments and myosin motors inside the stereocilia (Fig. 1). For stereocilia, steady-state conditions apply since the equilibration time is much shorter than the protrusions' lifetimes, while in short-lived protrusions the concentration profiles are dynamic.

The crystallike packing of the filaments in the actin core most likely confines the majority of the transport processes to a narrow space annulus between the actin core and surrounding membrane (Fig. 1). We assume that the local concentration of proteins in the thin space surrounding the actin core is uniform for a circular cross section at a given distance from the base. This allows us to reduce the diffusion process to one-dimensional diffusion inside the thin annulus along the stereocilia outer contour. We write the one-dimensional kinetic equations for such a process in terms of a concentration of proteins along the stereocilia length (z). The local concentration is c(z), the local radius of a cylindrically symmetric stereocilia is r(z), and the (small) thickness of the free volume is δ ∼ 10 nm (18). For membrane proteins, the diffusion is limited to the external membrane surrounding the actin core, and is therefore treated in exactly the same way.

Localization toward the stereocilia base due to actin retrograde motion

Proteins that directly bind to F-actin are dragged by its retrograde motion (Fig. 1, dashed box I) toward the stereocilia base caused by the treadmilling behavior of the filaments. The proteins can also be dragged by steric interactions with the bundling proteins that cross-link the actin filaments to each other or to the membrane. The direct interaction between these proteins and the actin filaments is described below by simple binding/unbinding kinetics. The retrograde motion of the filaments may induce an overall flow in the surrounding fluid, if the stereocilia membrane is permeable. We discuss this case in the Appendix, where we show that this case is not different in any essential way from the more general process of localization due to binding to the actin filaments. We therefore treat here the more general mechanism.

The flux of freely diffusing proteins, along the outer surface of the stereocilia, is given by J_f = −2πr(z)δD∂c_f(z)/∂s, whereas the total flux of actin-bound proteins is given by J_b = 2πr(z)δv_sc_b(z), where c_f and c_b are the local concentrations of the free and actin-bound proteins, respectively, at the height z along the stereocilia. The coordinate s is along the contour of the stereocilia outer surface (Fig. 1, box V). Using these fluxes, we write the kinetic conservation equations for a stereocilia of constant shape ()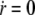

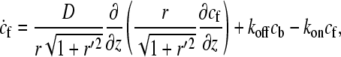(1)

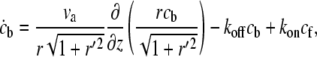(2)

where v_a is the retrograde velocity of actin toward the stereocilia base along the z axis, and r′ = ∂r/∂z and k_on,off are the on/off rates for the binding/unbinding of the AP to the F-actin. The derivatives along the outer contour of the stereocilia give rise to the factors of 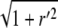in these equations. The flow velocity along the outer contour is given by the projection of the actin retrograde flow (Fig. 1), i.e., 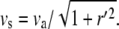Our convention is for positive velocity in the direction of the stereocilia tip, and negative velocity for the stereocilia base.

We assume here that the actin filaments are closely packed in the actin core, so that their local concentration is constant, as is therefore the concentration of binding sites. The tight packing of the filaments in the actin core of the stereocilia means that there are no gaps forming between the filaments, which therefore have a constant concentration along the length. This concentration of actin binding sites is included into k_on, i.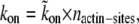e., where 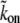is in units of s⁻¹ M⁻¹ and n_actin-sites is in units of M. Because the concentration of actin binding sites on the outer surface of the central actin-core is taken to be constant along the entire length of the stereocilia, it means that we do not describe here more complex processes whereby there is competition between different proteins and myosins on the available binding sites. These processes can be added in future elaborations of this model. (Note that the affinity of the AP to the actin filaments may depend on the internal state of the actin, i.e., either ATP-actin or ADP-actin, which changes along the length of the stereocilia; ATP-actin near the tip, and ADP-actin below. This will make the rates k_on and k_off height-dependent, but for simplicity, this is not included in the calculation. Since the ATP-cap is ∼180 nm (19), it can be neglected for the case of stereocilia.)

At steady state, Eqs. 1 and 2 reduce to the equations

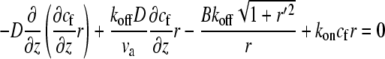(3)

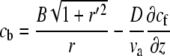(4)

for the bound and free protein densities. These equations can be solved numerically for a general shape, where r(z) ≠ const. For the special case of a simple cylinder, r(z) = const, Eqs. 3 and 4 can be solved analytically as

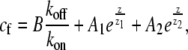(5)

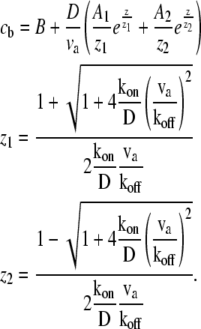(6)

For the case of localization due to actin treadmilling, the following boundary conditions apply:

1. A constant concentration of free proteins at the stereocilia base (equal to the concentration in the cell bulk) c_f (z = 0) = c_f,0; and

2. Zero fluxes of free and bound proteins at the stereocilia tip (z = h), J_b (z = h) = J_f(z = h) = 0.

For these particular boundary conditions, we get the coefficients

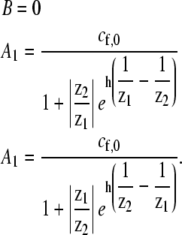(7)

For APs that bind to F-actin we find in a uniform cylinder an approximately exponentially decaying profile from the base (Eqs. 5 and 6; and Fig. 2 a). Note from Eq. 5 that the decay profile is determined by the ratios of k_off/v_a and k_on/D, and that z₁z₂ < 0. At the stereocilia tip we always get c_b(z = h) = 0. For actin retrograde motion to the stereocilia base we have v_a < 0, therefore z₁ < 0, and z₂ > 0. The dominant exponential term describing the decay of the concentration c_f from the stereocilia base is given by the second term in Eq. 5. In Fig. 2 a, we demonstrate the effect of stereocilia shape on the profile for a typical stereocilia shape, by solving numerically Eqs. 3 and 4. (Note that we solve the set of equations dynamically using an explicit finite difference scheme, which we evolve in time until steady state is reached.) We find that the distribution of the free proteins c_f is weakly affected by the shape, while the bound proteins c_b become highly localized at the narrow base.

FIGURE 2.

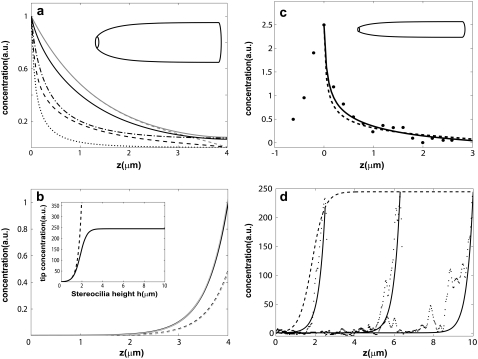
(a) Plot of the calculated profiles of proteins that localize to the stereocilia base due to actin treadmilling and due to myosin-VI self-localization. In the solid gray line, we plot the profile of free proteins for a cylindrical protrusion, and in the dashed gray line, we plot the profile of bound proteins given in Eqs. 5–7 for localization due to actin treadmilling. In the solid black line, we plot the profile of free proteins, and in the black dashed line we plot the profile of bound proteins for the shape shown in the upper part of the figure, by numerically solving Eqs. 3 and 4 using the same values for the parameters. In the dot-dashed (dotted) black line, we plot the profile of a free (bound) cargo protein that is localized to the base due to its binding to the myosin-VI, as described by Eqs. 9 and 10, which we solve numerically for the same shape (the myosin-VI profile is given in this case by the solid and dashed black line, for the free and actin-bound, respectively). (b) Plot of the calculated profiles of tip-directed myosins. In the solid (dashed) black line, we plot the profile of free (bound) myosins for the shape shown in the upper part of the figure, by numerically solving Eqs. 3 and 4. The gray lines show the same profiles for a cylindrical protrusion using the analytic expression of Eq. 8. In the inset we plot the concentration of tip-directed myosins at the tip as a function of the stereocilia height, with (solid line) and without (dashed line) deactivation at the tip, for a cylindrical stereocilia. (c) Calculated localization profile of a protein localized by actin treadmilling (solid line, Eqs. 3 and 4) and as cargo due to myosin-VI (dashed line, Eqs. 3 and 4), compared to the observed distribution of radixin (33) (solid circles). The profiles are calculated numerically for a shape similar to the stereocilia from which the data was measured (Fig. 4 b in (33)) as shown schematically by the shape drawn at the upper part of the figure. (d) Plot of the measured fluorescence intensity of myosin-III (black dots, Fig. 4 b of (22)) for three different stereocilia. The solid lines give the calculated profiles as a function of z using Eq. 19 for a cylindrical protrusion and the dashed line is the tip concentration as a function of the height h.

We consider another process whereby the free proteins also undergo a reaction at the stereocilia tip, which depletes their availability, which we will refer to simply as deactivation. The chemical process of deactivation renders the proteins inactive, and removes them from the population of available active proteins. The deactivation at the tip may arise due to reactions with the barbed ends of the actin filaments, or the associated proteins of the tip-complex. We assume that deactivated proteins leave the stereocilia by diffusion, coupling to actin treadmilling, or active transport to the base, and undergo continuous renewal from their source in the cell cytoplasm. Furthermore, we assume for simplicity that the rate of deactivation at the tip is constant with the stereocilia height, and is not affected for example by the membrane restoring force (which increases with height).

In this case the boundary condition at the tip is modified: the flux of free proteins at the tip is given by the balance between the diffusion and deactivation: −Nk_pc_f,h = 2πR_tipδD∂c_f,h/∂s, where k_p is the on-rate of the deactivation reaction occurring at N sites at the tip, of radius R_tip. To simplify the notation we redefine the effective deactivation rate to be k_p* = k_p(N/2πR_tipδ). The flux of actin-bound proteins is still zero at the tip. The solution for the concentration profile in a simple cylinder with such boundary conditions is given in the Appendix (Eq. 18). If the reaction sites are uniform in the stereocilia-tip cross section, as are the actin barbed ends for example, we have that N = (R_tip/a)², where a is the spacing between the reaction sites. The effective deactivation rate is therefore dependent on the stereocilia diameter.

Self-localization of myosin

Myosin molecular motors come in a large variety (20), but all share the ability to move along actin filaments using energy from ATP hydrolysis. Most myosins walk toward the plus-ends of actin filaments, while myosin-VI is unique in its tendency to walk toward the minus-ends (20,21). Some of these motors are known to move processively on their own, whereas others move only when attached to a cargo, or bundled together. For simplicity we will treat here the myosin motors as processive, so that their motion is that of free diffusion when not bound to the F-actin, and a directed motion at a constant velocity when actin-bound (Fig. 1, dashed box II). We will treat the myosin motors as moving only on the external surface of the actin bundle (Fig. 1). This behavior is supported by the observed distribution of myosins in stereocilia (22), where they are excluded from the actin core. Their motion along the external surface of the stereocilia bundle was demonstrated in Shepherd et al. (23).

Our calculation of steady-state myosin distributions assumes that there is a balance between the diffusion and active movement of myosins along the stereocilia, which is indicated by the observed continuous supply of motors to the tip (10). Since there are many different species of myosins on a single stereocilia, they may affect each other through excluded volume interactions, which can lead to a saturation of their concentration and to traffic-jams along the stereocilia length. These effects are not included in the simple diffusion treatment presented here.

For simplicity, we will neglect below the contribution of the actin treadmilling to the motion of the actin-bound myosins, although this process also affects the myosin distribution. The actin treadmilling motion simply adds to the processive motion of the actin-bound motors, and this is a small correction since the velocity of myosin motion (of ∼0.1–1 μm/s) is orders-of-magnitude larger than the treadmilling velocity inside stereocilia (of ∼10⁻⁴ μm/s). Nevertheless, there could be a fraction of nonprocessive (immobile) and actin-bound myosins that therefore move only with the actin treadmilling motion (24). If this fraction is large, the overall distribution of the myosin will be affected significantly by the actin treadmilling motion. Such processes are observed in filopodia for myosin-XV (10) and myosin-X (11), but due to lack of experimental data on these processes in stereocilia, this component is not treated here.

The distribution of such myosin motors along the stereocilia length is described by Eqs. 1 and 2, with the following replacements: v_m (velocity of actin-bound myosin) replaces v_a; D_m (the diffusion coefficient of free myosins) replaces D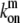; and and 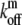(the on/off rates for the binding/unbinding of the myosin to the F-actin) replace k_on and k_off. The direction of motion of the myosin is given by the sign of v_m, where a positive sign stands for motion toward the plus-end (stereocilia tip), and a negative sign for motion toward the minus-end (stereocilia base). For base-directed myosins the boundary conditions are the same as for the proteins moving with the treadmilling actin, and in the simple cylindrical case we get the solution given by Eqs. 5–7. This results in the exponential self-localization of myosin-VI to the stereocilia base (10,25) (Fig. 2 a).

For tip-directed myosins (such as myosin-X, -XVa, -IIIa, etc.), the boundary conditions satisfied by the motors is modified to the following:

1. We assume that processive motors that get to the tip are released where the actin filaments end, and become freely diffusing myosins, m_b,hv_m = D_m∂m_f,h/∂z; and

2. The influx of processive motors at the stereocilia base is balanced by the outflux of free myosins, and is determined by the concentration of bound myosins at the base, i.e., J_b,z=0 = m_b,0v_m = m_f,0v_m().

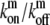We assume here that at the stereocilia base the ratios of bound and free motors is given by chemical equilibrium. The tip still functions as a reflecting wall, with zero overall flux. Using these boundary conditions we get the coefficients for the solution given in Eqs. 5 and 6,

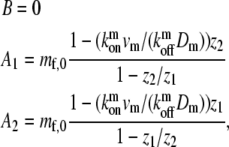(8)

where m_b, z₁, and z₂ are given by Eqs. 4–6 with the myosin parameters. This solution describes an exponential localization of the tip-directed myosins to the stereocilia tip (Fig. 2 b).

There is a crucial difference between the base and tip directed myosins regarding the conservation of the total number of myosins in the cell: for base-directed myosin-VI, due to the exponential localization at the base, the overall number of myosin motors in the stereocilia is finite, even in the limit of infinitely long stereocilia. For tip-directed myosins, the exponential localization to the tip results in an increasing overall number of motors in the stereocilia, as the height increases, leading to depletion of the motors in the bulk. Depletion of tip-directed myosins from the cell bulk will diminish the transport of cargo proteins to the tip.

A process of deactivation of the tip-directed motors at the stereocilia tip will limit this depletion effect. Such a process whereby a tip-directed myosin motor becomes nonprocessive and is then removed from the protrusion through the actin treadmilling, is observed for myosin-X (11) and myosin-XV (10) in filopodia. Here we include this process while limiting it to the stereocilia tip for simplicity, while in the future we can include it to occur throughout the length of the stereocilia. Adding this process to the equation for a cylindrical stereocilia, we get the following boundary condition at the tip: the influx of processive motors is balanced by the outflow of diffusing free motors and the deactivation process, m_b,hv_m = D_m∂m_f,h/∂z + k_p*m_f,h, where k_p* is the effective deactivation rate (see above). The solution for the concentration profile in a simple cylinder with such boundary conditions is given in the Appendix (Eq. 19). The motors are still exponentially concentrated at the tip, but their concentration there saturates to a finite value given by (for a cylindrical protrusion): 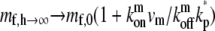(Fig. 2 b, inset).

Localization of proteins coupled to myosin motors

We now consider the concentration profile of a cargo protein that can bind to the myosin motors and be carried along the stereocilia (Fig. 1, dashed box III). To simplify the analysis we will assume that when the cargo binds to free myosin, both molecules diffuse as in their unbound forms, and when the cargo is bound to the actin-bound myosin the complex moves along the actin filaments with the myosin velocity v_m. This treatment basically assumes that the myosin motor has a concentration profile that is independent of the cargo (given by Eqs. 5, 6, and 8), and only serves as a background distribution of flow that affects the cargo concentration profile.

These assumptions lead to the kinetic equations for the cargo concentration,

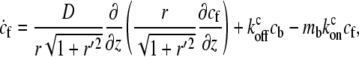(9)

(10)

where c_f,b are the local concentrations of free and myosin-bound cargo molecules, respectively, and 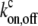are the on/off rates for the binding/unbinding of the AP to the actin-bound myosin, which has a local concentration m_b(z) from Eqs. 5, 6, and 8. For the general case, even in a simple cylinder, these equations can only be solved numerically.

Nevertheless, we can get an analytic approximation for a simple cylinder, which is valid for the limits given below. We first add Eqs. 9 and 10 to get

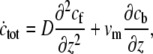(11)

where c_tot = c_b + c_f. This equation can be solved analytically in the limit of 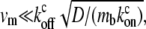which is equivalent to substituting: c_f = c_tot/(1 + 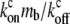), c_b = c_tot/(1 + 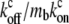), which means a local chemical equilibrium. This limit therefore describes the situation when the free and bound cargo undergo fast chemical kinetics, compared to the convective and diffusive flow processes. Furthermore, close to the stereocilia end where the myosin localizes (either base or tip, respectively), we can substitute for the myosin profile a single exponential of the form: m_b = m_b* exp(z/z_m), where z_m is determined by the dominant exponential term (Eqs. 5–8), i.e., z_m = z₁ and m_b* = A₁, for both base-directed and tip-directed myosins. In this limit we get the solution for the concentration profile of the cargo,

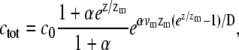(12)

where α = m_b* 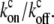We therefore find that the concentration profile of the cargo proteins decays more steeply than the simple exponential of the approximated myosin distribution (Eqs. 5, 6, and 8; and see Fig. 2 a). The concentration levels off to a constant: 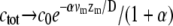at large distance from the concentration peak. The reason for this behavior is the exponential localization of the myosin, so that at large distances the remaining cargo proteins are free from the myosin-induced backflow.

RESULTS AND DISCUSSION

Experimental observations of active localization in stereocilia

Our calculated concentration profiles for the proteins and myosins indicate that the length-scales of their exponential localization, z₁ and z₂ (Eqs. 5 and 6), are determined by the combinations (k_off/v) = (z₁ + z₂)/|z₁z₂| and (k_on/D) = 2/|z₁z₂|. The dominant exponential localization length is given by z₁, and its value gives us a constraint on the values of the physical parameters.

Let us examine two simple limits: the first is 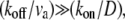where we get z₁ = (k_off/k_on)(D/v), in which v is the advection velocity either v_a or v_m. To have z₁ ∼ 1–10 μm in this limit, and using the observed treadmilling velocity in stereocilia (9) v_a ∼ 10⁻⁵−10⁻⁴ μm/s, the diffusion coefficient turns out to be D ∼ v_az₁(k_on/k_off) ∼ 10⁻⁵−10³ μm²/s, using (k_on/k_off) ∼ 1. We therefore find that the diffusion coefficient of proteins inside the stereocilia has to be extremely small compared to the values measured inside cells if the localization is driven by actin treadmilling, unless (k_on/k_off) is very large. The values of the diffusion coefficient measured in cells are D′ 1–10 μm²/s (26–28) for soluble proteins and 10⁻²−10⁻¹ μm²/s (29) for membrane proteins. Nevertheless, inside filopodia the diffusion coefficient of GFP was found to be one-tenth of that in the cytoplasm (26), indicating that the tight packing inside actin protrusions can greatly reduce the mobility of proteins. Stereocilia are notably even more tightly packed than filopodia, so a high reduction in diffusivity in stereocilia is certainly feasible, albeit undetermined as of yet. The diffusion inside the stereocilia is mostly confined to the narrow space between the bundle and the surrounding membrane, and is also hindered by numerous connecting proteins (steric barriers) (30). This may diminish the value of the diffusion coefficient significantly, but remains to be determined by future experiments.

The second limit is 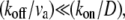where we get 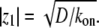In this limit, for reasonable values of D, very large values of (k_on/k_off) are required, as we got in the first limit. In general, within the above model, (k_on/k_off) is required to have large values if the advection velocity is small and D is given by characteristic values in cells. Despite these quantitative constraints, we cannot rule out the possible role of actin-treadmilling as an important localization process inside the stereocilia, for the following reasons:

1. The actual value of the diffusion coefficient D for both soluble and membrane proteins within the stereocilia is not known at present, and could potentially be very different from the cytoplasmic values.

2. The k_on/k_off ratio may be large, due to a large concentration (millimolar) of actin-binding sites along the outer surface of the actin bundle core. For example, if k_off ∼ 1 s⁻¹, 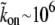s⁻¹ M⁻¹ (31), and n_{actin–sites} ∼ 1 mM, then we get a ratio of k_on/k_off ∼ 10³, which is the ratio used in the fits below.

The concentration of actin-binding sites used in this estimate is higher than in the bulk of the cell, and may occur due to the close confinement by the membrane surrounding the actin core in the stereocilia. Since there are many more actin-binding proteins than there are known proteins that are transported as cargo by myosin motors, localization due to actin treadmilling may still play a significant role.

Alternatively, for myosin localization, we have v_m ∼ 0.1–1 μm/s, which allows a much larger (smaller) value for the diffusion coefficient (for (k_on/k_off)), compared to the case of localization by actin treadmilling. Since the diffusion coefficients of the various components inside the stereocilia are not known at present, we will show below the possible consequences of localization due to both actin treadmilling and myosin motors.

We start with observations that indicate the self-localization of myosins. Myosin-VI localization to the stereocilia base was demonstrated and discussed in the literature (10,25). For tip-directed myosins we plot in Fig. 2 d several typical profiles of myosin-III (Fig. 4 b in (22)) along the stereocilia, compared to the calculated analytic distribution with deactivation at the tip (Eq. 19), assuming a cylindrical profile. Note that the narrower base of real stereocilia would give rise to a small modification of the above analytic results, while not changing their qualitative nature. The length-scale of the concentration profile, z₁ in Eqs. 5 and 6, depends on the myosin velocity, diffusion coefficient, and actin-binding kinetics. The data seems to support the result we get for tip-directed myosins that are deactivated at the tip, i.e., a saturation of the concentration at the tip as a function of stereocilia height (Fig. 2 d). The values of the parameters used in these calculations are: D_m = 0.1 μm²/s, v_m = 0.5 μm/s, k_m,on = 1 s⁻¹, k_m,off = 0.03 s⁻¹, and k_p* = 0.002 μm/s.

FIGURE 4.

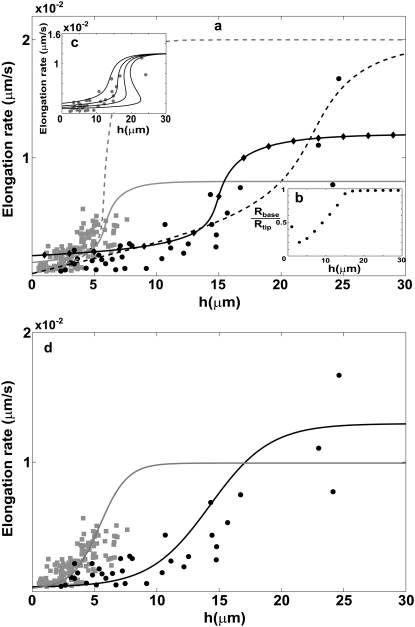
(a) Calculated dependence of the polymerization rate A(h) as a function of stereocilia height due to the localization of IPs to the base by the actin treadmilling (according to Eq. 15); the black lines are for the vestibular stereocilia; gray lines are for the auditory stereocilia. Solid lines give the solution for proteins without deactivation at the tip, and dashed lines indicate those with deactivation. Solid diamonds are a calculation for a shape with R_base/R_tip given in inset c. Solid circles show the observations of Rzadzinska et al. (9) for stereocilia in the vestibular part, and shaded squares show their observations for the auditory part. In inset c, we plot the polymerization rate dependence on the height for various values of 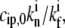where in the two rightmost graphs this parameter is larger than the critical value that gives multiple solutions. (d) Calculated dependence of the polymerization rate A(h) (according to Eq. 15) as a function of stereocilia height due to the localization of PPs to the tip by tip-directed myosins, with deactivation at the tip. Solid lines are for the vestibular stereocilia and shaded lines are for the auditory stereocilia; symbols are as in panel a.

There are several examples that indicate a localization of cargo proteins due to their coupling to myosin motors. One example of this phenomenon was found recently (25), where a strongly decaying profile of a membrane protein (PTPRQ) was measured at the stereocilia base, when myosin-VI was present. In the absence of myosin-VI, the concentration profile of this molecule became uniform, suggesting that its coupling to myosin-VI motion localizes it to the base, as we calculate.

Further examples of localization to the stereocilia base are 1), VLGR1 (32) which similar to PTPRQ has a large extracellular domain, and is a component of the ankle-link complex; and 2), radixin (33), which is a protein that is known to interact with various myosins (34), and could therefore be localized by myosin-VI or by coupling to the actin treadmilling. In Fig. 2 c we plot the observed distribution of radixin along the stereocilia (33), compared with the calculated distribution assuming 1), localization due to actin treadmilling (solid line, numerical solution of Eqs. 3 and 4), using; v_a = −3 × 10⁻⁵ μm/s, D = 1 μm²/s, k_on = 1 s⁻¹, k_off = 1.5 · 10⁻⁵ s⁻¹; and 2), localization due to myosin-VI motion (dashed line, numerical solution of Eqs. 9 and 10), using; D_m = 1.0 μm²/s, k_m,on = 1 s⁻¹, k_m,off = 0.5 s⁻¹, v_m = −0.2 μm/s, D_c = 1.4 μm²/s, k_c,on = 1.5 s⁻¹, and k_c,off = 0.5 s⁻¹. In both cases we calculate the distributions for the stereocilia shape shown at the top of Fig. 2 c. We find good agreement for both types of localization mechanisms.

In the next two sections we calculate the influence of localization of APs along the stereocilia length, on its overall shape and internal actin turnover. We assume here that inside the stereocilia there are proteins that influence the actin filaments by inhibiting or promoting its polymerization and depolymerization; 1), disassembling proteins (DP), such as Gelsolin, ADF/Cofilin, etc. (35), attach to the sides of F-actin and destabilize it so that it breaks and depolymerizes; and 2), polymerization-inhibiting proteins, such as barbed-ends capping proteins (35–39) (IP) and proteins that enhance/promote actin polymerization at the barbed ends (PP), such as VASP (40), WAVE, and Formins (36). The role of some of these proteins is still being investigated, but it is clear that they play a role in either increasing the rate of actin polymerization at the barbed ends or protecting these ends from capping, or both (12). Although the specific nature of all these proteins in the stereocilia is still being studied, they are well characterized in other cellular protrusions.

Actin filament disassembly determine stereocilia shape

Stereocilia have a distinct shape, whereby they have a narrow base and an almost cylindrical upper part (Fig. 3). This distinct shape may play a functional role in increasing the mechanical susceptibility to bending when the stereocilia are deflected.

FIGURE 3.

(a and b) EM pictures of two stereocilia from a frog saccular hair cell, with the calculated profiles superimposed: right dashed line gives the solution for localization of DPs due to actin treadmilling, while the left dashed line gives the solution for localization of DPs due to myosin-VI. The dot-dashed lines show the axis of the stereocilia. The scale bar in panels a and b is 200 nm and 2 μm, respectively. (c) A three-dimensional illustration of the calculated stereocilia profile of panel b using the fit using actin treadmilling localization. In panels d–i, we plot some illustrations of the stereocilia shape change due to different height, polymerization rate, and number of filaments for both actin-treadmilling localization (d–f) and myosin-VI localization (g–i) of the DPs. In all the illustrations we plot two stereocilia of different parameters (solid and dashed lines). In panels d and g, the number of filaments and polymerization rate are the same for two stereocilia of different heights. In panels e and h, the number of filaments is the same and the polymerization rate is 2 × 10⁻⁵ and 4 × 10⁻⁵ μm/s for the shorter and longer stereocilia, respectively. In panels f and i, the polymerization rate is the same, and the number of filaments is 800 and 2000 for the thinner and thicker stereocilia, respectively. All lengths are in microns.

In normal stereocilia the membrane is tightly wrapped around the actin core, so that it follows its shape (41). There are many actin-membrane linkers that ensure a tight wrapping of the inner actin core by the membrane (25,30). These protein linkers overcome the energetic cost of bending the membrane over the narrow and highly curved stereocilia base. The radius of the actin core r(z) at height z is proportional to the square root of the number of actin filaments at that height N(z), i.e., 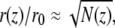where r₀ ≈ 10 nm is the interfilament distance inside the bundle (13). The number of filaments at the stereocilia tip is denoted as N(z = h) = N_tip.

In steady-state conditions the number of filaments at height z (Fig. 1) is a constant, due to a balance between the local rate of filament disassembly at this distance (right-hand side of Eq. 13), and the flux of filaments due to the treadmilling motion (left-hand side of Eq. 13). We consider here F-actin disassembly that is limited to the external surface of the actin bundle, due to the observed tight packing of the filaments inside the stereocilia core, which most likely prevents DPs from reaching inside the bundle. Additionally, severing or spontaneous depolymerization (due to actin aging in the filaments) inside the actin bundle would result in terminated filaments, which are not observed (30,42). Since the filaments are observed to terminate at the membrane, without any loose fragments, we assume in Eq. 13 that a severed filament quickly depolymerizes below the disassembly point, and is removed from the bundle (Fig. 1, box IV). A possible reason for this quick disassembly is that at the stereocilia base the filaments are entirely composed of ADP-actin, since the ATP-actin cap is usually estimated to be ∼180 nm (19).

Assuming disassembly at the outer surface of the actin core, we get at steady-state that

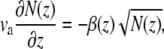(13)

where β(z) is the filament disassembly rate at height z, due to DPs, i.e., β(z) = k_ss_b(z), where s_b(z) is the local concentration of actin-bound DPs and k_s is the severing rate factor. If the rate of disassembly is a constant, either due to a uniform distribution of DPs, or due to spontaneous filament depolymerization, Eq. 13 results in a conical shape. This was found also in Prost et al. (17), and is in rough agreement with the shapes of short abnormal stereocilia, but does not agree with the shape of tall normal stereocilia. The disassembly rate is likely to depend also on the local concentration of the cross-linkers between the actin filaments and various APs that prevent disassembly. The concentration of these proteins could depend on the stereocilia height and also have a nonuniform profile, and these effects can be added to our model in the future.

We now calculate the effect of the localization of DPs to the stereocilia base, on the stereocilia shape. Such proteins have a known affinity to actin filaments, and are therefore inherently affected by the retrograde flow of actin and should be localized to the stereocilia base due to this mechanism (Fig. 1, box IV). Additionally they may be localized to the base by coupling to myosin-VI motors. We will show here that this localization of DPs can explain the observed narrow base of stereocilia (see Fig. 3 a). We solve self-consistently the equations for the concentration profile of the DPs (s_b(z)), and for the shape of the stereocilia actin core (Eq. 13). For the case of localization of the DPs due to actin treadmilling, the profile of actin-bound DPs s_b is given by Eqs. 3 and 4. If the DPs are mainly localized at the base by coupling to myosin-VI, the resulting concentration profile is given by Eqs. 9 and 10. In this case, the concentration of DPs becomes a constant beyond the length-scale of the myosin self-localization z₁, so that disassembly is not limited now to the stereocilia base. Beyond z₂ the concentration of DPs is roughly constant, s_b,∞, so the radius has a conical shape of the form: r(z) ∝ (β(∞)/2v_a)z. When the concentration of DPs beyond z₁ is small, this conical profile is indistinguishable from a cylinder. Note that we consider here either localization due to actin treadmilling or due to myosin-VI, but not the combination of both, since there is a huge difference in the velocities of the two processes. In reality, both processes can play a role simultaneously.

In Fig. 3, we plot the calculated stereocilia shape when DPs are localized to the base. The resulting stereocilia profile is of a roughly constant radius along the upper part, with a sharp narrowing at the base, as shown in Fig. 3, a and b, where we compare our calculations to observed stereocilia shapes. The values used in these calculations are

1. For actin treadmilling localization: β(z = 0) = s_f,0k_s = 1.1 × 10⁻⁷ s⁻¹; D_s = 1.2 μm²/s; v_a = −5 × 10⁻⁵ μm/s; k_on = 3 s⁻¹; and k_off = 10⁻⁴ s⁻¹.

2. For myosin-VI localization: β(z = 0) = 6 × 10⁻³ s⁻¹, D_s = 1.2 μm²/s, D_m = 1.0 μm²/s, v_a = 5 × 10⁻⁵ μm/s, v_m = −0.2 μm/s, m_f,0k_s,on = 4 s⁻¹, k_s,off = 10⁻⁴ s⁻¹, k_m,on = 1 s⁻¹, and k_m,off = 0.5 s⁻¹.

The number of filaments at the tip of these two stereocilia was estimated from the observed radius and the interfilament distance of ∼10 nm (13), to be N_tip = 1000 and 3000 for 1 and 2, respectively. The subscript s in the above parameters indicates that they are the values for the severing proteins (DPs).

In Fig. 3, d–i, we draw the calculated shapes of various stereocilia, when the DPs are localized due to actin treadmilling (Fig. 3, d–f), or due to myosin-VI (Fig. 3, g–i). We demonstrate the changes to the shape due to changing the stereocilia height or thickness, while keeping the actin treadmilling rate constant (Fig. 3, d, f, g, and i). We also show the changes in shape when the actin treadmilling increases with the stereocilia height, as is observed in Rzadzinska et al. (9) (see next section).

Height dependence of the actin elongation rate

It has been recently observed (9) that the actin polymerization rate increases with the height of stereocilia. This puzzling phenomenon is counterintuitive because, for one, the availability of G-actin monomers should decrease at the tip of the stereocilia as a function of the height when they are transported by free diffusion (2) and supplied at a constant concentration at the base. At steady state, the concentration of actin monomers under these conditions at the tip decreases with the stereocilia height, as n_mono(h) = n₀(1 + h/h_ac)⁻¹, where h_ac = 2πR_tipδD_ac/k_on,acN_b, n₀ is the monomer density in the bulk (stereocilia base), D_ac is the diffusion coefficient of actin monomers in the stereocilia, k_on,ac is the on-rate of actin monomers on the barbed ends at the stereocilia tip, and N_b is the total number of barbed ends at the tip. In principle, for long stereocilia this effect will eventually limit the elongation rate (2), but it seems from observations that in stereocilia this is not the dominant process, which means that the assumption of free diffusion of monomers is incorrect or that h_ac/h is large so that the decrease in monomer concentration at the tip is not significant. Furthermore, if the actin monomers are transported actively to the tip, then they could play a role in the increasing rate of polymerization with the height, in a similar manner to the action of proteins that promote actin polymerization (PP), which we discuss below.

Another process that we would expect to decrease the elongation rate at the tip with increasing stereocilia height (2) is the increase in the membrane restoring force acting on the barbed ends. The membrane of an elongated tube exerts a constant restoring force (44), but when the membrane area is finite the tension will eventually increase exponentially with the stereocilia height (45). The interplay between the membrane restoring force at the tip and the rate of polymerization was analyzed previously (17), and here we wish to investigate the role played by other mechanisms. Although the processes that reduce the polymerization rate with the increase in the stereocilia height can be easily included in our analysis, for the sake of clarity we concentrate below only on the mechanisms that can lead to an increase of the polymerization rate.

In the calculations we give here we assume that the stereocilia has a steady-state shape and height h, with the actin polymerization rate that we calculate. While the rate of polymerization depends on the stereocilia height, the steady-state height may also depend on the rate of polymerization. It is likely that the protrusive force due to actin increases with the rate of polymerization, thereby leading to increased height when the polymerization rate increases. Our model suggests that there may be a feedback effect that enhances height fluctuations in the stereocilia, leading to a large distribution of heights. The balance of forces that determines this steady-state shape is not treated here, and is deferred to a future study.

The rate of actin polymerization at the stereocilia tip complex is regulated by proteins that either inhibit (IP) or promote (PP) the actin polymerization process. The localization of PP to the tip could give an explicit height dependence of the PP concentration at the tip, and therefore a dependence of the polymerization rate on the height. Our analysis in Theory: Active Mechanisms of Localization Inside Stereocilia indicates that in a simple cylinder the concentration of tip-directed myosins at the tip increases exponentially for short stereocilia, and saturates to a constant value for tall ones when there is deactivation at the tip. Tip-directed cargo will therefore behave in a similar manner, as is observed for whirlin (10), which was suggested to act as an anticapping agent. The observed one-to-one correlation between the cargo and motor in this example leads us to a simple analysis where we will take the concentration of PP cargo to be simply proportional to the concentration of tip-directed myosins.

We therefore consider the rate of actin polymerization at the tip as proportional to the number of free barbed ends. The IPs at the tip will be described as undergoing a transient capping of those barbed ends, while the PPs that we consider here act to protect free barbed ends from the capping (other types of polymerization promotion by PPs are possible). These effects can be approximately described by the reaction equations,

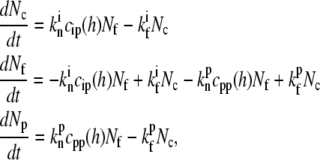(14)

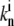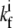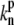where N_f is the number of free actin barbed ends; N_c is the number of IP-affected (capped) ends; N_p is the number of barbed ends that are protected from capping by the PPs; and N_tot = N_f + N_c + N_p is the total number of filaments in the stereocilia tip. The binding/unbinding rate constants of the IP (or PP) to the actin barbed-ends are and ( and 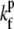), respectively, and the local concentration at the tip of free IP is c_ip(h) (or PP, in the case of c_pp(h)). At steady state we find that the average elongation rate is given by

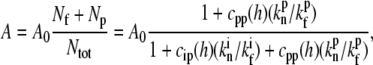(15)

where A₀ is the elongation rate in the absence of any IP and PP. To simplify the analysis we will compare this calculation to the observed data using either the base localization profile of IP (and zero PP concentration) or the tip localization profile of PP (and a constant IP concentration).

To have the polymerization rate depend on the stereocilia height over a range of many microns (as shown in Fig. 4), the localization of the IP should decay over the same length-scale. This cannot be accommodated by myosin-VI, which is localized over a distance of z_m ∼ 1 μm (25). We therefore conclude that IPs most likely contribute to the observed dependence of the polymerization rate on the height by coupling to the treadmilling actin core. When the IPs are localized due to the treadmilling actin flow, their concentration at the tip is given by the solution of Eqs. 3 and 4. Since at steady state we have v_a = A, Eq. 15 becomes an implicit equation for the polymerization rate A(h), which is now also dependent on the stereocilia shape.

Upon solving these equations we get the behavior shown in Fig. 4 a, where we compare to the observations in stereocilia (9). We plot the solutions for the case of a perfectly cylindrical protrusion (Eqs. 5 and 6) (solid lines), and when solving self-consistently for the stereocilia shape using Eq. 13 (solid diamonds). Our solution gives a linear increase of A(h) for small h, followed by a highly nonlinear increase, and a saturation to the free value of A₀ at large heights. We also calculate the dependence of the polymerization rate on the height when the IPs are deactivated at the stereocilia tip (dashed lines). As the deactivation rate increases, the increase in A as a function of h becomes more gradual, compared to the behavior without deactivation. For the self-consistent calculation of the stereocilia shape we used the localization of DP to the base due to actin treadmilling, and the resulting shapes are summarized by the ratio R_base/R_tip shown in the inset of Fig. 4 b, as a function of the stereocilia height. We find that even though this ratio drops to a small value for stereocilia of heights h ∼ 3–5 μm, the polymerization rate is almost unaffected. We find that our model gives a good fit to the observed polymerization rates.

The values of the parameters used in these calculations are

1. For the case without deactivation, D_c = 0.35 μm²/s, k_on = 1 s⁻¹, and

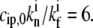
2. For the vestibular stereocilia, we used A₀ = 1.2 × 10⁻⁴ μm/s and k_off = 1.4 × 10⁻³ s⁻¹, whereas for auditory stereocilia we used A₀ = 8 × 10⁻⁵ μm/s and k_off = 3.5 · 10⁻⁴ s⁻¹.

3. For the case with deactivation, D_c = 0.75 μm²/s, k_on = 1 s⁻¹, 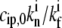= 100, and k_p* = 1 μm/s.

4. For the vestibular stereocilia, we used A₀ = 2 × 10⁻⁴ μm/s and k_off = 1.4 × 10⁻³ s⁻¹, whereas for auditory stereocilia we used A₀ = 2 × 10⁻⁴ μm/s and k_off = 1.5 × 10⁻⁴ s⁻¹.

Above a critical value of 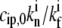there are multiple solutions for A(h) (Fig. 4 c, for no deactivation), which arises from the fact that the retrograde flow velocity is itself dependent on the concentration of IP at the tip: as the stereocilia grows higher, the polymerization rate increases and therefore the concentration profile of IP becomes even more localized at the base, until there is a divergent increase at some critical height, and a discontinuous jump to a higher value of the polymerization rate.

The concentration of PP at the stereocilia tip will be considered here to be simply proportional to the concentration at the tip of some tip-directed myosin that carries these proteins as cargo. This approximation is motivated by the observed one-to-one correlation between the cargo (whirlin) and motor (myosin-XV) (10). We assume that the PP act as anti-capping proteins, as described in Eq. 15, with a constant concentration of IP at the tip. We plot in Fig. 4 b the calculated polymerization rate A(h) for PP that undergo deactivation at the tip, so that their concentration profile is given by Eq. 19, assuming a cylindrical stereocilia (the profile of tip-directed myosins is not sensitive to the shape of the stereocilia base). The values used in these calculations are D_m = 1 μm²/s, v_m = 0.5 μm/s, k_on = 1 s⁻¹, k_p* = 10⁻⁴ s⁻¹, 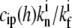= 40, and 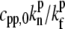= 0.1. For the vestibular stereocilia we used A₀ = 1.4 × 10⁻⁴ μm/s and k_off = 1 s⁻¹, whereas for the auditory stereocilia we used A₀ = 1 × 10⁻⁴ μm/s, k_off = 0.1 s⁻¹.

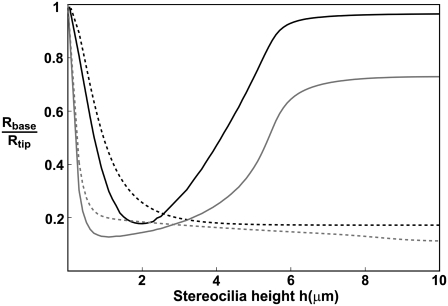
The increase in the rate of polymerization with the stereocilia height affects the shape of the stereocilia, as demonstrated in Fig. 5. In this figure we plot the ratio R_base/R_tip as a function of the stereocilia height, for a constant value of the polymerization rate, and when the polymerization rate increases with the height (using the analytic fit shown in Fig. 4 a, shaded line). We find that if the polymerization rate is independent of the height this ratio decreases monotonously as the height increases. When the polymerization rate does increase with the height (as observed), we find that the ratio recovers to a large value for tall stereocilia. The reason behind this behavior is that the increase in the actin treadmilling velocity leads to a shorter time that is available for the DPs to sever the filaments before they reach the base. For localization of DPs due to the actin treadmilling, there is also a stronger localization of the DPs to the base due to the increase in the polymerization rate, and consequently the actin disassembly is limited to a shorter length, resulting in a thicker base for long stereocilia compared to localization due to myosin-VI.

FIGURE 5.

The calculated ratios (R_base/R_tip) as a function of the stereocilia height. Black lines are for actin treadmilling, gray lines are for myosin-VI localization of the DPs to the base. Dashed lines are for a constant polymerization rate, and solid lines are for a polymerization rate that increases with the height according to the solid gray line in Fig. 4 a.

The values used in the calculations shown in Fig. 5 are

1. For localization of the DPs due to actin treadmilling, D_s = 0.4 μm²/s, k_on = 1 s⁻¹, and k_off = 3 × 10⁻⁵ s⁻¹, where for increasing polymerization rate β(z = 0) = 1.9 × 10⁻⁷ s⁻¹ and for the constant polymerization rate β(z = 0) = 0.5 × 10⁻⁷ s⁻¹ and v_a = −3 × 10⁻⁵ μm/s.

2. For localization of the DPs due to myosin-VI, D_s = 0.7 μm²/s, D_m = 0.5 μm²/s, v_m = −0.2 μm/s, m_f,0 k_s,on = 4 s⁻¹, k_s,off = 0.1 s⁻¹, k_m,on = 1 s⁻¹, and k_m,off = 0.3 s⁻¹, where for increasing polymerization rate β(z = 0) = 0.07 s⁻¹ and for constant polymerization rate β(z = 0) = 0.035 s⁻¹ and v_a = −3 × 10⁻⁵ μm/s.

The number of filaments at the tip that was used in all calculations was N_tip = 3000 (the same as for the stereocilia of Fig. 4 b).

CONCLUSIONS

In this article, we introduce the concept of active localization of proteins inside the stereocilia due to coupling to the actin retrograde flow and myosin motion. We show that these mechanisms lead to strong (exponential) localization at both the stereocilia base and tip of different myosins and proteins, as is observed. The aim of this article was to explore these two localization mechanisms, and since many of the kinetic parameters are not known at present inside the stereocilia, we cannot make a conclusion regarding which of these mechanisms is dominant. If the kinetic parameters turn out to be very similar inside the stereocilia and the bulk cytoplasm, then our work suggests that the most effective localization mechanism is due to myosin motors.

We then use this mechanism to explain two observed phenomena in stereocilia—the narrow shape of the stereocilia base, and the increase in the elongation rate with the stereocilia's height (9). Although we compare to experiments on stereocilia, our model is general and should apply to other types of cellular protrusions, such as microvilli and filopodia. The proposed mechanism can lead to the segregation of proteins inside cells, whenever the cytoskeleton is highly nonuniform, as appears, for example, in polarized cells, such as the lamellipodia of motile cells (46) and the microvilli of epithelial cells (47).

Several of our model predictions could possibly be tested experimentally. A direct test of our model would be to identify and label the IPs, PPs, and DPs in the stereocilia, and observe whether they are indeed localized as we propose, and that their localization profiles correlate with the observed shape and actin dynamics according to our calculations. These localization profiles should also be modified in cells with mutant myosins of different processivities and different chemical kinetics (48). Another prediction of our model that may be tested is that the rate of polymerization depends directly on the stereocilia height, and does not strongly depend on the stereocilia width (as proposed in (17)). This result could be tested by applying an external force on a tall stereocilia such that it is pushed down to a lower height, and then measuring the actin polymerization rate in the new position. Our model predicts that the polymerization rate should decline with the height, although the stereocilia width was unchanged. We also predict that the ratio between the stereocilia width at the tip and the base has a nonmonotonic dependence on the stereocilia height. This may be tested by systematically characterizing the shapes of stereocilia of different heights on the same cell with high resolution. Finally, we acknowledge that our model is by no means the whole story regarding this complex system, where many processes interact simultaneously. To advance our understanding of this system it is useful to characterize the consequences of each mechanism separately, as we do here. Even within the ideas raised in this article, we did not exhaust in this study all the possible reaction/diffusion possibilities that exist in this model, since we wished to focus on the main new features of the proposed active localization mechanisms.

APPENDIX

Localization to the stereocilia base due to hydrodynamic flow driven by actin retrograde motion

If water is free to flow (permeate) easily through the stereocilia membrane, then the actin retrograde flow will induce a hydrodynamic flow, which will affect all the proteins diffusing in the stereocilia, irrespective of the strength of their interaction with F-actin. In this case we have a simple one-dimensional diffusion equation for the total amount of protein per unit length along the stereocilia C(z)

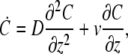(16)

where v is the advection velocity of the cytoplasm inside the stereocilia. The proteins are assumed to exist at a constant density in the cell cytoplasm (infinite reservoir), from which they diffuse into the stereocilia base. This gives the boundary condition C(z = 0) = C₀, whereas at the tip we have a condition of zero flux J(h) = 0. This gives the concentration profile at steady state,

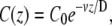(17)

and at the tip C(h) = C₀ exp(–h/h_d), where h_d = D/v is the decay length of the concentration profile. Nevertheless, inside stereocilia the flow of treadmilling actin is very slow ∼10⁻⁴ μm/s, so for h_d ∼ 1–10 μm we require extremely small diffusion coefficient: D ∼ 10⁻⁵−10⁻⁴ μm²/s. This result is similar to our calculation for localization to the base due to binding to actin filaments (see Localization Towards the Stereocilia Base Due to Actin Retrograde Motion), when z₁ = D/v and A₂ = 0.

Calculated profiles when there is a deactivation process at the stereocilia tip

We give here the solutions for the coefficients of the concentration profiles in a simple cylinder, when there is deactivation at the stereocilia tip.

The solution for the problem of base-directed localization with deactivation at the tip is given by the coefficients for Eqs. 5 and 6:

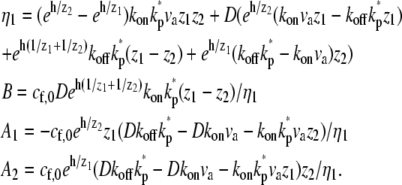(18)

The coefficients for the problem without deactivation (k_p* = 0) are given in Eq. 7.

Similarly for the case of tip-directed myosin localization with deactivation at the tip, we get the coefficients

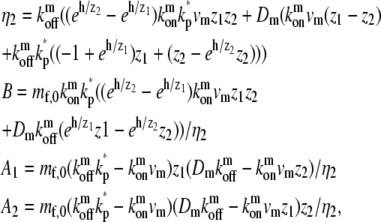(19)

which is equivalent to the solution given in Eq. 8 when there is no deactivation at the tip (k_p* = 0).