Abstract
Actin stress fibers (SFs) play an important role in many cellular functions, including morphological stability, adhesion, and motility. Because of their central role in force transmission, it is important to characterize the mechanical properties of SFs. However, most of the existing studies focus on properties of whole cells or of actin filaments isolated outside cells. In this study, we explored the mechanical properties of individual SFs in living endothelial cells by nanoindentation using an atomic force microscope. Our results demonstrate the pivotal role of SF actomyosin contractile level on mechanical properties. In the same SF, decreasing contractile level with 10 μM blebbistatin decreased stiffness, whereas increasing contractile level with 2 nM calyculin A increased stiffness. Incrementally stretching and indenting SFs made it possible to determine stiffness as a function of strain level and demonstrated that SFs have nearly linear stress-stain properties in the baseline state but nonlinear properties at a lower contractile level. The stiffnesses of peripheral and central portions of the same SF, which were nearly the same in the baseline state, became markedly different after contractile level was increased with calyculin A. Because these results pertain to effects of interventions in the same SF in a living cell, they provide important new understanding about cell mechanics.
INTRODUCTION
In nonmuscle cells, SFs are bundles of actin microfilaments assembled by actin-myosin interactions and cross-linked in a sarcomeric arrangement by α-actinin, myosin light chain, tropomyosin, and other proteins. Each end of a ventral SF is connected to a focal adhesion by proteins such as zyxin, vinculin, talin, and paxillin. This arrangement enables forces at the basal surface, where the cell interacts with the surrounding extracellular matrix (ECM), to be transmitted into and out of the cytoskeleton of the cell. This force transmission is critical for many cellular functions, such as shape stability, adhesion, wound healing, proliferation, apoptosis, motility, and responses to mechanical stimuli. Because of the central role of SFs in cell function, it is important to characterize their mechanical properties.
The mechanical properties of any material are embodied in the mathematical relationships among all the components of stresses and strains. Obtaining these relationships requires precise control and accurate measurements. In fact, a full three-dimensional characterization is very difficult and has not been achieved for any biological material. Even restricting attention to the simpler two-dimensional situation (1,2), this characterization is still extremely difficult to achieve in cells. Uniaxial test results, although mathematically not generalizable, can provide useful information. Hence, a first step toward characterizing mechanical properties of SFs is to obtain the uniaxial relationship between stress and strain in the axial direction. In some instances, stiffness (the ratio of stress to strain) is easier to measure than either stress or strain. For example, we and others have previously described the conditions under which transverse indentation can be used to measure the in-plane stiffness of a material and thereby enable estimation of mechanical properties (1,3).
One essential aspect of mechanical properties is determining whether or not the stress-strain relationship is linear. Linear materials have a constant stiffness that allows for easy quantification and enables one to calculate stress from the measured strain (or stiffness), or vice versa, as well as to extrapolate to other conditions. In contrast, nonlinear properties are much more difficult to quantify. Moreover, because stiffness is not constant, one cannot simply convert stress from strain or stiffness without knowing the specific functional form of the stress-strain relationship. Nearly all biological tissues have nonlinear stress-strain properties (2,4–6), but it is not known whether this is true for SFs.
In addition to linearity, another aspect of mechanical properties needs to be assessed. A recent study reported data consistent with heterogeneity of mechanical properties along the lengths of SFs (7). The spacing of the sarcomeric structures in fibroblasts were measured using green-fluorescent-protein-transfected α-actinin and a fluorescent-tagged myosin light chain (MLC) antibody before and after increasing the actomyosin contractile level. The intervention caused the spacing between α-actinin and myosin bands at the ends of the fibers (near the focal adhesions) to be smaller and those near the center of the SF to be larger than the homogeneous spacings observed before contractility was increased. This heterogeneity is compatible with different contractile levels, size, or material properties of the SF in the two regions. For example, regional differences in mechanical properties could allow the central region to stretch while the ends shorten. This interesting observation is a compelling rationale for directly ascertaining whether there are regional differences in mechanical properties in a SF.
Indirect assessment of cytoskeletal properties in living cells has been obtained using a variety of approaches, including traction microscopy, magnetic twisting cytometry, whole-cell perturbations, or atomic force microscope (AFM) measurements covering large regions of cells (8–12). Traction microscopy enables estimation of the forces applied at the focal-adhesion-ECM interface, but not direct assessment of how much of the force is transmitted to the SF. This, plus the difficulty in assessing strains in the SF, precludes use of this method to assess the stress-strain properties of SFs. Magnetic twisting cytometry enables estimation of the forces within a region of the cytoskeleton. Since this region contains many membranous, submembranous, and cytoplasmic structures, however, distinguishing the properties of any particular constituent requires a mechanical model with its attendant assumptions. Depending on the assumptions, model-derived estimates have their own limitations and uncertainties. A better method is to measure the mechanical properties as directly as possible.
Direct assessments of mechanical properties of actin filaments and SFs have been made mainly in vitro. One study examined the response of single actin filaments attached to glass microneedles subjected to 20 Hz sinusoidal perturbations and reported a dynamic stiffness of ∼44 pN/nm (13). These measurements were made at only one state, however, thereby providing incomplete information about linearity. Recently, more complete data on the stress-strain relationships of single actin filaments were obtained using microcantilevers (14). This study found highly nonlinear relationships at low strains and nearly linear responses at higher strains. Although these data provide valuable insights into the properties of single filaments, their relevance to the markedly different conditions in living cells is questionable. Moreover, one cannot necessarily infer the properties of a bundle of fibers from those of single filaments. A recent study directly measured the mechanical properties of isolated SFs (15), but again, the relevance to the intact cell is not clear.
AFM indentation offers the opportunity to examine SF mechanical properties in living cells. For example, elasticity maps were obtained under a variety of actin depolymerization and disrupting drugs (16). The results demonstrate general trends, but the properties of single SFs are difficult to ascertain from such maps. Moreover, the elasticity values were obtained under the severely constraining assumptions of Hertzian contact mechanics, rendering the absolute values of stiffness modulus questionable.
We have shown that when applied and interpreted correctly, AFM indentation allows reliable characterization of SF properties (17). Hence, in this study, we use AFM indentation to assess, for the first time, several important aspects of mechanical properties of the same SF in living cells. The three major findings are 1), decreasing or increasing contractile level decreases or increases, respectively, SF stiffness; 2), SFs have a nearly linear stress-strain relationship in the baseline state, whereas they exhibit nonlinear properties when the contractile level is decreased; and 3), in the baseline state, stiffness is nearly the same in the peripheral versus the central regions of the same SF, but becomes heterogeneous after the contractile level is increased. These results highlight the critical role of actomyosin contractile level in determining SF mechanical properties and should help us further understand the mechanical role of SFs under a variety of conditions.
MATERIALS AND METHODS
Cell culture
Human aortic endothelial cells from Lonza (Walkersville, MD) were cultured in endothelial cell basal medium plus 2% fetal bovine serum and other supplements (human epidermal growth factor, hydrocortisone, bovine brain extract, and gentamicin sulfate). The cells were used at passages 9–15 and grown in tissue-culture-treated polystyrene plates at 37°C in a humidified 5% carbon dioxide atmosphere.
Liposome preparation
We sought to obtain, as a reference, the softest possible biological structures that could be indented using AFM. Hence, we produced 2- to 5-μm-diameter unilamellar liposomes comprised of phosphatidylcholine/phosphatidylethanolamine at a 10:1 ratio containing fluorescein-5-isothiocyanate-distilled water according to a protocol modified from previous studies (18,19). At the time of study, 10–30 μl of a solution containing the liposome was injected into petri dishes that were pretreated for 5 min with 0.5 ml poly-L-lysine and rinsed with distilled water. The liposomes, which could be easily visualized under fluorescence microscopy, adhered sufficiently firmly to be indented with the AFM.
Indentation using atomic force microscopy
A Bioscope AFM (Veeco, Santa Barbara, CA) mounted on a Zeiss Axiovert 100 inverted microscope was used for both cell imaging and indentation. A silicon-nitride chip with an integrated cantilever (Veeco) was mounted on the fluid holder of the AFM scanner. A 220-μm-long, V-shaped cantilever with a pyramidal tip that has a hemispherical cap∼40 nm in diameter was usually selected for cell indentation. The semiangle of the pyramid is 32.5° (as measured separately by scanning electron microscopy). The probe was oscillated in air and its resonant frequency was determined from the dominant peak in the deflection amplitude spectrum. This frequency was used to calculate the cantilever spring constant, which was nominally 0.035 ± 0.002 N/m. Photodetector sensitivity was also determined from piezo position-deflection response on a clean glass dish filled with distilled water at a probing rate of 1 Hz. Preliminary studies revealed that indentation frequencies from 0.5 to 2 Hz did not produce discernibly different responses (results not shown). Hence, all indentations were performed at a frequency of 1 Hz. To minimize vibration, all the equipment was suspended on a platform above the counter during the experiments. To minimize the drift of the cantilever head, after turning on the instrument, we always waited at least an hour before beginning a study, since previous experience indicated that the largest amount of drift occurs in the first hour after the piezoelectric crystal driving the cantilever is energized. To avoid complications from neighboring interactions, we examined only cells or liposomes that were not in contact with any neighboring structures.
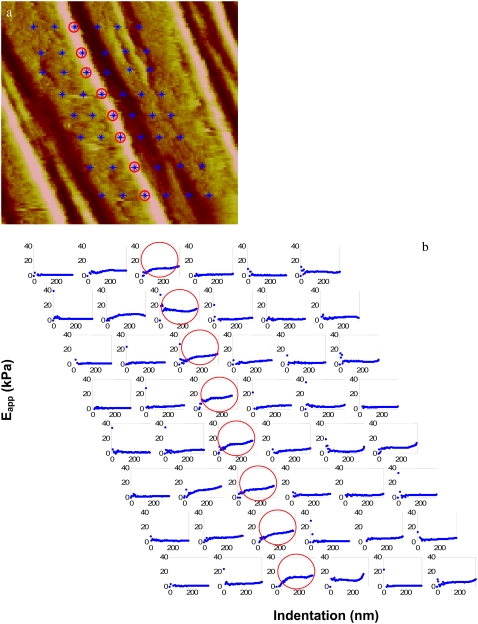
Using light or fluorescence microscopy, we identified a liposome or well-spread cell and positioned it under the AFM cantilever tip. For liposomes, we simply imposed an indentation and retraction at a rate of 1 Hz in several different regions of several different-sized liposomes. For cells, we first used contact mode at a scan rate of 1 Hz to obtain a 256 × 256-pixel deflection image of a small region of the cell between the peripheral margin and the nucleus. From this image, we identified the coordinates near a suitable SF and imposed an array of indentations covering a small region of the SF. The size and position of the array relative to the SF were chosen according to the following considerations. To ensure that an indentation was imposed on the SF despite possible horizontal drift of the AFM head between the times of imaging and indentation, each row of the array contained six or eight equally spaced indentations 300 nm apart. We chose this spacing because the contact area at an indentation depth of 200 nm is a square with an area of ∼200 × 200 nm2. Hence, indentations needed to be spaced at least this distance apart to ensure that the same portion of the target was not being interrogated by adjacent indentations. To be sure that one of the indentations probed the SF, we began and ended the row in a cytosolic region clearly off of the SF, i.e., we straddled the SF with the row of indentations and visually ascertained that only one SF was within the indentations. Because of possible vertical drift of the tip we could not ensure that a row of indentations would repeatedly probe the same axial location on the SF. Thus, rather than attempting to ascribe properties to a precise axial location, we chose to obtain the average properties over a small local region of the SF by imposing six to eight rows of indentations with each row spaced 600 nm apart. AFM force curves (i.e., deflection versus z-piezo position) were collected from each indentation and analyzed as described below. Fig. 1 a shows a representative example of an image of a SF. Superimposed on the image are the locations of the 8 × 6 array of indentations.
FIGURE 1.
(a) Contact-mode AFM deflection images (6 × 6 μm2) of a subregion of a living cell cultured on a petri dish. Asterisks mark the locations of individual indentations in an 8 × 6 array. (B) Pointwise modulus versus indentation depth responses for the regions demarcated in a. The circled responses are those characteristic of and corresponding to the large stress fibers shown in a.
Modulating actomyosin contractile level
Blebbistatin is a selective inhibitor of actomyosin interactions that has a high affinity for myosin II but does not perturb MLC kinase (20,21). Conversely, calyculin A, a serine/threonine phosphatase inhibitor, blocks dephosphorylation of MLC, and therefore elevates the level of phosphorylated MLC, resulting in enhanced contractile level (7,22–24). Hence, we used 10 μM blebbistatin or 2 nM calyculin A to decrease or increase SF contractile levels, respectively. We previously verified that these concentrations changed actin-dependent cellular responses without altering cell morphology (25). For these studies, adherent human aortic endothelial cells were removed from the culture dishes with trypsin (0.05%)/EDTA (0.02%) and transferred into a 60-mm culture dish at a low density (∼800 cells/cm2) and incubated for 24 h. The dish was then placed on the microscope stage under the AFM head. After identifying a suitable SF, we performed an array of indentations, as described above, over a central region of the SF as well as in a nearby cytosolic region devoid of SFs. Then, 1 ml of medium was carefully aspirated and replaced with the same volume of medium containing sufficient drug to achieve the desired final concentration. Using the original coordinates of the indentation array, we then imposed indentations in the same regions of the cell every 15 min for a total of 60 min for blebbistatin-treated cells and every 5 min for a total of 20 min for calyculin-A-treated cells. To serve as time controls, indentations of SFs and cytosol of untreated cells were imposed at 15-min intervals for a total of 60 min.
Assessing linearity
We have previously shown that the stress-strain relationships of passive cardiac muscle are highly nonlinear but become more linear upon activation as contractility is increased (26). Based on this observation, we examined the linearity of the SF stress-strain relationship during actomyosin contractile interactions at the baseline level, as well as those at a decreased contractile level. As discussed earlier, assessing linearity requires measuring stiffness at more than one strain level. Hence, to alter the SF strains, we used a custom-made hydraulic stretching apparatus (Fig. 2) positioned under the AFM head. Briefly, two independent, computer-controlled stepper motors are each connected to a master cylinder that is connected by stiff tubing filled with mineral oil to pistons that move a pair of orthogonally arranged carriages in opposite directions. The four edges of a square, prepunched deformable membrane are attached to corresponding pins on each of the carriages. Activating the stepper motors then produces in-plane biaxial stretch of the membrane. The central 15 × 15-mm2 region of a 40 × 40-mm2 square silicone membrane (Specialty Manufacturing, Saginaw, MI) is coated with 1 ml of a solution of phosphate-buffered saline consisting of 10 μg/ml fibronectin (Chemicon International, Temecula, CA), incubated for 1 h at 37°C, and then washed three times with phosphate-buffered saline. Cells are plated on the membrane at low density (∼800 cells/cm2) and incubated for 24 h at 37°C to allow firm attachment. Anti-fibronectin-coated beads (8 μm in diameter) are seeded sparsely on the membrane and allowed to attach for 3 h. Then the membrane is mounted onto the carriages of the stretching apparatus, which is placed on the stage of the AFM and filled with fresh CO2-independent medium at room temperature for study. We examined cells with at least three beads in their proximity. After imaging the beads, we obtained a 40 × 40-μm2 contact mode image of a region on the cell and then imposed an array of indentations on a single SF, as described above. For this portion of the study, we only examined SFs in the region of the cell midway between the periphery and the nucleus. After obtaining the baseline data, we stretched the membrane incrementally and equibiaxially in three small steps. Note that equibiaxial stretch minimizes translation and rotation of the cellular structures, and the small stretches keep the same cellular region in the field of view. After each stretch, the imaging and indentation procedure was repeated with the indentation array positioned as closely as possible to the same regions of the SF based on neighboring distinct landmarks. For each increment of stretch, the time from completion of imaging to completion of indentation was typically 5–10 min. Another group of cells was prepared and examined in a manner identical to that described above, except that these studies were done with medium containing 10 μM blebbistatin.
FIGURE 2.
Image of the hydraulic cell stretcher showing the stepper motors connected to the driving pistons (upper), which are connected, in turn, to a second set of pistons that move the two orthogonally positioned arms (lower) that stretch the deformable membrane. The latter is positioned under the AFM head during the study, enabling nearly simultaneous stretching and AFM indentation of living cells.
From the images of the beads after each incremental stretch, the displacement relative to the unstretched state is measured to enable calculation of the two-dimensional x- and y-strains of the membrane near the targeted cells using a custom-developed program in MATLAB (The MathWorks, Natick, MA). The local strain along the axis of the SF is then obtained by accounting for its orientation, as measured from the AFM scanning image. Each increment of SF strain was in the range of 2–3%.
Assessing heterogeneity
We compared the stiffness in two regions of the same SF before and after increasing contractile level. First, we obtained a large, e.g., 50 × 50 μm,2 contact mode image of a cell cultured on a plastic petri dish to identify a large, suitable SF. We then selected two small regions on such a SF to examine: a peripheral region within 20 μm of one end and a central region >45 μm from the end. After imposing an 8 × 6 array of indentations in the baseline state, the medium was changed to contain 2 nM calyculin A. Another image of the cell was obtained after 15 min, and using landmarks as a guide, indentations in the same two regions of the SF were imposed.
Data analysis
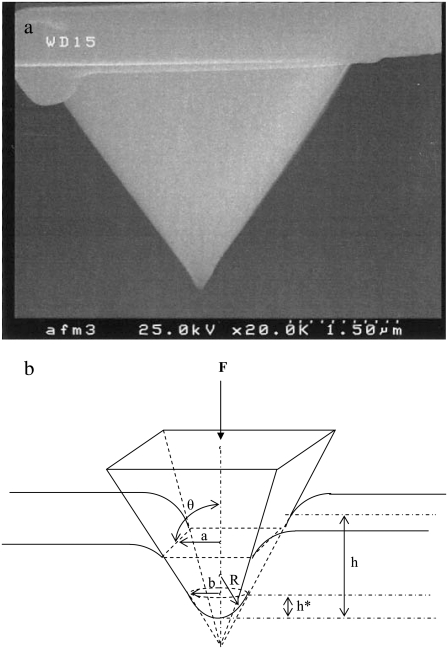
From each AFM deflection curve, the contact point was first identified using our previously developed algorithm (27). Based on that contact point, the deflection curve was converted to a force-indentation curve from which we calculated the apparent point-by-point modulus (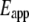 ) as a function of indentation depth (28). The tip of the cantilever we used is not a perfect pyramid, but has a hemispherical cap at its vertex (Fig. 3 a), a model of which is shown in Fig. 3 b. Consequently, depending on the indentation depth, two different formulas were used to calculate
) as a function of indentation depth (28). The tip of the cantilever we used is not a perfect pyramid, but has a hemispherical cap at its vertex (Fig. 3 a), a model of which is shown in Fig. 3 b. Consequently, depending on the indentation depth, two different formulas were used to calculate 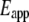 (29). If the indentation depth is only in the spherical region, the modulus is calculated using Eq. 1; otherwise, Eq. 2 is applied to account for the pyramidal shape:
(29). If the indentation depth is only in the spherical region, the modulus is calculated using Eq. 1; otherwise, Eq. 2 is applied to account for the pyramidal shape:
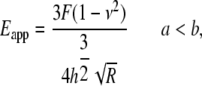 |
(1) |
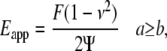 |
(2) |
where 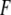 is indentation force, ν is Poisson's ratio, and
is indentation force, ν is Poisson's ratio, and
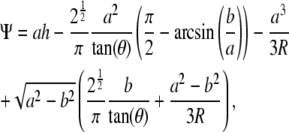 |
(3) |
where 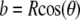 and a is a function of h, which is calculated from
and a is a function of h, which is calculated from
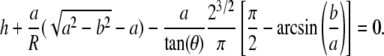 |
(4) |
Performing this calculation for each indentation depth makes it possible to plot the stiffness (modulus) as a function of indentation depth (i.e., a stiffness curve).
FIGURE 3.
Scanning electron micrograph of a typical AFM tip (a) and the corresponding model of a pyramid with an integrated hemispherical tip indenting an elastic half space (b). Within this panel, R is the radius of the spherical cap, a is the half-side length of the square contact area, b is the radius of the hemispherical tip where it merges smoothly into the pyramid, θ is the semiincluded angle of the pyramid, h* is the transition depth, F is the indentation force, and h is the indentation depth.
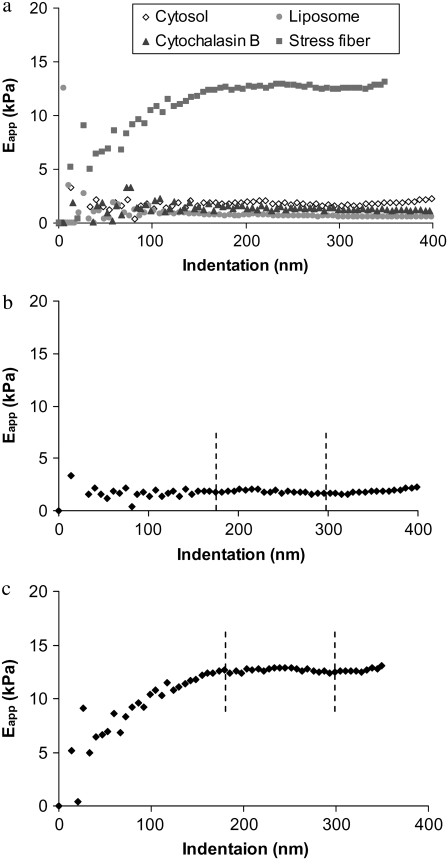
To help guide our data analysis, we performed some preliminary studies. In addition to data from 16 individual indentations on liposomes, we also treated a separate group of cells with 5 μM cytochalasin B for 1 h and obtained measurements from 12 arrays of indentations. In another group of cells, we obtained data from 18 arrays of indentations over SFs, as well as in regions of the cytosol devoid of SFs. The representative results shown in Fig. 4 a demonstrate two distinct types of stiffness curve. For liposomes, cells after cytochalasin treatment, and the cytosolic regions of cells—ignoring the noise in the first 50 nm of indentation, which is due to initial contact between the tip and sample, the stiffness was low and essentially independent of indentation depth. In contrast, for a SF, the stiffness began low and increased with depth until it reached a plateau. For clarity, the responses for cytosol and a SF are shown separately in Fig. 4, b and c. According to our previous numerical simulation study (28), the former response is characteristic of a uniform, linear soft material and the latter response is that of a linear, stiff material underneath a linear, softer material. Therefore, the stiffness of a SF was taken to be the averaged values in the plateau region only (∼180–300 nm), as shown in Fig. 4 c. For consistency, the stiffnesses of liposomes, treated cells, and cytosolic regions were computed similarly over the same range of indentations, as shown in Fig. 4 b.
FIGURE 4.
(a) Example of pointwise elastic modulus versus indentation depth responses obtained from liposomes, cytochalasin-treated cells, stress fiber, and cytosolic regions. (b) Response of a cytosolic region. (c) Response of a stress fiber.
Fig. 1 b illustrates the stiffness curves obtained for the array of indentations shown in Fig. 1 a. As intended, among the responses for each row of indentations, the ones at either end clearly represent those for cytosol. Among the remaining responses, there is one or more that is characteristic of a SF, with others showing mixed responses. Within each row, the largest averaged stiffness for all curves characteristic of SFs (circled response) is deemed to represent the stiffness of the SF at that axial location. Since the variation of the stiffnesses from different rows in the array was very small, we averaged the maximal value from each row to represent the stiffness of this region of the SF. In a similar way, we used the average values for the array of indentations to represent the stiffnesses of the other groups.
For the preliminary studies, the average stiffnesses for the liposomes, cytochalasin-treated cells, and cytosolic regions were 0.6, 1.2, and 2.0 kPa, respectively. The average value for these SFs was 11.3 kPa.
Statistical analysis
Student's t-test was used to compare two groups, and standard analysis of variance methods were used for the comparison of multiple groups. P < 0.05 was inferred as significantly different.
RESULTS
Modulating contractile level
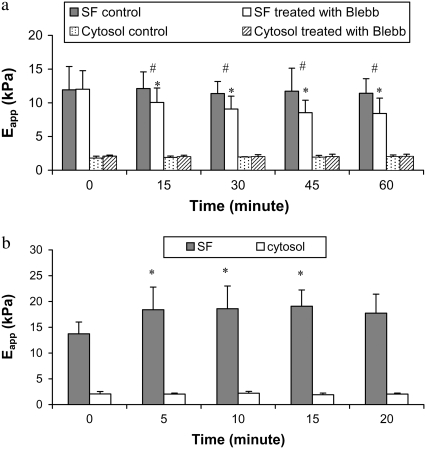
Fig. 5 a shows the time course of the effect of blebbistatin on the stiffnesses of 16 SFs and adjacent cytosolic regions in six cells, as well as SFs and cytosol in untreated cells. In the untreated cells, there was no significant change with time in either SF or cytosolic values. In the treated cells, SF stiffness gradually decreased for the first 30 min and then remained steady for the next 30 min. The 28% decrease in stiffness from the baseline value of ∼12 kPa to the steady-state value of ∼8 kPa at 60 min was highly significant. In contrast, there was no discernible effect on the stiffnesses of cytosolic regions and no difference between cytosolic stiffnesses of treated or untreated cells. Fig. 5 b shows the SF stiffnesses as a function of time after exposure to 2 nM calyculin A for 13 SFs and corresponding cytosol from five cells. SF stiffness progressively increased from a starting value of 13.7 kPa to a peak value of 19.1 kPa (P < 0.05) after 15 min, and then declined gradually afterward. There was no discernible change in the cytosol. These results demonstrate a direct dependence of SF stiffness on contractile level.
FIGURE 5.
(a) Averaged stiffness of stress fibers and cytoplasm as a function of time in untreated cells and cells treated with 10 μM blebbistatin (Blebb). The number symbols (#) denote significant differences between untreated and treated stress fibers. However, there were no differences in stiffness between the untreated and treated cytoplasm. (b) Averaged stiffness of stress fibers and cytosol as a function of time in cells treated with 2 nM calyculin A. Asterisks denote significant differences from the value at time 0. Error bars represent standard deviations.
Assessing linearity
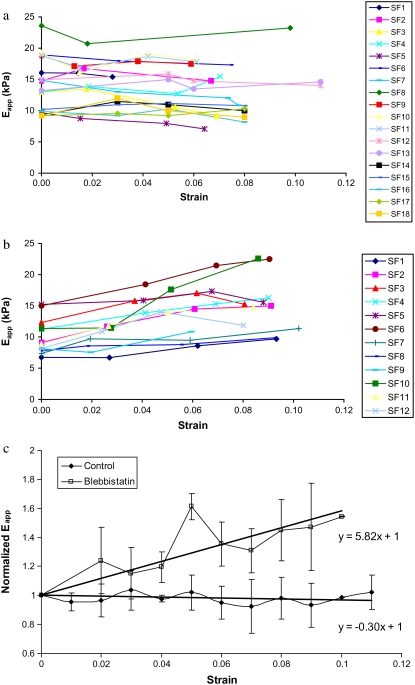
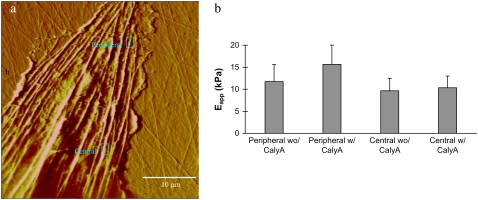
We examined 20 SFs from seven untreated cells and 13 SFs from five blebbistatin-treated cells. Fig. 6 shows representative deflection images of the same cell at four different strain levels. The small rectangles denote the regions on two different SFs where indentations were imposed and demonstrate that our methodology enables us to reliably probe nearly the same region of the same SF as it is being stretched. Fig. 7, a and b, shows the SF stiffness values for each increment of strain for both untreated and treated cells, respectively. The stiffness of the SFs in untreated cells is essentially independent of strain. In contrast, with few exceptions, the stiffness of SFs in the blebbistatin-treated cells increased progressively with increasing strain. The different responses are highlighted by plotting normalized stiffness (with respect to stiffness at zero strain) as well as the linear regressions of stiffness as a function of strain for both untreated and treated cells (Fig. 7 c). A strain-dependent stiffness is indicative of a nonlinear material response. These results demonstrate that the axial stress-strain relationship of SFs in untreated cells is linear and becomes slightly nonlinear when SF contractile level is decreased.
FIGURE 6.
AFM contact-mode deflection images 40 × 40 μm2 of the same region of a representative cell at the four different strain levels noted. The rectangles show the locations of indentations of two stress fibers for each strain increment.
FIGURE 7.
(a and b) Pointwise modulus versus strain in individual stress fibers in untreated cells (a) and cells treated with 10 μM blebbistatin (b). (c) Averaged normalized pointwise modulus versus strain along with linear regressions of the results for untreated and treated cells. Error bars denote standard deviations.
Assessing heterogeneity
Fig. 8 a shows a representative AFM deflection image of several long, thick SFs in a well-spread cell; the rectangles demarcate the peripheral and central regions of the SF where indentations were imposed. Fig. 8 b shows the averaged results of 18 SFs from seven cells. Before treatment with calyculin A, the average peripheral SF stiffness of 11.7 kPa barely differed from the average central stiffness of 9.7 kPa (P = 0.02). After exposure to calyculin A for 15 min, however, the stiffness of the peripheral regions increased significantly (P < 0.001) to 15.7 kPa, whereas stiffness in the central regions remained essentially unchanged at 10.3 kPa. This resulted in a highly significant (P < 0.0001) difference between the peripheral and central regions. These results indicate that the mechanical properties of SFs became much more heterogeneous after actomyosin contractile level was increased.
FIGURE 8.
(a) Representative 50 × 50-μm2 AFM contact mode deflection image of a living cell. The peripheral and central regions of the stress fiber are indicated by the rectangles. (b) Averaged stiffnesses of stress fibers measured from the peripheral and central regions in cells before (wo/) and after (w/) treatment with 2 nM calyculin A (CalyA). Error bars denote standard deviations.
DISCUSSION
Before discussing the implications of our results, there are some issues that deserve attention.
Deflection versus indentation
The thick SFs we examined, whose ends terminate in focal adhesions, are undoubtedly what are called ventral stress fibers located on the lowermost region of the cell closest to the substrate. If they were simply supported only at the focal adhesions and not resting on the substrate or supported by other structures, they could be deflected instead of being indented by the AFM tip. If that were the case, the interpretation of results would be quite different. However, the following theoretical considerations and experimental results provide compelling evidence that SF indentation, and not deflection, is produced by AFM tips.
Simple beam theory predicts a linear relationship between a lateral force applied anywhere along its length and the deflection at that point. Likewise, the lateral deflection of a string supported at its ends due to a force applied anywhere along its length is a linear function of force. In contrast, every study of AFM indentation of biological structures, including ours on SFs (data not shown), shows a nearly quadratic force-indentation response from which the stiffness is estimated. This nonlinear response is dominated by the tapered geometry of the tips indenting the underlying material. As we have discussed in detail in prior publications (17,28), regardless of the method used to analyze the data, the important point is that the response is nonlinear and not linear, as would be the case if one were simply deflecting a simply supported structure. Moreover, for a simply supported string or a beam, the force/deflection ratios (i.e., pseudostiffness) at the center compared to at 3/4 of its overall length should differ by 4/3 and by a factor of nearly 4, respectively. In contrast, our data shows that the stiffness of central and peripheral regions of SFs differ only by ∼20%. Even though the length of the stress fiber is not known, if it were being deflected rather than indented, the stiffnesses in regions separated by >20 μm should differ by much more than a few percent.
There are no theoretical solutions for large indentations with tapered tips, such as those pertaining to AFM studies, so the numerical simulations we reported previously (28), which account for large deformations and conditions very close to those for AFM, are as close to a gold standard for the mechanics of indentation as exists. Our experimental results closely mimic model predictions of the indentation responses expected of SFs. To be specific, linear materials that are homogeneous through the thickness display constant stiffness as a function of indentation depth, whereas materials with a stiffer layer underneath a softer top layer display stiffness-depth responses that gradually rise to a long plateau. Our findings that SFs have essentially linear properties, and that their stiffness-depth responses are indistinguishable from the simulations for a stiff linear material covered by a soft linear material, further support our contention that SFs are being indented rather than deflected.
Our results (Fig. 7) indicate that SF stiffness under control conditions is independent of axial strain. If the stress fibers were supported at their ends and were deflected rather than indented, the ratio of force to deflection, i.e., a “pseudostiffness”, should increase as axial strain is increased. This is clearly not the case. Hence, this is further experimental evidence that the stress fibers are not merely being deflected.
We have shown that completely unloading stress fibers causes them to “buckle” with a wavelength much shorter than the distances between focal adhesions. If the stress fibers were simply supported at their ends, they would buckle with a much, much longer wavelength. The short wavelength, or higher-order buckling is typical of the response of beams that are supported laterally, e.g., by an elastic foundation (25). We also demonstrated that disrupting the microtubule network did not affect the amount of prestretch in the SFs but caused the wavelength to increase significantly. The increased wavelength is consistent with decreasing the stiffness of the surrounding material, since wavelength is inversely proportional to the fourth root of the support material's stiffness. These completely independent experimental observations also suggest that SFs are not simply supported at their ends but rather are supported laterally by microtubules.
Effect of intervening structures
AFM indentation of cells obviously involves perturbing all intervening structures that are above the structure of interest, in this case the ventral SFs. For simplicity, we use the term cytosol, but in reality this includes the plasma membrane and all cytoskeletal constituents, including the actin cortical network and other proteins. It is reasonable to question how the mechanical properties of these structures affect the result. Our preliminary data provide insight into this issue. The stiffness of liposomes is likely the lower limit of a biological material. We show that cytochalasin treatment, which eliminates the contribution of both the cortical actin network and SFs, produces a result that is not too different from that of the cytosol of untreated cells. The difference between these two responses is most likely that of the other structures. Regardless, the important finding is that the value of the stiffness of SFs is severalfold greater than for all of the intervening structures combined.
Methodological issues
Even though we tried to minimize drift of the AFM head by turning on the instrument well before each study, we could not ascertain that drift did not occur during the time of a study, particularly for studies lasting an hour or more. As we described in the Methods section, rather than attempting to measure and correct for drift, which would have added to the study time, the use of an array of indentations coupled with imaging to guide positioning of the array both accommodated for possible drift and provided reasonable assurances that we were probing nearly the same portion of the same SF. This approach, of course, only enables us to discern the difference between axial regions that are much farther apart than the few micrometers covered by the indentation array. Whereas the AFM image is critical in enabling us to precisely locate the region of the cell to be interrogated, acquiring the image adds to the time needed to complete a study and could potentially alter the cell or some of its constituents. The fact that we could repeatedly impose interventions with consistent results, sometimes with intervening additional images, and without apparent damage to the cell or SF, suggests that the imaging did not produce marked changes. Moreover, we could repeatedly indent the same region of a cell for nearly an hour without any discernible change in response (data not shown).
As previously discussed, our pointwise method of data analysis (28) does not require limiting a priori assumptions of the material being linear as does the more commonly used Hertz contact method (30–34). Still, our method does assume infinitesimally small indentations, isotropy, and a planar geometry. Because of the assumption of small deformations, for indentations in thin parts of the cell, such as those examined in this study, there is a reasonable question of the contribution of the substrate. A very important result from our previous study (28) is the counterintuitive observation that for a material with linear stress-strain properties, one can indent at least 50% of the thickness and still be confident that the results match those predicted for large deformations. As our results demonstrated, SFs in control conditions have linear properties, so we are confident that limiting indentations to ∼300 nm obviates confounding effects of the substrate. Fig. 1 demonstrates that for some indentations at depths between 300 and 400 nm, the responses show a marked increase in stiffness. These responses are likely indicative of the tip beginning to sense the stiffer underlying substrate (28) and are the reason we limited analysis to depths of <300 nm.
Whether material anisotropy affects the results depends on relative scale. If the indenter contact area is much smaller than the length scale of the anisotropic structures in question, then what is measured can be considered to be locally isotropic and anisotropy is likely not a confounding factor. In our case, however, the contact area is likely larger than the diameter of the actin filaments comprising the SF. Thus, our methodology does not enable us to assess anisotropic effects of the actin filaments. In a previous publication (3), we demonstrated, however, that combining indentation and separate stretching in each direction could distinguish between the two different in-plane properties of a transversely isotropic rubber material with imbedded nylon fibers. Hence, to evaluate anisotropy due to actin filaments would require indenting while applying stretches in different directions at the molecular or individual filament level. This much more complicated experimental approach is, however, beyond the scope of the work presented here.
The SF is undoubtedly a more or less cylindrical structure and not a plane, as is assumed by our data analysis method, as well as all those presented previously. For SFs that are nominally ∼500–1000 nm in diameter, small indentations (<100 nm) can approximate planar conditions reasonably well, but indentations of 300 nm are not sufficiently small to ignore curvature effects. Since our indentations span this range, our results must be interpreted with this limitation of a planar approximation in mind. Nevertheless, the finding that at least one of the indentation responses demonstrates a plateau between ∼150 and 300 nm (Figs. 1 and 4) suggests that curvature effects are not sufficiently large to produce results substantially different from those assuming a planar geometry. In fact, some of the mixed responses observed (see Fig. 1) as the probe is moved across the SF may be due to such curvature effects.
The SF is undoubtedly viscoelastic. However, the stiffness for a given location varied by <4% over the frequency range of 0.25–4 Hz (data not shown). Hence, we indented at 1 Hz to minimize viscous effects and to enable the entire set of indentations and images to be obtained in <10 min.
Identifying the initial point of contact between the AMF tip and the target is a challenge. We recently developed a semiautomatic approach to address this issue (27). Doing so is critical, since indentation depth is inferred from an estimate of the contact point—which can be obscured by noise in the signal. Numerical simulations of nonlinear and linear materials with a range of stiffness demonstrated the consequences of misidentifying the contact point and the robustness of the algorithm to identify the contact point. We have adopted this scheme to analyze all our indentation data.
Our results are, to our knowledge, the first detailed studies about mechanical property changes in the same SF in intact cells before and after different types of intervention. The three major findings are: 1), decreasing or increasing contractile level decreases or increases, respectively, SF stiffness; 2), SFs have a nearly linear stress-strain relationship in the baseline state, whereas they exhibit slightly nonlinear properties when the contractile level is decreased; 3), in the baseline state, stiffness is nearly the same in the peripheral versus the central regions of the same SF, but becomes heterogeneous after the contractile level is increased.
It is useful to compare our findings with those of previous reports. Because we do not know the value of the Poisson's ratio for SFs (which could range from 0.1 to 0.5), there is some uncertainty as to the actual value of the stiffness modulus, since the apparent modulus we report differs from the true modulus by the factor (1 − ν2). Within this uncertainty range, given the unreliability of the Hertzian contact method of data analysis used in those studies, and since some of the authors report averaged cell stiffness rather than single SF stiffness, our stiffness values, which range from 10 to 15 kPa for stress fibers and are ∼3 kPa for cytosol, are reasonably close to the Young's moduli values of ∼5 kPa estimated for single SFs in fibroblasts (16), regions of fibroblast values ranging from 3 to 24 kPa (10), and endothelial cell values from 1.4 to 6.8 kPa (35). The two- to threefold decrease in stiffness after cytochalasin B treatment, and the lack of change after colchicine or taxol treatment (to disrupt or overpolymerize, respectively, microtubules) (16), are also consistent with our findings. A shift in regional fibroblast stiffness distributions from a median of ∼5 kPa to one of ∼10 kPa after a uniaxial 8% stretch differs from our finding of no effect of stretch, although the difference between methodologies and cell types makes comparison difficult. In contrast, however, there are reports of much higher values of SF stiffness. One study directly measured the force-extension response of isolated smooth muscle cell SFs and, based on an assumed radius of 100 nm, estimated a modulus of 1.4 MPa (15). The authors admitted, however, that it was difficult to accurately measure the diameter of the fibers and indicated that if the true radius was 250 nm, the modulus would only be ∼230 kPa. Even though this value is still more than an order of magnitude larger than our estimates, the distinctly different experimental conditions and cell types make direct comparisons difficult to interpret.
Since SFs are formed as the result of actomyosin interactions, their stiffnesses should be sensitive to the level of contractile level. The results shown in Fig. 5 confirm that single SF stiffness is sensitive to both increases and decreases in contractile level, and that AFM indentation can be used to quantify these effects. Although not surprising, to our knowledge, these results are the first to document this important aspect of single-SF mechanics in living cells. A previous study (12) reported consonant findings in smooth muscle cells consisting of an increase in cell stiffness with a contractile agonist (histamine) and a decrease in stiffness with a relaxing agonist (isoproterenol). However, because a different methodology was used, i.e., twisting magnetic cytometry that perturbed a region of a cell rather than a single SF, it is difficult to quantitatively compare our results with those of Wang et al.
As discussed above, key to both understanding mechanics and gaining confidence in AFM indentation results in thin materials such as regions of cells is whether the material used has linear stress-strain properties. As shown by our previous model predictions, the increase from low values to a plateau of the stiffness-depth response (Figs. 1 b and 4 c) is characteristic of a composite linear material. This is only indirect evidence of linearity, however. Our results are the first that we know of that directly assess the linearity of stress-strain relationships in living cells by combining stretching and indentation of the same SFs. The observation that the mechanical response is linear at normal contractile levels and becomes more nonlinear when contractile level is decreased is consistent with findings in muscles (26). Even though SFs are different than muscle, they likely use the same general actomyosin mechanism. That is, the nonlinear behavior could be due to structures other than the contractile apparatus. As an alternative, the nonlinear stress-strain behavior of individual actin filaments at low strain levels (14) could explain the nonlinear behavior of SFs. In contrast, as with muscular tissues, linear behavior likely represents the dominant effect of the actin-myosin contractile apparatus. These findings contribute new insight into cell mechanics, since they demonstrate that the material properties ascribable to SFs depend, to some extent, on their contractile level. These properties need to be accounted for in models of cell cytoskeletons that attempt, for example, to deduce levels of stress within cells. Moreover, as discussed below, the contractile-level-dependent shift from nonlinear to linear material properties could help explain how SFs can have heterogeneous properties along their length.
Our results demonstrate that increasing contractile levels above the baseline state results in heterogeneity of stiffness along a stress fiber, with the peripheral region being stiffer than the central region. This confirms indirect suggestions based purely on the spacing of α-actinin and MLC (7). Since the total force at any axial position must be the same for a SF to be in mechanical equilibrium, there are two possible scenarios that could explain the heterogeneity. One is that there is heterogeneity of SF cross-sectional area but essentially equal contractile levels in the peripheral versus the central region. However, this is rather unlikely, since if there were sufficient differences in cross-sectional area in the two regions, there should also have been different stiffnesses at the baseline state. As an alternative, there could be different cross-sectional areas in the two regions induced by increasing contractile levels, but it is difficult to envision how this might occur. The second, and more likely, possibility is that there is a higher contractile level near the periphery than at the center, with essentially the same cross-sectional areas. In fact, this possibility is consistent with previous observations of increased drug-induced MLC phosphorylation in the peripheral compared to the central region (7).
Assuming that the second of these scenarios is the correct one, it is reasonable to ask how a SF can have the same cross-sectional area and different contractile levels along its length. A possible explanation is related to our findings of both contractile-level-dependent stiffness and a degree of nonlinearity. Suppose that the center portion of a SF, because it has a lower contractile level, is more nonlinear than the periphery. The stress-strain relationship of the periphery is, however, shifted above and to the left of that of the central region. For equilibrium, the stresses in both regions of the SF must be the same. However, because the equilibrium strains associated with these stresses, as well as the stress-strain relationships, are different there is a higher stiffness in the periphery associated with a lower strain.
CONCLUSION
In summary, by combining insights from our previous analysis of AFM indentation with more detailed experimental measurements, we report new results about the mechanical properties of SFs in living cells. We demonstrate that 1), SF stiffness is dependent on the actomyosin contractile level; 2), decreasing contractile level below baseline values causes SF properties to become more nonlinear; and 3), increasing contractile level causes SF properties to become more heterogeneous. Taken together, these results demonstrate the important role of actomyosin contractile level in determining SF mechanical properties in living cells.
Acknowledgments
The authors express appreciation to Kevin Costa, who performed the studies and provided the data about indentation of liposomes.
Editor: Richard E. Waugh.
References
- 1.Humphrey, J. D., H. R. Halperin, and F. C. P. Yin. 1991. Small indentation superimposed on a finite equibiaxial stretch: implications for cardiac mechanics. J. Appl. Mech. 59:1108–1111. [Google Scholar]
- 2.Lanir, Y. 1979. Biaxial stress-strain relationship in the skin. Isr. J. Technol. 17:78–85. [Google Scholar]
- 3.Karduna, A., H. R. Halperin, and F. C. P. Yin. 1997. Experimental and numerical analyses of indentation in finite-sized isotropic and anisotropic rubber-like materials. Ann. Biomed. Eng. 25:1009–1016. [PubMed] [Google Scholar]
- 4.Fung, Y. C. 1967. Elasticity of soft tissues in simple elongation. Am. J. Physiol. 213:1532–1544. [DOI] [PubMed] [Google Scholar]
- 5.Lanir, Y., and Y. C. Fung. 1974. Two-dimensional mechanical properties of rabbit skin II. Experimental results. J. Biomech. 7:171–182. [DOI] [PubMed] [Google Scholar]
- 6.Yin, F. C. P., and Y. C. Fung. 1971. Mechanical properties of isolated mammalian ureteral segments. Am. J. Physiol. 221:1484–1493. [DOI] [PubMed] [Google Scholar]
- 7.Peterson, L., Z. Rajfur, A. S. Maddox, C. D. Freel, Y. Chen, M. Edlund, C. Otey, and K. Burridge. 2005. Simultaneous stretching and contraction of stress fibers in vivo. Mol. Biol. Cell. 15:3497–3508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dembo, M., and Y. L. Wang. 1999. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 76:2307–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fernandez, P., P. A. Pullarkat, and A. Ott. 2006. A master relation defines the nonlinear viscoelasticity of single fibroblasts. Biophys. J. 90:3796–3805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mizutani, T., H. Haga, and K. Kawabata. 2004. Cellular stiffness response to external deformation: tensional homeostasis in a single fibroblast. Cell Motil. Cytoskel. 59:242–248. [DOI] [PubMed] [Google Scholar]
- 11.Wang, N., and D. E. Ingber. 1995. Probing transmembrane mechanical coupling and cytomechanics using magnetic twisting cytometry. Biochem. Cell Biol. 73:327–335. [DOI] [PubMed] [Google Scholar]
- 12.Wang, N., I. M. Tolic-Norrelykke, J. Chen, S. M. Mijailovich, J. P. Butler, J. J. Fredberg, and D. Stamenovic. 2002. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. Am. J. Physiol. Cell Physiol. 282:C606–C616. [DOI] [PubMed] [Google Scholar]
- 13.Kojima, H., A. Ishijima, and T. Yanagida. 1994. Direct measurement of stiffness of single actin filaments with and without tropomyosin by in vitro nanomanipulation. Proc. Natl. Acad. Sci. USA. 91:12962–12966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu, X., and G. H. Pollack. 2002. Mechanics of F-actin characterized with microfabricated cantilevers. Biophys. J. 83:2705–2715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Deguchi, S., T. Ohashi, and M. Sato. 2006. Tensile properties of single stress fibers isolated from cultured vascular smooth muscle cells. J. Biomech. 39:2603–2610. [DOI] [PubMed] [Google Scholar]
- 16.Rotsch, C., and M. Radmacher. 2000. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: an atomic force microscopy study. Biophys. J. 78:520–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Costa, K. D., A. J. Sim, and F. C. P. Yin. 2006. Non-Hertzian mechanics of endothelial cells probed by atomic force microscopy. ASME J. Biomech. Eng. 128:176–184. [DOI] [PubMed] [Google Scholar]
- 18.Deamer, D., and A. D. Bangham. 1976. Large volume liposomes by an ether vaporization method. Biochim. Biophys. Acta. 443:629–634. [DOI] [PubMed] [Google Scholar]
- 19.Papahadjopoulos, D., and J. C. Watkins. 1967. Phospholipid model membranes. II. Permeability properties of hydrated liquid crystals. Biochim. Biophys. Acta. 135:639–652. [DOI] [PubMed] [Google Scholar]
- 20.Limouze, J., A. Straight, T. Mitchison, and J. Sellers. 2004. Specificity of blebbistatin, an inhibitor of myosin II. J. Muscle Res. Cell Motil. 25:337–341. [DOI] [PubMed] [Google Scholar]
- 21.Straight, A. F., A. Cheung, J. Limouze, I. Chen, N. J. Westwood, J. R. Sellers, and T. J. Mitchison. 2003. Dissecting temporal and spatial control of cytokinesis with a myosin II inhibitor. Science. 299:1743–1747. [DOI] [PubMed] [Google Scholar]
- 22.Chartier, L., L. L. Rankin, R. E. Allen, Y. Kato, N. Fusetani, H. Karaki, S. Watabe, and D. J. Hartshorne. 1991. Calyculin-A increases the level of protein phosphorylation and changes the shape of 3T3 fibroblasts. Cell Motil. Cytoskeleton. 18:26–40. [DOI] [PubMed] [Google Scholar]
- 23.Henson, J. H., S. E. Kolnik, C. A. Fried, R. Nazarian, J. McGreevy, K. L. Schulberg, M. Detweiler, and V. A. Trabosh. 2003. Actin-based centripetal flow: phosphatase inhibition by calyculin-A alters flow pattern, actin organization, and actomyosin distribution. Cell Motil. Cytoskeleton. 56:252–266. [DOI] [PubMed] [Google Scholar]
- 24.Leopoldt, D., H. F. Yee Jr., and E. Rozengurt. 2001. Calyculin-A induces focal adhesion assembly and tyrosine phosphorylation of p125(Fak), p130(Cas), and paxillin in Swiss 3T3 cells. J. Cell. Physiol. 188:106–119. [DOI] [PubMed] [Google Scholar]
- 25.Lu, L., Y. Feng, W. J. Hucker, S. J. Oswald, G. D. Longmore, and F. C. Yin. 2008. Actin stress fiber pre-extension in human aortic endothelial cells. Cell Motil. Cytoskel. 65:281–294. [DOI] [PubMed] [Google Scholar]
- 26.Lin, D. H. S., and F. C. P. Yin. 1998. A multiaxial constitutive law for actively contracting mammalian left ventricular myocardium. ASME J. Biomech. Eng. 120:504–517. [DOI] [PubMed] [Google Scholar]
- 27.Crick, S. L., and F. C. Yin. 2007. Assessing micromechanical properties of cells with atomic force microscopy: importance of the contact point. Biomech. Model. Mechanobiol. 6:199–210. [DOI] [PubMed] [Google Scholar]
- 28.Costa, K., and F. C. P. Yin. 1999. Analysis of indentation: implication for measuring mechanical properties with atomic force microscopy. J. Biomech. Eng. 121:462–471. [DOI] [PubMed] [Google Scholar]
- 29.Rico, F., P. Roca-Cusachs, N. Gavara, R. Farre, M. Rotger, and D. Navajas. 2005. Probing mechanical properties of living cells by atomic force microscopy with blunted pyramidal cantilever tips. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72:021914. [DOI] [PubMed] [Google Scholar]
- 30.Radmacher, M., M. Fritz, C. M. Kacher, J. P. Cleveland, and P. K. Hansma. 1996. Measuring the viscoelastic properties of human platelets with the atomic force microscope. Biophys. J. 70:556–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Radmacher, M. 1997. Measuring the elastic properties of biological samples with the AFM. IEEE Eng. Med. Biol. 16:47–57. [DOI] [PubMed] [Google Scholar]
- 32.Sato, M., K. Nagayama, N. Kataoka, M. Sasaki, and K. Hane. 2000. Local mechanical properties measured by atomic force microscopy for cultured bovine endothelial cells exposed to shear stress. J. Biomech. 33:127–135. [DOI] [PubMed] [Google Scholar]
- 33.Shroff, S. G., D. R. Saner, and R. Lal. 1995. Dynamic micromechanical properties of cultured rat atrial myocytes measured by atomic force microscopy. Am. J. Physiol. 269:C286–C292. [DOI] [PubMed] [Google Scholar]
- 34.Wu, H. W., T. Kuhn, and V. T. Moy. 1998. Mechanical properties of L929 cells measured by atomic force microscopy: effects of anticytoskeletal drugs and membrane crosslinking. Scanning. 20:389–397. [DOI] [PubMed] [Google Scholar]
- 35.Mathur, A. B., A. M. Collinsworth, W. M. Reichert, W. E. Kraus, and G. A. Truskey. 2001. Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J. Biomech. 34:1545–1553. [DOI] [PubMed] [Google Scholar]