Characterizing Aqueous Solution Conformations of a Peptide Backbone Using Raman Optical Activity Computations

Abstract

Mounting spectroscopic evidence indicates that alanine predominantly adopts extended polyproline II (PPII) conformations in short polypeptides. Here we analyze Raman optical activity (ROA) spectra of N-acetylalanine-N′-methylamide (Ala dipeptide) in H₂O and D₂O using density functional theory on Monte Carlo (MC) sampled geometries to examine the propensity of Ala dipeptide to adopt compact right-handed (α_R) and left-handed (α_L) helical conformations. The computed ROA spectra based on MC-sampled α_R and PPII peptide conformations contain all the key spectral features found in the measured spectra. However, there is no significant similarity between the measured and computed ROA spectra based on the α_L- and β-conformations sampled by the MC methods. This analysis suggests that Ala dipeptide populates the α_R and PPII conformations but no substantial population of α_L- or β-structures, despite sampling α_L- and β-structures in our MC simulations. Thus, ROA spectra combined with the theoretical analysis allow us to determine the dominant populated structures. Including explicit solute-solvent interactions in the theoretical analysis is essential for the success of this approach.

INTRODUCTION

Conformational analysis of alanine-containing polypeptides suggests that the polyproline II (PPII) is the major backbone conformation in aqueous solution. For example, Kallenbach and co-workers recently showed that alanine-containing peptides possess over 90% extended conformations (i.e., PPII and β-structures) (1). The authors, however, did not rule out the possibility of the presence of compact (α_R, α_L) conformations of alanine in aqueous solution and suggested that such compact structures are present, albeit not dominant. Here, we use Raman optical activity (ROA) to examine the propensity of Ala dipeptide, which contains a peptide backbone with a single alanine, to adopt compact structures like the right-handed (α_R) and left-handed (α_L) helical conformations in aqueous solution. We find that Ala dipeptide adopts both the extended PPII and compact α_R-conformations, which are the dominant conformations in aqueous solution.

Experimental and theoretical studies of polypeptides (2) suggest that short polypeptides can adopt secondary structures in aqueous solution. For example, the hepta-alanine polypeptide Ac-X₂A₇O₂-NH₂ (XAO; X and O denote diaminobutyric acid and ornithine, respectively) in aqueous solution was suggested to be an ensemble of β-turn, β-strand, and PPII conformations (3–5). A combination of Fourier transform infrared, vibrational circular dichroism, electronic circular dichroism, Raman, and NMR spectroscopic studies probed shorter alanine-based cationic peptides (e.g., trialanine, tetraalanine, and H-AAKA-OH). These studies indicated that these shorter peptides have a higher fraction of PPII than β-strand or α_R-conformations (6). ROA studies of a series of A₂-A₅ peptides suggest that the PPII population increases with the number of alanines (7). Taken together, these results provide compelling evidence that alanine-containing peptides in water populates PPII conformations. Molecular dynamics (MD) simulations of alanine-containing peptides in water indicate the sampling of α_R-motifs, in addition to the PPII and β-conformations (8).

Graf's combined MD and NMR studies, however, show that there is no detectable population of the α_R-conformation in aqueous solutions of A₃-A₇ peptides and that these short polyalanine peptides in water populate the PPII conformation almost exclusively (9). Following Graf's conformational analysis of A₃-A₇ peptides, Hummer and co-workers studied polyalanine peptide (A₅) conformations in aqueous solution using MD simulations to address the question of whether the commonly used force fields overpopulate the α-helical conformations of polyalanine peptides (10). They concluded that the NMR data are consistent with force fields that give a small α-helical population of polyalanine peptide and do not require exclusive formation of the PPII structure. Our combined Monte Carlo (MC) and ROA studies of Ala dipeptide show that the shortest alanine-containing peptide exists as a mixture of PPII and α_R-conformations in aqueous solution.

Chiroptical properties are sensitive to molecular geometry and to solvation (11–13). ROA is a chiroptical spectroscopy that measures the difference in the intensity of Raman scattered right- and left-circularly polarized light and is utilized to characterize aqueous solution conformations of the peptide backbone in polypeptides and proteins (14,15). ROA studies of polypeptides suggest that water promotes structural fluctuations between α_R-, PPII, and β-conformations (16). The ROA spectrum is the superposition of spectra arising from all conformations of polypeptides in solution (14), and thus, ROA analysis can be used to characterize solution conformations of peptide units in polypeptides.

The theoretical framework for ROA is well known (17–19). Accurate time-dependent density functional theory (TD-DFT) calculations of ROA are accessible using the resolution of identity approximation (RI-J) (20–22) and the Becke-Lee-Yang-Parr (BLYP) functional with the depolarized right-angle scattering (rDPS) basis set (23). ROA spectra are predicted to be very sensitive to both molecular conformation (24–28) and solvation, which were studied previously using continuum solvent models (29). Herrmann et al. (30) and Pecul et al. (29) analyzed ROA spectra of polypeptides using a single conformation in the gas phase and in an implicit solvent, respectively. Since ROA studies of polypeptides indicate that water facilitates conformational fluctuations (16), modeling polypeptide conformations in explicit solvent, and subsequently utilizing modeled structures to compute ROA spectra, may improve the effectiveness of ROA simulations for polypeptides.

Despite extensive experimental and theoretical study, there is no consensus on Ala dipeptide's structure in aqueous solution. NMR studies are consistent with both 1), an equal population of PPII and α_R-conformations (31,32), and 2), a dominant PPII conformation (33,34). The later composition is supported by two-dimensional (2D) infrared (IR) spectroscopy (35). However, Raman spectroscopy suggests that C7_eq, PPII, and α_R-conformations all exist in aqueous solution (36). MC and MD simulations of Ala dipeptide indicate either 1), PPII (8,37,38) or α_R-structures dominate (39–42), or 2), a comparable population of PPII and α_R-structures dominates (43–45), depending on the force field used. Thus, a debate remains as to whether PPII is the dominant conformation of Ala dipeptide in aqueous solution. The significant variation in the description of Ala dipeptide conformations warrants further analysis and suggests the utility of linking chiroptical simulations with experimental studies. Our ROA simulations combined with experimental data show that Ala dipeptide populates both the α_R and PPII conformations in aqueous solution; and hence, it is erroneous to ascribe all experimental signal to one dominant conformation, namely the PPII.

We present TD-DFT calculations of backscattered circular polarization (SCP) ROA based on MC simulation of Ala dipeptide in aqueous solution. Simulated Raman and ROA spectra constructed using the collection of H₂O-Ala clusters (see Methods for more details) with α_R and PPII conformations of Ala dipeptide are consistent with experiments. However, there is no significant similarity between the measured and computed Raman or ROA spectra for the set of H₂O-Ala clusters with α_L- and β-conformations of Ala dipeptide. Thus, these calculations facilitate assignment of the observed ROA spectral features to corresponding secondary structures that characterize the populated conformations of the peptide in aqueous solution. The interpretation of the experimental data enabled by the calculations helps in understanding the relationship between peptide conformations and ROA spectra. Our calculations also provide substantial predictive value. For example, our calculations demonstrate that ROA can distinguish between left- and right-handed helical conformations of peptides in aqueous solution; and hence, ROA can be used to differentiate the chirality associated with the handedness of helical conformations of peptides.

Previous ROA analysis using four Ala dipeptide conformations (β, α_R, α_L, PPII), each hydrogen bonded to four water molecules and embedded in an implicit solvent model, showed that the computed spectra of the PPII structure best explained the experimental ROA spectrum (46). It was also suggested that α_R, α_L, and “other conformations” of Ala dipeptide may be present in aqueous solution (46). Those ROA calculations were performed using restricted Hartree-Fock theory with a split valence plus basis set and neglected the effects of explicit water on the chiroptical response tensor (46). Pecul et al. showed recently that solvent influences on the chiroptical response tensor should be included when computing solvent effects on ROA (29). Jalkanen et al. recently computed the ROA spectra of a single (H₂O)₄-Ala dipeptide cluster, with the PPII conformation of the dipeptide, embedded in implicit solvent models using the B3PW91/B3LYP exchange correlation functionals with the aug-cc-pVDZ basis set (47). Those simulated ROA spectra (46–48) were in qualitative agreement with the experimental spectra, which provided the impetus for computing the ROA spectrum with improved accuracy for aqueous Ala dipeptide solutions using geometry sampling as an explicit part of the calculation. We now show that including explicit solute-solvent interactions is essential for computing the ROA of Ala dipeptide accurately in water and that TD-DFT computation (with the RI-J approximation and rDPS basis set) using MC-sampled geometries in aqueous solution provides a suitable means to analyze the ROA spectra of polypeptides and determine the dominant populated conformations of polypeptides in solution.

METHODS

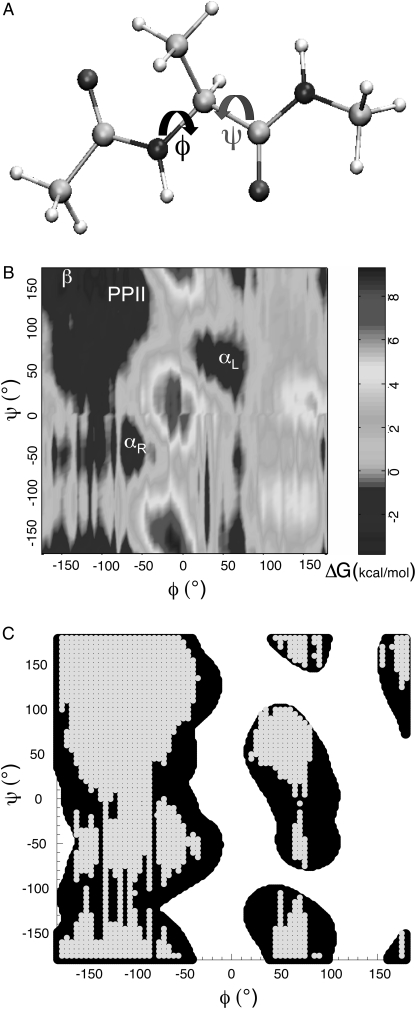
Two sets of MC computer simulations of Ala dipeptide in H₂O were performed using the optimized potential for liquid simulations-all atom (OPLS-AA) force field (49) and TIP4P water model (50). First, low-energy conformations of Ala dipeptide in H₂O were identified that characterize potentially populated regions of the Ramachandran map using MC free-energy simulations. Second, H₂O configurations were sampled with fixed backbone dihedral angles (φ and ψ; Fig. 1 A) for the dipeptide. The fixed peptide geometries were selected from low-energy regions of the Ramachandran map (Fig 1B). H₂O-Ala dipeptide cluster structures from the second set of MC simulations (sampling water configuration with fixed-peptide geometry) were optimized using DFT. Each H₂O-Ala dipeptide cluster has 10 water molecules within a cutoff distance of 0.5 nm from the hydrogen-bond donor (NH) and acceptor (O, N) atoms of Ala dipeptide (Fig. 1 A). Following geometry optimization of the H₂O-Ala dipeptide cluster, the structures were used to compute the backscattering ROA and Raman spectra using TD-DFT with the RI-J approximation, the BLYP functional, and the rDPS basis set.

FIGURE 1.

(A) Ball and stick model for the N-acetylalanine-N′-methylamide (Ala dipeptide). The peptide backbone structure in Ala dipeptide is defined by φ- and ψ-dihedral angles. (B) Free energy differences of Ala dipeptide conformations in water computed using MC simulations. α_R, α_L, β, and PPII conformational regions are shown on the Ramachandran map. (C) the computed φ- and ψ-distribution (gray) resembles the empirically derived φ, ψ distribution of amino acid residues (black) in neither canonical helix nor sheet secondary structures in protein x-ray crystal structures (61).

MC simulations

Free energy perturbation theory (51) was used to calculate the potential of mean force (PMF) that describes the relative free energy difference between Ala dipeptide conformations as a function of the peptide backbone dihedral angles. One-dimensional PMFs were calculated first with φ fixed and ψ varied from 0° to 360° in 5° increments. Then ψ was fixed and φ was varied from 0° to 360° in 5° increments. A 2D plot of the free energy difference for φ = 80°, ψ = 80°, the reference conformation, and all φ, ψ pairs were calculated from the one-dimensional PMFs. The resulting 2D plots identify low-energy conformations of Ala dipeptide in water.

MC simulations of Ala dipeptide in a box of 500 water molecules were performed using BOSS (51) at 25°C and 1 atm (NPT ensemble) with periodic boundary conditions. Long-range electrostatic interactions were evaluated by the Ewald method (52). The OPLS-AA force field, TIP4P water, and AM1 (53) based CM1A (54) partial atomic charges for the solute and solvent were used in the MC simulations. A more detailed description of the MC move and the atomic charge-partitioning scheme appears in Jorgensen and Tirado-Rives. (51).

DFT calculations of ROA

Zuber et al. recently demonstrated accurate and efficient prediction of ROA spectra using TD-DFT (22). The approach avoids calculating the four-center Coulomb integrals and omits contributions of the electric dipole-electric quadrupole polarizability tensor to the ROA differential scattering cross section. Luber et al. also showed recently that the contribution of the electric dipole-electric quadrupole polarizability tensor to the ROA intensities can be neglected for the amide I, amide II, and amide III vibrational modes for peptides (below 2000 cm⁻¹) (55). We use the same scheme in the off-resonance approximation (56) to calculate the circular difference differential scattering cross sections per unit solid angle 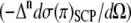for (57) SCP with naturally polarized (n) incident light:

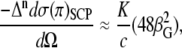(1)

where c is the speed of light, 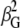is the anisotropic ROA invariant, and K is

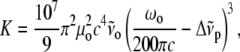(2)

where 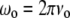is the frequency of the incident light, 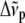is the Raman frequency shift (in cm⁻¹), c is the speed of light (in ms⁻¹), and 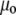is the permittivity of vacuum.

Placzek polarizability theory writes (58)

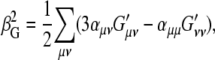(3)

where 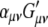is

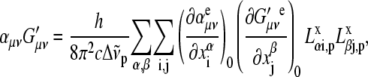(4)

where 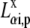is the ith component of the Cartesian displacement vector of nucleus α for normal mode p, and and 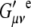are the elements of the electric dipole-electric dipole polarizability tensor and the imaginary part of the electric dipole-magnetic dipole polarizability tensor, respectively. The index 0 indicates that the derivatives of the electronic tensors are computed at the equilibrium nuclear geometry.

The geometries of H₂O-Ala dipeptide clusters from the second set of MC simulations were optimized using DFT implemented in TURBOMOLE (version 5.6) (59) with the BLYP correlation-exchange functional and the SVP basis set. The normal coordinates of the H₂O-Ala dipeptide clusters were computed from the molecular Hessian, which was determined for the optimized geometry. Optimizations of some of the H₂O-Ala dipeptide cluster structures lead to imaginary frequencies; and hence, such structures were not included in the ROA calculations. A 532 nm incident laser wavelength was used for tensor calculations, which were performed using TD-DFT with the BLYP functional, the rDPS basis set, and the [7s3p3d1f]/[3s2p1d] auxiliary basis set (60). All the calculations were performed in a gauge-independent dipole-velocity formulation using the RI-J. The Cartesian gradients of the polarizability tensors were evaluated numerically using the 6N-displaced geometries, where N is the number of atoms. The 6N geometries were obtained from the optimized geometries of the H₂O-Ala dipeptide clusters using a displacement of ±10⁻³ atomic units along the Cartesian coordinates.

The molecular Hessian of the optimized geometry of H₂O-Ala dipeptide clusters were used to compute the vibrational frequencies and normal coordinates of D₂O-Ala dipeptide structures. Thus, we used the H₂O-Ala dipeptide structures from the MC simulations to compute the ROA and Raman spectra of D₂O-Ala dipeptide clusters. The ROA and Raman spectra of the D₂O-Ala dipeptide clusters were then computed using Eq. 4.

The total Raman 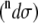and ROA 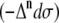scattering cross sections of a Ala dipeptide-water cluster is the sum of scattering cross sections of the peptide 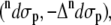water 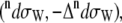and peptide-water interactions 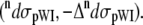Hence, the total Raman and ROA scattering cross sections is

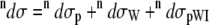(5)

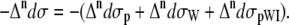(6)

Thus, the relative contributions of the Raman and ROA scattering cross sections of the dipeptide, water, and peptide-water interactions can be compared to the total ROA and Raman scattering cross sections of the Ala dipeptide-water cluster.

RESULTS

Low-energy conformations of Ala dipeptide in water

Fig. 1 shows the difference in free energy (ΔG) of Ala dipeptide conformations in water computed using MC simulations. The α_R, α_L, β, and PPII conformational regions are populated by the dipeptide (Fig. 1 B), in agreement with previous molecular mechanics force field simulations (38,43). Fig. 1 C shows that the computed distribution of φ- and ψ-dihedral angles (for Ala dipeptide conformations with ΔG < 0) also resembles the φ, ψ distribution of amino acid residues that are not found in either canonical helix or sheet secondary structures in protein x-ray crystal structures (61). Ala dipeptide explores both the right-handed (α_R) and left-handed (α_L) helical conformations, in agreement with previous MD and MC simulation studies (37,38,43). Thus, our MC simulations of aqueous Ala dipeptide indicate that the α-helical conformations are stabilized by solvation.

Structures of H₂O-Ala dipeptide clusters

H₂O-Ala dipeptide clusters from the MC simulations, corresponding to the low-energy regions (α_R, α_L, β, and PPII; Fig. 1 B) of the Ramachandran map, were optimized using quantum mechanical energy minimization (see Methods for details). The peptide backbone dihedral angles change upon geometry optimization. However, each peptide conformation, before and after geometry optimization, occupies the same region of the Ramachandran map (Supplementary Material, Fig. S1). Following geometry optimization of the H₂O-Ala dipeptide cluster, the structures were used for computing ROA and Raman spectra using TD-DFT (see Methods for details).

ROA and Raman spectra of H₂O- and D₂O-Ala dipeptide clusters

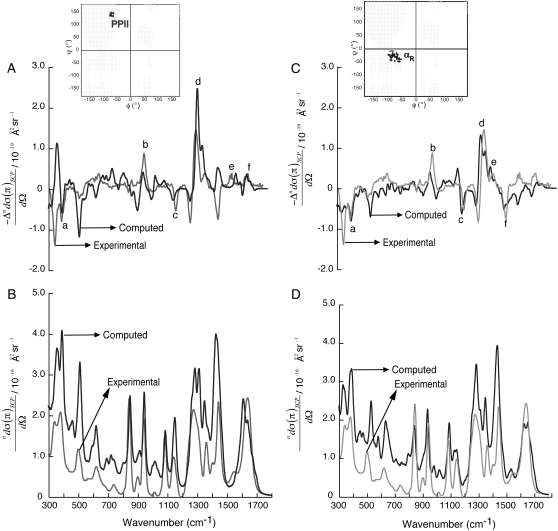
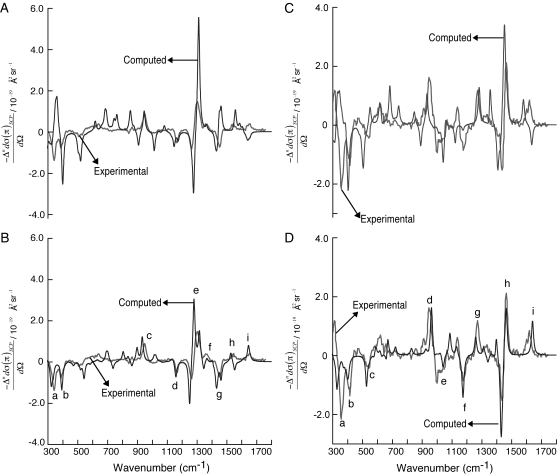
Fig. 2 shows the computed ROA (A and C) and the Raman (B and D) spectra using H₂O-Ala dipeptide clusters. The computed spectra are averaged over 30 H₂O-Ala dipeptide structures with φ- and ψ-dihedral angles from the PPII (inset in Fig. 2 A) and α_R (inset in Fig. 2 C) conformational regions of the Ramachandran map. The ROA spectra computed using both the PPII and α_R-conformations contain spectral features found in the measured spectrum. For example, ROA bands (a–f in Fig. 2 A) at 395 cm⁻¹ (a), 940 cm⁻¹ (b), 1140 cm⁻¹ (c), 1560 cm⁻¹ (e, amide II), 1665 cm⁻¹ (f, amide I), and the couplet centered at ∼1300 cm⁻¹ (d, extended amide III) are predicted in the computed spectrum using a set of Ala dipeptide conformations with −80° ≤ φ ≤ −60° and 130° ≤ ψ ≤ 150° (inset in Fig. 2 A), which is the set of structures from the PPII conformational region on the Ramachandran map. Thus, these ROA bands are attributed to the H₂O-Ala dipeptide structures with PPII conformations. The range of φ, ψ values (−80° ≤ φ ≤ −60° and 130° ≤ ψ ≤ 150°) for the PPII conformations of Ala dipeptide in aqueous solution determined from our ROA analysis is consistent with the range of values (−95° ≤ φ ≤ −45° and 95° ≤ ψ ≤ 145°) determined by 2D IR spectroscopy (35). Barron and co-workers have shown that positive ROA bands at ∼1318 cm⁻¹ and ∼1670 cm⁻¹ characterize PPII conformations of polypeptides (14,62), also consistent with our ROA analysis.

FIGURE 2.

SCP backscattering ROA (A and C) and Raman (B and D) spectra of H₂O-Ala dipeptide clusters. The computed spectra (black) are averaged over a collection of dipeptide conformations from PPII (A and B) and α_R (C and D) regions of the Ramachandran map (inset in A and C). The experimental spectra (gray; in arbitrary units) are from Deng et al. (48).

Fig. 2 C shows that the ROA bands (a–f) at 395 cm⁻¹ (a), 940 cm⁻¹ (b), 1140 cm⁻¹ (c), 1380 cm⁻¹ (e, Cα-H bend), 1450 cm⁻¹ (f), and the positive-negative couplet centered at ∼1300 cm⁻¹ (d, extended amide III) are predicted in the computed spectrum using a set of Ala dipeptide conformations (−50° ≤ φ ≤ −100° and −50° ≤ ψ ≤ 0°) from the α_R-region of the Ramachandran map (inset in Fig. 2 C). Thus, these ROA bands can be attributed to the H₂O-Ala dipeptide structures with α_R-conformations of the dipeptide. Interestingly, the ROA spectrum computed using the set of α_R-structures show a sequence of −/− bands in the frequency range of 300–400 cm⁻¹ (Fig. 2 C), consistent with the measured spectra. In contrast, the ROA spectrum computed using the set of PPII structures show a sequence of +/− bands in the same frequency range of 300–400 cm⁻¹ (Fig. 2 A).

Thus, the difference in the signs of the predicted ROA bands for the α_R and PPII conformations suggests that the ROA bands in the frequency range of 300–400 cm⁻¹ can be used to differentiate between the right-handed α_R and left-handed helical PPII conformations of Ala dipeptide (see Discussion for more detail). The Raman spectra computed using the PPII (Fig. 2 B) and α_R (Fig. 2 D) structures are also in good agreement with the measured spectrum. Fig. 2, B and D, shows only subtle differences in the computed Raman spectra using the PPII and α_R-conformations. For example, Raman bands at ∼1140 cm⁻¹ (Fig. 2 B) and ∼1540 cm⁻¹ (Fig. 2 D) are predicted for the PPII and α_R-conformations, respectively. Thus, ROA is a better probe of the secondary structure of peptides in aqueous solution than Raman scattering experiments. A more detailed analysis of the dependence of the computed ROA spectra on the φ and ψ dihedral angles of Ala dipeptide in H₂O appears in the Supplementary Material (Data S1) (Section 2).

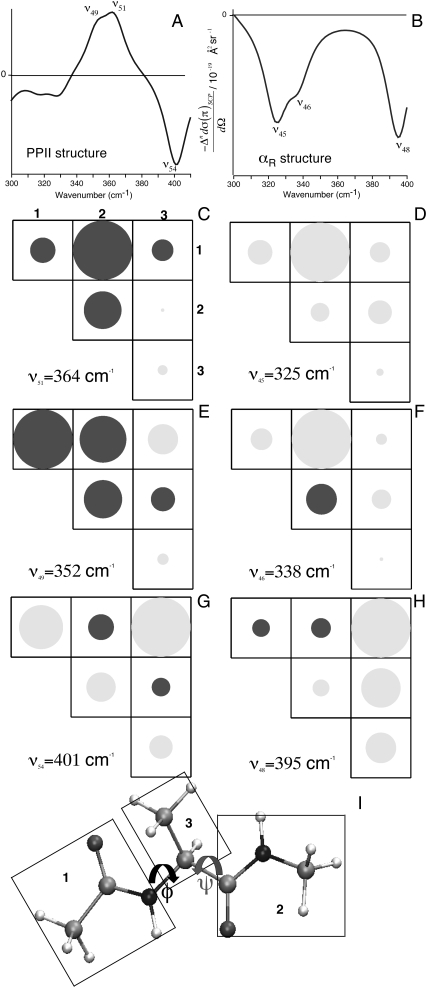
Fig. 3 shows the computed ROA (A and C) and the Raman (B and D) spectra using D₂O-Ala dipeptide clusters. The computed ROA spectra using both the PPII and α_R-conformations (insets in Fig. 3, A and C) contain spectral features found in the measured spectrum in D₂O. For example, ROA bands (peaks a–h in Fig. 3 A) at 340 cm⁻¹ (a), 395 cm⁻¹ (b), 500 cm⁻¹ (c), 950 cm⁻¹ (d), 1050 cm⁻¹ (e), 1280 cm⁻¹ (f, extended amide III), 1440 cm⁻¹ (g), and 1650 cm⁻¹ (h, amide I), are predicted in the computed spectrum using the set of PPII conformations. Similarly, ROA bands (peaks a–e in Fig. 3 C) at 340 cm⁻¹ (a), 395 cm⁻¹ (b), 500 cm⁻¹ (c), 1150 cm⁻¹ (d), and 1440 cm⁻¹ (e) are predicted in the computed spectrum using the set of α_R-conformations. Interestingly, the measured ROA spectrum of Ala dipeptide in D₂O also shows a sequence of +/−/− bands in the frequency range of 300–400 cm⁻¹. In contrast, the measured ROA spectrum in H₂O (Fig. 2) show a sequence of −/− bands between 300 cm⁻¹ and 400 cm⁻¹.

FIGURE 3.

SCP backscattering ROA (A and C) and Raman (B and D) spectra of D₂O-Ala dipeptide clusters. The computed spectra (black) are averaged over a collection of dipeptide conformations from PPII (A and B) and α_R (C and D) regions of the Ramachandran map (inset in A and C). The experimental spectra (gray; in arbitrary units) are from Deng et al. (48).

Thus, the ROA spectrum of Ala dipeptide in D₂O has an additional positive band in the frequency range of 300–400 cm⁻¹. The ROA spectra computed using the set of PPII (Fig. 3 A) and α_R (Fig. 3 C) structures in D₂O show a sequence of +/(−) and −/(−) bands in the frequency range of 300–400 cm⁻¹, respectively. The sign in parenthesis, (−), indicates the common negative ROA band predicted in the frequency range of 300–400 cm⁻¹ for the PPII and α_R-conformations. Thus, the computed ROA spectra based on PPII and α_R dipeptide conformations taken together contain the +/(−)/− spectral feature found in the frequency range of 300–400 cm⁻¹ of the measured spectrum in D₂O. The Raman spectra computed using the PPII (Fig. 3 B) and α_R (Fig. 3 D) structures are also in good agreement with the measured spectrum in D₂O. A more detailed analysis of the dependence of the computed ROA spectra on the φ and ψ dihedral angles of Ala dipeptide in D₂O appears in the Supplementary Material (Data S1) (Section 3).

There is no significant similarity between the measured and computed ROA and Raman spectra using the α_L (with 45° ≤ φ ≤ 65° and 25° ≤ ψ ≤ 55°) and β (with −180° ≤ φ ≤ −125° and 150° ≤ ψ ≤ 180°) conformations of H₂O-Ala dipeptide and D₂O-Ala dipeptide clusters (see Figs. S6 and S7 in Data S1). Thus, our ROA analysis suggests that Ala dipeptide in water populates α_R and PPII conformations without substantial α_L- and β-populations.

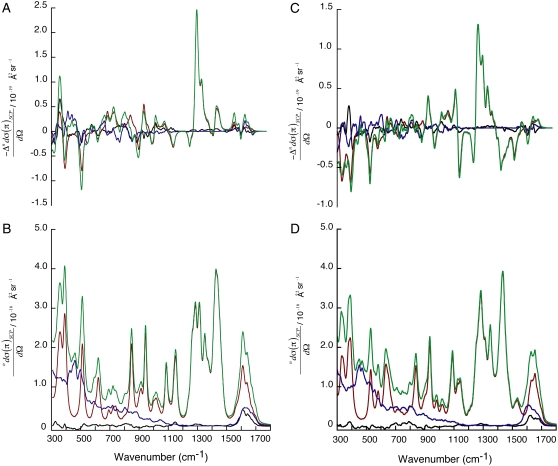
Fig. 4 shows the relative contributions of the dipeptide, water, and peptide-water interactions to the total ROA (A and C) and Raman (B and D) scattering cross sections of Ala dipeptide-water clusters (see Eqs. 5 and 6 in Methods for more detail), computed using the PPII (A and B) and α_R (C and D) conformations of Ala dipeptide. The ROA and Raman scattering cross sections are influenced by water in the low frequency range of 300–1100 cm⁻¹ and for the amide I and II bands. However, water makes no contribution to the Raman and ROA intensities from 1200 cm⁻¹ to 1500 cm⁻¹. Kapitán et al. recently showed that ROA bands in the 800–1600 cm⁻¹ range for the proline zwitterion in aqueous solution are not influenced by water (26), consistent with our ROA analysis, which also predicts the presence of ROA bands (1200–1500 cm⁻¹) for Ala dipeptide in aqueous solution that are not influenced by the solvent.

FIGURE 4.

ROA (A and C) and Raman (B and D) scattering cross section contributions of Ala dipeptide (red), water (blue), and peptide-water interactions (black) to the total ROA and Raman scattering cross sections of Ala dipeptide-water clusters (green). These computed spectra are averaged over a collection of dipeptide conformations from PPII (A and B) and α_R (C and D) regions of the Ramachandran map.

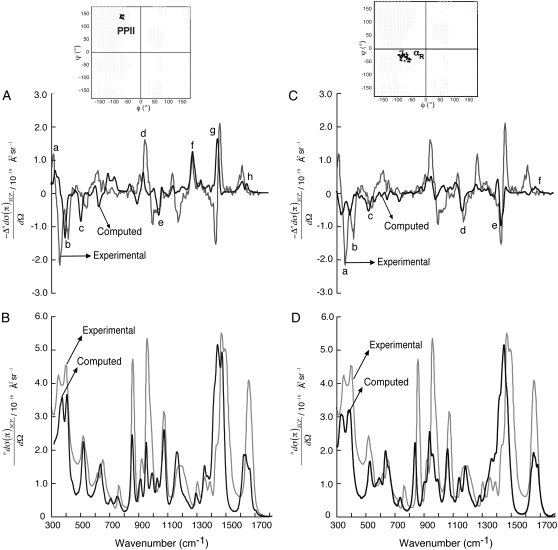
Fig. 5 shows the dipeptide contributions 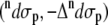of the total ROA and Raman scattering cross sections of Ala dipeptide-water cluster (see Eqs. 5 and 6 in Methods for more detail), computed using a PPII (φ = −68 and ψ = 135°; A and C) and an α_R (φ = −73° and ψ = −30°; B and D) conformation of Ala dipeptide. The computed ROA spectra using both PPII and α_R-conformations are in excellent agreement with the measured spectrum in both H₂O (A and B) and D₂O (C and D). For example, Fig. 5, B and D, shows that ROA bands a–i (including amides I, II, and III and the low frequency vibrational modes in the 300–400 cm⁻¹ range) predicted in the computed spectra using the α_R-conformations of Ala dipeptide conformation are in excellent agreement with the measured spectra in H₂O and D₂O.

FIGURE 5.

SCP backscattering ROA spectra computed (black) for a representative PPII (φ = −68° and ψ = 135°; A and C) and an α_R-conformation of Ala dipeptide (φ = −73° and ψ = −30°; B and D). Experimental spectra (gray; in arbitrary units) in H₂O (A and B) and D₂O (C and D) are from Deng et al. (48).

To understand the origin of the ROA intensity differences associated with the molecular vibrations in the low frequency range (300–400 cm⁻¹), we decomposed those intensity differences into contributions from groups of atoms in Ala dipeptide. As proposed by Hug (58,64), the ROA intensity decompositions is illustrated using the group coupling matrices for a PPII (φ = −68 and ψ = 135°; Fig. 6 A) and an α_R (φ = −73° and ψ = −30°; Fig. 6 B) conformation of Ala dipeptide (Fig. 6 I). The group coupling matrices show that the ROA intensity differences at ∼364 cm⁻¹ (Fig. 6 C) for the PPII (Fig. 6 A) and at ∼325 cm⁻¹ (Fig. 6 D) for the α_R (Fig. 6 B) are both dominated by contributions due to the relative motions of the atoms in groups 1 and 2 (Fig. 6 I), which is positive (black) and negative (gray) for the PPII and α_R-conformations, respectively. Fig. 6 also shows that the ROA intensity differences associated with molecular vibrations at ∼401 cm⁻¹ (Fig. 6 G) for the PPII and at ∼395 cm⁻¹ (Fig. 6 H) for the α_R are both dominated by contributions due to the relative motions of the atoms in groups 1 and 3 (Fig. 6 I) and are negative for both of these conformations. Fig. 6, E and F, shows the ROA intensity differences associated with molecular vibrations at ∼352 cm⁻¹ for the PPII conformation and at ∼338 cm⁻¹ for the α_R-conformation. The decomposition of the Raman intensities associated with the vibrations in these low wave number ranges for the groups of atoms in Ala dipeptide for the α_R and PPII conformations appear in the Supplementary Material (Data S1) (Section 5).

FIGURE 6.

Group coupling matrices for the ROA intensity differences associated with the vibrations in the low wave number range decomposed into contributions from groups of atoms in Ala dipeptide for a PPII (φ = −68° and ψ = 135°; A) and an α_R (φ = −73° and ψ = −30°; B) conformation. The groups of atoms in Ala dipeptide are shown in panel I. Positive and negative ROA intensity differences are shown as black and gray circles, respectively.

DISCUSSION

The aim of this study was to characterize Ala dipeptide conformations that are consistent with the measured ROA spectra in H₂O and D₂O. The ROA spectra were computed for H₂O- and D₂O-Ala dipeptide clusters with the PPII, α_R-, α_L-, and β-conformations of the dipeptide (Fig. 1 B) because the MC simulations found these structures in aqueous solution. Agreement between the measured and computed ROA spectra is used to characterize the populated conformations of Ala dipeptide in aqueous solution. The computed ROA spectra for the H₂O- and D₂O-Ala dipeptide clusters with the PPII and α_R-conformations are in excellent agreement (Fig. 5) with the measured spectra. There is no significant similarity between the measured and predicted ROA spectra for the α_L- and β-conformations. Thus, Ala dipeptide in aqueous solution dominantly populates α_R- and PPII conformations despite the fact that α_L- and β-structures are found in the MC simulations.

The conformational heterogeneity of Ala dipeptide has been probed using other spectroscopic methods. For example, the ¹³C-NMR spectra of Ala dipeptide in water and in liquid-crystalline media suggest that its structures in aqueous solution and in the liquid-crystalline state are very similar and that the structure is dominated by PPII conformations (33,34). However, these studies could not rule out the existence of α_R helical conformations in water. Following these NMR studies, Mehta et al. used ¹³C-NMR to show that Ala dipeptide in water exists in a mixture of PPII and α_R-conformations (31), consistent with our ROA analysis. Kim et al. used 2D IR to probe the conformational heterogeneity of Ala dipeptide in aqueous solution (35). Those authors concluded that the 2D IR experimental data and simulations are consistent with PPII-like conformations of Ala dipeptide in aqueous solution and ruled out the possibility of α_R helical conformations for Ala dipeptide in water. We emphasize that the 2D IR experiments were performed in D₂O, which stabilizes PPII conformations compared to H₂O. Chellgren and Creamer have also shown that D₂O stabilizes PPII conformations of alanine-containing peptides relative to H₂O (65). Those authors therefore suggested that conformational analysis of peptides using NMR, vibrational circular dichroism, IR, and Raman spectroscopy of peptides in D₂O is biased toward increased PPII populations.

Deng et al. suggested that the two negative ROA bands observed in the frequency range of 300–400 cm⁻¹ in the measured spectra of Ala dipeptide in H₂O and D₂O are indicative of its predominant conformation in aqueous solution (48). Our ROA computations predict the sequence of +/− and −/− ROA bands in the frequency range of 300–400 cm⁻¹ for the PPII and α_R helical conformations of Ala dipeptide, respectively (Fig. 5). Thus, the ROA analysis suggests that the two negative ROA bands observed in the frequency range of 300–400 cm⁻¹ in the measured spectra in H₂O and D₂O are characteristic of α_R helical conformations of Ala dipeptide. The measured ROA spectrum of Ala dipeptide in D₂O (Fig. 5, C and D) also shows a positive ROA band at ∼320 cm⁻¹ in addition to the two negative peaks in the frequency range of 300–400 cm⁻¹.

Our ROA spectrum computed using the PPII conformation of Ala dipeptide in D₂O (Fig. 5 C) predicts a positive ROA band in the frequency range of 300–400 cm⁻¹, consistent with the measured ROA spectrum in D₂O. Thus, the positive ROA band in the frequency range of 300–400 cm⁻¹ is a characteristic of the PPII conformations of Ala dipeptide. Since D₂O stabilizes PPII conformations of peptides relative to H₂O (see discussion in preceding paragraph), the positive ROA band observed in D₂O, is not observed in the measured spectrum in H₂O. The predicted ROA spectra using PPII and α_R helical conformations of Ala dipeptide have common spectral features found in the measured spectrum in H₂O, which indicate that Ala dipeptide in aqueous solution displays both conformations. We emphasize that the differential ROA response of Ala dipeptide in H₂O and D₂O—such as the key experimental spectral feature of −/− and +/−/− bands in the frequency range of 300–400 cm⁻¹ in H₂O and D₂O, respectively, predicted by our calculations—demonstrates that ROA can also differentiate the PPII- and α_R-dominant populated structures of Ala dipeptide in aqueous solution.

Han et al. also computed the ROA spectra of Ala dipeptide in H₂O, and their theoretical analysis of the ROA spectra suggests that PPII is the dominant conformation in aqueous solution (46). In contrast, our theoretical analysis of the ROA spectra of Ala dipeptide suggests that α_R is the dominant conformations in H₂O. If PPII dominated the conformational ensemble of Ala dipeptide in H₂O, then a positive ROA band in the frequency range of 300–400 cm⁻¹ would characterize it (see discussion in preceding paragraph). However, the measured ROA spectrum in H₂O (Fig. 5 B) shows two negative bands in that frequency range. The simulated ROA spectrum based on the H₂O-Ala dipeptide cluster with the α_R-conformation of the dipeptide (Fig. 5 B) shows negative ROA bands between 300 cm⁻¹ and 400 cm⁻¹, in agreement with the measured spectrum. Thus, our ROA calculations suggest a dominant population of α_R-conformation of Ala dipeptide in H₂O, which is also consistent with ¹³C-NMR studies (31).

Similarities between the observed and computed spectra (Figs. 2, 3, and 5) using the PPII and α_R-conformations of Ala dipeptide suggest that the pattern of +/− and −/− ROA bands in the frequency range of 300–400 cm⁻¹ are characteristic of the PPII and α_R helical conformations for Ala dipeptide, respectively. To correlate these spectral features to molecular structural elements, we decomposed the ROA intensity differences associated with vibrations in the frequency range of 300–400 cm⁻¹ into contributions from nuclei in groups of atoms in Ala dipeptide for an α_R and a PPII conformation. For example, the ROA band at ∼364 cm⁻¹ (Fig. 6 A) and ∼325 cm⁻¹ (Fig. 6 B) for the PPII and α_R, respectively, both originate from the relative motions of the nuclei in groups 1 and 2 (Fig. 6 I). ROA bands that are dominated by the relative motions of the nuclei in groups 1 and 2 in Ala dipeptide (Fig. 6 I) are also the probe of its secondary structure, since both of these groups contain the planar amide bonds that determine the φ and ψ dihedral angles. Thus, the ROA spectral features in the low frequency range of 300–400 cm⁻¹ provide structural information of the predominant conformations of Ala dipeptide in aqueous solution.

The ROA solvent dependence for chiral molecules was computed recently using DFT. Pecul et al. used DFT combined with a continuum solvent description to examine the influence of solvent on the ROA spectra of rigid molecules (29). The authors concluded that the solvent influence on the molecular geometry, the molecular Hessian, and the optical tensors should be included when computing solvent effects on ROA. Our computation of the geometry optimization, vibrational frequencies, normal modes, and derivatives of electric dipole-electric dipole polarizability and electric dipole-magnetic dipole polarizability tensors (Eq. 4 in Methods) were carried out using Ala dipeptide-water cluster structures. Thus, including explicit water in our ROA calculations accounts for the necessary solvent effects. We also find that the ROA and Raman scattering cross sections in the low frequency range of 300–1100 cm⁻¹ and for the amide I and II bands are influenced by water. In contrast, the ROA and Raman bands in the frequency range of 1200–1500 cm⁻¹ are not affected by water (Fig. 4).

The ROA and Raman scattering cross sections arising from the peptide-water interactions (see Eqs. 5 and 6 in Methods) are a minor fraction of the total ROA and Raman scattering cross sections of an Ala dipeptide-water cluster (Fig. 4). Fig. 4 also shows that the peptide-water hydrogen-bond interactions contribute to the Raman scattering cross section of the amide I band (Figs. 4, B and D). ROA computation of polypeptide including explicit solute-solvent interactions becomes extremely time consuming as the number of atoms grows. Efficient ROA computations of polypeptides may be achieved by excluding the water contribution to the Cartesian gradients of the electric dipole-electric dipole polarizability and electric dipole-magnetic dipole polarizability. However, the solvent influence on the geometry optimization of the solute and on the molecular Hessian must be included for accurate prediction of the ROA in solution.

The accurate prediction of ROA spectra of peptides in aqueous solution requires averaging over both solvent positions and peptide geometries (66). Thus, the computed ROA spectra (Figs. 2 and 3) averaged over H₂O- and D₂O-Ala dipeptide geometries predicts ROA spectral features of Ala dipeptide in aqueous solution. Fig. 5, B and D, shows that the ROA spectra computed using a single peptide conformation with φ = −73° and ψ = −30° correlates better with the observed spectrum than the computed spectrum averaged over a collection of Ala dipeptide structures with a wide range of φ- and ψ-values (−50° ≤ φ ≤ −100° and −50° ≤ ψ ≤ 0°; Figs. 2 C and 3 C) from the α_R-conformational region of the Ramachandran map. This suggests that the set of α_R-conformations of Ala dipeptide in aqueous solution constitutes a narrow distribution of peptide geometries around φ = −73° and ψ = −30°, rather than the broader distribution of structures with −50° ≤ φ ≤ −100° and −50° ≤ ψ ≤ 0°.

Our calculations show that the predicted ROA spectra using both the PPII and α_R-conformations of Ala dipeptide in H₂O and D₂O are in very good agreement with the measured spectra (Fig. 5) based on the overlap between the measured and computed spectra. Herrmann et al. recently showed that the ROA of helical peptides are dominated by the chirality associated with the peptide backbone conformation (30,67). Thus, based on the good agreement between the measured and computed spectra (Figs. 2–5) using the helical PPII and α_R-conformations of Ala dipeptide, we suggest that the backbone conformation of Ala dipeptide in aqueous solution is characterized by the compact α_R and extended PPII conformations, both of which dominate in aqueous solution.

Conformational analysis of Ala dipeptide is of fundamental importance to the question of the local conformational preference of unfolded polypeptides. Our ROA computational method could be used to interpret the ROA spectra of longer unfolded polypeptides in aqueous solution and to characterize their solution conformations. To characterize conformations of unfolded polypeptides, one has to determine residue-specific Ramachandran maps of the polypeptides. We demonstrate that ROA probes of molecular chirality can be used to determine the Ramachandran map of the shortest alanine-containing peptide. The accurate description of the conformational heterogeneity of Ala dipeptide backbone is an important step toward defining the residue-specific conformational preferences in unfolded polypeptides. In addition to the biological significance of dipeptide conformational analysis, combined experiments and simulations on short peptides can be used to determine the accuracy of commonly used force fields in MD and MC simulations.

For example, our MC and ROA studies of Ala dipeptide show that the shortest alanine-containing peptide exists as a mixture of PPII and α_R-conformations in aqueous solution, without a substantial population of left-handed α_L- or β-structures, despite sampling α_L- and β-structures in force field based MC simulations. Best et al. recently studied polyalanine peptide A₅ conformations in aqueous solution using MD simulations to address the question of whether the commonly used force fields overpopulate the α-helical conformations of polyalanine peptides (10). They concluded that the NMR data are consistent with force fields that produce α-helical populations of polyalanine peptides and that the data do not require exclusive formation of the PPII structure, consistent with our conformational analysis of Ala dipeptide in aqueous solution.

Growing access to commercial ROA spectrometers (68) and improved efficiency of ROA calculations, such as implementation of analytical derivative procedures for the computation of ROA (69), are likely to motivate further ROA analysis of aqueous polypeptide solutions. A combined conformational analysis and ROA study of polypeptides should be helpful for understanding more fully the relationship between peptide conformations and ROA spectra. A link of this kind may provide further insights into the connection between structure and dynamics.

CONCLUSIONS

SCP ROA analysis for Ala dipeptide based on TD-DFT/DFT calculations and MC-sampled peptide-water clusters were used with experimental ROA and Raman data to assign the dominant conformations of Ala dipeptide in aqueous solution. Agreement of observed and simulated ROA spectral features indicate the viability of screening plausible MC structures based on ROA data. We find that the computed ROA spectra using a single PPII conformation with φ = −68 and ψ = 135° and a single α_R-conformation with φ = −73° and ψ = −30° are in excellent agreement with the observed spectra. Thus, our ROA analysis shows that Ala dipeptide adopts both α_R and PPII conformations in aqueous solution, which are the dominant conformations in aqueous solution.

We also find that including explicit solute-solvent interactions is required for a), adequate quantum mechanical geometry optimization of the solute conformations in solution, b), computation of the molecular Hessian, and c), computation of the solvent influence on the optical tensor for predicting the ROA spectra of peptides in solution. The accurate prediction of the ROA spectra of Ala dipeptide based on the agreement between the observed and computed spectra using the PPII and α_R-conformations of the dipeptide in H₂O and D₂O suggest that our ROA computational method could be used to interpret measured ROA spectra of longer polypeptides in aqueous solution and to characterize their solution conformations.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.