Increasing Sensitivity of Ca²⁺ Spark Detection in Noisy Images by Application of a Matched-Filter Object Detection Algorithm

Abstract

Microscopic calcium (Ca²⁺) events (such as Ca²⁺ sparks) are an important area for study, as they help clarify the mechanism(s) underlying intracellular signaling. In the heart, Ca²⁺ sparks occur as a result of Ca²⁺ release from the sarcoendoplasmic reticulum, via ryanodine receptor channels. Measurement of Ca²⁺ spark properties can provide valuable information about the control of ryanodine receptor channel gating in situ, but requires high spatiotemporal resolution imaging, which produces noisy datasets that are problematic for spark detection. Automated detection algorithms may overcome visual detection bias, but missed and false-positive events can distort the distribution of measured Ca²⁺ spark properties. We present a sensitive and reliable method for the automated detection of Ca²⁺ sparks in datasets obtained using confocal line-scanning or total internal reflection fluorescence microscopy. This matched-filter detection algorithm (MFDA) employs a user-defined object, chosen to mimic Ca²⁺ spark properties, and the experimental dataset is searched for instances of the object. Detection certainty is provided by nonparametric statistical testing. The supplied codes can also refine the search object on the basis of those detected to further increase detection sensitivity. In comparison to a commonly used, intensity-thresholding algorithm, the MFDA is more sensitive and reliable, particularly at low signal/noise ratios. The MFDA can also be easily adapted to other signal-detection problems in noisy datasets.

INTRODUCTION

Localized calcium (Ca²⁺) release events, such as Ca²⁺ sparks (1), provide the basis for tight regulation between signaling proteins (2). In heart muscle, Ca²⁺ sparks are considered elementary events in excitation-contraction coupling and are due to sarcoendoplasmic reticulum Ca²⁺ release via ryanodine receptor channel (RyR) activation (1,3). Spatiotemporal summation of Ca²⁺ sparks results in the whole-cell Ca²⁺ transient (3) that initiates and controls muscle contraction (for review, see Bers (4)), and alterations in RyR function have been suggested to play a crucial role in some cardiac disease states (5–7). However, it has proven difficult to study RyRs in situ, so their gating properties have to be inferred from the Ca²⁺-release waveform associated with the Ca²⁺ spark (e.g. (8,9)).

Accurate and unbiased detection of Ca²⁺ sparks (and similar signaling events) is made problematic by their small spatial size, fast kinetics, and limited signal/noise ratio (SNR). A connected problem is that of “missed events”, as previously described for single-channel recording (10), which arise from small and/or fast events falling below the threshold for detection. Similarly, undetected sparks (which will, on average, be associated with a smaller fluorescence signal) may alter estimates of spark probability, average spark flux, and other parameters (11). On the other hand, if the detection threshold is too low, the resulting data is contaminated by “false positives” produced by noise. One way to minimize the occurrence of both missed events and false positives (assuming constant SNR) is to use a sensitive and reliable detection algorithm.

For 2D datasets, such as fluorescence images of Ca²⁺ sparks, an automated double-threshold method was developed (herein referred to as the “threshold-based” algorithm (11)). The first threshold defines contiguous areas large enough to be Ca²⁺ sparks, whereas the second, higher threshold, determines whether the signal has sufficient amplitude to be classified as a spark. However, this algorithm uses data smoothing and/or median filtering to reduce noise and false positives, and although such filtering increases the probability of the dataset passing the first threshold, it also decreases the signal amplitude so that the probability of passing the second threshold is reduced. These opposing effects can make the correct choice of filter and thresholds for any dataset problematic. To improve detection reliability against noise, a “live or die” filter (12) and a wavelet filter (13) have been added to threshold-based methods. Nevertheless, the process of selecting thresholds remains imprecise, although statistical significance for detected events can be determined if an adjacent Ca²⁺-spark-free region can be defined (14).

An optimal processor for a signal with additive noise is the signal itself, a “matched filter”, which maximizes the SNR of a dataset to facilitate detection and localization of the signal (15). We have implemented a matched-filter detection algorithm (MFDA) for detecting objects with known spatiotemporal properties in 2D images and applied it to the problem of detecting Ca²⁺ sparks in noisy data. To demonstrate the performance of the MFDA, we compare it to a commonly used threshold-based algorithm (11) using synthetic datasets over a range of SNR and spatial blur (to simulate out-of-focus events), as well as on Ca²⁺-spark datasets from rat ventricular myocytes. At an SNR of 1.0, the MFDA showed threefold improvement on both detection sensitivity (the probability that a given true event is positively detected) and positive predictive value (PPV, the probability that a given positive detection is correct). Further, since the search object can be refined after initial detection, the algorithm can be adaptive to the dataset. To facilitate examination of this detection approach, we include a stand-alone program (Windows-based), as well as annotated program listings that provide routines for model spark generation, Ca²⁺ spark detection, and model fitting (see the Supplementary Material, Data S1).

METHODS

Isolation and loading of cardiac ventricular myocytes

Wistar rats (250 g) were killed by lethal injection of sodium pentobarbitone (240 mg/kg intraperitoneally) in accordance with the University of Auckland Animal Ethics Committee guidelines. The enzymatic cell isolation method was as previously described (16). Briefly, the heart was perfused by a Langendorff perfusion system at 35°C with a modified Tyrode's solution containing 1.0 mg/ml collagenase (Type II, Worthington Biochemical, Lakewood, NJ) and 0.1 mg/ml protease (Type XXIV, Sigma Aldrich, St. Louis, MO) in 200 μM Ca²⁺. Cells were stored at room temperature in 1 mM Ca²⁺-Tyrode and aliquots were loaded with 5 μM Fluo-4-AM or Fluo-5F-AM (Invitrogen; Carlsbad, CA), followed by 20 min incubation and dilution (>64-fold) into 1 mM Ca²⁺-Tyrode. Ca²⁺-tolerant myocytes were selected based on good morphology (rod-shaped with clear striations) with no visible waves of contraction. For total internal reflection fluorescence (TIRF) imaging, 10 mM 2,3-butanedione monoxime (BDM, Sigma-Aldrich) was also added to reduce cell movement on stimulation. Stimulation, laser shutter, camera shutter, and acquisition were controlled by custom protocols written in pCLAMP 9.2 (Molecular Devices; Union City, CA).

Fluorescence imaging

For line-scanning confocal laser scanning microscopy (CLSM), a Zeiss LSM 410 was used (Carl Zeiss, Oberkochen, Germany) with a 40×, 1.25 N.A. oil objective. Illumination was provided by a 488-nm Ar⁺ laser (Uniphase, San Jose, CA) and fluorescence detected via a bandpass filter (535 ± 20 nm). For TIRF microscopy, an inverted microscope (TE-2000E, Nikon, Tokyo, Japan) was used, with a 60×, 1.49 N.A. oil objective. Illumination was provided by a 488-nm Ar⁺ laser (150M, Laser Physics, Cheshire, United Kingdom) coupled through a single-mode polarization-maintaining optical fiber (Oz Optics; Ottawa, Canada). The fluorescence detector was a cooled, backlit, frame-shift-enabled electron-multiplying charge-coupled device (EMCCD) (Ixon 487, Andor Technology, Belfast, Northern Ireland). The recording chamber was treated with 0.05% w/v poly-L-lysine (Sigma Aldrich) for 15 min and washed before cell addition. A micromanipulator was used to position a blunt fire-polished glass microtool to increase the area of contact between cell and coverslip.

Data processing

CLSM data was saved as 8-bit unsigned integer TIFF images, whereas TIRF camera data was converted to a 16-bit unsigned integer format. Data normalization was carried out before spark detection by dividing image data by an average intensity array (black-level subtracted for both types of data) that represents basal fluorescence. In the case of CLSM data, this was an average of 1024 lines; for TIRF data, a moving average over time (three frames immediately preceding the frame of interest) was used. Program development and data analyses were performed using Interactive Data Language (IDLV6.3, ITT Visual Information Solutions, Boulder, CO).

Automated detection of Ca²⁺ sparks

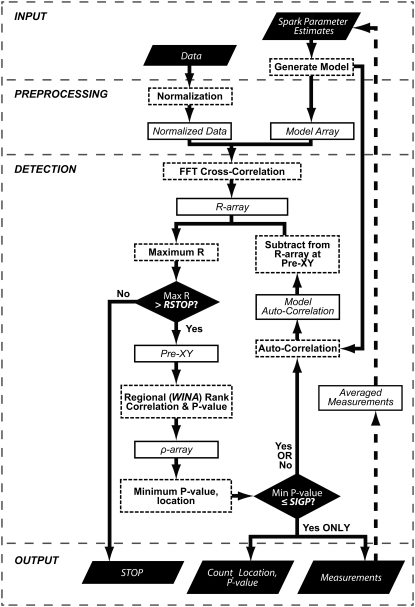
The MFDA involves two sequential cross-correlations between normalized data and model arrays (Fig. 1 shows the data processing path). The algorithm provides the most likely central location of a detected Ca²⁺ spark (or other event), which can then be the basis for further analysis of event properties. The event to be detected could be any arbitrary function of amplitude and time centered on the model array, but for this study, a model Ca²⁺ spark was used (generated by the flexible basis function MAKESPARK_FUNC (see Data S1)), although the event could also be based on actual experimental data.

FIGURE 1.

MFDA processing path. Solid lines indicate the normal algorithm processing path and dotted lines the path for utilizing model refinement (see text). The preprocessing steps usually involve data normalization, since a nonstationary background affects the magnitude of the cross-correlation whose value is used for initial site detection. RSTOP is a parameter that determines when all events have been detected, and SIGP sets the limit of detection reliability.

In the first step, input data and model arrays are cross-correlated to produce an initial array of correlation coefficients (array R₀). This quantifies the degree of similarity between the data and the model as a function of model position relative to the data. The calculation is performed by the routine FFTCORREL, which multiplies the Fourier transform of the data with the complex conjugate of the model transform. This first step is calculated with a fast Fourier transform (FFT) to allow efficient cross-correlation of large datasets and is mean-subtracted and normalized so that it is equivalent to Pearson's product-moment correlation coefficient.

To detect events, the cross-correlation array R_i (where i denotes the iteration count) is interrogated iteratively for the maximum value. A parameter RSTOP is used to define the minimum correlation coefficient so that if Max(R_i) ≤ RSTOP, the procedure stops and the detection count is i. RSTOP is determined by cross-correlating a randomized version of the normalized dataset with the model array to give correlation coefficients associated with noise of comparable power to the normalized dataset. The value of RSTOP is obtained from this correlation array by calculating at six standard deviations above the mean (which is ∼0). Because pixel randomization will be different for each MFDA run, the number of detected events for a given dataset and model may vary slightly if the dataset contains events that are near the limit of detection.

If Max(R_i) > RSTOP, the coordinates of this maximum value are used as the initial location of detected event i (which are stored as Pre-XY_i). To refine this estimate of position, further local cross-correlations are used to calculate the nonparametric Spearman rank correlation coefficient (ρ (Eq. 1)) as a function of position of a kernel containing the model object (computed by the routines STATMAP and RANK_CORREL, see Data S1):

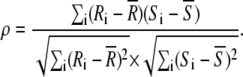(1)

The kernel is shifted relative to the data over a region surrounding Pre-XY_i. The kernel size in x and y is defined by the vector WINA (window area), which is determined within the algorithm such that WINA width and height are three times the full width at half-maximum (FWHM) in x and y of the model, but the kernel can be any shape. The region over which the kernel was shifted was a 10 × 10 area surrounding Pre-XY_i. At these values, execution time is minimized, although enough pixels are still processed to reliably determine object location. In these calculations, only model pixels significantly above background were used to avoid a large number of background pixels inflating the correlation coefficient. Since the tests were directed toward measuring Ca²⁺ sparks, the background of the model was normalized to 1.0, so that all pixels above this value were used. For example, in the spark model presented here, N = 435 pixels met this criterion (WINA = (15, 54), x = 0.4 μm/pixel, t = 1.4 ms/pixel).

At each shift, RANK_CORREL also calculates the two-tailed P-value for a nonzero value of ρ (Eq. 2), where t approximates a Student's t-distribution with N – 2 degrees of freedom (17):

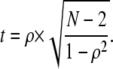(2)

The coordinates of the local P-value minimum are then the most likely location of the detected spark. If this P-value is less than or equal to a user-defined significance level, SIGP, then it is considered a detected event, otherwise, the event is rejected.

This process is repeated on a revised array, R_i+1, which is constructed by subtracting the model autocorrelation centered at Pre-XY_i. This enables the routine to sequentially examine all local maxima in the correlation array and the process continued automatically until the stop criterion is reached.

Spark model generation

Adjustable synthetic Ca²⁺ spark models were used as matched filters for the MFDA, as well as for generation of synthetic datasets for testing algorithm performance.

To simulate Ca²⁺ sparks recorded using a line-scanning CLSM system, the fluorescence signal (S), was given by

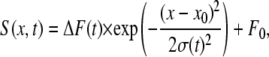(3)

where

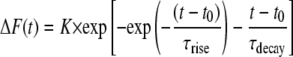(4)

and

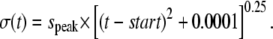(5)

FWHM in x was set to 2.0 μm, K was chosen so that the maximum of ΔF/F₀ was 1, F₀ was 1, and τ_rise and τ_decay were chosen so that time to peak was 10 ms and half time of decay was ∼20 ms. s_peak was determined from the FWHM, using the formula 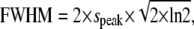whereas start was numerically determined from ΔF(t) as the initial start time for fluorescence increase.

These equations and partial derivatives (coded in the routines MAKESPARK_FUNC and MAKESPARK) were used in a nonlinear least-squares fitting method (CURVEFIT in IDL) to obtain measures of ΔF_, FWHM, τ_rise, τ_decay, x₀, t₀, and F₀ from aligned and averaged Ca²⁺ sparks in the original data.

To demonstrate the utility of the algorithm, fluorescence of Ca²⁺ sparks recorded using TIRF microscopy was also analyzed. In this case, the spark model was a 2D Gaussian function,

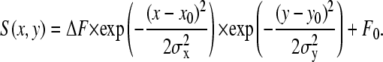(6)

Validation and comparison of the MFDA

Synthetic line-scanning CLSM Ca²⁺-spark datasets (512 × 512-pixel arrays), each with 10 sparks, were produced using the described CLSM spark model (Eqs. 3–5) as a template. Datasets over a range of SNR (defined here as the square root of the mean background photon count) were generated with Poisson-distributed noise. Of the many possible definitions of SNR, this was chosen to enable comparison with other algorithms (e.g., (11,13)). In addition to SNR, the effect of defocus (as occurs in confocal microscope imaging) on MFDA performance was investigated by blurring the template Ca²⁺ sparks before noise addition. This was achieved by convolution with a 2D Gaussian of width σ. Thus, as σ increased, spark amplitude decreased in an approximately inverse square relation, whereas spatial extent and time course increased proportionately (data not shown).

MFDA performance testing employed 100 datasets at each combination of SNR and blur. Alterations of SIGP (0.0005–0.002) and RSTOP (2–10 standard deviations) were examined for their effect on MFDA performance. To provide a benchmark, the threshold-based algorithm (11) was also used to process the same datasets. Performance measures included sensitivity and PPV. A detected spark location from the MFDA was considered correct if it was within the FWHM of the actual spark location. In a similar way, a detected spark region from the threshold-based algorithm was considered a positive result if it included the true spark location. Smooth curves illustrating data trends were manually fitted using Bezier splines and contours generated by the IDL CONTOUR routine.

RESULTS

MFDA performance

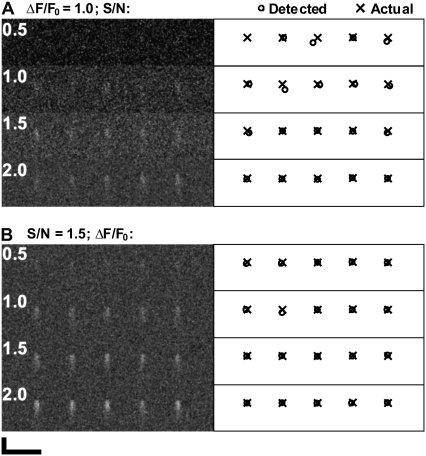
Detection of Ca²⁺ sparks in noisy datasets by eye can be compared to the performance of MFDA in Fig. 2, which shows Ca²⁺ sparks of fixed amplitude (ΔF/F₀ = 1.0) at various SNR (Fig. 2 A) and also at fixed background SNR (1.5) at varying ΔF/F₀ (Fig. 2 B). At an ΔF/F₀ of 1.0 and SNR of 0.5, sparks are detected with the automated algorithm, although they can hardly be seen by eye.

FIGURE 2.

MFDA Ca²⁺ spark detection (SIGP = 0.001), using the same spark model at varying SNR and ΔF/F₀. At left, raw data is shown to allow visual examination of the effect of varying SNR and signal strength. At right is shown the location (circles) of sparks detected by the MFDA, as well as the actual locations of the events (crosses). (A) Synthetic Ca²⁺ sparks with ΔF/F₀ = 1.0 at SNR levels (top to bottom) of 0.5, 1.0, 1.5, and 2.0. Note that the display is scaled to the maximum range. (B) Ca²⁺ sparks at SNR = 1.5, with ΔF/F₀ (top to bottom) of 0.5, 1.0, 1.5, and 2.0. Note that the display is scaled by the same factor. Scale bars: horizontal, 20 μm; vertical, 35 ms.

On a portable personal computer (Sony Vaio, 2.0 GHz Intel Core 2 processor, Windows XP Professional, 2.0 GB RAM), a total of 500 synthetic CLSM sparks in 50 data arrays required an average MFDA (SIGP = 0.001) execution time of 93 s to detect all sparks, which gives a detection rate of ∼5.4 sparks/s. This is slightly slower than the execution time of 36 s for the same dataset using the threshold-based algorithm, but yields fewer missed events (see below).

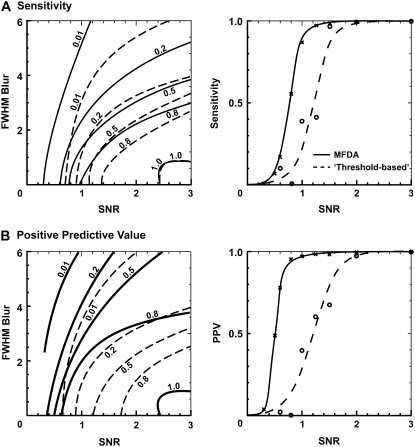
To further characterize MFDA performance (at SIGP = 0.001) and to compare it with the threshold-based algorithm (cri = 3.8 (11)), 100 synthetic datasets at each of nine SNRs and nine σ values were used. At an SNR of <0.6, the threshold-based algorithm would spontaneously halt and generate no detected events. Fig. 3, A and B, shows the sensitivity and PPV, respectively, of both algorithms as functions of SNR and blur (left panels; the extent of blurring is indicated by the approximate resulting spark FWHM on the vertical axis) and SNR only (right panels). In comparing these data, a contour shifted toward the top left indicates an improvement in the performance measure. For example, at SNR = 1.0, FWHM = 2 μm, the sensitivity and PPV of the MFDA were ∼0.55 and 0.85, respectively. In comparison, the threshold-based algorithm gave 0.2 and 0.25, respectively. This improvement further increased at lower SNR and increased blur (FWHM). As shown in the righthand panels in Fig. 3, the SNR (with no blurring) at which the MFDA offers half-maximal sensitivity (SEN₅₀) and PPV (PPV₅₀) were ∼0.8 and ∼0.5, respectively. With the threshold-based algorithm, SEN₅₀ and PPV₅₀ were approximately twice that of the MFDA (∼1.2 and ∼1.35 respectively), implying a fourfold increase in the required number of photons at the limits of spark detection.

FIGURE 3.

Comparison of the performance of the MFDA (solid lines; SIGP = 0.001) and the threshold-based algorithm (dashed lines; cri = 3.8) on synthetic CLSM datasets (n = 100). (A) The left panel shows a contour plot of sensitivity over a range of SNRs (tested at 0.3, 0.5, 0.6, 0.8, 1.0, 1.25, 1.5, 2.0, and 3.0) and Gaussian blur (indicated by the resulting FWHM as a factor of the original FWHM; tested at 2, 4, 6, 8, 10, 12, 14, 16, and 18 μm with an original FWHM of 2 μm). Right panels summarize the effect of SNR on sensitivity with no blur (i.e., the model spark is in focus). Standard errors were smaller than the symbol size. (B) Quantification of PPV over the same range of values for SNR and blur as in A. Both sensitivity and PPV curves for the MFDA show left-shifted behavior compared to the threshold-based algorithm, indicating improved performance, particularly at low SNR and/or blur extent. Note that blurring also affected spark amplitude (see Methods).

Implementing the MFDA with RSTOP from 4 to 10 standard deviations above the mean noise correlation increased SEN₅₀ from ∼0.7 to ∼1.3 and PPV₅₀ from ∼0.4 to ∼0.9. Increasing SIGP (0.0005–0.002) decreased both SEN₅₀ and PPV₅₀. The standard errors associated with these tests (n = 100 datasets) were on average 0.006 for sensitivity and 0.02 for PPV. The standard errors associated with the threshold-based algorithm were 0.004 for sensitivity and 0.005 for PPV.

The errors between actual and detected spark positions were also calculated, but there were no clear relationships between position errors and SNR or blur, and these errors were typically less than a single pixel (not shown).

Spark detection in CLSM and TIRF data

The MFDA was applied to Ca²⁺ spark data recorded from isolated myocytes using CLSM. Fig. 4 A shows raw fluorescence data, which was then normalized (Fig. 4 B) with the model Ca²⁺ spark shown as an inset. Intermediate and final outputs of the MFDA are shown in Fig. 4, C–E. Note that the MFDA detects more events than are easily discerned in the original data. The output of the threshold-based algorithm is shown in Fig. 4 F, and there are clear differences between this data and the output of the MFDA. Although the brightest events are detected by the threshold-based algorithm, a number of small detected regions are also present. For the events bounded by the square brackets (Fig. 4 F), the noise in the data leads to detected regions breaking into several smaller regions that are not always correctly identified as individual events, a problem not seen in the MFDA data (Fig. 4 D). Two events (Fig. 4 F, asterisks) were detected only by MFDA, whereas a number of small regions that were detected by the threshold-based algorithm (Fig. 4 F, arrows) were not present in the MFDA. The event at lower left (Fig. 4 F, lower asterisk) is visible by eye, suggesting that the MFDA is more sensitive. The smaller events (Fig. 4 F, arrows), detected only by the threshold-based algorithm, may be false positives since they appear to occupy a very small region.

FIGURE 4.

Detection of Fluo-4 Ca²⁺ sparks in CLSM data using the MFDA (SIGP = 0.001). (A) Raw intensity data. (B) Normalized data (ΔF/F₀). Inset shows (to the same scale) the model Ca²⁺ spark (matched filter). (C) Initial cross-correlation array, R₀, showing peak correlations at tentative spark locations. (D) Regional Spearman rank correlation array, ρ, with peaks indicating the most likely locations of the detected sparks. (E) Overlay of normalized data from B with detected locations of Ca²⁺ sparks and associated P-values. (F) Results from the threshold-based algorithm (cri = 3.8, black level = 25, N = 7). Arrows show events detected by the threshold-based algorithm but not by the MFDA. Asterisks indicate events that were detected by the MFDA but not by the threshold-based algorithm. Brackets show where a collection of discrete regions were identified by the threshold-based algorithm as two events. Scale bars: horizontal, 20 μm; vertical, 50 ms.

The MFDA was also used to detect Ca²⁺ sparks in data recorded by TIRF microscopy. Fig. 5 shows the raw data, averaged data, and normalized data (Fig. 5, A–C, respectively) together with intermediate and final outputs of the MFDA (Fig. 5, D–F). Comparison of Fig. 5, C and E, illustrates the comparative reliability of the MFDA against noise. Although the spark in Fig. 5 C is detectable by visual inspection, it would be hard to define either the center of the spark or its extent. However, Fig. 5 E shows a remarkably clean result, which makes possible accurate location of the spark center to be defined (Fig. 5 F).

FIGURE 5.

Detection of Fluo-5F Ca²⁺ sparks in TIRF data using the MFDA (SIGP = 0.001). (A) Raw image data. (B) Smoothed mean of three frames used for data normalization. (C) Normalized data (ΔF/F₀). Inset shows (to the same scale) the model Ca²⁺ spark (matched filter). (D) Initial FFT cross-correlation, R₀, showing a peak correlation at the tentative spark location. (E) Regional Spearman rank correlation array, ρ, with the peak indicating the most likely central location of the detected spark. (F) Overlay of normalized data shown in C, with the detected location of a Ca²⁺ spark with the associated P-value. Scale bar, 20 μm.

Model refinement

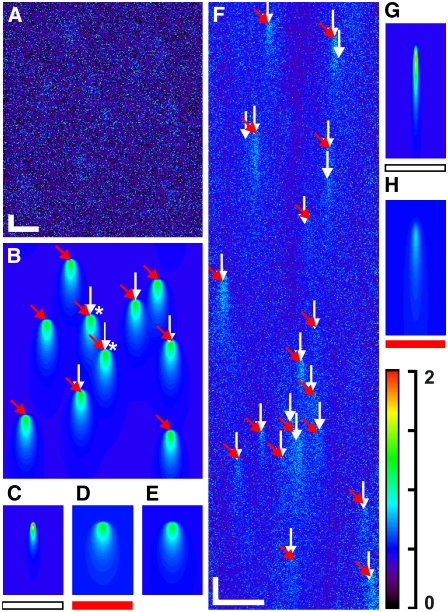
Although it is an optimal filter, the MFDA was also able to detect simulated out-of-focus events. Such events could be extracted and used to refine the model to further increase sensitivity. To demonstrate this adaptive ability, 10 synthetic sparks of known parameters (Fig. 6 B) were used to create a data array (SNR = 1.25 (Fig. 6 A)), which was then processed using an “incorrect” spark model (Fig. 6 C). This resulted in five detected events (Fig. 6 B, white arrows), but subsequent averaging of these five events and fitting the spark basis function (Eqs. 3–5) generated a refined model (Fig. 6 D) whose application resulted in detection of all 10 events (Fig. 6 B, red arrows). These 10 events were then averaged and the basis function refitted to give the results shown in Fig. 6 E, a spark that was very similar to the original synthetic spark (see Fig. 6 legend for parameters). The asterisks in Fig. 6 B show the two events detected with the threshold-based algorithm. The utility of model refinement is further illustrated in Fig. 6 F, which shows a normalized CLSM dataset. Processing the dataset with the initial model guess (Fig. 6 G) resulted in 22 detected events (Fig. 6 F, white arrows), whereas a refined model based on these events (Fig. 6 H) detected 17 events (Fig. 6 F, red arrows). Two of the four events detected in the first iteration and not in the second are seen to be in the tails of detected events, suggesting that the initial model was too short in duration and generated two false positives.

FIGURE 6.

Illustration of MFDA model refinement using detected events (SIGP = 0.001). (A) Synthetic dataset containing the sparks shown in B with Poisson noise (SNR = 1.25). (B) Synthetic data used to generate A, with spark parameters ΔF/F₀ = 0.5, FWHM = 6.0 μm, τ_rise = 3.6 ms, and τ_decay = 54.0 ms. White arrows indicate the positions of detected sparks (N = 5) using the initial model shown in C. Asterisks show sparks detected by the threshold-based algorithm (cri = 3.8). The five events detected by the MFDA were averaged to generate a new model (see D) and, with reprocessing using this refined model, detected all 10 sparks. (C) Initial spark model with parameters expected for a “typical” Ca²⁺ spark: ΔF/F₀ = 1.0, FWHM = 2.0 μm, τ_rise = 1.8 ms, and τ_decay = 28.0 ms. These values should be compared to those given for B. (D) Refined model derived from fitting the spark basis function to the first five detected events. The parameters of this model were ΔF/F₀ = 0.46, FWHM = 7.45 μm, τ_rise = 3.59 ms, and τ_decay = 44.64 ms. (E) Results of fitting the spark basis function to all detected events, giving a best estimate for the actual parameters underlying the noise-corrupted dataset shown in A: ΔF/F₀ = 0.46, FWHM = 7.15 μm, τ_rise = 3.63 ms, and τ_decay = 48.43 ms. (F) Real CLSM Ca²⁺ sparks obtained from isolated rat ventricular myocytes. These data are a subset of a continuous record of 12,000 lines. An initial model (see G) led to the MFDA detecting 21 sparks (white arrows). These sparks were averaged to generate a new model (see H), whose application led to the detection of 17 events. Visual examination of the data shows that two of the four extra events detected in the first pass of the MFDA arose in the tails of detected sparks, an effect that suggests that the initial model may be too short in duration. (G) Initial model, with parameters ΔF/F₀ = 1.0, FWHM = 0.66 μm, τ_rise = 1.95 ms, and τ_decay = 9.75 ms. (H) Refined model, with parameters ΔF/F₀ = 0.27, FWHM = 1.44 μm, τ_rise = 2.53 ms, and τ_decay = 13.44 ms. Note that the refined model suggests that the initial model was too short in duration, leading detection of extra events in the first pass. Note that A and F have intensities ranging from 0 to 7.02 and 4.21, respectively, using the same color table as shown in the color scale bar, which applies to B–E and G–H. This change in scale was used to enable features to be seen more clearly. Scale bars: (A–E) horizontal, 20 μm; vertical, 35 ms. (F–H) horizontal,10 μm; vertical, 10 ms.

DISCUSSION

The detection of events in noisy data is a common problem and has been the subject of a great deal of research. In the case of Ca²⁺-spark properties, detection and subsequent quantification of these microscopic and transient events is limited by the sensitivity, resolution, and noise profile of the sensing system, and measurement bias must be avoided. In this study, a matched-filter approach has been implemented as an improved method to automatically detect Ca²⁺ sparks, and the code provided here may be easily adapted to other 2D detection and localization problems.

As might be expected, decreasing SNR adversely affects the performance of both the MFDA and the threshold-based algorithm, but the MFDA is less sensitive to this problem (see Fig. 3). Though the SNRs of the CLSM and TIRF datasets presented here were ∼3.0, at which both algorithms have comparable sensitivity for in-focus events (see Fig. 3, upper right), a marked difference in performance was seen when events were blurred with smaller SNR. Since sparks are likely to be recorded with some degree of defocus, this improvement may be significant. In addition, we can compare the performance of both algorithms with that expected from the Rose criterion (18) of visual detection in the presence of noise. If a spark occupies a region of typically 60 pixels (∼2 μm by 20 ms), then the mean of those pixels must be five times larger than the background noise (18). Since the noise is Poisson, the mean equals the variance, so that we can estimate that the limit of human detection for a typical spark might occur at a SNR of 1–1.5 (see Fig. 2 A). At SNR = 1.0, the MFDA gave a sensitivity of ∼0.9 and PPV of ∼0.95, whereas the threshold-based algorithm gave ∼0.4 for both measures. This means that compared with the threshold-based algorithm, the MFDA would detect twice the number of events and generate half as many false positives. Put another way, the MFDA can outperform visual detection (see Fig. 2 A), because the MFDA showed improved performance over the threshold-based algorithm (Fig. 3), which in turn outperformed visual detection in tests presented in the study in which it was introduced (11). Comparison of our performance curves with those of a wavelet algorithm (13) shows that the MFDA has SEN₅₀ and PPV₅₀ at ΔF/F₀ of 0.35 and 0.27, compared to 0.29 and 0.22, respectively, for the wavelet (at SNR = 2.0 with Gaussian noise, δ = 4.0, τ = 3.25, see Fig. 4 of Wegner et al. (13)). Although these performance measures are similar, the MFDA requires only a model spark (which may be refined), whereas a wavelet approach requires (possibly extensive) testing of different wavelet functions to optimize detection efficiency.

An important feature of the MFDA is the use of a nonparametric statistical test to measure the reliability of the detected location. For a spark-background SNR of 1.5, the ∼0.98 sensitivity and ∼0.99 PPV of the MFDA (SIGP = 0.001 (see Fig. 3, right panels)) implies that only ∼2% of events should be false positives. It is notable that this high performance has been achieved without the need for the ad hoc selection of detection thresholds used in other algorithms.

The MFDA is based on the idea of knowing the spatiotemporal properties of the event of interest, so that one might expect that out-of-focus and/or nonstereotypically-shaped events would be poorly detected. However, the loss of signal amplitude associated with defocus affects threshold-based algorithms more strongly, and as a result, the MFDA is still able to outperform a threshold-based algorithm even when moderate blurring has altered event shape (see Fig. 3). In any case, it is possible to refine the model shape on the basis of detected events, in which case the MFDA would still further increase its PPV, as demonstrated in Fig. 6. The only penalty associated with model optimization in the MFDA is an increase in computer execution time, which increases in proportion to the number of models tested. It is possible that extensive testing of experimental data with a variety of models could provide greater insight into the statistical spatiotemporal variability of the underlying events. This is not possible, to our knowledge, with any other published algorithm for Ca²⁺ sparks.

It should be noted that the MFDA has to exclude data at the edges of the dataset due to the need to construct a cross-correlation between model and data. Since there would be no way to correctly pad the edge of a data set if an event were at the edge, we have to accept the slight reduction in the size of the analyzable data set and therefore, also, the number of detected events. Although this problem also exists for other algorithms, it can be minimized by ensuring that the region of interest is centered and completely covered in the field of view. A second problem arises from the effect of background changes that alter the amplitude of the cross-correlation so that normalization becomes problematic if the background is changing during the experiment. More sophisticated normalization routines that correct for a time-varying background could be developed, but such approaches are dataset specific and not examined here. As it stands, the MFDA prints a warning that “nonstationary” data has been detected but proceeds nonetheless. A related problem exists in cases where large numbers of line scans are taken when cell damage may appear. Therein lies an advantage of using a sensitive detector, as lower laser powers can be used while preserving event detection. In connection with this point, the data shown in Fig. 6 F is only a short segment of a 12,000-line line-scan image.

The MFDA offers improved sensitivity for low-amplitude events (see Fig. 2 B). The importance of this is underscored by the history of Ca²⁺ spark discovery; although Ca²⁺ had been imaged for some years with confocal microscopes, it was not until the laser power was increased closer to the damage threshold that sparks became visually apparent (M. B. Cannell, University of Auckland, personal communication). By increasing the sensitivity of the detector and detection algorithm, we can reduce the risk of sample damage. With modern high-quantum-efficiency dyes and the limits of numerical aperture set by the refractive index of biological media, it seems unlikely that improvements in instrumentation will provide a major increase in sensitivity. Therefore, development of more sensitive and reliable algorithms such as the MFDA may be crucial to increasing biophysical insight. Code listings are included in Data S1. A stand alone Windows demonstration program may be obtained by contacting the authors.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.