Abstract
The suggestion by Robert Cantor, that drug-induced pressure changes in lipid bilayers can change the conformational equilibrium between open and closed states of membrane proteins and thereby cause anesthesia, attracted much attention lately. Here, we studied the effect of both large external pressure and of 1-alkanols of different chain lengths—some of them anesthetics, others not—on the lateral pressure profiles across dimyristoylphosphatidylcholine (DMPC) bilayers by molecular dynamics simulations. For a pure DMPC bilayer, high pressure both reduced and broadened the tension at the interface hydrophobic/hydrophilic and diminished the repulsion between the phospholipid headgroups. Whereas the effect of ethanol on the lateral pressure profile was similar to the effect of a large external pressure on a DMPC bilayer, long-chain 1-alkanols significantly amplified local maxima and minima in the lateral pressure profile. For most 1-alkanols, external pressure had moderate effects and did not reverse the changes 1-alkanols exerted on the pressure profile. Nevertheless, assuming the bent helix model as a simple geometric model for the transmembrane region of a membrane protein, protein conformational equilibria were shifted in opposite directions by addition of 1-alkanols and additional application of external pressure.
INTRODUCTION
Although the phenomenon of general anesthesia has been known for a long time, the underlying mechanism is not yet understood (1). There is an ongoing debate about whether general anesthesia is caused by a specific binding of anesthetics—among them the 1-alkanols, up to a chain-length of ∼12 carbon atoms (see, e.g., Pringle et al. (2))—to membrane proteins (3) or by a nonspecific, lipid-mediated mode of action. In the latter case, the drugs are supposed to induce changes in lipid bilayers, which in turn alter the conformational equilibrium between different states of membrane proteins. A further alternative lipid-mediated mechanism for anesthetic action has recently been suggested on the basis of a soliton model for signal propagation in nerves (4): Assuming that nerve pulses travel as solitons along cell membranes, a melting point depression caused by anesthetics would impede signal transduction and thereby cause anesthesia (5,6).
General anesthesia can be reversed by the application of external pressure (7–11). These two antagonizing mechanisms—anesthesia and its pressure reversal—are not necessarily coupled, but it is likely that they are related in some way. Here, we tested whether the model for a lipid-mediated mode of operation suggested by Robert Cantor (12–14) can also account for pressure reversal of anesthesia in a simple manner.
Cantor's idea (12–14) is based on the premise that there is a variation of the cross-sectional area difference between the closed and the open conformation of membrane proteins in the direction of the bilayer normal. If this assumption is fulfilled, a change in the lateral pressure profile of lipid membranes caused by anesthetics could shift the equilibrium between the open and closed conformation of membrane ion channels and thereby cause anesthesia. A simple mechanism for pressure reversal of anesthesia would then be a shift of the conformational equilibrium of these membrane proteins in the opposite direction by external pressure.
Cantor's model has not been tested yet, as the lateral pressure profile of membranes or lipid bilayers is difficult to determine in experiments. Up to now, only qualitative measurements of the pressure distribution in the bilayer chain region were achieved: Templer et al. (15) doped mixed bilayers composed of varying concentrations of dioleoylphosphatidylcholine and dioleoylphosphatidylethanolamine with di-pyrenyl phosphatidylcholine probes of different chain lengths. These doped bilayers were then used for fluorescence measurements, where the rate of the eximer to monomer signal of the pyrenes was assumed to be a measure of the pressure in the bilayer. Upon increase of the dioleoylphosphatidylethanolamine concentration, the total lateral pressure in the chain region was increased and a transfer of lateral pressure away from the heads toward the ends of the carbon chains occurred. Applying a similar technique, Kamo et al. (16) found that the lateral pressure in mixed bilayers composed of 1-palmitoyl-2-oleoylphosphatidylcholine and 1-monoolein increased as a function of the monoolein fraction as long as the bilayer was in the lamellar phase, had a discontinuity in the phase transition regime, and was approximately constant in the cubic phase. Addition of the peptide 18A lowered the lateral pressure only in the acyl chain region at the bilayer interface.
In theoretical studies, analytical and statistical methods, mean-field approaches, Monte Carlo techniques, and coarse-grained models (12,14,17–28) as well as all-atom molecular dynamics (MD) simulations (29–37) have been used to calculate lateral pressure profiles of lipid bilayers. Based on all-atom MD simulations, Lindahl and Edholm (29) classified all terms contributing to the lateral pressure according to their physical origin (electrostatic, Lennard-Jones, dihedral, or other bonded interactions) and the interacting molecules (pairwise contributions of lipid chains, headgroups, or water molecules) and distinguished between energetic and entropic contributions to the surface tension. Similar studies have been performed by other authors: Gullingsrud and Schulten (30) explored the impact of simulation and analysis parameters on the calculation of pressure profiles across bilayers consisting of various lipids and studied the influence of the lateral pressure distribution on the gating process of the mechanosensitive channel MscL applying a simple geometric model. Later, Gullingsrud et al. (33) computed the pressure profile of a protein-lipid system (melittin embedded in a dimyristoylphosphatidylcholine (DMPC) bilayer) and found that the overall pressure distribution of this system was only moderately changed compared to a pure DMPC bilayer. Patra (31) investigated the changes in the lateral pressure profile of a dipalmitoylphosphatidylcholine (DPPC) bilayer upon addition of cholesterol. Carrillo-Tripp et al. (32) detected that the magnitude of the chain pressure near the headgroup-tail interface was enlarged for lipid bilayers containing docosahexaenoic acids (DHA) compared to simulations of bilayers made of only saturated or monounsaturated lipids. The usage of docosapentaenoic acid instead of docosahexaenoic acid, that is accompanied by a shift of the maximum density of unsaturated bonds toward the bilayer core, did not yield such effect. Niemela et al. (34) probed the pressure profiles of raft-like bilayers. Various sterols, all of them with a structure very similar to cholesterol, exerted significant changes on the pressure profiles of lipid bilayers, especially in the case of unsaturated bilayer lipids (35). Ollila et al. (36) observed that the central maximum in the lateral pressure profile decreased upon increasing lipid chain unsaturation whereas all other peaks increased in height. Recently, Terama et al. (37) reported that ethanol diminished the magnitude of the peaks in the lateral pressure profiles of DPPC and palmitoyl-docosahexaenoyl-phosphatidylcholine lipid bilayers in the region of the lipid headgroups.
Using a coarse-grained approach, Frischknecht and Frink (28) found that ethanol, butanol, and hexanol did not alter the shape of the pressure profile curve of the pure bilayer, but that these alcohols reduced the magnitude of all peaks. Thickness changes of the bilayers upon addition of alcohols were reflected by a shift of the pressure profile peaks along the bilayer normal.
Here, we investigated in all-atom MD simulations, in which way 1-alkanols modify the lateral pressure of lipid bilayers, and in particular whether observed changes are reversed by the application of external pressure. 1-Alkanols are an especially interesting test case, as it was suggested that small alcohols change the lateral pressure in membranes and thereby cause dissociation of embedded KcsA potassium channels (38). Changes in the structure, the dynamics, and in the local pressure distribution of lipid bilayers in response to anesthetics and external pressure were analyzed from MD simulations of lipid bilayers containing 1-alkanols of different chain lengths at two different pressures. Hypothetical shifts in the conformational equilibria for some simple geometric models of the transmembrane region of a membrane protein upon addition of 1-alkanols and application of large external pressure were calculated.
METHODS
Molecular dynamics simulations of membrane-alkanol systems
MD simulations of fully hydrated lipid bilayers containing 1-alkanols of different chain lengths have been carried out at pressures of 1 bar (see also a previous study (39)) and 1000 bar using the GROMACS software package version 3.3.1 (40–42). Each bilayer consisted of 512 DMPC lipids and was hydrated by a minimum of 22,600 water molecules; 288 molecules of ethanol, octanol, decanol, or tetradecanol were dissolved in each simulation system. The systems were built by quadruplicating equilibrated membrane-alkanol-water systems with 128 DMPC molecules (39). Additionally, control simulations without 1-alkanols were run. Simulations for the long-chain 1-alkanols octanol, decanol, and tetradecanol at normal pressure were taken from the previous study (39). Equilibrated snapshots of these simulations were chosen as starting structures for high-pressure simulations. A summary of all simulations is given in Table1.
TABLE 1.
All simulated systems containing various 1-alkanols
| System name | Number and type of 1-alkanol molecules | Number of water molecules | Pressure (bar) | Simulation time (ns) | Equilibration time (ns) |
|---|---|---|---|---|---|
| C1* | None | 22,692 | 1 | 52 | 6 |
| C1000 | None | 22,692 | 1000 | 32 | 6 |
| E1 | 288 ethanol | 24,584 | 1 | 53 | 10 |
| E1000 | 288 ethanol | 24,584 | 1000 | 75 | 20 |
| O1* | 288 octanol | 26,624 | 1 | 33 | 6 |
| O1000 | 288 octanol | 26,624 | 1000 | 70 | 45 |
| D1* | 288 decanol | 29,896 | 1 | 31 | 6 |
| D1000 | 288 decanol | 29,896 | 1000 | 32 | 6 |
| TD1* | 288 tetradecanol | 29,228 | 1 | 31 | 6 |
| TD1000 | 288 tetradecanol | 29,228 | 1000 | 34 | 6 |
Systems already partially analyzed in the previous study (39). All analysis was done with respect to the given equilibration times.
Hydrostatic pressures to reverse anesthesia in tadpoles range from 140 to 350 bar (8). Due to large pressure fluctuations (≈±200 bar) in MD simulations of nanoscopic systems, we chose an external pressure of 1000 bar. Experimentally, even higher pressures are applied to lipid bilayers.
All systems were simulated for a minimum of 31 ns using periodic boundary conditions, a rectangular simulation box, and a constant number of atoms at fixed pressure and temperature T = 310 K (NPT-like ensemble). Constraining the bond lengths by the LINCS (43) and SETTLE (44) methods allowed for an integration step size of 2 fs. The lipids and the water-alkanol solutions were separately coupled to a heat bath at 310 K using a coupling time constant of 0.1 ps (45). External pressures of 1 bar and 1000 bar (see Table 1) were applied using a weak semiisotropic coupling to a pressure bath (45) with a time constant of 1 ps and a compressibility of 4.5 × 10−5 bar−1.
The simple point charge water model (46) was chosen. The force field for the lipids was taken from Berger et al. and Chiu et al. (47,48). For the long chain 1-alkanols, the GROMACS force field (based on GROMOS87) was applied, modified for the partial atomic charges according to MacCallum and Tieleman (49). Ethanol was simulated using the recently developed GROMOS 53A6 force field (50), as this has been shown to result in a lower partition coefficient in better agreement with experimental values (39). Note that the Lennard-Jones parameter of the lipid hydrocarbon chains and of the 1-alkanols slightly differ from each other. For phospholipids, they were adjusted to reproduce the heat of vaporization for pentadecane (47).
To ensure a correct treatment of the long-range electrostatic interactions, the particle mesh Ewald (PME) method (51) was applied using a Fourier grid spacing of 0.12 nm, a fourth order cubic interpolation, and a relative accuracy of 1.0 × 10−5. The short-range van der Waals interactions have been accounted for with a cutoff-scheme using a cutoff radius of 1 nm. The neighbor list was updated every 10th integration step.
For details of the calculations of the lipid order parameter, the average headgroup-to-headgroup bilayer thickness dHH, the area per lipid, and the lateral lipid diffusion coefficient, please refer to the previous study (39). The orientation of the lipid chains was determined in terms of two angles γ and α. γ denotes the angle between the lipid chains and the membrane normal, whereas α is the angle between the lipid chain vector (defined by the centers of mass of the 3rd and 4th and the 11th and 12th carbon atom of the respective lipid chain), projected onto the membrane plane, and an arbitrarily chosen vector (1, 0, 0). The partition coefficient was calculated from the number of 1-alkanols inside and outside the bilayer at every time step. The criterion for inside/outside was based on the comparison of the z coordinates of the center of mass of the lipid headgroups (shifted by 0.2 nm to the bulk water phase) and of the 1-alkanols. The given error is the standard deviation of the partition coefficient obtained by block averaging (5 ns windows).
Calculation of lateral pressure profiles
The difference between the lateral and the normal pressure as a function of the normal coordinate of the bilayer, often referred to as local lateral pressure profile, was calculated analogous to the procedure described by Lindahl et al. (29): The pressure tensor is given by
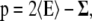 |
(1) |
where E is the kinetic energy density tensor and 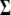 is the configurational stress tensor. In the case of exclusively pairwise interactions between the particles, the bilayer can be divided into horizontal slices of thickness Δz. Here, 100 slices per box were used, resulting in a thickness of ∼1 Å per slice. The local pressure tensor can then be calculated according to the formula (29):
is the configurational stress tensor. In the case of exclusively pairwise interactions between the particles, the bilayer can be divided into horizontal slices of thickness Δz. Here, 100 slices per box were used, resulting in a thickness of ∼1 Å per slice. The local pressure tensor can then be calculated according to the formula (29):
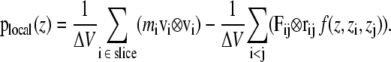 |
(2) |
The first sum is taken over all particles in the slice at z, whereas all particle pairs in the system contribute to the second term. The z coordinate, mass, and the velocity of particle i, and the force and the distance between particles i and j are denoted by zi, mi, vi, Fij, and rij, respectively. The volume of the slice is ΔV. The function 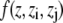 assigns a weight to the virial depending on the position of the two particles i and j. It is given by (21)
assigns a weight to the virial depending on the position of the two particles i and j. It is given by (21)
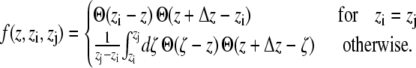 |
(3) |
Θ(z) denotes the Heaviside step function, with Θ(z) = 0 for z < 0, Θ(0) = 1/2, and Θ(z) = 1 for z > 0.
To obtain the pressure profiles from the simulations, reruns of the original trajectories were performed using a modified version of GROMACS 3.0.2, kindly provided by Lindahl and Edholm (29). Here, the SHAKE (52) algorithm was applied instead of LINCS (43), because pairwise interactions could then be extracted more easily (29). Sonne et al. (53) showed that the results obtained using PME for the simulations and a cutoff scheme in the reruns are converging toward the correct Ewald results as long as the chosen cutoff is large enough (rcutoff at the order of 1.6–2.0 nm). Here, electrostatic interactions in the reruns were truncated at a cutoff radius of 3.0 nm. For each bin, the diagonal elements of the local pressure tensor were calculated every 100 ps. The values were then averaged over time and a Gaussian smoothing over neighboring bins was performed. Finally, the profiles were symmetrized with respect to the bilayer center.
RESULTS
Equilibration times
All starting structures for the high pressure simulations had been equilibrated at a pressure of 1 bar in the previous study (39). The systems were further equilibrated at high pressure until the thermodynamic partition coefficient Kp of the 1-alkanols in the bilayer, the area per lipid, and the average lipid order parameter had become constant. An equilibration time of 6 ns was found to be sufficient for most of the systems (see Table 1). Exceptions were the simulations containing ethanol and the simulation with octanol at a pressure of 1000 bar with equilibration times between 10 ns and 45 ns. For octanol at high pressure, we observed a drastic decrease in the area per lipid and an increase in the lipid order parameter. These changes could possibly hint to a phase transition of the lipid bilayer, as discussed below.
Partition coefficients
For the simulations with ethanol, thermodynamic partition coefficients (ratio of the mole fraction of 1-alkanols inside the bilayer and the mole fraction of 1-alkanols in the surrounding water) of Kp = 68 ± 7 (1 bar) and Kp = 61 ± 5 (1000 bar) were determined (on average, 189 ± 8/182 ± 6 ethanol molecules were inside the bilayer at 1/1000 bar). Experimental values for the ethanol-lipid partition coefficient at normal pressure are considerably lower and range from Kp ≈ 2 to Kp ≈ 28 (37,39,54–57), depending on the kind of lipids and the experimental conditions. This discrepancy between experiments and simulations has also been observed and discussed in previous studies (37,38,58). Reasons for the overestimated ethanol partition coefficients in the simulations could be inconsistencies in current force fields (59,60), only implicit consideration of polarization effects in the region of the hydrophilic lipid headgroup (39), or artifacts due to the limited size of the simulation system as compared to experimental setups and the use of periodic boundary conditions (37). Also, at low ethanol concentrations, the partition coefficient strongly depends on the alcohol concentration (37), rendering high precision experiments in this regime difficult. Due to the too large partition coefficient for ethanol, observed effects are probably amplified with respect to experiments at comparable concentrations (39).
Also for the long-chain 1-alkanols, the partitioning between solvent and membrane was unaffected by the large external pressure. As for normal pressure, all 1-alkanols were located within the bilayer, their hydrocarbon chains being aligned with the phospholipid tail region.
Structural changes
It has been shown that the simulation of the pure DMPC bilayer at standard pressure (simulation C1, see Table 1) reproduces experimental values for the area per lipid, the bilayer thickness, the lipid order parameter, the lipid diffusion, and the bilayer elasticity quantitatively (39). Also, alkanol-induced changes of these parameters predicted in the simulations were in good agreement with the limited experimental data available (39).
High external pressure had a small to moderate effect on the structural properties of the ethanol-, decanol- and tetradecanol-phospholipid systems. For these membranes, the area per lipid and the bilayer thickness were reduced by 3.5–4.7% and 1–2% with respect to the systems at 1 bar (see Tables 2 and 3). The bilayer containing octanol (systems O1/O1000) underwent the largest changes with an area per lipid decrease of 7.9 Å2 and a thickness increase of 2.0 Å (see also Fig. 1).
TABLE 2.
Average area per lipid calculated from simulations of a DMPC bilayer containing different 1-alkanols at pressures of 1 bar and of 1000 bar
| Without 1-alkanols (Å2) | Ethanol (Å2) | Octanol (Å2) | Decanol (Å2) | Tetradecanol (Å2) | |
|---|---|---|---|---|---|
| 1 bar | 64.1 ± 0.4 | 67.8 ± 0.5 | 62.5 ± 0.4 | 59.3 ± 0.1 | 60.2 ± 0.1 |
| 1000 bar | 61.2 ± 0.6 | 64.6 ± 0.5 | 54.6 ± 0.1 | 56.6 ± 0.1 | 58.1 ± 0.1 |
TABLE 3.
Average headgroup-to-headgroup thickness of a DMPC bilayer containing various 1-alkanols at normal and high external pressures
| Without 1-alkanols (Å) | Ethanol (Å) | Octanol (Å) | Decanol (Å) | Tetradecanol (Å) | |
|---|---|---|---|---|---|
| 1 bar | 34.6 ± 0.2 | 34.0 ± 0.2 | 38.6 ± 0.2 | 40.5 ± 0.1 | 41.0 ± 0.1 |
| 1000 bar | 33.9 ± 0.3 | 33.3 ± 0.2 | 40.6 ± 0.1 | 40.1 ± 0.1 | 40.6 ± 0.1 |
FIGURE 1.
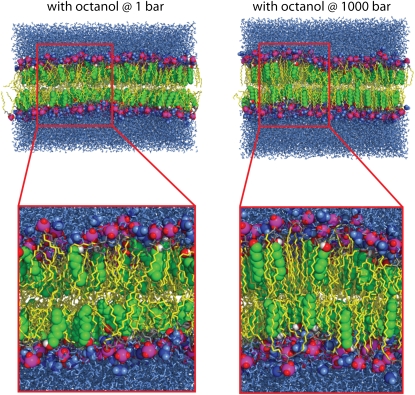
Simulation systems containing octanol at 1 bar (snapshot after 33 ns, left side) and at 1000 bar external pressure (70 ns, right side). The 1-alkanol carbon atoms are represented by green spheres, connected to the hydroxyl group (red and white spheres). Lipid tails are shown as yellow sticks. The lipid headgroup atoms are shown as spheres (phosphorus atoms, magenta; oxygen atoms, red; choline groups, blue) and yellow sticks (carbon atoms). The surrounding water is depicted as blue sticks. In the enlarged view, the increased order and the decreased tilt of the lipid chains with respect to the membrane normal can be seen.
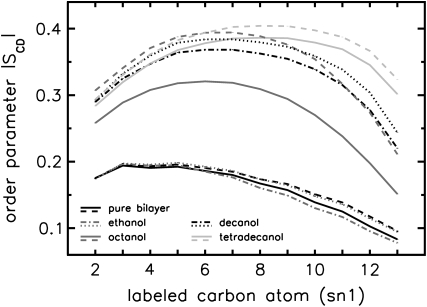
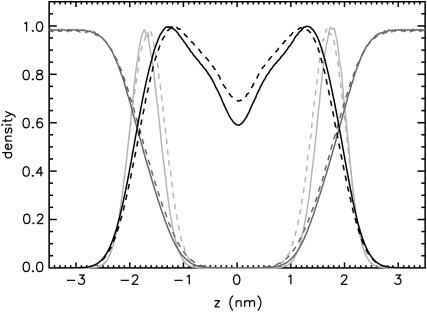
Application of external pressure exerted an ordering effect on the lipid tails by lateral compression of the bilayer. In agreement with the measurements of, e.g., Mateo et al. (61), the hydrocarbon chain order, measured by the deuterium lipid order parameter, was enlarged for all systems at 1000 bar (see Fig. 2). This order increase was additionally reflected in the reduction of the fraction of gauche dihedrals of the hydrocarbon chains (data not shown). Again, the largest changes induced by high external pressure were found for the octanol systems O1/O1000. The structural rearrangements of the bilayers under pressure were accompanied by an enhanced interdigitation of the lipid—and in the case of decanol and tetradecanol also of the 1-alkanol—chains. This is reflected by an increased density in the core region of the bilayer, exemplarily shown for DMPC in Fig. 3.
FIGURE 2.
Deuterium lipid order parameter (sn1 chain) for simulations with various 1-alkanols at external pressures of 1 bar (solid lines) and 1000 bar (dashed lines). Error bars are included, but are too small to be seen.
FIGURE 3.
Normalized number density profiles across the bilayer for the simulations of the pure DMPC systems (C1, solid lines; C1000, dashed lines). A Gaussian smoothing has been applied. The dark gray, black, and light gray lines represent the water, the lipid bilayer, and the phosphorus densities, respectively. Error bars are insignificantly small and are omitted here for clarity. The maxima of the phosphorus density curve mark the approximate headgroup location.
For the pure DMPC bilayer at standard pressure, the majority of the lipid chains were tilted with angles γ ranging from 0° to 20° with respect to the bilayer normal (Fig. 4). The angles α, a measure for the lateral orientation, were homogenously distributed for pure DMPC bilayers and for the ethanol-DMPC system. Addition of long-chain 1-alkanols to the bilayer decreased the tilting of the lipid chains. For tetradecanol (especially for the upper monolayer), the lateral distribution was narrowed.
FIGURE 4.
Orientation of the lipid chains (upper monolayer) of the different simulations. The chain orientation is given as a function of the angle γ between the lipid chains and the bilayer normal and the angle α defined by the projection of the lipid chains onto the bilayer plane and the arbitrarily chosen vector (1, 0, 0). The top row shows results from the simulations at standard pressure, the bottom row for the high pressure simulations. The color coding is chosen relative to an equal distribution in the angles α and γ. Occupancies with lower than two times this number are colored white, between two and four times this number are colored purple, between four and six times this number dark blue, etc.
High external pressure aligned the lipid tails with the membrane normal in the presence of long-chain 1-alkanols, reflected by a shift of the distribution toward smaller angles γ. The increased order in the octanol-phospholipid system (see Fig. 2) is additionally seen in the strong alignment of the hydrocarbon tails (pronounced maximum in the distribution of α for the upper monolayer; Fig. 4). The increase in lipid chain order, the increased packing density, and the alignment of the lipid tails for the octanol-DMPC system at high pressure are clearly seen in snapshots of the simulation system, too (Fig. 1).
Diffusion coefficient
At standard pressure, lipid diffusion was enhanced in a DMPC bilayer containing ethanol with respect to pure bilayers, whereas it was suppressed in systems containing octanol, decanol, or tetradecanol (see Table 4 and the previous study (39)). The diffusion coefficients predicted from the simulations were shown to be in agreement with values found in continuous photobleaching experiments (39). External pressures of 1000 bar decreased the lipid motion in all systems: for the pure DMPC, the ethanol-, the decanol-, and the tetradecanol-DMPC systems, the lipid diffusion was decreased by a factor of 1.6–2.3. In contrast, for the octanol-DMPC system, a ∼5-fold decrease in lipid diffusion was observed.
TABLE 4.
Lipid diffusion coefficients for simulations of a DMPC bilayer with various 1-alkanols at a pressure of 1 bar and of 1000 bar
Without 1-alkanols 
|
Ethanol 
|
Octanol 
|
Decanol 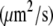
|
Tetradecanol 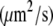
|
|
|---|---|---|---|---|---|
| 1 bar | 11.5 ± 0.6 | 17.0 ± 0.7 | 6.6 ± 0.4 | 2.9 ± 0.1 | 3.0 ± 0.1 |
| 1000 bar | 7.1 ± 0.3 | 7.5 ± 0.3 | 1.4 ± 0.1 | 1.7 ± 0.1 | 1.8 ± 0.2 |
Pressure profiles
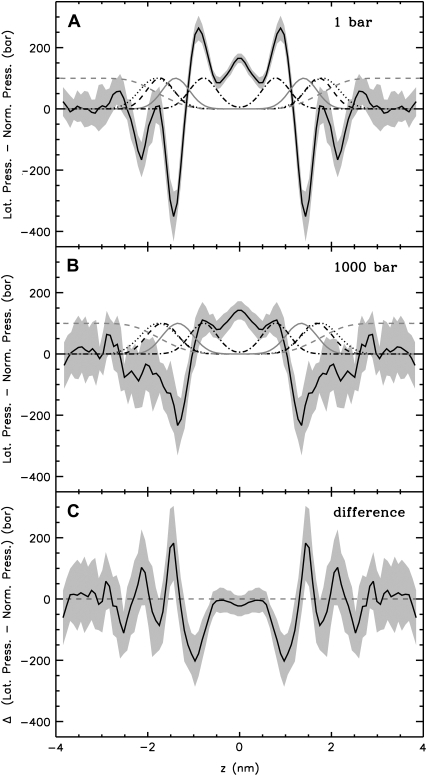
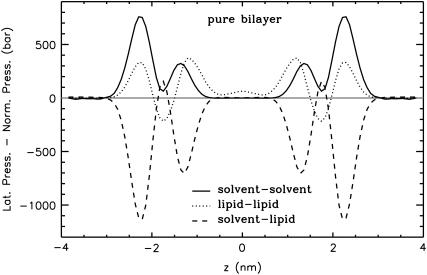
The symmetrized pressure profiles calculated from the MD simulations of the pure DMPC bilayer at 1 bar and at 1000 bar and the difference between them (for the calculation of the difference pressure profile, the bilayer at 1000 bar was scaled to the same thickness as the bilayer at 1 bar) are shown in Fig. 5. Results obtained at standard pressure (Fig. 5 A) are in agreement with previous studies (29–37,53): large tensions, which are due to strong electrostatic interactions and hydrophilic forces minimizing the contact between water and the hydrocarbons, were observed in the region of the glycerol group (z = ±1.44 nm). At the water-lipid interface (z ≈ ±2.2 nm) a second, slightly smaller tension peak was resolved. This two peak pattern was observed also in the separate contributions of the various interaction groups to the pressure profile (Fig. 6). The tension peaks are caused by solvent-lipid interactions forming a hydrogen-bonded network. Due to the increased order of interfacial water molecules (see, e.g., Siu et al. (60)), solvent-solvent interactions are repulsive at the interface (Fig. 6). Pressure maxima resulting from the entropic repulsion of the lipid chains were found in the region of the 5th–7th carbon atom. The vanishing pressure in the bulk water region may be used as a signature of full hydration of the lipid bilayer.
FIGURE 5.
Lateral pressure profiles of a DMPC bilayer consisting of 512 lipids at normal pressure (A) and at 1000 bar (B). The local lateral pressure, i.e., the difference between the lateral and normal components of the pressure tensor, is plotted as a function of the normal coordinate z of the bilayer (solid black line, z = 0 at the bilayer center). The error, calculated by averaging over time intervals and using error propagation for the smoothing procedure, is indicated by the gray shaded area. As a reference, the normalized, dimensionless number densities of various lipid components across the bilayer are given (dashed, black: phosphorus group; dotted, black: choline group; solid, gray: glycerol group; dot-dashed, black: sixth and seventh carbon atoms of the lipids; dashed, gray: water). C shows the difference between the pressure profiles at 1000 bar (bilayer at 1000 bar scaled to the thickness of the bilayer at normal pressure) and at 1 bar.
FIGURE 6.
Contributions of the different interaction groups to the total lateral pressure of the pure lipid bilayer at normal pressure. Errors are comparable to those for the total pressure profile.
At an external pressure of 1000 bar (see Fig. 5 B), the general shape of the curve was maintained, whereas the amplitudes of all local maxima and minima, especially the chain repulsion term, were strongly suppressed leading to a smoothed profile. The tension maxima in the headgroup region are merged and cover the whole headgroup region.
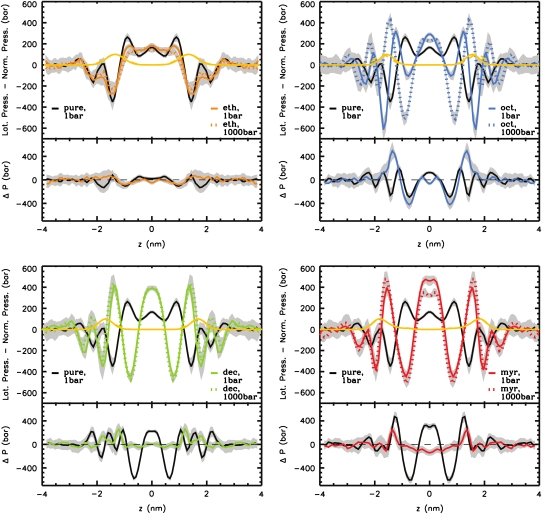
Inclusion of 1-alkanols into the bilayer strongly modified the pressure profiles (see Fig. 7). Ethanol mainly reduced the magnitude of the chain repulsion terms, which was, however, less pronounced if the GROMACS force field with modified partial charges (49) was used for ethanol (results not shown). This is in agreement with coarse-grained calculations of Frischknecht and Frink (28), whereas Terama et al. (37) found no significant changes at this peak in all-atom simulations using a DPPC bilayer. Both Frischknecht and Frink (28) and Terama et al. (37) reported a pronounced decrease of the interfacial tension upon addition of ethanol, whereas we observed only a slight, insignificant decrease. A splitting of the total pressure into the contributions from the interacting groups (data not shown) showed a decreased solvent-lipid tension at the interface and at the region of the glycerol group, and a peak for alkanol-lipid interactions in the latter region. Therefore it can be concluded that ethanol replaced solvent molecules in the region around the glycerol backbone. The above-mentioned difference in the total pressure profile to the study of Terama et al. (37) is probably due to different force fields used for ethanol and different cutoffs for Coulombic interactions.
FIGURE 7.
Upper section of each panel: Lateral pressure profiles of DMPC bilayers containing various 1-alkanols at external pressures of 1 bar (colored solid lines) and 1000 bar (colored dotted lines). For comparison, the lateral pressure profile of a pure DMPC bilayer is drawn (black solid line). Errors are indicated by gray shadows. The normalized dimensionless density of the lipid glycerol group is shown in yellow (solid line, 1 bar; dashed line, 1000 bar; mostly, these two curves overlap). Lower section of each panel: Difference between the lateral pressure profiles with and without 1-alkanols (black line) and the difference of the curves with 1-alkanols at 1000 bar and 1 bar (colored lines). For the calculation of the difference-pressure profiles, the contributing terms were scaled to the thickness of the pure bilayer at normal pressure.
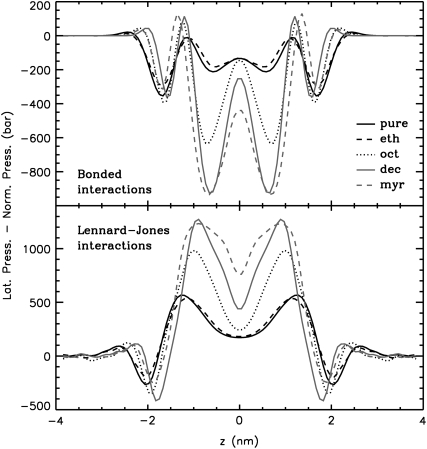
Addition of long-chain 1-alkanols amplified the local pressure maxima and minima in the bilayer core. Due to the thickening of the bilayers, the peaks were shifted outward. Remarkably, a tension peak was now seen within the hydrophobic core. This peak was caused by increased bonded interactions (see Fig. 8) from alkanol-alkanol and lipid-lipid interactions (data not shown). These bonded interactions are probably enlarged due to the increased order of the lipids and the 1-alkanols (see also the previous study (39)) (increased number of dihedrals in trans conformation). Upon addition of long-chain 1-alkanols, the repulsive Lennard-Jones interactions of the lipids and of the 1-alkanols were enhanced (see Fig. 8).
FIGURE 8.
Bonded and Lennard-Jones contributions to the total lateral pressure profile for all systems at normal pressure. All systems are scaled to the thickness of the pure bilayer at normal pressure. Errors are comparable to those for the total pressure profile.
With ethanol, decanol, and tetradecanol at high pressure, only moderate changes in the total pressure profile were found as compared to the respective pressure profile at 1 bar. The Lennard-Jones interactions in the high-pressure systems with decanol or tetradecanol are increased, but this change is compensated for by increased bonded interactions and decreased 1–4 interactions. Drastic changes in the lateral pressure profile were obtained for the octanol-DMPC system at high pressure: the interfacial tension minimum almost vanished, but the first minimum (counted from the center of the bilayer) became much more pronounced.
DISCUSSION
Partition coefficient
One hypothesis explaining the pressure reversal of anesthesia could have been a shift of the bilayer-water partitioning equilibrium of anesthetics such that less anesthetics dissolve in the lipid bilayer. Here, neither in the case of ethanol nor in the case of long-chain 1-alkanols, significant changes of the partition coefficients at a pressures of 1000 bar were observed. However, due to the large partition coefficients of long-chain 1-alkanols (62–64), moderate changes in the partition coefficient of these alkanols would hardly emerge in MD simulations with their inherent limited system size. Our results are in agreement with a study of Trudell et al. (65), where electron spin resonance techniques were used to investigate the partitioning of TEMPO (2,2,6,6 tetramethylpiperidine-1-oxyl) molecules in phospholipid vesicles. Only a very moderate shift of the distribution of TEMPO molecules between the aqueous and lipid phase, too small to account for the reversal of anesthesia, was found. Therefore, the assumption of reversal of anesthesia by a pressure-driven change of the 1-alkanols' partitioning behavior can be discarded, in agreement with the work by Miller et al. (10), who based on thermodynamic analysis showed in 1973 that a pressure-induced shift of partitioning is not able to explain the pressure-dependence of the anesthetic concentration.
Pressure profiles
The lateral pressure profile of a DMPC bilayer at normal pressure was not only largely modified by the addition of 1-alkanols studied here, but the long-chain 1-alkanols caused even a tension in the bilayer core. The conformational equilibrium of membrane-embedded proteins could easily be shifted by this effect. Therefore, the results presented here lend support to a lipid-mediated mode of anesthetic action via the lateral pressure inside a membrane as suggested by Cantor (12–14).
To illustrate this idea further, we calculated the hypothetical shift in the conformational equilibria of some model proteins (22,30) upon addition of 1-alkanols using the pressure profiles obtained from the MD simulations. For the notation and calculations, we follow the work by Cantor (22): At a given lateral pressure distribution p0, the conformational equilibrium between conformational states (s = r, t, …) of membrane proteins is given by 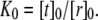 If the cross-sectional area difference ΔA(z) = At(z) − Ar(z) varies in the direction of the bilayer normal, a change in the lateral pressure profile p(z) results in the change of energy
If the cross-sectional area difference ΔA(z) = At(z) − Ar(z) varies in the direction of the bilayer normal, a change in the lateral pressure profile p(z) results in the change of energy
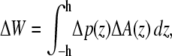 |
(4) |
with Δp(z) = p(z) − p0(z) and the thickness h of one monolayer. For ΔA(z) = const., it follows that
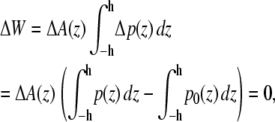 |
(5) |
since a self-assembled bilayer is always in a tension-free state (66). Induced by the change in lateral pressure, a new conformational equilibrium 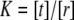 will be established. For the result of the integration (Eq. 4), the definition of the bilayer thickness d = 2h is crucial (see Fig. 9), as there exists a large tension at the lipid-water interface. Here, we defined the bilayer thickness by the maxima of the phosphorus density of the pure lipid bilayer at 1 bar and scaled the bilayers of all other simulations to the thickness of this bilayer. This approximation is reasonable, since lipid membranes in close vicinity of an embedded membrane protein adjust to its central hydrophobic surface. By equating the chemical potentials μr and μs of the two conformational states at each lateral pressure distribution p(z) and p0(z), and assuming that ΔA(z) is independent of Δp(z), Cantor deduced the relation
will be established. For the result of the integration (Eq. 4), the definition of the bilayer thickness d = 2h is crucial (see Fig. 9), as there exists a large tension at the lipid-water interface. Here, we defined the bilayer thickness by the maxima of the phosphorus density of the pure lipid bilayer at 1 bar and scaled the bilayers of all other simulations to the thickness of this bilayer. This approximation is reasonable, since lipid membranes in close vicinity of an embedded membrane protein adjust to its central hydrophobic surface. By equating the chemical potentials μr and μs of the two conformational states at each lateral pressure distribution p(z) and p0(z), and assuming that ΔA(z) is independent of Δp(z), Cantor deduced the relation 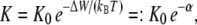 with kB and T denoting the Boltzmann constant and the temperature, respectively (12–14,22).
with kB and T denoting the Boltzmann constant and the temperature, respectively (12–14,22).
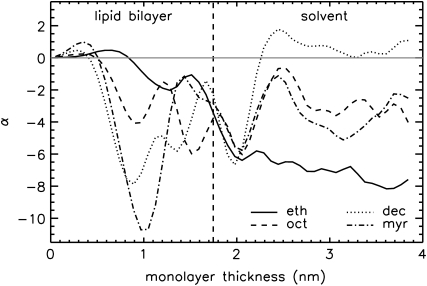
FIGURE 9.
Values of α = W/(kBT) (for the comparisons at 1 bar) as a function of the monolayer thickness chosen for the integration (see Eq. 4). The bilayer center is located at z = 0. The position of the phosphorus density maximum for the pure bilayer at 1 bar, used as the criterion for the monolayer thickness in our calculations, is marked by the dashed vertical line.
Assuming, as Cantor did (22), an expansion of the cross-sectional protein area in powers of z with different expansion coefficients in the two bilayer leaflets, i.e., 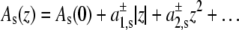 with
with 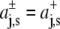 for z > 0 and
for z > 0 and 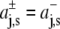 for z < 0, and a symmetrical bilayer (i.e., p(z) = p(−z)), α can be expressed in terms of the difference of the integral moments of p(z) and p0(z) (22)
for z < 0, and a symmetrical bilayer (i.e., p(z) = p(−z)), α can be expressed in terms of the difference of the integral moments of p(z) and p0(z) (22)
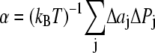 |
(6) |
with Δaj = 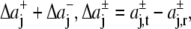 and
and 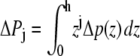 for j ≥ 1. ΔP0 is zero as the bilayer is always in a tension-free state (66). The first two integral moments of the DMPC bilayer at 1 bar, calculated from our pressure profiles, are P1/(kBT) = (−0.11 ± 0.04) Å−1 and P2/(kBT) = −3.26 ± 0.78. Using a statistical thermodynamic lattice model for bilayers, Cantor (22) derived values for P1/(kBT) = −1.74 Å−1 and P2/(kBT) = −29.4, about an order of magnitude smaller than the respective moments from the MD simulations. The differences probably arise from the simplified model and the neglected headgroup repulsion in the calculations of Cantor (22).
for j ≥ 1. ΔP0 is zero as the bilayer is always in a tension-free state (66). The first two integral moments of the DMPC bilayer at 1 bar, calculated from our pressure profiles, are P1/(kBT) = (−0.11 ± 0.04) Å−1 and P2/(kBT) = −3.26 ± 0.78. Using a statistical thermodynamic lattice model for bilayers, Cantor (22) derived values for P1/(kBT) = −1.74 Å−1 and P2/(kBT) = −29.4, about an order of magnitude smaller than the respective moments from the MD simulations. The differences probably arise from the simplified model and the neglected headgroup repulsion in the calculations of Cantor (22).
Three models for different membrane proteins have been suggested (22,30): The cooperative tilt model (22) describes a helix bundle, that is twisted along the bilayer normal (in opposite directions for the two monolayers). In the bent helix model (22), a membrane protein is built up by kinked helices forming a non-uniform bundle that can be inscribed by one truncated cone per monolayer. The cross-sectional area of such a membrane protein is 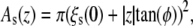 with the radius of the helix bundle ξs(0) and the angle φ = φ ± between the cone-shaped envelope of the kinked helix bundle at the upper/lower monolayer and the bilayer normal (for a more detailed description see (22)). The mechanosensitive channel MscL was approximated by a truncated cone stretching over the whole bilayer (conical shape model (30)). Different protein conformations are given by different slopes.
with the radius of the helix bundle ξs(0) and the angle φ = φ ± between the cone-shaped envelope of the kinked helix bundle at the upper/lower monolayer and the bilayer normal (for a more detailed description see (22)). The mechanosensitive channel MscL was approximated by a truncated cone stretching over the whole bilayer (conical shape model (30)). Different protein conformations are given by different slopes.
Using the results for the lateral pressure profiles from our simulations, we calculated the exponent α, characterizing the shift between two conformations of a protein, for these three protein models. As for the parameters of these models, we used values that were previously suggested from the respective authors: tan2(θt) − tan2(θr) = 0.05 for the cooperative tilt model ((22), corrected), with the twist angle θs of the respective conformation, a change of the cone slope from 0.0 to 0.2 for the MscL model of Gullingsrud and Schulten (30), and angles 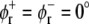 and
and 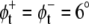 between the bilayer normal and the envelope of the kinked helices (assuming a symmetrical protein) for the bent helix model (22). A change in the conformational equilibria was considered as significant, if K and K0 differed by at least a factor of 2, i.e., if |α| ≥ ln(2) ≈ 0.69.
between the bilayer normal and the envelope of the kinked helices (assuming a symmetrical protein) for the bent helix model (22). A change in the conformational equilibria was considered as significant, if K and K0 differed by at least a factor of 2, i.e., if |α| ≥ ln(2) ≈ 0.69.
According to this definition, we found no significant changes in the protein conformational equilibrium upon addition of 1-alkanols or application of external pressure for the cooperative tilt and the conical shape model. However, assuming a bent helix model, the computed lateral pressure profiles for 1-alkanols and external pressure exert opposing effects on the conformational equilibrium of a hypothetical membrane protein, in line with the anesthetic action of 1-alkanols and the reversal of the anesthetic effect by external pressure (see Table 5): for addition of 1-alkanols at normal pressure, α was negative for all four investigated 1-alkanols.
TABLE 5.
Changes in the first and second integral moments upon the transition from p0(z) (reference system) to p(z) and corresponding changes in the conformational equilibrium of bent helix model proteins, measured by α
| System | Reference system | ΔP1/(kBT) (Å−1) | ΔP2/(kBT) | α | Significance |
|---|---|---|---|---|---|
| E1 | C1 | −0.125 ± 0.053 | −1.803 ± 0.794 | −3.43 ± 1.39 | Yes |
| O1 | C1 | −0.140 ± 0.060 | −1.048 ± 0.898 | −3.77 ± 1.60 | Yes |
| D1 | C1 | −0.088 ± 0.059 | 0.673 ± 0.853 | −2.27 ± 1.56 | Yes |
| TD1 | C1 | −0.109 ± 0.067 | 0.246 ± 1.017 | −2.86 ± 1.77 | Yes |
| C1000 | C1 | −0.112 ± 0.059 | −0.771 ± 0.860 | −3.02 ± 1.57 | Yes |
| E1000 | E1 | 0.011 ± 0.054 | 0.690 ± 0.828 | 0.33 ± 1.44 | No |
| O1000 | O1 | 0.293 ± 0.072 | 5.983 ± 1.077 | 8.16 ± 1.91 | Yes |
| D1000 | D1 | 0.225 ± 0.068 | 3.357 ± 0.976 | 6.17 ± 1.81 | Yes |
| TD1000 | TD1 | 0.041 ± 0.075 | 0.958 ± 1.139 | 1.16 ± 1.99 | No |
The error was calculated by error propagation.
The decreasing difference (within error margins) in the moments ΔP1 and ΔP2 for longer hydrocarbon chains of the 1-alkanols correlates with the cutoff effect for anesthetics, i.e., 1-alkanols with a chain length of 12 carbons or more do not show any anesthetic potency (see, e.g., Pringle et al. (2)). However, the cutoff is probably dependent on the membrane composition. Application of external pressure resulted—except for the control simulation—in positive values of α, and thus a reversal of the effect of 1-alkanols on the distribution of states, significant only for simulations containing octanol and decanol. The computed pressure-induced shift in the conformational equilibrium of a hypothetical protein in a pure lipid bilayer (negative α) correlates with the experimentally observed “pressure paralysis” (11).
Thus—although the application of external pressure did not reverse the alkanol-induced changes in the lateral pressure profile—a pressure-reversal mechanism of anesthesia for the bent helix model is seen: 1-alkanols moved the protein conformational equilibrium in one direction, whereas external pressure changed the equilibrium in the opposite direction. However, this pressure-reversal mechanism crucially depends on the type of change in protein shape upon activation or deactivation. Therefore, simulations of lipid bilayers containing explicit membrane proteins and eventually also different lipid species and cholesterol will be necessary.
Phase behavior
A different mechanism for anesthesia relies on shifts in the membrane phase transition temperatures by anesthetics (5). Depending on thermodynamic parameters such as temperature and pressure, lipid bilayers exist in different phases. Upon heating, pure DMPC bilayers at standard pressure exhibit a so-called pretransition from a gel to a ripple phase at 14°C and a main transition from a ripple to a liquid-disordered phase at 24°C (67–69). By application of external pressure, further distinct phases can be induced (70); for example, for saturated phosphatidylcholine bilayers with chain lengths of 13–18 carbon atoms, a pressure-induced interdigitated phase has been found (71).
Phase transitions of lipid bilayers have been observed successfully in dissipative particle dynamics simulations (72–74), as well as in coarse-grained and atomistic molecular dynamics simulations (75–78). In (MD) simulations, indications for phase transitions are drastic changes in the area per lipid, the bilayer thickness, the lipid chain order, and the lipid diffusion (78). Besides, the tilt angle of the lipid chains with respect to the membrane normal varies: in the gel Lβ and in the ripple Pβ′ phase, the lipid chains are tilted, whereas in the pressure-induced, partially interdigitated gel phase Lβi, they are aligned parallel to the bilayer normal. In the liquid crystalline phase Lα, the lipid chains are disordered (see Eisenblätter and Winter (70)).
In our simulations, we did not observe any signature for a phase transition of the pure DMPC bilayer and the bilayer with ethanol at 1000 bar. However, large structural changes were observed for the DMPC bilayer with octanol at high external pressure. Especially, the alignment of the lipid chains to the bilayer normal, the enhanced interdigitation, and the strong shrinking of the area per lipid indicate a transition to the partially interdigitated gel phase Lβi. Our previous simulations of DMPC bilayers with decanol and tetradecanol at 1 bar showed a drastic decrease in the area per lipid and an increase in the lipid order parameter. These systems probably underwent phase transitions to the gel state already at normal pressure. Therefore, for these systems, only moderate pressure-induced structural changes were found.
These results are in line with previous experiments: In accordance with the Clausius-Clapeyron relationship, Ichimori et al. (71) measured a linear increase of the gel to liquid-crystalline phase transition temperature with a slope of 21.2 K/kbar. At high pressures above 3 kbar, a partially interdigitated gel phase was observed. At normal pressure, addition of 1-alkanols up to the chain length of octanol caused a lowering of the main gel to liquid-crystalline phase transition temperature (39,79), depending linearly on the alkanol concentration (experiments with DPPC vesicle membranes) (80). Long-chain 1-alkanols from decanol up to tetradecanol exerted a biphasic dose-response effect on DPPC vesicles: at low concentrations they depressed, but at higher concentrations they elevated the phase transition temperature (81). Additional external pressure increased the phase transition temperatures with all 1-alkanols (80).
Since no phase transition was observed for pure DMPC at 1 kbar in the simulations, we conclude that in simulations, the main phase transition temperature for DMPC at normal pressure is significantly lower than obtained from experiment. Similarly decreased transition temperatures were found before for DPPC and DPPE bilayers applying a similar force field (78).
SUMMARY AND CONCLUSIONS
The influence of a large external pressure and of 1-alkanols of different chain lengths on the lateral pressure profile of a DMPC bilayer has been evaluated. Similar to the effect of a large external pressure on a pure bilayer, ethanol smoothed out the lateral pressure profile as compared to the profile of the pure bilayer. Long-chain 1-alkanols amplified local maxima and minima in such a way that a tension was created within the bilayer core. Except for the simulation with octanol, the pressure profiles for bilayers containing 1-alkanols were only moderately changed by a pressure of 1000 bar. External pressure slightly decreased both the area per lipid and, except for the simulation with octanol, the bilayer thickness. Lipid diffusion was strongly suppressed and an enhanced interdigitation of the lipid chains—for decanol and tetradecanol also of the 1-alkanol chains—was observed. At normal pressure, addition of long-chain 1-alkanols caused an alignment of the lipid chains in the direction of the bilayer normal. This effect was amplified by the application of an external pressure. For the octanol-DMPC system, external pressure probably caused a phase transition to the pressure-induced, partially interdigitated Lβi gel phase.
For the bent helix model of membrane proteins (22), changes in the lateral pressure profile caused by 1-alkanols and additional external pressure were found to shift the equilibrium between different protein conformations in opposite directions, consistent with an anesthetic effect of the 1-alkanols and the pressure reversal of anesthesia. Our results lend support to Cantor's model that anesthesia is mediated by local pressure changes. In this context, more complex simulations, including various lipid species and in particular membrane proteins, would be of interest, focusing on the effect of different anesthetics and external pressure on shifts in the main phase transition temperature and on their influence on embedded proteins.
Acknowledgments
We thank Volkhard Helms for support with computing time and Thomas Heimburg for valuable discussions.
Financial support by the Deutsche Forschungsgemeinschaft (Graduate School Structure Formation and Transport in Complex Systems, No. 1276/1) is gratefully acknowledged. As members of the Center for Bioinformatics, Rainer A. Böckmann and Beate Griepernau are supported by Deutsche Forschungsgemeinschaft grant BIZ 4/1.
Editor: Peter Tieleman.
References
- 1.Urban, B. W., M. Bleckwenn, and M. Barann. 2006. Interactions of anesthetics with their targets: non-specific, specific or both? Pharmacol. Ther. 111:729–770. [DOI] [PubMed] [Google Scholar]
- 2.Pringle, M. J., K. B. Brown, and K. W. Miller. 1980. Can the lipid theories of anesthesia account for the cutoff in anesthetic potency in homologous series of alcohols? Mol. Pharmacol. 19:49–55. [PubMed] [Google Scholar]
- 3.Franks, N., and W. R. Lieb. 1994. Molecular and cellular mechanisms of general anaesthesia. Nature. 367:607–614. [DOI] [PubMed] [Google Scholar]
- 4.Heimburg, T., and A. D. Jackson. 2005. On soliton propagation in biomembranes and nerves. Proc. Natl. Acad. Sci. USA. 102:9790–9795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Heimburg, T., and A. D. Jackson. 2007. The thermodynamics of general anesthesia. Biophys. J. 92:3159–3165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heimburg, T., and A. D. Jackson. 2007. On the action potential as a propagating density pulse and the role of anesthetics. Biophys. Rev. Lett. 2:57–78. [Google Scholar]
- 7.Johnson, F. H., D. Brown, and D. Marsland. 1942. A basic mechanism in the biological effects of temperature, pressure and narcotics. Science. 95:200–203. [DOI] [PubMed] [Google Scholar]
- 8.Johnson, F. H., and E. A. Flagler. 1950. Hydrostatic pressure reversal of narcosis in tadpoles. Science. 112:91–92. [DOI] [PubMed] [Google Scholar]
- 9.Lever, M. J., K. W. Miller, W. D. M. Paton, and E. B. Smith. 1971. Pressure reversal of anaesthesia. Nature. 231:368–371. [DOI] [PubMed] [Google Scholar]
- 10.Miller, K. W., W. D. M. Paton, R. A. Smith, and E. B. Smith. 1973. The pressure reversal of general anesthesia and the critical volume hypothesis. Mol. Pharmacol. 9:131–143. [PubMed] [Google Scholar]
- 11.Halsey, M. J., and B. Wardley-Smith. 1975. Pressure reversal of narcosis produced by anaesthetics, narcotics and tranquillisers. Nature. 257:811–813. [DOI] [PubMed] [Google Scholar]
- 12.Cantor, R. S. 1997. The lateral pressure profile in membranes: a physical mechanism of general anesthesia. Biochemistry. 36:2339–2344. [DOI] [PubMed] [Google Scholar]
- 13.Cantor, R. S. 1997. Lateral pressures in cell membranes: a mechanism for modulation of protein function. J. Phys. Chem. B. 101:1723–1725. [Google Scholar]
- 14.Cantor, R. S. 1998. The lateral pressure profile in membranes: a physical mechanism of general anesthesia. Toxicol. Lett. 100–101:451–458. [DOI] [PubMed] [Google Scholar]
- 15.Templer, R. H., S. J. Castle, A. R. Curran, G. Rumbles, and D. R. Klug. 1998. Sensing isothermal changes in the lateral pressure in model membranes using di-pyrenyl phosphatidylcholine. Faraday Discuss. 111:41–53. [DOI] [PubMed] [Google Scholar]
- 16.Kamo, T., M. Nakano, Y. Kuroda, and T. Handa. 2006. Effects of an amphipathic α-helical peptide on lateral pressure and water penetration in phosphatidylcholine and monoolein mixed membranes. J. Phys. Chem. B. 110:24987–24992. [DOI] [PubMed] [Google Scholar]
- 17.Szleifer, I., D. Kramer, A. Ben-Shaul, W. M. Gelbart, and S. A. Safran. 1990. Molecular theory of curvature elasticity in surfactant films. J. Chem. Phys. 92:6800–6817. [Google Scholar]
- 18.Szleifer, I., A. Ben-Shaul, and W. M. Gelbart. 1990. Chain packing statistics and thermodynamics of amphiphile monolayers. J. Phys. Chem. 94:5081–5089. [Google Scholar]
- 19.Xiang, T. X., and B. D. Anderson. 1994. Molecular distributions in interphases: statistical mechanical theory combined with molecular dynamics simulation of a model lipid bilayer. Biophys. J. 66:561–572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Harries, D., and A. Ben-Shaul. 1997. Conformational chain statistics in a model lipid bilayer: comparison between mean field and Monte Carlo calculations. J. Chem. Phys. 106:1609–1619. [Google Scholar]
- 21.Goetz, R., and R. Lipowsky. 1998. Computer simulations of bilayer membranes: self-assembly and interfacial tension. J. Chem. Phys. 108:7397–7409. [Google Scholar]
- 22.Cantor, R. S. 1999. The influence of membrane lateral pressures on simple geometric models of protein conformational equilibria. Chem. Phys. Lipids. 101:45–56. [DOI] [PubMed] [Google Scholar]
- 23.Cantor, R. S. 1999. Lipid composition and the lateral pressure profile in bilayers. Biophys. J. 76:2625–2639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Venturoli, M., and B. Smit. 1999. Simulating the self-assembly of model membranes. PhysChemComm. 10:45–49. [Google Scholar]
- 25.Cantor, R. S. 2002. Size distribution of barrel-stave aggregates of membrane peptides: influence of the bilayer lateral pressure profile. Biophys. J. 82:2520–2525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shillcock, J. C., and R. Lipowsky. 2002. Equilibrium structure and lateral stress distribution of amphiphilic bilayers from dissipative particle dynamics simulations. J. Chem. Phys. 117:5048–5061. [Google Scholar]
- 27.Mukhin, S. I., and S. Baoukina. 2005. Analytical derivation of thermodynamic characteristics of lipid bilayer from a flexible string model. Phys. Rev. E Stat. 71:061918. [DOI] [PubMed] [Google Scholar]
- 28.Frischknecht, A. L., and L. J. Douglas Frink. 2006. Alcohols reduce lateral membrane pressures: predictions from molecular theory. Biophys. J. 91:4081–4090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lindahl, E., and O. Edholm. 2000. Spatial and energetic-entropic decomposition of surface tension in lipid bilayers from molecular dynamics simulations. J. Chem. Phys. 113:3882–3893. [Google Scholar]
- 30.Gullingsrud, J., and K. Schulten. 2004. Lipid bilayer pressure profiles and mechanosensitive channel gating. Biophys. J. 86:3496–3509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Patra, M. 2005. Lateral pressure profiles in cholesterol-DPPC bilayers. Eur. Biophys. J. 35:79–88. [DOI] [PubMed] [Google Scholar]
- 32.Carrillo-Tripp, M., and S. E. Feller. 2005. Evidence for a mechanism by which ω-3 polyunsaturated lipids may affect membrane protein function. Biochemistry. 44:10164–10169. [DOI] [PubMed] [Google Scholar]
- 33.Gullingsrud, J., A. Babakhani, and J. A. McCammon. 2006. Computational investigation of pressure profiles in lipid bilayers with embedded proteins. Mol. Simul. 32:831–838. [Google Scholar]
- 34.Niemela, P. S., S. Ollila, M. T. Hyvönen, M. Karttunen, and I. Vattulainen. 2007. Assessing the nature of lipid raft membranes. PLoS Comput. Biol. 3:304–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ollila, O. H. S., T. Rog, M. Karttunen, and I. Vattulainen. 2007. Role of sterol type on lateral pressure profiles of lipid membranes affecting membrane functionality: comparison between cholesterol, desmosterol, 7-dehydrocholesterol and ketosterol. J. Struct. Biol. 159:311–323. [DOI] [PubMed] [Google Scholar]
- 36.Ollila, S., M. T. Hyvönen, and I. Vattulainen. 2007. Polyunsaturation in lipid membranes: dynamic properties and lateral pressure profiles. J. Phys. Chem. B. 111:3139–3150. [DOI] [PubMed] [Google Scholar]
- 37.Terama, E., O. H. S. Ollila, E. Salonen, A. C. Rowat, C. Trandum, P. Westh, M. Patra, M. Karttunen, and I. Vattulainen. 2008. Influence of ethanol on lipid membranes: from lateral pressure profiles to dynamics and partitioning. J. Phys. Chem. B. 112:4131–4139. [DOI] [PubMed] [Google Scholar]
- 38.van den Brink-van der Laan, E., V. Chupin, J. A. Killian, and B. de Kruijff. 2004. Small alcohols destabilize the KcsA tetramer via their effect on the membrane lateral pressure. Biochemistry. 43:5937–5942. [DOI] [PubMed] [Google Scholar]
- 39.Griepernau, B., S. Leis, M. F. Schneider, M. Sikor, D. Steppich, and R. A. Böckmann. 2007. 1-Alkanols and membranes: a story of attraction. Biochim. Biophys. Acta. 1768:2899–2913. [DOI] [PubMed] [Google Scholar]
- 40.Berendsen, H. J. C., D. van der Spoel, and R. van Drunen. 1995. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 91:43–56. [Google Scholar]
- 41.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7:306–317. [Google Scholar]
- 42.van der Spoel, D., E. Lindahl, B. Hess, G. Groenhof, A. E. Mark, and H. J. C. Berendsen. 2005. GROMACS: fast, flexible, and free. J. Comput. Chem. 26:1701–1718. [DOI] [PubMed] [Google Scholar]
- 43.Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
- 44.Miyamoto, S., and P. A. Kollman. 1992. SETTLE—an analytical version of the shake and rattle algorithm for rigid water models. J. Comput. Chem. 13:952–962. [Google Scholar]
- 45.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 46.Berendsen, H. J. C., J. P. M. Postma, W. F. Van Gunsteren, and J. Hermans. 1981. Interaction Model for Water in Relation to Protein Hydration. D. Reidel Publishing, Dordrecht, The Netherlands. 331–342.
- 47.Berger, O., O. Edholm, and F. Jähnig. 1997. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72:2002–2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chiu, S. W., M. Clark, V. Balaji, S. Subramaniam, H. L. Scott, and E. Jakobsson. 1995. Incorporation of surface tension into molecular dynamics simulation of an interface: a fluid phase lipid bilayer membrane. Biophys. J. 69:1230–1245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.MacCallum, J. L., and D. P. Tieleman. 2002. Structures of neat and hydrated 1-octanol from computer simulations. J. Am. Chem. Soc. 124:15085–15093. [DOI] [PubMed] [Google Scholar]
- 50.Oostenbrink, C., A. Villa, A. E. Mark, and W. F. van Gunsteren. 2004. A biomolecular force field based on the free enthalpy of hydration and solvation: the GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 25:1656–1676. [DOI] [PubMed] [Google Scholar]
- 51.Darden, T., D. York, and L. Pedersen. 1993. Particle Mesh Ewald—an N log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 52.Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- 53.Sonne, J., F. Y. Hansen, and G. H. Peters. 2005. Methodological problems in pressure profile calculations for lipid bilayers. J. Chem. Phys. 122:124903. [DOI] [PubMed] [Google Scholar]
- 54.Rowe, E. S. 1983. Lipid chain length and temperature dependence of ethanol-phosphatidylcholine interactions. Biochemistry. 22:3299–3305. [Google Scholar]
- 55.Trandum, C., P. Westh, K. Jorgensen, and O. G. Mouritsen. 1999. Association of ethanol with lipid membranes containing cholesterol, sphingomyelin and ganglioside: a titration calorimetry study. Biochim. Biophys. Acta. 1420:179–188. [DOI] [PubMed] [Google Scholar]
- 56.Trandum, C., P. Westh, K. Jorgensen, and O. G. Mouritsen. 2000. A thermodynamic study of the effects of cholesterol on the interaction between liposomes and ethanol. Biophys. J. 78:2486–2492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Koenig, B. W., and K. Gawrisch. 2005. Lipid-ethanol interaction studied by NMR on bicelles. J. Phys. Chem. B. 109:7540–7547. [DOI] [PubMed] [Google Scholar]
- 58.Patra, M., E. Salonen, E. Terama, I. Vattulainen, R. Faller, B. W. Lee, J. Holopainen, and M. Karttunen. 2006. Under the influence of alcohol: the effect of ethanol and methanol on lipid bilayers. Biophys. J. 90:1121–1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Tieleman, D. P., J. L. MacCallum, W. L. Ash, C. Kandt, Z. Xu, and L. Monticelli. 2006. Membrane protein simulations with an united-atom lipid and all-atom protein model: lipid-protein interactions, side chain transfer free energies and model proteins. J. Phys. Condens. Matter. 18:1221–1234. [DOI] [PubMed] [Google Scholar]
- 60.Siu, S. W. I., R. Vácha, P. Jungwirth, and R. A. Böckmann. 2008. Biomolecular simulations of membranes: physical properties from different force fields. J. Chem. Phys. 128:125103. [DOI] [PubMed] [Google Scholar]
- 61.Mateo, C. R., P. Tauc, and J.-C. Brochon. 1993. Pressure effects on the physical properties of lipid bilayers detected by trans-parinaric acid fluorescence decay. Biophys. J. 65:2248–2260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Seeman, P., S. Roth, and H. Schneider. 1971. The membrane concentrations of alcohol anesthetics. Biochim. Biophys. Acta. 225:171–184. [DOI] [PubMed] [Google Scholar]
- 63.Franks, N. P., and W. R. Lieb. 1986. Partitioning of long-chain alcohols into lipid bilayers: implications for mechanisms of general anesthesia. Proc. Natl. Acad. Sci. USA. 83:5116–5120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Rowe, E. S., F. Zhang, T. W. Leung, J. S. Parr, and P. T. Guy. 1998. Thermodynamics of membrane partitioning for a series of n-alcohols determined by titration calorimetry: role of hydrophobic effects. Biochemistry. 37:2430–2440. [DOI] [PubMed] [Google Scholar]
- 65.Trudell, J. R., W. L. Hubbell, E. N. Cohen, and J. J. Kendig. 1973. Pressure reversal of anesthesia: the extent of small-molecule exclusion from spin-labeled phospholipid model membranes. Anesthesiology. 38:207–211. [DOI] [PubMed] [Google Scholar]
- 66.Marsh, D. 1996. Lateral pressure in membranes. Biochim. Biophys. Acta. 1286:183–223. [DOI] [PubMed] [Google Scholar]
- 67.Wong, P. T. T., W. F. Murphy, and H. H. Mantsch. 1982. Pressure effects on the Raman spectra of phospholipid membranes: pressure induced phase transitions and structural changes in 1,2-dimyristoyl 3-sn-phophatidylcholine water dispersions. j. chem. phys. 76:5230–5237. [Google Scholar]
- 68.Ichimori, H., T. Hata, T. Yoshioka, H. Matsuki, and S. Kaneshina. 1997. Thermotropic and barotropic phase transition on bilayer membranes of phospholipids with varying acyl chain-lengths. Chem. Phys. Lipids. 89:97–105. [Google Scholar]
- 69.Heerklotz, H., and J. Seelig. 2002. Application of pressure perturbation calorimetry to lipid bilayers. Biophys. J. 82:1445–1452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Eisenblätter, J., and R. Winter. 2006. Pressure Effects on the structure and phase behavior of DMPC-gramicidin lipid bilayers: a synchrotron SAXS and 2H-NMR spectroscopy study. Biophys. J. 90:956–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Ichimori, H., T. Hata, H. Matsuki, and S. Kaneshina. 1998. Barotropic phase transitions and pressure-induced interdigitation on bilayer membranes of phopholipids with varying acyl chain lengths. Biochim. Biophys. Acta. 1414:165–174. [DOI] [PubMed] [Google Scholar]
- 72.Kranenburg, M., and B. Smit. 2004. Simulating the effect of alcohol on the structure of a membrane. FEBS Lett. 568:15–18. [DOI] [PubMed] [Google Scholar]
- 73.Kranenburg, M., M. Vlaar, and B. Smit. 2004. Simulating induced interdigitation in membranes. Biophys. J. 87:1596–1605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kranenburg, M., C. Laforge, and B. Smit. 2004. Mesoscopic simulations of phase transitions in lipid bilayers. Phys. Chem. Chem. Phys. 6:4531–4534. [Google Scholar]
- 75.Stevens, M. J. 2004. Coarse-grained simulations of lipid bilayers. J. Chem. Phys. 121:11942–11948. [DOI] [PubMed] [Google Scholar]
- 76.de Vries, A. H., S. Yefimov, A. E. Mark, and S. J. Marrink. 2005. Molecular structure of the lecithin ripple phase. Proc. Natl. Acad. Sci. USA. 102:5392–5396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Marrink, S. J., J. Risselada, and A. E. Mark. 2005. Simulation of gel phase formation and melting in lipid bilayers using a coarse grained model. Chem. Phys. Lipids. 135:223–244. [DOI] [PubMed] [Google Scholar]
- 78.Leekumjorn, S., and A. K. Sum. 2007. Molecular studies of the gel to liquid-crystalline phase transition for fully hydrated DPPC and DPPE bilayers. Biochim. Biophys. Acta. 1768:354–365. [DOI] [PubMed] [Google Scholar]
- 79.Lee, A. G. 1976. Interactions between anesthetics and lipid mixtures. Normal alcohols. Biochemistry. 15:2448–2454. [DOI] [PubMed] [Google Scholar]
- 80.Tamura, K., Y. Kaminoh, H. Kamaya, and I. Ueda. 1991. High Pressure antagonism of alcohol effects on the main phase-transition temperature of phospholipid membranes: biphasic response. Biochim. Biophys. Acta. 1066:219–224. [DOI] [PubMed] [Google Scholar]
- 81.Kamaya, H., N. Matubayasi, and I. Ueda. 1984. Biphasic effect of long-chain n-alkanols on the main phase transition of phospholipid vesicle membranes. J. Phys. Chem. 88:797–800. [Google Scholar]