The Geometry of Multisite Phosphorylation

Abstract

Reversible protein phosphorylation on multiple sites is a key regulatory mechanism in most cellular processes. We consider here a kinase-phosphatase-substrate system with two sites, under mass-action kinetics, with no restrictions on the order of phosphorylation or dephosphorylation. We show that the concentrations of the four phosphoforms at steady state satisfy an algebraic formula—an invariant—that is independent of the other chemical species, such as free enzymes or enzyme-substrate complexes, and holds irrespective of the starting conditions and the total amounts of enzymes and substrate. Such invariants allow stringent quantitative predictions to be made without requiring any knowledge of site-specific parameter values. We introduce what we believe are novel methods from algebraic geometry—Gröbner bases, rational curves—to calculate invariants. These methods are particularly significant because they make it possible to treat parameters symbolically without having to specify their numerical values, and thereby allow us to sidestep the parameter problem. We anticipate that this approach will have much wider applications in biological modeling.

INTRODUCTION

Reversible phosphorylation of proteins on serine, threonine, and tyrosine residues is one of the most significant forms of posttranslational regulation in eukaryotic cells (1,2). What is particularly striking about it is the extent of multisite modification, especially on substrates that play key regulatory roles. The epidermal growth factor receptor, a target of modern anticancer drugs, phosphorylates itself on 10 sites (3); the transcription factor p53, the “gatekeeper” of the genome, is phosphorylated on 16 sites (4); the tyrosine kinase Wee1, a key inhibitor of the G2/M transition in the cell cycle, is phosphorylated on 32 sites (5); the microtubule-associated protein tau becomes phosphorylated on 39–45 sites in Alzheimer's disease (6).

A single substrate molecule with n sites may be in one of 2ⁿ phosphoforms, each corresponding to a particular pattern of phosphorylated sites. However, the downstream response to phosphorylation samples the population of substrate molecules, not just any single molecule. It is therefore the state of the population of molecules that is biologically relevant, and this can be described by a distribution of concentrations of each of the 2ⁿ phosphoforms (7). Unlike the state of a single molecule, which may be treated in terms of protein sequence or structure, the phosphoform distribution is a dynamical quantity that is regulated by the collective interactions of the substrate with its cognate kinases and phosphatases. We wanted to understand the scope of this regulation and to determine in what way the phosphoform distribution changes in response to changes in enzyme activation and substrate availability.

We made preliminary progress toward answering these questions in a previous article (8). We considered a substrate, S, with two phosphorylation sites, which is phosphorylated by a kinase, E, and dephosphorylated by a phosphatase, F, as follows:

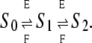(1)

This network of reactions is based on two assumptions. First, it is assumed that both enzymes act distributively, making at most one modification (addition or removal of a phosphate) in each collision between enzyme molecule and substrate molecule (9). Examples of both distributive phosphorylation and distributive dephosphorylation have been discussed in the literature (10–14). The MAPK layer of the MAP kinase cascade leading to Erk provides the canonical example of a two-site system—Mek kinase, MKP3 phosphatase, and Erk substrate—which satisfies the distributivity assumption (10,11,13). Second, it is assumed that the kinase phosphorylates in a strict order, while the phosphatase dephosphorylates in the reverse order. This implies that only three phosphoforms appear, not four. (The notation “S_i” in Eq. 1 signifies the phosphoform in which i sites have been phosphorylated in order.) Sequentiality is mathematically convenient—it reduces the number of phosphoforms from 2ⁿ to n + 1—and has been widely assumed in modeling studies, but its biological relevance remains unclear, as discussed below. In particular, the Mek-MKP3-Erk system is known not to be sequential (10,11).

Each enzyme is further assumed to act according to a standard biochemical scheme like that shown in Fig. 1 b. With mass-action kinetics, these assumptions give rise to a set of ordinary differential equations—a dynamical system—that describe the temporal changes in the concentrations of the nine chemical species in the system: three substrate phosphoforms, four enzyme-substrate complexes, and two free enzymes. The system has 12 parameters corresponding to the site-specific rate constants. Note that these parameter values are usually not known.

FIGURE 1.

Nonsequential multisite phosphorylation with two sites. (a) The four phosphoforms, S₀₀, S₀₁, S₁₀, S₁₁, are interconverted by the kinase, E, and the phosphatase, F. The dashed line indicates the possibility of processive modification by either kinase or phosphatase. (b) Each enzyme (X = E, F) acts through the standard biochemical mechanism shown. v has more bits than u when X = E and less bits than u when X = F, and u and v differ in only a single bit if the enzyme is distributive. Assuming mass-action kinetics, each reaction is annotated with the corresponding rate constants (a for “association”; b for “breakup”; c, for “catalysis”). Further details in the text.

We showed that the phosphoform distribution of this system has an unexpected property (8). Assume that it is started with some arbitrarily chosen concentrations of substrate and enzymes and allowed to reach a (stable) steady state. (Oscillations are not known in this system, although they are in related systems (15). Multistability, however, is possible: the same total amounts of substrate and enzymes may yield different steady states, depending on the initial conditions (7,16).) If the concentrations of the phosphoforms are measured at steady state and indicated by square brackets, then

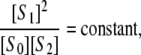(2)

where the constant depends only on the parameters. In particular, the quantity [S₁]²/[S₀][S₂] has exactly the same value in all experiments involving the same substrate and enzymes, independent of the total amounts of substrate and enzymes, the starting conditions, and the steady state that is reached. If a different substrate or different enzymes are used, satisfying the same assumptions, then Eq. 2 continues to hold, but the constant will change, reflecting the altered parameter values. Equation 2 is the first example of a steady-state invariant. It provides a stringent quantitative prediction without requiring knowledge of any parameter values.

If one or both of the enzymes in Eq. 1 is processive, so that more than one modification can be made in a collision between substrate and enzyme molecules, then there is the possibility of an additional reaction linking S₀ directly to S₂, or vice versa. In such a model, Eq. 2 no longer holds, but the way it changes can be used to determine each of the four possible cases in which the kinase or the phosphatase would be distributive or processive. Furthermore, this can still be done without requiring knowledge of any parameter values. Several processive kinases have been identified (17–19), although not, as yet, any phosphatases (which have traditionally been less well studied). The steady-state method of distinguishing enzyme mechanisms based on Eq. 2 has some advantages over the time-course methods normally used (10,11,17–19), as explained previously (8).

These results confirm the value of studying the steady-state phosphoform distribution, but the assumption of sequentiality in Eq. 1 limits their applicability. GSK3, in its “primed” phosphorylation mode, phosphorylates substrates in a strictly sequential C-to-N order (20). The kinase domain of the fibroblast growth factor receptor FGFR1 also autophosphorylates in a strict order in vitro (21). These examples suggest that phosphatases may also undertake ordered dephosphorylation. However, no such phosphatase has yet been identified. Accordingly, no kinase-phosphatase-substrate system is currently known to follow the model specified in Eq. 1.

In this article, we study the phosphoform distribution of a two-site system, making no assumptions about the order of phosphorylation or dephosphorylation. Several important examples exist, such as the MAPKK and MAPK layers of MAP kinase cascades, both of which are activated by double phosphorylation (22). The corresponding reaction network is shown in Fig. 1 a. The phosphoforms are now denoted S_u, where u is a bit string of length two encoding the pattern of phosphorylation on the two sites (0 or 1 for the absence or presence, respectively, of a phosphate). We show here that the phosphoform distribution satisfies the following striking geometric property when both enzymes are distributive. If the concentrations of the four phosphoforms are measured at steady state for varying total amounts of substrate and enzymes and varying initial conditions, then the points with coordinates

(3)

all lie on a plane that depends only on the parameters. Note the similarity in algebraic form between Eqs. 2 and 3, along with the considerable increase in geometric complexity in Eq. 3—a plane instead of a point—that arises from nonsequentiality. We show further that departures from this planarity arise, as previously, when one or the other of the enzymes is processive, and that this can be used to predict enzyme mechanisms without requiring knowledge of any parameter values (see Fig. 3). Although models like those in Fig. 1 have been widely used to study multisite phosphorylation, they have rarely been subjected to stringent quantitative tests. The results of this study provide the means for doing so.

FIGURE 3.

(y₁, y₂, y₃) curves for each of the four combinations of enzyme mechanisms, in the positive quadrant of R³. The paired labels indicate kinase/phosphatase, where D is distributive and P is processive. blue, D/D curve; cyan, D/P curve; red, P/D curve; purple, P/P curve. Each of the curves is based on the same core set of parameter values as in the D/D case. These values were drawn randomly from the uniform distribution on [0.00, 5.00] and are listed in the Mathematica notebook. The plane defined by Eq. 6 is shown with the D/D curve lying on it. The D/P curve has, in addition to the already chosen parameter values, whereas the P/D curve has The D/P and P/D curves look similar but have different behaviors for small and large t, as described in Fig. 2. The P/P curve has both 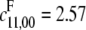and The value of t = [E]/[F] was varied in [0.01, 100]. This example was representative of 100 similarly generated ones. The Mathematica notebook allows the vantage point of the plot to be varied, which reveals the shape of the curves more clearly.

A crucial feature of our approach is that it does not require knowledge of parameter values. We have argued elsewhere that the “parameter problem” is one of the central difficulties in biological modeling (23). Models that reflect the molecular complexity of biological pathways usually have a large number of undetermined parameters. Methods for dealing with these vary from trying to avoid them by abstraction (24) or coarse graining (25), to fitting them to experimental data (26), to arguing for functional robustness to parameter values (27,28). None of these seems fully satisfactory as a general and systematic approach. In this article, we exploit a property of models that arise from biochemical networks with mass-action kinetics: their steady states form an algebraic variety that can hence be studied by the methods of algebraic geometry (29). Moreover, this can be done in such a way that the parameters are treated as symbolic quantities rather than as numbers. It is this flexibility which allows us to make stringent quantitative predictions without knowledge of parameter values.

Gröbner basis methods from algebraic geometry have previously been used to compute rate laws in metabolic control analysis (30,31) and to infer discrete models of molecular networks from time-series data (32,33), whereas toric varieties have been used to provide an alternative treatment of some aspects of chemical reaction network theory (34). Aside from these pioneering efforts, algebraic geometry has not been exploited in biological modeling. (It has stimulated recent developments in algebraic statistics and phylogenetic analysis (35).) We provide below an introduction to the algebraic geometry needed here. Our results suggest that these methods may well have wider applications beyond the particular problem of multisite phosphorylation discussed in this article.

MATERIALS AND METHODS

The results were obtained by mathematical analysis. The details of the calculations are reproduced in the accompanying Mathematica 6.0.0 notebook (Wolfram Research, Champaign, IL), which can be obtained from the corresponding author or downloaded from http://vcp.med.harvard.edu/papers.html.

RESULTS

The nonsequential model

The network of reactions for the nonsequential case is shown in Fig. 1 a. There are now four phosphoforms: S₀₀, S₀₁, S₁₀, and S₁₁. In the case where both enzymes are distributive, there are four phosphorylations by E and four dephosphorylations by F. If E is processive, there is an additional phosphorylation taking S₀₀ to S₁₁, whereas if F is processive, there is an additional dephosphorylation taking S₁₁ to S₀₀. These are indicated by the dotted line in Fig. 1 a. As previously described, each enzyme acts through a standard biochemical scheme (36), with reversible formation of a single enzyme-substrate complex and irreversible formation of product. ATP, ADP, and inorganic phosphate are assumed to be maintained at constant levels by some process that is not explicitly modeled. This is reasonable in vivo and is taken for granted in all models of phosphorylation. Accordingly, the total amount of substrate and total amounts of each enzyme are conserved, although these amounts become distributed among phosphoforms and enzyme-substrate complexes in a dynamic way as the reactions proceed.

In this model, it is possible for one substrate to yield multiple products. For instance, S₀₀ can produce either S₀₁ or S₁₀ and, if E is processive, also S₁₁. At the biochemical level, we assume that only a single enzyme-substrate complex is formed with different catalytic rates for each product. We could have assumed that a separate enzyme-substrate complex is formed for each potential product. However, this would have made no difference to our conclusions (results not shown) and would have considerably increased the number of parameters. Fig. 1 b shows the individual reactions annotated with their corresponding rate constants. Each rate constant has a superscript indicating either kinase or phosphatase and a subscript giving the bit string of the substrate. Because there may be several catalytic rates, corresponding to different products, the catalytic rate constant has a second subscript given by the bit string of its product. The model has 12 chemical species—four phosphoforms, six enzyme-substrate complexes, and two free enzymes—and 20 parameters when both enzymes are distributive with one extra parameter for each processive enzyme.

Previous models of phosphorylation have often relied on Michaelis-Menten rate functions in place of mass action. This is a dubious approximation, at best, and particularly suspect when enzymes have multiple substrates (37). We avoid it completely here.

With both enzymes processive, the dynamical system takes the form dx/dt = f(x; a), where x is the vector of species concentrations (x ∈ R¹²), a is the vector of parameters (a ∈ R²²) and f₁(x; a), ⋯, f₁₂(x; a) are the rate functions for each species. Here, R denotes the real numbers. If parameter values are chosen and an initial condition, x₀, is picked, then the dynamical system gives rise to a trajectory x(t) for which x(0) = x₀ (38). The total amounts of substrate and enzymes are conserved along any trajectory, and the trajectory is expected to always reach a steady state, at which dx/dt = 0 or, equivalently, f(x; a) = 0. Steady states may be stable or unstable (38). Only stable steady states will be experimentally realized but stability is not needed for the calculations below; the system may be in any steady state. Note that different initial conditions may lead to different steady states, even when the total amounts of enzymes and substrates are the same (multistability) (7,16). The set of steady states is denoted W ⊂ R¹² and depends on the choice of parameter values.

Of the 12 species concentrations, only those of the four phosphoforms are readily measurable, and it is their distribution with which we are particularly concerned. We denote the set of these distributions by π(W) ⊂ R⁴, considering it as the image of W under the projection 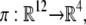which forgets the six enzyme-substrate complexes and the two free enzymes. What we seek to do in this study is to understand the geometry of π(W). Our first strategy will be to find algebraic formulae that are satisfied by all phosphoform distributions in π(W).

The steady-state equations provide formulae, f(x; a) = 0, which are satisfied in any steady state, but these formulae involve enzyme-substrate complexes and free enzymes as well as the phosphoforms. The enzyme-substrate complexes can be readily eliminated. If an enzyme-substrate complex is at steady state, then the reaction scheme in Fig. 1 b implies that

where the sum over catalytic rates allows for the possibility of multiple products S_v. It follows that

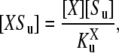(4)

where 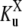is a generalized Michaelis-Menten constant,

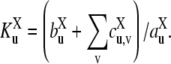(5)

This shows that at steady state, [XS_u] can be written in terms of [X] and [S_u]. The steady-state equations can therefore be rewritten so as to use only the four phosphoforms and the two free enzymes, [E] and [F]. The enzyme-substrate complexes have been eliminated. What is surprising is that the free enzymes can also be eliminated, leading to expressions like Eq. 3. This can be shown by direct calculation, which is how we first came across it, but it is hard to tell from this whether the resulting expressions are the only possibilities for eliminating the free enzymes. Algebraic geometry provides the framework in which such questions can be systematically answered.

Review of algebraic geometry

Readers familiar with algebraic geometry or Gröbner basis methods may wish to skip this section. The material summarized here is largely taken from Cox et al. (29), which may be consulted for more details.

An algebraic variety is the set of simultaneous solutions of a collection of polynomial equations in several variables. If we denote the variables x₁, ⋯, x_n (n no longer signifying the number of phosphorylation sites) then a polynomial in these variables is a finite linear combination of monomials, where α_i ≥ 0. It is convenient to write a monomial as x^α, where α = (α₁, ⋯, α_n) is an n-tuple of nonnegative exponents. A polynomial is then a finite sum of the form 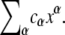The coefficients c_α may be drawn from any field, so that coefficients can be added, subtracted, multiplied and divided. The ability to work over an arbitrary field brings many advantages, particularly for dealing with parameters, as shown below.

Given a coefficient field, K, K[x₁, ⋯, x_n] will denote the algebra of polynomials in x₁, ⋯, x_n with coefficients in K. This will often be abbreviated to K[x]. If g₁, ⋯, g_m ∈ K[x] represents a collection of polynomials, then 𝒱(g₁,…,g_m) will denote the corresponding algebraic variety:

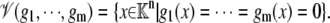For instance, in the real plane, 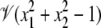is the unit circle, whereas, as we will shortly see, consists of just four points.

Polynomials, and hence algebraic varieties, arise from finite sums and products of variables. There are two contexts in molecular biology where this algebraic geometric viewpoint may be useful. The first is in models of molecular systems based on mass action. The rates of formation of chemical species are finite sums of production and consumption terms (finite because there is only a finite number of reactions in the system), while mass action implies that the production and consumption terms are monomials multiplied by (positive) real number coefficients (the rate constants). For this reason, when parameter values are specified, the set of steady states W ⊆ R¹² becomes an algebraic variety over R: 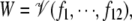where the polynomials f₁, ⋯, f₁₂ are the rate functions in the dynamical system dx/dt = f(x; a) described above.

The second context arises when state spaces are finite. In this case, functions on the state spaces can sometimes be represented as polynomials from which algebraic varieties naturally arise. This occurs in the study of finite statistical models, such as those used in gene finding, sequence alignment and phylogenetic tree construction (35), or when using finite-state models to reconstruct molecular regulatory networks (32,33). The field of algebraic statistics originated with the discovery of invariants for phylogenetic trees (39,40), which are similar in spirit to the invariants for multisite phosphorylation studied here.

One of the basic ideas in algebraic geometry is to associate to a geometric object those polynomials which vanish, or are “invariant”, on it. Given a variety the polynomials g₁, ⋯, g_m all vanish on V, by definition. However, any polynomial of the form 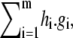where h_i are arbitrary polynomials in K[x], also vanishes on V. Here, h.g denotes multiplication of polynomials. The ideal generated by g₁, ⋯, g_m, denoted 〈g₁, ⋯, g_m〉, is the subset of K[x] consisting of all polynomials of the form 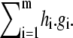In general, an ideal is any subset I ⊆ K[x] for which g + h ∈ I whenever g, h ∈ I, and g.h ∈ I whenever g ∈ I and h ∈ K[x]. It can easily be checked that these properties hold for 〈g₁, ⋯, g_m〉. One of the fundamental results that initiated algebraic geometry is David Hilbert's Basis Theorem: every ideal of K[x] is finitely generated and can therefore be expressed in the form 〈g₁, ⋯, g_m〉 (29). A set of generators for an ideal is called a basis.

One reason that ideals are so useful for studying geometric objects is that they allow a choice of different generators. If 〈g₁, ⋯, g_m〉 and 〈h₁, ⋯, h_l〉 are the same ideal (note that bases do not have to be the same size for this to be so), then it is easy to check that they define the same variety: Working with the ideal removes the dependency on any particular set of generators and allows generators to be chosen that are appropriate to the particular question being asked. For instance, it is not difficult to show that from which it follows immediately that the corresponding variety consists of {(±2, ±1)}.

The problem with which we are concerned is one of elimination. Given an ideal I ⊂ K[x₁, ⋯, x_n], we want to identify polynomials in I that do not use the variables x₁, ⋯, x_l. In our case, the ideal is 〈f₁, ⋯, f₁₂〉 and the variables to be eliminated are the enzyme-substrate complexes and the free enzymes. It is easy to check that I_l ∩ K[x_l+1, ⋯, x_n] is an ideal of K[x_l+1, ⋯, x_n]. It is called the l-th elimination ideal. Of course, this ideal could be empty. What we need is a basis for it. If we can find a basis for I, I = 〈g₁, ⋯, g_m〉, which is a Gröbner basis for the lexicographic order, then a basis for the elimination ideal consists simply of those g_i that lie in K[x_l+1, ⋯, x_n]: I_l = 〈{g₁, ⋯, g_m} ∩ K[x_l+1, ⋯, x_n]〉 (29). The significance of this is that it gives all the relevant polynomials: any polynomial in I that does not use the variables x₁, ⋯, x_l, can be generated from those g_i that are in the elimination ideal.

A Gröbner basis for an ideal I is one in which the polynomial remainder with respect to the basis determines membership of I. This is best understood in relation to polynomials in a single variable. If g, h ∈ K[x₁], then the analog of the “long-division” algorithm for numbers shows that h can always be divided by g with a remainder: there are unique polynomials, p, r ∈ K[x₁], such that h = p.g + r, where the degree of r—the highest power of x₁ in r—is strictly lower than the degree of g (29). This is extremely useful, because for instance, it solves the ideal membership problem. It is easy to check that h ∈ 〈g〉, if, and only if, r = 0. It further shows that any ideal I ⊂ K[x₁] is generated by a single polynomial. Simply take the polynomial in I of least degree and use the division algorithm to show that it generates I.

The division algorithm depends on the fact that monomials in x₁ have a natural order, corresponding to the normal order on their exponents: 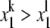if, and only if, k > l. Given any polynomial h ∈ K[x₁], this allows the largest monomial in h to be identified; its exponent is the degree of the polynomial. In contrast, monomials in more than one variable have no natural order on them. We can, however, impose various monomial orders, of which the lexicographic (lex) order is one of the most frequently used. In K[x₁, ⋯, x_n] we say that x^α> x^β if (α₁, ⋯, α_n) is lexicographically greater than (β₁, ⋯, β_n). That is, the first i for which α_i ≠ β_i satisfies α_i > β_i. Note that this implies x₁ > x₂ > ⋯> x_n. A monomial order is required to be a total order for which x^α > 1 and for which the order commutes with multiplication: if x^α > x^β, then x^α.x^γ > x^β.x^γ. It is easy to see that lex order satisfies these properties but there are many other monomial orders that are useful for different purposes.

Given a monomial order, it becomes possible to generalize the division algorithm to polynomials in more than one variable. Given a sequence of polynomials, g₁, ⋯, g_m ∈ K[x], and a polynomial h ∈ K[x], then there exist polynomials p₁, ⋯, p_m, r ∈ K[x], such that

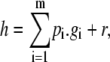where none of the monomials in r are divisible by the largest monomials in any of the g_i.

Although this generalized algorithm is helpful, it no longer determines ideal membership once n > 1. Consider the ideal, I = 〈x₁x₂ + 1, – 1〉 ⊂ K[x₁, x₂]. Although x₁() is evidently in I, the division algorithm for lex order gives

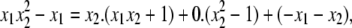which has a nonzero remainder. Unlike the single-variable case, the remainder upon division does not determine membership in the ideal. A Gröbner basis for a monomial order is a basis for which the remainder upon division is zero if, and only if, the dividend is in the ideal generated by the basis. It is a basic result of computational algebraic geometry that a Gröbner basis can always be found for any ideal and any monomial order (29). The facility to do this is provided in several computational tools, including Mathematica. In the next section, we will use Mathematica to compute a Gröbner basis for the lex order for the ideal 〈f₁, ⋯, f₁₂〉 ∈ R[x₁, ⋯, x₁₂] and thereby determine a basis for the required elimination ideal. This will lead us to invariants for π(W). (In fact, we will work over a different field to R (see below), but the method will be identical.)

Before proceeding, we note that π(W) itself need not necessarily be an algebraic variety. This is because it is obtained by projection. The variety 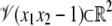is a hyperbola. If it is projected onto the x₁ variable, the resulting set is all of R except for the origin, because there is no x₂ for which 0 × x₂ = 1. The set R – {0} is not an algebraic variety, because no nonzero polynomial in one variable can have infinitely many solutions. Although projection may not preserve algebraicity, the elimination ideal still provides polynomials that vanish on π(W). The variety defined by the generators of the elimination ideal may, however, be strictly greater than π(W). We postpone determination of the geometric structure of π(W) to a later study. Our concern is to first show, by providing insights into enzyme mechanisms, that the geometric viewpoint being developed here has biological value.

Invariants for π(W)

To use the elimination theorem stated in the previous section, the variables to be eliminated must be highest in the lexicographic order, in which x₁ > ⋯> x₁₂. Let x₁, ⋯, x₈ represent the enzyme-substrate complexes and free enzymes and x₉, ⋯, x₁₂ represent the phosphoforms. The exact order is given in the Mathematica notebook that accompanies this article (see Materials and Methods). The notebook includes the other calculations discussed here. Instead of working over R, we will work over R(a), the field of rational functions in a₁, ⋯, a_m with coefficients in R. This will allow us to treat the parameters as symbolic quantities and to draw conclusions that are independent of the parameter values. Recall that a rational function is an expression of the form g/h where g, h ∈ R[a₁, ⋯, a_m] are polynomials. Because rational functions can be divided, as well as added, subtracted, and multiplied (as polynomials can), they form a perfectly respectable field of coefficients. Although we will formally work over R(a), we will continue to refer to W and π(W) as “real” and it should be kept in mind that this depends on parameter values.

Although working over R(a) has many advantages, an element like 1/(a₁ – 1), though well-defined in R(a), has no meaning in R when a₁ = 1. Care must be taken to ensure that coefficients remain well defined when specific numerical values are given to the parameters a₁, ⋯, a_m.

Let I = 〈f₁, ⋯, f₁₂〉 ⊆ R(a)[x₁, ⋯, x₁₂]. The required elimination ideal is I₈ = I ∩ R(a)[x₉, ⋯, x₁₂]. Mathematica's GroebnerBasis function readily computes a Gröbner basis for I for the lex order over R(a). It has 12 elements, as did the original basis. (Gröbner bases can become large and complex, particularly for the lex order.) We found on first inspection that I₈ = However, I₇ was generated by three polynomials, x₈.p₁, x₈.p₂, and x₈.p₃, where p₁, p₂, p₃ ∈ R(a)[x₉, ⋯, x₁₂]. Since [F] = x₈ can only be zero if there is no phosphatase in the system, which we may assume not to be the case, p₁, p₂, and p₃ must themselves vanish on π(W) and are therefore invariants for π(W). Let be the corresponding algebraic variety. Note that π(W) ⊆ V, but, recalling the discussion above, V may be strictly larger than π(W).

The polynomials p₁, p₂, and p₃ are each homogeneous quadrics. A polynomial 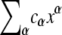is homogeneous if each monomial (for which c_α ≠ 0) has the same total degree, α₁ + ⋯ + α_n. It is a quadric if the total degree is 2. Hence, p₁, p₂, and p₃ are each sums of monomials of the form [S_u][S_v], for some u, v (including u = v). Homogeneity implies that V is a projective variety. If (x₉, ⋯, x₁₂) ∈ V, then so is the line through the origin to this point, given by (λx₉, ⋯, λx₁₂) for λ ∈ R. Projective geometry extends classical geometry by introducing “points at infinity”, which provides a more appropriate setting for some geometric constructions. The projective nature of V is surprising because the original dynamical system dx/dt = f(x; a) has no similar property. However, the projectivity can be seen to emerge at steady state by using Eq. 4.

Visualizing a projective variety in R⁴ is not straightforward. However, a simplification arises when both enzymes are distributive. If the Gröbner basis calculation is repeated after setting in f(x; a), then a suitable linear combination of the corresponding p₁, p₂, and p₃ invariants yields the polynomial

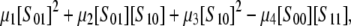where the coefficients μ_i are (polynomial) expressions in the parameters μ_i ∈ R[a]. Introducing new variables y₁, y₂, and y₃, the variety defined by the equation

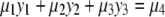(6)

is a plane in R³. Hence, making the identifications

(7)

we deduce the planarity result for Eq. 3 stated in the Introduction: when both enzymes are distributive, the points with coordinates (y₁, y₂, y₃) defined by Eq. 7 always lie on a plane, for varying total amounts of substrate and enzymes and varying initial conditions. In particular, this statement holds irrespective of the values of the parameters, which may change the plane but not the planarity. This provides a stringent quantitative test of the assumptions represented in Fig. 1 and immediately leads to testable predictions, as discussed below.

If either of the enzymes is processive, Eq. 6 no longer holds and the set of points defined by Eq. 7 is no longer confined to a plane. We were unable to find an invariant like Eq. 6 in these cases and turned, therefore, to a more explicit method for constructing points in π(W).

Rational parameterization of π(W)

The points in the variety are described implicitly as solutions of the equations g₁ = ⋯ = g_m = 0. It is sometimes possible to find explicit descriptions of the points of a variety. For instance, the unit circle in the plane is implicitly described as It can also be explicitly described as the locus of points of the form

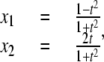(8)

where t ∈ R. It is easy to check that The parameter t can be interpreted as the x₂ coordinate of the point of intersection of the x₂ axis with the straight line joining (x₁, x₂) and (–1, 0) on the circle. The expressions used for x₁ and x₂ are no longer polynomials but rational functions of t, and Eq. 8 provides a rational parameterization of the circle over R. Such varieties are quite specialized and whether or not a given variety admits a rational parameterization is a subtle question. 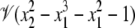For instance, in the real plane, the variety is rational, whereas is not (41).

A rational parameterization of π(W) can be constructed as follows. (The result proved here can be shown to hold in much greater generality for substrates with arbitrary numbers of sites (7,42).) Assume that both enzymes are processive and use Eq. 4 to rewrite the rate functions for the four phosphoforms in terms of just the phosphoforms and the free enzymes. Each monomial in these polynomial expressions then has the form α[X][S_u] where α ∈ R(a), X = E or F, and S_u is one of the four phosphoforms. Since we may assume that [F] ≠ 0 in any steady state (since this would correspond to absence of phosphatase), we may rewrite each monomial in the form [F]αtⁱ[S_u], where t = [E]/[F] and i = 0, 1. Hence, cancelling [F], each steady-state equation takes the form p = 0, where p is a linear expression in the phosphoform variables with coefficients in R(a, t), the field of rational functions of a₁, ⋯, a_m and t. The nonlinearity has been absorbed into the coefficient field.

With the usual ordering for the phosphoforms, [S₀₀], [S₀₁], [S₁₀], [S₁₁], these linear equations define a 4 × 4 matrix over R(a, t). Linear algebra can also be undertaken over an arbitrary coefficient field and it can be easily checked that this matrix has rank 3 over R(a, t). Hence, Gaussian elimination by elementary row operations simplifies the matrix to the form

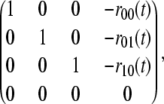(9)

where the coefficients r_u(t) ∈ R(a, t) can be written as rational functions of t with coefficients in R[a]. (Strictly speaking, the coefficients are rational functions in R(a) but their denominators can be cleared to make them polynomials in R[a].) The zero row in Eq. 9 arises because the rank is one less than maximal. (Had the linear expressions been treated as polynomials, then a Gröbner basis for the lexicographic order would have yielded the same result as Gaussian elimination (29).) Setting [S₁₁] = w, the corresponding simplified equations coming from Eq. 9 are [S_u] = w.r_u(t), for u ≠ 11, and [S₁₁] = w. This constitutes a rational parameterization of π(W) in the two variables w and t, with coefficients in R[a]. The rational functions r_u(t) are explicitly calculated in the Mathematica notebook.

As mentioned previously, care must be taken when giving numerical values to parameters. A general element p ∈ R[a], like 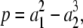may take positive or negative values for positive values of the parameters. However, if with c_α ∈ R, and c_α is always positive when it is nonzero, then, evidently, p takes only positive values for positive values of a₁, ⋯, a_m. Note that the converse is false. For instance, (a₁ – a₂)² + 1 is evidently positive for all values of a₁ and a₂ but is not a sum of positive monomials. We say that an element of p is positive if it is a sum of positive monomials (i.e., c_α > 0 when c_α ≠ 0) and is negative if it is a sum of negative monomials (i.e., c_α < 0 when c_α ≠ 0). Either assertion is a strong property of elements of R[a].

The numerator and denominator of each r_u(t) are both polynomials with coefficients in R[a] (because we cleared denominators, as explained above). The Mathematica notebook shows that the nonzero coefficients of these polynomials are all positive, in the sense defined above. This has two significant consequences. First, it shows that the denominator of r_u(t) can never be zero, for any positive parameter values, as long as [E] and [F] are positive. Hence, r_u(t) is always well defined and never becomes infinite for all biochemically realistic initial conditions and positive parameter values. Second, it shows that r_u(t) itself is always positive, for any positive parameter values, as long as [E] and [F] are positive. It is not difficult to see from this that all state variables must then be positive at steady state, provided that [E], [F], and the total amount of substrate are positive. This, of course, merely confirms what we would expect on biochemical grounds, but such properties are surprisingly hard to prove rigorously for nonlinear dynamical systems. (The positivity of the rational parameterization can be shown to hold in general for systems with any number of sites (42).)

The rational parameterization found here makes no distinction between stable and unstable steady states, but it is only the former that will be found experimentally or through numerical simulation. Stability is a dynamical property that can be determined for any steady state by examining the eigenvalues of the Jacobian matrix (38). It is an interesting open problem whether this local analytical method can be reinterpreted in algebraic terms, so that the stability can be detected algebraically.

Distinguishing enzyme mechanisms

The planarity invariant (Eq. 6) can now be directly calculated using the rational parameterization. The linear expression in Eq. 6 defines a plane in R³ perpendicular to the vector (μ₁, μ₂, μ₃). It can be checked that each μ_i ∈ R[a] is positive, in the sense explained above. Hence, the vector (μ₁, μ₂, μ₃) points into the positive quadrant. Furthermore, because μ₄ ≠ 0 (for positive values of the parameters), the plane lies at some distance from the origin. The discrepancy from planarity can be measured by

(10)

If Δ < 0, then the point (y₁, y₂, y₃) lies on the same side of the plane as the origin, whereas if Δ > 0, it lies on the opposite side. Because of the parameterization of the phosphoforms, each of y₁, y₂, y₃, and Δ can be expressed as a rational function of t with coefficients in R[a]. (Note that the w disappears because it is divided out in Eq. 7.)

The behavior of a rational function of t for large or small values of t is determined by the coefficients of the highest and lowest powers of t, respectively. Consider the rational function

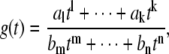(11)

which has been written to show only the nonzero monomials with the smallest and largest powers of t in the numerator and denominator: the exponents in the numerator lie between l < k and a_l, a_k ≠ 0, and the exponents in the denominator lie between m < n and b_m, b_n ≠ 0. The behavior of g(t) for large values of t (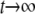) is given by

(12)

whereas for small values of t (), it is given by

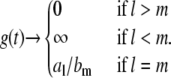(13)

The structures of y₁, y₂, y₃, and Δ as rational functions of t are tabulated in Table 1 for all four combinations of enzyme mechanisms (where X/Y indicates that the kinase uses mechanism X and the phosphatase uses mechanism Y). Since the (nonzero) coefficients of r_u(t) are all positive, as discussed previously, the same will be true of the coefficients of y₁, y₂, and y₃, in view of their definition in Eq. 7. It can also be checked that the coefficients of the nonzero monomials of Δ with the smallest and largest powers of t are each either positive or negative, in the sense explained previously. (The coefficients of the denominator of Δ are all positive, in view of its definition in Eq. 10. Hence, it is only the signs in the numerator that are relevant.) Table 1 describes these rational functions in a way similar to that seen in Eq. 11 but specifies only the sign (indicated by +tⁱ or –tⁱ) of the monomials with the smallest and largest powers of t.

TABLE 1.

Coordinates, y₁, y₂, y₃, and planar discrepancy, Δ, as rational functions of t = [E]/[F] for four combinations of enzyme mechanisms

	D/D	D/P	P/D	P/P
y1	–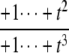
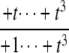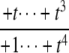y2	–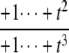
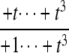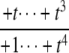y3	–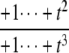
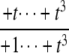Δ	0

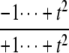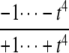The coordinates are defined by Eq. 7, and the planar discrepancy, Δ, by Eq. 10. D indicates a distributive and P a processive enzyme mechanism. The same format is used as in Eq. 11 but shows only the sign (indicated by +tⁱ or –tⁱ) of the monomials with the smallest and largest powers of t. Supporting calculations are provided in the accompanying Mathematica notebook. The “—” indicates a value that is not needed for the argument in the article but may be calculated using the notebook.

Note first that in the D/D case, Δ = 0, confirming what was discovered above by Gröbner basis methods: when both enzymes are distributive the steady states always lie on the plane defined by Eq. 6. In the D/P case, for small t, Eq. 13 shows that Δ becomes positive, because l = m = 0 and a_l and b_m are both positive. Hence, (y₁, y₂, y₃) lies on the far side of the plane for small t. For large t, Eq. 12 shows that Δ becomes negative because k = n = 2 and a_k is negative while b_n is positive. Hence, (y₁, y₂, y₃) comes closer to the origin for large t. The coordinate functions show how much closer. Indeed, each y_i goes to zero as t gets large, according to Eq. 12, because the degree of the largest monomial in the numerator, k = 2, is less than the degree of the largest monomial in the denominator, n = 3. Hence, as but remains beyond the plane for small t. In the P/D case, the situation is reversed. Using a similar argument, Δ shows that (y₁, y₂, y₃) remains on the far side of the plane for large t, whereas the coordinate functions show that it goes to zero for small t. Note that in both the D/P and P/D cases, the plane in question is that defined by Eq. 6, which depends only on the underlying D/D system and not on the processivity. Finally, the P/P case is a mixture of the previous cases. The coordinate functions show that (y₁, y₂, y₃) go to zero for both large and small values of t. The various possibilities are summarized in Fig. 2.

FIGURE 2.

Behavior of the point (y₁, y₂, y₃) ∈ R³ defined by Eq. 7 for large values (dark gray) and small values (light gray) of t = [E]/[F] for each of the four combinations of enzyme mechanism and arbitrary positive values of the relevant parameters. D indicates a distributive and P a processive enzyme mechanism. Each figure depicts in two dimensions the positive quadrant in R³ and the plane defined by the planarity invariant (Eq. 6). The hatched region on the far side of the plane relative to the origin is the locus of points for which the planar discrepancy Δ, defined in Eq. 10, is positive. The pyramidal region between the origin and the plane is the locus of points for which Δ < 0. The plane itself is defined by Eq. 6, corresponding to Δ = 0, and is the same in all cases.

The (y₁, y₂, y₃) curves for a representative sample are shown in Fig. 3. In the absence of experimentally measured site-specific parameter values for multisite substrates, we generated 100 examples by randomly selecting sets of parameter values. The association constants, with units of (concentration)⁻¹ (time)⁻¹, and the break-up and catalytic constants, and 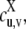with units of (time)⁻¹, were both drawn randomly from the uniform distribution on [0.00, 5.00]. The parameters for the D/D case were chosen first, followed by and 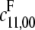for the remaining cases. The specific values for the example in Fig. 3 are listed in the Mathematica notebook. Fig. 3 also shows the plane defined by Eq. 6. As discussed above, this plane intersects the positive quadrant and does not contain the origin. The dispositions of the four curves with respect to this plane follow the limiting behavior summarized in Fig. 2. It can be seen that processivity in either or both of the enzymes is clearly distinguished by the geometry of the corresponding curve.

The curves in Fig. 3 were generated from the rational parameterization which, as mentioned previously, makes no distinction between stable and unstable steady states. If the (y₁, y₂, y₃) data were being obtained from an experiment, or if they were being generated from a numerical simulation of the equations, then only stable steady states would be found. We undertook such numerical simulations using randomly selected sets of parameter values, as previously, along with randomly chosen initial conditions. We found that for each set of parameter values, the (y₁, y₂, y₃) values of the stable states were distributed throughout the expected curves (data not shown). In particular, the stable states were not confined to any portion of the curve but were to be found everywhere along the curve. There was no difficulty in interpolating, by eye, the shape of the curve despite having a limited number of points on it corresponding to only the stable steady states.

Experimental tests

The above results make clear predictions about existing kinase-phosphatase-substrate systems. For instance, in the Mek-MKP3-Erk system, the substrate Erk is doubly phosphorylated and both enzymes act distributively (10,11,13). We therefore predict that this system satisfies the planarity invariant (Eq. 6). This can be tested in vitro using purified kinase, phosphatase, and substrate under conditions in which ATP is not limiting. It is remarkable that such “systems biochemistry” has rarely been attempted. Much has been understood about individual kinases and phosphatases through in vitro studies, but the two enzymes have rarely been brought together to study their systems properties. Although such experiments do not appear to be technically challenging, several issues need discussion.

First, although the experimenter can control the total amounts of substrate and enzymes and, to a lesser extent, the initial phosphorylation state of the substrate, the amounts of free enzymes at steady state are determined by the system's dynamics. The parameter t = [E]/[F] is not within the experimenter's direct control. However, it is not essential to trace the curve generated by t in Fig. 3 in any monotonic fashion. All that is required is to plot the (y₁, y₂, y₃) points defined by Eq. 7 as a set in R³. The t parameter can be exercised by varying the total amount of substrate and enzymes over as broad a range as possible.

Second, any method for detecting the substrate phosphorylation state, whether antibodies or 2D gels or mass spectrometry, will not preserve transient enzyme-substrate complexes. To avoid misquantifying the amounts of phosphoforms, it is necessary to maintain substrate in excess of enzymes. In this regime, any error arising from breakdown of enzyme-substrate complexes will be limited to no more than the total amount of enzyme.

Third, it is necessary to distinguish and quantify each of the four phosphoforms. Although antibodies and 2D gels have often been used to detect phosphorylation state, it can be difficult to distinguish intermediate phosphoforms (S₀₁ and S₁₀) with these methods. For instance, although commercial antibodies are available against all four phosphoforms of Erk1/2, those against the intermediate phosphoforms show poor specificity compared to the others (43). Mass spectrometry (MS) is a better option and has become the method of choice for detecting protein posttranslational modifications (44). Mayya et al studied the cyclin-dependent kinases CDK1/2, which are inhibited by double phosphorylation, and used MS to track all four phosphoforms dynamically over the cell cycle (45). However, quantification by MS requires particular care: the peak intensity of a peptide in the spectrometer bears little resemblance to its amount because different peptides ionize and “fly” with different efficiencies (46). Quantification requires either the introduction of exogenous heavy-isotope labeled standards, as in the AQUA method (45,47), or the use of internal peptide standards, as in the iQEM method introduced in Steen et al. (48).

Fourth, it is necessary to create steady states in vitro. Although in vivo reactions may be well represented by the model in Fig. 1, in vitro reactions consume ATP while producing ADP and inorganic phosphate, which are not explicitly modeled. If ATP is in sufficient excess, and the steady state is reached quickly, then a quasisteady state may be established that may be adequately represented by the model in Fig. 1. As an alternative, the system may be coupled to an ATP regenerating mechanism (49) that depletes some other phosphate source—phosphoenol pyruvate or creatine phosphate, for example—while buffering the kinase-phosphatase-substrate system from large variations in ATP, ADP, and inorganic phosphate. Experimental exploration will be needed to determine how best to create and maintain such steady states.

Finally, Figs. 2 and 3 show that processivity induces a discontinuous change in the geometry of the steady states. If 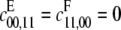(the D/D case), then (y₁, y₂, y₃) remains on the plane defined by Eq. 6 for all t > 0, but if 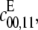say, becomes positive (the D/P case), even if it is only very slightly positive compared to other catalytic rates in the system, then (y₁, y₂, y₃) leaves the plane and moves to the origin for large t. What is not known, and depends on the values of the parameters, is how large t has to be for this to happen. It may require [E_tot] or [F_tot] values, which cannot be realized in practice. Hence, it may not be possible to detect a processivity rate that is very small compared to other catalytic rates in the system. Of course, conventional methods of detecting processivity (10,11,17–19) suffer from the same problem, without having a quantitative framework in which to study it. Further analysis may show how to back out information about the extent of processivity from the details of how (y₁, y₂, y₃) departs from the plane, as is possible in the sequential case (8).

Any experimental test is ultimately limited by the underlying errors of measurement. Although MS has proved extremely valuable for qualitative detection, its quantitative performance is not as good as one might expect. Mayya et al. find coefficients of variation in the range 12–22%, in their studies of CDK1/2 (45), despite using a high mass-accuracy hybrid ion trap Fourier transform spectrometer (Finnigan LTQ, Thermo Fisher Scientific, Waltham, MA). Measurement errors may dominate the feasibility of the tests discussed here.

DISCUSSION

We have argued elsewhere that the phosphoform distribution is the appropriate measure of the state of a multisite substrate and that one of the central questions is how the cognate kinases and phosphatases regulate this distribution (7). We have shown here that for a two-site system at steady state, the geometry of the set of distributions is determined by the mechanisms of the enzymes, as shown in Fig. 3. Although models of multisite phosphorylation have been widely used in the literature, they have often been judged on qualitative grounds and have not been subjected to stringent quantitative tests. The planarity invariant given by Eq. 6 is unusual in that it provides such a stringent test while not requiring any knowledge of site-specific parameter values. Furthermore, departures from the planarity invariant enable detection of processivity in either the kinase or the phosphatase or both.

We anticipate that the methods introduced here will have much wider application. At steady state, any mass-action model derived from a biochemical network gives rise to an algebraic variety. In contrast to analytical methods relying on differentiability, algebraic geometry is not tied to the real number field R but can be undertaken over any field of coefficients, such as the field R(a) used here. This amounts to treating the parameters as uninterpreted symbolic quantities. It is this flexibility that allows assertions to be made, such as the planarity invariant and the rational parameterization, which are valid for any assignment of positive values to the parameters. Algebraic geometry thereby provides a framework for formulating properties of a system in a parameter-independent manner. We believe this will be of considerable benefit in overcoming the parameter problem in biological modeling.