Vesicle Diffusion Close to a Membrane: Intermembrane Interactions Measured with Fluorescence Correlation Spectroscopy

Abstract

The protein machinery controlling membrane fusion (or fission) has been well studied; however, the role of vesicle diffusion near membranes in these critical processes remains unclear. We experimentally and theoretically investigated the dynamics of small vesicles (∼50 nm in diameter) that are diffusing near supported planar bilayers acting as “target” membranes. Using total internal reflection-fluorescence correlation spectroscopy, we examined the validity of theoretical analyses of vesicle–membrane interactions. Vesicles were hindered by hydrodynamic drag as a function of their proximity to the planar bilayer. The population distributions and diffusion kinetics of the vesicles were further affected by changing the ionic strength and pH of the buffer, as well as the lipid composition of the planar membrane. Effective surface charges on neutral bilayers were also analyzed by comparing experimental and theoretical data, and we show the possibility that vesicle dynamics can be modified by surface charge redistribution of the planar bilayer. Based on these results, we hypothesize that the dynamics of small vesicles, diffusing close to biomembranes, may be spatially restricted by altering local physiological conditions (e.g., salt concentration, lipid composition, and pH), which may represent an additional mechanism for controlling fusion (or fission) dynamics.

INTRODUCTION

Small vesicles (<100 nm in diameter) found inside cells participate in vital cellular processes such as exocytosis and endocytosis (1–5). During these processes, vesicles typically undergo two stages of dynamics, and for simplicity, we focus on the intermembrane interactions occurring before exocytosis: vesicles first must diffuse in close proximity with the target membrane; then the vesicles dock and fuse with membranes via specific protein-protein interactions to release their contents (6). (The steps for the intermembrane interactions occurring during postendocytotic fission are reversed.) The interactions of vesicles with membranes and their regulation at the second stage have been investigated widely using model systems and living cells (7,8). Although the first stage is also critical for these crucial biological processes, the physical interactions that must transpire between the two membranes remain poorly understood due, in part, to the complexity of the dynamics occurring within and between the biomembranes that depend on local lipid compositions, ion concentrations, and pH.

Because the cytoplasmic leaflet of the plasma membrane is enriched in anionic lipid (∼10–20 mol %) (9), electrostatic repulsion between opposing membranes is a primary intermembrane interaction, as well as interactions mediated by cytosolic calcium. Such interactions can be controlled by lipid compositions that characterize the surface charge density of each membrane (10,11). Ionic strength, pH, and chemical composition of the buffer have been known to alter membrane surface potential and Debye-Hückel screening length (12–14). In addition, hydration repulsive forces prevent vesicle aggregation in the primary Derjaguin-Landau-Verwey-Overbeek (DLVO) minimum (15). Van der Waals attraction forces (16) also play a key role in intermembrane interactions.

As a result, vesicle distributions near biomembranes are determined by the interaction potential energy between the two membrane systems, particularly in close proximity where hydrodynamic drag dominates (17–19). Although the hydrodynamic interaction between a sphere with a planar surface, which is similar to nonspecific interactions of vesicles with a target membrane, has been studied theoretically for almost a century, limited experimental studies have been reported. In addition, most research on the dynamics of spherical particles near a surface has been carried out with micron-sized particles primarily due to signal/noise ratio limitations (20–22). Some work has discussed hydrodynamic interactions of nanoparticles with a surface, but these measurements also suffered from low signal/noise ratio when the particle diameter was reduced to ∼50 nm (23,24).

In this study, we combined fluorescence correlation spectroscopy (FCS) with total internal reflection (TIR) (25–27) to investigate the interactions between small unilamellar vesicles (SUVs; 50–60 nm diameter) diffusing near supported lipid bilayers under different experimental conditions (e.g., ionic strength, pH, planar bilayer composition). TIR-FCS has previously been used to study interactions between diffusing fluorescent ligands with their receptors that had been reconstituted into supported planar bilayers (28), lateral diffusion of a membrane-binding fluorescent protein (29), and the kinetics of immobilized proteins at the single molecule level (30). We use TIR-FCS to overcome low signal/noise ratio limitations, while restricting our measurements to the interactions occurring between the fluorescently labeled vesicles and the target membrane surface that mimics the plasma membrane. In addition, we discuss, for what we believe is the first time, the theoretical interpretations of these mechanisms using hydrodynamic theory, in combination with modified DLVO theory.

MATERIALS AND METHODS

Materials

1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), 1-palmitoyl-2-oleoyl-sn-glycero-3-[phospho-l-serine] (POPS), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), and 1,2-dimyristoyl-sn-glycero-3-[phospho-l-serine] (DMPS) were purchased from Avanti Polar Lipids (Alabaster, AL). 1,1′-dihexadecyl-3,3,3′,3′-tetramethylindocarbocyanine (diI-C₁₆) (Invitrogen, Carlsbad, CA) was used as the fluorescent lipid analog. Lipids and fluorescent analogs were used without additional purification. Rhodamine green was purchased from Invitrogen.

Fluorescently labeled vesicle preparation

Chloroform solutions of lipids (79.9 mol % POPC, 20 mol % POPS, and 0.1 mol % diI-C₁₆) were dried under nitrogen in a test tube that had been previously cleaned in ethanolic potassium hydroxide, and stored under vacuum overnight. On the day of the experiment, the lipid film was resuspended in PBS (15 mM sodium phosphate, pH 7.4, 150 mM sodium chloride, and 10 mM sodium EDTA) at a 2 mM final lipid concentration. Lipid suspensions were bath sonicated at room temperature for 30 min and repeatedly extruded through a polycarbonate film with 30-nm or 50-nm diameter pores using a mini-extruder (Avanti Polar Lipids) to generate small unilamellar vesicles (SUVs) of a uniform size (25–30 nm radius). For experiments in which the ionic strength was varied, PBS (original ionic strength, 183 mM) was diluted 0.001×, 0.01×, and 0.1×, for final ionic strengths of 0.2 mM, 1.8 mM, and 18.3 mM, respectively. For experiments at pH 4, we used sodium acetate buffer with same ionic strength as 0.1× diluted PBS.

Target planar membrane preparation

Lipid mixtures of POPC containing 0, 5, 10, 15, or 20 mol % POPS were dried under nitrogen and stored under vacuum overnight. SUVs were prepared from resuspended lipid solutions using the above mentioned extrusion method or airfuge/probe sonication (31). On the day of an experiment, 50 μL of the SUV suspension was applied to a sandwich made of a detergent-cleaned 3 inch × 1 inch glass slide and a 22 mm × 22 mm glass coverslip, both of which were cleaned in argon plasma immediately before application of the SUV suspension. After a 30-min incubation in a humidified chamber, samples were exhaustively rinsed with the desired buffer to remove unfused SUVs. Subsequently, the glass slide was exchanged for a detergent-cleaned 24 mm × 50 mm glass coverslip under the desired buffer to further remove unfused vesicles and adjust the sample thickness to the microscope objective working distance. Before these unlabeled bilayer samples were sealed with VALAP (Vaseline/lanolin/paraffin (2:1:1, wt/wt)), 50 μL of the fluorescently labeled SUVs containing 20 mol % POPS in the desired buffer was applied to the coverslip sandwich. No subsequent fusion between the target membrane and the fluorescently labeled vesicles occurred, as indicated by the target membrane remaining unlabeled (data not shown).

Confocal fluorescence correlation spectroscopy

Fluorescence correlation spectroscopy experiments were carried out on a Nikon TE2000U inverted microscope as described previously (31). A laser beam (either the 488 nm line from a Coherent Innova 90C-6 argon ion laser (Santa Clara, CA) or the 543 nm HeNe laser from Meredith Instruments (Glendale, AZ)) was focused through the epi-port of the microscope and projected onto the sample by overfilling the back aperture of the objective (Nikon PlanApo IR 60× 1.4 NA). A 560 DRLP dichroic and 565 ALP emission filter (Chroma Technology, Rockingham, VT) were used to excite diI-C₁₆ and collect its emission, in addition to reducing the scattered light. Typical excitation power was ∼100 μW at the specimen plane with negligible photobleaching of diI-C₁₆ over the measurement period (typically 30–60 s). An optical fiber (50 μm diameter) was located in front of a GaAsP photomultiplier tube (Hamamatsu H7421-40, Bridgewater, NJ) in an image plane conjugate to the sample to exclude photons from outside of the detection volume. Autocorrelated data were obtained from a USB correlator (Flex02-12D, correlator.com, Bridgewater, NJ). Data were fit to three-dimensional diffusion with Igor Pro (WaveMetrics, Lake Oswego, OR) according to

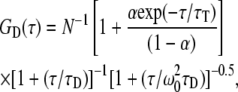(1)

where τ is the time interval, τ_D is the characteristic diffusion time and N is the average number of molecules in the open observation volume. The structural parameter, ω₀ (∼7.1), was obtained from autocorrelation measurements of an aqueous rhodamine green solution. α is the fraction of the fluorescent molecules in the triplet state with τ_T lifetime.

Vesicle hydrodynamic radii were determined to be 25.1 ± 1.7 nm (n = 28) by confocal FCS using the Stokes-Einstein relationship (32)

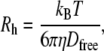(2)

where R_h is the hydrodynamic radius, D_free is the diffusion coefficient of unhindered Brownian motion, k_B is the Boltzmann constant, T is the temperature, and η is the solvent viscosity. These measurements were confirmed with dynamic light scattering (Nano zetasizer, Malvern Instruments, UK).

Total internal reflection-fluorescence correlation spectroscopy

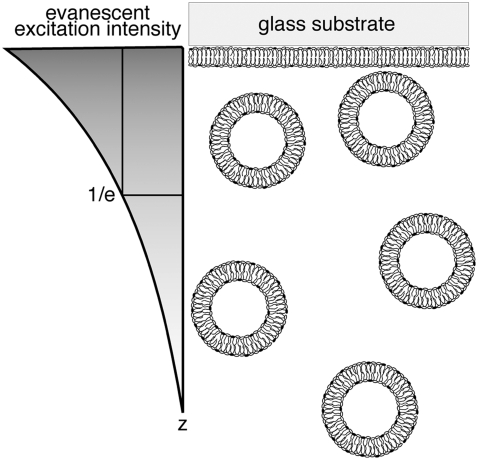
The TIR-FCS setup is described and characterized elsewhere (31,33). Briefly, a HeNe laser (0.4 mW, 543 nm, Meredith Instruments) was used for prism-based TIR. The beam, which was focused with a focusing lens (f = 100 mm), passed through a fused silica cube that was optically coupled, with glycerol, to a glass substrate to impinge on the solution/substrate interface at an angle greater than the critical angle (Fig. 1). The evanescent wave propagates into the solution with an exponentially decreasing intensity to selectively excite fluorophores within ∼100 nm of the substrate. The depth, d, of the evanescent field can be calculated as (26,34,35)

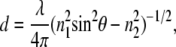(3)

where λ is the wavelength of the incident light in a vacuum, θ is the incident angle, and n₁ and n₂ are the refractive indices of the substrate and buffer, respectively. The depth of the evanescent field (that is, the 1/e intensity) for our experimental setup was calculated to be ∼65 nm. The fluorescence fluctuations originating from the sample near the interface were collected through an objective (Nikon CFI PlanApo IR 60×, 1.40 NA). To confine the detection volume along the x and y dimensions, an optical fiber (50 μm diameter) was placed in front of a GaAsP PMT (H7421-40, Hamamatsu, Japan) in a plane conjugate to the sample. The x-y position of the input end of the optical fiber was adjusted using a custom mount to maximize detection efficiency. The fluctuations in fluorescence signal were counted in reciprocal counter mode and autocorrelated.

FIGURE 1.

Schematic diagram depicting the z intensity profile of the evanescent wave and vesicle-supported planar bilayer system. Fluorescently labeled, anionic (20 mol % POPS) SUVs that are ∼50 nm in diameter diffuse close to the planar target membrane and are selectively excited by the evanescent field. The z dimension of the detection volume is determined by the depth of the evanescent wave, d; d at the 1/e intensity for our experimental setup is ∼65 nm. The x and y dimensions are defined by the confocal pinhole (i.e., the fiber diameter) and are not shown.

We maintained a constant distance between the objective and the coverglass surface by adjusting the z position of the sample stage to maximize photon counts from any given sample and maintain reproducibility. Measurements were carried out on fluorescently labeled, vesicle solutions (typical concentration ∼150 nM) near target planar bilayers in the desired buffer. The adsorption of vesicles to the planar bilayer itself was negligible under most experimental conditions as assessed by the constant number of vesicles freely diffusing near the surface over the measurement period. Confocal FCS measurements of SUVs were carried out to verify that fluorescence fluctuations originated from the diffusing SUVs and not from the diffusion of individual diI-C₁₆ molecules within the vesicular membrane (data not shown). Further, the FCS and TIR-FCS curves were fit to single-component diffusion, indicating that diI-C₁₆ molecules do not contribute to significant fluctuations in and of themselves. Therefore, the measured autocorrelation data from SUVs diffusing close to the target membrane were fit following (36)

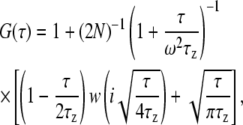(4)

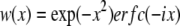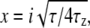where and N is the average number of SUVs in the detection volume, and τ_z is the characteristic diffusion time along the z axis (τ_z = d²/4D, where D is the diffusion coefficient of the vesicles diffusing in close proximity to the target membrane). (Note that we use D_free to indicate diffusion in bulk solution, as defined by Eqs. 1 and 2.) The depth of the evanescent wave, d, was calculated from Eq. 3, whereas the radius of the detection volume, ω_xy was determined from the radius of the optical fiber projected onto the sample plane. The geometrical factor ω was determined by ω = ω_xy/d. Chi-squared was calculated to assess the goodness-of-fit, unpaired, two-tailed Student's t-tests using Excel (Microsoft, Redmond, WA) were used for statistical analysis, and P ≤ 0.05 indicates that the means were statistically significantly different at a 95% confidence limit.

Theoretical analyses and background

The free diffusion (D_free) of spherical vesicles in a buffer with viscosity η is described by the Stokes-Einstein relationship, Eq. 2 (32). In contrast, when vesicles diffuse close to another membrane, Brownian motion of the vesicles can be significantly hindered by hydrodynamic interactions between the vesicle and its target membrane. These forces also include van der Waals, electrostatic and hydration repulsive interactions. Below we provide a summary of these forces and their projected effects on the diffusion kinetics of the vesicles.

Hydrodynamic interactions

Vesicle diffusion near the target membrane can be separated into parallel and perpendicular components with respect to the supported planar bilayer (i.e., the plasma membrane mimic). The diffusion coefficient for a vesicle moving parallel to a supported planar bilayer (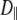) is

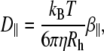(5)

where the correction 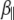describes the increased drag that occurs when particles diffuse parallel to the wall (19)

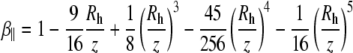(6)

and z is the shortest distance between the center of the SUV and the supported planar bilayer. Brenner derived the correction factor, 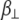for determining the diffusion coefficient of particles moving perpendicular to a wall (18), which is defined as

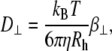(7)

where

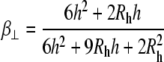(8)

and h = z − R_h, which is the separation between the vesicle and planar membrane surfaces. These corrected diffusion coefficients, 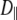and 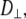describe the motion of a single vesicle at a well-defined distance from the target planar bilayer. In TIR-FCS measurements, the diffusion properties of vesicles and the distance of a vesicle from the supported planar bilayer are not fixed over the measurement period. In addition, the collected signal is an average of a number of vesicles that are moving throughout the detection volume. Thus, the calculated mean diffusion coefficient from the dispersed vesicles is more suitable as a comparison with the experimental data (see below, Eq. 14).

Driving forces controlling intermembrane interactions

To characterize the SUV distribution near the target membrane, we must also consider the driving forces that enhance vesicle–target interactions. The overall interaction energy 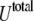includes the van der Waals energy 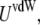the electrostatic energy 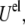and the hydration repulsion 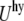such that

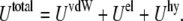(9)

The geometries associated with van der Waals interactions between membranes have been previously described (37). For two spherical shells, one of which has an infinite radius (that is, the supported planar bilayer), the van der Waals attractive energy can be described as

(10)

where r is the thickness of both membranes and A is the Hamaker constant, which is calculated as 6.7 × 10⁻²¹ J using Lifshitz theory (38) and is related to the dielectric constants (ɛ_buffer = 70 and ɛ_{lipid bilayer} = 2) (39) and the refractive indices of the lipid bilayers (n_{lipid bilayer} = 1.45) and buffer (n_buffer = 1.33) (40).

Electrostatic energy was based on the Derjaguin approximation (41). For sphere-wall interactions, recent studies suggested analytical expressions assuming that the surface maintains a uniform fixed surface charge density during the interaction. The electrostatic repulsion energy between two membrane systems is expressed as (22)

(11)

where e is the elemental electric charge, ɛ is the dielectric permittivity of water. is the surface potential of a vesicle (j = 1) and a supported planar bilayer (j = 2). φ is the mole fraction of charged lipid molecules and where l_D is the Debye-Hückel length, which is the inverse of κ, l_B is the Bjerrum length, and a is the cross-sectional area of a lipid molecule (42). In this work, surface potentials were regarded as Stern potentials for both membrane systems (43).

Hydration repulsion also affects the total potential energy. This short range interaction follows exponential law with a hydration decay length, ν of 0.2 nm (15). Hydration repulsion energy is given by (44)

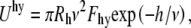(12)

where the pre-exponential 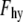= 4 × 10⁸ Pa. (15)

Statistical analysis of SUV distributions near the target membrane

By applying the Boltzmann distribution to calculate the total potential energy, we can calculate the probability density of vesicle distribution, 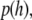in close proximity with the supported planar bilayer. Due to the selective TIR excitation (within ∼65 nm), we need to further consider the detection probability density of vesicles distributed as a function of distance from the supported planar bilayer. The normalized detection probability density, 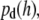decreases exponentially as the distance of vesicles from the supported planar bilayer increases as

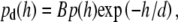(13)

where the prefactor 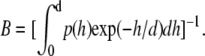As described by Eq. 4, experimentally determined diffusion coefficients are obtained from the measurement volume associated with d and detection area. To compare the measured diffusion coefficients with calculated ones, we assumed that the probability density of vesicle diffusion distribution is limited by the depth of the evanescent wave. Therefore, we normalized the detection probability from 0 to d. The mean diffusion coefficients of vesicles, as detected with TIR-FCS, can be expressed as

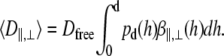(14)

As a result, the calculated averaged diffusion coefficient from the perpendicular and parallel motions with respect to the supported planar bilayer is compared to the measured vesicle diffusion near the target planar bilayer.

RESULTS AND DISCUSSION

Increasing ionic strength slows vesicle dynamics near target supported planar membranes

To evaluate the effect of ionic strength on intermembrane interactions, we used negatively charged SUVs and planar membranes that mimic a plasma membrane target. The surface charge density of the SUVs was constant with a fixed composition of POPC (79.9 mol %), POPS (20 mol %), which has a net negative charge at pH 7.4, and diI-C₁₆ (0.1 mol %). The diffusion of vesicles near planar bilayers composed of 80 mol % POPC and 20 mol % POPS was measured as a function of ionic strength using TIR-FCS, and representative curves are shown in Fig. 2. To determine and compare the effects of ionic strength on the SUV–planar membrane interactions without the effect of vesicle radius variation, we calibrated the measured diffusion coefficients by scaling the vesicle radius to be the same (25 nm) using Eq. 2.

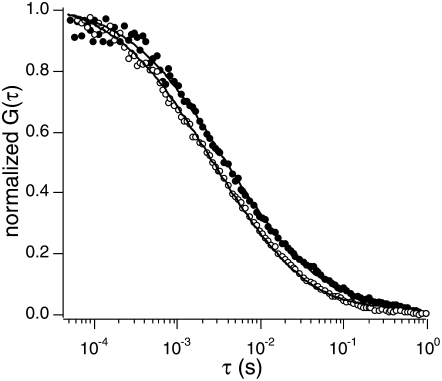
FIGURE 2.

Representative TIR-FCS curves of vesicles near a supported planar membrane (20 mol % POPS) in PBS (pH 7.4) at two different ionic strengths (183.4 (solid circles) and 18.3 mM (open circles)).

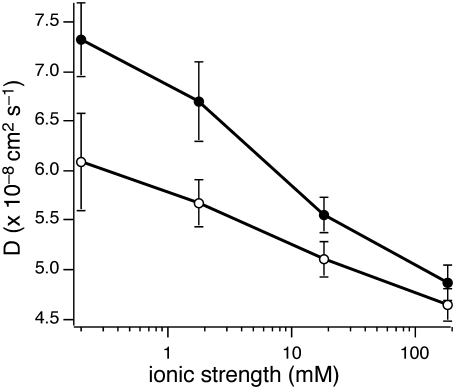
The measured diffusion coefficient of anionic SUVs close to the negatively charged target membrane as a function of ionic strength of PBS buffer is shown in Table 1 and as the solid circles in Fig. 3. For any given experimental condition, the measured SUV diffusion was slower than that measured in bulk solution far from the surface using conventional FCS of the same vesicle solutions (data not shown). At the highest ionic strength (183.4 mM), vesicle diffusion near the negatively charged planar bilayer was reduced by a factor of 1.7 (D = [4.9 ± 0.2] × 10⁻⁸ cm²/s, n = 30) as compared with D_free (D_free = [8.2 ± 0.7] × 10⁻⁸ cm²/s, n = 27)—that is, diffusion without the boundary condition. Vesicles experience a repulsive force when the electrical double layers associated with each membrane begin to overlap due to the surface charge of vesicles and supported planar bilayer that both contain 20 mol % POPS. The repulsive force decreases as a result of Debye screening that occurs when the ionic strength of the buffer increases. Thus, the average distance of vesicles from the planar bilayer and their diffusion coefficients decreased as ionic strength increased. These results indicate that vesicle motion becomes more hindered by hydrodynamic interactions with the supported planar bilayer.

TABLE 1.

Vesicle diffusion close to supported planar membranes as a function of ionic strength

Ionic strength (mM)	Measured D (× 10−8 cm2/s)	Calculated D (× 10−8 cm2/s)*	Calculated effective mol % of charged lipids*
20 mol % POPS planar bilayer
0.2 (n = 23)	7.3 ± 0.4†	6.3	20‡
1.8 (n = 29)	6.7 ± 0.4†	6.2	20‡
18.3 (n = 38)	5.5 ± 0.2†	5.6	20‡
183.4 (n = 30)	4.9 ± 0.2†	4.9	20‡
POPC planar bilayer
0.2 (n = 22)	6.1 ± 0.5	—§	—¶
1.8 (n = 30)	5.7 ± 0.2	—§	—¶
18.3 (n = 26)	5.1 ± 0.2	—§	1.2
183.4 (n = 33)	4.7 ± 0.2	—§	7.5

^*Values calculated from Eqs. 5–14.

^†There is a statistically significant difference in D as compared with paired samples of SUVs diffusing close to 100 mol % POPC supported bilayers. All the data have P < 4 × 10⁻⁴.

^‡Values are taken from the initial experimental conditions of the supported bilayers as prepared.

^§Because of the absence of surface charge on the planar bilayers, an ionic strength-dependent theoretical D cannot be calculated.

^¶Measured Ds are not valid because the thickness of the electrical double layer is comparable to the depth of evanescent field; therefore, we could not calculate effective mol %.

FIGURE 3.

Diffusion of vesicles near a planar target membrane as a function of ionic strength. Solid circles represent SUVs diffusing close to 20 mol % POPS supported bilayers, and open circles for SUV diffusion near 100 mol % POPC supported bilayers. Diffusion decreases as ionic strength increases, and this trend is enhanced when the target membrane is anionic. Note the pH of the buffer is 7.4.

We compared the observed data with theoretical calculations based on hydrodynamic interactions combined with the modified DLVO model described earlier (Eqs. 5–14). Due to the small volume fraction of SUVs (<1%), we did not observe any interactions between vesicles, which was further confirmed by confocal FCS measurements. In this control experiment, we observed no differences in the diffusion properties of SUVs when they were diluted 100-fold with buffer as compared with our standard SUV concentration (∼150 nM) (data not shown). Thus, we could calculate the potential energies without having to account for vesicle-vesicle interactions. Table 1 shows both measured and calculated diffusion coefficients of SUVs diffusing in close proximity to a target membrane containing 20 mol % POPS as a function of ionic strength. At high ionic strength (>18.3 mM), the theoretical calculations agree well with our observations, indicating that our theoretical approach and the assumptions made in Eqs. 13 and 14 for analyzing TIR-FCS data are appropriate. According to Eq. 11, the surface potential of vesicles and planar bilayers changes surface charge and the Debye-Hückel length that depends on ionic strength. When the Debye-Hückel lengths are very short (1.0 nm for 183.4 mM and 3.3 nm for 18.3 mM) and the majority of the vesicles is distributed relatively close to the planar bilayer, the short-range interactions, such as van der Waals and hydration repulsion interactions, become more important. However, in lower ionic strength environments (0.2 and 1.8 mM), where short-range interactions are less effective, theoretical predictions deviate from the experimental observations (Table 1). This disagreement becomes more apparent as ionic strength decreases and the distribution of vesicles has a low probability of interacting with the target membrane. (Note that the integrations in Eqs. 13 and 14 are carried out within the evanescent wave depth (∼65 nm), and Debye-Hückel lengths were 33.0 nm and 10.4 nm for 0.2 mM and 1.8 mM, respectively, which indicates that most vesicles are located outside the evanescent wave depth.) In other words, fewer vesicles diffuse through the evanescent wave because of the overlap between the thicker electrical double layers associated with the two membrane systems. As a result, the measured diffusion coefficients of the vesicles are greater than those determined solely from calculation and are less valid, in contrast to the diffusion coefficients measured in high ionic strength buffer.

We then carried out a similar series of experiments to characterize the effect of ionic strength on the interactions between negatively charged SUVs and neutral target membranes (100 mol % POPC) as a function of ionic strength (Table 1 and Fig. 3, open circles). Ionic strength effects were not expected in the case of POPS-containing vesicles interacting with POPC planar bilayers due to the absence of surface charge and electrical double layer contributions from the neutral planar bilayer. However, we unexpectedly observed that the negatively charged vesicles diffuse faster as ionic strength decreases, similar to the trend observed above when these vesicles diffuse close to negatively charged planar bilayers. These results suggested that the neutral planar bilayer also has an electrical double layer associated with it, thereby affecting the distance-dependent vesicle distribution from the planar bilayer as ionic strength changes. These results can be explained by the accumulation of an effective surface charge on the neutral, zwitterionic target membrane when anions are adsorbed from the buffer (12,45). The adsorbed anions form an electrical double layer on the neutral planar bilayer, and thus the bilayer exerts a repulsive force when it overlaps with the electrical double layer of the SUV.

The effective surface charge density of the neutral target membrane depends on ionic strength. We calculated the effective mol % of charged lipids, which is proportional to effective surface charge density in the neutral planar bilayer (Eq. 11). Table 1 shows the calculated effective percentage of charged lipids for high ionic strengths, where the theoretical predictions were valid for our experimental setup as previously discussed. At ionic strengths, 183.4 mM and 18.3 mM, the effective mol % of charged lipids was 7.5% and 1.2%, respectively (Table 1). Effective surface charge depends on ionic strength and can be interpreted by charge accumulation via anion adsorption to neutral bilayers (12,45). By increasing the ionic strength, the adsorbed salt increases and the charge-charge repulsion between two membranes is enhanced. Note that because the ionic strength effect is greater than the surface charge effect, we observed slower SUV diffusion at 183.4 mM ionic strength as compared to 18.3 mM. In addition, vesicle interactions with negatively charged target membranes are more sensitive to ionic strength changes as compared with their interactions with neutral target membranes. These results suggest that vesicle dynamics can be substantially altered by ionic strength when SUVs diffuse very close to negatively charged bilayers such as the cytoplasmic face of the plasma membrane.

Effect of lipid composition on the dynamics of small unilamellar vesicles near planar bilayers

To characterize the effect of lipid composition on the interactions between vesicles and supported planar bilayers, we varied the composition of the planar target bilayer from 0–20 mol % POPS (with the remainder as POPC). At pH 7.4, POPS has a net negative charge, and at pH 4, it is neutral. The ionic strength of the buffer was 18.3 mM, and the SUVs composition remained 79.9 mol % POPC, 20 mol % POPS, and 0.1 mol % diI-C₁₆ as in our other experiments. Table 2 shows the measured diffusion coefficients. At pH 7.4 (Fig. 4, solid circles), SUV diffusion increases with increasing POPS content in the target bilayer, indicating that the vesicles experience an enhanced repulsive force as the negative surface charge density in the planar bilayer increases. The average distance of vesicles from the planar bilayer also increases, weakening the drag forces on vesicles resulting in faster vesicle movements near the supported planar bilayer with higher surface charge density.

TABLE 2.

Vesicle diffusion near planar membranes as a function of pH and planar membrane mol % POPS content

POPS composition in planar membrane (mol %)	Measured D (× 10−8 cm2/s)	Calculated D (× 10−8 cm2/s)*	Calculated effective mol % of charged lipids*
pH 7.4
0 (n = 23)	5.1 ± 0.2	5.1†	1.2‡
5 (n = 38)	5.2 ± 0.1	5.5	1.7
10 (n = 29)	5.4 ± 0.1	5.5	3.3
15 (n = 38)	5.5 ± 0.1	5.6	15§
20 (n = 30)	5.5 ± 0.2	5.6	20§
pH 4
0 (n = 23)	4.8 ± 0.1¶	—‖	2.4
5 (n = 38)	4.9 ± 0.1¶	—‖	2.8
10 (n = 29)	4.9 ± 0.1¶	—‖	2.8
15 (n = 38)	4.9 ± 0.1¶	—‖	2.8
20 (n = 30)	4.8 ± 0.2¶	—‖	2.5

^*Values calculated from Eqs. 5–14.

^†Value is calculated from ^‡ value.

^‡Value indicates the surface charge density represented in Table 1.

^§Values are taken from initial experimental conditions of the prepared supported bilayers.

^¶P < 0.05, indicates a statistically significant difference in the diffusion coefficients between paired samples at pH 7.4 and pH 4.

^‖Due to the absence of surface charge on the planar bilayers, a theoretical D cannot be calculated.

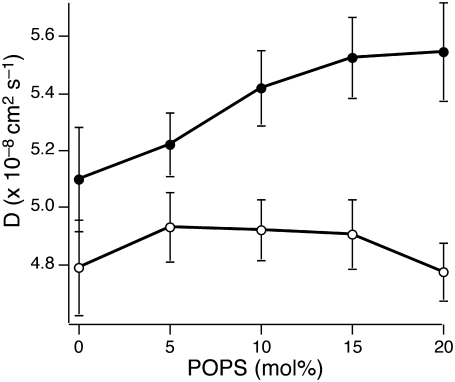
FIGURE 4.

Diffusion of SUVs near the supported planar membrane as a function of POPS. The mol % of POPS in the planar bilayer is varied and the vesicle diffusion measured. Solid circles are measured at pH 7.4, and open circles are measured at pH 4. At pH 7.4, as anionic lipid content in the planar bilayer increases, SUV diffusion increases, indicating that charge-charge repulsion increases; however, at pH 4, this trend is not observed.

When the lipid composition is varied, not only the surface charge density, but also the overall lipid characteristics of the planar bilayer, changes due to the POPS and POPC headgroups. To examine the role of electrostatic repulsion in influencing vesicle dynamics near the supported planar bilayer, we carried out the same series of experiments at pH 4. Because the apparent pKa of the POPS carboxyl group within the bilayer is higher than the intrinsic pKa (∼3.5) of carboxyl groups in bulk solution due to the lower local pH of the negatively charged membrane surface, most of the POPS headgroups are protonated at pH 4 (46). If electrostatic interactions dominate vesicle dynamics, vesicle movements should not change because the surface charge density is the same. Indeed, we observed no significant trend in vesicle diffusion on changing supported planar bilayer composition at pH 4 (Table 2 and Fig. 4, open circles), in contrast to pH 7.4 (Table 2 and Fig. 4, solid circles).

Due to the absence of charged lipids in both 0 mol % POPS planar bilayers at pH 7.4 and in planar bilayers with various POPS compositions at pH 4, the hindered diffusion of vesicles is expected to be the same. However, as shown in Fig. 4, we observed slower diffusion of vesicles near planar bilayers with various POPS compositions at pH 4 than of vesicles close to 100 mol % POPC planar bilayers at pH 7.4. At pH 7.4, SUVs remain highly charged due to their 20 mol % POPS content, and planar bilayer is neutral due to the absence of POPS; in contrast, both the vesicle and planar membranes are neutral at pH 4. Because effective surface charges accumulate on neutral lipid bilayers due to anion adsorption, electrostatic repulsion between the highly charged vesicles and neutral planar bilayers at pH 7.4 is greater than that between neutral vesicles and neutral planar bilayer at pH 4 (Table 2). A few possible reasons for this observation can be considered. First, not only the supported planar bilayers, but also the vesicles themselves, significantly lose their negative surface charge in an acidic environment due to protonation. Therefore the reduction of electrostatic repulsion is emphasized, as compared to vesicles with negative surface charge. Second, different anions (e.g., phosphate for pH 7.4 and acetate for pH 4 buffers) that eventually adsorb to the surface of neutral lipid bilayers can lead to different amounts of charge accumulation and cause dissimilar repulsion forces (45). To verify the dominant mechanism here, we calculated the effective mol % of charged lipids from the diffusion coefficients measured at pH 4 (Table 2). The surface charge densities of both the vesicles and planar bilayers were assumed to be identical due to POPS protonation at pH 4. Compared to the effective mol % of charged lipids in the neutral supported planar bilayer at pH 7.4 (1.2%), ∼2.4–2.8 mol % of effective charged lipid was measured for pH 4. Because the first possibility was already considered in our calculation, this disagreement can be attributed to the different anions, phosphate at pH 7.4 and acetate at pH 4, that adsorb to the bilayer surfaces. Although higher effective mol % of charged lipids at pH 4 was calculated than at pH 7.4, the possibility of incomplete protonation of acidic bilayer lipids cannot be considered because we did not observe a trend in vesicle diffusion on varying POPS content.

The surface potentials of the SUVs and target planar membrane directly affect the electrostatic repulsion energy (Eq. 11). To understand theoretically how lipid compositions of planar bilayers alter interactions with vesicles, we first calculated the averaged diffusion coefficients for each experimental condition (Eq. 14). Van der Waals and hydration energy were held constant under the assumption that characteristics of planar bilayers are not significantly different in our system. Table 2 shows measured and theoretically calculated diffusion coefficients of vesicles near supported planar bilayers of varying lipid compositions at pH 7.4. The theoretical expectations agree well with experimental data for planar bilayers containing 15 and 20 mol % POPS. (Note that the calculated value for 100 mol % POPC was obtained from the measured diffusion coefficient in Table 1.) However, for 5 and 10 mol % POPS target membranes, the calculated diffusion coefficients diverge from the experimentally determined values. Because the ionic strength was maintained at 18.3 mM, this deviation can be explained by lower than expected surface charge densities in planar bilayers (Eq. 11). The surface potential decreases and, as a result, the proximity of vesicles to the planar membrane increases via reduced charge-charge repulsion, thereby lowering vesicle diffusion.

We then calculated the effective mol % of POPS in the planar bilayers, using measured vesicle diffusion coefficients. Because the surface potential of vesicles is constant, vesicle dynamics reflect the surface properties of the planar bilayers. Table 2 shows that the effective mol % of POPS in the planar bilayers is ∼30% of the expected values. The reduction of surface charge that occurs when anionic vesicles interact with negatively charged membranes can be explained by the charge redistribution of the substrate when a charged object approaches it (47). As negatively charged vesicles move toward the planar bilayer, the charged POPS within the planar membrane target experiences strong electrostatic repulsion in the immediate area of the vesicle–target interface and thus, the POPS molecules diffuse laterally away from the interface to minimize the repulsion.

To test this hypothesis, we carried out a similar series of experiments using gel phase supported planar membranes composed of 0–20 mol % DMPS in DPPC. Both DMPS and DPPC are in the gel phase at room temperature and thus their lateral diffusion within the bilayer is several orders of magnitude slower than that of POPS and POPC. Table 3 shows the measured SUV diffusion coefficients and effective mol % of DMPS in the target membrane. For 5 and 10 mol % DMPS planar bilayers, the calculated effective mol % of DMPS in the targets were 3.8% and 6.2% (Table 3), respectively, as compared with 1.7% and 3.3% for 5 and 10 mol % POPS in the fluid bilayers (Table 2). These results suggest that the lateral mobility of POPS in the fluid target membrane leads to a reduction in the effective POPS concentration at the vesicle–target interface. (Note that the calculated mol % of DMPS was obtained under the assumption that the target membranes (DMPS/DPPC and POPS/POPC) are identical except for their phase behavior.) As a result of the transient reduction of the charged lipid population in the local bilayer, the vesicles move closer to the bilayer and the dynamics of vesicles are slower than expected. The driving force to redistribute the charged lipids in the planar bilayer on movement of the charged vesicles competes with the repulsion force created in the plane of the bilayer by surrounding charged lipids. This competition becomes amplified as the initial concentration of POPS molecules in the target membrane is increased. Thus, there is no significant reduction in effective charge density of supported planar bilayers with 15 and 20 mol % initial POPS composition.

TABLE 3.

Vesicle diffusion close to gel phase target supported planar membranes

DMPS composition in planar membrane (mol %)	Measured D (× 10−8 cm2/s)	Calculated D (× 10−8 cm2/s)*†	Calculated effective mol % of charged lipids*
0 (n = 15)	—‡	—‡	—‡
5 (n = 13)	5.4 ± 0.2	5.5	3.8
10 (n = 15)	5.5 ± 0.2	5.5	6.2
15 (n = 9)	5.5 ± 0.2	5.6	15§
20 (n = 30)	5.5 ± 0.1	5.6	20§

^*Values calculated from Eqs. 5–14.

^†Values are from Table 2 because there is no theoretical consideration of phase behavior of lipids in the target membranes.

^‡Due to the adsorption of vesicles to the target membrane, no data could be obtained.

^§Values are taken from initial experimental conditions of the prepared supported bilayers.

CONCLUSIONS

In this study, we provided experimental and theoretical studies to understand the physical underpinnings of intermembrane interactions that are essential for fusion (or fission) to occur. TIR-FCS provided the excitation selectivity and sensitivity to probe small vesicle dynamics near planar membrane under controlled environments. Using hydrodynamic theory, which explains the relationship between vesicle diffusion and the distance of vesicles from a planar membrane, we interpreted the underlying mechanism of vesicle dynamics near a planar membrane. Among the time-independent interactions that determine the population distributions of vesicles near the target membrane, electrostatic interactions were the most critical, particularly in a low ionic strength environment. When electrostatic repulsions governed vesicle-planar bilayer interactions, vesicle mobility became faster. Under conditions at which van der Waals and hydration interactions became more important, vesicles moved more slowly. Although surface charge densities of lipid bilayers were altered mainly by changing lipid compositions, neutral bilayers also had a weak surface charge density that was created by adsorbed anions. We also showed that lipid lateral diffusion may alter vesicle dynamics. These results suggest that vesicles do not simply move randomly near a membrane surface, but rather diffuse in a tightly controlled manner to enhance the probability of fusion leading to exocytosis. These theoretical and experimental studies support the hypothesis that the diffusion dynamics of vesicles as they approach the target membrane are regulated, in part, by driving forces and physiological conditions to increase the selectivity and efficiency of fusion (or fission). Further, this experimental system allows us to investigate systematically other molecular interactions that are critical for intermembrane interactions.