Abstract
A methodology for flexible fitting of all-atom high-resolution structures into low-resolution cryoelectron microscopy (cryo-EM) maps is presented. Flexibility of the modeled structure is simulated by classical molecular dynamics and an additional effective potential is introduced to enhance the fitting process. The additional potential is proportional to the correlation coefficient between the experimental cryo-EM map and a synthetic map generated for an all-atom structure being fitted to the map. The additional forces are calculated as a gradient of the correlation coefficient. During the molecular dynamics simulations under the additional forces, the molecule undergoes a conformational transition that maximizes the correlation coefficient, which results in a high-accuracy fit of all-atom structure into a cryo-EM map. Using five test proteins that exhibit structural rearrangement during their biological activity, we demonstrate performance of our method. We also test our method on the experimental cryo-EM of elongation factor G and show that the model obtained is comparable to previous studies. In addition, we show that overfitting can be avoided by assessing the quality of the fitted model in terms of correlation coefficient and secondary structure preservation.
INTRODUCTION
Development of experimental techniques, such as cryoelectron microscopy (cryo-EM), small-angle x-ray scattering, and fluorescence resonance energy transfer for medium to low-resolution structural studies of large biomolecules has been instrumental in unveiling functional mechanisms of these systems. In particular, cryo-EM has played a key role in identifying conformational states of macromolecular assemblies (1) such as the ribosome (2,3), GroEL, RNA polymerase (4), myosin (5), and viruses (6,7), among others.
The cryo-EM technique provides low-resolution structural information. In contrast to x-ray crystallography, which can provide atomic position, cryo-EM gives only the overall shape of the molecule. However, its significant advantage over x-ray crystallography is that it is easier to trap biological molecules in different conformational states and determine their structures.
Due to the low-resolution nature of cryo-EM data, there have been multiple efforts to establish methodologies combining information from high-resolution x-ray or NMR measurements with density maps from cryo-EM. Originally, the docking of high-resolution structures into EM maps was done manually, but several algorithms have been actively developed for objective and reproducible fitting.
Several quantitative docking methods have been developed to perform rigid-body fitting of atomic structures into low-resolutions maps (8–13). However, as resolution of cryo-EM data improves, conformations distinct from the known x-ray structures become apparent, and a simple rigid-body fitting is not sufficient to interpret the data.
The fitting of high-resolution structures into low-resolution cryo-EM maps, with conformational changes in the structure taken into account, has been approached in several ways, and has proven to be useful for understanding, at a near atomic-level of detail, conformational changes in several major biological systems. Multiple approaches have been employed to introduce flexibility. Studies in which the biological system is divided into domains that are independently fitted as separate rigid bodies have revealed conformational changes of several important biological systems (5,14–17). Some problems may arise using these methods, however. They require the relatively subjective partitioning of the system, and may often lead ultimately to models in which segments of biopolymer chain that were connected in the original conformation are now disjoint.
A more quantitative and objective technique based on the development of reduced models for the system of interest has also been introduced (8,18). In this approach, a reduced model is constructed based on vector quantization, and the model is deformed to fit the data. However, this method introduces ambiguity by embedding the full atomic structure into a reduced model to perform the flexible fitting.
Another quantitative approach combines real space refinement (RSRef) (19) with molecular dynamics (MD) simulations (20,21). Here, both the fit to the data and the stereochemical properties of the molecules are optimized. With this approach, conformation of N-ethyl-maleimide-sensitive factor was studied, allowing the flexibility of the linker between two domains, which are treated as rigid units (20). A possible drawback of such an approach is that the deformations obtained as a result of the flexible fitting may lead to conformations that are not physically realistic, because the mechanical properties of the molecules are not fully reflected in the deformation of the structure, as certain units are assumed to be rigid. In addition, most conformational changes that occur in biological molecules involve concerted motions between domains of the system. These sorts of concerted motions are poorly taken into account if domains are treated as independent rigid units.
More recently, partitioning proteins at the secondary-structure elements (SSE) level has been implemented in several optimization approaches. A molecular modeling technique based on Monte Carlo, simulated annealing, and coarse-grained models was used to refine structural models into cryo-EM maps (22). A method based on constrained geometric simulation was also recently introduced. Such an approach allows the flexibility of the protein, but certain elements, identified using FIRST (23,24), are kept rigid during the simulation to avoid nonphysical distortions (25).
Flexibility of protein structure has also been used to construct homology models based on iterative comparative modeling and cryo-EM fitting (26,27). In the most recent development, Topf et al., using Monte Carlo and simulated annealing models, applied a heuristic optimization to multilevel subdivisions of the structure from domains to SSEs (28). Structural variability of protein domains within the same family has also been used for flexible fitting (29). In such an approach, the conformational space of the superfamily is first determined. Decomposition of this conformational space is used to deform models by moving secondary structure elements. These methods have been tested on simulated data and experimental data and have been successful in predicting flexibility of the molecule. A common point to these approaches is that only rigid blocks of atoms (SSE) are allowed to move, and thus, interpretation of the mechanical properties of the molecules might be limited; if there are changes in SSEs, they are not detected. Rigid-block approximations would not be suitable to refine smaller-scale conformational changes that can be observed with higher-resolution data.
Recently, coarse-grained representation of the molecules has been used to incorporate full flexibility of the proteins into the fitting process with modest computational cost. Schröder et al. proposed the use of random-walk displacements with a simplified potential, elastic network model, and distance restraints to flexibly fit structures into cryo-EM data (30). This method has been successful in predicting conformational changes of the ribose-binding protein. Methods based on normal-mode analysis (NMA) also allow full protein flexibility during the refinement (31–35), and have proven to be useful in predicting the arrangement of the protein-conducting channel of Escherichia coli (36), GroEL (35,37), anthrax complex (38), and sarcoplasmic reticulum Ca-ATPase (34). Although NMA-based methods have been successfully applied to study motions of relevant biological systems, this approach has certain limitations. Higher-resolution cryo-EM data is now common (up to 4 Å for symmetric structures) and smaller-scale rearrangements are becoming visible (39). Although NMA techniques are useful for revealing very large conformational changes, they have some limitations in describing smaller-scale conformational changes (40).
In this article, we describe an optimization method with full protein flexibility to refine high-resolution structures into cryo-EM maps based on MD simulations, which is a well-established technique for investigating dynamics of biological molecules. Molecular dynamics with full protein flexibility is more expensive in terms of computational time compared to other methods, but it provides a more detailed description of the dynamics, as no rigid elements are considered, which is necessary with higher-resolution cryo-EM data. Recently, a method for steering MD using a minimum biasing function (Maxwell's demon MD) has been adapted to refine all-atom models in density maps from cryo-EM (41). In a different approach, atoms are steered by a potential map created from the cryo-EM data (42,43). To maintain the stereochemical quality of the structure, restraints are applied to coordinates relevant to SSEs (43). Here, our aim was to perform biased MD using correlation coefficients as the biasing potential. No restraint was imposed on the secondary structure during the simulation, and a physical description of the molecule is based solely on a standard molecular mechanics force field.
The results obtained using our molecular mechanics flexible-fitting approach are described below. Differences between the correlation-coefficient-based approach and the potential-map-based approach are discussed. Illustrative results of our studies on simulated EM data from several proteins, showing large conformational changes, are presented. We demonstrate that this flexible fitting method yields structures that agree remarkably well with the error-free simulated EM map, even for small conformational changes. In particular, we discuss the importance of not imposing secondary structure restraints to evaluate the quality of the fit. Finally, we discuss the results of our method as applied to experimental data of elongation factor G.
THEORY
The ultimate goal of our method is to obtain a high-resolution structure of the molecule captured in a cryo-EM experiment by fitting a known all-atom high-resolution structure to a cryo-EM electron density map of the same molecule, but in a different conformation. Often such conformational changes are significant and do not occur spontaneously in molecular dynamics simulations. An approach to solving this limitation is “biased” MD simulation, in which external forces are added to guide the system into a certain region of the conformational space. Targeted MD simulations (44,45) and steered MD simulations (46) have been successfully employed to study important conformational transitions of biological systems (47,48).
In our approach, we also use a biased technique. We employ classical molecular dynamics technique with a modified force field potential, V, which is calculated as a sum of the classical potential from the MD method, Vff, and a new effective potential, VFit:
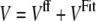 |
The additional effective potential is calculated according to the equation
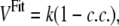 |
(1) |
where c.c. represents the correlation coefficient that describes similarity (overlap) of a target cryo-EM map to a cryo-EM map synthetically generated for an all-atom x-ray structure being fitted. The correlation coefficient is defined by
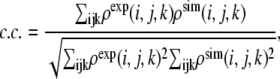 |
where ρexp (i, j, k) and ρsim (i, j, k) represent the experimental and synthetically simulated density of voxel (i,j,k). The synthetic cryo-EM map is generated from the all-atom structure; details are given in the Appendix.
In Eq. 1, k is a constant that regulates the magnitude of the effective potential, and it needs to be calibrated. The correlation coefficient is dimensionless, and therefore, k needs to be expressed in kcal/mol, which is the common unit in current force fields. This constant is the only arbitrary parameter introduced and needs to be provided as input to the simulations. In the Discussion section, we discuss the appropriate value of k that should be used to obtain optimal results from the fitting.
The described biasing potential is not the only choice. Other biasing potentials could be considered. In a different approach, considered by others, the biasing potential is simply proportional to the density (42,43)(C. C. Jolley and M. F. Thorpe, Arizona State University, personal communication, 2008). The idea is that atoms should be attracted toward the region where the density is high. Here, we will compare our approach (correlation-coefficient based) to that approach (density-based).
To clarify the expected behavior of each model, we will consider a simple two-dimensional system. First, we consider two atoms, 1 and 2, separated by 4 Å. We create a simulated low-resolution density map from those two atoms using a two-dimensional Gaussian kernel:
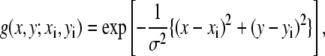 |
where (xi, yi) is the coordinate of the original atom i, and σ is the resolution parameter set to 4 Å.
We will examine how these two approaches fit those two atoms into their own simulated map. We would expect the atoms to be at their respective energy minimum. Fig. 1 a shows the biasing potential obtained defined as the negative of the density, Ud = –ρ. Its vector field shows forces from the biasing potential at each coordinate. Both atoms will be independently attracted toward the center, where the density is the highest.
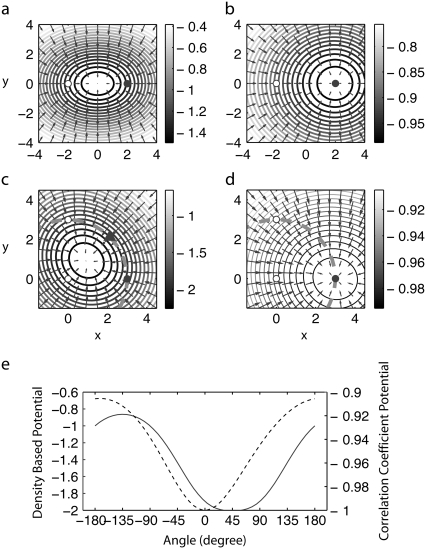
FIGURE 1.
(a) Potential map derived directly from the density map simulated from two atoms (2,0) and (−2,0) with σ = 4 is shown as a contour plot. Arrows show the force vectors from the potential. With this potential, each atom is attracted toward the center. (b) Potential map derived from the correlation coefficient between two atoms and their own simulated map. The potential map as a function of atom 1 with atom 2 fixed at (−2,0) is shown. With this potential, atom 1 is at the energy minimum at its original position; the two atoms are correlated in this potential, in other words, atom 1 knows the presence of atom 2. (c) The potential map from the density approach with three atoms: 1 (3,0), 2 (0,0), and 3 (0,3). The dotted line shows that the region that atom 1 can access, even the bond length between atoms 1 and 2, is fixed. The triangle indicates the energy minimum along the circle. (d) The potential map from the correlation coefficient approach with three atoms. (e) The potential energy along the line that atom 1 can access (dotted line in c and d) with the density approach (solid line) and with the correlation coefficient approach (dashed line). θ = 0 is the original position of atom 1. With the correlation coefficient approach, the original point is the energy minimum. With the density approach, the energy minimum is at θ = 45°, which is between atoms 1 and 3.
Fig. 1 b shows the biasing potential from the correlation-coefficient-based method. Here the two atoms are correlated, i.e., the potential that atom 1 experiences depends on the position of atom 2. The figure shows the potential function of atom 1 with atom 2 fixed at the original position. Unlike the potential obtained from density, atom 1 is at the energy minimum at its original position. This difference comes from the fact that with the correlation coefficient approach, the two atoms are correlated; in other words, atom 1 knows the existence of atom 2. In the direct density approach, the two atoms do not correlate.
The difference between these two approaches depends on the resolution. When σ is less than half of the distance between the atoms, the density map has two peaks at each atom, and thus the original coordinate is an energy minimum also with the density potential. However, such high resolution is not usually achievable in cryo-EM experiments.
Using the potential density-based approach in combination with a molecular mechanics potential, such as a bond interaction between these two atoms, would prevent the two atoms from colliding. However, as the biasing force is increased to enhance fitting, such compensation could become insufficient, which would make the calibration of biasing strength more difficult. In addition, even if a bond between the two atoms is considered as a rigid bond, such coordinate drift could still occur for more complex systems.
In the following, we consider three atoms, connected by two bonds as a chain, shown in Fig. 1, c and d. Fig. 1 c shows the potential from the density-based approach. Fig. 1 d shows the potential of atom 1 derived from the correlation coefficient (which depends on the positions of atoms 2 and 3). As was observed for the two-atom case, the atoms are not at the energy minimum for the density potential, whereas the original position of atom 1 is at its energy minimum with the potential derived from the correlation coefficient. In this case, even though the atoms are connected by rigid bonds, atoms 1 and 3 can rotate around atom 2. As Fig. 1 e shows, the energy minimum is rotated 45° inward. Again, with angle potential, such an artifact could be reduced. However, generally, angle potential is weaker than bond potential. Moreover, as those tests indicate, for a system with more atoms and complex flexibility, such as the one considered in this study, such an artifact could become difficult to eliminate.
In this work, we employ the potential based on correlation coefficient as it has proven to be effective in other works (16,21,32). It is intuitively straightforward, since the biasing forces are defined to increase the correlation coefficient, whereas with the density approach, the correlation coefficient is not guaranteed to increase at each step.
The effective potential gives additional contribution to the total forces that act on all atoms in the system during simulations:
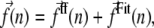 |
where n is an atom index. Additional forces are calculated as a gradient of VFit:
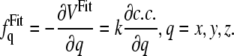 |
Complete derivation of the 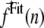 is given in the Appendix.
is given in the Appendix.
METHODS
Simulated maps
Synthetic maps are calculated by locating three-dimensional Gaussian functions on every atom and integrating these functions for every atom in each of the voxels as a given xn, yn, zn set of atomic coordinates (18):
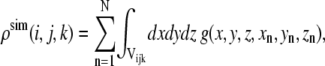 |
where n denotes the nth atom from a set of N atoms, (i,j,k) denotes a given voxel, and 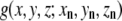 is the three-dimensional Gaussian function of the formula
is the three-dimensional Gaussian function of the formula
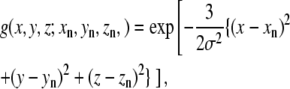 |
where σ is a resolution parameter. The resolution of a synthetic map is equal to 2σ (18). We note that the resolution parameter is set as a rough estimate and may not exactly coincide with the resolution reported using experimental data, since the resolution of the experimental data is often defined as a Fourier filter. However, previous studies with coarse-grained models have shown that the precise detail of the simulated maps do not affect the fitting performance (18,32,33).
Synthetic cryo-EM maps were generated at several resolutions, 4 Å, 6 Å, and 8Å, and used as target maps in the simulations. It has been shown that as long as the grid spacing is smaller than the resolution of the map, good-quality fits can be obtained (25). A 1-Å grid spacing was used for 4-Å resolution and a 2-Å grid for 6- and 8-Å resolution.
Simulations
To implement our approach, we modified the sander program source code from the Amber package (49), adding necessary procedures that read in cryo-EM maps, calculate gradient, and modify potential energy and forces by adding contributions due to the fitting.
All simulations were performed in vacuum with a distance-dependent dielectric constant. The force field parameters were taken from the parm99 parameters set (50). A cut-off of 100 Å for our five test proteins and 150 Å was used for the elongation factor G. The time step was set at 1 fs, with no rigid bonds treatment. Before the simulations, the initial structures were minimized to remove any internal strains. These minimizations resulted in small changes in the structures of the simulated systems. For each of the studied systems, we performed the simulations using synthetic cryo-EM maps of three different resolutions, i.e., 4 Å, 6 Å, and 8 Å.
Rigid-body fitting
We employed the Situs package (8) to perform rigid-body fitting of all-atom structures to cryo-EM maps. The Situs algorithm is based on the vector quantization approach in which three-dimensional structure is represented by a reduced representation of codebook vectors. Once both Protein Data Bank (PDB) structure and cryo-EM map are represented by two sets of a certain number of codebook vectors (in this work, we used 10 codebook vectors to represent a PDB structure and a cryo-EM map), qdock program from Situs can be used to fit a set of codebook vectors representing all-atom structure into a codebook vector set of cryo-EM maps. During this procedure, rotations and translations of the fitted codebook vectors are performed, and several possible initial orientations are obtained. Six of the best models were used to test our methods.
Secondary structure analysis
To perform analysis of the secondary structure content, we employed the Define Secondary Structure of Proteins (DSSP) program (51). In the DSSP approach, seven types of structural patterns in protein structures are specified. Each type is characterized by a set of structural parameters, e.g., distance between atoms, dihedral angles, etc., that allows assignment of one of the structural types to the protein conformation. All other conformations that cannot be classified according to one of these types belong to the group of unstructured conformations.
RESULTS
We have tested our procedure on simulated EM data. Several proteins have been used in the past for developing flexible fitting approaches (25,28,29,32,43). However, as our method targets higher-resolution data in which more detailed, i.e., smaller, conformational changes can be visible, we have decided to choose proteins for which only modest conformational changes have been observed. The successful prediction of those smaller conformational changes would demonstrate the suitability of our approach to study those higher-resolution and more detailed cryo-EM data. Larger conformational changes can be addressed using other approaches (25,29,32,34,35).
We choose five proteins for which a conformational change has been observed experimentally and high-resolution structures of the two states are available. The proteins are adenylate kinase (PDB codes 4ake and 1ake), LAO binding protein (1lst and 2lao), maltodextrin binding protein (1omp and 1anf), triacylglyceride lipase (3tgl and 4tgl), and mitochondrial aspartate aminotransferase (9aat and 1ama). The initial Cα root mean-square deviations (RMSDs) are 7.1 Å for adenylate kinase, 5.1 Å for LAO binding protein, 3.8 Å for maltodextrin binding protein, 2.8 Å for triacylglyceride lipase, and 1.8 Å for aminotransferase.
All structures of the test systems used in this work were taken from the Database of Macromolecular Movements, MolMovDB (52). A synthetic density map was constructed by convolution with a Gaussian kernel of σ = 2, 3, 4 (32). Lower-resolution data were not considered, because our approach targets the high-end resolution spectrum of cryo-EM data; lower-resolution data can be interpreted using normal-mode flexible fitting (NMFF). The fitting is done from the x-ray structures into the calculated error-free low-resolution maps. During the fitting, simulated maps from the deformed structures are created with the same resolution as the target map to evaluate the c.c.
The purpose of the method presented here is to fit the x-ray structure into a raw experimental (in this case, simulated) EM map of a different conformation of the same molecule. To examine the fitness between the atomic structure and the experimental map during the simulation, we examine the c.c. between the structure and the target EM map. In the following, we also examine the RMSD between the deformed structure and the original structure from which the target EM map was created. Ideally, when the c.c. reaches a maximum, the RMSD should reach a minimum. However, two different structures with different RMSDs can have the same c.c., since detailed information about the atomic coordinates is lost in the EM map and the EM map and atomic coordinates are not simply related by a linear transformation. Thus, to characterize the performance of our method, we examine both values.
Flexible fitting for structures aligned by RMSD
To separate the issues arising from identifying the correct orientation and positioning of the rigid atomic structure into the EM density from those associated with the successful flexible conforming of the structure into this map, we first examine the case where the deforming structure is optimally but rigidly superimposed onto the target structure so as to minimize initial RMSD between both structures. The structures were superimposed using the McLachlan algorithm (53) as implemented in the program ProFit (A. C. R. Martin, http://www.bioinf.org.uk/software/profit/), and the target maps were created from the fitted structures. This approach can be treated as a benchmark for our methodology, since before the simulations we use information about x-ray conformation of the final structure to superimpose the initial structure onto the final one. Results obtained from these simulations allowed us to test values that need to be considered for the weight, k, and to estimate the limits of accuracy of this approach.
Temperature
During the development of this method, we ran preliminary simulations at different temperatures, 100 and 300 K, and several weights k. In Table 1, results from refinements run using 100 K or 300 K are shown for adenylate kinase. Only a modest decrease in the RMSD is observed with simulations run at 300 K with weights, k, ranging from 1000 to 100,000, whereas simulations at 100 K produce models closer to the target. This observation indicates that at 300 K, thermal fluctuations increase RMSD, as seen in standard molecular dynamics simulations. Therefore, we have chosen to run simulations at the lower temperature, 100 K. In this way, our approach is more of an optimization. In the next section, we address in more detail the choice of the weighting factor.
TABLE 1.
RMSD (all-atom) as a function of temperature and weighting factor for adenylate kinase after RMSD alignment
| Final RMSD (Å)*
|
|||
|---|---|---|---|
| Resolution (Å)
|
|||
| K | Temperature (K) | 6 | 8 |
| 1000 | 100 | 4.1 | 4.9 |
| 300 | 6.5 | 6.4 | |
| 10,000 | 100 | 3.9 | 3.8 |
| 300 | 6.4 | 6.3 | |
| 100,000 | 100 | 6.1 | 4.2 |
| 300 | 6.1 | 6.5 | |
Initial all-atom RMSD was 7.3 Å.
Choice of weighting factor
In our implementation, the weight, k, is a parameter to adjust how strongly the system is biased to fit into the density. k needs to be calibrated so that sampling of conformations is enhanced while maintaining the structural integrity of the protein. Simulations with k ranging from 1000 to 300,000 were run for adenylate kinase undergoing a transition from the 4ake structure to 1ake (target simulated EM map), which are the open and closed forms of the enzyme, respectively. Three resolutions, at 4, 6 and 8 Å, were tested.
Table 2 shows the results obtained from those simulations. For the smaller weight tested, 1000, both the increase in c.c. and the decrease of the RMSD are modest relative to higher weights for each resolution. On the other hand, with the larger weights, the c.c. is easily increased, but the final structure does not necessarily agree better with the target conformation (RMSD > 4 Å). For adenylate kinase, a weight of 10,000 seems to be ideal, as both c.c. values increase to 0.93 and the RMSD decreased from 7.1 up to 1.2 Å for a map at 4 Å resolution. As the resolution decreases, the structural model obtained from our simulations has a larger final RMSD, but that value still remains close to that of the target structure (∼2 Å Cα RMSD). Simulations with the same weight were performed with other systems, and 10,000 consistently gave good accuracy in terms of c.c. and RMSD. With such weighting factors, the potential energy change and correlation coefficient energy change are of the same order of magnitude (results not shown). The forces resulting from the gradient of the c.c. are strong enough to overcome the energetic barriers separating the two structures. With a weight of 1000, the potential from the correlation coefficient is too small, which leads to a poor fit. With a weight of 100,000, the potential is too strong and the structure is distorted, with significant secondary structure loss.
TABLE 2.
RMSD (Cα atoms) and correlation coefficient as a function of weighting factor for adenylate kinase after RMSD alignment
| Resolution (Å) | Initial c.c. | Final RMSD (Å)*/Best c.c. | |
|---|---|---|---|
| 1000 | 4 | 0.61 | 2.65/0.85 |
| 6 | 0.76 | 3.04/0.94 | |
| 8 | 0.80 | 3.26/0.95 | |
| 10,000 | 4 | 0.61 | 1.23/0.93 |
| 6 | 0.76 | 1.66/0.98 | |
| 8 | 0.80 | 2.16/0/98 | |
| 100,000 | 4 | 0.61 | 3.53/0.95 |
| 6 | 0.76 | 3.89/0.99 | |
| 8 | 0.80 | 4.16/0.99 | |
| 200,000 | 4 | 0.61 | 3.30/0.95 |
| 6 | 0.76 | 4.65/0.99 | |
| 8 | 0.80 | 4.00/0.99 | |
| 300,000 | 4 | 0.61 | 4.40/0.94 |
| 6 | 0.76 | 4.00/0.99 | |
| 8 | 0.80 | 4.56/0.99 |
Initial RMSD was 7.1 Å.
Correlation coefficient versus RMSD
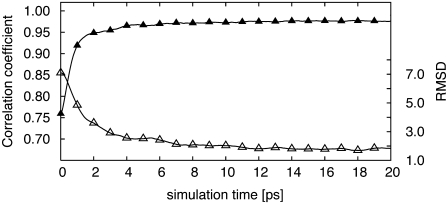
In this section, we discuss the evolution of the c.c. and RMSD as a function of time for the ideal weight, i.e., k = 10,000 simulations for adenylate kinase at 6 Å resolution. Fig. 2 clearly shows that as the RMSD decreases, the c.c. increases. After a rapid initial increase, c.c. stabilizes at ∼6 ps and fluctuates around a certain value. The same observation applies to the RMSD, which rapidly decreases and fluctuates around an RMSD value (1.7 Å at 6 Å resolution) close to the target structure. These rapid changes in the correlation coefficient and RMSD value show the effectiveness and robustness of our methodology. Though we run our simulations long enough to observe convergence of both the RMSD and the c.c., simulations could be terminated at 8 ps, and the final structure from such a simulation would be a very good fit to the target cryo-EM map.
FIGURE 2.
Simulations of adenylate kinase. RMSD (open triangles) and correlation coefficient (solid triangles) between the intermediate structure and the targeted structure at 6 Å resolution with a weight of 10,000 are shown as a function of molecular dynamics step. The initial Cα RMSD is 7.1 Å.
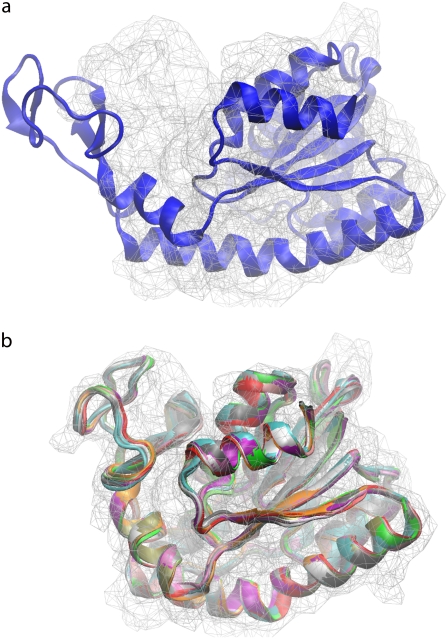
Fig. 3 shows the initial fit and twelve structures obtained from the fitting simulations for adenylate kinase using a target map at 4 Å resolution. These are the structures collected once the c.c. is stabilized, every 1 ps from 8 to 20 ps. These structures are all very similar to each other in terms of RMSD and c.c. The average difference in Cα RMSD between conformations of all these structures ranges from 0.4 Å to 0.8 Å and from 1.1 Å to 1.3 Å compared to the target structure. These RMSD measurements demonstrate that once the c.c. stabilizes, only minimal conformational differences occur, and any snapshot taken during that time would be a good fitting model to the target cryo-EM map. As previously demonstrated by Li and Frank, cryo-EM data can be interpreted as conformational averages (54).
FIGURE 3.
(a) Initial fit of the open form of adenylate kinase onto the closed simulated cryo-EM data at 4 Å resolution. (b) Ribbon representation of backbones of 12 snapshot conformations of adenylate kinase obtained from simulations and the corresponding low-resolution structures. Snapshots of the structures were taken every 1 ps from 8 ps to 20 ps of the simulation time. A better fit with the cryo-EM data is observed after refinement using our approach.
Frequency of force updates
In the results presented above, the additional forces due to the fitting to the cryo-EM data were updated at every step. One approach that can be considered with a view to speeding up simulations is to not update forces at every step. The assumption is reasonable, as at each step the structure only undergoes small conformational changes and the forces due to the fit to the density map would be affected only slightly. Such an assumption is similar to approaches in regular molecular dynamics simulations, where, to speed up the calculation, long-range interactions for electrostatic and Lennard Jones terms are not updated at every step.
We have run simulations with less frequent force updates. In Table 3, the final RMSD and computational time are shown for simulations with several frequency force updates. In every case, the final RMSDs are quite similar, but in terms of computational speed, less frequent force updates are clearly advantageous. In particular, with updates at every 20 steps, simulations are only ∼2 times slower than standard MD, whereas they are 20 times slower with updates at every step. In addition, we should note that the conformational transitions can be obtained within 20 ps, which does not require intensive computer resources. All simulations described in the following sections were run with force updates at every step, but less frequent updates will provide equivalent results.
TABLE 3.
Quality of fit and computational time as a function of additional force updates during the simulation for adenylate kinase after RMSD alignment
| Step frequency update | Final RMSD (Å)
|
Computational time relative to standard MD* | |
|---|---|---|---|
| 6 Å | 8 Å | ||
| 1 | 1.7 | 2.2 | 15.6 |
| 2 | 2.5 | 2.2 | 8.2 |
| 5 | 1.9 | 2.1 | 3.8 |
| 10 | 1.9 | 2.1 | 2.4 |
| 20 | 1.7 | 2.1 | 1.7 |
A 20-ps simulation without additional forces was run and used as reference.
Fitting tests for other systems
In Table 4 and Fig. 4, results from simulations are presented for all the systems studied in this work. The simulations were performed with a weighting factor equal to 10,000, with three different resolutions of the cryo-EM maps. As observed with adenylate kinase, both the c.c. and RMSD converge rapidly. In each case, the final structures agree well with the simulated cryo-EM map, as indicated by a high c.c., and are very close to the conformation from which those simulated maps were derived.
TABLE 4.
RMSD (Cα atoms) and correlation coefficient as a function of resolution
| Resolution (Å) | Initial RMSD/c.c. (Å) | Final RMSD/ best c.c. (Å) | |
|---|---|---|---|
| Adenylate kinase | 4 | 7.1/0.61 | 1.23/0.93 |
| 6 | 7.1/0.76 | 1.66/0.98 | |
| 8 | 7.1/0.80 | 2.16/0.99 | |
| LAO binding protein | 4 | 5.1/0.73 | 0.68/0.93 |
| 6 | 5.1/0.89 | 0.87/0.98 | |
| 8 | 5.1/0.92 | 1.16/0.99 | |
| Maltodextrin binding protein | 4 | 3.8/0.76 | 0.78/0.93 |
| 6 | 3.8/0.92 | 0.96/0.98 | |
| 8 | 3.8/0.95 | 1.22/0.99 | |
| Triacylglyceride lipase | 4 | 2.8/0.88 | 1.34/0.93 |
| 6 | 2.8/0.97 | 1.36/0.98 | |
| 8 | 2.8/0.98 | 1.39/0.99 | |
| Aspartate aminotransferase | 4 | 1.8/0.87 | 0.93/0.93 |
| 6 | 1.8/0.97 | 1.14/0.98 | |
| 8 | 1.8/0.98 | 1.59/0.99 |
FIGURE 4.
Simulations of the different systems with varied resolution. RMSD (open symbols) and correlation coefficient (solid symbols) between the intermediate structure and the targeted structure at 6 Å resolution, with k = 10,000, as a function of molecular dynamics step for adenylate kinase (triangles), LAO binding protein (squares), maltodextrin binding protein (circles), triacylglyceride lipase (inverted triangles), and aminotransferase (diamonds). The initial Cα RMSDs are 7.1 Å for adenylate kinase, 5.1 Å for LAO binding protein, 3.8 Å for maltodextrin binding protein, 2.8 Å for triacylglyceride lipase, and 1.8 Å for aminotransferase.
We should note that in the case of initial modest conformational changes (<3 Å), such as triacylglyceride lipase (3tgl/4tgl) and aspartate aminotransferase (9aat/1ama), even though the c.c. is already high, improvement in the fit can be obtained. In particular, for aspartate aminotransferase, for which the initial RMSD is only 1.8 Å, the RMSD decreases to <1 Å. Small conformational changes can be elucidated for high-resolution data, but as shown in Table 4, for lower-resolution (8 Å) data, no improvement is observed. Refinement, based on MD simulations, can capture small rearrangements only in high-resolution data. The elucidation of smaller conformational changes is quite significant, as higher-resolution data are now becoming available and reveal more details about the structure of biological molecules (39).
Flexible fitting with preliminary rigid-body fitting
The results just discussed represent the ideal case, where the two structures are in the same orientation. However, such will not be the case when dealing with real experimental data, since the target structure is not known. Thus, to test this situation, i.e., when the two structures have different initial orientations, we performed a preliminary rigid-body fitting of the x-ray structure into the simulated EM map using Situs (8,55). The rigid-body fitting yields optimal orientations of the high-resolution to low-resolution map (structure). Starting from those models, we performed fitting and analyzed the c.c. and the RMSD. Here, we should note that the RMSD is calculated without prior alignment, and thus not only includes the difference in conformation between the modeled structure and the target structure but also the difference in orientation of the two molecules. In the following, we will refer to this value as RMSD*, since it is different from the calculations we performed previously. Simulations were run for resolution at 4, 6, and 8 Å.
We should also note that initial rigid-body fitting cannot produce a unique answer; rather, several orientations with similar correlation coefficients are obtained. One could take the highest correlation coefficient model as a starting point of the flexible refinement, but in some cases, structure with similar c.c. values might display completely different orientations (32). Such issues often arise when the structure is rather symmetric. One should be concerned that an optimization protocol produces faulty models, as the structure is going to be deformed to maximize the c.c. even though the initial orientation might be wrong. Therefore, several flexible refinements starting from several rigid models with high c.c. should be run, and convergence toward a single conformation can assess the reliability of the model. In the following, six different best rigid fits obtained from Situs are studied as starting structures.
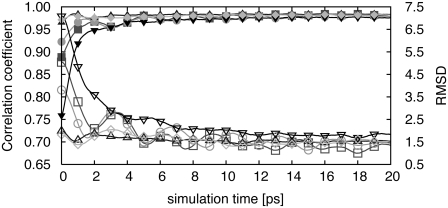
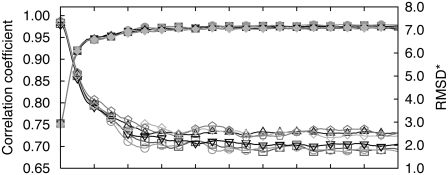
Fig. 5 and Table 5 contain results for adenylate kinase from simulations started from six different rigid-body fits. The initial RMSD* is higher, because it also includes the rotation/translation difference due to the rigid-body fitting. The simulations were performed for cryo-EM maps of resolutions equal to 4 Å, 6 Å, and 8 Å, respectively. Since the initial orientation was not perfect, during the simulation, the rotation and translation of the protein were allowed to possibly correct the initial misalignment. Overall, the refinements converge toward the same final RMSD*. The flexibly fitted structures are in good agreement with the target structure, with RMSD* as low as 1.5, 2.0, and 2.5 Å for target map resolutions equal to 4, 6, and 8 Å, respectively. Those values are almost comparable to the ideal case (1.2, 1.7, and 2.2 Å (Table 2)). As the resolution of the cryo-EM data is higher, the modeled structures are closer to the target data as more detailed information is contained in the higher-resolution data map. Although most of the structures are close to the target, 4 out of 3 × 6 independent refinements at 4 Å and 8 Å resolution give final structures that are very far from the target, the final RMSD* being on the order of 25 Å even though the correlation coefficient is high (0.83 for 4 Å and 0.96 for 8 Å resolution) and rather similar to values observed with good fits (see Table 5). Those structures also have a large initial RMSD* numbers (>25 Å), which is due to the fact that the initial alignment obtained by rigid-body fitting to the cryo-EM map deviates considerably from the ideal one. Even though rotation and translation of the protein are allowed during the simulation, the deviation from the ideal rigid fit was so large that the alignment, as well as the conformational changes, could not be obtained from the simulation.
FIGURE 5.
RMSD*s (open symbols) and correlation coefficients (solid symbols) between the intermediate structures and the targeted structures at 6 Å resolution, with k = 10,000, as a function of molecular dynamics step. Fittings were performed for several initial rigid-body fits for adenylate kinase.
TABLE 5.
Dependence of the resulting RMSD* (Cα atoms)/correlation coefficient on the initial structure for adenylate kinase at 4, 6, and 8 Å resolution
| Model | Initial RMSD*/c.c. | RMSD*/best c.c. |
|---|---|---|
| 4 Å | ||
| 1 | 7.24/0.60 | 1.83/0.92 |
| 2 | 7.21/0.61 | 0.95/0.93 |
| 3 | 7.31/0.60 | 1.90/0.91 |
| 4 | 29.43/0.51 | 26.37/ 0.82 |
| 5 | 29.02/0.53 | 25.74/ 0.83 |
| 6 | 7.23/0.60 | 0.87/0.94 |
| 6 Å | ||
| 1 | 7.34/0.75 | 1.74/0.98 |
| 2 | 7.33/0.75 | 1.81/0.98 |
| 3 | 7.29/0.75 | 2.57/0.97 |
| 4 | 7.22/0.75 | 1.97/0.98 |
| 5 | 7.29/0.75 | 2.39/0.97 |
| 6 | 7.38/0.75 | 2.69/0.97 |
| 8 Å | ||
| 1 | 7.34/0.79 | 2.85/0.98 |
| 2 | 7.33/0.79 | 2.53/0.98 |
| 3 | 7.34/0.79 | 2.99/0.98 |
| 4 | 28.57/0.72 | 24.98/0.96 |
| 5 | 29.43/0.71 | 26.38/0.96 |
| 6 | 7.30/0.79 | 2.51/0.99 |
RMSD* indicates that in addition to the conformational difference, the rotation and translation components due to the rigid-body fit are included in the RMSD.
Quality of the fitted model
In our simulations, the all-atom structure of the target was available, so we could calculate the RMSD* value between the target structure and the simulated one. However, when fitting to experimental cryo-EM data, one needs to have a methodology to determine quality of the models generated from our approach. This problem is not limited to our approach but applies also to other optimization fitting techniques.
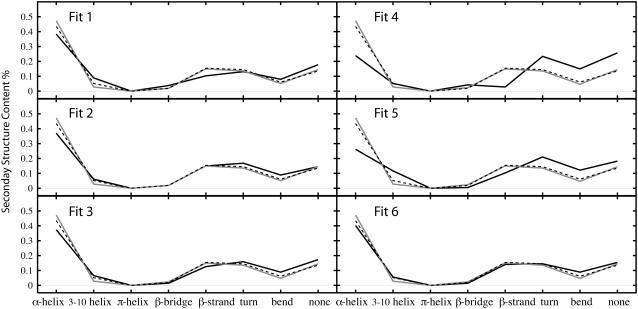
One of the factors that can be taken into account is the correlation coefficient value. However, differences in the correlation coefficients at 8 Å resolution between good (0.98) and poor (0.96) models, as observed for adenylate kinase, are not sufficiently large to differentiate them. Therefore, we performed further analysis of our simulation trajectories. To be more specific, we examined the conservation of the secondary structural motifs in the modeled structures. Since no structural restraints are imposed, forcible fitting easily distorts the structure, and it can be monitored through secondary structure motif inspection. Fig. 6 shows the results obtained from the DSSP analysis for adenylate kinase. We have analyzed initial, target, and best-fit structures. The percentage of structural patterns in initial and target conformations are almost identical, despite significant differences between each conformation. These two structures differ mostly in the different arrangement of their secondary structures. Structures with a low final RMSD*, Fit 1, Fit 2, Fit 3, and Fit 6 (Fig. 6), exhibit a secondary-structure pattern similar to those of the initial and final structures. On the other hand, in fits with high RMSD* values (Fit 4 and Fit 5), different secondary-structure contents, notably loss of α-helix contents and increase in the percentage of unstructured residues, are observed (Fig. 6). These results indicate that fitting starting with a wrong initial rigid-body fitting, which is too far from the ideal orientation, leads to loss of secondary structure. In such cases, the procedure still distorts the protein to maximize the c.c. at the cost of secondary structure conservation, whereas when the initial rigid-body fitting provides a good orientation, the c.c. is maximized with reasonable conformational transitions and the secondary structure is preserved. The c.c. and the secondary structure content should be used to evaluate the quality of the final model.
FIGURE 6.
Analysis of secondary-structure content for adenylate kinase. Secondary-structure contents are shown for each open initial conformation (gray line), closed target conformation (dotted line), and best structure obtained from the simulation (black line).
Tests with other systems
In Table 6, results from simulations initiated from several rigid fits are shown for all the other systems studied in this work. All the simulations presented in Table 6 were performed for resolution at 4 Å and a weighting factor equal to 10,000. As observed with adenylate kinase, significant decreases of the RMSD* can be obtained for all the proteins. For LAO binding protein, in particular, an RMSD* as low as 0.7 Å was observed. In a few cases, as previously observed, the initial RMSD* is so large at the beginning, because of a wrong initial orientation obtained from rigid fitting, that the misalignment cannot be corrected. Such structural models have a large RMSD*, with the target and lower final c.c. In addition, we have also observed loss of secondary-structure content. As discussed, the quality of the structure in terms of secondary structure in conjunction with c.c. value is a good indication of the correctness of the model.
TABLE 6.
Dependence of the resulting RMSD* (Cα atoms)/correlation coefficient on orientation of the initial structure
| Model | Initial RMSD*/c.c. | RMSD*/best c.c. |
|---|---|---|
| LAO binding protein | ||
| 1 | 5.85/0.70 | 0.62/0.94 |
| 2 | 12.87/0.63 | 10.89/0.80 |
| 3 | 32.28/0.61 | 33.93/0.81 |
| 4 | 22.20/0.63 | 21.83/0.80 |
| 5 | 5.87/0.70 | 0.68/0.94 |
| 6 | 5.80/0.71 | 0.74/0.93 |
| Maltodextrin binding protein | ||
| 1 | 8.24/0.68 | 0.77/0.93 |
| 2 | 8.45/0.68 | 0.83/0.93 |
| 3 | 35.91/0.62 | 34.45/0.79 |
| 4 | 7.80/0.70 | 0.81/0.93 |
| 5 | 8.30/0.69 | 0.80/0.93 |
| 6 | 6.62/0.69 | 0.81/0.93 |
| Triacylglyceride lipase | ||
| 1 | 2.42/0.86 | 1.42/0.93 |
| 2 | 25.72/0.70 | 25.35/0.83 |
| 3 | 25.59/0.69 | 27.31/0.82 |
| 4 | 2.63/0.85 | 1.26/0.93 |
| 5 | 23.70/0.68 | 24.67/0.84 |
| 6 | 27.63/0.70 | 26.58/0.83 |
| Aspartate aminotransferase | ||
| 1 | 4.88/0.73 | 1.16/0.92 |
| 2 | 4.07/0.75 | 0.89/0.93 |
| 3 | 3.19/0.79 | 0.90/0.93 |
| 4 | 4.14/0.76 | 0.94/0.92 |
| 5 | 4.23/0.74 | 1.03/0.93 |
| 6 | 3.66/0.77 | 1.14/0.92 |
DISCUSSION
Self-fitting
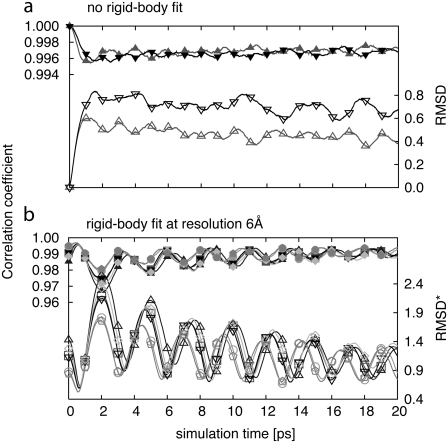
In performing fitting to reflect the conformational dynamics of biological molecules, the case could arise in which the coordinates are drifting. To address this concern, we performed a series of simulations in which initial PDB structure was fitted to its own synthetic cryo-EM map. In a manner similar to that used in all other test cases presented in this article, we performed two different kinds of simulations. In the first simulations, the initial all-atom structure is superimposed onto the target all-atom structure before the simulations by minimizing the RMSD. Since in this case we applied the method to fit the initial structure to its own cryo-EM map, the preliminary RMSD fitting was not necessary. In the second simulations, we employed the Situs package to preliminarily align PDB structures to the synthetic cryo-EM maps. In such cases, the initial PDB structures are not perfectly aligned to the target maps. All the simulations were performed for resolutions at 6 and 8 Å.
Fig. 7 a shows the c.c. and RMSD for fitting started from the perfectly aligned PDB structure to its own cryo-EM map for maps at resolutions of 6 and 8 Å, whereas Fig. 7 b shows the c.c. and RMSD from simulations where the initial structures were obtained in the Situs preliminary fitting for the simulated map at 6 Å resolution. Overall, only small deformations from the initial structures are observed in all simulations. For structures perfectly aligned, the RMSD quickly reaches a plateau. The deformations are minimal (<1 Å) and the higher the resolution, the lower the deformations, since the structure is better resolved. In the case of the rigid-body fitted structures, where the overall orientation of the molecule is not ideal, we also see that the RMSD reaches a plateau after a short period and the deformations remain minimal. Such results indicate that there is no coordinate drift during the simulation.
FIGURE 7.
Correlation coefficient (solid symbols) and RMSD (open symbols) for self-fitting of adenylate kinase at 6 Å (triangles) and 8 Å (inverted triangles) resolution (a) and after preliminary rigid-body fitting (b). The refinement was performed for six different initial fits.
In addition, such simulations are indicative of the type of fluctuation that can occur once the structure is in good agreement with the low-resolution data. For higher-resolution maps, fluctuations are smaller and less frequent than for lower-resolution maps. Such fluctuations are representative of the effects on protein mobility under external restraints. Similar characteristic fluctuations when fitting experimental data would be indicative that the structure has reached equilibrium.
Quality of models: evaluation
We performed our tests on error-free simulated EM maps. However, there is always the concern of overfitting the data with experimental data. Overfitting arises when one deforms the structure using unrealistic motions to maximize the c.c. As we mentioned, flexible refinement of x-ray structure into low-resolution data depends on the initial structure obtained from rigid-body fitting. Indeed, rather than giving a unique answer to the fitting, rigid-body fitting gives a set of initial possible starting orientations. Therefore, rather than running one single refinement, it is preferable to run several refinements using several starting orientations obtained from rigid-body fitting. Convergence of several simulations toward a single conformation attest to the reliability of the conformational change predicted from fitting techniques, even in the cases that cannot be differentiated solely based on the final correlation coefficient value (32). In addition, a faulty refinement process leads to an unreasonable protein structure, as indicated by secondary structure loss. Because our approach finds the correct balance between force due to the potential energy function of the protein and force of the fitting, structural models consistent with the low-resolution data can be differentiated from faulty models by evaluating secondary-structure contents, which shows the importance of not imposing restraint during the refinement.
Fitting to experimental data: elongation factor G
To perform accurate fitting, flexible fitting techniques should be able to tolerate noise in the map. Jolley et al. have analyzed the effect of noise on the result of fitting with a correlation coefficient optimization (25). Though a high level of noise, signal/noise ratio (S/N) = 1, is detrimental for fitting, with a higher level, S/N > 2, little impact is observed. Similarly, Schroder et al. have compared fitting with and without noise and have observed that their method is robust against noise (30). Although we have shown that our approach works with noise-free simulated EM data, we also need to demonstrate its applicability to experimental data, which contains noise and thus may hinder fitting.
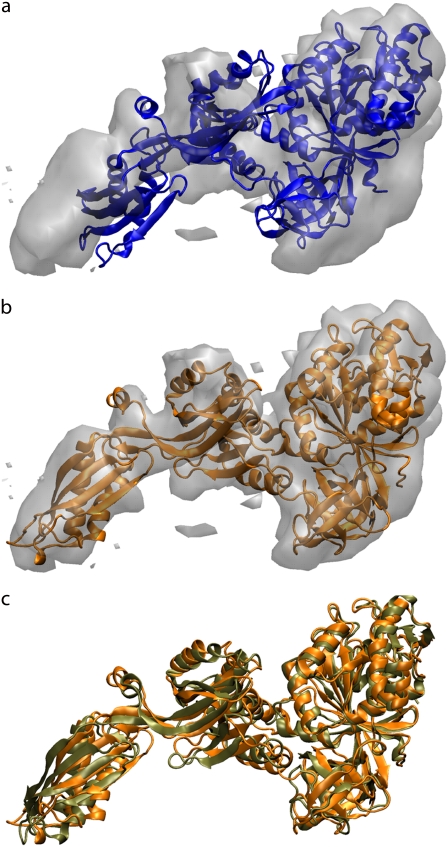
We have applied our approach to the fitting of elongation factor G (EF-G), an 844-residue protein. EF-G plays a key role in the translocation event related to protein synthesis. Upon binding of EF-G and subsequent hydrolysis, the ribosome undergoes a conformational change (ratchetlike motion) and translocation of the tRNAs occurs (2). The cryo-EM reconstruction at 11.8 Å resolution of EF-G bound to the ribosome revealed a conformation different from the known x-ray structure (56). We performed flexible fitting into the isolated EF-G map using the x-ray structure of a mutant factor (57). The PDB entry code for this structure was 1FNM. The initial correlation coefficient between the experimental EM-map and the x-ray structure, calculated for the inside of the molecular envelope (58), after rigid-body fitting using Situs is 0.62. The correlation coefficient converged after 20 ps to a value of 0.82. The all-atom RMSD between the starting and the fitted structure is 8.9 Å, and the secondary structure of the protein has been preserved. Fig. 8 a shows the original rigid-body fitting; some regions of the density remain unaccounted for. Fig. 8 b illustrates the model obtained from our simulation, in which significant improvement of the fit to the density is observed. The flexible fitting reveals large rearrangements between domains II, IV, and V. In particular, we observe a large displacement (up to 20 Å) of domain IV, which is correlated with rotations of domains II and V. In addition, as shown in Fig. 8 c, the final fit is structurally similar to that obtained using a different approach, NMFF, in which a simplified representation of the protein is taken into account and instead of MD simulation normal modes are used for optimization (33). We should also note that the visual comparison with the results from Velazquez-Muriel et al. reveals a similar structural rearrangement (29).
FIGURE 8.
Flexible fitting of EF-G into the cryo-EM map at 11.8 Å. (a) Structure rigidly fitted into the experimental EM map using the Situs package with 12 codebook vectors. (b) The final flexibly fitted structure using MD simulation. (c) Comparison of final flexibly fitted structure with the model obtained using NMFF (tan). Even though the fitting techniques employed are different, both models are structurally similar.
CONCLUSIONS
We introduced a method for the flexible fitting of high-resolution structures into low-resolution electron density maps from cryo-EM based on molecular dynamics simulations. This method targets higher-resolution cryo-EM maps for which more structural details are available (8 Å and higher). We show its success in predicting conformational changes of simulated and experimental cryo-EM data. In particular, smaller conformational changes (<3 Å RMSD) that can be experimentally observed in higher-resolution cryo-EM data are successfully predicted by our approach. As demonstrated in this article, this procedure provides a robust way to flexibly fit proteins while maintaining the overall architectural integrity. Due to the use of molecular dynamics simulations, only feasible deformations are possible, i.e., correlated motions between distant parts of the biological system are taken into account. In addition, we can evaluate the reliability of the obtained models by examining secondary structure conservation during the fitting.
In terms of computational time, although this method adds some overhead to standard MD, fitting is achieved on a relatively short timescale and large systems could be easily handled. The primary motivation for the development of this method is to model smaller-scale conformational changes observed in cryo-EM. Therefore, for large systems undergoing large conformational changes, normal-mode methods such as NMFF and MD-simulation-based methods should be combined to obtain an optimal fit. If a large conformational change is present, NMFF can be used to accomplish most of the conformational change. The MD-simulation-based method could then be used to model detailed changes within domains, such as helix movements, which are difficult to obtain within the low-frequency normal-mode regime. Therefore, these approaches provide a useful tool for the determination of conformational changes for large biological macromolecular assemblies in the context of experimental restraints from low-resolution structural data and the furtherance of our understanding of the underlying functional mechanisms in these systems.
Acknowledgments
The authors thank Osamu Miyashita for helpful discussions regarding this work.
Financial support from the National Science Foundation (grant 0744732) is greatly appreciated.
APPENDIX
In this approach, due to the additional effective potential, VFit, forces acting on each of the atoms in the system are calculated as a negative gradient of the potential VFit. Taking into account expression for VFit in Eq. 1 to calculate forces, it is necessary to calculate the gradient of the correlation coefficient, c.c.:
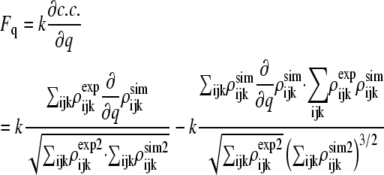 |
Calculation of the derivative of the correlation coefficient resolves to calculating the derivative of the synthetically generated density map ρsim. Synthetic maps are calculated by locating three-dimensional Gaussian functions on every atom and integrating these functions for every atom in each of the voxels as a given xn, yn, zn set of atomic coordinates:
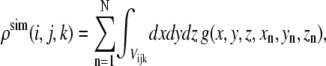 |
where n denotes nth atom from a set of N atoms, (i,j,k) denotes a given voxel, and 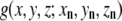 is the three-dimensional Gaussian function of the formula
is the three-dimensional Gaussian function of the formula
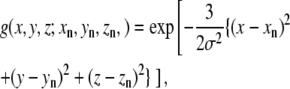 |
where σ is a resolution parameter. The resolution of a synthetic map is equal to 2σ.
When the volume, Vijk, of voxel (i,j,k) is defined as 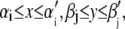 and
and 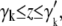 we can calculate the density as
we can calculate the density as
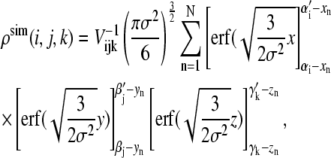 |
where 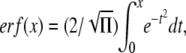 and the derivative of the density map is given as
and the derivative of the density map is given as
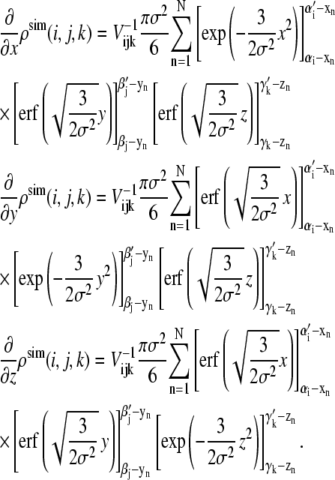 |
Editor: Ruth Nussinov.
References
- 1.Saibil, H. R. 2000. Conformational changes studied by cryo-electron microscopy. Nat. Struct. Biol. 7:711–714. [DOI] [PubMed] [Google Scholar]
- 2.Frank, J., and R. K. Agrawal. 2000. A ratchet-like inter-subunit reorganization of the ribosome during translocation. Nature. 406:318–322. [DOI] [PubMed] [Google Scholar]
- 3.Valle, M., R. Gillet, S. Kaur, A. Henne, V. Ramakrishnan, and J. Frank. 2003. Visualizing tmRNA entry into a stalled ribosome. Science. 300:127–130. [DOI] [PubMed] [Google Scholar]
- 4.Darst, S. A., N. Opalka, P. Chacon, A. Polyakov, C. Richter, G. Y. Zhang, and W. Wriggers. 2002. Conformational flexibility of bacterial RNA polymerase. Proc. Natl. Acad. Sci. USA. 99:4296–4301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wendt, T., D. Taylor, K. M. Trybus, and K. Taylor. 2001. Three-dimensional image reconstruction of dephosphorylated smooth muscle heavy meromyosin reveals asymmetry in the interaction between myosin heads and placement of subfragment 2. Proc. Natl. Acad. Sci. USA. 98:4361–4366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Conway, J. F., W. R. Wikoff, N. Cheng, R. L. Duda, R. W. Hendrix, J. E. Johnson, and A. C. Steven. 2001. Virus maturation involving large subunit rotations and local refolding. Science. 292:744–748. [DOI] [PubMed] [Google Scholar]
- 7.Lee, K. K., and J. E. Johnson. 2003. Complementary approaches to structure determination of icosahedral viruses. Curr. Opin. Struct. Biol. 13:558–569. [DOI] [PubMed] [Google Scholar]
- 8.Wriggers, W., R. A. Milligan, and J. A. McCammon. 1999. Situs: a package for docking crystal structures into low-resolution maps from electron microscopy. J. Struct. Biol. 125:185–195. [DOI] [PubMed] [Google Scholar]
- 9.Volkmann, N., and D. Hanein. 1999. Quantitative fitting of atomic models into observed densities derived by electron microscopy. J. Struct. Biol. 125:176–184. [DOI] [PubMed] [Google Scholar]
- 10.Rossmann, M. G. 2000. Fitting atomic models into electron-microscopy maps. Acta Crystallogr. D Biol. Crystallogr. 56:1341–1349. [DOI] [PubMed] [Google Scholar]
- 11.Rossmann, M. G., R. Bernal, and S. V. Pletnev. 2001. Combining electron microscopic with x-ray crystallographic structures. J. Struct. Biol. 136:190–200. [DOI] [PubMed] [Google Scholar]
- 12.Jiang, W., M. L. Baker, S. J. Ludtke, and W. Chiu. 2001. Bridging the information gap: computational tools for intermediate resolution structure interpretation. J. Mol. Biol. 308:1033–1044. [DOI] [PubMed] [Google Scholar]
- 13.Chacon, P., and W. Wriggers. 2002. Multi-resolution contour-based fitting of macromolecular structures. J. Mol. Biol. 317:375–384. [DOI] [PubMed] [Google Scholar]
- 14.Volkmann, N., D. Hanein, G. Ouyang, K. M. Trybus, D. J. DeRosier, and S. Lowey. 2000. Evidence for cleft closure in actomyosin upon ADP release. Nat. Struct. Biol. 7:1147–1155. [DOI] [PubMed] [Google Scholar]
- 15.Rawat, U. B. S., A. V. Zavialov, J. Sengupta, M. Valle, R. A. Grassucci, J. Linde, B. Vestergaard, M. Ehrenberg, and J. Frank. 2003. A cryo-electron microscopic study of ribosome-bound termination factor RF2. Nature. 421:87–90. [DOI] [PubMed] [Google Scholar]
- 16.Gao, H., J. Sengupta, M. Valle, A. Korostelev, N. Eswar, S. M. Stagg, P. Van Roey, R. K. Agrawal, S. C. Harvey, A. Sali, M. S. Chapman, and J. Frank. 2003. Study of the structural dynamics of the E. coli 70S ribosome using real-space refinement. Cell. 113:789–801. [DOI] [PubMed] [Google Scholar]
- 17.Gao, H., and J. Frank. 2005. Molding atomic structures into intermediate-resolution cryo-EM density maps of ribosomal complexes using real-space refinement. Structure. 13:401–406. [DOI] [PubMed] [Google Scholar]
- 18.Wriggers, W., and S. Birmanns. 2001. Using Situs for flexible and rigid-body fitting of multiresolution single-molecule data. J. Struct. Biol. 133:193–202. [DOI] [PubMed] [Google Scholar]
- 19.Chapman, M. S. 1995. Restrained real-space macromolecular atomic refinement using a new resolution-dependent electron-density function. Acta Crystallogr. A. 51:69–80. [Google Scholar]
- 20.Chen, J. Z., J. Fürst, M. S. Chapman, and N. Grigorieff. 2003. Low-resolution structure refinement in electron microscopy. J. Struct. Biol. 144:144–151. [DOI] [PubMed] [Google Scholar]
- 21.Fabiola, F., and M. S. Chapman. 2005. Fitting of high-resolution structures into electron microscopy reconstruction images. Structure. 13:389–400. [DOI] [PubMed] [Google Scholar]
- 22.Mears, J. A., M. R. Sharma, R. R. Gutell, A. S. McCook, P. E. Richardson, T. R. Caulfield, R. K. Agrawal, and S. C. Harvey. 2006. A structural model for the large subunit of the mammalian mitochondrial ribosome. J. Mol. Biol. 358:193–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jacobs, D. J., and M. F. Thorpe. 1995. Generic rigidity percolation: the pebble game. Phys. Rev. Lett. 75:4051–4054. [DOI] [PubMed] [Google Scholar]
- 24.Jacobs, D. J., A. J. Rader, L. A. Kuhn, and M. F. Thorpe. 2001. Protein flexibility predictions using graph theory. Proteins. 44:150–165. [DOI] [PubMed] [Google Scholar]
- 25.Jolley, C. C., S. A. Wells, P. Fromme, and M. F. Thorpe. 2008. Fitting low-resolution cryo-EM maps of proteins using constrained geometric simulations. Biophys. J. 94:1613–1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Topf, M., M. L. Baker, B. John, W. Chiu, and A. Sali. 2005. Structural characterization of components of protein assemblies by comparative modeling and electron cryo-microscopy. J. Struct. Biol. 149:191–203. [DOI] [PubMed] [Google Scholar]
- 27.Topf, M., M. L. Baker, M. A. Marti-Renom, W. Chiu, and A. Sali. 2006. Refinement of protein structures by iterative comparative modeling and cryoEM density fitting. J. Mol. Biol. 357:1655–1668. [DOI] [PubMed] [Google Scholar]
- 28.Topf, M., K. Lasker, B. Webb, H. Wolfson, W. Chiu, and A. Sali. 2008. Protein structure fitting and refinement guided by cryo-EM density. Structure. 16:295–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Velazquez-Muriel, J. A., M. Valle, A. Santamaría-Pang, I. A. Kakadiaris, and J. M. Carazo. 2006. Flexible fitting in 3D-EM guided by the structural variability of protein superfamilies. Structure. 14:1115–1126. [DOI] [PubMed] [Google Scholar]
- 30.Schröder, G. F., A. T. Brunger, and M. Levitt. 2007. Combining efficient conformational sampling with a deformable elastic network model facilitates structure refinement at low resolution. Structure. 15:1630–1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Delarue, M., and P. Dumas. 2004. On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models. Proc. Natl. Acad. Sci. USA. 101:6957–6962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tama, F., O. Miyashita, and C. L. Brooks III. 2004. Flexible multi-scale fitting of atomic structures into low-resolution electron density maps with elastic network normal mode analysis. J. Mol. Biol. 337:985–999. [DOI] [PubMed] [Google Scholar]
- 33.Tama, F., O. Miyashita, and C. L. Brooks III. 2004. NMFF: flexible high-resolution annotation of low-resolution experimental data from cryo-EM maps using normal mode analysis. J. Struct. Biol. 147:315–326. [DOI] [PubMed] [Google Scholar]
- 34.Hinsen, K., N. Reuter, J. Navaza, D. L. Stokes, and J. J. Lacapere. 2005. Normal mode-based fitting of atomic structure into electron density maps: application to sarcoplasmic reticulum Ca-ATPase. Biophys. J. 88:818–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Suhre, K., J. Navaza, and Y. H. Sanejouand. 2006. NORMA: a tool for flexible fitting of high-resolution protein structures into low-resolution electron-microscopy-derived density maps. Acta Crystallogr. D Biol. Crystallogr. 62:1098–1100. [DOI] [PubMed] [Google Scholar]
- 36.Mitra, K., C. Schaffitzel, T. Shaikh, F. Tama, S. Jenni, C. L. Brooks III, N. Ban, and J. Frank. 2005. Structure of the E. coli protein-conducting channel bound to a translating ribosome. Nature. 438:318–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Falke, S., F. Tama, C. L. Brooks, E. P. Gogol, and M. T. Fisher. 2005. The 13 Å structure of a chaperonin GroEL-protein substrate complex by cryo-electron microscopy. J. Mol. Biol. 348:219–230. [DOI] [PubMed] [Google Scholar]
- 38.Tama, F., G. Ren, C. L. Brooks III, and A. K. Mitra 2006. Model of the toxic complex of anthrax: responsive conformational changes in both the lethal factor and the protective antigen heptamer. Protein. Sci. 15:2190–2200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stahlberg, H., and T. Walz. 2008. Molecular electron microscopy: state of the art and current challenges. ACS Chem. Biol. 3:268–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tama, F., and Y. H. Sanejouand. 2001. Conformational change of proteins arising from normal mode calculations. Protein Eng. 14:1–6. [DOI] [PubMed] [Google Scholar]
- 41.Caulfield, T. R., and S. C. Harvey. 2007. Conformational fitting of atomic models to cryogenic-electron microscopy maps using Maxwell's demon molecular dynamics. 2007 Biophysical Society Meeting Abstracts. Biophys. J., Supplement, 368a, Abstract, 1735-Plat.
- 42.Noda, K., M. Nakamura, R. Nishida, Y. Yoneda, Y. Yamaguchi, Y. Tamura, H. Nakamura, and T. Yasunaga. 2006. Atomic model construction of protein complexes from electron micrographs and visualization of their 3D structure using a virtual reality system. J. Plasma Phys. 72:1037–1040. [Google Scholar]
- 43.Trabuco, L. G., E. Villa, K. Mitra, J. Frank, and K. Schulten 2008. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure. 16:673–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schlitter, J., M. Engels, and P. Krüger. 1994. Targeted molecular dynamics: a new approach for searching pathways of conformational transitions. J. Mol. Graph. 12:84–89. [DOI] [PubMed] [Google Scholar]
- 45.Ma, J., P. B. Sigler, Z. Xu, and M. Karplus. 2000. A dynamic model for the allosteric mechanism of GroEL. J. Mol. Biol. 302:303–313. [DOI] [PubMed] [Google Scholar]
- 46.Isralewitz, B., M. Gao, and K. Schulten. 2001. Steered molecular dynamics and mechanical functions of proteins. Curr. Opin. Struct. Biol. 11:224–230. [DOI] [PubMed] [Google Scholar]
- 47.Krammer, A., H. Lu, B. Isralewitz, K. Schulten, and V. Vogel. 1999. Forced unfolding of the fibronectin type III module reveals a tensile molecular recognition switch. Proc. Natl. Acad. Sci. USA. 96:1351–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sanbonmatsu, K. Y., S. Joseph, and C. S. Tung. 2005. Simulating movement of tRNA into the ribosome during decoding. Proc. Natl. Acad. Sci. USA. 102:15854–15859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Case, D. A., T. E. Cheatham, T. Darden, H. Gohlke, R. Luo, K. M. Merz, A. Onufriev, C. Simmerling, B. Wang, and R. J. Woods. 2005. The Amber biomolecular simulation programs. J. Comput. Chem. 26:1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A 2nd generation force-field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
- 51.Kabsch, W., and C. Sander. 1983. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 22:2577–2637. [DOI] [PubMed] [Google Scholar]
- 52.Gerstein, M., and W. Krebs. 1998. A database of macromolecular motions. Nucleic Acids Res. 26:4280–4290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.McLachlan, A. D. 1982. Rapid comparison of protein structures. Acta Crystallogr. A. 38:871–873. [Google Scholar]
- 54.Li, W., and J. Frank. 2007. Transfer RNA in the hybrid P/E state: correlating molecular dynamics simulations with cryo-EM data. Proc. Natl. Acad. Sci. USA. 104:16540–16545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Reference deleted in proof.
- 56.Valle, M., A. Zavialov, J. Sengupta, U. Rawat, M. Ehrenberg, and J. Frank. 2003. Locking and unlocking of ribosomal motions. Cell. 114:123–134. [DOI] [PubMed] [Google Scholar]
- 57.Laurberg, M., O. Kristensen, K. Martemyanov, A. T. Gudkov, I. Nagaev, D. Hughes, and A. Liljas. 2000. Structure of a mutant EF-G reveals domain III and possibly the fusidic acid binding site. J. Mol. Biol. 303:593–603. [DOI] [PubMed] [Google Scholar]
- 58.Roseman, A. M. 2000. Docking structures of domains into maps from cryo-electron microscopy using local correlation. Acta Crystallogr. D Biol. Crystallogr. 56:1332–1340. [DOI] [PubMed] [Google Scholar]