Cell-Cell Mechanical Communication through Compliant Substrates

Abstract

The role of matrix mechanics on cell behavior is under intense investigation. Cells exert contractile forces on their matrix and the matrix elasticity can alter these forces and cell migratory behavior. However, little is known about the contribution of matrix mechanics and cell-generated forces to stable cell-cell contact and tissue formation. Using matrices of varying stiffness and measurements of endothelial cell migration and traction stresses, we find that cells can detect and respond to substrate strains created by the traction stresses of a neighboring cell, and that this response is dependent on matrix stiffness. Specifically, pairs of endothelial cells display hindered migration on gels with elasticity below 5500 Pa in comparison to individual cells, suggesting these cells sense each other through the matrix. We believe that these results show for the first time that matrix mechanics can foster tissue formation by altering the relative motion between cells, promoting the formation of cell-cell contacts. Moreover, our data indicate that cells have the ability to communicate mechanically through their matrix. These findings are critical for the understanding of cell-cell adhesion during tissue formation and disease progression, and for the design of biomaterials intended to support both cell-matrix and cell-cell adhesion.

INTRODUCTION

The organization of cells into tissues is one of the most fundamental questions in developmental biology and tissue engineering. Although knowledge of cell migration from tissues is critical to the treatment of a number of diseases, little is known about how the balance between cell-cell association, dissociation, and cell-substrate adhesion is physiologically maintained and disrupted. The importance of matrix chemistry in mediating this differential adhesion is well-studied, however, less is known about the role of matrix mechanics in mediating tissue architecture (1–3).

In a previous study, we established a role for matrix mechanics in mediating tumor progression through the modulation of cell adhesion and contractility (2). Interestingly, tumors are stiffer and cell contractility is increased in comparison to normal tissue. Additionally, Wang et al. (1) have shown that cells are likely to adhere more strongly and migrate faster on stiffer substrates. This is because on softer substrates, cells are more weakly adherent to the matrix, unable to exert significant traction to produce motion, and the cells adhere to each other rather than to the substrate. Although this work shows that substrate mechanics can affect cell-cell cohesion by shifting the balance of cell-cell and cell-substrate adhesion, the exact mechanisms by which cells are driven to interact on compliant matrices and disperse on stiffer matrices is not understood.

Because cells are capable of responding to gradients in compliance through durotaxis (4), and because cells create strains within the matrix by exerting contractile forces (5–8), we hypothesized that cells are capable of sensing and responding to these strains created by neighboring cells. The relationship between matrix compliance, cell contractility, and cell-cell interactions is not obvious. Cells on stiffer substrates exert more force, but the substrate disturbances do not extend as far. On softer substrates, cells have been shown to exert less force (2), but these disturbances reach farther. However, what has not been measured is whether cells are capable of exerting contractile forces that are sufficiently strong to generate substrate strains from the cell edge that alter the adhesion and migration of an adjacent cell. To test this, we investigated endothelial cell-cell interaction, migration, and traction generation as a function of substrate compliance. Our data indicate that endothelial cells are capable of sensing mechanical forces exerted by adjacent cells and that this sensing mechanism can drive cells to interact. Although our data is specific to endothelial cells, it suggests a novel mechanism of cell communication that should be explored in other systems.

MATERIALS AND METHODS

Cell culture

Bovine aortic endothelial cells (BAECs) (VEC Technologies, Rensselaer, NY) were cultured as described previously (5).

Surface preparation

Glass surfaces were prepared as described previously (5,6) with minor modifications, using a method adapted from the protocol described by Wang and Pelham (9). 6-((Acryloyl)amino)hexanoic acid (N-6) was synthesized using the method described by Pless et al. (10). The N-6 copolymerizes with the acrylamide to form a reactive polyacrylamide gel. The N-6 contains an N-succinimidyl ester that is displaced by a primary amine, linking the amine-containing ligand to the polyacrylamide substrates.

Gels were prepared using varying ratios of acrylamide (40% w/v solution) and bis-acrylamide (2% w/v solution), based on the desired gel compliance. To minimize background fluorescence due to out-of-plane beads, gels were made in two stages as described previously (11) to produce a 100-μm gel without beads beneath a gel containing beads within a single focal plane. The modulus was determined experimentally as described previously (6) and matched closely with the moduli published elsewhere (12). Briefly, a small steel ball was placed atop the gel and the depth of indentation was measured using the micrometer on the microscope. An arginine-glycine-aspartic acid (RGD)-containing nonapeptide (with a sequence of NH₂-Tyr-Ala-Val-Thr-Gly-Arg-Gly-Asp-Ser-OH) was covalently linked to the polyacrylamide gels to permit cell adhesion.

Cell plating for microscopy

BAECs were plated at a density of 2500 cells/cm² 24 h before experimentation. The standard media was exchanged with Leibovitz L-15 media (Invitrogen, Carlsbad, CA) supplemented with 10% calf serum, 0.5% penicillin-streptomycin, and 1% 200 mM L-glutamine. Cells were immediately placed on an Olympus Inverted IX70 Microscope stage (Olympus America, Melville, NY) equipped with a chamber maintained at 37°C and a Spot RT camera (Diagnostic Instruments, Sterling Heights, MI) for observation.

Migration studies

For determination of single cell migration parameters, only cells that remained in isolation (>100 μm from other cells) were measured. For migration studies of cell pairs, those cells pairs that were chosen for observation begin in contact and are isolated from other adjacent cells by at least 100 μm for the duration of observation. Cell centroid position was determined based on cell outlines created using ImageJ software (National Institutes of Health, Bethesda, MD) and used to calculate the mean-square displacement (MSD) for a range of time intervals (13). The speed, S, and direction persistence time, P, were determined by fitting the MSD (〈d²〉) and the time interval, t, to the persistent random walk equation (14,15):

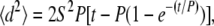(1)

using nonlinear least squares regression analysis. The MSD calculation was used for cell pairs despite the influence of the adjacent cell, similar to previous work investigating Brownian diffusion (16). The dispersion of a cell population (S²P) was determined by calculating individual cell dispersion values and reported as the mean of the individual cell values (17).

Calculation of detectable substrate deformations from the cell edge

The average distance of bead displacement from the cell edge, was measured as

(2)

where Area_beads and Area_perimeter are based on the region of bead movements determined by overlaying the unstressed images of the beads onto the stressed image of the beads. Inspection of the equation shows that it is a measurement of the average distance of displacement from the cell edge, and is calculated based on the area between the cell and the border of the detectable bead displacements and dividing by the average perimeter of this area.

Traction force microscopy

Traction force microscopy was used as has been described (6,7), based on deformations in the polyacrylamide substrate relative to the relaxed substrate as detected by movements of 0.5-μm beads embedded in the gel.

Statistical tests

All statistical comparisons were done using unpaired Student's t-test at α = 0.05 for statistical significance.

RESULTS

Cell-cell contact behavior is a function of matrix compliance and density

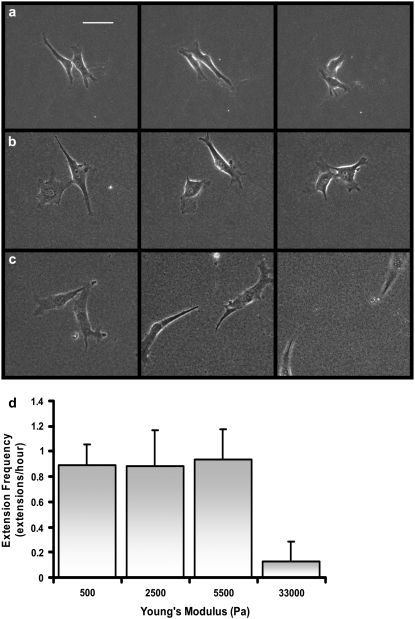
To investigate the influence of substrate compliance on cell-cell interactions, pairs of cells on varying compliance gels, ranging from very soft (Young's modulus (E) of 500 Pa) to very stiff (E = 33,000 Pa) were examined. Three qualitatively different behaviors were observed. On the softest gels (500 Pa), cells touch and remain in contact for the duration of the experiment (Fig. 1 a). Once in contact, cells may extend additional pseudopodia toward the adjacent cell, but the cells generally do not lose contact. Cells on the intermediate compliances studied (2500 and 5500 Pa) tend to contact, separate and retouch repeatedly (Fig. 1 b). Once the cells contact, they generally do not migrate significantly far from each other unless a third cell migrates within close proximity of the pair. On the stiffest gels (33,000 Pa), cells contact and migrate away from each other, without the same repeated contact behavior described for cells on intermediate compliance substrates (Fig. 1 c). In general, cells on the stiffest substrate touch only once before migrating away from each other.

FIGURE 1.

Endothelial cell-cell interactions on substrates of varying mechanical compliance. Endothelial cell-cell interactions on (a) soft (500 Pa), (b) intermediate compliance (5500 Pa), and (c) stiff (33,000 Pa) substrates. Images are of representative cell pairs taken at time of 0, 3 h, and 6 h. It should be noted that in b, cells repeatedly disconnect and reconnect throughout the 6-h period more often than is depicted. Scale bar = 50 μm. (d) Cells on more compliant substrates tend to repeatedly contact neighboring cells through pseudopodial extension. The number of cell extensions sent out toward an adjacent cell that result in cell-cell contact was counted for a period of 6 h as a function of substrate compliance (n = 5–8 at each compliance).

The average number of cell-cell contact events between nearby cells over a 6-h period on the different stiffness gels was measured (Fig. 1 d). On the low and intermediate compliance gels, cells tend to extend a pseudopodium resulting in cell contact ∼1 h⁻¹. In contrast, cells on the stiffest substrate tend to touch only once before separating.

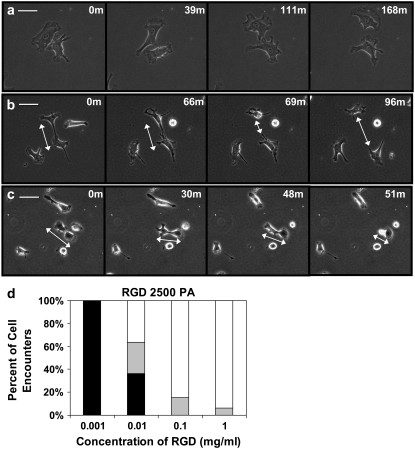
Cell-cell contact events were also measured as a function of extracellular matrix density on gels with E = 2500 Pa. Contact between two migratory cells results in one of three behaviors: “weak” interaction, where no qualitative shape change occurs (Fig. 2 a), “repulsive tether formation”, where one cell withdraws from following contact (Fig. 2 b), and “attractive tether formation”, where a cell is pulled toward an adjacent cell (Fig. 2 c). This interaction is peptide-density dependent (Fig. 2 d).

FIGURE 2.

Endothelial cell-cell interactions on substrates of varying matrix densities. BAECs on 2500 Pascal gels of differing RGD densities were visualized during cell-cell contact. Contact results in one of three behaviors depicted. (a) “Weakly” interacting cells: cells approach, touch, and move away from each other without a significant change in shape. (b) “Repulsive” tether formation: cells touch, resulting in the formation of a tether. Breakage of the tether results in one of the two cells snapping away and rounding. (c) “Attractive” tether formation: cells touch, resulting in the formation of a tether. The tether eventually pulls one cell off of the surface toward the adjacent cell causing the cell to round. Scale bar = 50 μm. (d) Cell-cell encounters were recorded at each ligand density. Weakly interacting cells are in white, repulsive tether formations are in gray, and attractive tether formations are in black. Between 15 to 24 cell-cell interactions were observed at each concentration. Chi-squared analysis indicates P < 0.001, indicating that the distributions of cell encounters at the four separate ligand densities are statistically significantly different.

Cell migration of isolated and paired cells varies as a function of matrix compliance

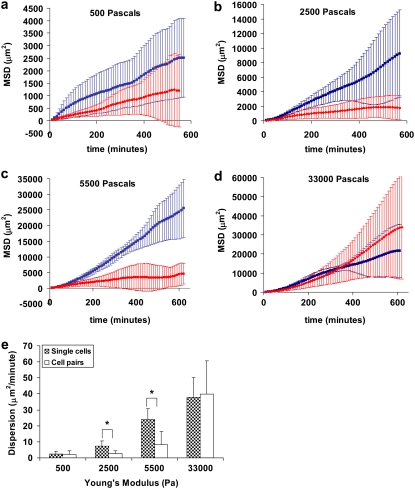
Because cell-cell interaction behavior varies based on the stiffness of the substrate (Fig. 1), it is logical that the migration behavior of cells in close proximity to an adjacent cell will also vary based on stiffness. To test this, we quantified the MSD of individual cells in the vicinity of another cell; the likelihood of cell-cell interactions was modulated by cell plating density. If cells are plated too sparsely, then the likelihood of finding two cells in close proximity is rare. If too many cells are plated, then it is difficult to find cell pairs in isolation, which is essential to prevent the influence of adjacent cells. As a control, the behavior of individual cells in isolation was also measured. In Fig. 3, we plot the MSD as a function of time for individual cells (blue) and cells in pairs (red) for four gel compliances, showing that MSD increases with gel stiffness. We were unable to parse the origin of this increased displacement into cell speed or persistence, as published by others (18).

FIGURE 3.

Migratory behavior of single cells versus cell pairs on compliant substrates. Mean-square displacements of single cells (blue squares) and cells in pairs (red diamonds) are plotted against time for cells on gels of (a) 500 Pa, (b) 2500, (c) 5500, and (d) 33,000. (e) The dispersion rates of cells in isolation and cells in pairs are plotted against the Young's Modulus of the substrate. Gels are coated with 1.0 mg/ml RGD-peptide. Error bars represent SD of n = 6–10 cells and the RGD concentration is 1.0 mg/ml. *P < 0.05.

Comparing the MSD of single cells and cells in pairs shows a clear difference in migration behavior. On the softest (E = 500 Pa; Fig. 3 a) and stiffest (E = 33,000 Pa; Fig. 3 d) substrates, the migratory behaviors of individual and interacting cells are very similar. However, at the two intermediate compliances tested (Fig. 3, b and c), single cells migrate farther than those cells in close proximity to an adjacent cell. The difference in MSD of isolated versus cells in pairs on intermediate stiffness gels shows that interacting cells remain close to an adjacent cell rather than migrating away as is the case on stiff substrates, consistent with the behavior observed in Fig. 1. One might speculate that cells in pairs on the intermediate stiffness gels exhibit a smaller change in MSD over time in comparison to single cells because cell-cell adhesion hinders cell separation, thereby preventing migration. However, as depicted in Fig. 1 b, interacting cells at intermediate compliances can and do disconnect from each other. This cycle of breaking and reforming connections repeats throughout the observation period (Fig. 1 d) indicating that cells could disconnect and migrate away. Instead, cells in pairs on intermediate compliance substrates stay near to each other and continue to interact, breaking and reforming connections. Therefore the difference in MSD of a single cell in comparison to cell pairs on intermediate compliance gels is not simply due to an inability to separate, but rather indicates that the cells prefer to remain in close proximity.

An alternative measure of cell migration is the dispersion (17), which quantifies the ability of a cell to scatter from its origin. Migratory cells display greater dispersion. The dispersion of single cells (depicted in Fig. 3 e, gray) increases with substrate stiffness indicating that cells on stiffer substrates migrate farther from their origin than those on softer gels. This result is not surprising, as it is well-established that motility is impaired on softer substrates (18–20). We compared the dispersion of single cells to cells interacting in pairs as a function of gel stiffness. On the stiffest substrate, the difference between the dispersion of single cells and cell pairs is statistically indistinguishable (Fig. 3 e) and resembles the migratory behavior of endothelial cells on tissue culture plastic (13). Similarly on the softest substrate, the dispersion of single cells and cells in pairs is statistically indistinguishable. On the two intermediate compliances, where the touch-release-touch behavior is observed, single cell dispersion is significantly greater than the dispersion of cells within close range of an adjacent cell. These data quantify the behavior depicted in Fig. 1 b, that cell dispersion on intermediate compliance substrates is reduced by the presence of another cell. Notably, the dispersion of cells in pairs on intermediate compliance is significant, indicating that cells in pairs do migrate, but do not disperse to the same degree as isolated cells. If the cells were unable to migrate because they are adherent to an adjacent cell, one would expect the dispersion of cells in pairs to approach zero as migration is inhibited.

Substrate deformations created by cell contractility increase with decreasing substrate modulus and correlate with cell-cell separation distance

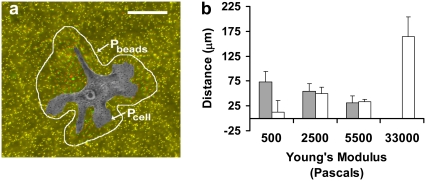
Because cells in pairs on intermediate compliances repeatedly touch and release (Fig. 1) and do not migrate far from each other (Fig. 3 e), we hypothesized that the two cells might be communicating through the substrate by exerting traction stresses, causing tension gradients in the substrate detectable by the adjacent cell. It is now well-established that cells exert larger traction forces on stiffer substrates (1,2,7,21,22), but the disturbance field (strain) on a stiff substrate is less than on a soft substrate. Therefore, because of these two competing factors, it was not clear how the average distance of detectable substrate deformation created by a cell scales with substrate compliance. Additionally, it was unclear if the deformations created in the substrate by one cell are sufficiently long range that they can be mechanically detected by an adjacent cell. To test our hypothesis that the cells are communicating mechanically through the substrate, we first quantified the distance that cells can deform their matrix to determine if these displacements are significantly large to displace the substrate under a nearby cell (Fig. 4 a). As shown in Fig. 4 b (gray), substrate strains decrease with increasing Young's modulus; cells on softer substrates displace the substrate more than cells on stiffer substrates, despite exerting weaker forces.

FIGURE 4.

Cells migrate within reach of the disturbances created by traction stresses. (a) The distance of bead displacement was measured as described in Materials and Methods, using the perimeter of the cell and the perimeter of the region of detectable bead movements. (b) The average distance of bead displacement from the cell edge (gray) and the maximum separation distance of interacting cells (white) are plotted against the Young's Modulus of the substrate. To measure the maximum cell-cell separation distance, pairs of cells initially beginning in contact and located at least 100 μm away from any adjacent cells throughout the duration of the experiment are observed for 6 h. Gels are coated with 1.0 mg/ml RGD-peptide. Error bars represent SD of n = 6.

We next compared the disturbance field to the cell-cell separation distance. We quantified the maximum separation distance of two cells initially in contact over 6hrs (Fig. 4 b, white). Notably, at both 2500 Pa and 5500 Pa, where the touch and release behavior is observed, the distance of substrate displacement from the cell edge and the maximum cell-cell substrate separation distance are statistically indistinguishable (P = 0.60 and 0.79, respectively). Disturbances created by cells on 5500 Pa gels, for example, are detectable 31.2 ± 13.7 μm from the cell edge and the average maximum cell-cell separation distance is 33.1 ± 4.8 μm, suggesting that at this compliance the mechanical influence of one cell, as observed in the cell's strain field, is close to the average cell-cell separation distance between cells. On the stiffest substrate (E = 33,000 Pa), where disturbances on the stiffest substrate do not propagate a detectable distance from the cell edge (Fig. 4 b), and the cells do not typically contact more than once (Fig. 1 d), the separation distance over a 6-h period is 164.2 ± 39.4 μm. On the most compliant substrates, no clear relationship between cell separation distance and substrate disturbance exists, but this is perhaps due to impaired migration of the cell on extremely soft surfaces (18). Summarizing these data, cells on gels of 2500 and 5500 Pa generally do not separate farther than the reach of their traction forces.

In determining the average reach of a cell's traction forces, the RGD concentration applied to the gels in Figs. 3 and 4 is 1.0 mg/ml. Although a range of ligand densities was not tested, we would expect that as long as there is sufficient ligand for the cells to adhere and migrate, the relationship between separation distance and substrate displacements would not change. Notably, if less ligand is available, cells will not spread as far. We have shown previously that spread area positively correlates with contractile force (6), therefore, if less ligand is present, cells generate less force, and the reach of their traction forces decreases. We would expect cells to sense each other mechanically on substrates conjugated with less ligand, but the region of sensing and mechanical transmission would be decreased.

Cells have the ability to sense traction stresses exerted by neighboring cells

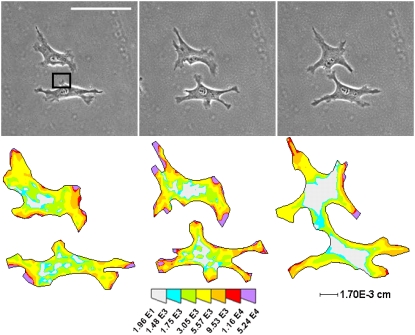
To determine if cells can exert tractions of significant magnitude capable of creating displacements detectable by an adjacent cell, traction force microscopy was used to quantify the force exerted by a pseudopod reaching to contact an adjacent cell. Fig. 5 illustrates an example of a cell extending a pseudopod from the interior of its cell body toward another cell on a 5500 Pa gel. This particular cell pair was chosen for analysis because of the unusual “reaching” behavior, which was often seen on softer gels (5500, 2500, and 500 Pa) and not typically seen on glass or stiff substrates (33,000 Pa). The directed motion of the pseudopod hints at mechanical sensing. There are many instances where cells, led by their large lamellipod, come into contact. The force exerted by the lamellipod is relatively large compared to the forces exerted by a smaller pseudopod. Therefore in these instances, it would be difficult to speculate on whether the cells came into contact because they could mechanically sense each other or because they touched as a result of random migration. Additionally, a lamellipod exerts significantly larger forces than a smaller pseudopod, so it would not be surprising if this force could be sensed by an adjacent cell. To truly determine whether cell tractions could result in changes in cell behavior, it was necessary to analyze incidences whether the cell migration pattern deviated from what would be expected. In the image depicted, the cell extends a small pseudopod directly toward an adjacent cell counter to the direction of motion. Because this behavior is atypical of an isolated cell, we investigated whether this motion could be due to the presence of another cell.

FIGURE 5.

Traction stress distribution supports mechanical cell-cell communication. Phase images and corresponding traction maps of an example of two cells coming into contact over time on 5500 Pa gels conjugated with 1.0 mg/ml RGD peptide. Box indicates early the pseudopodium analyzed for substrate disturbances as described in the Appendix. Scale bar = 100 μm. Color map is in units of dynes/cm².

Over a 6-h period, the cells touched six separate times. In the extension event depicted, the total force at (t = 0) exerted by the indicated, early forming pseudopodium is F = 4.8 × 10⁻³ dynes directed at an angle of −36° from the horizontal. To determine the distance of significant strain produced by an early forming pseudopod, the force exerted by the pseudopodium can be approximated as a point force originating at its center. Our previous data indicates that the most significant force is at the tip of the pseudopod (6), so approximating the force at the center of the pseudopod is a conservative estimate. Given this approximation, the distance of significant transmission through the substrate is ∼29.5 μm (see Appendix for details). Interestingly, the distance from the point force to the adjacent cell at the point of cell-cell contact is 25 μm, indicating that it is possible for one cell to exert tractions detectable by an adjacent cell and supporting our hypothesis that cells communicate mechanically through their substrate.

DISCUSSION

This study explores the influence of substrate mechanics and cell-generated traction stresses on endothelial cell-cell contact. The results presented here show for the first time that cells can mechanically influence the behavior of neighboring cells through cues generated by cellular traction stresses extending through the substrate. Our data show a novel form of cell-cell communication by which deformations created in the substrate by one cell can be detected by an adjacent cell. Moreover, we have established that endothelial cell-cell contacts are more likely to break on stiffer substrates.

One might speculate that cells in this study are responding to chemical gradients through paracrine signaling (13,23,24) rather than cell-generated mechanical cues. However, if cells were excreting a chemoattractant into the medium independently of the matrix compliance, we would expect cells to exhibit the same touch-release-touch behavior on stiff substrates as occurs on intermediate compliances, which is not the case. However, we cannot eliminate the possibility that cells secrete different amounts or types of chemoattractants based on compliance that in turn affect migration. To address this possibility, we also carried out separate experiments exchanging media between cells on different compliant substrates to rule out any effect of substrate-induced changes in chemoattractant production, and found no differences in cell behavior. One might also speculate that differences in cell behavior relates to remodeling of the substrates. However, work by Nelson et al. (25) has shown that remodeling of polyacrylamide is minimal and additional work by Vernon et al. (26) indicates that collagen production at the mRNA level does not change in response to matrix compliance. Therefore it is unlikely that the changes in cell contact behavior that we observe are due to changes in matrix deposition or substrate remodeling.

It is important to note that our results indicating that substrate mechanics alters cell contact behavior may be specific to BAECs. BAECs migrate slowly (27) and tend to migrate away from each other in culture, whereas epithelial cells, for example, tend to form stable cell contacts when plated subconfluently (3,28) and may behave differently than BAECs on deformable substrates. We believe the principles elucidated in this study are significant for understanding BAECs substrate-mediated processes and need to be examined for other cell types.

The results in this study are directly relevant to wound healing and angiogenesis, where the balance between cell-cell and cell-substrate adhesion is desired or disrupted (29–32). Our results indicate that endothelial cells tend to prefer to remain in contact at tissue-like stiffness, but prefer to migrate away from neighboring cells on stiffer substrates. Our results indicate that not only is the rigidity of the substrate important, but also the traction forces and subsequent substrate strains created by cells. Cell-cell adhesion is promoted by the contractile forces of cells on their substrate. These results are critical in understanding the relative contributions of matrix chemistry and mechanics in dictating cell behavior, and such insights are the basis for intelligent biomaterial design, where cell-material interactions are tightly controlled. Future studies of cell migration and tissue formation should not only include consideration of the effects of substrate chemistry and mechanics, but also the effects of individual cell contractility on the collective behavior of cells.

APPENDIX

It is of interest to determine whether the strains in the substrate propagate in such a way as to cause significant, detectable relative motions within the body of the adjacent cell. In theory, the displacements created by the pseudopod extend indefinitely through the substrate. To determine the distance of significant motion from the edge of the transmitting cell, we approximated the distance between the two “antennae” on the receiving cell (D) as 10 nm, which is a modest estimate of the spacing of integrins in a focal adhesion, and the distance of relative motion between the two antennae (u_r) as the length of a typical covalent bond, 0.1 nm. Approximating the substrate displacement due to a point force (u) in a linearly elastic material as

(A1)

r is the distance from the point force, F is the force and E is the elastic modulus (33,34), the relative motion (u_r) between two points can be approximated as

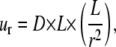(A2)

where, again, D is the separation distance between two “antennae” points on the receiving cell. This relation implies that two adhesion sites on the receiving cell, which are initially separated by a distance D, will experience a relative motion of order D(L/r)².

In the example cell shown in Fig. 5, D can be approximated as 10 nm and a meaningful relative motion (u_r) as the length of a typical covalent bond, 0.1 nm. Substituting back into Eq. A2, the typical distance of significant transmission through the substrate (r) is thus

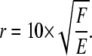(A3)

Given the force exerted by the pseudopodium depicted in Fig. 5 as calculated by traction force microscopy, the distance of significant transmission is approximately 29.5 μm. The center of the pseudopodium is located approximately 25 μm from the edge of the cell in the direction of maximum substrate disturbance, which is within the predicted range of significant detectable substrate disturbance. These data indicate that the force exerted by one cell is detectable by an adjacent cell, and supports our hypothesis that cells are communicating mechanically through the substrate.