The Role of Extracellular Matrix in Glioma Invasion: A Cellular Potts Model Approach

Abstract

In this work, a cellular Potts model based on the differential adhesion hypothesis is employed to analyze the relative importance of select cell-cell and cell-extracellular matrix (ECM) contacts in glioma invasion. To perform these simulations, three types of cells and two ECM components are included. The inclusion of explicit ECM with an inhomogeneous fibrous component and a homogeneously dispersed afibrous component allows exploration of the importance of relative energies of cell-cell and cell-ECM contacts in a variety of environments relevant to in vitro and in vivo experimental investigations of glioma invasion. Simulations performed here focus chiefly on reproducing findings of in vitro experiments on glioma spheroids embedded in collagen I gels. For a given range and set ordering of energies associated with key cell-cell and cell-ECM interactions, our model qualitatively reproduces the dispersed glioma invasion patterns found for most glioma cell lines embedded as spheroids in collagen I gels of moderate concentration. In our model, we find that invasion is maximized at intermediate collagen concentrations, as occurs experimentally. This effect is seen more strongly in model gels composed of short collagen fibers than in those composed of long fibers, which retain significant connectivity even at low density. Additional simulations in aligned model matrices further elucidate how matrix structure dictates invasive patterns. Finally, simulations that allow invading cells to both dissolve and deposit ECM components demonstrate how Q-Potts models may be elaborated to allow active cell alteration of their surroundings. The model employed here provides a quantitative framework with which to bound the relative values of cell-cell and cell-ECM interactions and investigate how varying the magnitude and type of these interactions, as well as ECM structure, could potentially curtail glioma invasion.

INTRODUCTION

In this work, we investigate the complex interplay between glioma cells and their extracellular environment using a Q-Potts model of a multicellular tumor spheroid in heterogeneous extracellular matrix (ECM). Gliomas are the most common primary brain tumor, and high-grade gliomas are almost invariably fatal (1,2). One key reason that prognosis for high-grade glioma patients is so poor is that the tumors are highly invasive and cannot generally be fully removed via surgical resection. Much research has thus focused on understanding and limiting glioma invasion; nevertheless, substantial changes in prognosis have not yet been realized. Although in vivo studies are crucial for determining which approaches may best curb invasion clinically, in vitro experiments are also important, as they allow well-controlled studies of individual parameters that may be key determinants of glioma invasion. Because cell behavior may differ on 2D substrates compared to 3D environments (3–7), and because both cell-cell and cell-environment contacts are likely important in determining glioma migration patterns, a number of in vitro studies have used 3D multicellular glioma tumor spheroids embedded in 3D approximations of ECM to elucidate the mechanisms that drive glioma invasion (8–18).

In silico studies allow even further dissection of the complex questions surrounding glioma invasion, and such studies have allowed new insights in this area. Many of these studies employ sets of reaction-diffusion equations to model tumor proliferation and/or tumor cell chemotaxis (18–28), although other approaches have been used as well (29–31). Although such approaches can qualitatively reproduce glioma invasive behavior, they do not access cellular-level behavior. A smaller number of computational glioma studies have employed cellular automaton models. These models are typically more patent, but each cell is represented by an independent site, and thus subcellular behavior can neither be taken into account nor predicted. An approach that has been used previously to model avascular tumor growth but has not yet been used to investigate glioma invasion is the Q-Potts model (32–35). In Q-Potts models, cells are delineated as assemblages of contiguous like spins on a spin lattice. Adjacent unlike spins are assigned energies of adhesion (the key input parameters) according to their spin states, and cells evolve so as to minimize the energy of the lattice according to the differential adhesion hypothesis (DAH) (36). The chief advantages of such a model are ease of use, transparency, and access to subcellular detail. The adhesion energy input parameters in large measure can be inferred from previous experimental results and can then be further refined via simulation in an iterative fashion. Although one recent Q-Potts model explored how the inhomogeneous structure of the ECM affects tumor angiogenesis (37), the importance of ECM in tumor invasion has thus far only been studied with a cellular automaton approach (38–40). Such an approach lends itself to capturing emergent phenomena in tumor invasion through ECM but does not allow explicit modeling of subcellular behavior.

Here, we use a Q-Potts model to elucidate the relationship between glioma invasiveness and glioma cells' interactions with an extracellular environment. Model tumor cells are introduced into a lattice representing ECM with two components and particular structure, and the tumor cells are permitted to grow, proliferate, and invade according to the energetics of the system. The model ECM used contains two components, one that forms a fibrous scaffold and is inhomogeneous on the cellular length scale, and another that is distributed homogeneously throughout the environment and forms no large-scale structures. Such an extracellular environment is consistent with that found in a variety of tissues, as well as tissue approximations composed of self-assembling fibrous proteins commonly used to study cell migratory behavior in vitro (41–45). In particular, the model ECM used in this study is meant to recapitulate the structure of collagen I gels that have been used in in vitro studies investigating the effects of collagen matrix density on glioma invasion (16,17). In one such study, glioma spheroids grown from U87dEGFR glioblastoma multiforme (GBM) cells were investigated. These cells have a truncated epidermal growth factor receptor (EGFR) gene. When embedded in collagen I gels these spheroids displayed increased invasive cell density and migratory speed as a function of collagen concentration in the range 0.5–1.5 mg/ml collagen (16). More recent experiments on spheroids grown from rat-derived C6 glioma cells embedded in collagen I gels have yielded similar results in this concentration range. These studies also reveal that C6 spheroids grown at higher collagen concentrations (>3 mg/ml) exhibit high invasive cell density. However, these invasive cells are considerably less motile than those that invade at lower collagen concentration and fail to migrate far from the spheroid body (C. B. Gluck, C. Guo, and L. J. Kaufman, unpublished results), a finding similar to that of Friedl et al. for fibrosarcoma spheroids (45).

The finding that intermediate collagen concentration encourages the greatest C6 invasion is consistent with findings for fibroblasts and smooth muscle cells plated on 2D substrates coated with collagen. Here, maximum cell spreading and migratory speed are found at intermediate collagen concentration (47–49). As described in these studies, such findings likely relate to the number, distribution, and adhesive force capacity of cell-collagen surface receptors. The reasons spheroids embedded in 3D gels maximally invade at intermediate collagen concentration is likely more complex. In addition to considerations of cell-collagen adhesion, cell-cell adhesion must be considered. Additionally, steric and mechanical factors likely play a role. For example, in the presence of large numbers of collagen fibers, the pore size in the extracellular environment will be smaller than the average cell size. This may require cells to alter their mode of migration and/or reorganize their surroundings for invasion to occur, and in extreme cases, small pores may arrest invasion entirely. Such considerations are not only important in understanding in vitro spheroid invasion but are also likely relevant in vivo, as brain tissue is highly crowded with a network of healthy cells, ECM molecules, and large-scale structures such as blood vessels (50). In vivo, gliomas tend to invade along blood vessels and white matter tracts (51), and the reasons for the preferential invasion along these structures may include increased perivascular space, the presence of chemoattractants, the presence of ECM molecules to which glioma cells can adhere (haptoattractants), and/or the presence of directionally permissive (aligned, contiguous) cellular or extracellular surfaces in these regions.

In this work, we begin with a discussion of the Q-Potts model and its underlying assumptions. We present findings on basic model parameters and show that the density and invasiveness of a tumor in any given model collagen lattice is most affected by the tumor's ability to shed its cells, which is mediated by the relative values of proliferative cell cohesion and proliferative cell-ECM adhesion energies. We then explore glioma growth and invasion as a function of amount and organization of model collagen in the surroundings. We show that glioma invasion patterns seen in vitro can be reproduced by the Q-Potts model employed here. In particular, we find that invasiveness of model tumor spheroids in all of the lattices examined is profoundly influenced by the amount and distribution of model collagen fibers. We furthermore illustrate that tumor invasiveness is inhibited by energy costs associated with very high collagen and invasive cell density. This reproduces the experimental finding that intermediate collagen concentrations maximize cell invasion in vitro. Finally, we independently assess the importance of two key cell-ECM interactions in determining glioma invasion: matrix dissolution, as may be carried out by degradative matrix metalloproteases (MMPs), and matrix deposition.

MODEL

The Q-Potts model

It has been recognized that during certain biological processes, cells may sort according to the same basic thermodynamic principles that govern mixing or demixing of a two-phase liquid system (36). According to the differential adhesion hypothesis, assortments of different types of sufficiently motile cells ergodically explore their potential energy landscape and organize such that the lowest energy configuration is achieved (36). Evidence supporting the DAH has been observed in a wide array of biological systems (52–55). It is reasonable to expect that the DAH can capture characteristics of tumor invasion into ECM, as such behavior is largely determined by cell-cell and cell-ECM molecular interactions. These interactions are driven by cell adhesion molecules and integrins, the number and distribution (and forces associated with engaged bonds) of which determine relative cell-cell and cell-ECM affinities. These affinities can be captured by the energies of adhesion and cohesion that are minimized according to the DAH.

Because the DAH is predicated on thermodynamic arguments, it readily avails itself to modeling using Monte Carlo methods. Glazier and Graner first demonstrated that many cell sorting events may be described by embedding the principles of the DAH into a Q-Potts model (56,57). In a generic Q-state Potts model, discrete sites on a lattice can assume any of Q different spins (58). Spins at lattice sites chosen at random are flipped from a spin state to a spin state These flips are accepted, as in any Monte Carlo model, with a probability, 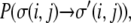according to the following rules:

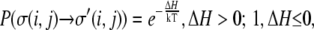(1)

where H is the system's Hamiltonian and T is its temperature. The Hamiltonian governing spin flipping in the general Q-Potts model is

(2)

where J is the spin-spin coupling energy constant. In the Glazier and Graner model, different spin states represent different cells. Each cell and, in our model, ECM element, is assigned a type, 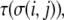and the interactions among sites in cells are governed by type-dependent bond energies, 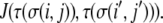Cells and ECM components then sort based on the Hamiltonian

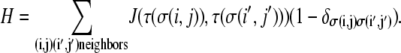(3)

Our model accounts for a number of tumor spheroid-specific properties. Spheroids prepared as described by Freyer and Sutherland are initially composed solely of proliferative cells (59). As the spheroid matures, changes occur that are specific to the cell line and spheroid preparation (12,60). Typically, the spheroid grows increasingly dense. In the process, the inner cells fill with waste and, simultaneously, few nutrients reach these cells. In response, the inner cells evolve first into passive, nondividing quiescent cells and, eventually, into necrotic cells (12,60–62). Spheroids thus become layered: necrotic cells form the core, quiescent cells surround this core, and invasive or shed proliferative cells line the rim. When glioma cells are prepared as spheroids they will invade 3D ECM approximations such as collagen I gels. The invading, proliferative cells appear phenotypically similar to the invasive cells found in gliomas in vivo.

With these considerations in mind, we permit lattice sites to flip among three cell spin states—the proliferative spin state (p), the quiescent spin state (q), and the necrotic spin state (n)—and two ECM spin states. The ECM spin states are the “collagen” spin state (c) and the “matrix” spin state (m). The collagen spin state represents assemblies of macromolecules such as collagen I that associate into long fibrous structures. These long fibrous structures provide the structure and mechanical properties of collagen I based tissues as well as of collagen I gels in which glioma invasion has been investigated (16–18). The matrix spin state represents ECM lacking any such fibrous scaffolds. This inclusion of explicit two-component inhomogeneous ECM is a novel aspect of our Q-Potts model that allows elaboration of and insight into how gliomas invade.

At the start of each simulation, a specified number of collagen threads of a given length are arranged randomly to create a 2D background ECM that reproduces the structure of collagen I gels employed for in vitro cell migration and tumor invasion studies. A spheroid of proliferative cells is subsequently planted at the center of the lattice, and it is permitted to develop according to the Hamiltonian

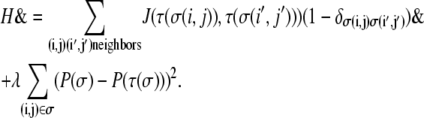(4)

Here, the summation is over a site's four nearest and four next-nearest neighbors, 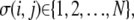and 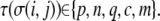N is the total number of cells. λ is an elasticity constant that moderates the energetic penalty associated with a cell perimeter varying from its target value, 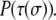Although other formulations of the Q-Potts model constrain cell area, we constrain the perimeter through the quadratic term to encourage more symmetric cells even when significant contact guidance is present. This reproduces the rounded cell body dictated by the shape of the nucleus, since nuclear dimensions are an important consideration in determining how cells traverse crowded environs (4,63). We note that in our perimeter-constrained simulations, cell area is also effectively constrained via energetic considerations associated with the first term of the Hamiltonian.

In addition to the rules enforced by the Hamiltonian, there are several other experimentally inspired rules. Cells that have attained their prescribed perimeters, 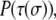and touch at least one collagen or matrix site are required to divide in half at fixed intervals. Cells randomly divide from either top to bottom or right to left to preserve the symmetry of the system. This frees only full-grown cells with sufficient space to divide and permits their progeny to grow into the surrounding ECM. Unlike several other treatments (29,34), here cell phenotypes are not altered through each phase of mitosis. Additionally, each cell type consumes a set amount of nutrients and produces a set amount of waste at regular intervals. When a lattice site in a cell surpasses a waste or nutrient threshold, all the cell spins are flipped from either the proliferative to quiescent or quiescent to necrotic state. Once cells become necrotic, their nutritional states are frozen. More subtle treatments describing nutrient usage, waste production, and diffusion of nutrients and waste have been employed previously and are necessary for realistic and multiscale modeling of tumor growth and invasion as it occurs in vivo (34). Our simplified treatments of both mitosis and nutrition allow us to focus in more detail on how spheroid invasiveness depends on extracellular environment. It is important to note that our simplified treatment yields the same tumor growth curve achieved in more sophisticated treatments, since the ratio of the number of proliferative cells that divide to the number that become quiescent is the prime determinant of total number of cells in the system. Finally, in our initial simulations, cells can only occupy, but not modify, the contents or positions of collagen sites. If a cell moves from a site previously occupied by collagen, the site is restored to its collagen spin state. The collagen sites therefore may be said to be conserved. As will be described in Results and Discussion, we later permit for more complex interactions between the cells and model collagen.

It should be noted that although the model employed here is a 2D model, the results presented may roughly be considered as slices through the centers of 3D spheroids, as our model replicates the structure of, and aims to reproduce behaviors associated with, 3D spheroids grown in 3D ECM approximations, rather than that of glioma cells plated on 2D substrates. Although there is no barrier to extending this model to 3D, the fact that the current 2D version well reproduces behavior seen when confocal microscopy is used to image 2D slices of 3D tumors grown in 3D environments confirms that this approach allows us to detail the relationship between properties of a tumor's extracellular environs and tumor invasion.

Simulation details

We employ a 500 × 500-site 2D lattice with periodic boundary conditions, with each lattice site set to be 2 μm. For the model parameters we typically use, as will be discussed below, this results in spheroid growth consistent with that seen experimentally for spheroids in collagen I gels (60,64). The perimeters of cells are approximated from experimental data (64). As necrotic and quiescent cells are more rounded than proliferative cells, they are assigned a perimeter of 40μm, whereas proliferative cells are assigned a perimeter of 50μm. Before planting proliferative cells in the center of a matrix, the cells are annealed in a bare (collagen-free) matrix for 400 Monte Carlo sweeps (MCS (1 MCS = 250,000 spin flips)) from a wall-like pattern of 5 × 6 lattice site bricks according to the following rules:

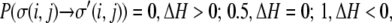(5)

with T = 0, λ = 1, γ = 0, J_mm = 0, J_pp = 2, and J_mp = 9. Such annealing prevents matrix spins from intermixing with cell spins and allows formation of natural-looking cell boundaries (57).

After annealing, a 50-μm circle of 65 proliferative cells, each composed of 30 sites on average, is placed at the center of the lattice of interest. To create isotropic collagen lattices, positions of the centers of the collagen threads to be used are randomly selected from the sites of the lattice. Although collagen fibers formed in vitro are generally between 100 nm and 1 μm (41,65–67), here they are accorded the width of a single site (2 μm), the minimum width permitted by our lattice. The angles at which the threads will be oriented are also randomly selected, and the threads are grown outward from the center into a lattice large enough to accommodate the fully grown threads. Once all of the threads are laid down, the inner 500 × 500 sites of the lattice are selected. Because the threads are arranged randomly, with no constraints imposed to make them self-avoiding, threads can overlap. The average number of overlap sites, which are treated identically to nonoverlap collagen sites, is a function of the number and length of threads used. Even in simulations using identical thread number and length, the number of overlap sites and sites of outgrowth into the larger initial lattice vary from simulation to simulation. Therefore, we refer to the total number of sites that would have been occupied, excluding overlap and outgrowth into the larger initial lattice.

Simulations employing the Hamiltonian in Eq. 4 and the probability rule in Eq. 1 are then run using the parameters shown in Table 1. The radius of the initial spheroid and the bond energies listed in Table 1 were determined through preliminary simulations calibrating the diameter of the simulated spheroids on a bare lattice with that of a glioma line grown as spheroids in nonadherent petri dishes over the course of 4 weeks (64). With these bond energies implemented at T = 4, spheroids develop in accordance with the experimental growth kinetics of spheroids detailed in previous work, as will be described below. Time is incorporated into the model with the assumption that cells divide on average once every 12 h. For T = 4, λ =1, and the energies of adhesion and cohesion (to be referred to as J parameters) given in Table 1, proliferative cells on average attain 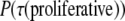every 144 MCS. As cells may divide only upon reaching their set perimeter, we set 144 MCS equal to 12 h. The ratio of time interval between divisions to time interval until a cell becomes quiescent is set to be ∼1:6. This permits proliferative cells to replicate a sufficient number of times to sustain their population before becoming quiescent. If this ratio is increased, the spheroid expands more quickly than is seen in experiment; if this ratio is decreased, the spheroid succumbs more quickly than is seen in experiments. A rudimentary treatment of nutrition is employed to set the time to quiescence and time to necrosis. Given that diffusion of nutrients and waste is not included in our treatment, published values for nutrient use, waste production, and necrotic thresholds in spheroids result in unphysically rapid necrosis (59,68). Thus, we use effective rates that set time to quiescence at ∼3 days and time to necrosis at ∼4.5 days. Although this behavior could be accomplished in the model with just two rules, to make the model easily extensible to a more complex treatment of nutrition, we embed the time to quiescence and necrosis in a kinetic model of nutrient usage and waste production. The lattice is initially seeded with a set amount of nutrients, and rates of nutrient consumption and waste production, and quiescent and necrotic thresholds, are chosen to be consistent with the times to quiescence and necrosis described above.

TABLE 1.

Adhesion and cohesion energies (J parameters) used in simulations

Jij	c	m	p	q	n
c	10
m	3	3
p	1	2*	30*
q	5	5	30	8*
n	5	5	15	1*	0

The J parameters applied to all simulations except as specifically noted. Proliferative, quiescent, and necrotic cells are denoted by p, q, and n, respectively. Model collagen and collagen-free ECM areas are denoted by c and m, respectively. Values with asterisks are varied, as explicitly discussed in Results and Discussion.

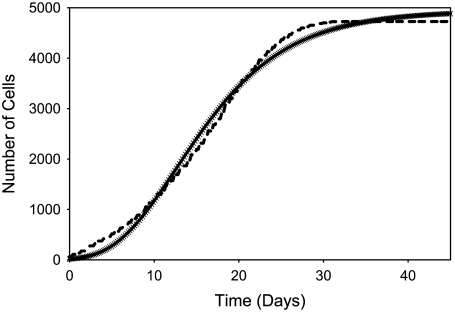
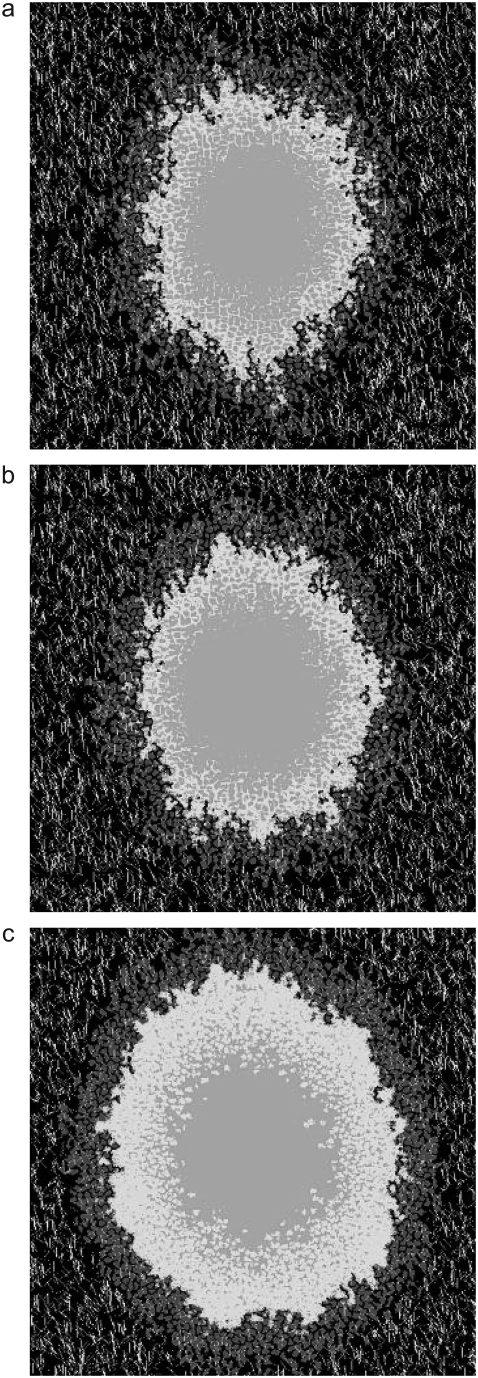
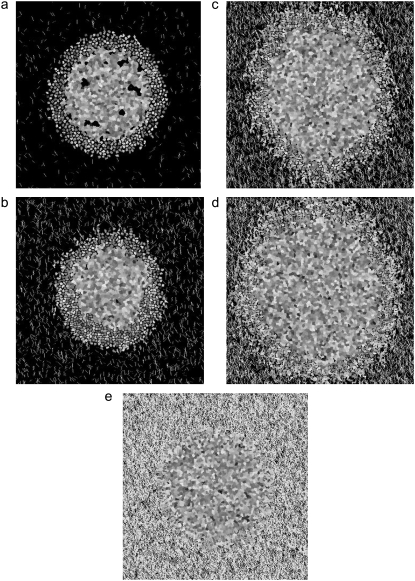
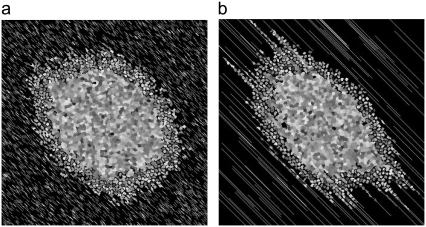
With these parameters and rules in place, we first simulate the growth of a spheroid in the absence of collagen fibers. The vast difference in bond energies between J_pp and J_mp (Table 1) causes the spheroid to shed cells even in the absence of collagen fibers (Fig. 1, a and b). This behavior is consistent with spheroid growth in ECM models lacking large-scale structure or inhomogeneity (69) and suggests that the relative values of the cell-cell (J_ij, with i,j ∈ n, p, q) and cell-matrix (J_im, with i ∈ n, p, q) energies are reasonable. Next, we simulate the growth of a spheroid on moderately dense lattices bearing 7500 12-μm-long “collagen” threads (Fig. 1, c and d). Fig. 1 demonstrates that proliferative cells are actively stimulated to both elongate and replicate by the presence of collagen in the model implemented here for the values reported in Table 1. Cells shed in the absence of collagen remain relatively compact and wade just outside the spheroid in the extracellular matrix space, whereas in the presence of collagen, cells become elongated and intermingle with the collagen. Just as the difference in the J_pp and J_mp bond energies allows for spheroids to shed cells in the absence of collagen, the difference between J_pp and J_cp prompts cells to invade along the lattice's model collagen fibers. Fig. 2 shows how a spheroid develops over 14 days and shows that that these preliminary simulations qualitatively capture invasive patterns that develop in experiments on glioma spheroids embedded in collagen I gels (16–18). In addition, the simulated spheroid observes Gompertz growth kinetics, as do glioma cells cultured in 2D and spheroids implanted in mice (70–72) (Fig. 3). Such agreement occurs even without exact bookkeeping of diffusing nutrients and waste or detailed inclusion of the cell cycle. For the parameters in this simulation, the number of proliferative cells increases until about day 16, at which point the nutrients in the system are not sufficient to sustain continued increases in proliferative cells, which then begin to decrease even as total cell number continues to rise. Such behavior is consistent with that measured for a variety of cell lines grown as spheroids in spinner culture (12,64).

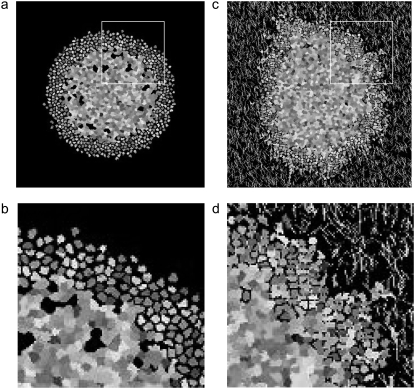
FIGURE 1.

Spheroids simulated according to Eqs. 6 and 9 and rules discussed in the text, with bond energies given in Table 1 at T = 4 and λ = 1. Spheroids are shown after 14 days of development. Individual cells can be differentiated, as they are depicted in grayscale. (a) Entire spheroid on a bare lattice. A number of proliferative cells have been shed into the spheroid periphery. (b) Detail of area enclosed by white box in a. (c) Entire spheroid on lattice containing 7500 12-μm threads. Many proliferative cells are invading along collagen threads, which are depicted in white. (d) Detail of area enclosed by white box in c.

FIGURE 2.

Time-lapse images of the development of the spheroid shown in Fig. 1 c at 0 days (a and d), 7 days (b and e), and 14 days development (c and f). (Left) Individual cells of all cell types are depicted in different colors. Yellow, collagen; black, afibrous ECM. (Right) Cell types are depicted in different shades: purple, proliferative cells, blue, quiescent cells; and green, necrotic cells.

FIGURE 3.

Regression of the growth curve (solid crosses) for the spheroid depicted in Fig. 2 against a three-parameter Gompertz equation (dashed line).

To interpret the simulations performed, spheroid radius and invasive distance are measured. Spheroid radius is defined as the radius of the circle completely circumscribing the dense portion of the spheroid. Computationally, this is assumed to be the closest distance from the center of the spheroid to 30 or more matrix or collagen sites. The number 30 is used to preclude the spheroid radius being measured as the distance between the center of the spheroid and its nearest small hole. Similarly, the invasive distance is defined as the radius of the circle completely circumscribing all spheroid cells, including invasive cells, minus the spheroid radius, as was done in Kaufman et al. (16). Although this metric biases the invasive distance toward accounting for outlier cells, in practice this bias is only observed on sparse or anisotropic collagen matrices. To determine how various factors influence the number and type of cells, the total number of cells, N, and number of cells of each type, N_p, N_q, and N_n, are counted. Cell position is quantified by calculating the cell centroid. The x and y coordinates of the centroid of a cell whose sites are denoted by i,j, with i representing the site's row and j the site's column, are determined by 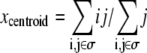and 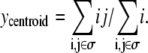The average number of nearest- and next-nearest-neighbor sites of collagen, matrix, and other cells abutting proliferative cells is also quantified as a metric of these cells' average environs.

In certain simulations, quantities are averaged over three simulations, and means and standard deviations are presented. In all cases, standard deviations are small, and thus, in certain simulations, results are reported for one simulation, the same one that gives rise to the spheroid images presented.

RESULTS AND DISCUSSION

Varying elasticity and temperature

Before discussing how spheroid growth and invasion change as a function of amount and distribution of model collagen, we address how spheroid growth changes in the same moderately dense lattice above (7500 12-μm threads) as a function of elasticity (λ), temperature (T), and select J parameters to validate the parameters used in subsequent simulations. Increasing the temperature of the system allows cells to more efficiently explore their potential energy landscape. In a similar way, decreasing elasticity, and thus allowing greater cell shape changes at low energy cost, allows individual cells to more efficiently explore the energy landscape described by the first term of the Hamiltonian. Although neither of these parameters is precisely related to a particular biological parameter, temperature broadly correlates to the overall growth rate of the tumor, and elasticity describes the degree of cell membrane rigidity.

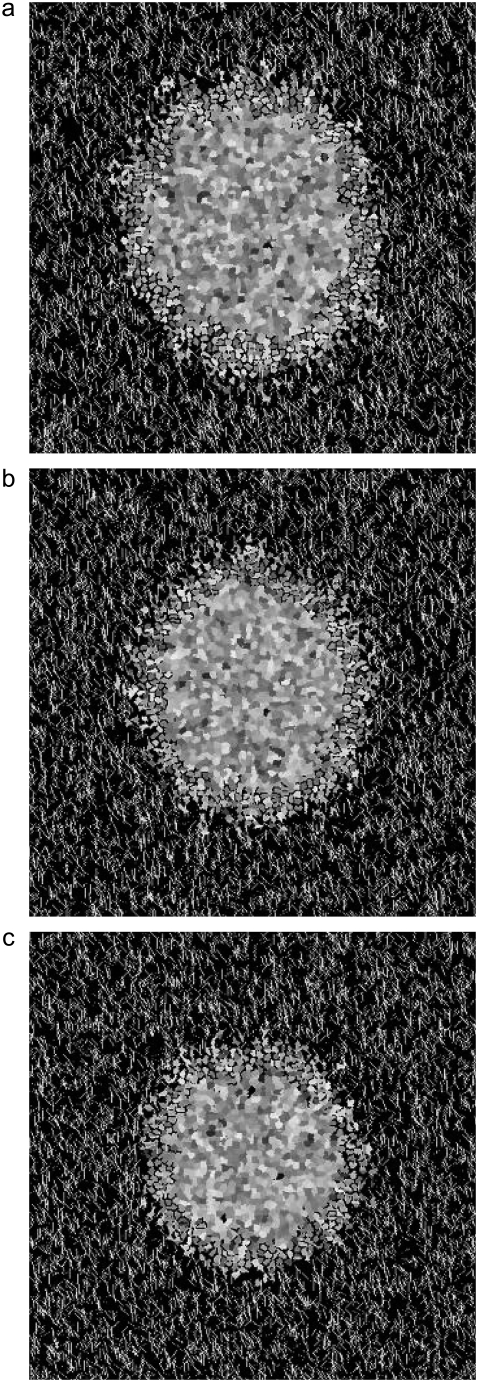
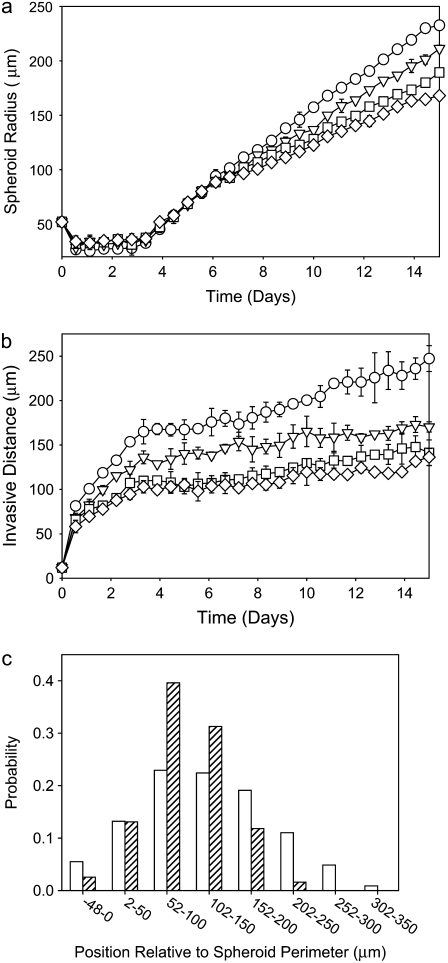
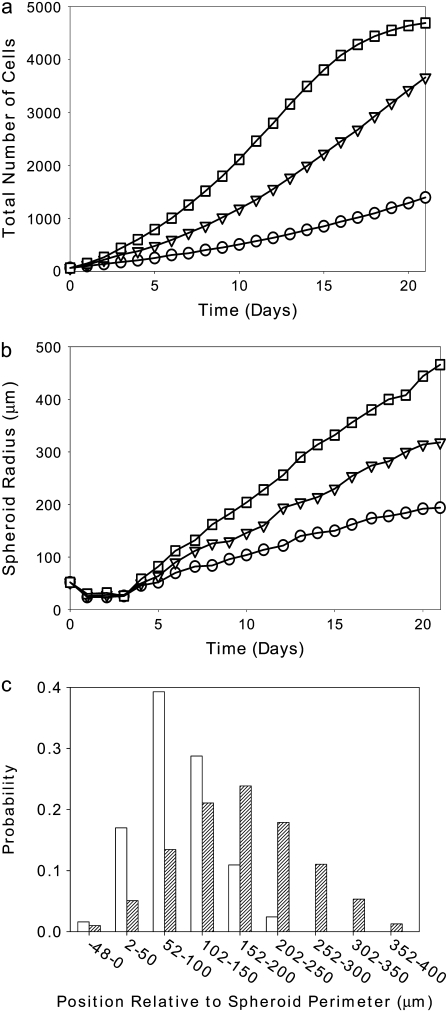
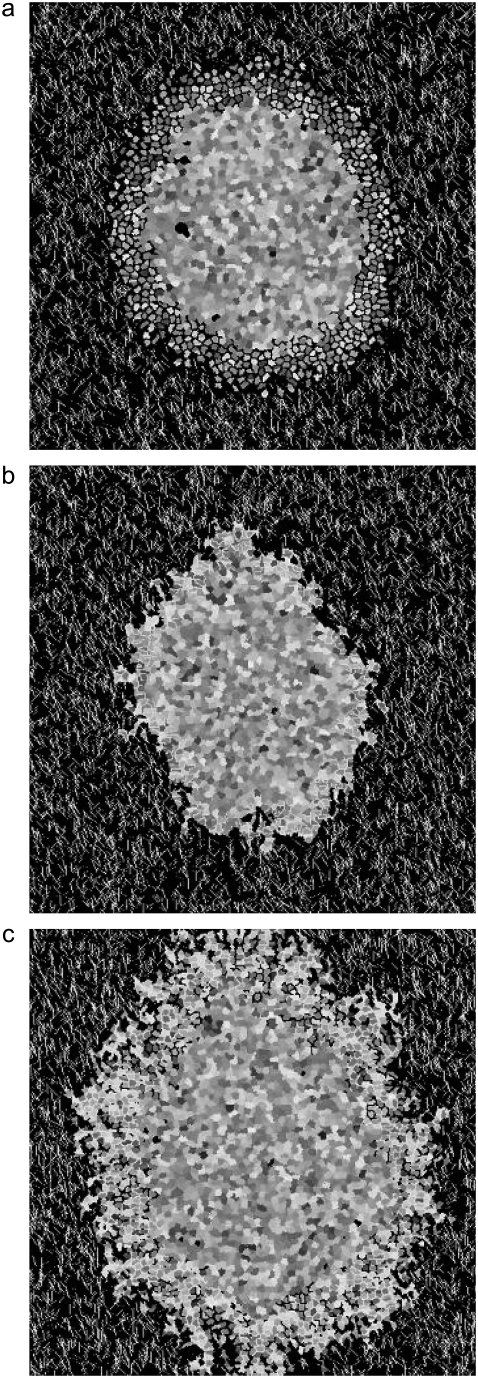
More precisely, given the use of a perimeter constraint to limit cell elongation, in our model elasticity is related to small-length-scale membrane fluctuations, akin to membrane ruffling. Fig. 4 demonstrates that at high λ, a decrease of both spheroid radius and invasive distance occurs, demonstrating that at high λ, the cells cannot expand into their environs efficiently, even in the presence of extracellular matrix elements to which they are attracted. Fig. 4 shows spheroids resulting from one set of simulations at λ = 3, 5, and 7 after 14 days of development (Fig. 2, c and f, shows such a spheroid with λ = 1). Fig. 5 shows spheroid radius and invasive distance for three sets of such simulations at values of λ from 1 to 7 as they develop over 16 days. A small value of λ allows the cells' perimeters to fluctuate more substantially, and in a modestly dense collagen lattice, cells far from the spheroid center will inevitably find a collagen strand to which to adhere. This permits these cells to traverse the lattice more readily than cells with a higher λ, leading to the greater invasive distance at smaller values of λ. This can be seen in the distribution of proliferative-cell positions relative to the spheroid edge (Fig. 5 c). There are also more cells (and more proliferative cells) in systems with a small value of λ. This occurs because cell growth is encouraged by a small value of λ, which results in a smaller energy penalty for larger cells relative to that which would be incurred at large values of λ. Cell growth in turn promotes cell division. For the 14-day spheroids with λ = 1 and λ = 7 shown in Figs. 2 c and 4 c, the total number of cells is 1991 and 861, respectively. In addition, the proportion of cells that is proliferative changes with λ. The percentages of proliferative cells for these two spheroids are 41.1% and 34.0%, respectively. Of the proliferative cells, there is also a clear difference in position relative to the spheroid edge, as shown in Fig. 5 c, with the proliferative cells in the system with greater shape flexibility venturing further from the spheroid center. Differences in λ chiefly affect the time necessary for spheroid radius and invasive distance growth; thus, to accelerate simulations, we set λ = 1 for the simulations investigating the effect of matrix variations on cell invasion that are presented below.

FIGURE 4.

Spheroids simulated on lattices containing 7500 12-μm threads after 14 days development. All parameters are as given in Table 1, with T = 4, and elasticity, λ, varied: (a) λ = 3, (b) λ = 5, and (c) λ = 7.

FIGURE 5.

Spheroid development as a function of elasticity, λ, for spheroids simulated on a lattice containing 7500 12-μm threads after 14 days development, as shown in Fig. 4. (a and b) Spheroid radius (a) and invasive distance (b), with λ = 1 (circles), λ = 3 (inverted triangles), λ = 5 (squares), and λ = 7 (diamonds). Standard deviations are plotted behind symbols and are not visible when smaller than the symbol. (c) Proliferative cell position relative to spheroid edge for one spheroid with λ = 1 (open bars) and one spheroid with λ = 7 (hatched bars).

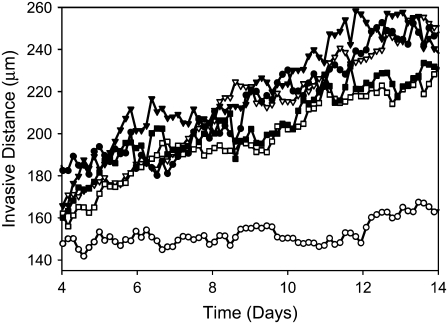
Next we varied temperature (T), which appears in Eq. 1 and sets the likelihood of accepting a move associated with an increase in system energy. The primary effect of raising the temperature of the system is that cells can divide more frequently, as the ability to surmount the energy barrier to cell growth and thus cell division increases with temperature, even though there is an energy cost associated with increased cell population. This is manifested as an increase in cell number (Fig. 6 a) and an increase in spheroid radius (Fig. 6 b) with increasing T. Increases in average cell velocity and invasive radius also occur, as is demonstrated by the distribution of proliferative-cell positions (Fig. 6 c). This cannot be well quantified for temperatures above T = 4 at 14 days, because the invasive cells reach the edge of the simulation box and interact with other invasive cells in a manner that is not physical. The cell velocity, invasive distance, and proliferative-cell positions all increase with increased T, since the probability that any given move is accepted increases, and thus cells can traverse the lattice more quickly at higher temperatures. Because increased T leads chiefly to increased cell proliferation, it is reasonable to consider the possible biological relevance of this parameter. In GBM cells, common mutations to the EGFR gene lead to increased cell proliferation and decreased apoptosis (73,74). It is believed that these two factors then lead to increased tumor invasiveness in vivo, though a recent study shows decreased invasion of U87dEGFR cells in a collagen I matrix (18). We find that increasing T, and thus increasing cell proliferation, in model collagen matrices increases spheroid radius substantially without substantially enhancing invasive radius, a finding in agreement with Stein et al. (18).

FIGURE 6.

Spheroid development as a function of temperature, T, for spheroids simulated on a lattice containing 7500 12-μm threads. (a) Total number of cells versus time for spheroids that develop at T = 2 (circles), T = 4 (inverted triangles), and T = 6 (squares). (b) Spheroid radii for T = 2 (circles), T = 4 (inverted triangles), and T = 6 (squares). (c) Proliferative cell position relative to spheroid edge for a spheroid grown with T = 2 (open bars) and T = 4 (hatched bars).

All simulations described below were conducted with λ = 1 and T = 4. Such values, together with the J parameters given in Table 1, allow for efficient increase in the number of cells, growth of the spheroid, and invasion of proliferative cells, at the same time qualitatively reproducing experimental results of glioma spheroid development in collagen I gels (16–18).

Varying bond energies

The values of the cell-cell and cell-environment adhesion and cohesion energies are crucial in determining spheroid behavior in the model. In addition, these J parameters have clear biological relevance, as they describe the relative preferences of cells for other cells and for ECM components. On a molecular level, these preferences are determined via expression and engagement of cell adhesion molecules including integrins and cadherins. Varying the J parameters related only to cell-cell adhesion may have a substantial effect on overall spheroid invasion, since cell shedding is a necessary step for invasion, and a number of in vitro experiments have recently highlighted how cell-cell adhesion relates to tumor invasiveness and metastasis (75–77). The downregulation of E-cadherin has been implicated in a variety of invasive and metastatic cancers (78). In gliomas, the differential activity of E-cadherin and N-cadherin, the most common adhesion molecule in neurons, has been described (79). In addition, it has been shown that glioma cell lines with low N-cadherin expression, low surface tension, and presumably low cell-cell adhesion invade low-concentration collagen I gels (0.5 mg/ml) in a dispersed pattern (17). This dispersed pattern is seen for U87 (17), U87dEGFR (16), and C6 cells (C. B. Gluck, C. Guo, and L. J. Kaufman, unpublished results) at all collagen concentrations between 0.5 and 1.5 mg/ml. On the other hand, Hegedus et al. showed that cells with high N-cadherin expression invade in a ring at 0.5 mg/ml collagen, effectively maintaining more cell-cell contacts among the proliferative, invading cells than exist in the starburst shaped dispersed pattern. These same cell lines, however, invade 1.5 mg/ml collagen gels in a dispersed pattern (17), indicating that varying cell-cell adhesion within a certain range is only important in sparse collagen gels. Indeed, in higher-concentration collagen gels (1.5 mg/ml), cell-matrix adhesions dominate invasion patterns of cells regardless of N-cadherin level.

These experimental findings, together with the fact that the simulation may be expected to be very sensitive to adhesion energy parameter values, prompt our investigation of the effects of independent variation of bond energies. Although one can theoretically vary all of the bond energies, we only detail variation of the bond energies of the most common—and therefore most influential—interactions in the model. One can also vary these parameters beyond the ranges discussed below, and doing so produces alternative forms of growth, many of which have been described already in detail by Glazier and Graner (57) and are inconsistent with tumor invasion. First, we vary the necrotic-quiescent bond energy (J_nq), the quiescent-quiescent bond energy (J_qq), and the proliferative-proliferative bond energy (J_pp), which are set to be 1, 8, and 30, respectively, in all simulations not discussed in this section. Varying both J_qq and J_nq over a wide range from their initial values up to 30 has very little effect on the dynamics of spheroid invasion in this model (data not shown). However, at greater J_nq and J_qq values, the spheroid does expand somewhat more quickly. Increasing J_nq increases the repulsion among necrotic and quiescent cells, altering spheroid density by causing islands of matrix to form within the body of the spheroid. In a similar way, as J_qq is increased, quiescent cells begin to increasingly repel one another, leaving ECM segments within the spheroid. These areas tend to be larger at high J_qq than at high J_nq, since quiescent cells are more likely to be adjacent to each other than to necrotic cells by the 14th day of spheroid development. Even in the presence of large J_qq and J_nq values, the islands of extracellular matrix are temporary, eventually filled in by newly divided cells. The islands of ECM are reminiscent of those seen by Hegedus et al. in invasion of the high-N-cadherin-expressing GBM lines at low collagen concentration, in which the ring invasion pattern surrounds areas of digested collagen (17). However, the noncontiguousness of the cells in spheroids with high J_nq and J_qq values is not consistent with most glioma invasion patterns found in in vitro collagen I matrices. Thus, we choose a relative ordering of cell-cell adhesion energies that inhibit the formation of such islands within the spheroid body: J_nq < J_qq < J_pp < J_pq. This assures that inner (necrotic and quiescent) spheroid cells are more likely to reside next to each other than next to outer cells. This ordering may accurately reflect the number and strength of cell-cell adhesion molecules among the necrotic, quiescent, and proliferative cells in low-cadherin-expressing gliomas, but is likely not consistent with that in high-cadherin-expressing lines.

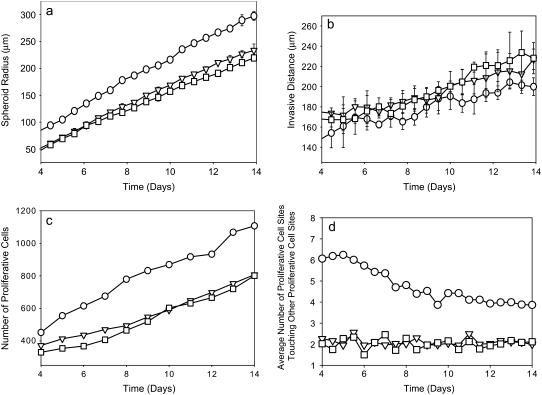
We now vary J_pp. Although this quantity sets energies only between proliferative cells, the fact that proliferative cells typically have contact with many matrix and collagen sites makes the value of J_pp crucial in determining invasive properties of the spheroid. Fig. 7 shows images of spheroids simulated with different values of J_pp after 14 days of development. Small J_pp values lead to increased spheroid radius, slightly decreased invasive distance, and increased proliferative-cell density in the invasive region relative to simulations using large values of J_pp (Fig. 8). At high J_pp, the proliferative cells spread away from one another in a dispersed pattern, and fewer proliferative cells are in contact with one another, as demonstrated by Fig. 8 d. This is because increasing J_pp increases the surface tension between proliferative cells relative to that between proliferative cells and both collagen and matrix elements, increasing the bias toward invasion. At low J_pp values, the population of proliferative cells increases quickly over time as a result of the relatively low energy cost of contacts between proliferative cells. These proliferative cells clump along the spheroid rim rather than invading significantly into the surroundings, as can be seen in Fig. 7. Thus, the relatively subtle effect that J_pp has on invasive distance, as illustrated in Fig. 8 b, is due to competing effects. At low J_pp, there is an increase in proliferative-cell number, but those proliferative cells tend to remain close to the central spheroid body, whereas at high J_pp, there are fewer proliferative cells, but those cells do invade the surroundings more substantially. The fact that changing J_pp alone can lead to drastic differences in spheroid structure over time shows that cell-cell affinity is as important a consideration as cell-ECM element affinity in determining invasive behavior.

FIGURE 7.

Spheroids simulated on lattices containing 7500 12-μm threads after 14 days development. All parameters are as given in Table 1, except as noted. T = 4 and λ = 1. (a) J_pp = 30. (b) J_pp = 20. (c) J_pp = 10. Necrotic, quiescent, and proliferative cells are differentiated in grayscale as in the right panel of Fig. 2 (in color).

FIGURE 8.

Spheroid development as a function of proliferative cell-proliferative cell adhesion energy, J_pp, for spheroids simulated on a lattice containing 7500 12-μm threads. Measures are shown for days 4–14. J_pp = 10 (circles), J_pp = 20 (inverted triangles), and J_pp = 30 (squares). (a and b) Spheroid radius (a) and invasive distance (b) averaged over three simulations. Error bars are standard deviations and are plotted behind the symbols. (c and d) Number of proliferative cells (c) and average number of proliferative cells (d) a given proliferative cell is adjacent to for the single set of simulations shown in Fig. 7.

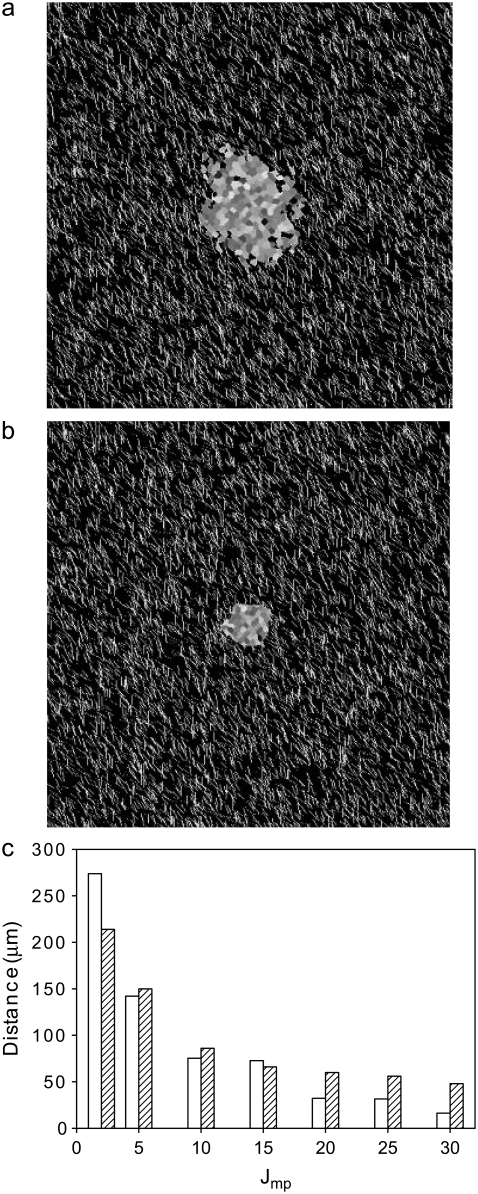
Next, we vary J_mp. Fig. 9 shows that increasing J_mp from the value of 2 used in all other simulations described decreases not only spheroid radius but invasive distance as well, essentially concentrating the cells into one extremely dense spheroid body with occasional dense protrusions outside the spheroid. This behavior is not consistent with any in vitro experiments of spheroid growth in collagen gels and supports the use of a low value of J_mp in our simulations. In all experiments in which spheroids invade collagen gels, regardless of particulars of the invasive pattern, cells invade preferentially along collagen fibers and do not substantially invade into collagen-free matrix regions. This might suggest that J_mp should not have such a strong effect on invasion. However, all invading cells (and particularly those that cannot elongate substantially) will touch both collagen and collagen-free (matrix) areas of the environment, or sites of the lattice. Thus, at high J_mp values, invasion is discouraged. If our model allowed for greater change of proliferative cell shape upon invasion, increasing J_mp would be expected to have less effect. Although at the collagen density investigated for the varied J parameter simulations (7500 12μm threads) increasing J_mp has more significant effect than increasing J_cp (data not shown), at higher collagen density, the behavior would be inverted. In the absence of large quantities of other fibrous ECM scaffold, the situation in many brain regions in vivo, increasing the J_mp bond energy, by either altering the relative amounts of various glycoproteins in the matrix or introducing a drug that binds cell-matrix or tumor cell-healthy cell adhesion molecules overexpressed by the tumor cells, could limit invasion, rendering these tumors more partial to resection.

FIGURE 9.

Spheroids simulated on lattices containing 7500 12-μm threads after 14 days development. All parameters are as given in Table 1 except as noted, and T = 4 and λ = 1. (a) J_mp = 10. (b) J_mp = 30. (c) Invasive distance (open bars) and spheroid radius (hatched bars) as a function of J_mp.

Collagen concentration

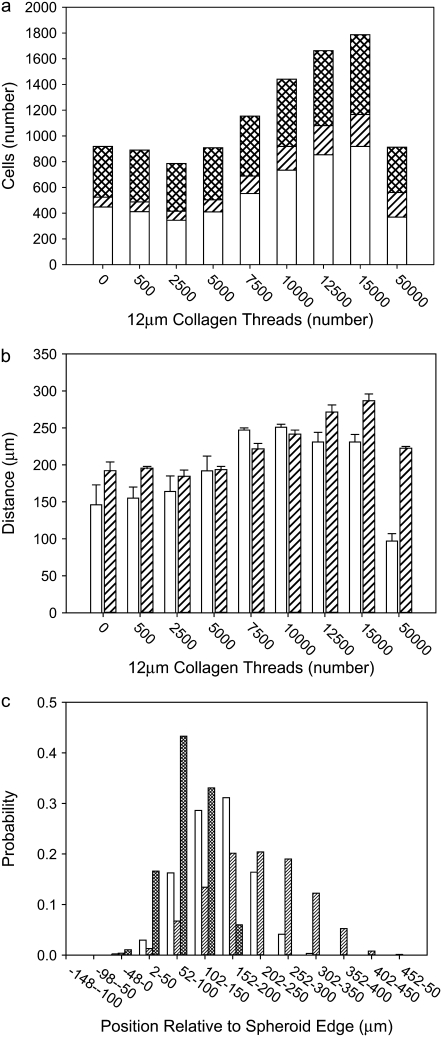
Having fixed T, λ, and the J parameters such that spheroid invasion patterns in vitro are qualitatively reproduced by the model, we are now in a position to predict glioma invasion into environments of given structure. In particular, we now consider the effect of varying collagen-thread density and length. In this model, the number of collagen threads is a stand-in for collagen concentration: the more threads, the higher the collagen concentration for any given thread length. To study the effects of increasing collagen concentration, spheroids are planted on lattices with increasing numbers of threads. Fig. 10 presents images of model spheroids after 14 days of development in matrices of different numbers of 12-μm threads, from a low-density unpercolated matrix to a very high-density matrix. These simulations show that spheroid development in surroundings containing model collagen arranged into fibers of length on the order of cell length can be sorted into three regimes. Under a certain collagen threshold, cells can be shed from the spheroid but cannot successfully invade. At moderate collagen concentrations, cells can both be shed and invade. Finally, above a certain threshold, cells cannot be shed and therefore cannot invade.

FIGURE 10.

Spheroid development at 14 days as a function of number of 12-μm collagen threads, for (a) 500, (b) 2500, (c) 10,000, (d) 15,000, and (e) 50,000 threads. (Fig. 2 b shows spheroid development in a lattice of 7500 12-μm threads).

At 500 and 2500 collagen threads (Fig. 10, a and b), the lattice is undersaturated and not percolated. Spheroid development in the 500-thread system bears much similarity to that in a collagen-free environment (Fig. 1 a), as few cells at the edge of the initial spheroid have collagen neighbors. We note here that one way in which our model does not well represent the 3D environment glioma cells encounter in 3D in vitro experiments is that here, a collagen network that does not appear percolated in 2D is not percolated. On the other hand, a 2D slice of a 3D system may reveal a seemingly unpercolated network that is percolated through connections to collagen fibers outside the imaged plane. Such collagen interconnections in vitro allow a cell attracted to collagen to invade through the matrix along different paths than would be allowed in the absence of such out-of-plane percolation. At 2500 12-μm threads, a few cells invade along the interconnected threads (Fig. 10 b). The low invasive cell density is affected by the fact that cell growth and proliferation are limited in environments of little collagen in our model, since there is a higher energy cost associated with proliferative cell growth into bare matrix (as dictated by J_mp) than along collagen (as dictated by J_cp).

At moderate collagen concentrations (5000–15,000 12-μm threads), many more cells traverse one of a profusion of interconnected collagen threads. Fig. 10, c and d, shows that these spheroids have a more rounded, symmetric morphology. This is in part due to the fact that proliferative and total cell number increase almost linearly with collagen-thread number in this regime (Fig. 11 a), since the low J_cp value encourages cell growth and division when cells touch collagen. The increase in cell number is tracked by the increase in spheroid radius (Fig. 11 b), which also increases monotonically with collagen-thread number in this concentration regime. The invasive radius in this intermediate collagen concentration regime is higher than in the undersaturated lattices but is quite similar over the 5000–15,000 range, though the invasive cell density is higher at the higher collagen concentrations. The similarity in invasive distance occurs because in this intermediate concentration regime, cells radiate outward on the longest continuously interconnected threads locally available, which will be of similar length in all intermediate-concentration matrices with threads of a given length.

FIGURE 11.

Measures of spheroid development at 14 days as a function of number of 12-μm collagen threads. (a) Number of cells: proliferative cells (open), quiescent cells (hatched), and necrotic cells (solid). Means are given for three simulations. (b) Invasive distance (open) and spheroid radius (hatched). Means and standard deviations are reported for three simulations. (c) Proliferative cell position relative to spheroid edge for 2500 (open), 15000 (hatched), and 50,000 (cross-hatched) 12-μm collagen threads for the simulations that give rise to the spheroid images in Fig. 10.

Finally, at the highest collagen concentration investigated, 50,000 12-μm threads, the numbers of total cells and proliferative cells, the spheroid radius, and the invasive radius are all substantially lower than they are in the intermediate collagen concentration matrices (Fig. 11). In the model, this is because the abundance of collagen threads allows cells to maximize their collagen contacts (and thus decrease their energy contribution to the system) by slight alterations in shape that do not lead to extension and eventual invasion. In addition, invasion in such a crowded environment would increase the ratio of proliferative cell-proliferative cell to proliferative cell-matrix contacts relative to that in somewhat sparser matrices. Given that J_pp = 30 and J_mp= 2 in these simulations, this would substantially increase total energy.

In comparison to experiments, two things are noteworthy in the results illustrated by Figs. 10 and 11, which show that there are three regimes for spheroid growth and invasion as a function of collagen concentration. First, the simulations here suggest that given the simple assumption that in a two-component ECM, invasion is driven by the preference of cells for a fibrous component rather than each other, there will be maximal invasion at an intermediate density of collagen fibers. This finding is consistent with our unpublished results and the finding of maximal cell spreading and migratory speed on 2D substrates at intermediate collagen concentration (47–49). It has been suggested that decreased cell spreading on a substrate coated with a high concentration of surface ligands is driven by the fact that at high collagen density, cell collagen receptors can be engaged without maximal cell spreading (48,49). The decrease of migratory speed on 2D surfaces with high surface ligand concentration has been explained somewhat differently in other studies (49,80,81), where the authors proposed that cell migration is limited at low ligand density by inability of the cell to form sufficient attachments to spread and generate traction to move forward. At high ligand densities, however, according to those studies, an overabundance of contacts prevents cell detachment and thus migration. This description of inhibited migration at both very low and very high ligand densities is consistent with the mechanism of inhibited invasion in our model. Here, each cell perimeter site has a certain affinity for each collagen, matrix, or other cell site. This is equivalent to assuming that each cell has a certain number of collagen, matrix, and cell adhesion sites on its surface. A cell in an environment with few cell-collagen contacts has limited invasive potential, as described previously. Also, for a cell with many cell-collagen contacts, as proliferative cells will have at high environmental collagen concentration, there is no energetic benefit associated with further invasion.

Another factor in determining cell invasion through tissue or in vitro approximations to tissue partially captured in our model is related to cellular ability to move through small pores. This issue is not important in 2D spreading and migration but is of critical importance in 3D migration both in vitro and in vivo. In vivo and in high-concentration collagen I gels, in an experimental setting, glioma cells invade their surroundings despite the fact that the pore size in those surroundings is smaller on average than cell size. Cells move through such environments by dissolving structural proteins, reorganizing structures, and/or squeezing through small pores in their surroundings. Thus far, we have not allowed either of the first two processes in our simulations. However, because the cells in our model can change shape, cell contractility that may allow motion through small, stiff pores is included in the model. Although we cannot capture the full 3D motion of a cell moving through a small pore in our 2D simulation, we do capture cell contractility that allows motion through channels of collagen that are narrower than the cell body. Such motion may be similar to the motion glioma cells use to move along blood vessels and bundled axons of the corpus callosum in brain in vivo or through small pores in vivo and in vitro (63). Our results suggest that at very high collagen density, cell shape alteration to the extent allowed in our model is not sufficient to overcome small pore size or the disinclination for cells to deadhere from collagen to migrate, in agreement with recent experimental findings (45).

Experimentally, in addition to (and often coupled to) the steric effects described above, mechanical properties of cell surroundings may affect cellular ability to invade 3D environments. On 2D substrates, cell spreading is independently affected by substrate stiffness and ligand density. For example, at a given collagen density, it has been shown that smooth muscle cells spread maximally on surfaces of high stiffness (49). Additionally, it has been shown that cells may exhibit durotaxis, the tendency to move along gradients of increasing stiffness (82). Experiments decoupling the effects of stiffness and ligand density in 3D are difficult to design and perform, yet early experiments of this type suggest that maximal stiffness does not correlate with maximal cell movement (83). Our model neither explicitly includes nor excludes durotaxis. Thus far, we have described the J parameters defining cell preference for collagen as being driven by cell-collagen receptors, and thus cell migration from an area of low to high ligand density would be driven by haptotaxis. However, it is equally possible to describe cell preference for collagen, as contained in the low value of J_cp, as being driven by cell preference for a stiff substrate. In that formulation, cell migration is driven by durotaxis. Thus, our simulations show that a single type of cell preference for structures in the extratumoral environment (whether haptotactic or durotactic in nature) is sufficient to reproduce spheroid invasive patterns seen in vitro.

In addition to the potential effects of stiffness on single-cell migration, mechanical properties of the environment may affect multicellular aspects of tumor development as well. It was suggested by Kaufman et al. that in 1.5-mg/ml and 2-mg/ml collagen concentration matrices, volumetric expansion of the spheroid is curtailed due to pressure exerted by bundled collagen at the spheroid edge, a finding consistent with work showing that solid stress inhibits tumor growth through a variety of mechanisms (84,85). In our model, there is no stress or pressure associated with collagen present alongside the spheroid body. Despite this, as Figs. 10 and 11 show, spheroid radius growth is curtailed in matrices of high collagen concentration in our model. This is due to the tendency for static cells to exhibit limited growth and proliferation when the tendency to migrate is reduced, as it is here due to the high number of cell-collagen contacts. Thus, we find that cell-cell, cell-matrix, and cell-collagen preferences alone are sufficient to curtail spheroid radius growth at high collagen concentrations.

Matrix structure

Before we compare collagen concentration in our model to that used in in vitro experiments, we first isolate the effects of the collagen thread length from that of collagen concentration on spheroid development. To this end, spheroids are planted on matrices with the same number of initial collagen sites (15,000, 60,000, and 90,000) composed of threads of different lengths, 12-μm and 52-μm. Comparing Fig. 12, a–c, to Fig. 10, b–d, reveals the independent influence of concentration and thread length in our model, as these figures depict spheroids grown on lattices of identical number of collagen sites, or collagen concentration, organized into either many short fibers or fewer longer fibers. For low-concentration collagen matrices, qualitatively, it is evident that cells invade along interconnected fibers in the matrix. The longer the interconnected fiber, the greater the invasive radius, and thus, at low collagen concentrations, longer fibers encourage invasion (Fig. 13). At higher collagen concentrations, long interconnected fibers may emerge from threads of any length, and therefore invasive radii become independent of thread length, as there are sufficient threads that even short ones intersect and form the long connected structures to which the invasive radius is most sensitive.

FIGURE 12.

Spheroid development at 14 days as a function of number of 52-μm collagen threads, for (a) 577, (b) 2308, and (c) 3462 threads. Number of collagen sites is identical to those of Fig. 10, b–d, respectively.

FIGURE 13.

Invasive distance for spheroids that develop in lattices of 15,000 (circles), 60,000 (inverted triangles), and 90,000 (squares) collagen sites. Open symbols depict invasive distance for lattices with 12-μm threads and solid symbols depict those for lattices with 52-μm threads. Only the spheroid grown on the low-concentration lattice populated by short threads exhibits a significantly smaller invasive radius.

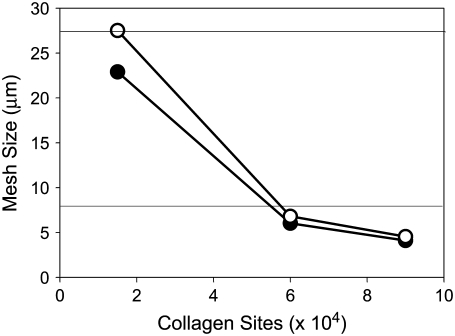
In considering how matrix structure changes as a function of collagen thread length, and to further correlate our model lattices with experimental collagen matrices, we also examine matrix mesh size. We define mesh size as the approximate distance between nearest collagen sites. The mesh sizes of the model collagen lattices used here are calculated as described by Kaufman et al. (16). Cell free lattices are constructed that have a given number and length of collagen threads, and the distances between adjacent collagen sites in each separate row and column are calculated. A histogram of these distances is compiled, and the mesh size of a given lattice is approximated by fitting the distributions to exponentials of the form 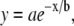where b is the mesh size. Slight differences in distribution across rows and columns are found, particularly at low collagen concentration. This is ostensibly due to lack of complete randomness in placement of collagen threads. In all cases, distribution across rows is reported. All mesh size distributions are fit to exponential decays with R² > 0.99. Fig. 14 shows that mesh size determined in this manner depends strongly on collagen concentration and weakly on collagen thread length. Moreover, the mesh sizes found suggest that the models here have “concentration” similar to those used in experiment. Experimentally, determining mesh size from 2D slices of 0.5- to 2.0-mg/ml 3D collagen matrices yields mesh sizes from 28 to 8 μm, respectively (16). Thus, the 60,000-site model collagen matrices may be considered similar in concentration to 2.0-mg/ml experimental gels, and the 15,000-site collagen concentration matrices are similar to the 0.5-mg/ml collagen gels. We find that the model lattice with shorter threads better reproduces the clear differential in invasive distances seen experimentally in gels of 0.5- and 2-mg/ml collagen than does the model lattice with long threads, which is consistent with the presence of fibers with an average length between branching or entanglement points of <10 μm, as found in the experimental collagen gels of these concentrations (16).

FIGURE 14.

Mesh size versus number of collagen sites for 12-μm (open circles) and 52-μm (solid circles) threads. Horizontal lines are drawn at mesh sizes of experimental matrices of 0.5- and 2.0-mg/ml collagen I gels as described in Kaufman et al. (16).

In addition to interrogating how spheroid development changes as a function of collagen thread length in isotropic matrices, we also do so in anisotropic (aligned) matrices. Although such work has not been done experimentally with spheroids, it is well known that single cells will align with and migrate along aligned collagen fibers (86–90). In addition, glioma cells are known to preferentially invade along blood vessels and the bundled axons present in the corpus callosum, due perhaps to the contiguous surface these structures present. If this is due at least in part to attraction between the cells and the fibers, as opposed to, for example, changes in nutrient and waste diffusion in these regions, our simulations should show effects when collagen-thread organization is altered. Fig. 15 shows spheroids simulated on lattices with parallel collagen threads of 12 μm and 202 μm. These lengths are comparable to cell size and spheroid size, respectively. Although in this work threads generally stand in for collagen fibers, as are present in in vitro experiments on spheroid growth, the gross anisotropy of the long threads used here is meant to recapitulate the geometry glioma cells may encounter in vivo along blood vessels or within the corpus callosum. We find that when spheroids invade in environments composed of parallel collagen structures significantly longer than their own diameter, cells do align along those threads. However, because the cells divide and are shed from the spheroid symmetrically, despite the increased tendency for the proliferative cells to invade unidimensionally, there is some invasion perpendicular to the collagen threads as well. This is consistent with the fact that cells are shed even in the absence of collagen threads in our model. When thread lengths are similar to cell length, cells cannot effectively grow alongside them and therefore do not significantly assume the orientations of the threads.

FIGURE 15.

Spheroid development at 14 days on aligned collagen matrices composed of (a) 12-μm and (b) 202-μm collagen threads.

Collagen dissolution and deposition

In the simulations presented thus far, certain cell-ECM interactions that are likely important in vitro and in vivo have not been included. Indeed, the ability of high-grade gliomas to aggressively invade brain tissue is likely due, at least in part, to their ability to alter their environments in a manner that leads to further growth and invasion. For glioma cells, there are at least three potential cell-environment interactions that could greatly affect invasion both in 3D gels and in vivo. These are 1), matrix structure dissolution, as may be effected by the action of proteases; 2), matrix molecule deposition; and 3), matrix remodeling in which cells move ECM structures through tractional forces.

In all simulations to this point, the lattice surrounding cells was static; cells could only change the lattice by occupying sites, and even so, once a cell abandoned a particular site, it returned to its initial (matrix or collagen) state. In the following simulations, cells are permitted to alter the lattice by flips of lattice sites adjacent to cells from collagen to matrix or vice versa with probability described by Eq. 1. A cell flipping a collagen site to a matrix site is effecting changes to its environment similar to those caused by a cell producing proteases that dissolve structural entities in the ECM. A cell flipping a matrix site into a collagen site is equivalent to a cell secreting an ECM molecule into its environment. Because the secreted “collagen” may not be associated with other collagen threads in our model, one might more broadly consider this type of move to be similar to cell secretion not only of a haptoattractant or duroattractant, but also of a chemoattractant. Thus, in the set of simulations we present here, cells are allowed to alter their energetics not by changing their own constitutions in response to their environment, but by directly changing their environment.

The dissolution of ECM in vitro or in vivo may increase migration by removing ECM structures that provide structural and/or mechanical barriers to invasive cells. However, these same ECM structures facilitate cell invasion via cell-ECM adhesion. Thus, both experimentally and in silico, large-scale dissolution of structural proteins in the environment would not necessarily increase invasion. As described above, we investigate matrix dissolution in our model by turning on a cell's ability to flip collagen sites adjacent to matrix sites into matrix sites. In particular, we allow such flips to be attempted 25, 50, 75, or 100% of the time a proliferative-cell site abuts a collagen site. We find that allowing dissolution does not change spheroid radius and decreases invasive distance (data not shown). We find no significant differences between allowing collagen dissolution 25% of the time and 100% of the time, and Fig. 16 a shows a spheroid at 14 days, in which dissolution is allowed 50% of the time. When dissolution is permitted, proliferative cells remain more spherical, as they end up in relatively collagen-free environs. The fact that we find decreased invasion at all levels of collagen dissolution investigated may be related to differences between our simplified model and the situation in vivo. In our model, the substrate for dissolution and the preferred substrate for adhesion are identical; they are the collagen sites on the lattice. However, in vivo, a particular protease may act on one ECM component at the same time that other cell-ECM interactions continue to permit for effective invasion. Moreover, in vivo, collagen dissolution may occur only at select locations, rather than at random sites adjacent to proliferative cells.

FIGURE 16.

Spheroid development at 14 days allowing (a) matrix dissolution 50% of the time, (b) matrix deposition 50% of the time, and (c) both matrix dissolution and deposition 50% of the time, as described in the text.

Experimentally, deposition of ECM molecules may also allow gliomas to tune their environments in a variety of ways that could increase ease of invasion. For example, cells can deposit ECM molecules like tenascin and hyaluronan, whose presence has been shown to correlate with increased invasion in vivo (91). As described above, we approximate such activity by allowing cells to flip matrix to collagen 25%, 50%, 75%, and 100% of the time proliferative cells abut matrix lattice sites. We find that spheroid radius growth is curtailed similarly when collagen deposition occurs between 25% and 100% of the time. Invasive distance decreases with increased deposition rates (data not shown). Fig. 16 b shows the result of a simulation in which deposition flips are allowed 50% of the time. The collagen deposition has effects on spheroid development similar to those of high collagen density, except that the effects seen here are focused locally, wherever proliferative cells were invading and dividing. Thus, the result is an anisotropic spheroid with very limited invasion. Again, the effect of collagen deposition here may be different from that of ECM deposition in vivo, in part because in vivo there are many ECM components, and the deposition of one of these need not result in structural barriers as it does in our model, which includes only large-scale collagen structures.

Finally, we allow both collagen dissolution and deposition. This is in some ways equivalent to matrix reorganization, for collagen is dissolved in one location and produced in another, with locations chosen at random from lattice sites adjacent to proliferative cells. As in the cases of 50% collagen dissolution and 50% collagen production, depicted in Fig. 16, a and b, respectively, allowing simultaneous production and dissolution 50% of the time effects gross changes in spheroid invasive pattern (Fig. 16 c). Although these invasive patterns are not consistent with invasive patterns seen in any in vitro experiments of glioma spheroids to date, they do show increased invasive radius relative to spheroids in which either collagen dissolution or collagen deposition occurs, suggesting that incorporating matrix remodeling into a Q-Potts model of this type may reproduce realistic invasion patterns, especially if more than two types of ECM component are included.

CONCLUSION

In this article, we have employed an intuitive version of the Q-Potts model on a lattice containing an explicit, two-component ECM containing a fibrous component and a homogeneous afibrous component to independently assess the importance of cell-cell and cell-ECM adhesion and cohesion energies in spheroid growth and invasion. The fundamental assumptions underlying our model are that tumors develop to minimize their bond energies, and that tumor cells may invade due to haptotaxis or durotaxis, with cells showing an affinity for structural proteins in their environment. First, we have demonstrated that we can qualitatively reproduce the spheroid growth and invasion patterns that most glioma spheroids demonstrate in collagen I matrices of varying concentration. This occurs despite the fact that nutrient usage, waste production, and the cell cycle are treated at only the most basic levels in our model.

To reproduce spheroid growth and invasion patterns consistent with experiment in our model requires the ordering of cell-cell and cell-environment adhesive and cohesive energies such that J_cp < J_mp < J_nq < J_qq < J_pp < J_pq. Among these adhesion and cohesion energies, we find that the geometry of invasion in environments of low and intermediate collagen concentration is most strongly affected by J_mp due to the large number of proliferative cell-matrix contacts. Increasing the difference between J_pp and J_mp or J_pp and J_cp while maintaining J_cp < J_mp results in increased tumor cell proliferation and invasion along model collagen structures.

For a set of J parameters that qualitatively result in invasive patterns consistent with glioma spheroid invasion in vitro, we find that collagen concentration and organization affect invasion in a manner consistent with that seen in in vitro experiments. The concentration and mesh size at which the maximal volumetric spheroid growth and invasion occur are consistent with those measured in vitro. This suggests that proliferative cell haptotactic or durotactic affinity for collagen structures in their surroundings is sufficient to describe many of the features seen in spheroid invasion in vitro. At collagen thread lengths consistent with those used in in vitro experiments on glioma invasion in collagen I gels, little invasion is seen at low collagen concentration, effective invasion occurs at intermediate concentration, and invasion is limited by structural obstacles at high concentration. Although at moderate and high collagen concentration invasion is largely independent of collagen thread length, at low concentration this is not the case, and increasing a lattice's interconnectedness results in increased tumor cell proliferation and invasion. Finally, we extend the Q-Potts model to allow cells to alter their environment through dissolution and/or deposition of explicit ECM. Although we find only limited agreement with changes that occur experimentally, we propose that a Q-Potts model incorporating a three-component explicit matrix may more fully capture the effects of these processes.