Small- and Large-Scale Conformational Changes of Adenylate Kinase: A Molecular Dynamics Study of the Subdomain Motion and Mechanics

Abstract

Adenylate kinase, an enzyme that catalyzes the phosphoryl transfer between ATP and AMP, can interconvert between the open and catalytically potent (closed) forms even without binding ligands. Several aspects of the enzyme elasticity and internal dynamics are analyzed here by atomistic molecular dynamics simulations covering a total time span of 100 ns. This duration is sufficiently long to reveal a partial conversion of the enzyme that proceeds through jumps between structurally different substates. The intra- and intersubstates contributions to the enzyme's structural fluctuations are analyzed and compared both in magnitude and directionality. It is found that, despite the structural heterogeneity of the visited conformers, the generalized directions accounting for conformational fluctuations within and across the substates are mutually consistent and can be described by a limited set of collective modes. The functional-oriented nature of the consensus modes is suggested by their good overlap with the deformation vector bridging the open and closed crystal structures. The consistency of adenylate kinase's internal dynamics over timescales wide enough to capture intra- and intersubstates fluctuations adds elements in favor of the recent proposal that the free (apo) enzyme possesses an innate ability to sustain the open/close conformational changes.

INTRODUCTION

Adenylate kinase (Adk) is a monomeric enzyme that regulates the energy charge of the cell by balancing the relative abundance of AMP, ADP, and ATP. The concentration of the three nucleotides is controlled by the enzyme through the catalysis of the phosphoryl transfer reaction:

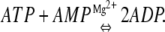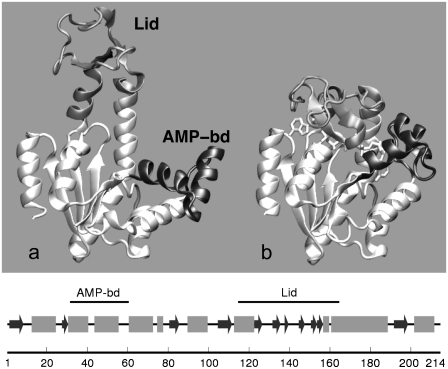
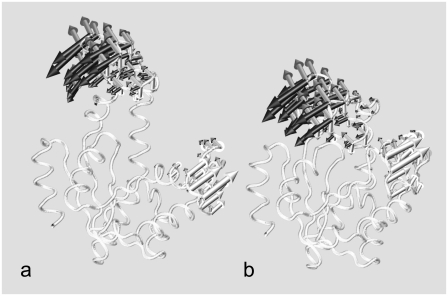
The differences in structural arrangement between the free Escherichia coli adenylate kinase (AKE) and the enzyme complexed with an inhibitor mimicking both ATP and AMP are illustrated in Fig. 1 (1,2). By comparing the two portrayed crystal structures, it is apparent that the formation of the ternary complex stabilizes the enzyme in a form where the mobile Lid and AMP-binding subdomains (highlighted in Fig. 1) close over the remainder core region. This rearrangement of the two mobile subdomains is necessary for the accommodation of the nucleotides in an optimal catalytic geometry and the resulting closed enzyme conformation provides a solvent-free environment for the phosphoryl transfer.

FIGURE 1.

Cartoon representation (51) of crystallographic structures of Escherichia coli adenylate kinase in: (a) the open apo form and (b) the closed holo form. The PDB codes for the two structures are 4ake and 1ake, respectively (1,2). The flexible Lid (amino acids 114–164) and AMP-binding (amino acids 31–60) domains are colored in shaded and solid representation, respectively. The succession of secondary elements is shown in the bottom panel. Helices are indicated as shaded boxes while β-strands are shown as solid arrows.

The conformational change sustained by adenylate kinase upon complexation with ATP and AMP, and its reopening upon unbinding of the processed nucleotides, represent the rate-limiting step in the reaction turnover (3). A large number of experimental studies have consequently addressed the functional implications of Adk structural elasticity (1–11). In particular, recent investigations, based on a wide range of techniques, have provided converging evidence for the fact that, even in the absence of the bound nucleotides, the free enzyme is capable of interconverting between the open and closed forms. These investigations have led to formulating the hypothesis that evolutionary pressure has endowed Adk, and arguably other enzymes (12,13), with the innate ability to interconvert between distinct biologically relevant forms.

These observations have stimulated this numerical study of the dynamical evolution of the free (apo) AKE molecule in solution. By means of two 50-ns-long molecular dynamics (MD), simulations started from the available crystal structures we characterize, over various timescales, the conformational fluctuations sustained by the enzyme and analyze the extent to which they indicate the suggested innate predisposition to connect the open and closed forms.

Several previous computational investigations of the flexibility of Adk exist and include both mesoscopic and atomistic approaches. Coarse-grained models have, for instance, been applied to model the pathways connecting the open and closed forms of the enzyme (14–17). Atomistic simulations have instead been used to probe the free energy landscape in the neighborhood of several known enzyme conformers, as in the recent investigations by Lou et al. (18), Arora et al. (19), and Henzler-Wildman et al. (9). In the first study (18), an advanced sampling technique was used to show that the enzyme populated conformations compatible with the holo-form geometry, as probed by FRET experiments (10). Arora et al. (19) further showed that the free energy landscape along a preassigned reaction coordinate connecting the open-closed forms of AKE is approximately flat for the apo-form while, upon ligand binding, it changes, favoring the closed state. Finally, in the study of Henzler-Wildman et al. (9), carried out on Adk extracted from hyperthermophile Aquifex aeolicus, a variety of experimental and computational probes have indicated the existence of several metastable configurations bridging open and closed states.

In this study, by analyzing the recorded trajectories with a series of novel methods, it is found that the enzyme dynamics proceeds by hopping through distinct conformational substates where the system dwells typically for 5–10 ns. The internal dynamics within the substates and the discontinuous jumps across them are analyzed in detail. As dynamics progresses, the intersubstates conformational variability accounts for an increasing, and ultimately dominant, fraction of conformational fluctuations of the system.

These facts, besides indicating the progressive increase of the structural heterogeneity of visited conformational phase space, pose the question of understanding what relationship, if any, exists among 1), the directions of largest structural variability within the substates; 2), the difference vectors that connect the substate representatives; and 3), the functional conformational change associated to the deformation vector bridging the available apo/holo crystal structures. These questions are at the heart of the multiscale spirit of this analysis aimed at characterizing the connection between the system conformational fluctuations at the smallest scale (within the substates) and at the largest, functional one, embodied by the open/close rearrangement.

Despite the diversity of structures belonging to different substates, which can differ by as much as 12 Å RMSD, it is found that virtually the same limited set of collective modes controls 1), the structural fluctuations within all substates; 2), the intersubstates structural transitions; and 3), the apo/holo conformational changes.

The analysis indicates that the free enzyme can be efficiently driven through various substates bridging the open and catalytically potent states through the thermal excitation of a limited number of collective modes. The results provide support to the recent hypothesis of the innate capability of apo AKE to sustain the apo/holo structural change and give a vivid illustration of how this predisposition is embodied in specific properties of the system internal dynamics.

The novel methodological tools introduced to identify the visited conformational substates and the consensus modes accounting for the intra- and intersubstate fluctuations have a general and transferable character. They hence ought to be applicable to the growing number of proteins and enzymes that, like Adk, have been recently argued to be capable of spontaneously interconverting between different biologically relevant forms (12,13,20).

METHODS

Molecular dynamics simulations

The atomistic MD evolution of E. coli adenylate kinase, AKE, was followed starting from two distinct initial structures, corresponding to the open and closed form of the enzyme. More precisely, the initial conformation of the first simulation was the free (apo form) enzyme from the 4akeA PDB crystal structure (21). The second simulation followed, instead, the evolution of the free closed form of the enzyme obtained by removing the Ap5A inhibitor from the 1akeA PDB structure file. In the following, for simplicity, we shall refer to the two simulations as the open and closed trajectories. The terminology is only meant as a reminder of the starting configuration as, in fact, for both trajectories a partial conversion to the complementary (open or closed) state is observed.

Each system was parameterized with OPLSS-(AA)/L force field (22–24) and was energy-minimized after solvation by 17,694 simple point charge water (25) molecules in a cubic box. Periodic boundary conditions were applied and the overall charge neutrality was ensured by the presence of four Na⁺ cations. The system was gradually heated up to 300 K. The temperature was next adjusted, along with the system density, in a 500-ps-long MD evolution at constant temperature (300 K) and pressure (1 bar). The coupling times to the Nosé-Hoover thermostat (26,27) and Berendsen barostat (28) were 0.2 ps and 0.5 ps, respectively. After equilibration, the barostat was removed and the system dynamics was followed in the NVT ensemble with a cubic simulation box of side l = 8.35 nm for 52 ns. The dynamics was integrated with the GROMACS software (Ver. 3.3.1) (29) with an integration time-step of 1 fs. Constraints on bond lengths were enforced with the LINCS algorithm (30) and water internal degrees of freedom were controlled with the SETTLE algorithms (31). Long-range electrostatic interaction was treated with the particle-mesh Ewald method (32,33). The initial 2 ns of each trajectory were not considered for analysis, which was instead performed on the subsequent 50-ns-long production runs. The sampling time for the structural data (atomic coordinates of the enzyme and water) was equal to 0.5 ps for a total of 10⁵ frames.

Structural fluctuations and a phenomenological model for mechanical strain

The overall mobility of individual amino acids in each trajectory was characterized by means of the root mean-square fluctuation (RMSF) profile of their α-carbon atoms. The RMSF of the i^th C_α, whose instantaneous coordinate at time t is indicated by 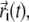is given by 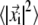where the brackets denote the time average and 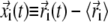is the instantaneous displacement from its time-averaged (reference) position. The average was taken after removing the rigid-body motions of the enzyme. Following Henzler-Wildman et al. (9), each recorded frame was oriented so to align the rigid core (for definition of the domains, see Fig. 1 legend) against the core of the open crystal structure.

The overall mobility information provided by the RMSF profile is complemented with a phenomenological analysis of the instantaneous geometrical strain experienced by the various amino acids. Specifically, for the i^th amino acid, we compute a geometric parameter, q_i(t), providing a measure of how much its instantaneous distance from neighboring amino acids differs with respect to the time-average,

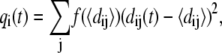(1)

where d_ij is the distance of the C_α atoms of amino acids i and j and 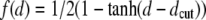is a sigmoidal function weighting the average spatial proximity of the two amino acids. Its point of inflection is set at the cutoff distance d_c = 7.5 Å.

Structural clustering

The K-medoids clustering scheme (34) was used to partition each trajectory in structurally homogeneous groups. The pairwise RMSD distances between all pairs of the 10³ recorded structures (one every 50 ps) are taken as input. The returned output consists of the grouping of the structures in a preassigned number of nonempty clusters, K. A representative conformation for each cluster is also provided. The clusters and their representatives are identified by minimizing the dissimilarity score obtained by summing the RMSD of each structure from its cluster representative. The method is commonly implemented in an iterative fashion through the following steps:

• Step 1. The members of the K clusters are first assigned randomly.

• Step 2. The cluster representatives are next identified by picking, in each cluster, the element with smallest total distance from the other cluster members.

• Step 3. The clusters are finally redefined by assigning each data-set member to the closest representative.

Steps 2 and 3 are repeated until the dissimilarity score no longer decreases. To avoid trapping (in local minima) of the dissimilarity score, the method is repeatedly applied for several initial random groupings. We emphasize that the clustering returned by standard K-medoids scheme described above is based solely on the input of the RMSD distance of any pair of structures (aligned over the core region), and hence does not consider their succession in time along the trajectory.

Accounting for the time-order of the structures is essential for partitioning the recorded trajectories in a succession of progressively-visited substates. The K-medoids scheme was accordingly modified to ensure that each cluster gathered structures spanning an uninterrupted time interval of the simulation. The introduction of the time-continuity constraint simplifies the definition of the cluster members, which are unambiguously specified by introducing K – 1 time subdivisions of the trajectory.

The minimization of the dissimilarity score subject to the time-continuity constraint is performed within a greedy stochastic minimization scheme. Given the K – 1 time-subdivisions (initially equispaced), the representative of each cluster is defined as in Step 2 of the standard K-medoids scheme and the resulting dissimilarity score is computed. At variance with Step 3 of the original method, a new clustering is proposed by randomly reassigning one or more of the K – 1 subdivisions and ensuring that no two subdivisions coincide as empty clusters would result. The new cluster representatives are found and the new dissimilarity score is calculated. The proposed clustering is kept if it leads to a decrease of the dissimilarity score, otherwise the previous one is retained and a new partitioning is proposed. The procedure is iterated until convergence of the dissimilarity score (10⁵ iterations were typically sufficient to reach convergence for partitioning 1000 structures in K = 10 clusters, requiring a few minutes of computation on present-day personal computers). The modified algorithm was run for 2 ≤ K ≤ 15 and the consensus of the emerging cluster subdivisions with the original method (see Supplementary Material, Data S1) was considered for a robust definition of the conformational substates (see Results and Discussion).

Covariance matrix

A principal component analysis was used to identify the collective variables capturing the most prominent structural fluctuations of the MD trajectories (35). These collective coordinates, also termed essential dynamical spaces or low-energy modes, are provided by the top eigenvectors (typically those associated with the largest 10 eigenvalues) of the covariance matrix, C. The latter is defined as

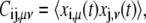(2)

where x_i,μ(t) indicates the μ^th component of the vector displacement (at time t) of the i^th C_α from its reference position, computed averaging over all configurations after an optimal structural superimposition of the core region.

The covariance matrix of Eq. 2 can be processed to separate the contributions arising from the structural fluctuations within the substates and across them, in analogy with the “jumping among minima” model of Kitao et al. (36) and with the subsequent study of the consistency of the multiscale internal dynamics of protein G of Pontiggia et al. (37). For brevity, we shall refer to these contributions as intra- and intersubstates, respectively. More precisely, following the notation of Pontiggia et al. (37), Eq. 2 can be written as

(3)

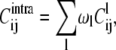(4)

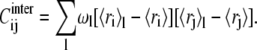(5)

In the above expressions, l runs over the substates; w_l is the weight of the l^th substate, which is the fraction of simulation time spent by the system in it; 〈〉_l denotes the average taken over the conformations of the l^th substate; and 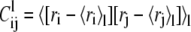is the covariance matrix of the l^th substate itself.

The first term in the decomposition of the covariance matrix is the contribution arising from structural fluctuations within substates. It consists of the weighted sum of the covariance matrices of the individual clusters. The second, intersubstate term, arises instead from the structural differences of the substates representatives. It should be noted that the intersubstate contribution runs over all pairs of representatives, and not only over time-consecutive ones.

RMSIP

We have compared the essential dynamical spaces of pairs of covariance matrices calculated over various time intervals of the trajectories. We shall indicate two such sets of essential dynamical spaces as 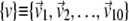and 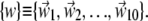Their common orientation, induced by the superposition of the corresponding reference structures, will also be assumed. The consistency of {v} and {w} was quantified, as customary, via the root mean-square inner product (RMSIP),

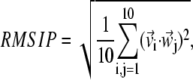(6)

which ranges from 0, for complete orthogonality of the {v} and {w} spaces, to 1 in case of their perfect overlap.

We have considered the question of whether the RMSIP of two essential spaces is likely to have arisen by a mere consistency of nonspecific dynamical features, such as the overall mobility of amino acids. This, in turn, could be ascribed to an expected relatedness, among the substates, of the local density around each amino acid (38). However, recent analysis of high-quality crystal structures have shown that the mean-square fluctuation profile, though impacted upon by density effects, is not indicative of uncoordinated local diffusive motion. Rather, it is largely ascribable to specific relative movements of nearly-rigid subdomains (39). Prompted by these considerations we have considered whether a given RMSIP value reflects the consistency of the magnitudes of amino acid fluctuations alone, or if it reflects the consistency of the directions of their displacements as well.

A specific test was devised for addressing this issue. It consists of computing the distribution of RMSIP values that arise when the essential dynamical spaces of {v} and {w} are modified so to 1), preserve the normalized mean-square fluctuation profiles of each mode, while 2), retaining the orthonormal relationships within the new sets {v′} and {w′} and 3), ensuring the orthogonality of {v′} and {w′} with the zero-energy modes associated to translations and rotations of the system.

The algorithm used for this purpose is described hereafter. For each amino acid we performed a random reorientation of its three-dimensional displacement appearing in all modes of each set (i.e., the randomization is carried out separately for {v} and {w}). It is important to stress that the rotation differs from site to site but the same rotation is applied to the displacements of one particular site (amino acid) in all 10 modes.

This random reorientation procedure realizes requirements 1 and 2, above. In fact, it preserves the normalized mean-square fluctuation profiles of each mode and the randomized modes are still orthonormal. However, the new modes, in general, will have nonzero overlap with the six zero-energy modes associated to the rigid-body motions of the system. From a practical point of view, the orthogonality condition can be enforced in an approximate way by retaining, out of a large number of randomly-generated sets of modes, those in which each mode has a projection smaller than 0.05 on the six-dimensional linear space of the zero-energy modes.

In this way, the RMSIP value of two original sets of modes, {v} and {w}, can be compared against the distribution of RMSIP values of randomized sets that, mode by mode, still possess the same RMSF profile. This reference distribution therefore provides an indication of how much the mere specification of the normalized RMSF profiles of all the modes, constrains the possible RMSIP values.

Optimal mixing

Equation 6 provides an average measure of accord of two essential dynamical spaces, as the top 10 eigenvectors of C are treated on equal footing (degeneracy) (40). This implies that the same value of RMSIP may be attained with different detailed levels of accord of two spaces. To characterize, with a finer resolution, the consistency of two sets of modes we introduce a variational scheme that identifies their maximally consistent (or inconsistent) subspaces. The scheme, explained in detail in the Appendix, is used to redefine two new bases 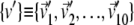and 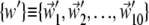for the same linear spaces described by v and w. The redefined bases, {v′} and {w′}, possess two noteworthy properties:

1. A basis vector of one set is orthogonal to all basis elements of the other set except the one with the same index and

2. The index provides a natural ordering of the basis vectors in terms of decreasing mutual consistency; note that the RMSIP of the new basis vectors is the same as the original vector.

The method is employed here to identify the maximally overlapping essential dynamical subspace(s) of the entire trajectories started from open and closed configurations. The algorithm is, however, amenable to many other possible applications, such as the dynamics-based alignment (41), which is the comparison of large-scale movements in pairs of proteins for which a one-to-one correspondence between a substantial number of their amino acids can be established based on purely structural (42,43) or structural-dynamical (41) criteria.

The source code of the program is available upon request.

RESULTS AND DISCUSSION

In the following, we will present a detailed analysis of the MD results for AKE. We shall primarily focus on the 50-ns-long simulation started from the crystallographic structure (PDB:4ake) of the open free enzyme. The resulting salient properties will be compared with the second simulation started from a closed, again ligand-free, configuration (prepared starting from the structure in PDB:1ake).

Flexibility and structural heterogeneity

The recorded trajectories were first analyzed to assess the level of overall conformational heterogeneity encountered during the time evolution. The structural differences between the two starting crystal structures reflect the different orientation of the Lid and AMP-binding subdomains (corresponding to residues 114–164 and 31–60, respectively). The remainder Core region, consisting of 133 amino acids, presents minor differences in the two crystal structures (1.61 Å RMSD). The RMSD of the full C_α trace of 1ake and 4ake is 8.14 Å (see Fig. 1).

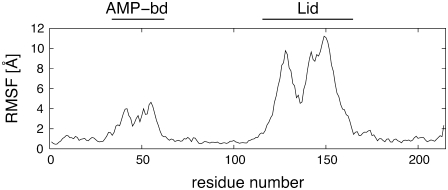
Fig. 2 shows the RMSF of each amino acid calculated for the entire 50-ns-long open trajectory after removing the rigid-body motions of the Core region. The structural deviations are accumulated in correspondence of the Lid and AMP-binding regions. The core is, by converse, very stable as its amino acids have root mean-square fluctuations (RMSFs) of <2 Å. The rigidity of this region is consistent with NMR and x-ray studies, as well as with previous topology-based characterizations of the protein's elasticity (14–16,44,45). Analogous results emerge from the analysis of the fluctuations in the closed simulation (see Data S1).

FIGURE 2.

Root mean-square fluctuations of the C_α atoms observed in the 50-ns-long open trajectory. The fluctuations have been calculated after an optimal structural superposition of the C_α trace of the Core region of the enzyme.

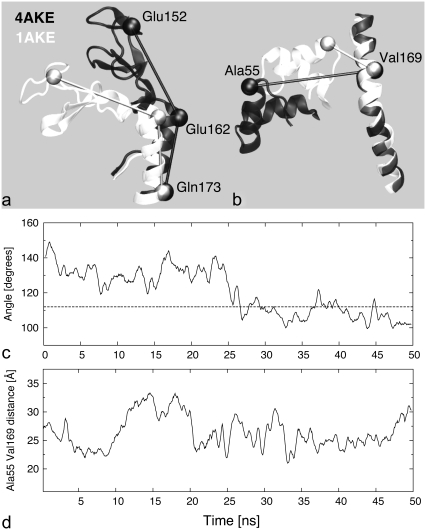
The rearrangements experienced by the two mobile subdomains are aptly summarized by the time evolution of two independent geometric parameters that discriminate between the open and closed configurations of the Lid and AMP-binding regions, respectively. The degree of bending of the Lid toward the core was measured by the angle formed by two virtual bonds connecting the C_α values of amino acids (152 and 162) and (162 and 173), see Fig. 3 a, and its time evolution is shown in Fig. 3 c. The arrangement of the AMP-binding subdomain relative to the core was captured by the distance between the C_α values of amino acids 55 and 169, as illustrated in Fig. 3 b. The time evolution of this second parameter, which was previously considered also in FRET experiments and computational studies for AKE (10,18), is shown in Fig. 3 d. By comparison with the initial structure, during the second half of the simulation, the Lid is bent toward the core and the Lid-Core geometric parameter frequently takes on values that are compatible with the closed (holo) form (dashed reference line in Fig. 3 c). The AMP-bd–Core distance, instead, fluctuates within a fairly constant range throughout the trajectory (Fig. 3 d).

FIGURE 3.

To discriminate between open (solid) and closed (open) conformations of the Lid and AMP-binding subdomains, two independent geometric parameters are introduced. (a) The Lid orientation is captured by the angle between the virtual bonds formed by the C_α values of amino acids 152, 162, and 173. (b) The AMP-bd arrangement is captured by the distance between C_α values of Ala⁵⁵ and Val¹⁶⁹, which attains the value of 12 Å for the closed conformation. The time series of the Lid and AMP-bd geometric parameters during the open trajectory are shown in panels c and d, respectively. Open (closed) conformations of the AMP-bd and Lid subdomains are associated with values of the parameters greater (smaller) than 12 Å and 116° (dashed line in c), respectively. The lack of correlation of the time series in panels c and d suggest the independent motion of the two subdomains.

Consistently with previous reports on the approximately-independent motion of the two subdomains on the nanosecond scale (9), also from this analysis no significant correlation emerges among the two time evolutions of Fig. 3, c and d. In fact, the Kendall correlation coefficient of the data set constituted by 100 pairs at equal times of the two geometric parameters (i.e., sampled at 0.5 ns) was equal to τ = 0.065. The probability to observe a Kendall's τ having modulus smaller or equal to 0.065 in random sets of 100 elements is equal to 67% (46).

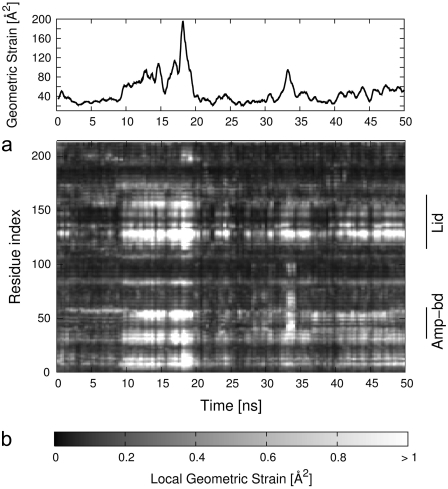
To characterize with finer detail the structural fluctuations of AKE, we investigated how extensive, as a function of time, are the changes to the local structural environment of each amino acid (represented by the C_α atoms). In particular, we quantify the changes to the set of distances between one amino acid and its neighbors (i.e., those within 7.5 Å). The distortions of the contact network of the i^th amino acid are quantified with the geometric-strain parameter, q_i, defined in Eq. 1. By analyzing the time evolution of the geometric strain profile, it is possible to identify the regions of the enzyme that undergo a rigidlike motion. The pairwise distances of amino acids within such regions would be highly conserved in time, regardless of the amplitude of the motion of the region with respect to a fixed reference frame. Consequently, by cross-referencing the RMSF and the geometric strain analysis it is possible to identify a posteriori the amino acids (if any) that act as hinges for the articulated motion for AKE. The time evolution of the geometric strain profile q_i is shown in the bottom panel of Fig. 4, along with the profile of the cumulative strain of the full protein chain (top panel of the same figure).

FIGURE 4.

(a) Time evolution of the geometric strain (see Eq. 1) summed over all amino acids. The strain of each individual amino acid is shown in panel b.

Fig. 4 illustrates two notable features of adenylate kinase dynamics that are hereafter discussed in detail. First, the geometric strain is mostly concentrated on specific regions of the protein chain and, secondly, the patterns of geometric strain evolve discontinuously in time.

Six sets of amino acids, labeled a–f, are associated with significant strain, namely group a, amino acids 8–15; group b, 28–35; group c, 53–60; group d, 123–130; group e, 135–137; and group f, 153–158. In particular, group d corresponds to the Lid-Core interface, while sets b and c corresponds to the AMP-Core interface; hence, these groups of residues act as primary hinges for the motion of the two mobile subdomains. It is worth noticing that a further region of high geometric strain (group e) is found in the middle of the Lid subdomain, indicating an articulated motion of the latter around this joint.

We now turn to the observation that the buildup/release of geometric deformations of these regions is discontinuous in time. For example, at t = 9 ns there is a rapid increase of the geometric strain in correspondence of all above-mentioned groups, which persists up to t = 19 ns. At this time another coordinated change of these regions is observed.

These facts indicate that the system evolution proceeds by visiting distinct conformational substates through which the systems hops with rapid transitions, signaled by discontinuities in the geometric strain profiles.

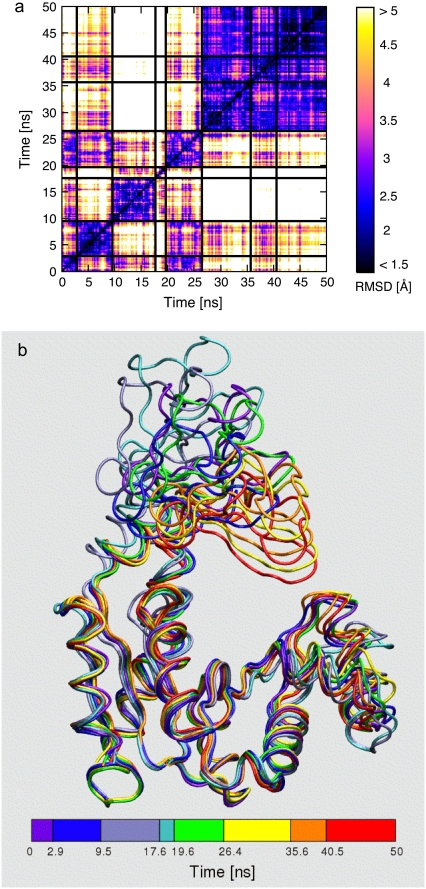
This conclusion is supported by the analysis of the density plot in Fig. 5 a, which provides the RMSD between each pair of conformations sampled from the open trajectory. The block character of the matrix suggests that distinct conformational groups are explored during the dynamical evolution. Consistently with this qualitative observation, the analysis of the distribution of the pairwise distances (47) suggests that the system populates conformational basins where the internal structural heterogeneity is ∼2.5 Å RMSD while the RMSD of conformations in different basins is mostly in the range (4–7 Å) (see Data S1). As a quantitative method to identify the conformational basins visited by the trajectory we have applied the two structural clustering schemes described in Methods.

FIGURE 5.

(a) Density plot of the pairwise RMSD of 1000 time-equispaced conformations from the open trajectory (time labels are shown on both axes). Solid black lines are used to separate the substates identified with the structural clustering procedure. The structures representing the substates are shown in panel b and are colored according to the time subdivision (clustering) shown at the bottom.

First, we have applied the original K-medoids scheme, which yields an optimal partitioning of structures into a preassigned number of clusters, K. The grouping relies on a purely structural measure of similarity of two given structures (their RMSD), irrespective of their time separation along the trajectory.

The clustering was performed by varying K from 2 to 15. Values of K > 6 resulted in a noticeable intermittent assignment to different clusters of structures contained in time intervals smaller than 0.5 ns. This effect was taken as indicating an excessively fine subdivision of the conformational substates. For values of K ≤ 6, instead, each cluster comprised structures covering, with only sporadic outliers, continuous time intervals of duration not smaller than 2 ns.

The robustness of the K-medoids structural partitioning was compared against the one returned with the second clustering scheme described in Methods, which enforced the time continuity of the clustered structures. The algorithm returns a subdivision of the trajectory into a fixed number K of nonoverlapping intervals (clusters) with maximal internal structural homogeneity.

A good consistency with the original K-medoids partitioning was obtained using K = 8 nonoverlapping intervals. The emerging consensus time subdivision, shown in Fig. 5 a, was consequently used to identify the most prominent conformational substates explored by the trajectory.

The typical RMSD of structures belonging to the same cluster was equal to 1.9 Å while structures belonging to different substates differed from 3 Å up to 12 Å RMSD (after alignment of the core region). The representatives of the clusters are shown in Fig. 5 b. The figure conveys the large variability of conformations encountered; nonetheless the average structure of the whole trajectory is at only 2.2 Å RMSD from the starting crystallographic conformation.

The trajectory started from the closed structure presented qualitative parallels with the above results. In particular (see Data S1), the closed trajectory visits approximately eight substates, characterized by residence times of ∼5–10 ns. However, due to its more compact arrangement, the structural fluctuations of the closed enzyme are smaller than for the open form. This reverberates in a smaller global mean-square fluctuation (i.e., summed over all C_α fluctuations), which is 2838 Ų and 908 Ų for the open and closed trajectory, respectively. In addition, the RMSD distances between the substate representatives are smaller, typically ∼3 Å. Though the ensembles of conformations explored by the two simulations do not strictly overlap, it is worth noticing that the RMSD between pairs of structures in the two trajectories can be as low as 2.5 Å.

Intra- and intersubstates structural fluctuations

Starting from the identification of the substates visited by the trajectory, it is possible to analyze the relative extent to which structural fluctuations within the substates and across them impact on the breadth of visited conformational space.

We first analyzed the intra- and intersubstates contributions to the global mean-square fluctuation (MSF) of the molecule (i.e., the sum of the mean-squared displacements of each C_α).

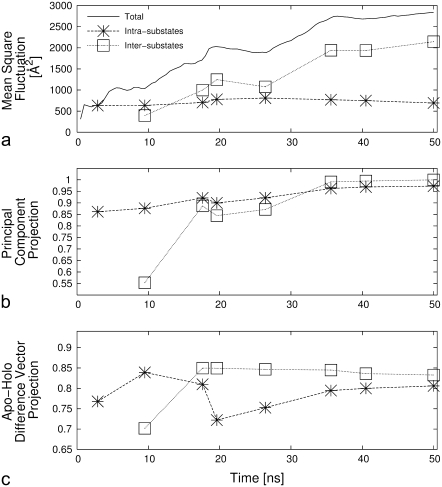
It may be anticipated that the relative interplay of the intra- and intersubstates fluctuations depends on the duration of the simulations (which, e.g., affects the number of visited substates). We have accordingly computed the intra- and intersubstates contributions to the MSF, for increasing duration of the trajectory, i.e., for each of the time subdivisions indicated in Fig. 5 b, bottom. The global MSF calculated at all stages of the trajectory is also reported in Fig. 6 a.

FIGURE 6.

(a) Time evolution of the total mean-square fluctuation of the enzyme and of its intra- and intersubstates contributions. The other panels portray the evolution of the scalar product (in modulus) between the first intra- and intersubstates essential modes and the principal mode of the entire trajectory (b) and the normalized apo/holo difference vector (c).

Over the 50-ns-long trajectory, the fraction of global MSF accounted for by the seven intersubstates hops is 70%. The result is striking, as the intersubstates contribution is computed merely on the basis of the eight structures representing the visited substates and their representation weight (i.e., the time-intervals duration). Aside from the specific case of AKE, it will be interesting to apply the methodology introduced and discussed here to other proteins/enzymes as well to check if, in general, a minimal number of key configurations can capture most of the structural fluctuations encountered in multinanosecond trajectories.

Finally, besides indicating that the jumps across substates represent a key aspect of the equilibrium dynamics of the system, the increasing trend of the global MSF in Fig. 6 indicates that the progressive broadening of the visited configuration space is still ongoing after 50 ns. This aspect is consistent with the experimental indication that an exhaustive exploration of the available structural space of the apo form of AKE occurs over timescales that largely exceed the one covered by the simulation (4,11,48).

Comparing intra- and intersubstates essential dynamics

The intra/intersubstate decomposition discussed above stimulates the investigation as to which relationship, if any, exists among the generalized coordinates that correspond to the essential dynamical spaces calculated separately for each of the eight substates as well as the difference vectors between the representative structures of the clusters. To address this issue we have first calculated the RMSIP between the essential dynamical spaces of the 28 distinct possible pairs of substates. The average RMSIP was equal to 0.83 with a standard deviation of 0.03. The value indicates a very high degree of consistency of the fluctuations within the various clusters. The consistency remarkably extends also to the intercluster structural fluctuations in analogy with that recently established for the smaller and globular protein G (37). A stringent verification of this point is given in Fig. 6 b, which shows, as a function of time, the modulus of the scalar product between the first principal component of the intra- and intersubstates matrix, and the first principal component of the covariance of the entire trajectory. Despite considering only one space, the principal direction of the intracluster covariance matrix computed with as few as two substates is already well aligned with the one of the total trajectory (scalar product equal to ∼0.9). The quality of the accord does not deteriorate as more and more substates are visited.

The consistency of the directionality of the structural fluctuations within and across the substates appears remarkable in consideration of the increasing breadth and diversity of the visited conformational space (see Fig. 6 a).

The above considerations further prompt the conclusion that a limited set of collective coordinates, indicated by the consensus of the inter/intracluster essential dynamics, would be adequate to describe the salient conformational fluctuations over a range of timescale wide enough to capture the (subnanosecond) dynamics within substates and the transitions across them (occurring at the multinanosecond level).

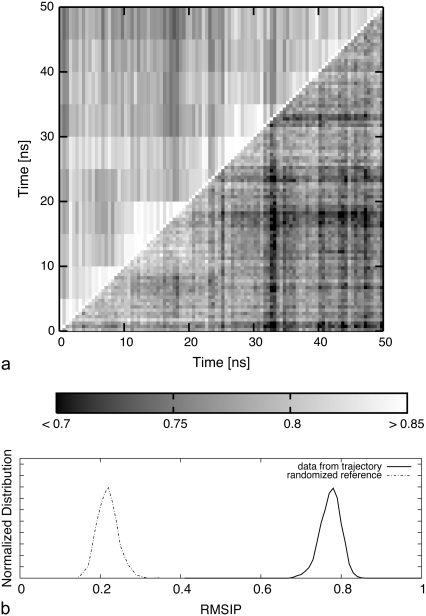
This expectation is verified and illustrated in Fig. 7, which shows the highly consistent RMSIP between the essential dynamical spaces of pairs of intervals of 0.5 ns or 5 ns from the trajectory (that is, with time-subdivisions covering a wide range of durations and unrelated to the substates partitioning).

FIGURE 7.

(a) Density plot of the RMSIP between essential dynamical spaces (EDS) of 0.5-ns-long intervals of the open trajectory (time labels on the abscissas) against themselves (lower triangle), and against the EDS of 5-ns-long intervals (upper triangle). (b) The distribution of RMSIP values from the lower triangle of the matrix (pairs of 0.5-ns-long intervals) is shown with a solid curve. The dashed curve shows the distribution of RMSIP values obtained by randomizing (in a way that preserves the mobility profiles of the amino acids) the original EDS.

It is to be noted that the high RMSIP values observed here (which are comparable to those usually found in statistically significant matches of essential dynamical spaces in MD trajectories (49)) do not reflect the mere correspondence of the profiles of structural mean-square fluctuations of the amino acids (which, being partly related to their degree of burial/coordination, might be expected not to change dramatically during the simulation). In fact, the distribution of RMSIP values that would follow from specifying only the MSF profiles of each mode is provided in Fig. 7 and covers a region of values much lower that those observed here, confirming the statistical significance of the observed RMSIP values. The results of an analogous analysis, carried out over the top 20 modes, in place of 10, are provided in Fig. S6 of Data S1.

Substates dynamics and the open/closed conformational change

A naturally emerging question is whether the observed degree of consistency is functionally oriented, i.e., related to the prominent structural rearrangement between the open and closed forms of the enzyme. To establish this property, and in analogy with the analysis of Fig. 6 b, we have computed, as a function of time, the fraction of the norm of the difference vector between the apo-holo crystal structures projected onto the first essential eigenvector of the intra- and intersubstate covariance matrices. The results are plotted in Fig. 6 c and indicate that the fraction of captured norm is ∼0.8 throughout the trajectory, supporting the functional relevance of the molecules' internal dynamics.

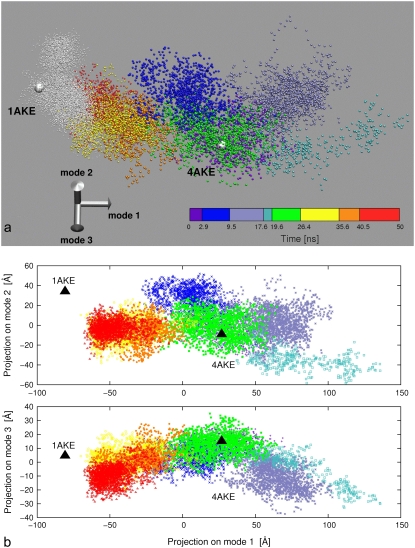
Fig. 6 c reveals the interesting aspect that the intersubstate hops are typically better aligned along the apo/holo conformational changes than the intracluster principal directions. Over the entire 50-ns-long trajectory, 82% of the open/closed conformational change is already captured by the first low-energy mode, while considering the top 10 modes capture 96% of the norm. The fact that the conformational changes within and across the substates occur mostly along the direction bridging the open and closed conformers, is illustrated in the scatter plots of Fig. 8. In Fig. 8 a, the substates visited by the open trajectory are represented, with different colors, in the space of the three lowest-energy modes. The trajectory started from the closed structure is also shown for comparison. For clarity, two bidimensional projections of the scatter plot are provided in Fig. 8 b (and an animated three-dimensional view of Fig. 8 a is provided in Movie S1, Movie S2, and Movie S3). The discrete character of the clouds associated to each substates is readily perceivable, as well as their preferential elongation along the apo/holo difference vectors. This anisotropy is particularly apparent for the trajectory as a whole.

FIGURE 8.

(a) Representation of the open and closed dynamical trajectories in the space of the three lowest-energy modes of the open trajectory. Each point represents an MD configuration and its coordinates are obtained by projecting the instantaneous deformation vector from the average structure of the open trajectory onto the three modes. White points are used to represent the closed trajectory, while different colors are used to distinguish the substates of the open trajectory. The open and closed crystal structures are represented as large spheres. An animated three-dimensional view of the portrayed set of points is provided as Movie S1, Movie S2, and Movie S3. Two bidimensional projections (mode 1 versus mode 2 and mode 1 versus mode 3) of the three-dimensional scatter plot are provided in panel b.

It is important to notice that, despite the good orientation of the principal dynamical directions along the apo/holo change, the succession of visited substates does not proceed in a directed manner in that, for instance, no constant progression of the open to the closed conformation is seen. As a consequence of the nondirected character of the dynamics, it is expected that the full interconversion occurs over much longer timescales than those accessed here, consistent with experimental indications (11).

Consensus essential dynamics of the open and closed trajectories

As a final stage of our analysis, we proceeded to identify the consensus set of collective modes that best capture the common structural fluctuations of AKE encountered in the two 50-ns-long trajectories. The essential dynamics analysis applied to the two merged trajectories is not adequate to this purpose, as it is not designed to extract the dynamical features that are shared by the two separate trajectories. This problem is tackled by means of the novel variational scheme, specifically developed for this study, which is described in Methods and in the Appendix. The method provides an optimal redefinition of the basis vectors in the two sets of modes that are returned in order of decreasing mutual consistency. We stress that the new bases span the same linear spaces of the original sets so that the original RMSIP, equal to 0.786, is unaltered by the redefinition.

It was found that the 10 lowest-energy modes of the two trajectories share, with almost perfect overlap, a three-dimensional subspace. In fact, the scalar products of the first, second, and third pairs of redefined modes have scalar products equal to 0.972, 0.951, and 0.925, respectively (see Fig. 9).

FIGURE 9.

The three consensus low-energy modes of the open and closed trajectories are shown respectively with solid, shaded, and open arrows superposed to the average structure of the (a) open and (b) closed trajectories.

For each trajectory, this three-dimensional consensus space is sufficient to account for 1), >57% of the total mean-square fluctuations; 2), >50% of the intrasubstate MSF; 3), >60% of the intersubstate MSF; and it also captures 4), 77% of the norm of the apo/holo difference vector.

The consensus modes thus constitute an extremely limited set of generalized coordinates that account for the system internal dynamics over a wide range of timescales (encompassing both intra- and intersubstates fluctuations) and indicates their relatedness to the major functional conformational change between the open and closed structures.

From a practical point of view, the findings also suggest the use of the consensus collective modes as natural candidates for profiling the free energy of the system in terms of a reduced number of generalized variables.

CONCLUSIONS

The predisposition of adenylate kinase to undergo major, functionally oriented, conformational changes was investigated through extensive molecular dynamics simulations of the free enzyme. Available crystal structures of AKE were taken as starting points for two MD simulations covering a total time-span of 100 ns. The analysis of the data collected over this previously unaccessed MD timescale has exposed interesting functionally oriented characteristics of the internal dynamics of the enzyme and of the organization of its free energy landscape.

During the free dynamical evolution, the enzyme populates distinct conformational substates with residence times of 5–10 ns. The ensemble of different conformers is structurally heterogeneous (with intersubstates differences up to 12 Å RMSD), reflecting the pronounced mobility of the AMP-binding and Lid subdomains.

We have carried out a covariance analysis of structural fluctuations recorded over a temporal range wide enough to cover both the collective small scale fluctuations within the substates and the larger-scale ones associated with intersubstate transitions. Strikingly, irrespective of the probed timescale, all intra- and intersubstate essential dynamical spaces turned out to be highly consistent. The functional relevance of this consistency, which does not originate from unspecific properties of overall amino acid mobility, is underscored by the high overlap that the essential dynamical spaces have with the deformation vector connecting the available apo/holo crystal structures.

The results support the recent suggestion of Adén and Wolf-Watz (50) that functionally oriented conformational fluctuations are innate properties of the free (apo) Adk. In fact, the analysis indicates that the free enzyme can be driven through various conformational substates bridging the inactive and catalytically potent states through the thermal excitation of a limited number of collective modes. The consistency of the salient features of the enzyme's internal dynamics within and across substates leads us to speculate that these properties may have been promoted by evolutionary pressure.

SUPPLEMENTARY MATERIAL

Structural heterogeneity of the open and closed trajectories; subdivision of the open and closed trajectories into structurally homogeneous groups (substates); distribution of RMSD of structures from the two trajectories; movie of the backbone during the open and closed trajectories; animated three-dimensional view of the scatter plot of Fig. 8 a. PDB files containing the C_α coordinates of 10³ frames (one every 50 ps) from each trajectory are available upon request.

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX

Consider the linear vector spaces V and W, spanned by the top N essential dynamical vectors, {v₁, v₂, …, v_N} and {w₁, w₂, …, w_N}, respectively. We wish to establish if, or to what approximation, V and W share a common subspace. The problem amounts to finding new orthonormal basis vectors for V and W, {v′₁, v′₂, …, v′_N} and {w′₁, w′₂, …, w′_N}, respectively, which are ranked according to decreasing mutual consistency. The problem could be solved through an iterative procedure where the first pair of vectors, v′₁ (belonging to V) and w′₁ (belonging to W), is picked to have the largest possible scalar product. This optimal selection procedure would then be repeated in the remaining complementary spaces of V and W and so on. In practice, the iterative scheme is avoidable, as the new basis vectors can be identified by requiring the stationarity of the functional

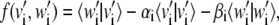(7)

which leads to the maximization of the overlap of the new basis vectors with same index subject to the normalization constraint enforced by the Lagrange multipliers α_i and β_i. Let A_i,j and B_i,j be the two N × N orthogonal matrices representing the basis change: 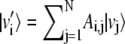and 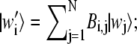and let and 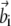be the rows of matrices A and B, respectively. Defining the nonsymmetric N × N matrix C as C_ij = 〈w_i|v_j〉, the functional in Eq. 7 can be rewritten as

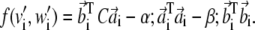(8)

The stationary condition gives the following set of eigenvalue equations,

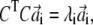(9)

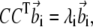(10)

with i = 1; …N, 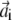and 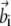are vectors with unit norm; and the coefficient λ_i equals 4α_iβ_i. Notice that the two solutions are not independent: if 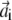is a solution for Eq. 9, then 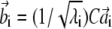is a solution for Eq. 10; furthermore, the scalar product of the vectors v′_i and w′_i associated with this solution is 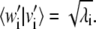As C^TC is an N × N symmetric matrix, we have a complete solution to the eigen-problem of Eq. 9 and the orthogonality of the new basis vectors is hence guaranteed.

Let us consider the nondegenerate case with λ_i ≠ λ_j ∀ i ≠ j and order the eigenvalues in descending order as λ₁ > λ₂ > ··· > λ_N. Vectors v′_i and w′_i are defined by the i^th solution of Eq. 9, as

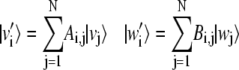(11)

and their scalar product is 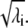Notice also that 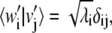in the case of no degeneracy in solutions of Eq. 9.