Two arms are better than one: parasite variation leads to combined inducible and constitutive innate immune responses

Abstract

Parasites represent a major threat to all organisms which has led to the evolution of an array of complex and effective defence mechanisms. Common to both vertebrates and invertebrates are innate immune mechanisms that can be either constitutively expressed or induced on exposure to infection. In nature, we find that a combination of both induced and constitutive responses are employed by vertebrates, invertebrates and, to an extent, plants when they are exposed to a parasite. Here we use a simple within-host model motivated by the insect immune system, consisting of both constitutive and induced responses, to address the question of why both types of response are maintained so ubiquitously. Generally, induced responses are thought to be advantageous because they are only used when required but are too costly to maintain constantly, while constitutive responses are advantageous because they are always ready to act. However, using a simple cost function but with no a priori assumptions about relative costs, we show that variability in parasite growth rates selects for a strategy that combines both constitutive and induced defences. Differential costs are therefore not necessary to explain the adoption of both forms of defence. Clearly, hosts are likely to be challenged by variable parasites in nature and this is sufficient to explain why it is optimal to deploy both arms of the innate immune system.

1. Introduction

Since parasites are ubiquitous in nature and, by definition, harm their hosts, organisms have developed a range of diverse mechanisms with which they defend themselves. A mechanistic understanding of these various immune components is vital to human and animal health and to our understanding of the role of disease in natural systems. Along with all other traits, the structures of the immune system have been shaped by evolution; selection pressures and constraints determine their evolutionary trajectory and govern their organizational complexity (Frank 2002). It is, therefore, important to understand how the costs and benefits of the production, maintenance and use of immune constituents may have lead to the mechanisms that we observe (Sheldon & Verhulst 1996; Frank 2002). Here we use a mathematical model to show how a simple mechanism can explain the need for both constitutive and induced responses in the innate immune system.

A major component of defence for all animals is the suite of innate immune effector systems which, in vertebrates, are also crucial for the mediation of the adaptive immune response. Invertebrates lack acquired immune responses but their mechanistically simple innate effectors are highly efficient and more functionally sophisticated than had been thought (Kurtz 2004; Jiravanichpaisal et al. 2006). Innate immune mechanisms in both vertebrates and invertebrates consist of constitutive responses (which are always ready to act) and induced responses (which are expressed only after the host has been exposed to infection). This distinction can also be seen in plant defences where some compounds involved in defence are expressed constitutively but can be further induced in response to elicitors (Zavala et al. 2004; Nurnberger & Lipka 2005), thus leading to analogies made between animal and plant defences (Dangl & Jones 2001; Gomez-Gomez & Boller 2002; Nurnberger & Lipka 2005). In insects, the phenoloxidase (PO) cascade is the most prominent component of constitutive innate defence. This enzyme cascade is triggered via a serine protease cascade solicited by key pathogen markers (e.g. Cerenius & Soderhall 2004): the cascade produces melanin and, in the process, releases a suite of potent cytotoxins (e.g. Sadd & Siva-Jothy 2006). The overall effect is the death and melanotic encapsulation of the pathogen very soon after exposure. Although activated by the presence of pathogens, the PO response has been demonstrated to have constitutive properties; previously activated plasma from a larval lepidopteran showed no increased antiviral activity over naive controls (Popham et al. 2004). Perhaps the best studied induced responses in insects are the antimicrobial peptides (Hoffmann 2003). These are relatively small peptides that are targeted at narrow groupings of pathogens (e.g. either gram-negative or gram-positive bacteria) which are expressed in quantity after insult (Hoffmann 2003).

Given that all organisms rely on innate immunity, it is surprising that relatively little work has examined why this facet of defence is organized the way it is. Fundamental to any theory of the evolution of the immune system is the fact that immune investment is costly (Sheldon & Verhulst 1996). Primarily, these costs will consist of the energetic costs of activation and maintenance of the response and the cost of diverting resources away from other traits, for example, feeding or sexual behaviour (Tschirren & Richner 2006). There is also evidence of genetic correlations between traits that result in trade-offs when one is optimized at the cost of another (Boots & Begon 1993; Kraaijeveld & Godfray 1997) either with another immune component (Cotter et al. 2004) or with other life-history traits (Hosken 2001). Finally, costs may also be incurred because the host's immune system targets its own tissue, through autoimmunity (Janeway et al. 2004) and/or autoreactivity (Sadd & Siva-Jothy 2006), for example. Recent work on insects, for example, has revealed that a potentially major, but non-metabolic cost of using the constitutive phenoloxidase cascade is that it melanizes, and so impairs the function of, the insect's kidney analogue (Sadd & Siva-Jothy 2006). Homeostasis and water balance are particularly important for insects, so damage of this type is likely to have important fitness implications. Obviously, these immune system costs will be exceeded by the benefits gained by optimal investment in, and the organization of, immunity.

Clearly, inducible defences have an advantage over constitutive defences in that they can be deployed only when needed, resulting in cost ‘savings’ when the pathogen is absent. This notion assumes (i) that there is a cost to the host of being parasitized, otherwise there would be no need to evolve and maintain defence mechanisms, (ii) that there is a cost to expressing inducible defences (if there is no cost one would expect them to be always maintained, i.e. constitutive), and (iii) that it is costly to maintain a constitutive response, otherwise there would be no need to evolve induced responses. Existing theoretical work on inducible defences has highlighted the importance of organism size, reproductive state and the abundance of natural enemies (Clark & Harvell 1992) but has tended to focus on predator–prey (Clark & Harvell 1992; Broom et al. 2005; Irie & Iwasa 2005; Longson & Joss 2006) or plant–herbivory systems (Adler & Karban 1994). Previous theory has looked at optimal allocation between multiple defence options (Shudo & Iwasa 2001) including constitutive responses and inducible defences with different time delays. Here we adopt a similar approach and develop a model of the innate immune system, including constitutive and inducible defences, to address the question of why defences of both types are maintained so ubiquitously. The model was developed assuming an invertebrate host for a number of reasons; insect systems have already been identified as useful tools for studying human diseases (Scully & Bidochka 2006) but as vectors of many serious diseases, understanding insect immunology is important in its own right. Further, homologues have been identified between vertebrate and insect innate immune components (Rock et al. 1998; as well as plant components; Dangl & Jones 2001), suggesting that insect systems are tractable models for studying the evolution and organization of innate immunity in general. The model uses a cost function to examine the optimal combination of both (constitutive and induced) arms and shows that the possession of both is optimal when faced with a range of parasites that show variation in their growth rates.

2. Model and results

Functionally, the immune response of an insect host consists of induced and constitutive responses. Phenoloxidase activity fulfils the criteria of a constitutive response in that it uses factors that are present without previous contact with a parasite (Brown et al. 2003; Popham et al. 2004). Further, several invertebrate species have been shown to be plastic in their levels of phenoloxidase activity either in response to selection (Schwarzenbach & Ward 2006) or density dependence (Reeson et al. 1998). Induced responses rely on the production of peptides, specific to either gram-negative or gram-positive organisms, after exposure to a pathogen (Brown et al. 2003). Anti-microbial peptides produced after infection with sub-lethal doses of a pathogenic yeast have been shown to protect larvae from a subsequent lethal dose of the same yeast (Bergin et al. 2006). This contrasts to constitutive responses where previously activated plasma showed no increased virucidal phenoloxidase activity over naive controls (Popham et al. 2004).

In this paper, we are interested in the effect of pathogen growth rates on the optimal combination of constitutive and induced, non-specific immune responses in invertebrate hosts. To this end, we adopt a simple model to describe the interaction of the immune responses of the host with the pathogen. We make the assumption that the constitutive response is fixed at a pre-determined level of activity but that this level may vary between organisms, perhaps reflecting different developmental or environmental conditions. Induced responses are then produced in direct proportion to the amount of pathogen present but have a finite lifespan. The parsimonious assumption is that the two responses act additively to counter parasites and that they do this in a manner proportional to the parasite load and to the sum of their levels of activity. This can be described in a simple two-variable model defining the dynamics of a pathogen population within the host and the extent of the immune response stimulated. The within-host dynamics of a parasite population, P, and the induced response, R, of a host with a constitutive response, k, are described by the following equations:

$$\frac{\text{d}P}{\text{d}t}=rP-g(R+k)P,$$ (2.1)

$$\frac{\text{d}R}{\text{d}t}=aP-bR.$$ (2.2)

The parasite population is assumed to grow exponentially at a rate r, meanwhile parasites are removed from the population with an efficiency, g, proportional to the density of parasites and the total activity of the combined immune responses, R and k. The induced response is stimulated in the presence of parasites at a rate, a, and decays at a rate, b.

This system has two equilibria, a trivial one where $\hat{P}=0$ and $\hat{R}=0$, the other is non-trivial where $\hat{R}=(r/g)-k$ and $\hat{P}=(b/a)((r/g)-k)$. When k≥r/g, the trivial equilibrium of $\hat{P}=0$ is stable and the infection is eliminated. Under the circumstances where k<r/g, however, $\hat{P}$ is unstable and shows oscillatory behaviour with long periodicity. This implies that the induced response is unable to clear the infection when the constitutive response is overwhelmed (k<r/g). We would expect, however, demographic stochasticity to eliminate the parasite at very low levels hence we introduce a threshold, P_thresh, below which the parasite is assumed to be eliminated. Here we therefore assume a threshold such that the induced response clears the infection and that oscillations do not occur.

It is assumed that being parasitized is costly to the host and that this cost is proportional to the size of the parasite burden, additionally both types of immune response exact a cost; the cost of the constitutive response is fixed proportional to its level and the cost of the induced response is proportional to the level of induced response at that point in time, such that at any point in time the cost to the host is given by

$$C_t=c_P{P}_t+c_{k}k+c_R{R}_t,$$ (2.3)

and where c_P+c_k+c_R=1.

The total lifetime cost to the host can then be defined as

$$C_{\text{total}}={\int }_{t=0}^T(c_P{P}_t+c_{k}k+c_R{R}_t).$$ (2.4)

To find the optimal allocation of host resources into constitutive and induced responses, the model is iterated over a range of values for the parameters r, k and a governing parasite growth rate (we assume that this relates to damage, and therefore cost, to the host and is thus linked to virulence), constitutive response level and rate of stimulation of induced response. For each parasite growth rate, the parameter combination C_total is calculated and the optimal combination of immune response parameters can be found by minimizing C_total. We assume that the initial inoculant size, P₀, is constant and that, in the absence of parasites, the level of induced activity, R₀, is 0.

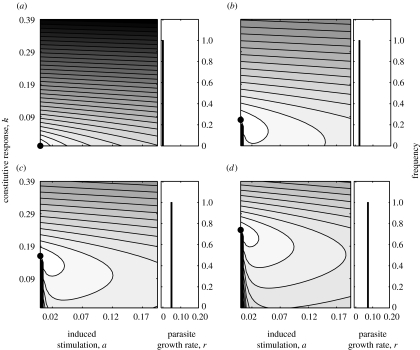
Over a given time period, we can calculate the cumulative cost to the host, C_total, of different combinations of parameter values for a and k and for increasing values of r. In figure 1, the value of C_total is plotted for different values of a and k, for a range of parasite growth rates. In the extreme case of r=0, there is no parasite growth within the host, and, as would be expected, the optimal strategy for the host is to not invest in immune responses of either type (figure 1a). Figure 1b–d shows same plot for three arbitrary values of r when r>0. It shows that for parasite growth rates greater than 0, the ‘cheapest’ combination of immune responses is to only invest in a constitutive response. That optimal constitutive response, k, is just high enough to counter the infection, such that k≥r/g, with k increasing as r increases.

Figure 1.

(a–d) The optimal combination of investment into constitutive, k, and induced, a, responses is shown in terms of minimizing total cost in the face of parasites with different growth rates, r (a, 0; b, 0.024; c, 0.048; d, 0.072). In each case, cost is shown on a scale from high (grey) to low cost (white), the combination of parameters with the lowest overall cost is marked by a filled circle. Parameter values are g=0.3, b=0.001, P₀=0.01, c_p=c_k=c_r=0.333, a ranges from 0.0 to 0.195 and k from 0.0 to 0.39.

This occurs under the assumption that the host encounters an entirely predictable pathogen whose growth rate is known. It is clearly more realistic to expect a host to encounter a range of pathogens with differing, growth rates—either reflecting variation within a parasite species or between different pathogen species. By summing the cost across the different values of r, we can calculate the average cost to the host of each parameter combination over the range of parasite growth rates, this assumes that the fitness cost does not affect mortality and is not influenced by other life-history variable such as host age. To reflect a more realistic distribution of growth rates, weightings can be applied such that the host encounters pathogens with different growth rates according to some assumed distribution. One simple assumption is that the growth rates of the pathogens a host encounters are distributed normally about a mean.

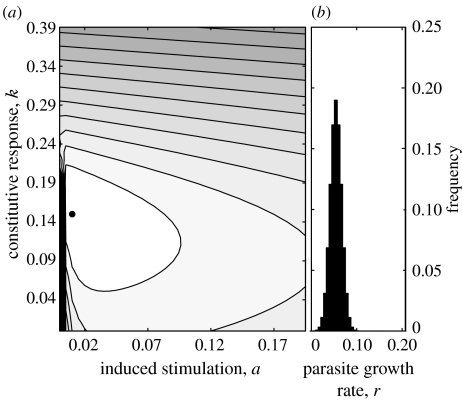
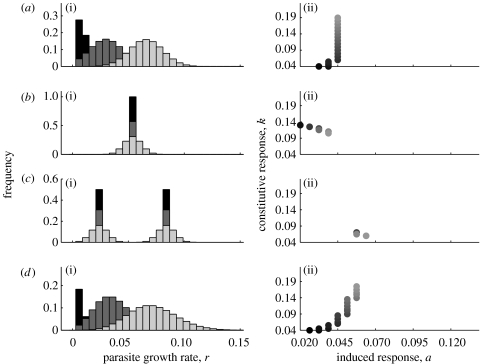
In figure 2a, we plot the cost function for a host encountering parasites with growth rates distributed normally about a mean (r_mean), as shown in figure 2b. Under this assumption, the optimal strategy for a host is to adopt both constitutive and induced defences. We can further explore this assumption by adjusting the shape and the position of the normal distribution and by looking at other distributions. In figure 3, we show the effect of these assumptions on the optimal combinations of immune responses. Increasing the mean of the distribution has no effect on the induced parameter, a, with the host adjusting the degree of constitutive investment (figure 3a(ii)). However, if we adjust the variance of the distribution (figure 3b), the optimal investment in both constitutive and induced responses are affected (figure 3b(ii)); initially, with a very narrow distribution, because there is very little variation, it is sufficient to have only a constitutive response. As the variance of the distribution increases, the host reduces investment in constitutive responses and increases investment in induced responses. A similar pattern is seen for a host whose parasites have bi-modally distributed growth rates (figure 3c), a situation perhaps reflecting a host with two distinct parasite species. In this case, the effect is much reduced as the host is already coping with two widely disparate growth rates so increasing the variance around them has a relatively small effect overall (figure 3c(ii)). In the final case, growth rates are distributed leptokurtically by means of a Poisson distribution (figure 3d), allowing us to follow a skewed, asymmetrical distribution. Here, as the mean increases, the variance also increases resulting in the optimal investment in both responses increasing (figure 3d(ii)). The results presented here assume an equivalence between c_P, c_k and c_R. Although not shown, over the course of an infection the total cost of being parasitized is of the same order as the total cost expended on constitutive response and on the induced response. By adjusting the values of c_P, c_k and c_R, we can increase and decrease their relative costs. As expected, this has the effect of shifting the optimal combination, however, the qualitative pattern is not changed (data not shown).

Figure 2.

(a) Plot of cost to host of investment in constitutive and induced responses when encountering parasites with varying virulence (reflected by differing growth rates, r_mean=0.054). Parameter combination with minimum cost is marked by a filled circle. (b) Distribution of parasite growth rates, r_mean=0.054. Parameter values are the same as given in figure legend 1.

Figure 3.

The effect of changing distribution characteristics are shown for different assumptions about parasite growth rate distribution. (i) Distributions are shown, with changing distribution characteristics shading from black to light grey, for: (a) normal distribution with increasing mean and constant variance; (b) normal distribution with increasing variance and constant mean; (c) bimodal distribution, each peak has an increasing variance and constant mean; and (d) leptokurtically skewed distribution with increasing variance. (ii) The optimal combination of induced, a, and constitutive, k, parameters are shown for each distribution (a–d) with the effect of changing distribution characteristics reflected by shading from black to light grey.

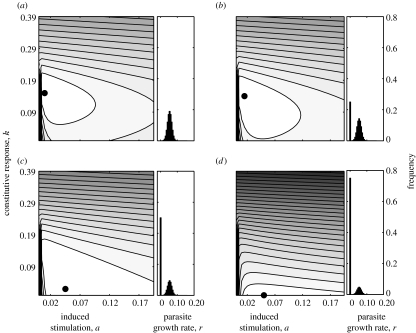
The method used here makes an inherent assumption that the host is always parasitized, it may be more realistic to expect hosts to be free from parasitism for some proportion of the time. We can use the case where r=0 to approximate to a situation where the host is uninfected; with a parasite growth rate of 0 the optimal strategy for the host is not to invest in immune defences of either type (figure 1a) thus mimicking what we would expect in the complete absence of parasitism. If we assume p to reflect the proportion of time a host is parasitized, then the amount of time they are uninfected is equal to 1−p. In figure 4 we show, for different values of p, the result of fixing a proportion (1−p) of the parasite growth rate distribution at r=0, the remaining proportion, p, is then distributed normally about r_mean. As the frequency with which the host is parasitized reduces, the proportion of resources invested in constitutive responses also decreases, until, at low levels of parasitism, only induced responses are favoured (figure 4d).

Figure 4.

Effect of parasite encounter frequency on optimal investment in immune responses with parasite growth rates normally distributed. (a–d) Optimal investment in constitutive, k, and induced, a, responses are shown for decreasing rates of parasitism, p (a, p=1.0; b, p=0.75; c, p=0.5; d, p=0.25). Rate of parasitism, p, reflects the proportion of time the host is infected by a parasite whose growth rate is greater than 0. Parameter combination with minimum cost is marked by a filled circle. Parameter values are the same as given in figure legend 1.

As presented, the model makes baseline assumptions about the nature of the interaction between the parasite and the immune response. We explored the implications of changing some of these assumptions including saturating-induced responses, time-delayed-induced responses and density-dependent parasite growth, but found no qualitative difference in the outcome described for the basic model. One could also consider an ‘induced-type’ response that can be maintained independent of the parasite dynamics once activated. However, this is essentially functioning in the same manner as a constitutive response whose intensity can be adjusted for each infection encountered and is eventually deactivated. As such, it would always be cheaper than a true constitutive response that is constantly maintained but does not reflect a truly induced response.

3. Discussion

We have shown how variability in parasite growth rates leads to an organism evolving to combine both constitutive and induced defences rather than relying on one or the other. Previous theory predicts that in a predator-free environment inducible defences are favoured over constitutive defences while a purely constitutive strategy would be most likely to occur in an unchanging, highly predictable environment with high predator abundance (Clark & Harvell 1992; Adler & Karban 1994). However, these studies have assumed defence strategies to be either constitutive or induced, here we are interested in what has driven the combination of both constitutive and induced defences together that is found extensively through out the animal kingdom. We have focused on the challenge a host faces from parasites and have shown that when a host is faced with an environment where the parasites it encounters have different growth rates, it becomes optimal, in terms of energetic cost to the host, to adopt both a constitutive and an induced response. This result is robust to assumptions about the distribution of encountered parasite growth rates and, above a threshold, for variable parasite encounter rates.

Surprisingly, empirical investigation into parasite growth rates has been largely neglected. However, in vitro growth rates have been found to differ not only between virulent and avirulent strains of Toxoplasma gondii (Kaufman et al. 1959) but also between three virulent strains with little identifiable polymorphism (Appleford & Smith 1997). In vivo growth rates are much harder to ascertain. A study on rodent malaria, Plasmodium chabaudi, found that parasitemia (a measure of the parasite's replication rate) in the rodent host varied significantly between different parasite clones (Mackinnon & Read 1999). Parasitemia also correlated with anaemia and weight loss in the host, two other virulence-related traits, adding further support to the commonly assumed correlation between parasite growth rate and virulence (Mackinnon & Read 1999). In Schistosoma mansoni, high virulence was associated with high replication rates in definitive hosts but not intermediate hosts, although replication rates did vary across substrains in both intermediate and definitive hosts (Davies et al. 2001). Measurements of parasite virulence in vivo can be confounded with genotypic interactions between host and parasite influencing observed virulence, this has been shown most clearly in plant–pathogen systems (Salvaudon et al. 2005) and also in animal models (Carius et al. 2001; Lambrechts et al. 2005) and may be a factor for future consideration. However, it is clear that the potential for variation in virulence exists within parasite species.

The amount of variation in pathogen virulence in natural insect pathogens is even less well studied than growth rates themselves. However, a number of insects, such as bumble-bees (Bombus terrestris; Colla et al. 2006), Daphnia (Little & Ebert 2000) and, among others, Plodia interpunctella, Culex sp. and Tenebrio sp. (Onstad 2006) have been shown to be natural hosts to a diversity of parasite species suggesting that they are regularly exposed to a variety of pathogens. Studies on cockroaches (Blatella germanica; Cloarec et al. 1992) and bedbugs (Cimex lectularius; Reinhardt et al. 2005) have found a diversity of bacterial species associated with their cuticle, in cockroaches these are largely considered to be benign. In bedbugs, however, traumatic insemination of females allows the introduction of the cuticular bacteria to the haemolymph with the likelihood that the female bedbug is exposed to the diverse cuticular fauna on a regular basis. Variance in growth rates may also exist within a parasitic species, although there is very little quantifiable information on parasite growth rates, particularly in vivo. A study on bumble-bees found that 16% of all individuals and over half of the populations sampled were infected by more than one genotype of a trypanosome parasite (Schmid-Hempel & Funk 2004). Additionally, condition-dependent virulence has been documented in the same system (Brown et al. 2000), suggesting that there may be scope for variation in virulence within parasite species.

Shudo & Iwasa (2001) looked at optimal allocation between an inducible and a constitutive defence and demonstrate that a combination of induced and constitutive defences is predicted for severe pathogen attack, that is, when the initial dose is large and the pathogen is both fast growing and has a high cost to the host. In a later study, they show that variation in pathogen dose can affect the optimal amount of stored defence proteins versus newly produced proteins (Shudo & Iwasa 2002). Further, uncertainty in the size of the inoculant dose allows a decrease in the amount of stored proteins. Although couched in terms of defence proteins, this model is analogous to their previous model and suggests that constitutively expressed responses (in the form of stored proteins) may be reduced in the face of unpredictable infective dose. Our work shows that unpredictability in other relevant factors can also favour increased investment in inducible responses over constitutive responses, we suggest that over multiple infections a combination of responses is optimal owing to the diversity in pathogens that might be encountered. Our interpretation of these results suggests that constitutive responses are sufficient to combat the majority of infections, however, a number of infections are able to swamp these primary responses and, without the induction of further defences would overwhelm the host. Further empirical and theoretical research is clearly necessary to dissect the relative importance of infection size and pathogen variation.

All of the models predict higher probability of infection leads to greater relative investment in constitutive responses (Shudo & Iwasa 2001, 2002). Elevated cuticular melanization and phenoloxidase activity, both elements of constitutive defences, have been measured in populations reared at high larval density (Reeson et al. 1998; Barnes & Siva-Jothy 2000; Wilson et al. 2001). The density-dependent prophylaxis hypothesis proposes that increased host density results in a higher risk of infection, and, as a result, rearing density may be used as a cue to assess infection risk (Wilson & Reeson 1998). We would predict that this should coincide with a reduced investment in induced responses such as anti-microbial peptides (figure 4) though this has not been experimentally assessed. Increased antimicrobial activity has been demonstrated in the offspring of parents challenged by lipopolysaccharide (LPS; Moret 2006). This counters general predictions, and more specific ones from this model, which suggest investment in induced responses should be reduced with both increased risk of infection and high predictability of parasite fauna (both of which might be suggested by parental infection). There are several reasons why this discrepancy might be observed. Firstly, LPS is a non-pathogenic, non-living molecule derived from bacterial cell walls thus, while it is a cue for invertebrate immune systems, it will show none of the other traits of a pathogenic organism. How this might affect the control and feedbacks of the immune response is unknown. Secondly, our model does not include specificity between pathogen and induced response, while this is not close to the scale of vertebrate specificity, it has been demonstrated in insects (Little et al. 2003) and, although very broad, may have an affect that is not captured by a simple model.

This work has parallels in some predator–prey and plant–herbivory systems (Clark & Harvell 1992; Adler & Karban 1994). However, while there are obvious analogies between defences that are induced in response to predation or herbivory and those that are induced to counter pathogenic invasions, there are also distinctions that must be made. In predator–prey systems, the size of the prey has been found to be key while induced defences are generally structural (Harvell 1990) and most frequently found in aquatic invertebrates. The importance, if any, of host size in parasitic attack is by contrast unknown. Further, the fitness cost for an unsuccessful parasite (i.e. no transmission) is different from that of an unsuccessful predator (having to find another prey item). A common assumption is that some responses are induced because, while they are very effective, they are also very dangerous for the host and would cause serious damage if they were expressed constitutively. In this model, we have shown that induced responses can be optimal even when the cost to the host is not significantly different than those of constitutive responses.

Here we have assumed a compartmentalized immune response whose two parts are independent of each other. In reality, the purely constitutive and purely induced responses can be considered to be the ends of a continuum with some pathways having elements of both; for example, the constitutively expressed phenoloxidase precursor is rapidly catalysed by immune insult (Hultmark 1993) but further expression can be induced. One might also expect there to be some direct interaction between them; the presence of induced responses, for example, might downregulate the expression of constitutive responses. In this model, we assumed that the induced response was directly linked to pathogen load, an alternative approach adopted the assumption that the production of specific immune cells was not linked to pathogen load in a direct manner (Shudo & Iwasa 2004). We have also assumed that the level of constitutive response expressed is fixed for a host irrespective of its state of infection but that this level can vary between individuals, perhaps in response to the developmental environment or life-history cues such as gender or age. The importance of these different assumptions will be examined in future modelling. The model is currently being developed to allow the role of ecological feedbacks to be examined, this would allow us to extend the theory to cover situations where the prevalence of the pathogen is linked to the infection dynamics. This is currently not a feature of this model, however, the model remains valid for a range of situations where such feedbacks do not occur such as with opportunistic and generalist pathogens. This is particularly relevant in insects where single host pathogens are rare.

The development of this model has highlighted some key areas that are underinvestigated in natural systems. Parasite diversity has previously been highlighted as having a role in the allocation of defences, in particular the switch from tolerance to defence (Jokela et al. 2000) and is a fundamental assumption to the Red Queen theory of the maintenance of variation in populations (Jaenike 1978). While variation in immunity in mammalian host species is an area of great interest (Norris & Evans 2000; Tella et al. 2002; Smith & Hunt 2004), very little attention has been paid to the extent of individual variation in invertebrate hosts, and, to an even lesser extent their parasite species. It is crucial that we gain more empirical understanding of the growth kinetics of invertebrate parasite species and host immune dynamics. In the absence of such data, we can, however, investigate other assumptions of the model theoretically. In particular, a key question is the integration of the induced response. Here, we have assumed that the induced response is directly proportional to the parasite load so that adjusting the induced response parameter, a, affects the intensity of the response. An alternative assumption might be that it is the sensitivity or the timing of the response that varies. In mammalian systems, it is common to assume the host is an infinite resource from the parasite's point of view. For many invertebrates, the size discrepancy between host and parasite may not be as extreme. Therefore, it may be appropriate to model the host as a limiting resource, leading to questions about dose dependency.

Most theory on immune response organization has focused on the adaptive response of vertebrates, however, as the innate response underlies immunity in both vertebrates and invertebrates it is important to develop the theoretical understanding of the criteria that underpin its organization. We would argue that this is likely to be particularly fruitful owing to the potential for combining theoretical predictions with tractable invertebrate model systems. Here we have begun this process by identifying a parsimonious process that can explain the seemingly ubiquitous possession of both induced and constitutive innate immune responses. Organisms would not need both of them if they were only faced with parasites with predictable growth rates however, parasites vary. Hosts therefore need both arms to cope with an uncertain world.