Estimating Time to Event From Longitudinal Categorical Data: An Analysis of Multiple Sclerosis Progression

Abstract

The expanded disability status scale (EDSS) is an ordinal score that measures progression in multiple sclerosis (MS). Progression is defined as reaching EDSS of a certain level (absolute progression) or increasing of one point of EDSS (relative progression). Survival methods for time to progression are not adequate for such data since they do not exploit the EDSS level at the end of follow-up. Instead, we suggest a Markov transitional model applicable for repeated categorical or ordinal data. This approach enables derivation of covariate-specific survival curves, obtained after estimation of the regression coefficients and manipulations of the resulting transition matrix. Large sample theory and resampling methods are employed to derive pointwise confidence intervals, which perform well in simulation. Methods for generating survival curves for time to EDSS of a certain level, time to increase of EDSS of at least one point, and time to two consecutive visits with EDSS greater than three are described explicitly. The regression models described are easily implemented using standard software packages. Survival curves are obtained from the regression results using packages that support simple matrix calculation. We present and demonstrate our method on data collected at the Partners MS center in Boston, MA. We apply our approach to progression defined by time to two consecutive visits with EDSS greater than three, and calculate crude (without covariates) and covariate-specific curves.

1 INTRODUCTION

Multiple sclerosis (MS) is a chronic inflammatory disease of central nervous system myelin. Symptoms include weakness, sensory symptoms, gait disturbance, visual symptoms, bladder dysfunction, and sexual dysfunction. MS occurs in 0.1% of the US population, with onset usually in early adulthood. About 85% of MS patients have the Relapsing-Remitting (RR) form of MS at time of initial diagnosis. On average, RR MS patients have 1.5 attacks every two years in which symptoms grow more severe for a few days or weeks. Without treatment, about fifty percent of the RR MS patients will progress within 10 years to a steadily worsening disease course called Secondary Progressive (SP). The remaining 15% of MS patients experience a steadily worsening disease from the onset with (progressive-relapsing MS) or without (primary-progressive MS) attacks. A disability status scale (EDSS) measures the functioning ability of a patient and ranges from 0 (normal neurological exam) to 9 (bedridden). The EDSS fluctuates in the short term, but tends to increase over time. Both short and long term prediction of EDSS are of great importance to physicians and patients. In particular, estimates of the distribution of (1) time to increase of EDSS of one point, (2) time to EDSS of three, and (3) time to sustained EDSS of three, are of interest. Such outcomes have been widely used to study MS progression in observational studies and in Phase III clinical trials (e.g., Confavreux, Vukusic and Adeleine, 2003, Andersen, et al., 2004). The EDSS trajectories are very different for the RR patients versus the remaining 15% and SP patients, and in this paper we consider the RR form of the disease only.

We consider data that were collected from February 2000 to April 2005 by the Partners Multiple Sclerosis Center in Boston, MA. These data are part of an ongoing study that aims to understand the natural history of MS in the current era of FDA-approved disease modifying therapy (Gauthier, Glanz, Mandel, and Weiner, in press). Data contain semi-annual measures of EDSS for 267 patients with a clinically isolated syndrome or a diagnosis of RR MS at early stages of their disease, brain MRI metrics and other clinical and demographic covariates. Figure 1 displays the EDSS process of two subjects during 8 visits.

Figure 1.

EDSS profiles of two patients who had at least 8 out of 9 potential visits.

Previous studies used survival analysis methods to estimate time to a certain level of EDSS and time to increase of one point of EDSS (Weinshenker et.al., 1989, Runmarker, Andersson, Oden, and Andersen, 1994, Kremenchutzky et.al. 1999, Confavreux et.al., 2003). This approach is problematic for several reasons. First, the EDSS is an ordinal measure for which an increase of one point has different meanings at different EDSS levels. An increase from EDSS of zero to EDSS of one, for example, is not as important of an indicator of progression as is an increase from EDSS of two to three. Stratification by baseline EDSS level results in small stratum sizes, hence is rarely employed. Second, not all patients reach the terminating event before the end of follow-up. The EDSS at the end of follow-up is informative with respect to the EDSS event of interest and by simply censoring such individuals, as is the current practice in MS studies, information is lost. In Figure 1, the patient on the left had an EDSS of zero when the study ended while the patient on the right had an EDSS of two. When trying to estimate the survival function of time to EDSS of three, for example, one should not ignore this information. Interestingly, both patients began at the same EDSS level. Third, EDSS is a reversible process, meaning that it is not necessarily increasing over time (although it has a tendency to increase in the long run). This complicates the definition of the end point and the treatment of missing values. For example, it is not at all clear what to do with a missing EDSS value. If the EDSS process were progressive, then survival analysis methods tailored to interval censored data would apply. Such methods are not adequate for reversible processes.

In this paper, we suggest a method for estimating time to event that circumvents these difficulties in applying survival analysis methods through more natural modelling of the repeated categorical EDSS values. A transitional model (Diggle, Liang and Zeger, 1994) is fitted first to describe the influence of covariates on six months fluctuations of EDSS. Using its results and simple manipulations of the estimated transition probabilities, we provide covariate specific probability curves for time to progression. These are important descriptive statistics of the natural history of a disease, and are easily understood and interpreted by physicians and patients. We adopt the Markovian assumption because of its clinical plausibility and to simplify estimation and interpretation, but extensions are also considered. Although time to event is of primary interest in MS studies, in other situations, quantities such as mean occupation time or steady state probabilities may be of interest, and can be calculated from the transitional model results by using properties of Markov chains (see Albert, 1994).

Transitional models use the conditional distribution of the sequence of observations as their building blocks and are the natural model-of-choice when the primary focus is that of prediction. For repeated categorical data, such models have received little attention relative to marginal and random effect models (Agresti, 1999). Diggle et. al. (1994) describe transitional models mostly for normal and binary outcomes. Albert (1994) applies transitional models to ordinal outcomes using data from a study of experimental allergic encephalomyelitis, which is an animal model of MS. His focus is on methods to deal with the relapsing remitting nature of the disease. He also shows how to estimate interesting features of the disease such as the mean occupation time in a state. Zeghnoun, Czernichow and Declercq (2003) describe the transitional model in the context of ordinal responses and use it to check the influence of ozone on respiratory symptoms (a binary outcome). Yu, Morgenstern, Hurwitz and Berlin (2003) use a transitional model to analyze longitudinal low-back pain data, but the method they employ does not exploit the ordinal scale. Heagerty (2002) studies a marginalized transition model for serial categorical data and uses Markov dependency between consecutive values. His focus is on the marginal mean and the transition part is modelled in order to facilitate likelihood based inference. Transitional models can be regarded as discrete time multi-state models in survival analysis (Hougaard, 2000), where each level of the response (e.g., EDSS) corresponds to a state. Here the survival time to first visit to state j is the time (discrete) until the response changes to level j. Andersen, Borgan, Gill and Keiding (1993) give an extensive discussion of Markov models in the framework of survival analysis and supply many references. They also demonstrate their use on several real data sets. Their main focus is on studying estimates for continuous time data subject to censoring. Another related field in which similar models have been studied is time series. Fokianos and Kedem (2003) review models for categorical time series which are essentially transitional models with one long series rather than many short ones. Estimation methods presented by Kaufmann (1987) and Fokianos and Kedem (1998, 2003) in the framework of time series analysis can be directly applied to our model. The focus of time series analysis, however, is somewhat different than our focus on time to a terminating event.

Section 2 presents the notation, the model and the method of estimation. Although it focuses on a proportional odds model for an ordinal response, extensions to nominal outcomes and to models other than proportional odds are straightforward and discussed briefly. Section 3 describes construction of survival curves based on Markov transition models given an estimate of the transition matrix and its corresponding variance-covariance matrix. Simple manipulations of the transition matrix enable calculation of the survival of many clinically interesting end points. Pointwise confidence intervals are calculated based on the delta method under the assumption that transition matrix estimators have an asymptotic normal distribution. The proposed confidence intervals are easy to calculate and are accurate. This is discussed in Section 4, where we apply our method to the MS data. We conclude the paper with a discussion on topics for further research.

2 MODELLING AND ESTIMATION

In this section, we present parametric transitional models for categorical data, giving special treatment for ordinal responses. The notation and methods follow models studied in time series, and for more details the reader is referred to Kaufmann (1987), Diggle et.al. (1994) and Fokianos and Kedem (1998, 2003).

2.1 Transitional Models

Let t = 0, 1, 2, … index visit times, e.g., semiannual visits, and let Y_t and x_t denote the response variable and an m dimensional covariate vector measured at visit t, respectively. The variable of interest, Y_t, is categorical, and takes on one of the values 1, 2, …, J, which can be measured either on a nominal or an ordinal scale. At times, it will be convenient to replace Y_t with its indicator vector $Y_t^{•}=(Y_t^1,\dots ,Y_t^J{)}^{\prime }$, where $Y_t^j=I\{Y_t=j\}$ and I{∙} is the indicator function. Denote by ${ℱ}_{\mathcal{t}}=\{(Y_0,{\mathrm{x}}_0),\dots ,(Y_t,{\mathrm{x}}_t)\}$ the history up to time t and let ${\pi }_{tj}=P(Y_t=j|{ℱ}_{\mathcal{t}-1})$, ${\pi }_t=({\pi }_{t1},\dots ,{\pi }_{tJ-1}{)}^{\prime }$. Transitional models are defined for the conditional probabilities π_t. This is most commonly done by first defining a covariate reduction Z_t = D(ℱ_t), where Z_t is a design matrix having J − 1 rows, and then specifying a parametric model of the form

$${\pi }_t(\theta )=\left(\begin{array}{c}{\pi }_{t1}(\theta )\\ ⋮\\ {\pi }_{tJ-1}(\theta )\end{array}\right)=\left(\begin{array}{c}{h}_1({\mathbf{Z}}_{t-1}^{\prime }\theta )\\ ⋮\\ h_{J-1}({\mathbf{Z}}_{t-1}^{\prime }\theta )\end{array}\right)=\mathbf{h}({\mathbf{Z}}_{t-1}^{\prime }\theta ),$$ (1)

where h is a link function takes on values on the (J − 1)-simplex, i.e., a probability function.

Fokianos and Kedem (2003) review models of the form of (1) in the framework of time series and give various examples of the data reduction D and of the link function h. In contrast to one long time series, many longitudinal data sets, such as our MS example, comprise of many short time series of differing lengths, and there is much less flexibility in modelling. The most frequently used data reduction is through the Markov dependency model (e.g., Diggle, et.al., 1994); i.e., Z_t depends only on (Y_t, x_t). The following section gives examples of models for ordinal responses under a Markov model of order one that will be applied later to the MS data. Section 2.3 discusses inference under these models using longitudinal data. Extensions to Markov model of a higher order and to non-Markovian models are discussed briefly in Section 2.4

2.2 The Proportional-Odds Model for Ordinal Response

In this section, we assume that P(Y_t = j∣ℱ_t−1) = P_θ(Y_t = j∣Y_t−1, x_t−1) and discuss several models for an ordinal outcome. Our aim is to explore several simple alternatives of the popular proportional odds model, and to discuss their advantages and drawbacks in terms of parsimony and interpretation. Alternative models can be found in Agresti (1990) and Fokianos and Kedem (2003).

For ordinal responses, the cumulative distribution function is commonly used as the building block for modelling (Agresti, 1990). Using the logit link, a possible model is:

$${\eta }_{tj}\equiv logit\{P(Y_t\le j|Y_{t-1}=k,{\mathbf{x}}_{t-1})\}={\alpha }_{kj}+{\mathbf{x}}_{t-1}^{\prime }{\beta }_k\hspace{0.17em}(k=1,\dots ,J;j=1,\dots ,J-1),$$ (2)

where the α_kj’s are scalars and the β_k’s are m dimensional vectors. Letting $\theta ={({\alpha }_{11},{\alpha }_{21},\dots ,{\alpha }_{J1},{\alpha }_{12},\dots ,{\alpha }_{J2},\cdots ,{\alpha }_{1J-1},\dots ,{\alpha }_{JJ-1},{\beta }_1^{\prime },\dots ,{\beta }_J^{\prime })}^{\prime }$, $F(\eta )=exp(\eta )/[1+exp(\eta )]$ (the logistic distribution function), h₁(η₁, …, η_J−1) = F (η₁) and h_j(η₁, …, η_J−1) = F(η_j) − F(η_j−1) for j > 1, it is easy to verify that (2) is a special case of (1) with ${\mathbf{Z}}_{t-1}^{\prime }=({\mathbf{I}}_{J-1}\otimes {Y^{•\prime }}_{t-1},1_{J-1}\otimes {Y^{•\prime }}_{t-1}\otimes {{\mathbf{x}}^{\prime }}_{t-1})$, where I_j is the identity matrix of order j, 1_j is a vector of ones of length j, and ⊗ is the Kronecker product operator.

Equation (2) defines a separate model for each past response k; in each model (i.e., for each k) proportional-odds are assumed to hold with respect to the covariates. This is the saturated proportional odds model where all interactions of $Y_{t-1}^{•}$ with x_t−1 are present and the total number of parameters is J(m + J − 1), where m is the number of covariates.

Since (2) results in a large number of parameters, a more parsimonious model is desirable. A natural simplification is to assume that the effect of a covariate, after controlling for the baseline transition probabilities, is independent of the specific transition. This model takes the form

$${\eta }_{tj}={\alpha }_{kj}+{\mathbf{x}}_{t-1}^{\prime }\beta \hspace{0.17em}(k=1,\dots ,J;j=1,\dots ,J-1).$$ (3)

The model is a partial proportional-odds model (Peterson and Harrell, 1990) in which several of the conditioned variables have proportional odds (x_t−1) and the other do not $\left(Y_{t-1}^{•}\right)$. It has m + J(J − 1) parameters and can be shown to be a special case of (1).

Viennet, Ménard and Thomas (1998) and Zeghnoun, Czernichow and Declercq (2003) assume the proportional odds property also for $Y_{t-1}^{•}$ by defining the model

$${\eta }_{tj}={\alpha }_j+{\mathbf{x}}_{t-1}^{\prime }\beta +{\gamma }_k\hspace{0.17em}(k=1,\dots ,J-1;j=1,\dots ,J-1).$$ (4)

The total number of parameters reduces to m + 2(J − 1).

A referee pointed out that a further parsimony can be achieved by utilizing the ordinal scale of the last state. Specifically, let s_k be a score corresponding to state k, then the model

$${\eta }_{tj}={\alpha }_j+{\mathbf{x}}_{t-1}^{\prime }\beta +\gamma s_k\hspace{0.17em}(j=1,\dots ,J-1)$$ (5)

further reduces the number of parameters to only m + J. The scores s_k should be chosen to linearize the ordinal categories and are ideally based on prior physical knowledge (see Agresti, 1990 chapter 8).

Both models (4) and (5) restrict the parameters by assuming a constant odds ratio at each row and at each column of the transition matrix. In particular, they assume that

$${\eta }_{tj}-{\eta }_{{\mathit{tj}}^{\prime }}={\alpha }_j-{\alpha }_{j^{\prime }}$$

is independent of the value of the past response Y_t−1 and the covariate vector x_t−1. While the assumption of proportional-odds for the covariates x_t−1 may be reasonable in several applications, the assumption that the difference in log-odds for different groups of the current response is independent of the past response (demonstrated by the equation above) seems unrealistic in the MS example and in many other cases. Thus, although models (4) and (5) are the most parsimonious and the easiest to interpret, in practice, models (2) and (3) need to be considered. For the case of a homogeneous population (no covariates), the latter models are the most general ones, while the models (4) and (5) impose constraints on the transition probabilities as discussed above.

2.3 Estimation

Let i = 1, …, N index subjects, and let n_i denote the number of visits made by subject i. The likelihood under the Markov model of order one is

$$\prod _{i=1}^N\prod _{t=1}^{n_i}{P}_{\theta }(Y_{it}=y_{it}|y_{it-1},{\mathbf{x}}_{it-1})\times \prod _{i=1}^{N}P(Y_{i0}=y_{i0}|{\mathbf{x}}_{i0}),$$ (6)

where y_it is the observed value of subject i at visit t. If the parameters of P(y_i0∣x_i0) in (6) are independent of θ, inference can be carried out using the first term only without loss of efficiency (Kaufmann, 1987):

$$\mathrm{PL}=\prod _{i=1}^N\prod _{t=1}^{n_i}{P}_{\theta }(Y_{it}=y_{it}|{\mathbf{x}}_{it-1},y_{it-1}).$$ (7)

Fokianos and Kedem (1998) justify maximization of (7) using partial likelihood arguments. In practice, one should treat past responses as covariates and implement regression models tailored for categorical data treating the terms in the product of (7) as independent. Under mild regularity conditions, (7) has the usual asymptotic properties of a likelihood and standard inference methods apply (Kaufmann, 1987, Fokianos and Kedem, 1998).

Models (2), (4) and (5) are proportional-odds models and estimation can be easily carried out using statistical software packages such as SAS and R (e.g., proc logistic in SAS and the function polr in the MASS package of R). For model (2), J different models should be fitted independently, with the k’th model using only transitions from state k. For models (4) and (5), one overall proportional-odds model should be fitted. Model (3) can be estimated using proc nlmixed in SAS. Alternatively, partial proportional-odds models can be estimated using SAS proc genmod in conjunction with Generalized Estimating Equations (GEE), after manipulating the data as discussed by Stokes, Davis and Koch (2000).

2.4 Beyond Markov Models of Order One

The family of models (1) is much richer than the models considered in Section 2.2. Estimation and inference are implemented as described in Section 2.3, with ${\mathbf{Z}}_{it-1}^{\prime }$ replacing x_it−1, Y_it−1 on the right side of the conditioning sign of (7). We discuss two examples that are relevant to MS. For simplicity, we present the models without covariates.

An important extension is to Markov models of a higher order q:

$$P(Y_t=j|Y_0=y_0,\dots ,Y_{t-1}=y_{t-1})=P(Y_t=j|Y_{t-q}=y_{t-q},\dots ,Y_{t-1}=y_{t-1}).$$

Diggle et.al. (1994) discuss such models for the special important case J = 2 and the extension for J ≥ 3 is straightforward. In practice, the difficulty in such modelling is in the step from (6) to (7). The term omitted in that step involves the marginal distribution of the first q observations (Y₀, …, Y_q−1) and it usually contains a large portion of the data (note that this is less problematic for time series data). Furthermore, the number of parameters usually increases with q. Thus, a large data set is needed in order to well estimate such models.

As a second extension consider the non-Markovian model:

$$P(Y_t=j|Y_0=y_0,\dots ,Y_{t-1}=y_{t-1})=P(Y_t=j|Y_{t-1}=y_{t-1},\max (Y_0,\dots ,Y_{t-1})=y_{\max }).$$ (8)

If the probability depends on y_max only through I{y_max ≥ c}, for some c, then the model is similar to a capture-recapture model studied by Yang and Chao (2005). It can be used to describe the behavior of benign MS patients who spend a long time in state 1 before their disease becomes active. This model recognizes the importance of the greatest degree of progression in the patients history for prediction of future progression. We note that the model is Markovian on the extended state space {(j, m)∣j = 1, …, J, j ≤ m ≤ J} of the process (Y_t, max(Y₀, …, Y_t)).

3 ESTIMATING TIME TO PROGRESSION

In the previous section we modelled the transition probabilities as a function of the process’s history and covariates. In this section we show how the regression results can be used to estimate time to progression for groups of patients.

After choosing a model and estimating its parameters, one can calculate the time-dependent transition matrix for a subject given his/her covariates. For example, under model (3), the (k, j) entry of the transition matrix at time t is given by

$$P(Y_t=j|Y_{t-1}=k,{\mathbf{x}}_{t-1})=\frac{exp({\alpha }_{kj}+x_{t-1}^{\prime }\beta )}{1+exp({\alpha }_{kj}+x_{t-1}^{\prime }\beta )}-\frac{exp({\alpha }_{kj-1}+x_{t-1}^{\prime }\beta )}{1+exp({\alpha }_{kj-1}+x_{t-1}^{\prime }\beta )},$$ (9)

where α_k0 = −∞ and α_kJ = ∞. In this section, we explore ways to use this matrix for survival estimation. Our discussion starts from a given estimated transition matrix P̂ that depends on a covariate matrix z and a parameter vector θ. We assume a Markov model and defer the discussion of time dependent covariates to Section 3.3.

3.1 Estimating t-Step Probabilities

Let vec denote the vectorize operator that stacks the rows of a matrix one on the other and let P = (p̂_kj) be the estimated transition matrix. Typically, P̂ = P(z^′θ̂) is a covariate-specific matrix defined by a model such as (2)-(5). Most estimation methods yield an asymptotic normal distribution for θ̂; i.e., with a covariance matrix Σ_θ, $\sqrt{N}(\widehat{\theta }-\theta )\to N(0,{\mathbf{\sum }}_{\theta })$. Applying the delta method and using the transformation P(z′θ) defined by the model, we arrive at

$$\sqrt{N}[\mathrm{vec}(\widehat{\mathbf{P}})-\mathrm{vec}(\mathbf{P})]\to \mathrm{N}(0,\mathbf{\sum })$$ (10)

where Σ is a J² × J² matrix containing the covariance of p̂_kj and p̂_k′j′ in its (k − 1) × J + j row and (k′ − 1) × J + j′ column. Technical details for the calculation of Σ for model (3) are given in the appendix. The survival estimators discussed in this section make use of P̂ and Σ and (10), i.e., they are subject-specific but exploit the asymptotic results of the whole sample.

The estimated probability of a subject occupying state j at time t given occupation of state k at time 0 is simply ${\widehat{p}}_{kj}^t$, the (k, j) cell of the estimated t-step transition matrix P̂^t. Viewing P^t as a continuous mapping from ℝ^J×J to ℝ^J×J, it follows from the delta method that

$$\sqrt{N}[\mathrm{vec}({\widehat{\mathbf{P}}}^t)-\mathrm{vec}({\mathbf{P}}^t)]\to \mathrm{N}(0,{\mathbf{D}}_t\mathbf{\sum }{\mathbf{D}}_t^T),$$

where D_t is the matrix of the partial derivatives of vec(P^t) with respect to vec(P). For example, for J = 3 there are J² = 9 transition probabilities and for each t, J² = 9 functions of these probabilities. The functions for t = 1, 2 are:

$$\mathrm{vec}(\mathbf{P})=\left(\begin{array}{c}{p}_{11}\\ p_{12}\\ p_{13}\\ ⋮\end{array}\right)\hspace{0.17em}\text{and}\hspace{0.17em}\mathrm{vec}({\mathbf{P}}^2)=\left(\begin{array}{c}{p}_{11}^2+p_{12}{p}_{21}+p_{13}{p}_{31}\\ p_{11}{p}_{12}+p_{12}{p}_{22}+p_{13}{p}_{32}\\ p_{11}{p}_{13}+p_{12}{p}_{23}+p_{13}{p}_{33}\\ ⋮\end{array}\right),$$

and the corresponding matrices of derivatives are D₁ = I₉, the identity matrix, and

$${\mathbf{D}}_2=\left(\begin{array}{ccccccccc}2p_{11}& p_{21}& p_{31}& p_{12}& 0& 0& p_{13}& 0& 0\\ p_{12}& p_{11}+p_{22}& p_{32}& 0& p_{12}& 0& 0& p_{13}& 0\\ p_{13}& p_{23}& p_{11}+p_{33}& 0& 0& p_{12}& 0& 0& p_{13}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right).$$

Calculation of D_t is very simple. Let Δ_kj be a J × J matrix whose elements are all zeros except the (k, j) cell which is one, it follows that

$$\frac{\partial \mathrm{vec}({\mathbf{P}}^t)}{\partial p_{kj}}=\mathrm{vec}\left(\underset{h\to 0}{\lim }{h}^{-1}[{(\mathbf{P}+h{\mathbf{\Delta }}_{kj})}^t-{\mathbf{P}}^t]\right)=\mathrm{vec}\left(\sum _{\ell =0}^{t-1}{\mathbf{P}}^{\ell }{\mathbf{\Delta }}_{kj}{\mathbf{P}}^{t-\ell -1}\right),$$ (11)

where P⁰ is the identity matrix with the same dimension as P. This corresponds to the (k − 1)J + j’th column of D_t. A typical matrix in the sum at the right-hand side of (11) is the Kronecker product of the k’th row of P^ℓ with the j’th column of P^t−ℓ−1.

Equation (11) provides a simple algorithm for estimation of D_t using P̂, P̂², …, P̂^t−1, and (10) and the discussion below it suggests simple normal-based pointwise confidence intervals for the t-step transition probabilities. In the following sections we show how this result, together with simple manipulations of P̂, produces estimates and pointwise confidence intervals for different survival curves of interest. In Section 4.4 we show that the confidence intervals have good coverage. An alternative approach for estimating the variance of P̂^t and constructing confidence intervals via resampling methods is discussed in Section 3.3.

3.2 Time to a State

Simple manipulations of the transition matrix and its covariance estimate yield estimators of survival curves and their variances. The following three examples illustrate the utility and simplicity of the method.

3.2.1 Time to State J

An important clinical parameter is the distribution of time until the first visit to some state. In MS, particular interest lies in time to reaching EDSS of three since it may indicate the initiation of moderate disability.

Without lost of generality, we consider the distribution of time to first reaching state J. To do this, we replace the J’th row of P̂ with a vector with zeros everywhere except the J’th element which we set to one, i.e., we make J an absorbing state. If we denote this matrix by Q̂ and the distribution of time to first visit to J given initial state k by F_J (∙∣k), then we have

$${\widehat{F}}_J(t|k)={\widehat{q}}_{k,J}^t,$$

where ${\widehat{q}}_{k,j}^t$ is the (k, J)’th element of the t’th power of Q̂. The variance-covariance matrix of vec(Q̂) is required for estimation of pointwise confidence intervals for F̂_J(t∣k). This is obtained by replacing the entries of Σ corresponding to the J’th row of P̂ with zeros.

3.2.2 Time to Two Consecutive Visits at J

EDSS of three may indicate sustained progression, or it may represent a transient event caused by an attack. It thus may be of greater interest to estimate the time to an EDSS of three at two consecutive visits. Here we show how to adjust P̂ in order to generate survival curves for time to two consecutive visits at J.

Define P* to be P̂ with the (J, J) element set to zero and let a be a column vector with P̂_JJ as its J’th element and all its other elements 0. Defining

$$\widehat{\mathbf{Q}}=\left(\begin{array}{cc}{\mathbf{P}}^{\ast }& \mathbf{a}\\ {\mathbf{0}}_{1,J}& 1\end{array}\right),$$

where 0_{(r, c)} is a matrix of zeros with r rows and c columns, we have as before

$${\widehat{F}}_{JJ}(t|k)={\widehat{q}}_{k,J+1}^t,$$ (12)

where F_JJ (∙∣k) is the distribution of time to the first two consecutive visits to J starting at k. Note that F̂_JJ (1∣j) equals 0 for j < J. Calculation of the covariance matrix of vec(Q̂) based on Σ is similar to the previous example. The covariance matrix should be expanded to a (J +1)² ×(J +1)² matrix with zero rows and columns corresponding to the structured 0’s and 1’s elements.

3.2.3 Time to a Higher State

While an EDSS of three measures absolute progression, there is also interest in relative progression. This corresponds to calculating the first time to an increase of EDSS of at least one point. Thus, for a subject starting at state k, the first time to one of the states k + 1, k + 2, …, J, is of interest.

Define a vector a_k to be the sum of the rows of P̂ from the k + 1’th column onward, i.e., ${\mathbf{a}}_k(i)={\mathrm{\sum }}_{k^{\prime }=k+1}^J{\widehat{p}}_{i{k}^{\prime }}$ for i = 1, …, k. Define ${\mathbf{P}}_k^{\ast }$ to be the k × k upper left block of P̂, that is, the transition probabilities among the first k states, and let

$$\widehat{\mathbf{Q}}=\left(\begin{array}{cc}{\mathbf{P}}_k^{\ast }& {\mathbf{a}}_k\\ {\mathbf{0}}_{1,k}& 1\end{array}\right)$$

(we omit the subscript k from Q̂ for simplicity), so that we have

$${\widehat{F}}_{k+}(t)={\widehat{q}}_{k,k+1}^t,$$

where F_k+ is the distribution of time to a higher state given the initial state is k. Note that here we need a different matrix Q̂ for each initial state, and that F_J+ is undefined. In order to calculate the covariance matrix of vec(Q̂), we first define the (k + 1)² × J² matrix

$$\mathbf{B}=\left(\begin{array}{ccccc}{\mathbf{I}}_k& {\mathbf{0}}_{(k,J-k)}& {\mathbf{0}}_{(k,k)}& {\mathbf{0}}_{(k,J-k)}& \cdots \\ {\mathbf{0}}_{(1,k)}& {{\mathbf{1}}^{\prime }}_{J-k}& {\mathbf{0}}_{(1,k)}& {\mathbf{0}}_{(1,J-k)}& \cdots \\ {\mathbf{0}}_{(k,k)}& {\mathbf{0}}_{(k,J-k)}& {\mathbf{I}}_k& {\mathbf{0}}_{(k,J-k)}& \cdots \\ {\mathbf{0}}_{(1,k)}& {\mathbf{0}}_{1,J-k}& {\mathbf{0}}_{(1,k)}& {{\mathbf{1}}^{\prime }}_{J-k}& \cdots \\ ⋮& ⋮& ⋮& ⋮& ⋮\end{array}\right)$$

where the entries of the last k + 1’th rows are all zeros. B is constructed such that B × vec(P̂) + (0, 0, …, 0, 1)^T = vec(Q̂), and hence the covariance matrix of vec(Q̂) is BΣB^T.

Calculation of the marginal distribution of reaching a higher state (unconditional on the initial state) requires estimation of the initial state distribution. The empirical distribution based on the second term of (6) can be used or it can be obtained through modelling (for example, assuming stationarity). Although easily estimable, this marginal distribution seems less interesting than the conditional distributions described above.

3.3 Time Dependent Covariates

Our discussion on survival estimation has started from a transition matrix P̂ = P(z^′θ̂), and we have described estimation of survival curves that are suitable for fixed (baseline) covariates. However, it is usually of interest to incorporate into the model covariates that change over time. Classic examples are age and disease duration. In this section, we extend our method by allowing time-dependent covariates. This enables more flexibility in modelling but requires more effort in estimation and confidence interval calculation.

Denote by ${\mathbf{z}}_t^{\prime }$ the matrix of covariates at time t and assume that z_t includes only external covariates, that is, covariates that can be determined independently of the outcome process (EDSS). Estimates should be interpreted in conjunction with this covariate process, where a different survival curve is generated for each such process. For internal covariates, such as MRI metrics which cannot be determined independently of progression, one can still estimate the one-step transition matrix, but in order to generate survival curves, a joint model for covariates and outcome is required. This is beyond the scope of the current paper. A formal distinction between internal and external covariates is given by Kalbfleisch and Prentice (2002).

Given the covariate process (z₀, z₁, …, z_t−1) and the parameter estimate θ̂, the estimated probability of occupying a given state at time t is calculated from $\mathbf{P}({\mathbf{z}}_0^{\prime }\widehat{\theta })\times \mathbf{P}({\mathbf{z}}_1^{\prime }\widehat{\theta })\times \dots \times \mathbf{P}({\mathbf{z}}_{t-1}^{\prime }\widehat{\theta })$. If quantities such as those discussed in Section 3.2 are of interest, P̂ is replaced with the appropriate Q̂ in the product. The derivation of pointwise confidence intervals for the survival curves are comprised of two steps (see the discussion at the beginning of Section 3). The first step concerns estimation of the parameters θ, for which time-dependent covariates pose no difficulty. In the second step, the delta method is used to estimate the variance of the t’th transition probabilities. This second step is complicated in examples with time-dependent covariates. Thus, instead of analytically calculating the linear approximation of $\theta \mapsto \mathbf{P}({\mathbf{z}}_0^{\prime }\theta )\times \mathbf{P}({\mathbf{z}}_1^{\prime }\theta )\times \cdots \times \mathbf{P}({\mathbf{z}}_{t-1}^{\prime }\theta )$, a sampling based approximation is suggested. This simulation procedure takes the following steps:

1. Fit the model and calculate θ̂ and Σ̂_θ.

2. Generate B θ*’s from N(θ̂, Σ̂_θ), and denote them by ${\theta }_1^{\ast },\dots ,{\theta }_B^{\ast }$.

3. For each ${\theta }_b^{\ast }$, calculate the target parameter from $\mathbf{P}({\mathbf{z}}_0^{\prime }{\theta }_b^{\ast })\times \mathbf{P}({\mathbf{z}}_1^{\prime }{\theta }_b^{\ast })\times \cdots \times \mathbf{P}({\mathbf{z}}_{t-1}^{\prime }{\theta }_b^{\ast })$ or from $\mathbf{Q}({\mathbf{z}}_0^{\prime }{\theta }_b^{\ast })\times \mathbf{Q}({\mathbf{z}}_1^{\prime }{\theta }_b^{\ast })\times \cdots \times \mathbf{Q}({\mathbf{z}}_{t-1}^{\prime }{\theta }_b^{\ast })$ and denote it by $p_b^{\ast }$. For example, if the target parameter is the transition probability from k to J in t steps, $p_b^{\ast }$ is the (k, J) entry of $\mathbf{P}({\mathbf{z}}_0^{\prime }{\theta }_b^{\ast })\times \mathbf{P}({\mathbf{z}}_1^{\prime }{\theta }_b^{\ast })\times \cdots \times \mathbf{P}({\mathbf{z}}_{t-1}^{\prime }{\theta }_b^{\ast })$.

4. Calculate the confidence interval using the variance of $p_1^{\ast },\dots ,p_B^{\ast }$.

Step 4 can be replaced by calculating the confidence interval using the percentiles of $p_1^{\ast },\dots ,p_B^{\ast }$. This approach does not rely on the linear approximation of the delta method and in practice often gives better results. It, however, still relies on the asymptotic normality of θ̂. An alternative that does not rely on the normal assumption is to calculate bootstrap percentile confidence intervals. The simulation method for estimating confidence intervals is faster and easier to implement than bootstrap methods. The idea is due to Yosef Rinott who has used it in a complex simulation study (personal communication).

4 ILLUSTRATION - THE MS DATA

In this section, we apply the methods described in the previous sections to the MS data. The data consist of semi-annual measures of EDSS on 267 subjects aged≥18 years with a clinically isolated syndrome or the diagnosis of relapsing-remitting MS who were enrolled within the CLIMB study currently ongoing at the Partners Multiple Sclerosis Center in Boston, MA. All patients have data at baseline visit, but due to staggered entry to the study, the numbers of follow-up visits for each subject range from one to ten. Here we consider 1107 follow-up visits (or transitions) with frequencies per subject (from 1 to 10, respectively) of 37, 42, 39, 45, 19, 32, 29, 18, 5, 1. Among them, there are 53 missing visits for which information on EDSS before and after the missed visit is available. We excluded from the raw data two observations with two and three consecutive visits missing. Thus, the analysis is based on 1001 one-step transitions and 53 two-step transitions (Table 1). Since the subjects were selected to be at the beginning of their disease, only a few patients had high levels of EDSS. Therefore, we treat EDSS levels of three and higher as one category. We also combine EDSS levels of zero and one since the distinction between them is ambiguous.

Table 1.

Observed and row proportions of transitions of MS patients between EDSS scores. One-step for complete data and two-step for missing visits.

		EDSS≤1	EDSS=2	EDSS≥3
EDSS≤1	one-step frequency	568	68	11
	one-step proportion	.878	.105	.017
	two-step frequency	31	6	0
EDSS=2	one-step frequency	76	126	27
	one-step proportion	.332	.550	.118
	two-step frequency	5	4	1
EDSS≥3	one-step frequency	8	32	85
	one-step proportion	.064	.256	.680
	two-step frequency	0	1	5

Available covariates are brain parenchymal fraction (BPF) and T2 lesion volume (T2LV) which measure tissue loss and lesion accrual in the brain, respectively, and age, sex and disease duration (from first symptoms). The brain MRI metrics have acquired a central role in the understanding of MS disease evolution, pathogenesis of symptoms, and prediction of clinical outcomes. They were measured at enrollment and yearly thereafter.

We demonstrate our method using the time to two consecutive visits with EDSS level of three or higher as the outcome (Section 3.2.2). At first, we treat the population as homogeneous (i.e., without covariates) and produce crude survival curves and pointwise confidence intervals. These are similar to the Kaplan-Meier curve and its pointwise confidence intervals that are commonly used as descriptive statistics for survival data. We then calculate curves for different subgroups defined by baseline BPF, as a graphical tool for a simple comparison. Finally, we estimate a regression model based on (3) using age and disease duration as time-dependent covariates, and demonstrate calculation of the survival curve and pointwise confidence intervals for specific sets of covariates. For illustration, we calculate and depict the survival curves up to ten years. This relies heavily on the parametric assumptions of our model and the utility of such long term prediction needs more investigation.

The analysis is based on the missing at random (MAR) assumption, and estimation was conducted by direct maximization of the likelihood. Thus, the contribution to the likelihood of an observation with a missing visit is based on the two-step transition matrix $\mathbf{P}({\mathbf{z}}_{\mathbf{t}-\mathbf{2}}^{\prime }\theta )\mathbf{P}({\mathbf{z}}_{\mathbf{t}-\mathbf{1}}^{\prime }\theta )$. Discussion on missing values and other aspects of the analysis is given in Section 5

4.1 Crude Estimation of Transition Probabilities

We first calculated the survival curve and its pointwise confidence intervals using model (3) with no covariates. The estimated parameters are

$$\widehat{\alpha }=({\widehat{\alpha }}_{11},{\widehat{\alpha }}_{12},{\widehat{\alpha }}_{21},{\widehat{\alpha }}_{22},{\widehat{\alpha }}_{31},{\widehat{\alpha }}_{32})=(1.99,4.15,-0.68,2.05,-2.76,-0.83),$$ (13)

and by using (9) we obtain our working transition matrix to time to two consecutive visits in state 3 (see Section 3.2.2)

$$\widehat{\mathbf{Q}}=\left(\begin{array}{cccc}.880& .104& .016& .000\\ .336& .550& .114& .000\\ .059& .245& .000& .696\\ .000& .000& .000& 1.00\end{array}\right).$$ (14)

If no missing data were present, the (asymptotic) variance-covariance matrices of α̂ and vec(Q̂) would be block diagonal with the k’th block of Cov[vec(Q̂)] given by $N_k^{-1}[\mathrm{diag}({\widehat{Q}}_{(k\cdot )})-{\widehat{Q}}_{(k\cdot )}{\widehat{Q}}_{(k\cdot )}^{\prime }]$, where N_k is the number of transitions from state k and Q̂_(k∙) is the k’th row of Q̂. Due to the missing visits, however, the components of α̂ are all correlated and the estimated covariance matrix is

$${\widehat{\mathbf{\sum }}}_{\alpha }=\mathrm{Cov}(\widehat{\alpha })={100}^{-1}\left(\begin{array}{cccccc}1.346& 1.189& -0.022& -0.012& -0.012& -0.002\\ 1.189& 9.237& -0.009& -0.011& -0.044& -0.047\\ -0.022& -0.009& 1.863& 0.694& -0.017& -0.012\\ -0.012& -0.011& 0.694& 4.060& -0.034& -0.070\\ -0.012& -0.044& -0.017& -0.034& 13.29& 2.591\\ -0.002& -0.047& -0.012& -0.070& 2.591& 3.531\end{array}\right).$$ (15)

To approximate the variance of vec(Q̂), first the variance of vec(P̂) is estimated as described by (21) in the appendix, and then the matrix is expanded and rearranged as described in Section 3.2.2. Based on the estimate of Q and its variance, the (1 − α) level confidence interval for the probability of having EDSS level of three or higher in two consecutive visits before time t, for a subject who had EDSS level of one at baseline is

$${\widehat{q}}_{14}^t\pm z_{\alpha /2}\sqrt{{({\mathbf{D}}_t[\mathrm{V}\widehat{\mathrm{a}}\mathrm{r}\{\mathrm{vec(}\widehat{\mathbf{Q}})\}]{\mathbf{D}}_t^T)}_{(4,4)}},$$ (16)

where z_α is the α quantile of the standard normal distribution and the term under the square-root is the fourth entry in the diagonal of the matrix in parenthesis, and corresponds to the variance of ${\widehat{q}}_{14}^t$ (in general, to calculate the variance corresponding to EDSS of j at baseline, the j(J +1) element of the diagonal of the matrix in the square-root of (16) should be used).

We found that the confidence interval

$$exp[exp\{\pm z_{\alpha /2}\frac{\sqrt{\mathrm{V}\widehat{\mathrm{a}}\mathrm{r}({\widehat{q}}_{14}^t)}}{{\widehat{q}}_{14}^{t}log({\widehat{q}}_{14}^t)}\}log({\widehat{q}}_{14}^t)]$$ (17)

usually performs better than (16). This confidence interval uses the log(-log) transform and it is commonly employed in survival analysis (e.g., Kalbfleisch and Prentice, 2002).

For comparison, we calculated bootstrap confidence intervals and simulation based confidence intervals as described in Section (3.3). The bootstrap confidence intervals were calculated by resampling transitions from the estimated transition matrix, preserving the data structure, i.e., the number of transitions for each person, his/her baseline state and the missing visits. Thus, a person who had baseline EDSS of 1, had four visits, and missed visit 2 in the data set, also had this structure in the bootstrap samples. We generated 5000 bootstrap samples b = 1, …, 5000 where for each b, we estimated the transition matrix Q̂_b and calculated the survival curve using the appropriate entry of ${\widehat{\mathrm{Q}}}_b^t$. The variance of the bootstrap estimates was used to construct the confidence intervals. The confidence intervals of the simulation method were also based on 5000 simulations, where in each simulation we generated α_b from the normal distribution N(α̂, Σ̂_α) (see (13) and (15)).

The results of the analysis are shown in Figure 2. The similarity between the different confidence intervals is remarkable. The estimated probabilities of experiencing sustained EDSS of three or higher before 5 years (10 visits) are 0.18 and 0.29 given baseline EDSS levels of one and two, respectively. These relatively low probabilities reflect the low progression rate of MS. The estimated probabilities of EDSS of three or higher before 5 years (not shown, see Section 3.2.1) are larger (0.28 and 0.41). This reflects the nature of MS as a relapsing remitting disease and the possibility of a recovery after a relapse.

Figure 2.

Probability of reaching EDSS level of three or higher in two consecutive visits. Left - starting at EDSS level of one, right- starting at EDSS level of two. The pointwise confidence intervals based on the delta method (solid lines), simulation method (circles) and parametric bootstrap (pluses).

4.2 Comparing Groups of Patients

Formal comparison of patient groups is done by testing equality of group-specific transition matrices. As an example, we defined sub-groups according to BPF at first visit. Previous studies and preliminary analysis showed that BPF is highly associated with the EDSS level. We divided the transitions according to quartiles of baseline BPF and for each quartile we calculated the transition matrix. Using the likelihood-ratio test, we found a significant difference between the transition matrices (P-value<0.001). Specifically, the lower quartile group appears different from the other groups, suggesting a possible classification based on small BPF (smaller BPF indicate more tissue loss in the brain). The result of such a test is not as easily interpreted as visual tools. Computing and drawing the survival curves of different groups on the same axis system is a useful graphical analysis, similar to stratified Kaplan-Meier plots.

Figure 3 depicts the estimated distribution functions of time to first sustained EDSS of three or higher accompanied by 95% pointwise confidence intervals calculated by the delta method. Since the group sizes are relatively small, particulary in the low BPF stratum, the confidence intervals are wide. However, it is still apparent that patients with low BPF are approximately 1.5 times as likely to have deteriorated as compared to others at each time point.

Figure 3.

Probability of reaching EDSS of three or higher in two consecutive visits by BPF group. Left - starting at EDSS of one, right - starting at EDSS of two. ○ ○ ○ probability for the low BPF stratum, ● ● ● probability for the normal-high BPF stratum, ⋯ 95% pointwise confidence intervals for the low BPF stratum, – – – 95% pointwise confidence intervals for the normal-high BPF stratum.

4.3 Regression Models

Next we fit the regression model (3) to the MS data using BPF, T2LV, sex, age and disease duration as covariates. All covariates except sex are time dependent. While age and disease duration are external covariates, BPF and T2LV are undoubtedly internal ones. However, these variables change slowly in time and are highly correlated across different time points. The Pearson correlations of BPF at baseline with BPF after one, two, and three years are 0.98, 0.96 and 0.9, respectively. These correlations for T2LV are 0.91, 0.94, and 0.97. We thus, treated these variables as fixed biological markers of disease severity, at least for purposes of estimating short term survival, and used only the baseline values in the model. Only 250 of the 267 individuals (1025 transitions) could be used due to missing covariate values. Table 2 contains the estimated transition matrix of the average person and the odds ratios (ORs) of the covariates (the estimated parameters are roughly ORs minus one). Covariates were grouped according to quartiles, with the quartile of high risk serving as reference. According to (3), an odds ratio smaller than one (a negative coefficient) indicates a tendency to increase the EDSS and the corresponding covariate should be interpreted as a risk factor. Using two standard errors as our threshold (i.e., significant level of 5%), none of the covariates’ coefficients is significant. However, the coefficient of the lowest quartile of BPF, and the coefficients corresponding to lesion volume are almost significant, reinforcing the known relation between tissue loss and lesions in the brain and disability.

Table 2.

Results of model (3), covariates were grouped according to their quartiles. Left - odds ratios (OR) and 95% confidence intervals (CI). Right - estimated transition matrix for the ‘average person’.

Variable	OR	95% CI
sex=female	1.26	(0.84,1.90)
32<age≤38	1.05	(0.59,1.86)
38<age≤46	1.08	(0.59,1.95)
46<age	0.67	(0.37,1.19)
3 <MS duration≤6	0.74	(0.47,1.15)
6 <MS duration≤10	0.68	(0.42,1.11)
10 <MS duration	0.66	(0.40,1.08)
BPF≤.860	0.61	(0.35,1.04)
0.860<BPF≤0.884	0.92	(0.53,1.58)
0.884<BPF≤0.912	0.96	(0.57,1.64)
1.81<T2LV≤2.95	0.61	(0.37,1.00)
2.95<T2LV≤5.08	0.62	(0.38,1.02)
5.08<T2LV	0.62	(0.38,1.04)
	EDSS≤1	EDSS=2	EDSS≥3
EDSS≤1	.861	.119	.019
EDSS=2	.332	.568	.099
EDSS≥3	.066	.270	.664
transitions matrix for the average person:
sex=female
age=39 Yrs
MS duration=5 Yrs
BPF=0.880
T2LV=4.23

Figure 4 compares the survival curve of a subject with BPF in the highest quartile to that of a subject with BPF in the lowest one. The values of the other covariates at enrollment taken to be female, age 35, MS duration of one year, and T2LV in the second quartile. The confidence intervals were calculated by the simulation method described in Section 3.3 with B = 5000 and by using percentiles instead of the variance in step 4. The conclusions are quit similar to that obtained from Figure 3, where tissue loss in the brain predicts faster progression.

Figure 4.

Probability of reaching EDSS of three or higher in two consecutive visits based on model (3), comparing lowest and highest BPF quartile for a female aged 35 and MS duration of one year at enrollment and T2LV of 2. Left - starting at EDSS of one, right - starting at EDSS of two. ○ ○ ○ probability for the lowest BPF quartile, ● ● ● probability for highest BPF quartile, ⋯ 95% pointwise confidence interval for the lowest BPF quartile, – – – 95% pointwise confidence interval for the highest BPF quartile.

4.4 Accuracy of the Confidence Intervals

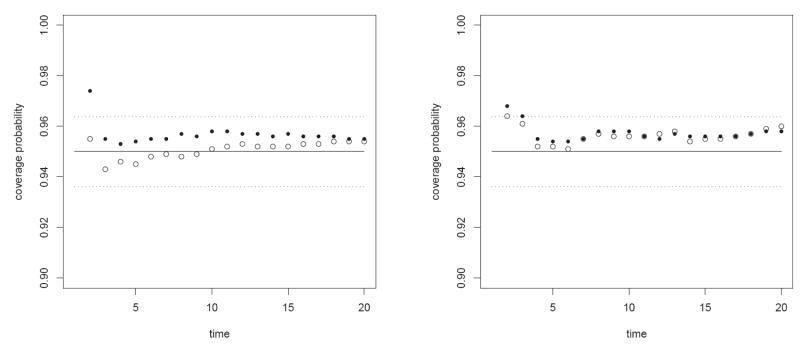
We conducted a simulation study to assess the correctness of the declared coverage probability of the suggested confidence intervals in our data. We simulated data sets with the same structure as our original data according to the first order model with parameters equal to those obtained in Section 4.1. In particular, we simply used the first 1000 bootstrap data sets that we simulated for the parametric bootstrap of section 4.1. For each sample we fitted the first order model, derived the pointwise confidence intervals of the probability of time to two consecutive visits to state 3, and counted for t = 1, …, 20 the number of confidence intervals that covered the true parameter (i.e., probability at step t).

Figure 5 presents the proportion of confidence intervals that covered the true parameter starting at states one and two. The figure compares the performance of the confidence interval (17) with $\mathrm{Var}({\widehat{q}}_{14}^t)$ estimated by the delta method and by the simulation method described in Section 3. Also drawn are the target coverage probability of 0.95 (solid line) and a band that represents two standard deviations of a binomial experiment with n = 1000 and p = 0.95 (dotted lines). The declared coverage seems very accurate. Similar calculation for the confidence interval (16) reveals a certain anti-conservative coverage at the first two time points. The simulation based method is slightly more conservative than the analytical delta method.

Figure 5.

Coverage probabilities of time to first two consecutive visits in state 3 starting from state 1 (left) and two (right). ○ ○ ○ - confidence intervals based on the analytical delta method, ● ● ● - confidence intervals based on the simulation method.

Calculation of confidence intervals by reproducing the parameters from their approximate normal distribution, as described in Section 3.3, affords substantial computational efficiency. The use of 5000 simulated samples in the analysis of Section 4.3 took less than 100 seconds using R 1.9.1 on a PC with 1200 MHz Pentium processor. This was considerably faster than the bootstrap calculation. As this method relies on the normal approximation to the distribution of the parameters’ estimator, its performance in small samples is of interest. In a small simulation study, we compared this method to a parametric bootstrap and found that the confidence intervals were very similar (results are not shown). We also checked the performance when several entries of the transition matrix were small and found anti-conservative coverage at the early time points. Further investigation of the performance of different normal based and bootstrap based confidence intervals for θ̂ under different scenarios is needed and planned.

4.5 Model Selection and Goodness-of-Fit

A priori, model (3) was chosen as a compromise between parsimony and biological interpretability. In consideration of goodness-of-fit, first note that Model (5) ⊂ Model (4) ⊂ Model (3) ⊂ Model (2), and these models have 16, 17, 19 and 45 parameters, respectively. We did not consider model (5) in our analysis, because it is not clear what score to use for the ordinal response. It is obvious that progression from EDSS of 2 to EDSS of 3 is a larger step than progression from EDSS of 1 to EDSS of 2, but this is difficult to quantify and does not seem worth the reduction of one parameter that this additional assumption affords. We obtained a P-value of 0.03 when comparing model (3) and (4) and a P-value of 0.12 when comparing models (3) and (2) (all the P-values in this section correspond to likelihood ratio tests). Thus, our choice of model (3) seems reasonable.

The more interesting question concerns the Markov assumption about the dependency among transitions within each subject (conditional on the covariates). The common alternatives for the one-step Markov assumption are a Markov model of higher order and an inhomogeneous Markov process. These can be tested by embedding the model in a larger model and using likelihood ratio or chi-square tests (i.e., Anderson and Goodman, 1957, Fokianos and Kedem, 2003).

We tested our Markov model of order one by comparing it to a second order model. We used a straightforward modification of model (3) by defining each state as the EDSS at two consecutive visits. Several complications arose that are typical to such an extension. First, the number of parameters increased from m + J(J − 1) to m + J²(J − 1). In our case (m = 13, J = 3) and the number of parameters increased from 19 to 31. Second, the number of available transitions decreased because the initial state comprises now the first two EDSS values. Thus, we had one less transition for each subject which corresponded to approximately a 25% reduction in transition data. Third, while all of our subjects had information on the EDSS at baseline, several had missing data on their six month visit. Thus, the likelihood (7) cannot be used since the factorization shown in (6) does not hold, and in order to maximize the likelihood the distribution of the initial state, which is a nuisance parameter, must be estimated.

Because of the reduction in the number of transitions and the increase in the number of parameters described above, the transition probabilities from state (1,3) were assumed equal to those from state (2,3), and similarly the transition probabilities from state (2,1) and (3,1) were assumed equal. We estimated jointly the transition probabilities and the distribution of the initial state (first two EDSS values); the latter was estimated without reference to covariates. The likelihood ratio test yielded a P-value of < 0.001 favoring the second order model.

Although the sample size is too small for valid inference based on the second order model, it is still of interest to look at its crude results. Figure 6 presents the crude progression curves for the different initial states. Here time to hitting state (3,3) is the parameter of interest and calculations are performed as described in Section 3.2.1. As expected, the curves are ordered by the current EDSS and then by the previous EDSS.

Figure 6.

Crude probabilities of reaching EDSS of three or higher in two consecutive visits based on the second order model. Different lines for different baseline states.

To test time homogeneity, one can replace α_kj in (3) with α_tkj, i.e., consider a baseline transition matrix that is time dependent, and test α_tkj = α_0kj for all t. This approach substantially increases the number of parameters and hence is problematic. An alternative that is often used to test the proportional hazards assumption in survival analysis, is to introduce a time related covariate to the model, say u(t), and to test its influence. Thus, one replaces (3) by

$${\eta }_{tj}={\alpha }_{kj}+{\mathbf{x}}_{t-1}^{\prime }\beta +u(t)\gamma ,$$ (18)

and tests H₀ : γ = 0. Of course, combinations of the two approaches or interaction of time and covariates can also be used. For example, one can define different baseline transition matrices in the beginning and end of the process and test for their equity, i.e.,

$${\eta }_{tj}={\alpha }_{0kj}I\{t\le t_0\}+{\alpha }_{1kj}I\{t>t_0\}+x_{t-1}^{\prime }\beta ,$$ (19)

where t₀ is a user defined cutoff point, and H₀ : α_0kj = α_1kj.

We tested time homogeneity of our model using (18) with u(t) = t and u(t) = log(t), and (19) with t₀ = 2 and obtained P-values of 0.24, 0.22 and 0.28, respectively. Since our model contains age and disease duration as time dependent variables, our interpretation of the test is that there is no evidence of time inhomogeneity of the process that is not captured by age and disease duration.

Finally, we fit a non-Markov model of the form of (8) by including dichotomous time dependent covariates indicating whether the patient ever reached EDSS greater than or equal to two and three:

$${\eta }_{tj}^{\ast }={\alpha }_{kj}+x_{t-1}^{\prime }\beta +I\{\max (y_0,\dots ,y_{t-1})\ge 2\}{\gamma }_1+I\{\max (y_0,\dots ,y_{t-1})\ge 3\}{\gamma }_2,$$

where ${\eta }_{tj}^{\ast }=P(Y_t=j|{\mathrm{x}}_{t-1},Y_{t-1}=k,{ℱ}_{t-2})$. The likelihood ratio test revealed a significant effect of these variables (P-value<0.001) with estimated coefficients γ̂₁ = −0.50 and γ̂₂ = −1.37. The coefficients of the other covariates were similar to those of Table 2, but the baseline probabilities differed. The motivation of this model is to allow for a different pattern of progression for a benign subpopulation of MS patients as compared to typical RR MS patients. It also shows that among RR MS patients disability tends to accumulate, since patients who have experienced progression in EDSS (earlier in the disease) and then recovered have a higher risk of progression as compared to those who have not.

5 DISCUSSION

MS is a heterogeneous chronic disease whose nature is not completely understood. One of the difficulties in MS research is the necessity for long-term studies due to the slow progression rate of the disease. FDA approved treatments are now in a wide use and the CLIMB study, ongoing at the Partners MS Center in Boston, is one of the first large scale studies that aims to understand the natural history of treated MS. The current paper suggests a new method of combining MRI metrics and clinical covariates for estimation of six months progression probabilities. The approach is applied to data from a short term follow-up of a moderate number of early stage patients. The limited amount of data necessitates the use of models that are likely only rough approximations of nature. Evidently, a second-order process, which possibly relaxes the proportional-odds assumption of several covariates, and includes covariates which indicate a benign disease subtype describes the data better than model (3). However, for interpretation of covariate effects, we found that both first and second order Markov models give the same results. More complicated models can utilize our method as their starting point with only slight modifications. When more data are available, such models can be fitted and evaluated with greater accuracy. It will be of interest to check whether inclusion of age and disease duration truly captures the time inhomogeneity of the EDSS process, or this finding is a consequence of the short follow-up period. It is also not clear whether a similar model provides a good approximation to the EDSS process at the higher end of the scale and in more progressive stages of MS. Confavreux, Vukusic, Moreau and Adeleine (2000) show that most MS patients appear to progress at the same rate beyond EDSS of 4 and the disease becomes more of a degenerative process less influenced by any of the previous covariates. We plan to assess these questions using the additional transitions that will be available in the near future.

Eighty percent of our patients were treated at enrollment with one of the therapies for MS. As the decision to start or change treatment is based on the progression of the disease, it is problematic to include treatment as a covariate in a model for progression. A simple comparison of untreated and treated patients revealed that the former are older (42.6 vs. 38.5 mean age) with a longer disease duration (7.3 vs. 4.9 mean disease duration) and have a lower EDSS level at baseline. The CLIMB study and our analysis aim to describe the natural history of MS in the current era of available treatments. It is conducted under the assumption that every patient’s disease is treated (or not treated) optimally (Pittock et.al., 2006). Currently, the database does not contain information on variables that determine treatment assignment. However, such variables will be collected in the future and a matching on a propensity score developed from such additional data will enable us to incorporate treatment into the model (D’Agostino, 1998).

At enrollment, patients were asked to come to the MS center once every six months, but the original data contain missing visits and dropouts. Thirty one patients dropped out from the study. The most common reason for dropping out is leaving the MS center (11 patients) because of either moving out of state or switching provider. Other reasons are time commitment (4 patients), unwillingness to give blood (2 patients), death during the study (1 patient, unrelated to MS) and feeling healthy (1 patient). Other patients did not specify a reason or did not respond to phone calls. Since the data were limited to RR MS and the patients are in the beginning of their disease and have moderate disability, it is reasonable to assume that missing occurred at random. The majority of MS patients having EDSS in the range 1-3 maintain their normal lifestyle and the reasons for dropping out reflect that. However, we expect that missing values for patients having EDSS in the range 6-9 will not be at random. Such patients have difficulties with travel that may cause them to miss a visit or to drop out from the study. Understanding the reasons for intermittent missing and dropouts and incorporating them into the model will be needed when fitting models for the MS population in later, progressive stages.

Even if the EDSS of each patient follows a Markov process, the model assumptions are not satisfied when subject-specific unmeasured variables determine the transition matrix. In such cases, it is natural to fit a random effects model (Diggle et.al.,1994), in which a random latent variable is related to each subject. Random effects models for two state Markov models have been considered by several authors (see Albert and Follmann 2003, Aitkin and Alfó, 2003 and references therein). Albert and Waclawiw (1998) estimate the first passage time of a Markov process with random effects, but this parameter is estimated without reference to subject specific history. A method for estimating probability curves similar to that presented here, but based on a random effects model is currently under study. Under this approach, a subject specific curve may be fitted using his history, i.e., the observed transitions help to predict the value of the latent random variable which in turn is used to predict future responses. Such models are much more computationally demanding and are naturally studied and estimated using the Bayesian paradigm.

The EDSS process is not a discrete time process but rather a continuous one that is observed at approximately equally spaced time points. Kalbfleisch and Lawless (1985) studied such data and derived the maximum likelihood estimator of the intensity matrix. They illustrated the difficulties in obtaining the intensity matrix given an estimate of the discrete time probability matrix, and recommended to estimate directly the intensity matrix. It is of interest to define events similar to those presented in Section 3.2 in a continuous time space and to develop methods for inference.

In our analysis, the state space has three values, but the EDSS scale ranges from 0 to 9. When the ordinal variables takes one of many values, the method presented here becomes more complicated with respect to both computation and interpretation. An attractive alternative is to assign scores for the ordinal variable and to fit to that score a model for continuous outcomes (same reasoning motivated model (5). Transitional models for continuous outcomes are well studied (e.g., Diggle, et.al., 1994). However, we are not aware of any attempt to use such models to estimate time-to-events of the type discussed in Section 3.2.

Finally, we remark that although we present survival estimates and pointwise confidence intervals for proportional-odds models fit to ordinal data, our method is more general and can be easily applied to many other types of longitudinal categorical data under a wide variety of models.

A Appendix

This appendix provides technical details for calculation of the variance of vec(P(z^′θ̂)) under the model (9). First consider calculation of the derivative of the map $\theta \mapsto \mathrm{vec}\left[\mathrm{P}\right({\mathrm{z}}^{\prime }\theta \mathrm{)]}$ defined by (9). Let α = (α_kj) (k = 1, …, J; j = 1, …, J − 1), θ = (α, β) and let F(j, k, x; θ) = exp(α_jk+xβ)/[1 + exp(α_jk + xβ)] for j = 1, …, J − 1, k = 1, …, J. Let V (θ) = diag(F(j, k, x; θ)[1 − F(j, k, x; θ)]) be a J(J − 1) × J(J − 1) matrix containing the binomial variances in its diagonal (in the alphabetical order of jk). Let A be a J × (J − 1) matrix with (i, i) elements equal to 1, (i, i − 1) elements equal -1 and all other entries 0. For example, for J = 3

$$A=\left(\begin{array}{c}1\\ -1\\ 0\end{array}\begin{array}{c}0\\ 1\\ -1\end{array}\right).$$

Let B = I_J ⊗ A, where ⊗ denotes the Kronecker product, and denote by 1_a the vector of ones of length a, then

$$\nabla (\theta )=\frac{\partial }{\partial \theta }\mathrm{vec}(\mathbf{P}({\mathbf{z}}^{\prime }\theta ))=\left(BV(\theta ),(BV(\theta )1_{J(J-1)})\otimes \mathbf{x}\right).$$ (20)

The variance is estimated by

$$\mathrm{V}\widehat{\mathrm{a}}\mathrm{r}[\mathrm{vec}(\mathbf{P}({\mathbf{z}}^{\prime }\widehat{\theta }))]=N^{-1}\nabla (\widehat{\theta }){\widehat{\sum }}_{\theta }\nabla (\widehat{\theta })\text{'}.$$ (21)