Time-dependent mechanical characterization of poly(2-hydroxyethyl methacrylate) hydrogels using nanoindentation and unconfined compression

Abstract

Hydrogels pose unique challenges to nanoindentation including sample preparation, control of experimental parameters, and limitations imposed by mechanical testing instruments and data analysis originally intended for harder materials. The artifacts that occur during nanoindentation of hydrated samples have been described, but the material properties obtained from hydrated nanoindentation have not yet been related to the material properties obtained from macroscale testing. To evaluate the best method for correlating results from microscale and macroscale tests of soft materials, nanoindentation and unconfined compression stress-relaxation tests were performed on poly-2-hydroxyethyl methacrylate (pHEMA) hydrogels with a range of cross-linker concentrations. The nanoindentation data were analyzed with the Oliver–Pharr elastic model and the Maxwell–Wiechert (j = 2) viscoelastic model. The unconfined compression data were analyzed with the Maxwell–Wiechert model. This viscoelastic model provided an excellent fit for the stress-relaxation curves from both tests. The time constants from nanoindentation and unconfined compression were significantly different, and we propose that these differences are due to differences in equilibration time between the microscale and macroscale experiments and in sample geometry. The Maxwell–Wiechert equilibrium modulus provided the best agreement between nanoindentation and unconfined compression. Also, both nanoindentation analyses showed an increase in modulus with each increasing cross-linker concentration, validating that nanoindentation can discriminate between similar, low-modulus, hydrated samples.

I. INTRODUCTION

Many factors contribute to the difficulty of measuring the mechanical properties of biomaterials on the scale of cellular interactions.¹ As with all polymers, the mechanical properties of biomaterials depend on loading rate and temperature. In addition, materials incorporating biological monomers such as sugars or proteins may be too expensive to produce in the large amounts needed for conventional testing. Also, as in the cases of bioMEMs (microelectromechanical systems with biological or chemical applications) and drug delivery devices, the structures fabricated from these materials are themselves small in scale. Small scale is also an issue when the local mechanical properties of heterogeneous tissues are sought. Nanoindentation provides an excellent method for probing mechanical properties at a biological scale.

Since nanoindentation may be the only method available to characterize the material properties of a new biomaterial, it is important that the nanoindentation material properties can be related to the properties from macroscale experiments. This correlation is especially important since it has been shown that small changes in the mechanical stiffness of a substrate can affect cell phenotype. For example, myotube formation in myoblasts¹ and the differentiation of mesenchymal stem cells are affected by substrate stiffness.² Further, vascular smooth muscle cells exhibit durotaxis when cultured on a hydrogel with a gradient of stiffnesses.³ With polymer-based microdevices, nanoindentation techniques are particularly well suited for determining the mechanical properties of materials that may vary on the microscale and nanoscale.^4,5 Specifically, we propose to use pHEMA as a calibration material for nanoindentation experiments performed on tissues. To show that pHEMA gels of varying cross-link density are suitable as standard materials, we have conducted experiments on the microscale and macroscale using various fitting methodologies. In this paper we discuss experimental difficulties and open questions about the best modeling practices to compare nanoindentation to macroscale tests.⁵

A. Current challenges with nanoindentation

There are several unique challenges associated with nanoindentation of hydrated, compliant materials. Major sources of uncertainty include evaluating the appropriateness of viscoelastic models, defining suitable calibration materials, and eliminating sources of experimental error in the measurements. Each of these issues is addressed here. Material viscoelasticity can be addressed by modeling the time-dependent mechanical behavior rather than by assuming a purely linear, elastic response. Several groups have successfully analyzed nanoindentation experiments using viscoelastic models. Oyen⁶ examined nanoindentation creep experiments in polymers following ramp loading. Cheng et al. derived a solution for standard linear solid materials indented with both a flatpunch⁷ and spherical tip⁸ geometry. Fujisawa and Swain. studied the viscoelasticity of poly(methyl methacrylate) (PMMA) by quantifying the strain dependence of the elastic modulus from nanoindentation.⁹

With soft, hydrated samples, adhesion can become a significant factor. In Gupta et al., adhesion was shown to have a significant effect on the elastic modulus of polydimethylsiloxane (PDMS) at different peak loads.¹⁰ When the adhesion was taken into consideration, the scatter in elastic modulus was greatly reduced. In Carillo et al., the work due to adhesion was shown to be smaller when materials are hydrated and better agreement was seen between aqueous nanoindentation and unconfined compression.^11,12

To accurately use nanoindentation to quantify mechanical properties, it is essential to correctly calculate a tip-area function¹³ and determine of the point of initial contact.^13,14 With soft materials, it is especially important to use a calibration material that has a similar compliance to define the tip-area function¹⁵ over the full displacement range that will be used in the tests. In addition, determining the point of contact for soft materials may also require modifications to the standard testing protocols used for stiff materials.^5,16 Nanoindentation was initially used to study stiff materials, such as metals and ceramics.¹⁷ When using the TriboIndenter (Hysitron, Inc, Minneapolis, MN) microscope to locate an indent position, the instrument moves the tip to the sample surface and applies a preload force for preset time periods to allow the piezo scanner thermal drift to settle and to measure the electronic drift prior to the start of the experiment. While these steps reduce error for indents in harder materials, the minimum preload force of 0.1 µN is large enough to cause significant creep into hydrogels. This causes indents to begin at a considerable depth into the material, as much as several microns.

Polymeric hydrogels are particularly important to study in hydrated state because the effect of swelling on the mechanical properties is so significant. By adjusting the percentage of ethanol in the storage solution for bone samples, Bembey et al. showed that the mechanical properties of the bone changed with the level of hydration.¹⁸ Hydration history can also affect the mechanical properties of hydrogels as shown in Thomas et al.¹⁹

Others have addressed these problems in a variety of ways. Dynamic nanoindentation has also been used to describe time-dependent mechanical properties of polymers. White et al. obtained good agreement for the storage and loss modulus from dynamic nanoindentation and rheometry for epoxy, PDMS, and PMMA.²⁰ Dynamic nanoindentation was used to distinguish small differences in the storage moduli of eight engineering polymers with different material densities in Odegard et al.²¹ In Bouaita et al. several polyolefins were tested using dynamic stiffness measurement method where an alternating current (ac) signal is applied on top of the direct current (dc) actuation of a traditional nanoindentation test.²² An alternative approach to spring-dashpot models is to characterize two independent material properties using different testing methods. In Huang and Lu, this approach was used to characterize polymers indented with both Berkovich and spherical tips to calculate the bulk and shear relaxation moduli.²³ Here we do not consider dynamic methods.

B. Research objectives

We examined how nanoindentation can be used to discriminate between compliant and hydrated samples of pHEMA hydrogels with different cross-linker concentrations. In addition, we determined the best model to describe the time-dependent behavior of these hydrogels and the most appropriate method to compare microscale and macroscale material properties. The difficulties of testing polymeric and hydrated materials with nanoindentation often result in errors that are larger than the actual test result. This can lead to indistinguishable modulus values from nanoindentation for similar materials. We chose to examine four pHEMA hydrogels with a narrow range of cross-linker concentrations to ensure that the nanoindentation methods used were able to discriminate between similar materials. The pHEMA hydrogels studied here are viscoelastic and thus provided an excellent way to evaluate which viscoelastic model best described the stress relaxation of pHEMA in both nanoindentation and unconfined compression. To apply nanoindentation results to materials selection, the relationship between the mechanical properties from nanoindentation and a conventional macroscale test, such as unconfined compression, must be understood.

II. THEORY

A. Spherical tip solution

Nanoindentation of soft materials is optimized with conospherical tips that minimize fracture or plastic deformation of the sample.²⁴ Several viscoelastic models have been applied to nanoindentation data with spherical indenter tips. Cheng et al.⁸ outline in detail the solution for nanoindentation with a spherical indenter on a standard linear solid material. Here this solution is expanded to include the more generalized Maxwell–Wiechert model. For a spherical indenter tip, the load–displacement relationship for a Hertzian elastic solid is⁸:

$$P=\frac{8G\sqrt{R{\delta }^3(t)}}{3(1-\nu )},$$ (1)

where G is the shear modulus, R is the indenter radius, ν is the Poisson’s ratio, and δ(t) is the displacement as a function of time. For the generalized Maxwell–Wiechert viscoelastic model, this equation can be rewritten in terms of a time-dependent relaxation modulus function, G_rel(t), for the stress-relaxation response to an instantaneous ramp displacement, δ₀.

$$P(t)=\frac{4\sqrt{R{\delta }_0^3}}{3}{G}_{\text{rel}}(t).$$ (2)

B. Maxwell–Wiechert model

In Bembey et al.¹⁸ and Oyen,⁶ nanoindentation creep experiments are modeled with a generalized viscoelastic model. Here, stress-relaxation data was fit using a five-parameter (j = 2) Maxwell–Wiechert model.²⁵ The generalized Maxwell–Wiechert mechanical model is shown in Fig. 1. The standard linear solid (SLS) model is equivalent to the Maxwell–Wiechert model in which j = 1. Although integral models with an infinite number of elements can provide the best mathematical fit to stress-relaxation behavior, we chose to use the smallest number of spring-dashpot elements that fit the data well. With a finite number of material parameters, the relaxation time constants may be associated with particular phenomena, something that is more difficult when using integral models.

FIG. 1.

Maxwell–Wiechert spring-dashpot model.

For this analysis, the number of Maxwell elements is set equal to 2 so that the model consists of three springs and two dashpots. In the Maxwell–Wiechert model, each of the three arms shares the applied stress such that:

$$\sigma ={\sigma }_e+{\displaystyle \sum _j{\sigma }_j}.$$ (3)

This leads to the following uniaxial relationship between stress and strain for the stress-relaxation case, where ∈₀ represents the constant strain.²⁵

$$\sigma (t)=\left\{k_e+{\displaystyle \sum _j{k}_j}\text{exp}\left(\frac{-t}{{\tau }_j}\right)\right\}{\in }_0.$$ (4)

From Eq. (3), the relaxation modulus can be derived by dividing both sides by the constant strain. By substituting Eq. (5), as shown below, into Eq. (1), we can model the behavior of soft materials exposed to a ramp displacement and long hold period at the peak displacement.²⁵

$$G_{\text{rel}}(t)=k_e+{\displaystyle \sum _j{k}_j\text{exp}\left(\frac{-t}{{\tau }_j}\right)}.$$ (5)

III. EXPERIMENTS

A. Gel synthesis

Four different types of poly-2-hydroxyethyl methacrylate gels were synthesized. Twenty milligrams of the ultraviolet (UV) photoinitiator, dimethoxyphenylacetophenone (DMPAP), were weighed out in a 2 mL centrifuge tube and melted at 85 °C in a digital dry bath. Then 900 mL of 2-hydroxyethyl methacrylate (HEMA) (Sigma-Aldrich, St. Louis, MO) were added to the tube. The HEMA had previously been run through an inhibitor-removal column (Sigma-Aldrich) and stored with beads of Molecular Sieve Type 4A (Sigma-Aldrich) to remove most of the monomethyl ether hydroquinone (MEHQ) polymerization inhibitor. Then 600 mL ethylene glycol were added to the centrifuge tube. Four different amounts of the cross-linker, ethylene glycol dimethacrylate (EGMDA), were used to synthesize gels with a 1.3, 1.6, 1.9, and 2.3 vol% cross-linker. Each tube was then vortexed, and the solution was carefully pipetted into a 0.25 in. diam poly(tetrafluoroethylene) (PTFE) mold. The solution was polymerized under UV light for 3 min. The polymerized gel was immediately transferred to a well filled with 30% ethanol in deionized water to remove unreacted components and avoid crack propagation in the gels during swelling. After equilibrating in the 30% ethanol solution, the gel was moved to a 10% ethanol solution and finally to deionized water. The gel was kept fully submerged until testing was completed. An example of a typical pHEMA gel is shown in Fig. 2.

FIG. 2.

Top and side view of a representative pHEMA hydrogel sample.

B. Nanoindentation

Nanoindentation of hydrated materials poses several challenges to extracting mechanical properties. One source of error comes from the machine’s ability to sense the surface of a soft material.¹⁶ The sources of error discussed here are specific to the Hysitron Triboindenter and the Triboindenter software, but similar sources of error are present in other instrumentation. When the indenter tip first makes contact with a soft material (<100 MPa), the tip may travel hundreds of nanometers into the surface before the start of data collection. As the tip slowly approaches the surface, the Z-axis of the Tribo-Scanner is placed in feedback mode. When the Z piezo voltage reaches 0, the stepper motor is stopped and the tip is held on the surface with constant force for 60 s. The tip is then held at the surface for an additional 50 to 80 s for feedback sensing and drift correction. This long contact period has little effect on the starting displacement in harder materials, but on a soft surface such as a hydrogel the pretest displacement can be significant when compared with the total displacement during the test.

In very compliant materials, the surface may be indented a significant amount before the test begins. This unmeasured initial displacement results in an apparent contact depth that is less than the actual contact depth.¹⁶ To accurately define the initial contact point, displacement-controlled experiments were performed as described in Cao et al.¹⁴ Briefly, the tip is manually moved to be in contact with the sample by monitoring the force display on the transducer controller to determine the Z location of the surface. The tip is then moved up slightly above the sample surface, and a displacement-controlled “air” indent is performed. From now on, we will refer to the above procedure as the manual method and the procedure of initiating indents using the Hysitron microscope as the tip-optics method.

Since each indent begins above the gel surface, it was necessary to offset the displacement and force to be zero at the surface of gel. Ideally, the surface location would be determined on the loading curve at the point at which the tip snaps to contact, but this point was not clearly visible on load–displacement curves, as shown in Fig. 3. Instead, sample engagement was seen as a gradual change in the loading curve slope. Therefore, the displacement and force are offset so that the point of lowest force on the unloading curve (point of last contact) is at zero displacement and zero force. The points of last contact for four example indents are shown in Fig. 3.

FIG. 3.

Examples of load–displacement data for each of the four cross-linker concentrations. As expected, we see an increase in load with increasing cross-linker concentration for four indents with the same displacement. With these hydrated pHEMA samples, we do not see the snap-to-contact feature often seen with adhesive materials. As a result, the curves were offset so the point of last contact (minimum load on the unloading curve) was set to zero displacement and zero load.

A 50-µm diamond conospherical fluid cell tip was used for all experiments. The Oliver–Pharr fitting method used by the Hysitron software²⁶ bases its calculation and measurements on the tip-area calibration. A quartz sample with a reduced modulus of 69.6 GPa is most often used as a nanoindentation calibration standard. For the wide, rounded tips used on softer biomaterials, this results in calibration of the tip-area function for only a small range of depths. To perform the tip-area calibration over a wide range of depths, a photoelastic coating, PS-6 (Vishay Micro-Measurements, Malvern, PA), was used to characterize the 50-µm fluid cell tip to depths up to 5 µm. In Klapperich et al., polycarbonate is suggested as an alternative calibration material.¹⁵ Polycarbonate (E = 3 GPa) would still require significant extrapolation of the area function to the depths used in this study. Agarose²⁴ and photoelastic films⁶ have been suggested as softer calibration standards to ameliorate this issue. Here, a photoelastic coating with a nominal elastic modulus of 700 kPa (PS-6, Vishay Micro-Measurements, Malvern, PA) was used to empirically characterize the tip geometry at depths up to 5 µm. The tip area is defined as a function of contact depth, h_c, as shown in Eq. (6) below. The constants for the 50-µm spherical tip were C₀ = 173.4140, C₁ = 0.10009, and C₂ = 3.5029 × 10⁷.

$$A(h_c)=C_0{h}_c^2+C_1{h}_c+C_2{h}_c^{1/2}.$$ (6)

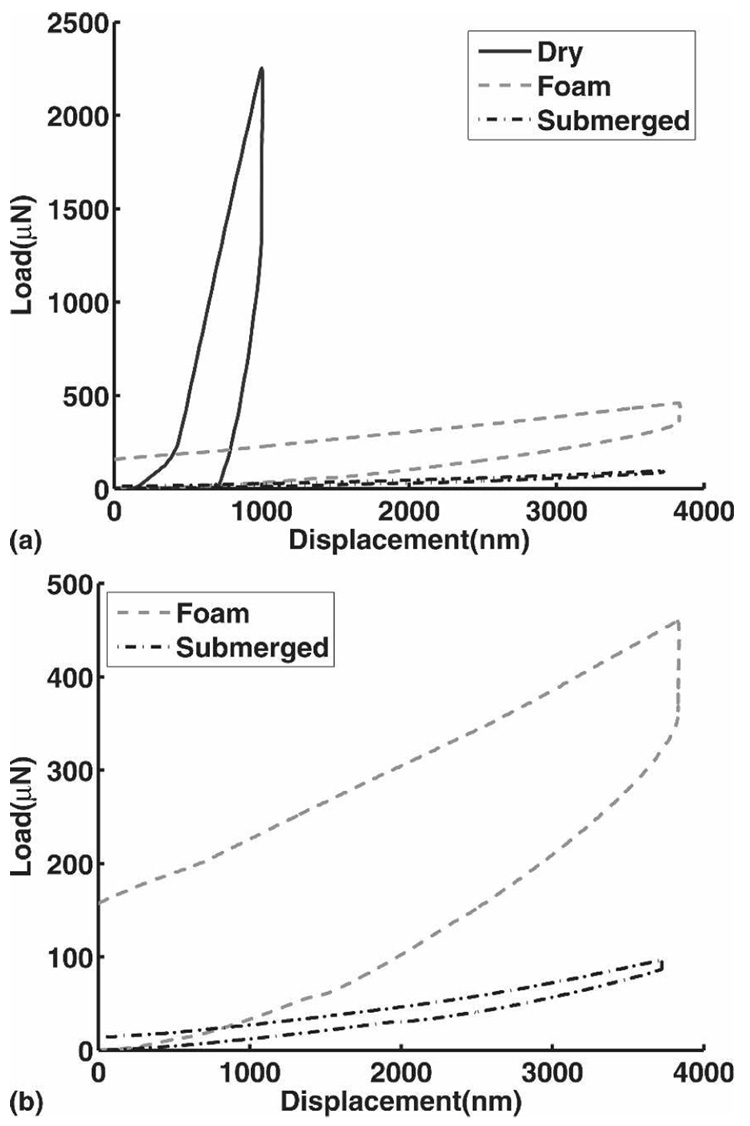
Samples were completely submerged in Millipore water during testing. In our experiments, small changes in hydration caused a markedly different load–displacement response, so equilibrium hydration was maintained through complete submersion. Although we expected a large difference between a submerged and a dry gel, we were surprised to also see a large difference after surrounding a hydrogel with OASIS hydrating foam as described by others as a method of sample hydration (Smithers-Oasis, Kent, OH).²⁴ A series of three indents on a single pHEMA gel at various levels of hydration are shown in Fig. 4. The data suggest that the foam hydration method may not be ideal for pHEMA hydrogels, although it has previously been shown to be useful for other materials.²⁴ The hydrogels used in these experiments were continuously submerged after synthesis to ensure that dehydration and rehydration did not change the mechanical properties.

FIG. 4.

Effect of hydration on nanoindentation of pHEMA hydrogels. (a) Three indents on the 1.9% cross-linker pHEMA hydrogel at three different levels of hydrations are shown above. The 1.9% cross-linker gel was indented while fully submerged, after approximately 10 min surrounded with hydrated OASIS foam, and after drying out completely at ambient conditions. All of the indents were manual, displacement-controlled, air indents with maximum displacement of 1000 or 4000 nm and a 5 s hold period. The peak displacement was adjusted to avoid exceeding machine force limits. (b) The OASIS foam and hydrated indents only.

Each gel was indented using a displacement ramp function with a 500-nm/s loading and unloading rate, a 4000-nm peak displacement, and a 300 s hold period. The indents were repeated for at least three locations on each gel with at least five indents per location. Indents where the tip obviously started in the gel or did not make contact with the gel were excluded from further analysis.

C. Unconfined compression

To verify the mechanical properties measured through nanoindentation, unconfined compression tests were performed on the four pHEMA gels. Both linear and viscoelastic models were used to fit the stress-relaxation data from the unconfined compression testing. Unconfined compression testing was performed on each gel using a custom-designed testing system as shown in Fig. 5.²⁷ In preparation for testing, the initial thickness of each sample was measured using a voltage-sensing micrometer at three locations to provide an average value. The gel was then placed in a polycarbonate well filled with deionized water and compressed between two PTFE platens. The bottom platen was affixed to the floor of the polycarbonate well. Movement of the top platen was controlled by a precision stepping motor (Compumotor model 57–83, 25,000 steps per revolution, Parker Hannifin, Rohnert Park, CA) in series with a precision screw (10 rev/in.) equipped with an antibacklash assembly (Universal Thread and Grinding Co., Fairfield, CT) to provide a displacement resolution of 102 nm/step.

FIG. 5.

The experimental setup for the unconfined compression measurements uses an automated compression apparatus with the sample placed between two PTFE platens. The compression chamber is filled with deionized water. Movement of the top platen was controlled by a precision stepping motor and stress was recorded at 2 Hz by a load cell mounted beneath the polycarbonate well. The entire testing system was contained inside a Styrofoam housing during testing to reduce the effects of ambient-temperature fluctuations on the force signal. In addition, the temperature was recorded throughout the experiment using a digital thermometer.

The top platen was lowered until initial contact with the sample was detected, then an axial compressive prestrain of 2% strain was applied at a rate of 500 nm/s. This strain was held constant for 10 min. Subsequently, a stress-relaxation protocol was carried out that involved a ramp to 12% strain at a displacement rate of 500 nm/s followed by a hold period of 1 h. Axial force was recorded at 2 Hz by a load cell mounted beneath the polycarbonate well (model SML-5lb, Interface Inc., Scottsdale, AZ). The entire testing system was contained inside a Styrofoam housing during testing to reduce the effects of ambient-temperature fluctuations on the force signal. In addition, the temperature was recorded throughout the experiment using a digital thermometer (Dual Thermometer, VWR International Inc., West Chester, PA).

The Poisson’s ratio of the pHEMA gels was calculated using digital images of the four gels (two each of 1.3% and 2.3% cross-linker gels) in the compression well immediately prior to and at the end of the relaxation period. The images were obtained using a digital camera (PowerShot A80 4.0 megapixels, Canon Inc., Lake Success, NY) and were analyzed using ImageJ software (National Institutes of Health, Bethesda, MD) to measure the radial strain. The Poisson’s ratio for each gel was calculated as the negative of the ratio of radial and axial strains and was averaged to be 0.29.

D. Data analysis

Although identifying the location of initial contact on the nanoindentation loading curve would be ideal, we could not find a repeatable method for doing so because of the lack of the snap-to-contact feature usually seen in adhesive materials (see Fig. 3). Offsetting the load is necessary to ensure that all equilibrium moduli are positive and thus physically meaningful. Prior to fitting in Matlab (MathWorks, Natick, MA), all nanoindentation data was rezeroed so that the load and displacement at the point of last contact were set to 0. In future work, we hope to improve upon the procedure by possibly starting farther off the gel to clearly identify the surface location on the loading curve.

The reduced modulus was calculated by fitting the unloading curve from 20% to 95% with a power-law fit and calculating the derivative of this function at the beginning of the unloading curve. This slope is equal to the stiffness of the gel. The reduced modulus was then calculated from the stiffness and the tip area at the contact depth using the same method as the Hysitron analysis software. The Young’s modulus for each indent was determined from the reduced modulus according to Eq. (7) using a Poisson’s ratio of 0.29 as determined previously. A Poisson’s ratio of 0.07 and elastic modulus of 1141 GPa were used for the diamond indenter tip.²⁶

$$\frac{1}{E_r}=\frac{1-{\nu }_i^2}{E_i}+\frac{1-{\nu }_s^2}{E_s}.$$ (7)

Both the nanoindenter and unconfined compression apparatus experience some degree of electronic drift. To correct for this error, the slope of the stress-relaxation curve at the end of the hold period was calculated and a linear drift function was subtracted from the stress-relaxation curves. This subtraction was done in place of monitoring the nanoindentation drift at the surface of the gel prior to the experiment, which allows the tip to creep into the material significantly. Tests with nonlinear drift during the hold period were excluded from further analysis. Drift was subtracted prior to any fitting in Matlab for all data sets. The Maxwell–Wiechert parameters were determined using the fit function with Eq. (5).

IV. RESULTS AND DISCUSSION

A. Nanoindentation

Using the Oliver–Pharr fit of the nanoindentation data, we see an increase in the Young’s modulus values with the addition of cross-linker, as shown in Fig. 6. The pHEMA hydrogels are viscoelastic, but the linearly elastic model is able to discern between the different cross-linker concentrations and show a similar trend to the unconfined compression data. In Gupta et al., a finite element analysis of soft tissue nanoindentation showed that the Oliver–Pharr method was not a suitable method of analysis for viscoelastic materials.²⁸ These results show that the Oliver–Pharr method may be suitable for discerning differences between some viscoelastic materials, even if the method is not capable of determining time-dependent properties.

FIG. 6.

Comparison of the modulus values for each cross-linker concentration. Both the Oliver–Pharr and Maxwell–Wiechert nanoindentation analyses result in a statistically significant increase in modulus with cross-linker concentration from 1.3% to 1.6% cross-linker and from 1.6% to 1.9% cross-linker. Only the nanoindentation equilibrium modulus shows a statistically significant increase from 1.9% to 2.3% cross-linker. *p value < 5 × 10⁻⁸, **p value < 5 × 10⁻⁹, ⁺p value < 5 × E⁻⁶, ⁺⁺p value < 5 × ⁻⁷, ⁺⁺⁺p value < 5 × E⁻³.

There is a reasonable correlation (R² = 0.95) between the Young’s modulus obtained from the Oliver–Pharr method and the equilibrium modulus obtained from the Maxwell–Wiechert model, as shown in Fig. 7. The Young’s modulus shows a statistically significant increase in modulus from the 1.3% to the 1.6% gels and from the 1.6% to the 1.9% gels (p < 5E–8). The equilibrium modulus, k_e, shows a statistically significant increase in modulus with increasing cross-linker concentration for all gels (p < 5E−3). The equilibrium modulus is better at discerning between the two highest cross-linker concentrations as shown in Fig. 6. It is important to note that while the standard deviations for both moduli from nanoindentation were quite high, the standard deviations at most locations were considerably smaller, as shown in Fig. 7. This observation indicates that although the gel itself might be mechanically heterogeneous across its surface, the indentation test gives repeatable results at each indent location.

FIG. 7.

The average Young’s and equilibrium modulus at each nanoindentation position is shown above. Each point on the graph represents a single position on a gel and each gel is shown with a different data marker. Error bars are shown for both the Young’s modulus and equilibrium modulus at each position. Two to five indents were performed at each position.

Surface tension forces from water and sample adhesion are another source of error in hydrated testing. To avoid the error introduced by strong adhesive forces seen at the air–water interface, here all experiments were performed on submerged samples with the tip remaining several millimeters below the surface of the water. An advanced Z-axis calibration (using the Hysitron software) was performed in water above the sample at the beginning of each day of testing. By analyzing only the stress-relaxation data during the hold period, the effect of errors caused by creep during unloading period²⁹ were minimized.

B. Maxwell–Wiechert model

The Maxwell–Wiechert model provides a robust fit for the stress-relaxation curve for both macroscale and microscale experiments. Both nanoindentation and unconfined compression stress-relaxation curves were modeled using the three-parameter (j = 1) and a five-parameter (j = 2) Maxwell–Wiechert models. In both cases, the five-parameter (j = 2) model provided a superior fit as shown in Fig. 8. Expanding the Maxwell–Wiechert model to seven parameters did not provide any measurable improvement. The results of the Maxwell–Wiechert fit are shown in Table I. The equilibrium modulus values from the macroscale and microscale tests increased with increasing cross-linker concentration and were in good agreement.

FIG. 8.

Typical curve fits for Maxwell–Wiechert Model. (a) On nanoindentation data. (b) On unconfined compression data. For j = 1, the Maxwell–Wiechert model is equivalent to the standard linear solid (SLS) model. Both tests were performed on the same 1.6% pHEMA gel. Only every 100th data point is plotted for readability.

TABLE I.

Summary of results from Maxwell–Wiechert model (j = 2).

PHEMA–co-EGDMA	Test	ke (kPa)	k1 (kPa)	τ1 (s)	k2 (kPa)	τ2 (s)
1.3%	Nanoindentation (n = 15)	342 ± 96	53 ± 20	5 ± 1	69 ± 38	62 ± 22
	Unconfined compression (n = 3)	611 ± 156	28 ± 7	760 ± 691	23 ± 10	658 ± 990
1.6%	Nanoindentation (n = 15)	586 ± 122	49 ± 12	6 ± 2	58 ± 21	72 ± 30
	Unconfined compression (n = 3)	721 ± 58	32 ± 13	64 ± 31	46 ± 10	881 ± 559
1.9%	Nanoindentation (n = 13)	897 ± 107	83 ± 12	4 ± 2	85 ± 37	63 ± 32
	Unconfined compression (n = 3)	783 ± 80	47 ± 16	389 ± 556	48 ± 11	531 ± 535
2.3%	Nanoindentation (n = 10)	1044 ± 99	67 ± 10	5 ± 3	52 ± 21	106 ± 175
	Unconfined compression (n = 4)	894 ± 88	50 ± 10	638 ± 430	47 ± 9	247 ± 323

The first spring constant, k_e, corresponds to the equilibrium relaxation modulus. The second spring constant, k₁, and its time constant, τ₁, correspond to the elements in the first Maxwell arm of the model. The third spring constant, k₂, and its time constant, τ₂, correspond to the elements in the second Maxwell arm of the model.

There was no clear trend with changing cross-linker concentration for the two smaller spring constants and the two time constants. This may be because the relaxation rate is dependent on the test geometry. In Sasaki, the relaxation time constant for a poly (N-isopropyl acrylamide) hydrogel is found to be proportional to the square of the sample radius.³⁰ In Mak et al.,³¹ nanoindentation experiments with larger indenter tips took longer to reach equilibrium than those with smaller indenter tips. The nanoindentation time constants, therefore, should be smaller than unconfined compression time constants, as shown in Table I, since the sampled region in nanoindentation is much smaller than the entire sample diameter. If the peak force in stress-relaxation tests is also greater with a larger surface area, this may help to explain why the unconfined compression equilibrium modulus is consistently higher than the nanoindentation equilibrium modulus.

In the future, we seek to apply this multiscale approach to characterize hydrogels for tissue engineering applications to quantify how cellular traction on a hydrogel affects phenotype and gene expression. Without a good understanding of the mechanics of these substrate materials in a hydrated state, interpretations of cellular response to different mechanical environments will be impossible to study. The time-dependent model of stress–strain behavior will provide more information to characterize cell–biomaterial interactions, while the equilibrium modulus can be used to compare the material with others tested at the macroscale.

C. Comparison of microscale and macroscale tests

The best agreement between the microscale and macroscale tests was between the nanoindentation and unconfined compression equilibrium modulus, k_e, as shown in Fig. 6. This result is consistent with that of Simha et al.,³² which found that the nanoindentation and unconfined compression equilibrium modulus of urethane, 4.41 MPa, were in good agreement. However, it is important to note that the values from nanoindentation and unconfined compression of these pHEMA hydrogels are not exactly the same. It is still important to use caution in comparing mechanical properties from nanoindentation to those from macroscale experiments without using a reference sample that can be tested with both methods.

In general, the moduli for the 1.9% and 2.3% gels were in better agreement than for the softer gels. Since unconfined compression averages the properties of the entire gel, it may be necessary to greatly increase the number of nanoindentation tests to get better agreement. Unfortunately, the manual method of initiating indents makes large numbers of indents very difficult. This problem could be greatly ameliorated by changes to the instrument software. The unconfined compression equilibrium modulus for the 1.3% gel had the largest difference from the nanoindentation equilibrium modulus. This may be partly caused by the force resolution of the nanoindenter. As the magnitude of the force decreases, the force error becomes more significant. Although the exact value varies, a typical error in measuring the force is 1 µN. The average peak load for the 1.3% gel is 16 µN, while the average peak load for the 2.3% gel is 47 µN. Some of the 1.3% gel indents had peak loads as low as 7 µN. This means that the machine error was greater than 10% of the peak load for these indents and may have had a significant effect on the calculated modulus value. The peak load itself may also be overestimated by the selection of the point of last contact as the zero-load point, causing an overestimation of modulus for indents with a large pull-off force. For some curves, the pull-off force can be the same order of magnitude as the peak load.

It is important to note that some differences between nanoindentation and unconfined compression may be due to actual differences between the bulk and surface mechanical properties. A greater degree of hydration near the surface could be responsible for the lower nanoindentation elastic modulus values for the 1.3% and 1.6% gels. Because small areas are sampled in each test, the local modulus values when correctly calculated can vary greatly from the bulk modulus obtained in other experiments.

D. Johnson–Kendall–Roberts adhesion models

Nanoindentation of soft materials is often evaluated using adhesion models.^{10–12,14,33,34} To evaluate the appropriateness of adhesion models for pHEMA hydrogels, the load–displacement data were also analyzed using the solutions for the linearly elastic Johnson–Kendall–Roberts (JKR) adhesion model presented in Ebenstein and Wahl³³ and Gupta et al.¹⁰ These models were applied to the original data before rezeroing, so that the pull-off force, P_adh, could be measured. The results of these analyses are shown in Table II. The Ebenstein and Wahl³³ method used three points from the load–displacement data, P_adh, δ_adh, and δ₀ where the adhesion values occur at the minimum load for the unloading segment and δ₀ is the displacement on the unloading curve when the force is equal to 0.³³ Using these points, the reduced modulus, E_r, can then be calculated from Eq. (8)³³:

$$E_r=\frac{-3P_{\text{adh}}}{\sqrt{R}}{\left[\frac{3({\delta }_0-{\delta }_{\text{adh}}}{1+4^{-2/3}}\right]}^{-3/2}.$$ (8)

TABLE II.

Comparison of the different nanoindentation analysis methods.

PHEMA–co-EGDMA, method/value	Maxwell–Wiechert, ke (kPa)	Oliver–Pharr, E (kPa)	Ebenstein, et al., EJKR (kPa)	Gupta, et al., EJKR (kPa)
1.3% (n = 15)	342 ± 96	355 ± 47	818 ± 87a	671 ± 81b
1.6% (n = 15)	586 ± 122	505 ± 54	1221 ± 186a	966 ± 183b
1.9% (n = 13)	897 ± 107	712 ± 61	1446 ± 101a	1553 ± 187b
2.3% (n = 10)	1044 ± 99	751 ± 44	1565 ± 400	1597 ± 87

^ap value <5 × 10⁻³.

^bp value <5 × 10⁻⁶.

In Gupta et al.,¹⁰ the elastic modulus was calculated from the stiffness and initial unloading force, as well as the pull-off force. Both JKR methods discriminate between the four cross-linker concentrations, but give larger values than the unconfined compression. We believe this result is partly due to errors in determining a point of zero force that is meaningful. The preindentation force is nonzero for almost all indents since the tip is interacting with water as it approaches the gel surface. The variation of the preindentation force curve for four example indents is shown in Fig. 3. Because the data sets are not offset prior to fitting, there is a greater variability in the JKR results, especially for the 2.3% cross-linker gel using the Ebenstein and Wahl³³ method. Both JKR methods assume that the tip is an ideal sphere, but this is not the case for the tip used in these studies as shown in Eq. (6). The JKR modulus is typically lower than the elastic modulus for adhesive materials,¹⁰ but the errors in calculating the pull-off force and tip area may cause an overestimation. It may also be that the Young’s and equilibrium modulus values calculated with the rezeroed curves are lower than in other studies, because the surface location is more accurately determined.

V. CONCLUSIONS

While nanoindentation is a convenient tool for mechanical characterization of biomaterials, hydrated testing still poses some unique challenges. We have shown here that nanoindentation can be used to discriminate between similar, low-modulus samples when the issues with the hydrated testing of soft materials are addressed. The pHEMA hydrogels synthesized here are modeled well by a five-parameter Maxwell–Wiechert viscoelastic model in both nanoindentation and unconfined compression stress-relaxation tests. The equilibrium moduli from the Maxwell–Wiechert model provided the best correlation between nanoindentation and unconfined compression, as shown in Fig. 6. The additional Maxwell–Wiechert spring and time constants seem to be more dependent on test geometry than on cross-linking density. Since the relaxation equilibrium modulus can be determined without fitting the relaxation curve to a five-parameter Maxwell–Wiechert model, this material property provides an efficient method to compare the results from nanoindentation and macroscale experiments. It is important to note that challenges still remain in directly correlating properties from experiments at different size scales and that the equilibrium modulus from nanoindentation is not equal to that from unconfined compression. The methods presented here provide a way to discriminate between similar low-modulus materials using nanoindentation. Finally, by identifying and controlling for the experimental errors we have discussed here, it may be easier to identify when surface versus bulk differences in mechanical properties are significant for soft, hydrated samples.