The Pulsatile Propagation of a Finger of Air Within a Fluid-Occluded Cylindrical Tube

Abstract

We computationally investigate the unsteady pulsatile propagation of a finger of air through a liquid-filled cylindrical rigid tube using a combined boundary element method and lubrication theory approach. The flow-field is governed by the dimensionless parameters Ca_Q(t) = Ca_M + Ca_Ω sin(Ωt) = μQ*(t*)/πR²γ, Ω = μωR/γ and A = 2Ca_Ω/Ω. Here, Ca_Q(t) consists of both mean (Ca_M) and oscillatory (Ca_Ω) components. It is shown that the behavior of this system is appropriately described by steady-state responses until the onset of reverse flow, wherein the system operates in the unsteady regime (Ca_Ω > Ca_M). When flows in this regime are considered, converging and diverging stagnation points move dynamically throughout the cycle and may temporarily separate from the interface at high Ω. We have also found that for Ca_Ω < 10Ca_M the bubble tip pressure drop ΔP_tip may be estimated accurately from the pressure measured downstream of the bubble tip when corrections for the pressure drop due to Poiseuille flow are applied. The normal stress gradient at the tube wall (∂τ_n/∂z) is discussed in detail, as this is believed to be the primary factor in airway epithelial cell damage (Bilek et al 2003). In the unsteady regime we find that local film-thinning produces high ∂τ_n/∂z at low Ca_Ω. Film thickening at moderate Ca_Ω in the unsteady regime protects the tube wall from the large gradients near the bubble tip, therefore reducing ∂τ_n/∂z. We find that the stress field is highly dynamic and exhibits intriguing spatial and temporal characteristics that may be of interest to our field of study, pulmonary airway reopening.

1. Introduction

The goal of this paper is to elucidate a solution of the pulsatile propagation of a semi-infinite air finger through a fluid occluded rigid circular tube. Solution of the free surface problem is achieved with an axisymmetric formulation of the boundary element method (BEM) coupled to lubrication theory in the upstream thin film region. The model formulation and solution methods discussed herein may be of underlying importance to various applications including flow through porous media and the design of microfluidic devices. These studies may also be of importance to biological fluid mechanics applications such as pulmonary airway reopening, erythrocyte migration and embolic events in distal capillaries. The relevance of these studies to problems of physiologic importance can be found in review articles by (Gaver III et al 2006; Grotberg 2001).

Initial experimental investigations conducted by Fairbrother & Stubbs (1935), Bretherton (1961), and Cox (1962) of steady, semi-infinite bubble propagation through a rigid tube demonstrated a correlation between residual film thickness far upstream of the bubble $h_0^{\ast }$ and the dimensionless fluid capillary number $Ca=\mu U_{AVG}^{\ast }∕\gamma$. Ca is a function of fluid viscosity (μ), surface tension (γ), and the average fluid velocity downstream of the bubble tip $U_{AVG}^{\ast }$; representing the balance of viscous and surface tension induced forces. Bretherton extended experimental results to the limit of vanishing Ca via matched asymptotic analysis, determining that $\underset{Ca\to 0}{\lim }{h}_0^{\ast }\propto C{a}^{2∕3}$. Park & Homsy (1984) followed Bretherton's groundbreaking work to formalize the low Ca asymptotic analysis with perturbation theory. Ratulowski & Chang (1989) used an arclength-angle formulation of a composite lubrication equation to extend the asymptotic analysis to higher Ca.

We simulate this system to capture the complex interfacial and flow field dynamics. Mesh based computational studies using finite difference routines (Reinelt & Saffman 1985; Wassmuth et al 1993) and the finite element method (Giavedoni & Saitia 1997; Heil 2001; Shen & Udell 1985) have been successfully employed under steady state conditions. Application of the boundary element method (BEM), our chosen technique, to air finger propagation in channels was pioneered by Lu & Chang (1988) and followed by Ingham et al (1992) and Halpern & Gaver III (1994). This computational scheme was selected because of the inherent efficiency of the method, which requires meshing and computations only at node points along the boundary of the domain. With axial symmetry and the addition of lubrication theory approximations in the thin film region, where BEM computations demand excessive resources, computational costs for the time-dependent simulation are tractable.

In the Results section we investigate the following characteristics: the dimensionless bubble tip pressure drop ΔP_tip, extrapolated ΔP_tip (defined below), curvature κ_tip, velocity U_tip, and upstream bubble radius β. We consider the time-dependent behavior of these properties as well as trends occurring at fixed mean capillary number Ca_M and oscillatory amplitude A over a range of dimensionless frequencies Ω. In the Discussion section we explore the implications of these flows on the temporally and spatially dependent normal stress gradient ∂τ_n/∂z, because this mechanical stress component has been shown to be of fundamental importance to the damage of pulmonary epithelial cells that may relate to ventilator-induced lung injury (Gaver III et al 2006).

2. Problem Formulation

We examine the oscillatory progression of a semi-infinite finger of air through a rigid, cylindrical tube of radius R containing a Newtonian fluid of viscosity μ and a constant surface tension γ (Figure 1). The dynamics of the air phase are neglected and the reference pressure in this region is P = 0. We assume axial symmetry (r* = (r*, z*)). s* defines the arc-length coordinate along the air-liquid interface, originating at the bubble tip and spanning through the boundary element method (BEM) and lubrication theory (LUBE) regions.

Figure 1.

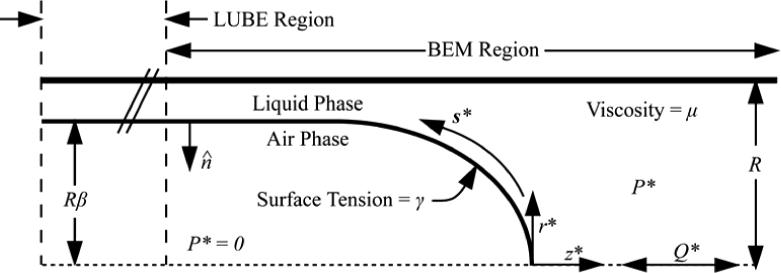
Model

Bubble motion is induced by downstream flow, dictating the behavior of the air finger by conservation of mass. The downstream flow rate (Q*(t*)) is defined according to [2.1], consisting of mean ($Q_M^{\ast }$) and oscillatory ($Q_{\omega }^{\ast }$) components.

$$Q^{\ast }\left(t^{\ast }\right)=Q_M^{\ast }+Q_{\omega }^{\ast }\sin \left(\omega t^{\ast }\right)$$ [2.1]

The dimensional frequency ω determines the period of oscillation. The reopened region far upstream of the bubble tip is of radius r_men = Rβ. Since the interface is a free surface, β is determined as part of the solution.

2.1 Governing equations, BEM region

Governing equations for fluid motion are scaled using the parameters shown in [2.2], with dimensional quantities denoted with an asterisk (*).

$$\begin{array}{c}\hfill {\mathit{u}}_z^{\ast }=U{\mathit{u}}_z=\left(\frac{\gamma }{\mu }\right){\mathit{u}}_z,{\mathit{u}}_r^{\ast }=\left(\frac{\gamma }{\mu }\right){\mathit{u}}_r,r^{\ast }=Rr,z^{\ast }=Rz,r_{men}^{\ast }=R{r}_{men},\hfill \\ \hfill P^{\ast }=\frac{\gamma }{R}P,t^{\ast }=\left(\frac{R\mu }{\gamma }\right)t,{\kappa }^{\ast }=\frac{1}{R}\kappa ,{\tau }^{\ast }=\frac{\gamma }{R}\tau \hfill \end{array}$$ [2.2]

The velocity scale U = γ/μ, a balance between surface tension and viscous forces, represents the interfacial relaxation velocity. All lengths are scaled by the tube radius R, and time is scaled naturally with velocity and length. The Law of Laplace defines the pressure scale. We pose the governing equations and boundary conditions in the laboratory frame of reference. Below (§3.5, §3.6) time stepping is described, which will allow our simulations to focus on the bubble tip region of interest.

We assume inertial effects are negligible and the unsteadiness in the problem arises from the kinematic boundary condition (limitations associated with this assumption are addressed in §5.3). The flow field is thus described by the dimensionless Stokes equation [2.3] and continuity equation [2.4].

$$\nabla \mathit{P}={\nabla }^2\mathit{u}$$ [2.3]

$$\nabla \cdot \mathit{u}=0$$ [2.4]

The flow is driven far downstream with an imposed velocity profile

$$\mathit{u}(r,t)=2C{a}_Q\left(t\right)(1-r^2),$$ [2.5]

scaling [2.1] yields the dimensionless downstream flow rate

$$C{a}_Q\left(t\right)=C{a}_M+C{a}_{\Omega }\sin \left(\Omega t\right).$$ [2.6]

The dimensionless parameters describing the system are:

$$C{a}_Q\left(t\right)=\frac{\mu U_{AVG}^{\ast }\left(t^{\ast }\right)}{\gamma }=\frac{\mu Q^{\ast }\left(t^{\ast }\right)}{\pi R^2\gamma },\Omega =\frac{\mu \omega R}{\gamma },A=\frac{2C{a}_{\Omega }}{\Omega }.$$ [2.7]

Ca_Q(t) is a capillary number that represents balance between viscous and surface tension effects, consisting of mean (Ca_M) and sinusoidal oscillatory (Ca_Ω) components. U_AVG(t) represents the average velocity across a cross-section in the downstream region, equal to Q*(t)/πR². By conservation of mass Q*(t) also represents the gas flow rate into the finger of air from the upstream end. The dimensionless frequency (Ω) and amplitude (A) parameterize bubble oscillation. A specifies the peak to peak oscillatory stroke length of the bubble tip $L_{stroke}\approx A\stackrel{‒}{\beta }R$, where $\stackrel{‒}{\beta }$ is the average bubble radius. In our simulations we define A, L_stroke and $\stackrel{‒}{\beta }$ are determined through the solution process.

No slip and no penetration are enforced at tube wall [2.8]:

$${\mathit{u}(\mathit{r},t)\mid }_{r=R}=0.$$ [2.8]

The interfacial stress jump condition is defined as

$$\left[\sigma \cdot {\widehat{n}}_{men}\right]=-\kappa {\widehat{n}}_{men}$$ [2.9]

where σ is the stress tensor for the for the viscous occluding fluid, n̂_men is the outward facing interfacial normal vector, and κ is the 3-dimensional interfacial curvature.

2.2 Governing equations, LUBE region

In the region of the model governed by lubrication theory the evolution equation for the radial position of the meniscus [2.13] is obtained from the z-component of the full Navier-Stokes equation. We simplify by assuming radial symmetry (as dictated by the BEM formulation), viscous dominated flow, and that the ratio of radial to axial length scales is small following a long-wavelength approximation

$$\frac{\partial P^{\ast }}{\partial z^{\ast }}=\mu \left(\frac{1}{r^{\ast }}\frac{\partial }{\partial r^{\ast }}\left(r^{\ast }\frac{\partial u_z^{\ast }}{\partial r^{\ast }}\right)\right).$$ [2.10]

Integrating [2.10] twice w.r.t. r, applying the boundary conditions $\partial v_z^{\ast }∕\partial z^{\ast }=0$ and $v_z^{\ast }=0$, then scaling with [2.2] yields the axial velocity in the lubrication region:

$$v_z=\frac{{\kappa }_z}{2Ca}\left(\frac{r^2-1}{2}-r_{men}^2\ln \left(r\right)\right),$$ [2.11]

where κ_z is the curvature derivative in the z-direction. We integrate the velocity over the cross-sectional area of the fluid to determine the flow rate Q, from which we attain the flow derivative in the z direction ∂Q/∂z.

Differentiating Q w.r.t. z and applying Leibnitz's rule produces the relationship between the evolution equation and the flow derivative

$$\frac{\partial r_{men}}{\partial t}=\frac{1}{2\pi r_{men}}\frac{\partial Q}{\partial z},$$ [2.12]

into which we substitute ∂Q/∂z to obtain the evolution equation in the lubrication region

$$\frac{\partial r_{men}}{\partial t}=\left(\frac{1}{16r_{men}}\right)\left[\begin{array}{c}{\kappa }_z\left(8r_{men}\frac{\partial r_{men}}{\partial z}-8r_{men}^3\frac{\partial r_{men}}{\partial z}+16\ln \left[r_{men}\right]r_{men}^3\frac{\partial r_{men}}{\partial z}\right)\hfill \\ +{\kappa }_{zz}\left(-1+4r_{men}^2-3r_{men}^4+4\ln \left[r_{men}\right]r_{men}^4\right)\hfill \end{array}\right]$$ [2.13]

It should be noted that if the bubble speed varies too rapidly, spatial gradients in film thickness will be created that may violate the (implicit) lubrication approximation by having too short a lengthscale. By introducing the lubrication region far upstream of the bubble tip, the significance of these errors is reduced in the bubble tip region that is modeled using the BEM formulation.

3. Method of Solution

We pose a problem formulation base in the laboratory frame of reference (i.e. fixed walls), which would result in inappropriately large domains when solved over long periods of time. To prevent this, the governing equations are solved in the laboratory frame and kinematically translated into the bubble tip frame of reference (i.e. the velocity of the bubble tip is zero). This process is further described below in §3.5.

3.1 Boundary element method (BEM)

The boundary element method is utilized to determine the flow field in the region of the model surrounding the bubble tip (Figure 1 and Figure 2). Ladyzhenskaya (1963) showed that

$$u_k\left(\mathbf{x}\right)={\int }_S{T}_{ik}(\mathbf{x},\mathbf{y})u_{i}dS-\frac{1}{Ca}{\int }_S{U}_{ik}(\mathbf{x},\mathbf{y}){\tau }_{i}dS,$$ [2.14]

where T_ik and U_ik are the traction and velocity kernels, u_i is the velocity vector, and τ_i is the traction vector τ = σ_fluid•n̂. The axisymmetric form of the kernels used in this simulation may be found on pages 132−135 and appendix D in Becker (1992). Integrals are evaluated over positions y that describe the boundary S. The solution vector u_k = f(x) describes points x within the bounded domain. Near the boundary of the domain [2.14] is re-written as

$$c_{ik}{u}_k\left(\mathbf{x}\right)={\int }_S{T}_{ik}(\mathbf{x},\mathbf{y})u_{i}dS-\frac{1}{Ca}{\int }_S{U}_{ik}(\mathbf{x},\mathbf{y}){\tau }_{i}dS,$$ [2.15]

where c_ik accounts for the stress discontinuities occurring at the boundary. To numerically implement this formulation the axisymmetric domain is discretized into N_elm 3-node quadratic elements as shown in Figure 2. Four degrees of freedom (DOF) exist at each BEM node: u_r, u_z, τ_r, τ_z. Velocity (u) and/or stress (τ) boundary conditions are applied on two of the four degrees of freedom. Nodes adjacent to two surfaces (Figure 2) have 4 DOF for each surface, as discussed in Zimmer et al (2005). The discrete formulation of [2.15]

$$C_{ki}{U}_i\left(\mathbf{x}\right)-\sum _{m=1}^{N_{elm}}{\int }_{S_m}{T}_{ik}(\mathbf{x},\mathbf{y})u_{i}d{S}_m=-\frac{1}{Ca}\sum _{m=1}^{N_{elm}}{\int }_{S_m}{U}_{ik}(\mathbf{x},\mathbf{y}){\tau }_{i}d{S}_m.$$ [2.16]

is then evaluated for each node, where S_m represents the boundary of element m. Numeric evaluation of the integrands in [2.16] for each element using standard Gaussian quadrature techniques yields

$$\mathbf{T}w=\mathbf{U}t.$$ [2.17]

The matrices T and U are of size 2N × 2N and 2N × 3N respectively, where N is the number of nodes. The vector w contains the velocities in the form w_2j-1 = u_zj, w_2j = u_rj and t contains stress data t_2j-1 = τ_zj and t_2j = τ_rj, where and j = 1,2,...,N. U is 2N × 3N so that two stresses may defined at the corner nodes. Either the velocity or stress is known at each corner. With this [2.17] can be arranged into the Ax = b form where A is 2N × 2N, x is 2N and contains the unknown velocities and stresses, and b hold the known velocities and stresses obtained from the boundary conditions. We then solve for the unknown velocities and stresses with Gaussian elimination. When the solution at the boundary has been obtained, [2.14] can be used to determine the internal velocity field.

Figure 2.

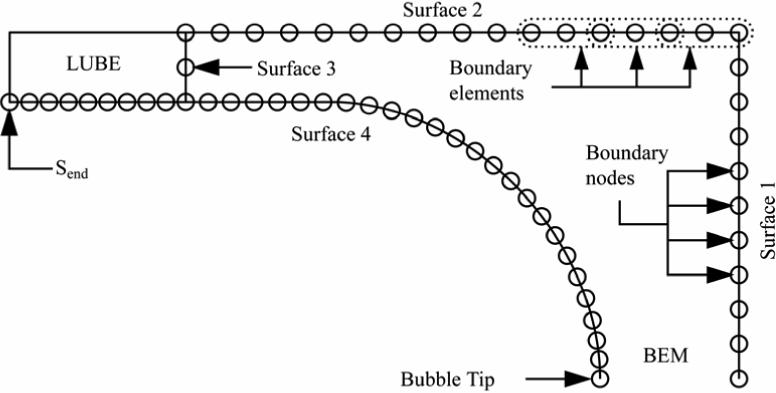
Computational Domain

3.2 Boundary conditions: BEM region

As described in Halpern & Gaver III (1994) and Zimmer et al (2005), boundary conditions must be carefully set to generate accurate results. This entails the definition of mixed conditions at the corner points as described in the Appendix. Flow through the downstream surface of the model (Surface 1 in Figure 2) is defined by the instantaneous capillary number Ca_Q(t) [2.6]. Along the tube wall no slip and no penetration are enforced via velocity conditions. At the interface (Surface 4 in Figure 2), τ_r and τ_z are obtained from [2.9]. For a complete description of the boundary conditions in the BEM domain see Table 1 in the Appendix.

3.3 Lubrication theory

Lubrication theory is used to describe the flow field in the upstream region of the model, reducing the length of the BEM domain and providing boundary conditions on the adjacent BEM region (Figure 2, surface 3). Following standard lubrication theory approximations, the evolution equation [2.13] is obtained as described in §2.2. The curvature κ and the curvature spatial derivatives κ_z and κ_zz are continuous throughout the BEM and LUBE regions of the model due to the implementation of a master surface spanning the length of the domain.

3.4 Boundary conditions: LUBE region, BEM/LUBE boundary

In the LUBE region, nodes are fixed axially; the radial velocity is defined by the evolution equation [2.13]. Connection of the two domains through the master cubic spline and the shared boundary condition produces a continuous description of the flow field and interfacial behavior. At the boundary between the BEM and LUBE regions axial velocity and radial stress conditions are enforced. As at the downstream end of the BEM region, shear stress is defined on the corner nodes by differentiating the velocity profile.

3.5 Kinematic translation, tip frame of reference

Solution of the boundary integral equations for a given time step produces a quasi-steady-state solution. To analyze time-dependant behavior a kinematic boundary condition is applied to the free surface in conjunction with the time-dependant flow rate. To prevent elongation of the computational domain nodal positions are kinematically translated in the bubble tip frame of reference by subtracting the tip velocity from the axial velocity at each node point. This allows the tip of the bubble to remain fixed at the origin while solving the equations of motion in the laboratory frame of reference. In the BEM region we apply the following condition:

$$\frac{d\mathit{M}}{dt}=\left[\left(u_z-u_{tip}\right)n_z+u_r{n}_r\right]\widehat{n},$$ [2.18]

where M = (r_m(s,t), z_m(s,t)) is the interfacial position vector. Details of this technique are provided by (Zimmer et al 2005). Likewise, in the lubrication region we apply

$$\begin{array}{cc}\hfill u_r^{interface}& =\left(\frac{\partial r_{men}}{\partial t}-u_{tip}{n}_z\right)n_r\hfill \\ \hfill u_z^{interface}& =0.\hfill \end{array}$$ [2.19]

3.6 Time stepping

The time-dependent evolution of the meniscus and flow field is determined by the NetLib routine DLSODES (Double precision Livermore Solver for Ordinary Differential Equations with general Sparse Jacobian matrices), operating on a master domain spanning the BEM and LUBE regions. Nodal positions are redistributed every ¼ cycle, with increased nodal density in the tip region.

3.7 Convergence

We assessed the convergence of our solutions by investigating the impact of critical properties of our solutions (bubble tip pressure drop ΔP_tip, bubble tip curvature κ_tip, tip velocity U_tip) as a function of the nodal density and extent of the boundary element domain. Nodal density on the free surface was determined by iterating the steady state solution of Ca(t) = 0.1 with an increasing number of interfacial nodes. The interfacial nodal density was selected so that the maximum change in the solution variables per additional element was less than 5e-5. Comparison of steady state results over 0.01 < Ca_Q < 1.3 with the simulations of Reinelt & Saffman (1985) show a maximum difference in predicted film thickness < 0.5% and bubble tip pressure drop < 1.6%, demonstrating excellent agreement between the two methods.

The normal component of velocity at the air-liquid interface in the frame of reference of the moving tip was used to define convergence in steady state simulations. When the maximum normal velocity throughout the BEM and LUBE regions was less than 5×10⁻⁸, the steady state was considered converged. Convergence in oscillatory simulations was determined by comparing results from previous cycles. ΔP_tip, κ_tip, and U_tip were compared at 144 temporal points per cycle; when the maximum difference of these characteristics varied by less than 10⁻⁵ between cycles the oscillatory simulation was considered converged.

In order to determine the appropriate domain length for the BEM region, solutions were calculated for BEM regions over z_LFT < z < z_RT, where z_LFT defines the juncture between the BEM region and the thin-film region that is modeled using lubrication approximations, and z_RT is the downstream extent of the BEM domain (typically, z_RT = 3). Solutions for A = 1, Ca_M = 0.01, Ω = 0.06 were calculated with the length of the domain ranging over −14 < z_LFT < −0.6 with a fixed nodal density. Bubble tip parameters ΔP_tip, U_tip, and κ_tip were insensitive to z_LFT for z_LFT < −3, so solutions were calculated with the BEM region over −4 < z < 3.

4. Results

4.1 Flow field

As a baseline, we consider the flow field occurring at Ca_M = 0.01, Ω = 0.04, A = 5. In Figure 3 the dynamic nature of the flow field is introduced by demonstrating the time-dependent streamlines at points throughout the oscillatory cycle. As such, panels a-f present instantaneous streamlines every 1/6^th cycle, and identify the time-dependent locations of converging (+) and diverging (-) stagnation points as well a separatrix (X) that temporarily exists during deceleration. These stagnation points are emphasized because of their importance in interfacial transport (Stebe & Barthes-Biesel 1995; Stebe & Maldarelli 1994; Zimmer et al 2005). Note that since this is an unsteady flow, the interface is not a streamline and therefore streamlines may intersect the free surface.

Figure 3.

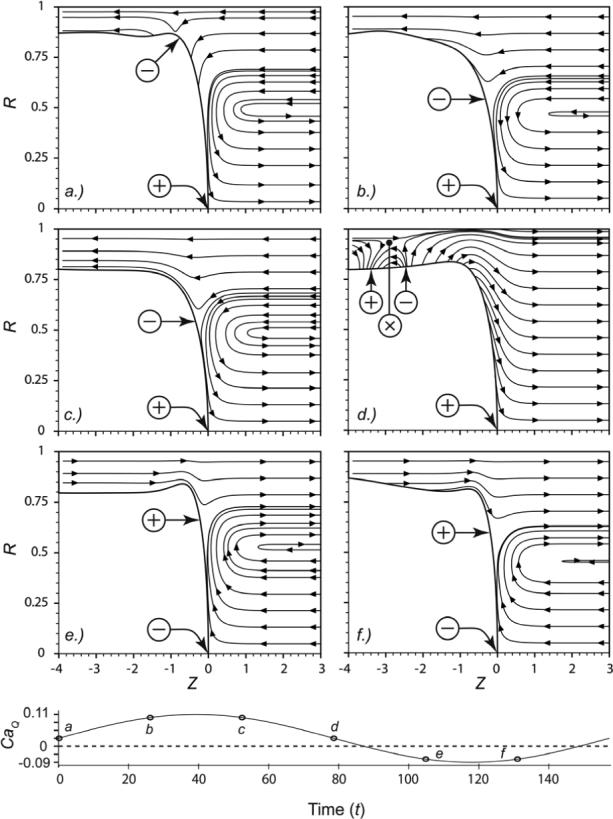
Instantaneous streamlines, bubble tip frame of reference. Ca_M = 0.01, Ω = 0.04, A = 5, Ca_Ω = 0.1. Converging stagnation points are represented with (+), diverging stagnation points with (-), and stagnation points separated from the interface (separatrices) are indicated with (X).

Figure 3a shows flows that exist at Ca_Q = Ca_M in the accelerating phase produce a converging stagnation point (+) at the bubble tip and a diverging stagnation point (-) in the transition region between the bubble tip to the thin-film (similar to steady-state flows). As the flow rate is increased to a maximum of Ca_Q(t) = Ca_M + Ca_Ω (Figure 3a –b) the transition region diverging stagnation point (-) migrates towards the bubble tip. Subsequently, as Ca_Q(t) decreases towards Ca_M (Figure 3c and d) the transition region stagnation point migrates along the interface away from the bubble tip, eventually separating from the free surface to create a separatrix (denoted by X in Figure 3d) and ultimately dissipating at the wall. It is important to note the dissimilarities between Figure 3a and Figure 3d. While both of these flows occur at Ca_Q(t) = Ca_M – unlike the accelerating phase, the decelerating phase bears little similarity to the steady-state flow field that would exist at Ca_M, as it includes two converging stagnation points in addition to the separatrix. This behavior clearly demonstrates that the time-dependent nature of the system modifies the interfacial geometry and flow field even though inertia is not included in this model. In addition, the separatrix was not observed in prior 2-D planar investigations of pulsatile flow (Zimmer et al 2005), highlighting the importance of geometry on the flow fields.

When flow reversal occurs (Ca_Q(t) < 0), the stagnation points change polarity with the bubble tip transforming from convergent (+) to divergent (-), and the transition region stagnation point becoming convergent (Figure 3e and f). With increasing Ω, the reverse-flow transition region stagnation point (+) may also separate from the interface and convect into the bulk of the fluid. The local film thinning occurring in the accelerating phase of the reverse stroke (Figure 3e) plays a significant role in the normal stress gradient ∂τ_n/∂z, this effect is discussed in §5.1

4.2 Hysteresis Loops

Figure 4 presents hysteresis loops that demonstrate the dynamic relationship between the key system responses ΔP_tip, extrapolated ΔP_tip, κ_tip, and Ca_Q(t). The extrapolated ΔP_tip, (ΔP_tip)_ext, is determined from the pressure at the downstream boundary by subtracting the instantaneous Poiseuille flow viscous pressure drop P_μ = 8L_DOWNCa_Q(t) that occurs between bubble tip and downstream end of the domain, L_DOWN = z_RT. Practically, (ΔP_tip)_ext is an important quantity because this characteristic is measurable experimentally, while it is not possible to directly measure ΔP_tip. We therefore seek to determine whether (ΔP_tip)_ext is an adequate measure of the tip pressure drop.

Figure 4.

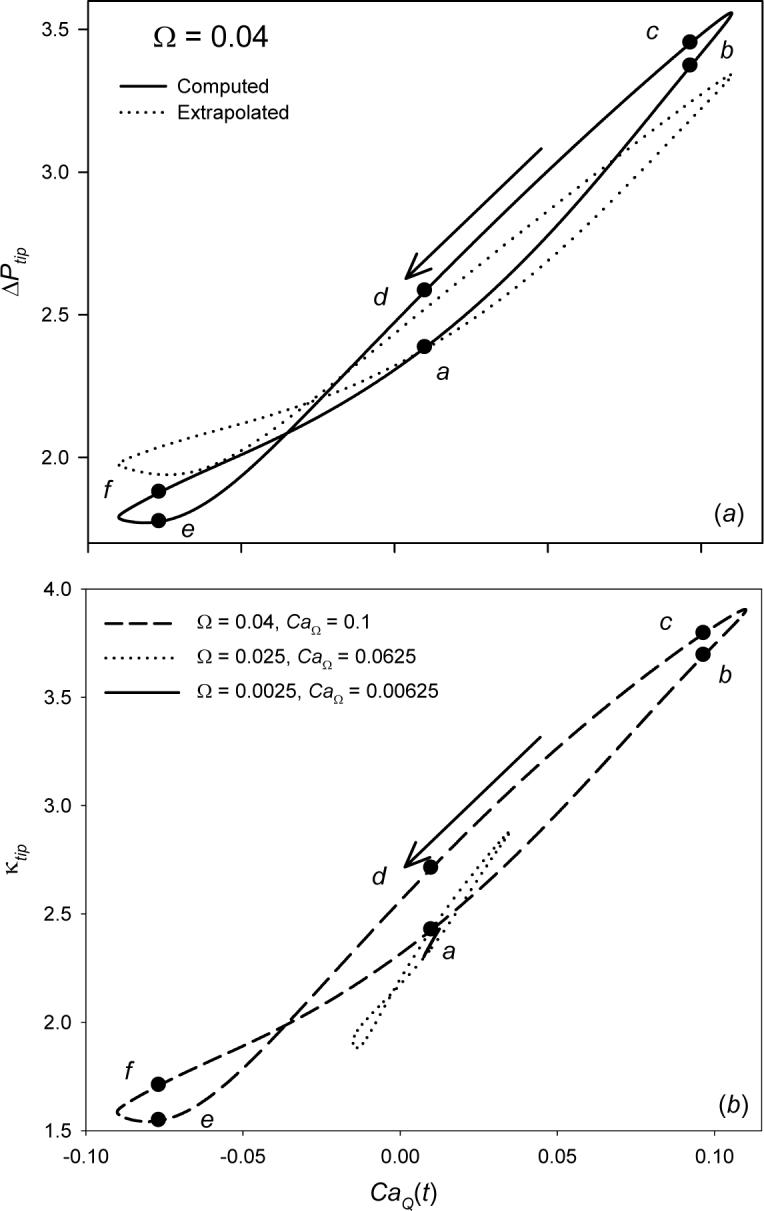
Bubble tip pressure drop ΔP_tip (a) and curvature κ_tip (b) hysteresis loops for Ca_M = 0.01, A = 5. Symbols a-f correspond to streamlines shown in Figure 3.

Figure 4a shows hysteresis loops of ΔP_tip and (ΔP_tip)_ext over one cycle for Ca_M = 0.01, A = 5, and Ω = 0.04. (ΔP_tip)_ext follows the same qualitative pattern as ΔP_tip, indicating that downstream pressure measurements can be used to experimentally evaluate interfacial pressure jumps (cycle-averaged quantitative comparison is provided below). In the region Ca_Q(t) ≥ Ca_M the hysteresis loop rotates in the counter-clockwise direction, and ΔP_tip increases with Ca_Q(t) so that ΔP_tip is greater on the deceleration phase. Streamlines corresponding to this behavior are shown in Figure 3a-d, which correspond to the points a-d in Figure 4. We find that at large Ca_M or small A the entire hysteresis loop rotates in the counter-clockwise direction. However, as shown in Figure 3 and Figure 4, for small Ca_M or large A the hysteresis loops cross in the reverse flow region (Ca_Q < 0, points e and f). This results in a portion of the hysteresis loop that rotates in the clockwise direction. Note that the large A is critical to this behavior, as it allows for a significant region of film thickening during the cycle. For example, if one fixes Ca_Ω = AΩ/2 by decreasing A and increasing Ω, then the hysteresis area increases and the cross-over region is eventually eliminated.

In order to fully understand the behavior of ΔP_tip, it is instructive to investigate the dynamic tip curvature, κ_tip (Figure 4b). Clearly, ΔP_tip is consistent with κ_tip – this occurs because curvature is a major component of the interfacial stress condition [2.9]; qualitative differences arising between κ_tip and ΔP_tip are a result of viscous effects that become more significant as Ω is increased. In the forward portion of the oscillatory cycle, κ_tip increases with increasing Ca_Q(t) until the maximum velocity (Ca_Q = Ca_M + Ca_Ω) is reached. Subsequent deceleration results in local film thickening that increases the tip curvature (compare Figure 3a to Figure 3d) and, hence, increases ΔP_tip. This behavior results in the counterclockwise direction of the hysteresis loop.

The clockwise rotation of the ΔP_tip and κ_tip hysteresis loops occur in the portion of the cycle where Ca_Q(t) < 0 when A is large (see above). The κ_tip response shows that the curvature is reduced as the bubble travels in the –z direction (which results in the blunting of the bubble tip), causing a commensurate decrease in ΔP_tip. κ_tip (and hence ΔP_tip) increases in the accelerating phase near the minimum velocity (compare Figure 3e to Figure 3f), yielding the clockwise orientation.

4.3 Cycle-averaged results

To elucidate the trends present over the range of parameters considered herein (Ca_M = 0.01, 0.05, 0.1; A = 1, 5 and 5 × 10⁻⁴ ≤ Ω ≤ 10), we present the cycle-averaged results in Figure 5 -Figure 7. Generally, when Ca_Ω < Ca_M quasi-steady behavior is observed and when Ca_Ω > Ca_M the cycle-averaged data are modified from the steady-state response. This modification results from the reverse flow that exists during a portion of the cycle when Ca_Ω > Ca_M, we term this the ‘unsteady regime.’

Figure 5.

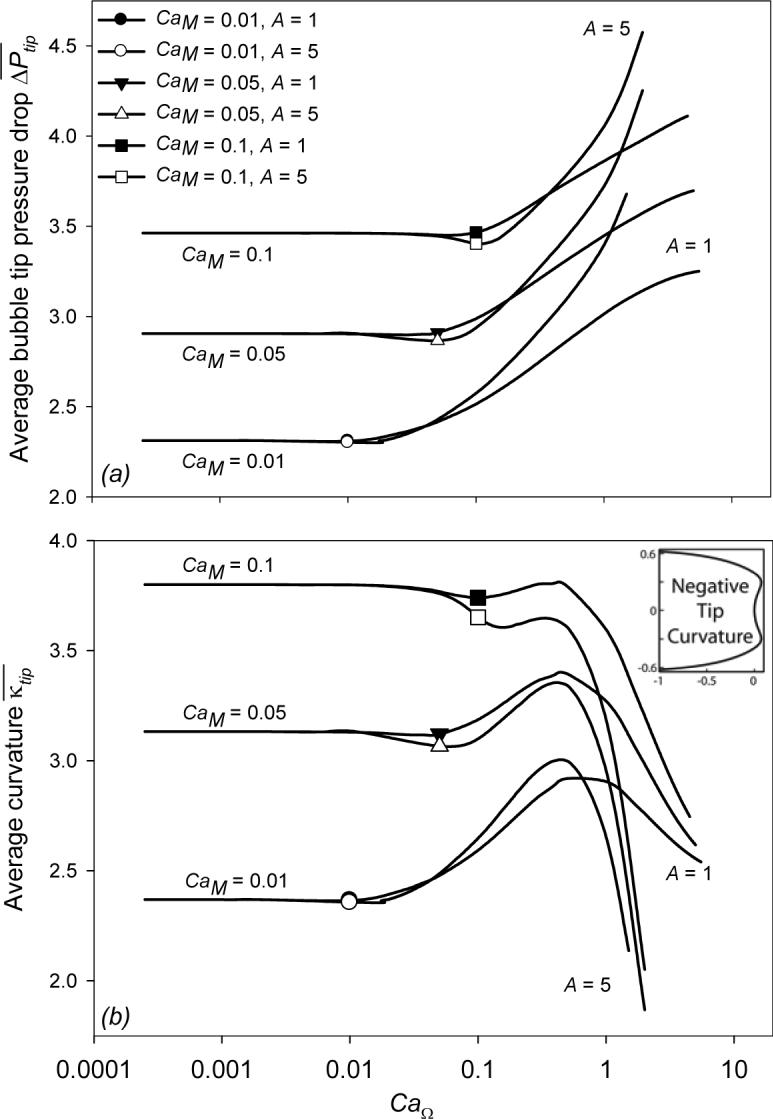
Cycle averaged bubble tip pressure drop ΔP̄_tip (a) and curvature ${\stackrel{‒}{\kappa }}_{tip}$ (b). Symbols indicate the dimensionless frequency where Ca_Ω = Ca_M, data to the right of symbols indicate the unsteady regime and the presence of reverse flow. Inset region is representative of the interfacial geometry when κ_tip < 0.

Figure 7.

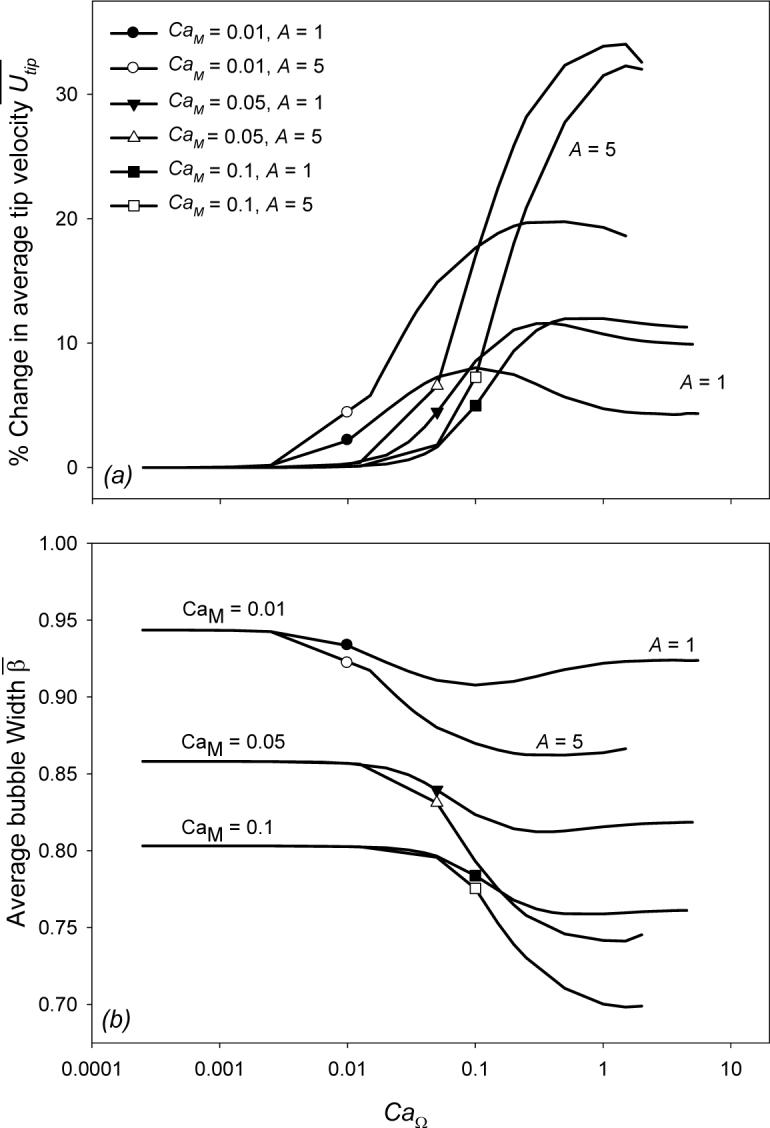
Cycle averaged percent change in bubble tip velocity ΔŪ_tip (a) and bubble half width $\stackrel{‒}{\beta }$ (b). Symbols indicate the dimensionless frequency where Ca_Ω = Ca_M, data to the right of symbols indicate the unsteady regime and the presence of reverse flow.

In the unsteady regime the cycle-averaged bubble tip curvature ${\stackrel{‒}{\kappa }}_{tip}$ (Figure 5b) initially increases with Ca_Ω. This increase in ${\stackrel{‒}{\kappa }}_{tip}$ is consistent with the hysteresis loops shown in Figure 4b, which clearly demonstrates that an increase in Ca_Ω leads to a net upward shift of the hysteresis loops. Subsequently, Figure 5b demonstrates that a further increase in Ca_Ω yields a precipitous reduction in ${\stackrel{‒}{\kappa }}_{tip}$. This behavior occurs because κ_tip becomes negative for a portion of the oscillatory cycle (see inset of Figure 5b); meanwhile, κ_tip during the large Ca_Q forward stroke approaches a constant (Halpern & Gaver III 1994). As a result, the ${\stackrel{‒}{\kappa }}_{tip}$ is reduced. As A is increased the reduction in ${\stackrel{‒}{\kappa }}_{tip}$ is more abrupt because the bubble tip becomes inverted for an extended period of the cycle.

Analogous to ${\stackrel{‒}{\kappa }}_{tip}$, The cycle-averaged bubble tip pressure drop ΔP̄_tip (Figure 5a) is unaffected by frequency unless reverse flow occurs (Ca_Ω > Ca_M). In this unsteady regime, ΔP̄_tip exhibits a monotonic increase, with ΔP̄_tip initially increasing in concert with ${\stackrel{‒}{\kappa }}_{tip}$. This correlation between ΔP̄_tip and ${\stackrel{‒}{\kappa }}_{tip}$ is consistent with the hysteresis loops shown in Figure 4. However, at high Ca_Ω this correlation is broken – ΔP̄_tip increases while ${\stackrel{‒}{\kappa }}_{tip}$ decreases. This occurs because of the increasing effect of viscous forces as velocity increases, as discussed in §4.2.

To assess the accuracy of (ΔP̄_tip)_ext as an estimate of ΔP̄_tip as discussed above, we compare ΔP̄_tip to (ΔP̄_tip)_ext in Figure 6. This comparison demonstrates that (ΔP̄_tip)_ext may be used to predict ΔP̄_tip at Ca_Ω well within the unsteady regime. In fact, our calculations show that the deviation is very low when Ω < 1 for A = 1 or Ω < 0.1 for A = 5 with Ca_M = 0.01. This large range of correlation holds true for all Ca_M considered in this study, indicating that one may confidently use (ΔP̄_tip)_ext to estimate ΔP̄_tip when Ca_Ω < 10Ca_M.

Figure 6.

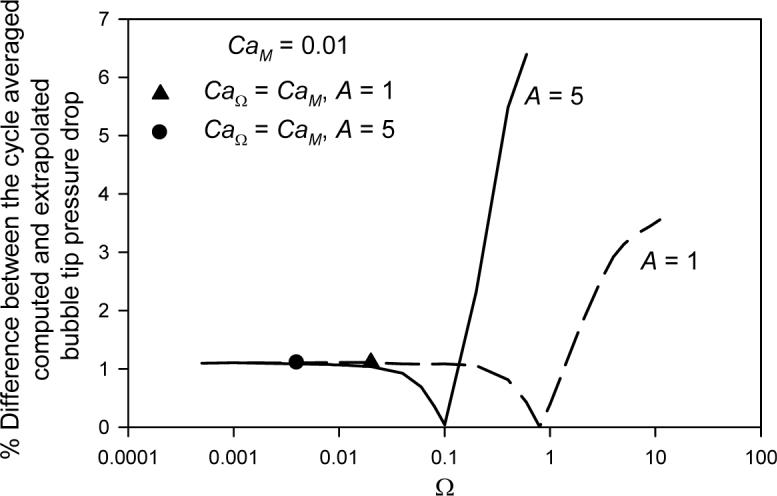
Percent difference between the cycle-averaged pressure drop ΔP̄_tip and extrapolated ΔP̄_tip for Ca_M = 0.01. Data to the right of symbols indicate the unsteady regime and the presence of reverse flow.

Figure 7 provides the a) cycle-averaged percent change in bubble tip velocity ΔŪ_tip and the b) cycle-averaged bubble half width $\stackrel{‒}{\beta }$. $\stackrel{‒}{\beta }$ was calculated by conservation of mass within the system. Flow through the upstream (z_LFT) and downstream (z_RT) boundaries

$$\begin{array}{cc}\hfill {\stackrel{‒}{Q}}_{LET}^{\ast }& =\pi {\beta }^2{\stackrel{‒}{U}}_{tip}\hfill \\ \hfill {\stackrel{‒}{Q}}_{RT}^{\ast }& =\pi R^{2}C{a}_M\hfill \end{array}$$ [4.1]

must be equal as both the air and liquid phases are considered to be incompressible. Therefore,

$$\stackrel{‒}{\beta }=\sqrt{C{a}_M∕{\stackrel{‒}{U}}_{tip}}.$$ [4.2]

Figure 7a shows that ΔŪ_tip increases significantly with increasing Ca_Ω. At A = 1, ΔŪ_tip stabilizes at high frequencies to a value independent of Ω, but decreases with Ca_M. Similar trends exist for A = 5; however, direct observations of the plateau region were not feasible. Figure 7b shows a commensurate decrease in $\stackrel{‒}{\beta }$ with increasing Ca_Ω. Obviously, pulsatile flow results in a net film thickening, which is observable in Figure 3. As expected, this film thickening response occurs largely in the unsteady regime and is related to the increasing film thickness that is observed under high-Ca steady propagation (Halpern & Gaver III 1994). The effects of bubble thickening are far more pronounced with increasing A because high amplitude cycling modifies the bubble geometry over a region that extends far upstream of the bubble tip. In contrast, low A only perturbs the geometry in the immediate vicinity of the tip and thus does not greatly modify the residual film deposited on the wall.

5. Discussion

Above we have discussed the behavior of the flow field and bubble tip properties (U_tip, ΔP_tip, κ) that are important to understanding the fluid mechanical interactions fundamental to this analysis. These fundamental characteristics are clearly modified by the presence of pulsatile flow, especially when reverse-flow conditions exist. In this section we focus on the implications of these flow characteristics on the mechanical stresses that exist on the tube wall. As we will demonstrate, these stress fields are highly dependent on the flow parameters, which exhibit both spatial and temporal dependence. These responses are of fundamental interest and may also be of physiological significance, particularly in relation to pulmonary airway reopening. Specifically, we consider the normal stress gradient (§5.1) and shear stress (§5.2) along the tube wall. We then explore the limitations related to our assumptions of Stokes flow (§5.3).

5.1 Normal stress gradient

Magnitude

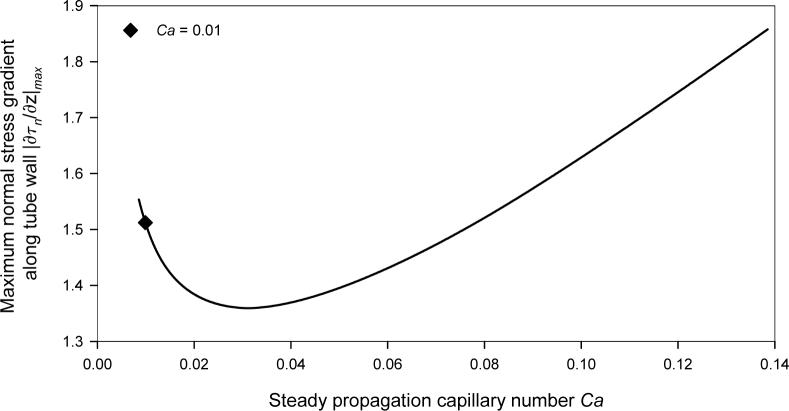
Our interest in the normal stress gradient stems from its importance to damage emanating from the reopening of fluid-occluded airways. Bilek et al (2003) demonstrated that an increased normal stress gradient ∂τ_n/∂z along a channel wall is directly correlated to increased cell mortality. Those studies focused on very small values of Ca (2.7 × 10⁻⁵ ≤ Ca ≤ 6.8 × 10⁻⁴), and showed that a decrease in Ca resulted in an increase in ∂τ_n/∂z (corresponding to increased cell damage). Figure 8 shows that ∂τ_n/∂z is a minimum along the tube wall under steady reopening conditions near Ca = 0.03. In the present study, we focus on low-Ca behavior (Ca_M = 0.01) because this region is of most interest in physiological systems.

Figure 8.

Maximum normal stress gradient magnitude |∂τ_n/∂z|_max along tube wall, steady state bubble propagation

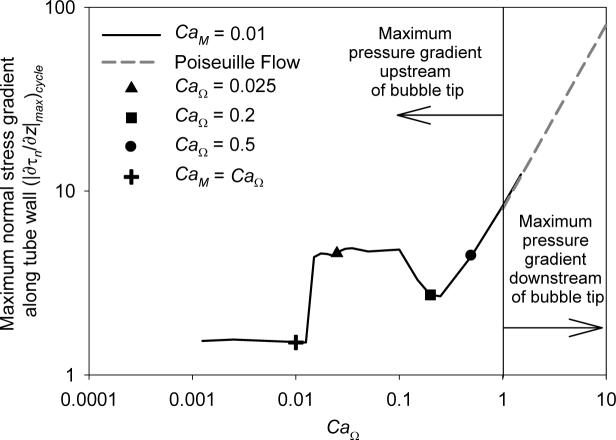
Figure 9 shows the maximum normal stress gradient along the wall at any point in the oscillatory cycle, (|∂τ_n/∂z|_max)_cycle as a function of Ca_Ω for Ca_M = 0.01 and A = 5. This figure shows that the system exhibits a quasi-steady regime (Ca_Ω < Ca_M, to the left of +) wherein (|∂τ_n/∂z|_max)_cycle is approximated by the steady-state results shown in Figure 8. The unsteady regime can be sub-divided into three regions:

Figure 9.

Maximum magnitude of the normal stress gradient along the tube wall at any point in the cycle (|∂τ_n/∂z|_max)_cycle where A = 5 and Ca_M = 0.01. + indicates the onset of reverse flow (Ca_Ω = Ca_M), data to the right of this point exhibits reverse flow. Dashed line indicates the region where the maximum normal stress gradient may be predicted by (|∂τ_n/∂z|_max)_cycle = 8(Ca_M + Ca_Ω).

Unsteady regime I

At low Ca_Ω (Ca_M < Ca_Ω ≤ 0.1), (|∂τ_n/∂z|_max)_cycle is increased dramatically due to interfacial flows near the bubble tip. The plateau region that occurs over Ca_M < Ca_Ω < 0.1 diminishes with increasing Ca_M (data not shown);

Unsteady regime II

At moderate Ca_Ω (0.1 < Ca_Ω < 0.5), the system evolves from the low Ca_Ω plateau region to the high Ca_Ω response due to local film thickening, and

Unsteady regime III

At high Ca_Ω (Ca_Ω ≥ 0.5): (|∂τ_n/∂z|_max)_cycle is equivalent to the pressure gradient due to the Poiseuille flow downstream of the bubble tip, following the form (|∂τ_n/∂z|_max)_cycle = 8(Ca_M + Ca_Ω).

Below we elucidate the relationships between the normal stress gradient and interfacial geometry in the unsteady regime as they relate to the driving parameters A and Ω.

In order to identify the interfacial characteristics that result in (|∂τ_n/∂z|_max)_cycle, we explore the behavior of |∂τ_n/∂z|_max as a function of Ca_Q(t) for Ca_Ω = 0.025, 0.2 and 0.5, which represent unsteady regimes I-III, respectively. The time-dependent responses are provided in Figure 10, where the symbols (▲, ■, • as in Figure 9) identify the specific portion of the cycle (Ca_Q(t)) associated with (|∂τ_n/∂z|_max)_cycle. Finally, in Figure 11, we plot a) ∂τ_n/∂z vs. z and b) interfacial geometry at the Ca_Q(t) corresponding to (|∂τ_n/∂z|_max)_cycle, where the symbols (▲, ■, •) precisely identify the location of (|∂τ_n/∂z|_max)_cycle.

Figure 10.

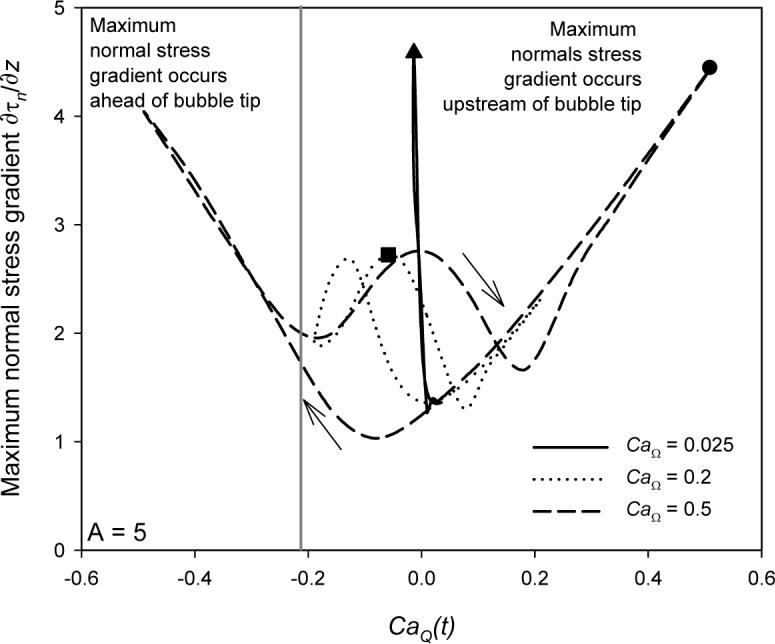
Normal stress gradient hysteresis loops for Ca_M = 0.01, A = 5. Symbols ▲, ■, and • indicate the location of (|∂τ_n/∂z|_max)_cycle for Ca_Ω = 0.025, 0.2, and 0.5 respectively.

Figure 11.

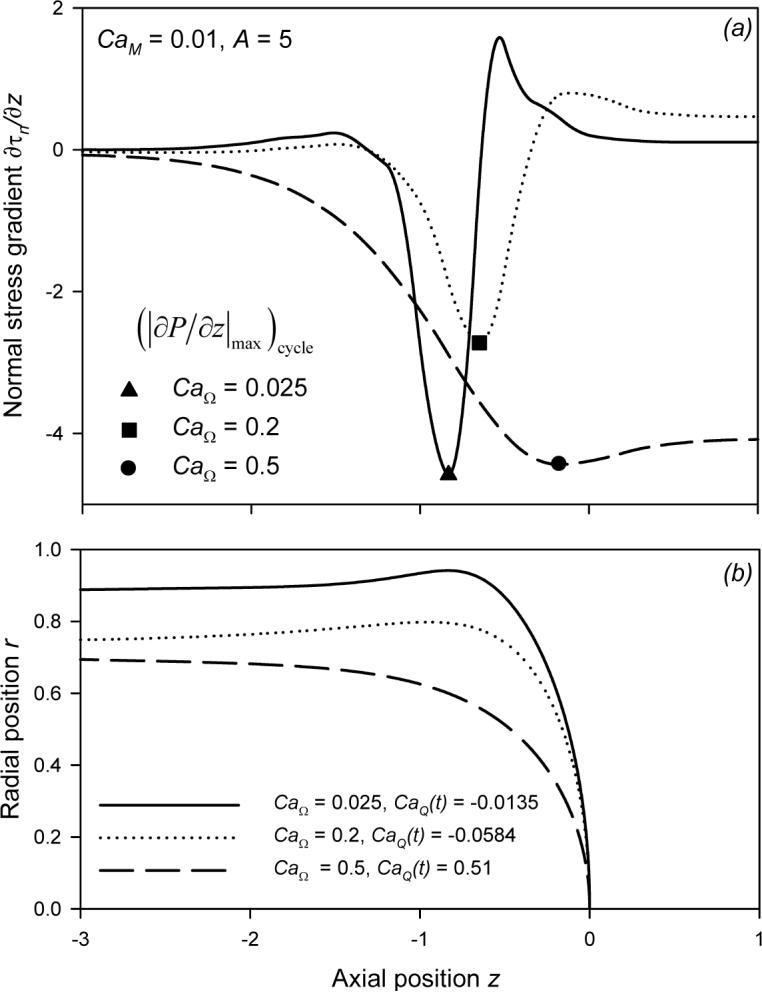
Normal stress gradient ∂τ_n/∂z (a) and interfacial geometry (b) occurring at (|∂τ_n/∂z|_max)_cycle for Ca_M = 0.01, A = 5. Symbols identify the location of (|∂τ_n/∂z|_max)_cycle and correspond to those in Figures 9 and 10.

Unsteady regime I

The time-dependent response in Figure 10 at Ca_Ω = 0.025 (solid line) corresponds to the sharp increase in the (|∂τ_n/∂z|_max)_cycle shown in Figure 9 (▲). This response demonstrates that |∂τ_n/∂z|_max varies substantially over the cycle, with the maximum value (|∂τ_n/∂z|_max)_cycle (▲) occurring as a spike on the retracting stroke near Ca_Q(t) = Ca_M - Ca_Ω. This magnitude far exceeds the |∂τ_n/∂z| that exists over the remainder of the cycle. The bubble tip geometry at this instant (Figure 11b, solid line) shows the extraordinary film thinning that occurs during this part of the reverse stroke. ∂τ_n/∂z (Figure 11a, solid line) demonstrates the extremely large normal-stress gradient that is exacerbated by this local film thinning. Therefore, the very large increase in (|∂τ_n/∂z|_max)_cycle occurs as a result of very slow bubble retraction that induces a high resistance region in the transition region between the bubble cap and thin film. The large magnitude of ∂τ_n/∂z is consistent with the predictions of the stresses that exist in the leading edge of plug propagation (Fujioka & Grotberg 2004).

Unsteady regime II

A local minimum in (|∂τ_n/∂z|_max)_cycle occurs near Ca_Ω = 0.2. The time-dependent response (Figure 10) demonstrates that this increase in frequency modifies |∂τ_n/∂z|_max substantially. Local maxima occur at several points in the cycle, but the absolute maximum (|∂τ_n/∂z|_max)_cycle occurs near Ca_Q = −0.06 (■). It is evident from the interfacial geometry (Figure 11b, dotted line) that this marked reduction in |∂τ_n/∂z|_max occurs because oscillation has caused the film to thicken, which is consistent with Figure 7b.

Unsteady regime III

With Ca_Ω = 0.5, Figure 10 shows that |∂τ_n/∂z|_max has local maxima occurring at velocity extrema and at Ca_Q = 0. (|∂τ_n/∂z|_max)_cycle (•) occurs at the maximum forward velocity. At this rate, the film has thickened substantially (Figure 11b), but the normal stress gradient remains very large due to the elevated velocity that occurs from the high Ca_Ω. This corresponds to the large-Ca_Q behavior in Figure 9 (•). In this regime (|∂τ_n/∂z|_max)_cycle is equivalent to the Poiseuille viscous pressure gradient in the tube downstream of the bubble tip, following the form (|∂τ_n/∂z|_max)_cycle = 8(Ca_M + Ca_Ω). This relationship is provided by in Figure 9.

Spatial and Temporal Behavior

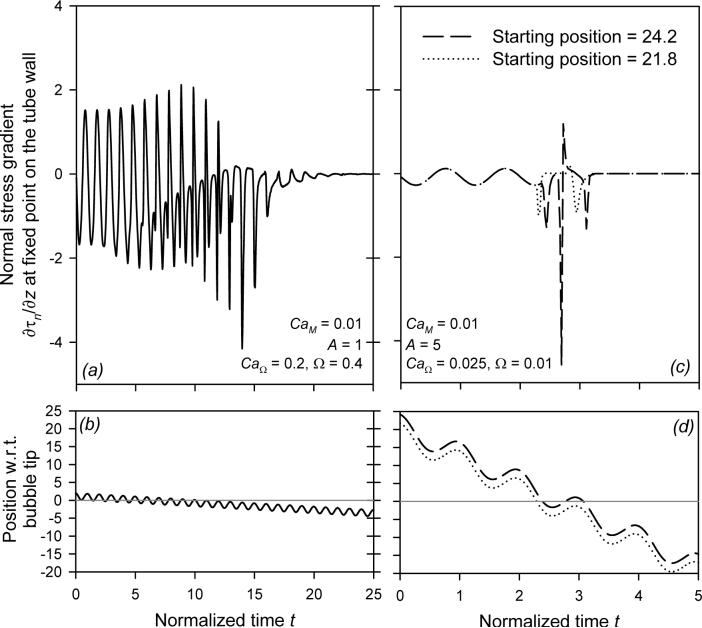
Bilek et al (2003) and Kay et al (2004) have demonstrated that the normal stress gradient is the mechanical stimulus that leads to cellular membrane disruption caused by a finger of air passing over epithelial cells in a fluid-filled channel. In this sub-section, we investigate the implications of the temporal and spatial variation of ∂τ_n/∂z, which leads to the complex signature described in Figure 12a,c.

Figure 12.

Normal stress gradient ∂τ_n/∂z at a point fixed on the tube wall (a,c) and position with respect to the bubble tip (b,d). Time is normalized so that oscillations have a period of 1.

In Figure 12a we provide the time-dependent ∂τ_n/∂z at a point fixed on the tube wall for Ca_Ω = 0.2 and A = 1. Initially this point is downstream of the bubble tip and experiences the gradient induced by the Poiseuille velocity profile. As the bubble tip approaches the fixed point (position decreasing to zero in Figure 12b), ∂τ_n/∂z is modified from pure oscillation as the interfacial ∂τ_n/∂z sweeps across the cell (see Figure 11a for an example of ∂τ_n/∂z at one instant). In this low amplitude, high frequency scenario the bubble tip repeatedly passes over the fixed point, greatly increasing the potential for trauma. After the bubble tip has passed over the fixed point the high-resistance transition region induces a large magnitude time-dependent stress. For example, near t = 14 the magnitude of ∂τ_n/∂z is at a maximum, and is qualitatively associated with the local film thinning and high resistance region that exists during the reverse flow. With increased t, the fixed point resides solely beneath a nearly uniform thin film. Only a constant τ_n exists from the radial component of the bubble curvature, ∂τ_n/∂z| ∼ 0.

To explore the spatial dependency of the stress-field, we consider the magnitude of ∂τ_n/∂z affecting two points separated by a small distance (z = 24.2 and 21.8) at A = 5 and Ca_Ω = 0.025 (Figure 12c). This small variation in location results in significantly different transient ∂τ_n/∂z during the time at which the bubble tip is passing over the points. This response occurs because each point on the wall is associated with different profiles of the time-dependent stress-field as a result of the Lagrangian translation of the bubble tip. As a result, adjoining points on the wall experience significantly different ∂τ_n/∂z signatures. The wavelength of the spatial-dependency is approximately A, but would be slightly larger due to the residual film which extends the stroke of the bubble tip according to Figure 7.

When comparing Figure 12a to Figure 12c, it is evident that both Ca_Ω and A greatly influence the stresses observed at a fixed point on the wall. For Ca_Ω = 0.2 and A = 1 (Figure 12a) the bubble passes a point on the wall 19 times, while for Ca_Ω = 0.025 and A = 5 (Figure 12c) the bubble passes by only three times. High frequency causes a region of the wall to experience more frequent exposure to the bubble tip, while increasing A leads to an extended range of bubble motion. As a result, high amplitudes and high frequency may induce repeated trauma.

5.2 Shear stress

Bilek et al (2003) and Kay et al (2004) demonstrate that normal stress gradient, not shear stress (τ_t) is primarily responsible for cellular damage in a simplified model of airway reopening. Nevertheless, other systems (i.e. epithelial cells in the vasculature) demonstrate effects that are triggered by τ_t. For this reason, we consider the relationship between τ_t and the flow parameters of our system. In the range investigated (10⁻¹ > Ca_M > 10⁻²) a strong linear correlation exists between Ca_Ω + Ca_M (the maximum Ca_Q(t)) and the maximum shear stress (τ_t)_max along the tube wall at any point in the oscillatory cycle:

$${\left({\tau }_t\right)}_{max}=4(C{a}_{\Omega }+C{a}_M).$$ [4.3]

We find that (τ_t)_max occurs upstream of the bubble tip only at low reopening velocities (Ca_Ω + Ca_M < 0.3). Note that the linear relationship between (τ_t)_max and the maximum Ca_Q(t) is likely to exist only at large Ca_Q(t); the results of Bilek et al (2003) demonstrate a weaker dependence with reducing Ca.

5.3 Limitations

In the model investigated herein we assume Stokes flow with time-dependent forcing and interfacial response dictated by the KBC (§3.5). In order to investigate the validity of the Stokes flow hypothesis, we rescale the Navier-Stokes equations with velocity- and time-scales relevant to system forcing. Scaling the Navier-Stokes equation with u* = ū_tipu and t* = (1/ω)t yields

$${\alpha }^2\frac{\partial \mathit{u}}{\partial t}+Re(\mathit{u}\cdot \nabla )\mathit{u}=-\frac{1}{C{a}_U}\nabla P+{\nabla }^2\mathit{u}$$ [4.4]

where Ca_U = μū_tip/γ. The Womersley parameter α, describing the unsteady nature of the system, is equal to

$$\alpha =R\sqrt{\frac{\omega }{\upsilon }}$$ [4.5]

where ν is the kinematic viscosity. The Reynolds number Re, the ratio of inertial to viscous forces, is defined as

$$Re=\frac{R{\stackrel{‒}{u}}_{tip}}{\upsilon }$$ [4.6]

Since the present investigation considers a balance between pressure and viscous interactions which ignores temporal and convective acceleration [2.3], Stokes flow is an appropriate approximation if the following conditions are satisfied:

$${\alpha }^{2}C{a}_U\ll 1{\alpha }^2\ll 1ReC{a}_U=We\ll 1Re\ll 1$$ [4.7]

Here the Weber number We = ReCa represents the ratio of inertial forces to surface tension.

The Womersley parameter (α) describes the balance between unsteady inertial and viscous effects. For α < 1 the downstream flow is quasi-steady and maintains a nearly parabolic profile. As α is increased the downstream flow profile will assume a more plug-like configuration and become increasingly out of phase with the driving pressure gradient. In this study we assume the flow profile downstream of the bubble is parabolic, valid when α < 1.

Heil (2001) systematically investigated the effect of Re on steady air finger propagation through a rigid channel. It was shown that variations in Re produced small variations in residual film thickness and significant changes in bubble tip pressure drop and flow field. Closed vortices were observed downstream of the bubble tip, not present in Stokes simulations. In the present investigation we neglect these inertial effects, and it is plausible that these may become significant at Re > 1. The present study provides the baseline from which inertial effects can be investigated.

While our computational methods have provided a robust means for exploring a range of parameters, at high Ω and low Ca_M numerical difficulties may interfere with the solution process. In particular, the boundary element method may suffer from poor accuracy when two boundaries are in very close proximity. This can occur at low Ca_M because the exceedingly thin film results in adjacent boundaries being separated by very small distances (r < 0.05). As a result, the time-dependent solver (DLSODES, §3.6) may fail to converge at the specified error tolerances and iteration limits. To investigate this range of parameters, one could increase the level of Gauss quadrature for integration of the boundary integral equations [2.15].

6. Conclusions

In this paper we investigate the pulsatile motion of a finger of air propagating within a rigid tube filled with a viscous Newtonian fluid. We present a two-dimensional axisymmetric model incorporating the boundary element method coupled to lubrication theory in the upstream thin-film region, driven by pulsatile flow at the downstream boundary.

We consider the time-dependent behavior of the flow field and bubble geometry throughout the course of the oscillatory cycle. The behavior of this system is well approximated by steady-state responses until the system enters the unsteady regime, Ca_Ω > Ca_M. We explore ΔP_tip, κ_tip, U_tip, and β throughout the cycle. We find that ΔP_tip may be estimated accurately ((ΔP_tip)_ext) from the pressure measured downstream of the bubble tip after correction for the viscous losses between the measuring point and the bubble tip. This relationship holds true far into the unsteady regime (Ca_Ω < 10Ca_M) and validates the use of (ΔP_tip)_ext in experimental investigation. Furthermore, we find that an increase in Ca_Ω increases the residual film ($1\text{-}\stackrel{‒}{\beta }$) that is associated with a significant increase in Ū_tip. Even though $\stackrel{‒}{\beta }$ increases during dynamic oscillation, extreme film thinning may occur at instances in the cycle. This, in turn, is correlated with a highly dynamic stress field that has very interesting temporal and spatial characteristics that may have implications to pulmonary airway damage associated with ventilator-induced lung injury. Further research will investigate the influence of coupling surfactant physicochemical hydrodynamics to this system, which may allow the predication of optimal ventilation strategies for the treatment of obstructive pulmonary disease.

Appendix

Table 1.

Boundary conditions

Region	ur	uz	τr	τz
Surface 1	0	2Ca(1 — r2)	-	-
Surface 1−2 Corner on Surface 1	-	0	−4CaR	-
Surface 1−2 Corner on Surface 2	0	-	-	−4CaR
Surface 2	0	0	-	-
Surface 2−3 Corner on Surface 2	0	-	-	$\left(\frac{{\kappa }_z}{2}\right)\left(r-\frac{r_{men}^2}{r}\right)$
Surface 2−3 Corner on Surface 3	-	0	$-\left(\frac{{\kappa }_z}{2}\right)\left(r-\frac{r_{men}^2}{r}\right)$	-
Surface 3	-	$\frac{{\kappa }_z}{2}\left(\frac{\left(r^2-1\right)}{2}-r_{men}^2\ln \left[r\right]\right)$	$-\left(\frac{{\kappa }_z}{2}\right)\left(r-\frac{r_{men}^2}{r}\right)$	-
Surface 3−4 Corner on Surface 3	-	$\frac{{\kappa }_z}{2}\left(\frac{\left(r^2-1\right)}{2}-r_{men}^2\ln \left[r\right]\right)$	0	-
Surface 3−4 Corner on Surface 4	-	-	-κnr	-κnz
Surface 4	-	-	-κnr	-κnz