Spectral Characteristics of a 140-GHz Long-Pulsed Gyrotron

Abstract

Gyrotrons operating in the millimeter and submillimeter wavelength ranges are the promising sources for applications that are requiring good spectral characteristics and a wide range of output power. We report the precise measurement results of gyrotron spectra. Experiments were conducted using a 140-GHz long-pulse gyrotron that is developed for the dynamic nuclear polarization/nuclear-magnetic-resonance spectroscopy at the Massachusetts Institute of Technology. Transient downshift of the frequency by 12 MHz with a time constant of 3 s was observed. After reaching equilibrium, the frequency was maintained within 1 ppm for over 20 s. The coefficient of the frequency change with cavity temperature was −2.0 MHz/K, which shows that fine tuning of the gyrotron frequency is plausible by cavity-temperature control. Frequency pulling by the beam current was observed, but it was shown to be masked by the downward shift of the gyrotron frequency with temperature. The linewidth was measured to be much less than 1 MHz at 60 dB relative to the carrier power [in decibels relative to carrier (dBc)] and 4.3 MHz at 75 dBc, which is the largest dynamic range to date for the measurement of gyrotron linewidth to our knowledge.

I. Introduction

IN RECENT years, an intensive search for radiation sources with good spectral characteristics and reasonable output power at millimeter and submillimeter wavelengths has been conducted for a great number of research projects and practical applications [1], [2]. In a number of recent successful applications using gyrotrons, such as dynamic nuclear polarization enhanced nuclear magnetic resonance [dynamic nuclear polarization (DNP)/nuclear magnetic resonance (NMR)] to investigate the structures of bio-molecular systems [3], [4] and collective Thomson scattering (CTS) to diagnose the plasmas [5]–[7], an improved knowledge of the source spectral characteristics and cleaner more stable frequency operation are of critical importance. To satisfy these challenging requirements, Massachusetts Institute of Technology (MIT) has been developing gyrotrons [8]–[12] and measurement systems [13], [14].

The gyrotron is a vacuum electron device based on the cyclotron resonance interaction between an electron beam and electromagnetic waves in a resonant cavity [15]. Using a smooth wall interaction structure, whose transverse dimensions are many wavelengths at the operating frequency, gyrotrons have the ability to generate very high power when compared to the slow wave microwave tubes such as klystrons, backward wave oscillators, or solid-state devices at the millimeter and submillimeter wavelength regions.

For the applications listed previously, a knowledge of the spectral characteristics of gyrotrons is very important. For example, for the CTS to diagnose ion energy distribution and instabilities in plasmas, it requires high spectral purity and narrow linewidth over a large dynamic range to insure that the measured signals only originate from the plasma and not from a stray reflection [14]. In the DNP/NMR experiments, significant enhancement of the signal-to-noise ratio only occurs when the highly populated spin polarization of the electrons can be transferred to the less populated nuclear one. Consequently, the DNP mechanism also needs high spectral resolution and stability to match the driving frequency to the electron-spin-resonance spectrum of the paramagnetic species in the sample [3].

Therefore, we report the precise measurements of gyrotron spectra bearing those applications in mind and discuss the physical mechanism and its implications. This paper is organized as follows. In Section II, the experimental setups, including the 140-GHz long-pulse gyrotron and the heterodyne frequency measurement system, are briefly overviewed. Detailed results on frequency downshifts, frequency control by cavity temperature, and frequency pulling by current are presented in Section III, followed by the linewidth measurement in the largest dynamic range. In the final section, the results are summarized.

II. Experimental Setups

To study the spectral characteristics of gyrotron emission, we used a 140-GHz gyrotron operating in pulses with a duration of 30 s (Figs. 1 and 2). To date, this 140-GHz gyrotron has been employed in DNP experiments with a 212-MHz (5-T) NMR spectrometer at MIT. The typical operating parameters are listed in Table I. The 140-GHz gyrotron is capable of producing 15-s long output pulses at 50% duty cycle. For single pulse operation, an output pulse as long as 5 min is readily achievable. The TE₀₃ operating mode in the cavity is converted into the TE₀₁ mode by an internal mode converter. Outside the gyrotron, the TE₀₁ mode is converted to the TE₁₁ mode using a serpentine rippled wall mode converter. Details of this gyrotron are given in [8].

Fig. 1.

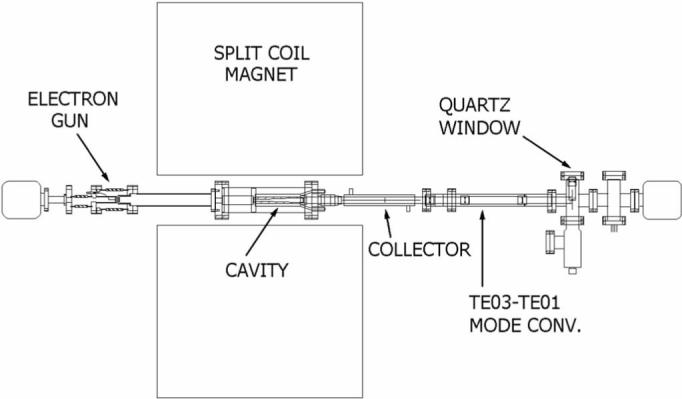
Schematic diagram of the gyrotron used for this experiment. The basic components of the gyrotron include a magnet, an electron gun, and a vacuum tube which consists of a beam tunnel, a resonator, and a mode converter and collector.

Fig. 2.

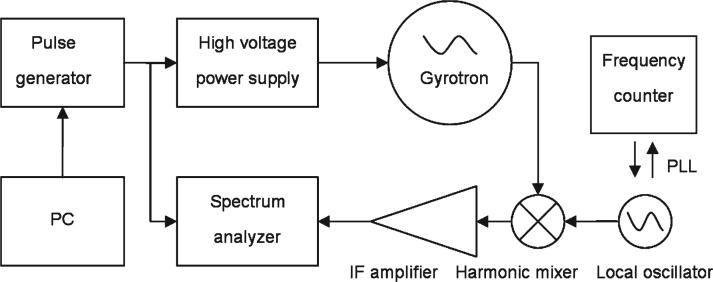
Block diagram of the heterodyne system that is used to measure the spectral characteristics of the pulsed gyrotron. A trigger signal with a repetition rate of 0.01 Hz is generated by the computer and sent to the pulse generator, which is used to control the pulse of the high-voltage power supply and to gate the SA. A segmented sweep over the duration of the pulse was made by changing the delay of the time gate in the SA.

TABLE I.

Operational Parameters and Resulting Output Power of the 140-GHz Gyrotron for the DNP/NMR Experiments

	140 GHz
Operation voltage, Vo (kV)	12
Beam current, Io (mA)	25
Operating mode	TE031
Tube output mode	TE01
Magnetic field, Bo (T)	5.1
Cyclotron harmonic number	1
Output power (W)	14

The gyrotron output was sampled by a mirror and a 1.5-m long Ka-band waveguide and delivered to the area where the fringe magnetic field intensity is below 5 G. This pickoff sample of the gyrotron beam was frequency downshifted by a heterodyne receiver. The harmonic heterodyne-receiver system employed a low-frequency local oscillator (LO) between 18 and 26.5 GHz and a harmonic mixer to mix the gyrotron signal with the seventh harmonic of the LO (Micro-Lambda YIG oscillator). The LO frequency was counted by a frequency counter (Phase Matrix EIP 578 B) and locked by a phased-locked loop stabilizing the LO to 10 kHz. The intermediate frequency (IF) from the mixer was amplified by a series of low noise amplifiers and detected by a spectrum analyzer (SA) with a dynamic range of 90 dB. To keep the 10-kHz resolution of the locked LO, the sweep time of the SA (Agilent E4404B) was set to over 1 ms, and the resolution bandwidth is fixed at 10 kHz.

III. Frequency Variation

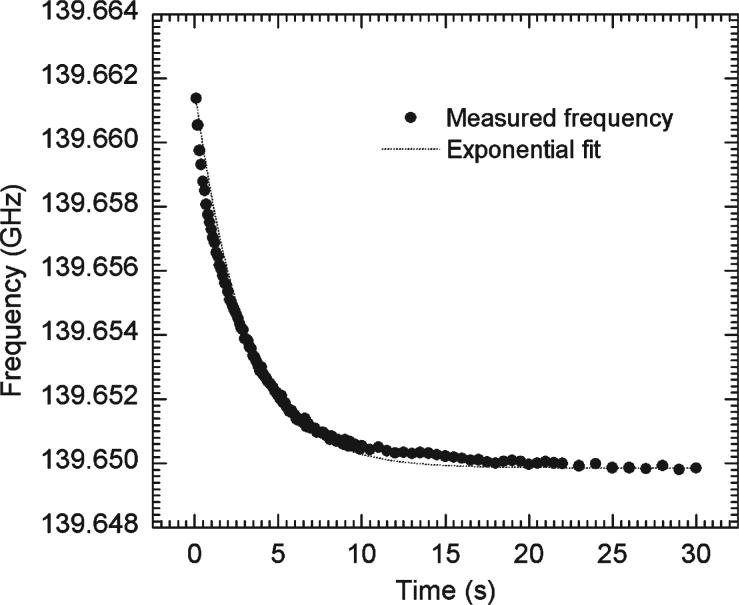
Fig. 3 shows the frequency variation over the duration of the gyrotron pulse. A transient downward frequency shift of 12 MHz has been observed. In comparison with the exponential fitting curve, the time constant is estimated to be approximately 3 s. After several tens of seconds, the frequency reaches equilibrium and remains stable to within 1 ppm for the rest of the pulse.

Fig. 3.

Frequency shift over the duration of a pulse at 12.9 kV, 30 mA, and repetition rate of 0.01 Hz. Solid dots represent the measured data, and the solid line is a curve fitted to an exponential function. The SA is set to a 14-ms sweep time and 30-kHz resolution bandwidth.

For the long-pulse gyrotrons, a frequency downshift with longer time constant (> 1 s) is a common feature [16]–[18], but the physical mechanism of the slow-frequency downshift is still not completely understood, as mentioned in [19] and [20]. Possible explanations for the frequency downshift in this system are the following: 1) thermal expansion of the resonant cavity due to ohmic heating of the cavity walls; 2) neutralization of dc space charge fields of electron beam by impact ionization; and 3) resonance frequency modification of the cavity by the background plasma.

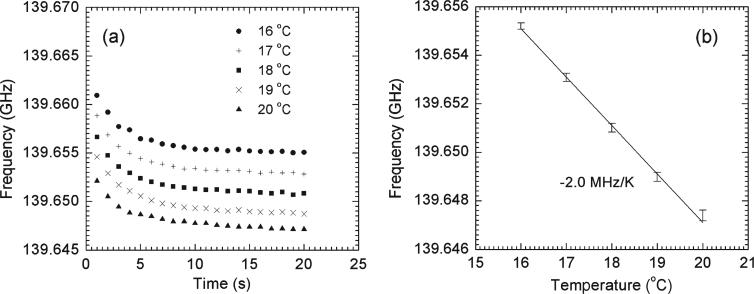
The sensitivity of the frequency shift due to thermal expansion was measured by changing the temperature of the cavity coolant, which is water in our case (Fig. 4). A recirculating chiller with the temperature precision of ±0.1° controls the cavity temperature during operation. Averaging the frequencies after saturation (from 10 to 20 s), a linear coefficient of −2 MHz/K was obtained, which is consistent with the theoretical value of −2.3 MHz/K, assuming a thermal expansion coefficient of ideal copper without external constraints. This demonstrates that frequency fine tuning of a gyrotron could be possible with precise cavity-temperature control. The observed frequency downshift in Fig. 3 could be explained by the thermal expansion of the resonant cavity if the temperature rise of the cavity was about 6 °C.

Fig. 4.

(a) Frequency variation over the duration of the pulse with respect to the cavity temperature (the temperatures are set values in the recirculating chiller). (b) Frequency change as a function of the temperature, where the frequencies are averaged values after reaching equilibrium (from 10 to 20 s).

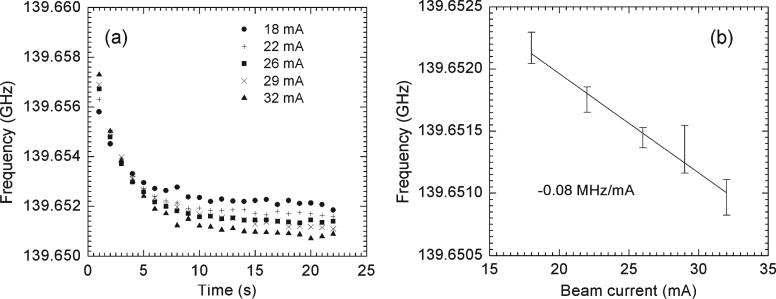
Fig. 5 shows the frequency variation as the electron beam current was changed. At the start of a pulse, frequency pulling by beam current [21]–[23] was observed with a coefficient of +0.1 MHz/mA. From the simulations using a nonlinear gyrotron code that is called Maryland Gyrotron (MAGY) [24], a positive slope of frequency pulling by the beam current was predicted to be +0.5 MHz/mA. However, the frequency downshift due to the thermal expansion of the cavity and/or plasma formation overwhelms the frequency pulling by the electron beam within a few seconds after the onset of emission. As a consequence, a negative coefficient of −80 kHz/mA was observed after the frequency reached equilibrium, as shown in Fig. 5(b), which explains why MAGY results, ignoring the frequency downshift due to higher power and cavity thermal effect, have a higher coefficient than measured at 1 s.

Fig. 5.

(a) Frequency variation over the duration of the pulse with respect to the beam current. The beam current was maintained by controlling the heater current. (b) Frequency change as a function of the beam current, where the frequencies are averaged values after reaching equilibrium.

IV. Linewidth Measurement

Gyrotron radiation has a finite linewidth which can be attributed to both intrinsic noise sources such as the shot effect of the electron beam and thermal noise, as well as the extrinsic technical noise sources such as fluctuations in the operating parameters [25]. Linewidth and lineshape measurements of the gyrotron are very important in applications that are utilizing a frequency shift by scattering, for example, radar [26] and CTS [5]–[7]. DNP/NMR also require a narrow linewidth to match the exact frequency in the EPR spectrum for maximum signal enhancement in NMR [3]. In order to measure the linewidth of the gyrotron over a large dynamic range, we used a low noise harmonic-mixer receiver. The input power to the mixer was increased to maximize the observable dynamic range. The resulting strong IF signal caused the IF amplifier to gain compression, lowering the SA noise floor down to −80 dBm from the −70 dBm small signal level. As a consequence, we had a conservative observable dynamic range of up to 80 dB.

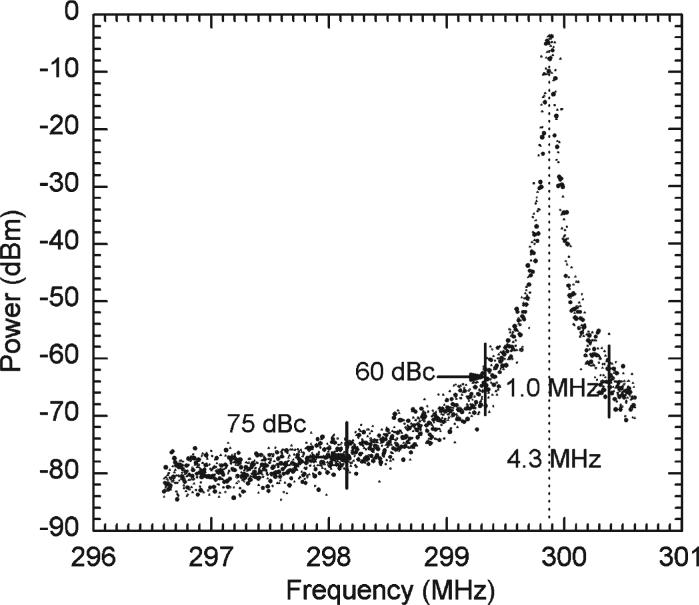
Three separate frequency sweeps lasting 0.1 s each have been overlapped in Fig. 6 to estimate the linewidth and lineshape. The power level of the center frequency (299.87854 MHz) in the IF domain is about −3.5 dBm. Therefore, the 60-dB relative to the carrier-power [in decibels relative to carrier (dBc)] linewidth at −63.5 dBm is measured to be around 1.0 MHz, and the 75-dBc linewidth at −78.5 dBm is estimated to be 4.3 MHz, respectively, which is the largest dynamic range for the measurement of gyrotron spectra to our knowledge. After converting the power scale into a linear ratio relative to the peak power, the full-width at half-maximum (FWHM) linewidth is calculated to be 72 kHz. The true FWHM linewidth of the gyrotron could be narrower, as shown in [27] and [28], because the linewidth in the heterodyne measurement is the convolution of the LO with the gyrotron, i.e., the detection limit is set by the phase noise of the LO circuit and harmonic noise in the mixer. The linewidth of the LO was directly measured to be 0.14 MHz at 60 dBc, using the SA ranging the frequency from 10 kHz to 26.5 GHz. Multiplication of the LO linewidth by the harmonic number (0.14 MHz multiplied by 7) is approximately equal to the linewidth of the gyrotron (1 MHz) that is measured using the LO. This means that the true linewidth of the gyrotron is likely to be narrower than the measured one.

Fig. 6.

Spectral linewidth of the 140-GHz gyrotron in the IF domain, in which the LO frequency was locked at 19.99400 GHz, and its seventh harmonic was mixed with the gyrotron frequency. For this measurement, the SA was set to 10 kHz of resolution bandwidth and 100 ms of sweep time. Sweeping was delayed by 10 s to wait until the frequency was stabilized after the onset of radiation.

V. Summary

In this paper, we reported the spectral characteristics of gyrotron emission using the 140-GHz long-pulsed gyrotron that is developed for the DNP/NMR spectroscopy at MIT. As with other long-pulse gyrotrons, the frequency was down-shifted during the pulse. In our measurements using the 10-W 140-GHz gyrotron, the measured frequency downshift was 12 MHz and saturated after 10 s with a time constant estimated to be about 3 s. After reaching equilibrium, the gyrotron frequency remained stable to within 1 ppm for the remainder of the 30-s pulse. The coefficient of the frequency tuning as a function of the cavity temperature was measured to be −2.0 MHz/K, which is consistent with that expected for the thermal expansion of the cavity. This observation supports the possibility of fine tuning the gyrotron frequency by cavity-temperature control. Frequency pulling by beam current was observed, but this effect was shown to be hidden by the frequency pulling due to thermal expansion or other effect such as background plasma formation. In addition, the linewidth was shown to be much less than 1 and 4.3 MHz at 60 and 75 dBc, respectively, which is the largest dynamic range for the fine resolution measurement of gyrotron spectra to our knowledge. These results show that gyrotrons operating in the millimeter and submillimeter wavelength ranges are the promising sources for applications requiring good spectral characteristics and reasonable output power.

Biography

Seong-Tae Han received the B.S. degree in physics education and the M.S. and Ph.D. degrees in physics from Seoul National University (SNU), Seoul, Korea, in 1999, 2001, and 2005, respectively.

As a Research Assistant, he participated in developing the ultrawideband TWTs for jamming and satellite communication. In addition, he built the first-working lithographie galvanoformung und abformung (LIGA)-fabricated folded waveguide TWT and developed a delayed feedback oscillator at Ka-band. He was a Researcher in the Research Institute of Basic Science, SNU, in 2005, where his research focused on developing the advanced vacuum electron devices to bridge the terahertz gap by employing recent innovations such as photonic crystal concept and nano/MEMS fabrication. Since September 2005, he has been a Postdoctoral Research Associate in the Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge. He currently works on the development of subterahertz continuous-wave gyrotrons and their applications, including imaging and hyperthermia. Other research interests cover high-power RF applications such as electron cyclotron heating of fusion plasmas and charged particle acceleration for medical use.

Robert G. Griffin received the B.S. degree in chemistry from University of Arkansas, Fayetteville, in 1964, and the Ph.D. degree in physical chemistry from Washington University, St. Louis, MO, in 1969. He did his postdoctoral research in physical chemistry at the Massachusetts Institute of Technology (MIT), Cambridge, with Prof. J. S. Waugh.

In 1972, after completing his postdoctoral training, he assumed a staff position at the Francis Bitter National Magnet Laboratory (FBML), MIT. In 1984, he was promoted as the Senior Research Scientist and was appointed to the faculty in the Department of Chemistry, MIT, in 1989. In 1992, he became the Director of the FBML and is concurrently the Director of the MIT-Harvard Center for Magnetic Resonance, where he has been the Associate Director since 1989. He has published more than 300 articles concerned with the magnetic resonance methodology and applications of magnetic resonance [nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR)] to studies of the structure and function of a variety of chemical, physical, and biological systems. In the last decade, this research has focused on the development of methods to perform the structural studies of membrane and amyloid proteins and on the utilization of high-frequency (> 100 GHz) microwaves in EPR experiments and in the development of dynamic nuclear polarization/NMR experiments at these frequencies. He has served on numerous advisory and review panels for the National Science Foundation and the National Institutes of Health.

Kan-Nian Hu received the B.A. and M.S. degrees in chemistry from National Taiwan University, Taipei, Taiwan, R.O.C., in 1996 and 1998, respectively, and the Ph.D. degree in physical chemistry from Massachusetts Institute of Technology (MIT), Cambridge, in 2006.

Since he joined the field of magnetic resonance in 1996, he has been involved in projects, including pulsed field gradient nuclear magnetic resonance (NMR) for diffusion phenomena, solid-state multiple quantum magic angle spinning NMR, high-field (> 5 T) dynamic nuclear polarization in solids, and electron spin resonance for distance measurements. He is currently a Visiting Fellow at the National Institutes of Health, Bethesda, MD.

Chan-Gyu Joo received the B.S. and M.S. degrees in chemistry from Korea University, Seoul, Korea, and the Ph.D. degree in physical chemistry from Indiana University, Bloomington.

Since 2002, he has been a Postdoctoral Researcher in the Francis Bitter Magnet Laboratory, Massachusetts Institute of Technology, Cambridge. His principal research interest is dynamic-nuclear-polarization NMR spectroscopy in liquid and solid state.

Colin D. Joye (S'03) received the B.S. degree in electrical engineering and computer science from Villanova University, Villanova, PA, in 2002, and the M.S. degree in electrical engineering and computer science from Massachusetts Institute of Technology (MIT), Cambridge, in 2004, where he is currently working toward the Ph.D. degree.

In 2002, he was with the Waves and Beams Division, Plasma Science and Fusion Center, MIT, as a Research Assistant. His current research interests include gyrotron oscillator and amplifier sources at the millimeter and submillimeter wavelengths.

Jagadishwar R. Sirigiri (S'98–M'02) received the B.Tech. degree in electronics and communication engineering from Institute of Technology, Banaras Hindu University (BHU), Varanasi, India, in 1996, and the M.S. and Ph.D. degrees in electrical engineering and computer science from Massachusetts Institute of Technology (MIT), Cambridge, in 1999 and 2002, respectively.

From 1994 to 1996, he was associated with the Center of Research in Microwave Tubes, BHU, where his research areas included TWTs and gyro-TWTs. He is currently a Research Scientist in the Plasma Science and Fusion Center, MIT. He is involved in the design and development of novel high-power gyrotrons and gyrotron amplifiers at millimeter-wave frequencies. His research interests include novel microwave sources and amplifiers in the millimeter and terahertz regime, quasi-optical structures and photonic-band-gap structures, and their applications in microwave vacuum electronics.

Richard J. Temkin (M'87–F'94) received the B.A. degree in physics from Harvard College, Cambridge, MA, and the Ph.D. degree in physics from Massachusetts Institute of Technology (MIT), Cambridge.

From 1971 to 1974, he was a Postdoctoral Research Fellow in the Division of Engineering and Applied Physics, Harvard University, Cambridge. Since 1974, he has been at MIT, first at the Francis Bitter National Magnet Laboratory and later at the Plasma Science and Fusion Center (PSFC) and the Department of Physics. He currently serves as a Senior Scientist in the Physics Department, as Associate Director of the PSFC, and Head of the Waves and Beams Division, PSFC. His research interests include novel vacuum electron devices such as the gyrotron and free electron laser, advanced high-gradient electron accelerators, quasi-optical waveguides and antennas at millimeter wavelengths, plasma heating, and electron spin resonance spectroscopy. He has been the author or coauthor of over 200 published journal articles and book chapters and has been the editor of six books and conference proceedings.

Dr. Temkin is a Fellow of the American Physical Society and The Institute of Physics, London, U.K. He was the recipient of the Kenneth J. Button Prize and Medal of The Institute of Physics, London, and the Robert L. Woods Award of the Department of Defense for Excellence in Vacuum Electronics Research.

Antonio C. Torrezan (S'04) received the B.S. and M.S. degrees in electrical engineering from State University of Campinas, Campinas, Brazil, in 2004 and 2005, respectively. He is currently working toward the Ph.D. degree at the Massachusetts Institute of Technology (MIT), Cambridge.

From 2003 to 2005, he was associated with the Brazilian Synchrotron Light Laboratory where his research was focused on the development of an X-band electron-paramagnetic-resonance spectrometer for samples with small number of spins. In 2004, he worked as an intern at the Brazilian Aeronautics Company (Embraer) in the area of control systems. Since 2005, he has been a Research Assistant in the Plasma Science and Fusion Center, MIT. His research interests include millimeter-wave technologies and submillimeter-wave sources such as the gyrotron.

Paul P. Woskov (S'74–M'76–SM'99) received the Ph.D. degree in electrical engineering from Rensselaer Polytechnic Institute, Troy, NY, in 1976.

In 1976, he was with the Francis Bitter National Magnet Laboratory, Massachusetts Institute of Technology (MIT), Cambridge, where, since 1980, he has been in the Plasma Science and Fusion Center, MIT. He is currently a Principal Research Engineer and Associate Division Head in the Plasma Technology Division. His principal interests include plasma diagnostics, fusion energy, millimeter-wave technologies, and environmental applications of plasmas and millimeter waves.

Dr. Woskov is a member of the American Physical Society, the American Chemical Society, and the American Association for the Advancement of Science.