The response of a spherical tissue-equivalent proportional counter to different heavy ions having similar velocities

Abstract

A tissue-equivalent proportional counter (TEPC) has been used as a dosimeter in mixed radiation fields. Since it does not measure LET directly, the response function must be characterized in order to estimate quality factor and thus equivalent dose for the incident radiation. The objectives of this study were to measure the response of a spherical TEPC for different high-energy heavy ions (HZE) having similar velocity and to determine how quality factors can be determined. Data were obtained at the HIMAC heavy ion accelerator for ⁴He and ¹²C at 220 ± 5 MeV/nucleon (β = 0.59) and ¹²C, ¹⁶O, ²⁸Si and ⁵⁶Fe at 376 ± 15 MeV/nucleon (β = 0.70). A particle spectrometer recorded the charge and position of each incident beam particle. Events with low energy deposition were observed for particles that passed through the wall of the TEPC but not through the sensitive volume. The frequency averaged lineal energy, ȳ_f, was always less than the LET of the incident particles. The dose averaged lineal energy, ȳ_D, was approximately equal to LET for particles with LET greater than 10 keV/μm, whereas ȳ_D was larger than LET for the lighter particles with lower LET. Part of this effect is due to detector resolution and energy straggling that increases the variance of the response function. Although the TEPC is not a LET spectrometer, it can provide real time measurements of dose and provide estimates of quality factors for HZE particles using averaged values of lineal energy.

1. Introduction

Exposure to radiation fields consisting of high-atomic-number and high-energy (HZE) particles can exist during manned space missions and near particle accelerators used for research and radiation therapy. Human exposure to HZE particles from galactic cosmic radiation (GCR) is of concern because the frequency and duration of manned space activities is increasing (NRCSSB, 1996). Although the relative number of HZE particles heavier than helium is only about 1% of the GCR, their contribution to dose can be significant (Wefel, 1978). Medical facilities are using accelerators to produce clinical beams of protons and carbon ions for tumor therapy (Proton Beam Therapy, 2004; GSI, 2004; NIRS, 2004). In addition to dosimetry for these situations, it is necessary to determine the quality of the incident radiations in order to characterize their relative biological effectiveness (RBE). For radiation protection, a radiation weighting factor, w_r, has been defined to compensate for differences in RBE between different types of radiation (NCRP, 1993). Multiplying the absorbed dose by the proper w_r yields an equivalent dose that relates the radiation risk of stochastic effects to the specific exposure. For mixed fields and radiations without a defined w_r, the ICRP gives a formula for calculating a radiation quality factor, Q, which is a function of the linear energy transfer (LET) of the incident particle (NCRP, 1993; ICRP, 1991).

LET only describes energy loss occurring along the trajectory of the primary charged particle. In this sense, energy deposition can only be described when the particle intercepts a point or volume of interest. It neglects the radial dimensions of a track caused by secondary electrons (delta-rays) that can have considerable range when the velocity of the heavy particle is large. There have been attempts to address this problem by introducing the concept of restricted linear energy transfer (LET_Δ), but this has never been applied to recommendations that formally assess radiation quality (ICRU, 1968).

The ideal approach to radiation protection in mixed fields is to use a detector that can measure patterns of energy deposition within volumes of material that are important for biological considerations. It should respond to particles that pass through the volume of interest as well as to delta-rays from particles that pass near but not through this volume. One solution is a tissue-equivalent proportional counter (TEPC). Rossi and Rosenzweig (1955) developed the first TEPC to simulate the measurement of energy deposition in volumes of tissue with dimensions similar to the nucleus of a mammalian cell. The conventional TEPC¹ used today has a rigid wall made of tissue-equivalent plastic, surrounding a gas-filled cavity. An anode wire extends through the center of this gas cavity. Spherical detectors often have a helical grid wire surrounding the anode in order to form a uniform electrical field for ion-pair multiplication. Simulation of energy deposition in volumes with dimensions of a few micrometers is accomplished by operating the TEPC at a low pressure. However, the density difference between the solid wall and the gas cavity can alter the pattern of energy deposition from that in a homogenous medium since the spatial distribution of delta-rays produced in a volume of material is directly related to density of the material. Nevertheless, this type of detector has found wide applications in applied dosimetry (Cucinotta et al., 2000; Badhwar, 2000, 2002; Doke et al., 2001; Chee et al., 2000; Walters et al., 2000; Tume et al., 2000; Lindborg et al., 1999; Burmeister et al., 2002).

Galactic cosmic rays encountered in space range in Z from 1 to 26 with energies from 50 MeV/nucleon to over 1000 MeV/nucleon. It would not be practicable to measure the response of a TEPC to the complete spectrum of particles. We have undertaken a systematic approach to determining the effects of charge and velocity (MeV/nucleon) on detector response:

1. Determine the response as a function of velocity for fixed Z.

2. Determine the response as a function of Z for fixed velocity.

3. Determine the response as a function of Z and velocity for fixed LET.

Parts 1 and 3 have reported in the literature (Rademacher et al., 1998; Gersey et al., 2002; Guetersloh et al., 2004; Nikjoo et al., 2002). These experiments were unique because the TEPC was part of a charged-particle spectrometer that recorded the location and identity of each incident particle. This made it possible to recall data and reconstruct the trajectory of each particle as it passed near or through the TEPC.

The work presented here is a description of experiments in part (2) described above. The objective was to examine the response of the same spherical TEPC to particles with different atomic number but with similar velocities. Thus the energy distribution of secondary electrons remained the same but the intensity would scale as Z² or LET. The data consisted of response functions for two ions, ¹²C and ⁴He, at 220±7 MeV/nucleon (β = 0.59) and four ions, ⁵⁶Fe, ²⁸Si, ¹⁶O and ¹²C, at 376 ± 15 MeV/nucleon (β = 0.70).

The ultimate goal is to form a complete understanding of detector response to HZE particles that can be used to design a comprehensive dosimeter for radiation protection in space and near high energy particle accelerators.

2. Materials and methods

Experiments were performed at the heavy ion medical accelerator (HIMAC) operated by the National Institute of Radiological Sciences in Chiba, Japan (NIRS, 2004). The facility is capable of accelerating a large selection of ions from protons to xenon with energies ranging from 100 to 800 MeV/nucleon. It is therefore possible to design research experiments for physics and radiation biology using heavy ions that are similar to primary particles in the space radiation environment.

The original objective was to study the response of a spherical TEPC to monoenergetic particles from Z = 2 to 26 at an energy of 376 MeV/nucleon. Because of shielding constraints, it was not possible to obtain the lighter ions at this energy. Thus the experiment was divided into two groups. One group consisted of ⁴He and ¹²C, at 220 ± 5 MeV/nucleon (β = 0.59) and the other group consisted of ¹²C, ¹⁶O, ²⁸Si and ⁵⁶Fe at 376 ± 15 MeV/nucleon (β = 0.70). The reasoning was that the two carbon beams would serve as link between the two energies. A summary of the beam characteristics is included in Table 1. The beam intensity was controlled to about 1000 heavy ions per spill. The beams were defocused to a uniform distribution approximately 20 mm in diameter.

Table 1.

Properties of the particle beams

Ion	E (MeV/n)	β	Diameter (μm)	εmin (keV)	LET (keV/μm)	ȳf (keV/μm)	ȳD (keV/μm)
4He	225	0.59	3	0.30	1.68	1.56	2.58
12C	215	0.58	3	0.60	15.6	13.4	16.1
12C	389	0.71	1	0.35	11.2	9.93	12.4
16O	385	0.71	1	0.40	19.9	17.9	20.8
28Si	375	0.70	1	0.45	61.9	50.4	59.8
56Fe	355	0.69	1	3.0	219	184	224

The orientation of the detectors used in this investigation is shown in Fig. 1. A spherical TEPC with a sensitive volume diameter of 12.7 mm and wall thickness of 2.54 mm was used in all experiments and was identical to the instrument used in previous studies (Rademacher et al., 1998; Gersey et al., 2002; Guetersloh et al., 2004; Borak et al., 2004). The high voltage for the TEPC was set to 595 V for the β = 0.70 ions and 610 V for the β = 0.59 ions. The density of the propane-based tissue-equivalent gas was set to 33 Torr to simulate a tissue diameter of 1 μm for the higher-velocity ions and 99 Torr to simulate a tissue diameter of 3 μm for the lower-velocity ions (Waker, 1995). Over 5 × 10⁵ events were recorded for each ion.

Fig. 1.

Schematic diagram of the experimental arrangement showing the position of the TEPC relative to the position-sensitive detectors, PSD.

The TEPC was calibrated using an internal ²⁴⁴Cm alpha source as well as an external Pu–Be neutron source, giving a total of four calibration points. Alpha particles from an internal source passed through a collimator giving trajectories through the center of the gas cavity and thus a simulated path of 1 μm or 3 μm for a density of 1 g/cm³. A distribution of alpha particles interacting with the central anode of the TEPC provided a calibration point corresponding to a path of approximately one half of the diameter since these alpha particles stopped in the anode. An alpha edge was also observed for alpha particles nearing the end of their range. For the external neutron source, the point of maximum energy deposition by recoil protons, the proton edge, was the fourth calibration point. An EG&G ORTEC² research pulser was also used to further establish linearity of the data acquisition system, ensuring that the four calibration points found by the source method could be related to energy deposition events in all other channels.

The TEPC was located between four pairs of position-sensitive lithium-drifted silicon detectors (PSDs) that served as a charged-particle spectrometer (Zeitlin et al., 1994; Wong et al., 1990). Two PSD pairs were mounted upstream of the TEPC, and two downstream. The PSDs were fabricated in the shape of circular disks with radii of 22 mm and thicknesses between 800 and 1050 μm. The total charge collected on one side of the detector was proportional to the total amount of energy deposited in the PSD by the particle and was used in off-line analysis to identify the particle. On the other side of the detector, charge was divided between the top (q₁) and bottom (q₂) of each vertical PSD, or left (q₁) and right (q₂) of each horizontal PSD. The amounts of charge collected in q₁ and q₂ were related to the horizontal (U_i) or vertical (V_i) position of the incident ion. The energy imparted as well as the transverse locations within the detectors were recorded and stored for each incident particle. The location of the PSD along the beam axis provided the third spatial dimension (Z₀) of the particle.

An additional lithium-drifted silicon detector, labeled “3 mm” in Fig. 1, was mounted downstream of the TEPC. This detector had a thickness of 3.0 mm and a radius of 12.7 mm and was used to increase the efficiency of triggering by ensuring that incident ions well outside the detection capability of the TEPC were not processed by the data acquisition logic.

Triggering was done both with and without the TEPC in coincidence with the 3mm detector. For each trigger, the signal from the TEPC was sent to an external EG&G ORTEC 142AH charge-sensitive preamplifier and then split into two EG&G ORTEC 572 shaping amplifiers. The difference in amplification was optimally set to obtain detailed information on the full spectrum of energy deposition events. The signals from each PSD, the 3 mm detector, and each shaping amplifier were sent to analog-to-digital converters. The data were saved to disk on an event-by-event basis.

Off-line data processing began with an analysis of the information recorded by each PSD. Since energy deposited in the PSD was proportional to the square of the charge of the ion, a peak was observed for the primary accelerated ion. Fragments and noise contributed to smaller, less developed peaks and wide tails. Elimination of all events that are not in the peak corresponding to the primary particle for each PSD ensured that the incident particle passed through the entire spectrometer.

Cartesian coordinates were also returned by the PSDs. A procedure using a carefully machined 25.4-mm-thick brass grid collimator was used to calibrate each PSD (Wong et al., 1990). A third-order multiple regression model was selected using SAS,³ taking into account the results of both the backward elimination method (Ott, 1993) with α = 0.5 and minimizing the C_p statistic (Mallows, 1973). All interaction terms were considered in the model selection, and lower-order hierarchical terms were included in the final models. The result was in effect a mapping of the measured coordinates, U_i and V_i into the true coordinates, X_i and Y_i, within the PSD. PSD2 and PSD3 were used to reconstruct the transverse coordinates, X₀ and Y₀, of the particle at a longitudinal position corresponding to the center of the TEPC. The impact parameter was defined as the radial distance from the center of the TEPC.

3. Results

There was no attempt to actively suppress electronic noise in the TEPC and amplifiers. During each run, the data acquisition system was also triggered by a pulse generator running at a fixed rate of either 1 or 10 Hz. These events were identified in the off-line analysis as a signal in the TEPC with no energy signal above noise in any of the silicon detectors. This distribution of signals in the TEPC constituted background and noise. Based on these data, a threshold was determined such that signals corresponding to energy depositions below this value could not be distinguished from noise. The values of the threshold, ε_min, for each ion are shown in Table 1. The values were different for each particle depending on amplifier gains and radiation background levels during each experiment. It was observed that particles, which missed the detector entirely (i.e., b > 8.9 mm), provided signals that were essentially identical to background.

The distribution of energy deposition events for a broad uniform beam of ¹²C particles at 389 MeV/nucleon (LET = 11.2 keV/μm) is shown in Fig. 2. The solid line in Fig. 2 shows the expected distribution of energy depositions if ε = LET • x, where x is the path length through the gas cavity. The shape of this response function is similar to those reported earlier. The broad peak indicated as region A, is populated by events in which the particle passed through the gas cavity of the TEPC. Region B, corresponding to small values of ε, is populated by events where the incident particles miss the gas cavity but pass through the side walls of the detector (b > radius) and produce delta-rays that do enter the gas cavity. Region C, corresponding to very large values of ε, is populated by events where the incident particles either the just graze the inside wall of the gas cavity (b ≈ radius) or happen to hit the anode or helical grid wires within the cavity (Rademacher et al., 1998; Gersey et al., 2002).

Fig. 2.

The distribution of energy deposition, ε, for events measured in the TEPC operating with a simulated diameter of 3 μm for ¹²C ions at 389 MeV/nucleon. Three regions A, B, and C represent events with different trajectories through the detector.

The grazing particles that produce large energy depositions must have an impact parameter very close to the radius of the gas cavity. Otherwise, the soft delta-rays contributing to the large energy deposition would be stopped in the wall before reaching the gas cavity. A track model for the radial extension of a particle in water indicated that the dose from delta-rays is reduced by a factor of 10⁴ at a distance of 10 nm from the trajectory of a particle at 400 MeV/nucleon and by a factor of 1.3 × 10⁴ for particles at 240 MeV/nucleon (Cucinotta et al., 1995). This provides a narrow limit on the location of the track for grazing events. Fig. 3 shows an example of the distribution of impact parameters in region C for ⁵⁶Fe at 355 MeV/nucleon. When these data are re-plotted as a two-dimensional function of the transverse dimensions, X and Y, it was seen that the broad plateau occurring for impact parameter less than 5.5 mm is due to wire hits and the peak centered near 6.26 mm is due to grazing events. Events in this peak can be used to determine the spatial resolution of track reconstruction assuming that these events occur exactly at the radius of the gas cavity. Fig. 4 shows the full width at half maximum (FWHM = 2.36σ) divided by the mean value in the peak for these events as a function of the LET for all of the incident particles in this study. For particles with an LET greater than 10 keV/μm in water (i.e., Z≥6), the resolution using this figure-of-merit is around 10%. There is a large increase in the FWHM for the ⁴He ions due to the limitations of the charge separation technique used with the silicon PSDs. For this reason, position-related analyses were not performed with the ⁴He data.

Fig. 3.

The distribution of impact parameters for ⁵⁶Fe at 389 MeV/nucleon for events with large energy deposition corresponding region C (see Fig. 2) for this ion.

Fig. 4.

The spatial resolution of the position sensitive detectors as a function of LET in tissue using the width of the distribution of impact parameters for events with large energy deposition corresponding to region C (see Fig. 2).

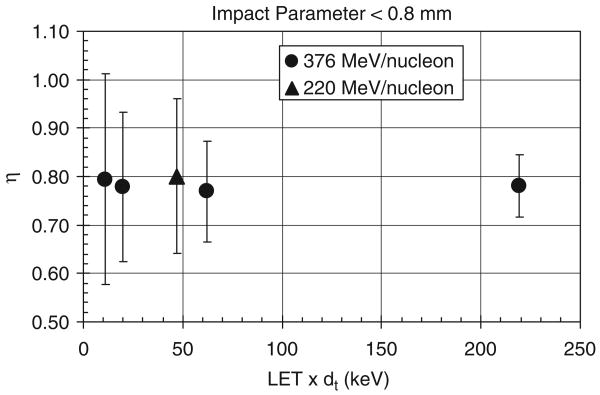
Energy deposition recorded in the TEPC can be standardized to the product of LET and the simulated diameter, d_t. This allows a comparison of the response functions using a dimensionless variable based on the energy loss of the particle and density of the gas in the detector. We define the variable η ≡ ε/(LET × d_t).

Particles with impact parameters less than 0.8 mm passed near the center of the detector (b ≈ 0) and had trajectories through the gas cavity that were within 1% of the diameter. Fig. 5 shows the mean value of energy deposition for these events expressed in terms of η as a function of LET × d_t. Data for ⁴He have been omitted because the spatial resolution in the position sensitive detectors was greater than 10%. The standard error of the mean is smaller than the size of the symbols because of the large number of events used to compute the mean. The error bars represent the standard deviation of the sample of events. It can be seen that η is always less than 0.80. There does not appear to be any trend in this data if the results are plotted as a function of Z, β, β² or LET.

Fig. 5.

The mean energy deposition, ε, in the TEPC for events where the incident particle passed through the center of the detector. The data have been standardized using the variable η = ε/LET • d_t.

Fig. 6 compares the response function of the TEPC in terms of η for ¹²C and ⁵⁶Fe ions with velocity, β = 0.70 and ⁴He ions with β = 0.59. Data are presented as complimentary cumulative distribution functions (CCDF) such that the ordinate represents the probability that η will be greater than or equal to the value on the abscissa. The results show that at high LET (⁵⁶Fe) there are a larger number of low energy deposition events that can be distinguished from noise. The interval between η = 0.2 and 1.1, represents the region where particles are passing through the gas cavity of the TEPC. Data in this region reflect a convolution of energy loss straggling by the primary particle, delta-ray effects in the sphere and detector resolution due to ion pair multiplication. The slopes decrease as the LET decreases even when the velocities are similar.

Fig. 6.

The complimentary cumulative distribution for the response function, f (η), measured by the TEPC for ¹²C and ⁵⁶Fe at 376 MeV/nucleon and ⁴He at 225 MeV/nucleon. The ordinate is the probability that events will have energy deposition greater the corresponding value of η on the abscissa.

The distributions of energy deposition for all ions were converted into lineal energy, y, and mean values were computed. Fig. 7 shows a plot of the frequency averaged lineal energy, ȳ_f, and the dose averaged lineal energy, ȳ_D, as a function of charge, Z, for all ions. In each case, the averaged values of y are divided by LET for standardization. Data for protons at β = 0.53 (172 MeV/nucleon) (Borak et al., 2004) were also included in the same plot. It can be seen that ȳ_f consistently underestimated LET by as much as 20%. There is a slight indication that ȳ_f approaches LET as Z decreases. For Z = 6 and higher, ȳ_D was within 5% of LET. However, ȳ_D was substantially greater than LET for ⁴He and protons.

Fig. 7.

Values of frequency averaged lineal energy, ȳ_f (open symbols) and dose averaged lineal energy, ȳ_D (solid symbols) as a function of charge, Z. The circles are for particles at 376 ± 15 MeV/nucleon. The squares are for particles at 220 ± 7 MeV/nucleon. The triangles are for protons at 172 MeV (Borak et al., 2004).

The measured distributions of lineal energy were used to estimate quality factors, Q, for applications in radiation protection. The recommended value of Q was determined from the LET of each mono-energetic ion using the relationship for quality factor versus LET, Q(L), recommended by the ICRP (1991). Quality factors based on lineal energy were determined using four approaches. One approach was to assume that LET is equal to ȳ_F and then determine Q(ȳ_f). This was repeated by assuming that LET is equal to ȳ_D and then determining Q(ȳ_D). The third method was based on computing an averaged value, Q̄, using the complete dose response function of the TEPC, D(y), and the assumption that y was numerically equivalent to LET, Q̄[D(L) = D(y)]. The fourth method used a radiation quality function based on lineal energy, q(y), recommended by the ICRU (1986) such that Q̄[q(D(y))].

The results for all ions in this study are shown in Fig. 8. At 376 MeV/nucleon (β = 0.70), Q(ȳ_f) underestimated the recommended value of Q for each ion except for ⁵⁶Fe. This was because ȳ_f was always about 20–30% less than LET. When the LET of the incident particle is less than 100 keV/μm (i.e., Q(L) with positive slope), Q(ȳ_f) will be less than Q(L), and when the LET of the particle is greater than 100 keV/μm (i.e., Q(L) with negative slope), Q[ȳ_f] will be greater than Q(L). Q(ȳ_D) provided the most consistent estimation of Q with the exception of ¹²C, which overestimated Q by 28%. Even though ȳ_D is significantly greater than LET for ⁴He, it does not influence Q because Q(L) has constant value of 1.0 below 10 keV/μm. For the ions in this study, Q̄[D(L) = D(y)] followed a pattern similar to Q[ȳ_D].

Fig. 8.

Bar graph showing estimates of quality factor. The recommended quality factor is obtained from the exact value of LET for each particle and the Q(L) relationship recommended by the ICRP. Q(LET = ȳ_f) and Q(LET = ȳ_D) used the averaged values of lineal energy to estimate LET. Q̄[D(L) = D(y)] used the complete response function of the TEPC and the assumption that f(L) = f(y). Q̄[q(D(y))] is based on the ICRU method of determining quality factor directly from lineal energy.

4. Discussion

The response of a spherical tissue-equivalent proportional counter was measured for several ions that had different charge, Z, but with similar velocities. Specifically, data was collected for ⁴He and ¹²C at 220 ± 7 MeV/nucleon (β = 0.59) and ¹²C, ¹⁶O, ²⁸Si and ⁵⁶Fe at 376 ± 15 MeV/nucleon (β = 0.70). The gas pressure was adjusted to simulate a volume of tissue having a diameter of 1 μm for particles with velocity, β = 0.70, and 3 μm for particles with velocity, β = 0.59. Position-sensitive detectors were used to determine the trajectory of the incident particles through the detector. The spatial resolution based on FWHM/mean was about 10% for all particles except ⁴He.

Particles that passed through the center of the detector deposited only about 80% of the energy expected from the product of the LET and the diameter. This was attributed to high-energy delta-rays escaping from the sensitive volume and the fact that electrons produced in the front and rear wall of the detector did not provide complete energy compensation. However, energy compensation from the wall exceeded energy loss from the gas when the impact parameter was greater than about 85% of the radius.

The response of the detector in terms of energy deposition, f(ε), was similar in shape for all ions. All had events with small values of energy deposition corresponding to particles that passed through the side-wall of the detector but not through the gas cavity. Events with very large energy deposition were from particles that just grazed the inside wall of the detector or intercepted the anode or helical grid wires. The effects of energy straggling and ion-pair multiplication increased as the charge, Z, of the particle decreased when the velocity was kept constant.

The frequency mean lineal energy, ȳ_f, was about 8–15% lower than the corresponding value of LET for all ions. It was noted that this quantity was particularly sensitive to the low energy threshold that was used to distinguish events with small energy depositions from background and noise. For example, by increasing the lower threshold from 0.1 to 3 keV, the ratio of ȳ_f to LET changed by a factor of 1.8, from 0.47 to 0.83, for ⁵⁶Fe (LET = 219 keV/μm) and a factor of 3.2, from 0.5 to 1.60, for ⁴He (LET = 1.7 keV/μm).

It was observed that ȳ_D was within 10% of LET for Z = 6 to 26. However, ȳ_D was about 50% greater than LET for ⁴He. Previous results showed that ȳ_D was more than a factor of two greater than LET for protons (Borak et al., 2004). We have investigated the possible influence of using a simulated diameter of 3 μm for the ions at 220 MeV/nucleon as opposed to 1 μm for the ions at 376 MeV/nucleon. When the simulated diameter was increased from 1 to 3μm for ⁵⁶Fe ions at 1050 MeV/nucleon, ȳ_f decreased by about 4% and ȳ_D decreased by about 2%.⁴ The data for ¹²C, shown in Table 1, were consistent with these observations. It is thus concluded that the increase in ȳ_D observed for ⁴He was not due to changes in the simulated diameter.

Ions with the same velocity should have the same energy distribution of secondary electrons. Thus the response function for ions at β = 0.7 should be similar when energy deposition plotted as the standardized variable, η. There are however pronounced differences as a function of LET because of detector resolution and energy straggling. Fig. 6 indicates that less than 1% of the events were greater than η = 1 for ⁵⁶Fe (LET = 219 keV/μm) whereas about 7% were greater than η = 1 for ¹²C (LET = 11.2 keV/μm) and 14% were greater than η = 1 for ⁴He (LET = 1.68 keV/μm). The dose averaged lineal energy, ȳ_D, is the second moment of the frequency distribution, $\overline{y^2}$, divided by the first moment, ȳ. The second moment is very sensitive to the relative number of events with large energy depositions. Even though there are compensating events with reduced energy deposition, there is an increase in the spread or variance of the response functions as the LET becomes small (Fig. 6). This increased variance causes ȳ_D to increase relative to LET.

The data were used to estimate quality factors for applications in radiation protection. All the methods using the data from this TEPC produced results that were within 20% of the value of the quality factor based on the true value of LET for each ion and Q(L) from the ICRP. When LET was greater than 20, Q(ȳ_D) seemed to be the most consistent estimator of quality factor since ȳ_D is not strongly influenced by changes in the number of very small energy deposition events recorded by the TEPC. Although ȳ_D is significantly larger than LET for ⁴He and ¹H, this result fortuitously did not affect quality factor since Q(L) has a constant value equal to 1.0 in that domain of LET.