Semiparametric Estimation of Treatment Effect in a Pretest–Posttest Study with Missing Data

Abstract

The pretest–posttest study is commonplace in numerous applications. Typically, subjects are randomized to two treatments, and response is measured at baseline, prior to intervention with the randomized treatment (pretest), and at prespecified follow-up time (posttest). Interest focuses on the effect of treatments on the change between mean baseline and follow-up response. Missing posttest response for some subjects is routine, and disregarding missing cases can lead to invalid inference. Despite the popularity of this design, a consensus on an appropriate analysis when no data are missing, let alone for taking into account missing follow-up, does not exist. Under a semiparametric perspective on the pretest–posttest model, in which limited distributional assumptions on pretest or posttest response are made, we show how the theory of Robins, Rotnitzky and Zhao may be used to characterize a class of consistent treatment effect estimators and to identify the efficient estimator in the class. We then describe how the theoretical results translate into practice. The development not only shows how a unified framework for inference in this setting emerges from the Robins, Rotnitzky and Zhao theory, but also provides a review and demonstration of the key aspects of this theory in a familiar context. The results are also relevant to the problem of comparing two treatment means with adjustment for baseline covariates.

1. INTRODUCTION

1.1 Background and Motivation

The so-called pretest–posttest trial arises in a host of applications. Subjects are randomized to one of two interventions, denoted here by “control” and “treatment,” and the response is recorded at baseline, prior to intervention (pretest response), and again after a prespecified follow-up period (posttest response). We use the terms “baseline/pretest” and “follow-up/posttest” interchangeably. The effect of interest is usually stated as “difference in change of (mean) response from baseline to follow-up between treatment and control.”

For instance, in studies of HIV disease, a common objective is to determine whether the change in measures of immunologic status such as CD4 cell count from baseline to some subsequent time following initiation of antiretroviral therapy is different for different treatments. Depressed CD4 counts indicate impairment of the immune system, so larger, positive such changes are thought to reflect more effective treatment. To exemplify this situation, we consider data from 2139 patients from AIDS Clinical Trials Group (ACTG) protocol 175 (Hammer et al., 1996), a study that randomizes patients to four antiretroviral regimens in equal proportions. The findings of ACTG 175 indicate that zidovudine (ZDV) monotherapy is inferior to the other three [ZDV+didanosine (ddI), ZDV+zalcitabine, ddI] therapies, which showed no differences on the basis of the primary study endpoint of progression to AIDS or death. Accordingly, we consider two groups: subjects who receive ZDV alone (control) and those who receive any of the other three therapies (treatment). As is routine in HIV clinical studies, measures such as CD4 count were collected on all participants periodically throughout, and interest also focused on secondary questions regarding changes in immunologic and virologic status. An important secondary endpoint was change in CD4 count from baseline to 96±5 weeks.

To formalize this situation, let Y₁ and Y₂ denote baseline and follow-up response (e.g., baseline and 96±5 week CD4 count) and let Z = 0 or 1 indicate assignment to control or treatment, respectively. Because, under proper randomization, pretest mean response should not differ by intervention, it is reasonable to assume that E(Y₁|Z = 0) = E(Y₁|Z = 1) = E(Y₁) = µ₁. Letting E(Y₂|Z) = µ₂ + βZ, the desired effect may then be expressed as

$$\begin{array}{c}\hfill \{E(Y_2\mid Z=1)-{\mu }_1\}-\{E(Y_2\mid Z=0)-{\mu }_1\}\hfill \\ \hfill =E(Y_2\mid Z=1)-E(Y_2\mid Z=0)=\beta \hfill \end{array}$$ (1)

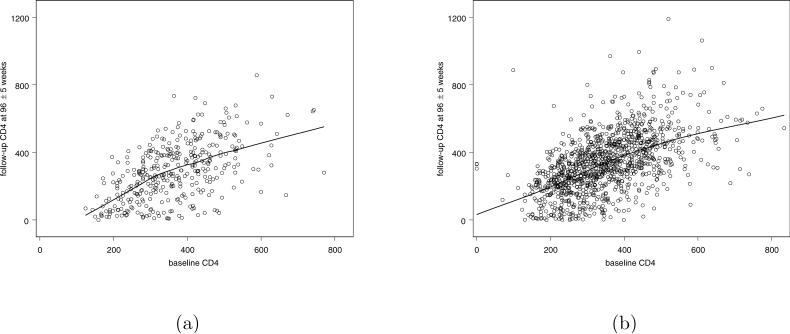
and interest focuses on the parameter β. A number of ways to make inference on β have been proposed. Because the question is usually posed in terms of difference in change from baseline, analysis is often based on the “paired t test” estimator for β found by taking the difference of the sample averages of (Y₂ − Y₁) in each group. The second expression in (1) involves only posttest treatment means, suggesting estimating β in the spirit of the two-sample t test by the difference of Y₂ sample means for each treatment (ignoring baseline responses altogether). However, if baseline response is correlated with change in response or posttest response itself, intuition suggests taking this into account. For continuous response, this has led many researchers to advocate the use of analysis of covariance (ANCOVA) techniques, in which one estimates β directly by fitting the linear model E(Y₂|Y₁, Z) = α₀ + α₁Y₁ + βZ. A variation is to include an interaction term involving Y₁Z; here, β is estimated as the coefficient of (Z − Z̄) in the regression of Y₂ − Ȳ₂ on Y₁ − Ȳ₁, (Z − Z̄), where the overbars denote overall sample average. Singer and Andrade (1997) mentioned a “generalized estimating equation” (GEE) approach (see also Koch, Tangen, Jung and Amara, 1998), where (Y₁,Y₂)^T is viewed as a multivariate response vector with mean (µ₁,µ₂ + βZ)^T and standard GEE methods are used to make inference on β. Yang and Tsiatis (2001) and Leon, Tsiatis and Davidian (2003) provided further details on all of these methods. The two-sample t test approach implicitly assumes pre- and posttest responses are uncorrelated, which may be unrealistic, while the paired t test and ANCOVA evidently assume linear dependence of Y₁ and Y₂, which may not hold in practice; for example, Figure 1 shows baseline and follow-up CD4 counts in ACTG 175 and suggests a mild curvilinear relationship between them in each group. Numerous authors (e.g., Brogan and Kutner, 1980; Crager, 1987; Laird, 1983; Stanek, 1988; Stein, 1989; Follmann, 1991; Yang and Tsiatis, 2001) have studied these “popular” procedures under various assumptions, yet no general consensus has emerged regarding a preferred approach, providing little guidance for practice.

Fig. 1.

CD4 counts after 96±5 weeks versus baseline CD4 counts for complete cases for (a) ZDV alone and (b) the combination of ZDV+ddI, ZDV+ddC or ddI alone, ACTG 175. Solid lines were obtained using the Splus function loess() (Cleveland, Grosse and Shyu, 1993).

A further complication facing the data analyst, particularly in lengthy studies, is that of missing follow-up response Y₂ for some subjects. In the ACTG 175 data, for example, although baseline CD4 (Y₁) is available for all 2139 participants, 37% are missing CD4 count at 96±5 weeks (Y₂) due to dropout from the study. A common approach in this situation is to undertake a complete-case analysis, applying one of the above techniques only to the data from subjects for whom both the pre- and posttest responses are observed. In the GEE method, one may in fact include data from all subjects by defining the “multivariate response” for those with missing Y₂ to be simply Y₁, with mean µ₁. However, as is well known, for all of these approaches, unless the data are missing completely at random (Rubin, 1976), which implies that missingness is not associated with any observed or unobserved subject characteristics, these strategies may yield biased inference on β.

Often, baseline demographic and physiologic characteristics X₁, say, are collected on each participant. Moreover, during the intervening period from baseline to follow-up, additional covariate information X₂, say, including intermediate measures of the response, may be obtained. In ACTG 175, at baseline CD4 count (Y₁) and covariates (X₁), including weight; age; indicators of intravenous drug use, HIV symptoms, prior experience with antiretroviral therapy, hemophilia, sexual preference, gender and race; CD8 count (another measure of immune status); and Karnofsky score (an index that reflects a subject's ability to perform activities of daily living) were recorded for each participant. In addition, CD4 and CD8 counts and treatment status (on/off assigned treatment) were recorded intermittently between baseline and 96±5 weeks (X₂). Missingness at follow-up is often associated with baseline response and baseline and intermediate covariates, and this relationship may be differential by intervention. For example, HIV-infected patients who are worse off at baseline as suggested by low baseline CD4 count may be more likely to drop out, particularly if they receive the less effective treatment. Moreover, HIV-infected patients may base a decision to drop out on post-baseline intermediate measures of immunologic or virologic status (e.g., CD4 counts), which themselves may reflect the effectiveness of their assigned therapy. Here, the assumption that follow-up is missing at random (MAR; Rubin, 1976), associated only with these observable quantities and not the missing response, may be reasonable.

If one is willing to adopt the MAR assumption, methods that take appropriate account of the missingness should be used to ensure valid inference. A standard approach to missing data problems is maximum likelihood, which in the pretest–posttest setting with Y₂ MAR involves full (parametric) specification of the joint distribution of V = (X₁,Y₁,X₂,Y₂,Z). Alternatively, adaptation of popular estimators such as ANCOVA to handle MAR Y₂ on a case-by-case basis may be possible. Maximum likelihood techniques are known to suffer potential sensitivity to deviations from modeling assumptions, and neither approach has been widely applied by practitioners in the pretest–posttest context.

In summary, although missing follow-up response is commonplace in the pretest–posttest setting, there is no widely accepted or used methodology for handling it. In this paper we demonstrate how a unified framework for pretest–posttest analysis under MAR may be developed by exploiting the results in a landmark paper by Robins, Rotnitzky and Zhao (1994).

1.2 Semiparametric Models, Influence Functions, and Robins, Rotnitzky and Zhao

A popular modeling approach that acknowledges concerns over sensitivity to parametric assumptions is to take a semiparametric perspective. A semiparametric model may involve both parametric and nonparametric components, where the nonparametric component represents features on which the analyst is unwilling or unable to make parametric assumptions, and interest may focus on a parametric component or on some functional of the nonparametric component. For example, in a regression context one may adopt a parametric model for the conditional expectation of a continuous response given covariates and seek inference on the model parameters but be uncomfortable assuming the full conditional distribution is normal, instead leaving it unspecified. Under the semiparametric model for the pretest–posttest trial we consider, features of the joint distribution of V = (X₁,Y₁,X₂,Y₂,Z) beyond the independence of (X₁,Y₁) and Z induced by randomization are left unspecified and thus constitute the nonparametric component, and interest focuses on the functional β of this distribution defined in (1). When Y₂ is MAR, this semi-parametric view not only offers protection against incorrect assumptions on V , but allows us to exploit the theory of Robins, Rotnitzky and Zhao (1994) to deduce estimators for β. These authors derived an asymptotic theory for inference in general semiparametric models with data MAR that may be used to identify a class of consistent estimators for parametric components or such functionals, as we now outline.

Robins, Rotnitzky and Zhao (1994) restricted attention to estimators that are regular and asymptotically linear. Regularity is a technical condition that rules out “pathological” estimators with undesirable local properties (Newey, 1990), such as the “superefficient” estimator of Hodges (e.g., Casella and Berger, 2002, page 515). Generically, an estimator $\widehat{\beta }$ for β (p × 1) in a parametric or semiparametric statistical model for a random vector W based on i.i.d. data W_i, i = 1,...,n, is asympotically linear if it satisfies, for a function φ(W),

$$n^{1∕2}(\widehat{\beta }-{\beta }_0)=n^{-1∕2}\sum _{i=1}^n\phi \left(W_i\right)+o_p\left(1\right),$$ (2)

where β₀ is the true value of β generating the data, E{φ(W)} = 0, E{φ^T (W)φ(W)} < ∞ and expectation is with respect to the true distribution of W . The function φ(W) is referred to as the influence function of $\widehat{\beta }$, as to a first-order φ(W) is the influence of a single observation on $\widehat{\beta }$ in the sense given in Casella and Berger (2002, Section 10.6.4). An estimator that is both regular and asymptotically linear (RAL) with influence function φ(W) is consistent and asymptotically normal with asymptotic covariance matrix E{φ(W)φ^T (W)} . Although not all consistent estimators need be RAL, almost all reasonable estimators are. For RAL estimators, there exists an influence function φ^eff(W) such that E{φ(W)φ^T (W)} − E{φ^eff(W)φ^effT (W)} is nonnegative definite for any influence function φ(W); φ^eff(W) is referred to as the efficient influence function and the corresponding estimator is called the efficient estimator. In fact, for any regular estimator, asymptotically linear or not, with asymptotic covariance matrix ∑, ∑ − E{φ^eff(W)φ^effT (W) is nonnegative definite; thus, the best estimator in }the sense of “smallest” asymptotic covariance matrix is RAL, so that restricting attention to RAL estimators is not a limitation. We use the term “influence function” unqualified to mean the influence function of an RAL estimator.

As indicated by (2), there is a relationship between influence functions and consistent and asymptotically normal estimators; thus, by identifying influence functions, one may deduce corresponding estimators. In missing data problems, Robins, Rotnitzky and Zhao (1994) distinguished between full-data and observed-data influence functions. “Full data” refers to the data that would be observed if there were no missingness; in the pretest–posttest setting the full data are V . Accordingly, full-data influence functions correspond to estimators that could be calculated if full data were available and are hence functions of the full data. “Observed data” refers to the data observed when some components of the full data are potentially missing; hence observed-data influence functions correspond to estimators that can be computed from observed data only and are functions of the observed data. For a general semiparametric model, the pioneering contribution of Robins, Rotnitzky and Zhao (1994) was to characterize the class of all observed-data influence functions when data are MAR, including the efficient influence function, and to demonstrate that observed-data influence functions may be expressed in terms of full-data influence functions. Because for many popular semiparametric models the form of full-data influence functions is known or straightforwardly derived, this provides an attractive basis for identifying estimators when data are MAR, including the efficient one.

In summary, the Robins, Rotnitzky and Zhao (1994) theory provides a series of steps for deducing estimators for a semiparametric model of interest when data are MAR: (1) Characterize the class of full-data influence functions, (2) characterize the observed data under MAR and apply the Robins, Rotnitzky and Zhao theory to obtain the class of observed-data influence functions, including the efficient one and (3) identify observed-data estimators with influence functions in this class. In this paper, for the semiparametric pretest–posttest model when Y₂ is MAR, β is a scalar (p = 1), and we carry out each of these steps and show how they lead to closed-form estimators for β suitable for routine practical use. Interestingly, despite the ubiquity of the pretest–posttest study and the simplicity of the model when no data are missing, to our knowledge explicit application of this powerful theory to pretest–posttest inference with data MAR with an eye toward developing practical estimators has not been reported.

1.3 Objectives and Summary

The goals of this paper are twofold. The first main objective is to develop accessible practical strategies for inference on β in a semiparametric pretest–posttest model with follow-up data MAR by using the fundamental theory of Robins, Rotnitzky and Zhao (1994) as described above. Although this theory is well known to experts, many researchers have only passing familiarity with its essential elements. Thus, the second main goal of this paper is to use the pretest–posttest problem as a backdrop to provide a detailed and mostly self-contained demonstration of application of the theory of semiparametric models and the powerful, general Robins, Rotnitzky and Zhao results in a concrete, familiar context. This account hopefully will serve as a resource to researchers and practitioners wishing to appreciate the scope and underpinnings of the Robins, Rotnitzky and Zhao theory by systematically tracing the key concepts and steps involved in its application and explicating how it can lead to practical insight and tools.

In Section 2 we summarize the semiparametric pretest–posttest model and outline how the class of full-data influence functions for estimators for β may be derived. In Section 3 we characterize the observed data when Y₂ is MAR, review the essential Robins, Rotnitzky and Zhao (1994) results and apply them to derive the class of observed-data influence functions. Sections 4 and 5 present strategies for constructing estimators based on observed-data influence functions, and we demonstrate the new estimators by application to the ACTG 175 data in Section 6. Results and practical implications are presented in the main narrative; technical supporting material and details of derivations are given in the Appendix.

As in any missing-data context, validity of the assumption of MAR follow-up response is critical and is best justified with availability of rich baseline and intervening information. We assume throughout that the analyst is well equipped to invoke this assumption.

2. MODEL AND FULL-DATA INFLUENCE FUNCTIONS

2.1 Semiparametric Pretest–Posttest Model

First, consider the full data (no missing posttest response). Suppose each subject i = 1,...,n is randomized to treatment with known probability δ, so Z_i = 0 or 1 as i is assigned to control or treatment; in ACTG 175, δ = 0.75. Then Y_1i and Y_2i are i's pretest and posttest responses (baseline and 96±5 week CD4 in ACTG 175), X_1i is i's vector of baseline covariates and X_2i is the vector of additional covariates collected on i after intervention but prior to follow-up, which may include intermediate measures of response. Assuming subjects' responses evolve independently, the full data on i are V_i = (X_1i,Y_1i,X_2i,Y_2i,Z_i), i.i.d. across i with density p(v) = p(x₁,y₁,x₂,y₂,z); we often suppress the subscript i for brevity. From (1) interest focuses on $\beta =E(Y_2\mid Z=1)-E(Y_2\mid Z=0)={\mu }_2^{\left(1\right)}-{\mu }_2^{\left(0\right)}$, ${\mu }_2^{\left(1\right)}={\mu }_2+\beta \text{and}{\mu }_2^{\left(0\right)}={\mu }_2$; throughout, expectation and variance are with respect to the true distribution of V.

From Section 1.2, under a semiparametric perspective the analyst may be unwilling to make specific parametric assumptions on p(x₁,y₁,x₂,y₂,z) such as normality or equality of variances of Y₁ and Y₂. For example, in HIV research it is customary to assume that CD4 counts are normally distributed on some transformed scale and to carry out analyses on this scale; however, as there is no consensus on an appropriate transformation, methods that do not require this assumption are desirable. Thus, in arguments to deduce the form of full- and observed-data influence functions here and in Sections 3 and 4, we do not impose any specific assumptions beyond independence of (X₁,Y₁) and Z induced by randomization and assumptions on the form of the mechanism governing missingness. As our objective is to outline the salient features of the arguments without dwelling on technicalities, we assume needed moments, derivatives and matrix inverses exist without comment.

2.2 Full-Data Influence Functions

As presented in Section 1.2, our first step in applying the Robins, Rotnitzky and Zhao (1994) theory is to characterize the class of all full-data influence functions for RAL estimators for β; these will be functions of V . This may be accomplished by appealing to the theory of semiparametric models (e.g., Newey, 1990; Bickel, Klaassen, Ritov and Wellner, 1993), which provides a formal framework for characterizing influence functions for RAL estimators in such models, including the efficient influence function. The theory takes a geometric perspective, where, generically, influence functions based on data V for RAL estimators for a p-dimensional parameter or functional β in a statistical model for V are viewed as elements of a particular “space” of mean-zero, p-dimensional functions of V for which there is a certain relationship between the distance of any element of the space from the origin and the covariance matrix of the function. From (2), as the covariance matrix of an influence function is equal to the asymptotic covariance matrix of the corresponding estimator, the search for estimators with small covariance matrices, especially the efficient estimator, may thus be focused on functions in this space and guided by geometric distance considerations.

In Appendix A.1 we first sketch an argument that demonstrates that any RAL estimator has a unique influence function, supporting the premise of working with influence functions. We then review familiar results for fully parametric models and show how they may be regarded from this geometric perspective. Finally, we indicate how this perspective is extended to handle semiparametric models. The key results are a representation of the form of all influence functions for RAL estimators in a particular model and a convenient characterization of the efficient influence function that corresponds to the efficient estimator.

In Appendix A.2 we apply these results to show that all full-data influence functions for estimators for β in the semiparametric pretest–posttest model must be of the form

$$\left\{\frac{Z(Y_2-{\mu }_2-\beta )}{\delta }-\frac{(Z-\delta )}{\delta }{h}^{\left(1\right)}(X_1,Y_1)\right\}-\left\{\frac{(1-Z)(Y_2-{\mu }_2)}{1-\delta }-\frac{\{(1-Z)-(1-\delta )\}}{1-\delta }{h}^{\left(0\right)}(X_1,Y_1)\right\},$$ (3)

where h^(c)(X₁,Y₁), c = 0, 1, are arbitrary functions with var{h^(c)(X₁,Y₁)} < ∞. Technically, the influence function (3) depends on µ₂ and β through their true values. As is conventional, here and in the sequel we write influence functions as functions of parameters, which highlights their practical use as the basis for deriving estimators, shown in Section 5. From (3), influence functions and hence all RAL estimators for β are functions only of (X₁,Y₁,Y₂,Z) and hence do not depend on X₂. This is intuitively reasonable; because X₂ is a post-intervention covariate, we would not expect it to play a role in estimation of β when Y₂ is observed on all subjects. In Section 3, however, we will observe that when Y₂ is MAR for some subjects, such covariates are important not only for validating the MAR assumption, but for increasing efficiency of estimation of β, as discussed in Robins, Rotnitzky and Zhao (1994, page 848).

The results in Appendix A.2 also show that the efficient influence function, that with smallest variance among all influence functions in class (3), is found by taking

$$\begin{array}{c}\hfill h^{\left(c\right)}(X_1,Y_1)=E(Y_2\mid X_1,Y_1,Z=c)-{\mu }_2^{\left(c\right)},\hfill \\ \hfill c=0,1,{\mu }_2^{\left(1\right)}={\mu }_2+\beta ,{\mu }_2^{\left(0\right)}={\mu }_2.\hfill \end{array}$$ (4)

Thus, if full data were available in ACTG 175, the optimal estimator for β would involve the true regression of 96±5 week CD4 on pretest CD4 and other baseline covariates listed in Section 1.1. Leon, Tsiatis and Davidian (2003) identified class (3) when no intervening covariate X₂ is observed and showed that influence functions for the popular estimators discussed in Section 1.1 are members; for example, the two-sample t test estimator

$$\begin{array}{cc}\hfill {\widehat{\beta }}_{2s}& =n_1^{-1}\sum _{i=1}^n{Z}_i{Y}_{2i}-n_0^{-1}\sum _{i=1}^n(1-Z_i)Y_{2i},\hfill \\ \hfill n_c& =\sum _{i=1}^{n}I(Z_i=c),c=0,1,\hfill \end{array}$$ (5)

has influence function (3) with h^(c) ≡ 0, c = 0, 1 (see Appendix A.2). Thus, popular estimators are=RAL and valid under the semiparametric model, and hence contrary to widespread belief, are consistent and asymptotically normal even if Y₁ and Y₂ are not normally distributed. Leon, Tsiatis and Davidian (2003) also showed that none of the popular estimators has the efficient influence function, suggesting that improved estimators are possible, and proposed estimators based on (4) that offer dramatic efficiency gains over popular methods.

In fact, (3) is the difference of the forms of all influence functions for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$, respectively, which may themselves be deduced separately by arguments analogous to those in Appendix A.2. In Appendix A.3 we argue that, for the purposes of identifying observed-data estimators for β, it suffices to identify observed-data influence functions for estimators for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$ separately. We thus focus for simplicity in Section 3 on estimation of ${\mu }_2^{\left(1\right)}$.

3. OBSERVED DATA INFLUENCE FUNCTIONS

3.1 Semiparametric Pretest–Posttest Model with MAR Follow-Up Response

Suppose now that Y₂ is missing for some subjects, with all other variables observed, and define R = 0 or 1 as Y₂ is missing or observed. Then the observed data for subject i are O_i = (X_0i,Y_1i,X_1i,R_i,R_iY_2i,Z_i), i.i.d. across i. We represent the assumption that Y₂ is MAR as

$$\begin{array}{cc}\hfill & P(R=1\mid X_1,Y_1,X_2,Y_2,Z)\hfill \\ \hfill & =P(R=1\mid X_1,Y_1,X_2,Z)\hfill \\ \hfill & =\pi (X_1,Y_1,X_2,Z)\ge \epsilon >0,\hfill \end{array}$$ (6)

reflecting the reasonable view for a pretest–posttest trial that there is a positive probability of observing Y₂ for any subject. Equation (6) formalizes that missingness does not depend on the unobserved Y₂, but may be associated with baseline and intermediate characteristics and be differential by intervention, the latter highlighted by the equivalent representation

$$\begin{array}{c}\hfill \pi (X_1,Y_1,X_2,Z)=Z{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\hfill \\ \hfill +(1-Z){\pi }^{\left(0\right)}(X_1,Y_1,X_2)\hfill \end{array}$$ (7)

for π^(c)(X₁,Y₁,X₂) = π(X₁,Y₁,X₂,c) ≥ ε > 0, c = 0, 1. For ACTG 175, (6) and (7) make explicit the belief that subjects may have been more or less likely to drop out (and hence be missing CD4 at 96±5 weeks) depending on their baseline CD4 and other characteristics as well as intermediate measures of CD4 and CD8 and off-treatment status, where this relationship may be different for patients treated with ZDV only versus the other therapies, but that dropout does not depend on unobserved 96±5 week CD4. Relaxation of the assumption that X₁,Y₁,X₂ are observed for all subjects is discussed in Section 7.

3.2 Complete-Case Analysis and Inverse Weighting

As noted in Section 1.1, a naive approach under these conditions is to conduct a complete-case analysis. For example, using the two-sample t test, estimate β by

$$\begin{array}{cc}\hfill & n_{R1}^{-1}\sum _{i=1}^n{R}_i{Z}_i{Y}_{2i}-n_{R0}^{-1}\sum _{i=1}^n{R}_i(1-Z_i)Y_{2i},\hfill \\ \hfill & n_{Rc}=\sum _{i=1}^n{R}_{i}I(Z_i=c),c=0,1,\hfill \end{array}$$ (8)

the difference in sample means based only on data for subjects with Y₂ observed. Under the semiparametric model, as E(RZY₂) = E{ZY₂E(R|X₁,Y₁,X₂,Y₂,Z)}= E{ZY_2π⁽¹⁾(X₁,Y₁,X₂)} by (6) and (7), and E{RI(Z = 1)} = E(RZ) = E{Zπ⁽¹⁾(X₁,Y₁,X₂), the first term in (8) converges in probability to E{ZY₂ · π⁽¹⁾(X₁,Y₁,X₂)}/(X₁,Y₁,X₂)}, which is not equal to $E(Y_2\mid Z=1)={\mu }_2^{\left(1\right)}$ in general. Similarly, the second term is not consistent for ${\mu }_2^{\left(0\right)}$. Thus, (8) is not a consistent estimator for β in general.

A simple remedy is to incorporate inverse weighting of the complete cases (IWCC; e.g., Horvitz and Thompson, 1952). Here, whereas the estimator for ${\mu }_2^{\left(1\right)}$ in (8) solves ${\sum }_{i=1}^n{R}_i{Z}_i(Y_{2i}-{\mu }_2^{\left(1\right)})=0$, weight each contribution by the inverse of the probability of seeing a complete case; that is, solve ${\sum }_{i=1}^n{R}_i{Z}_i(Y_{2i}-{\mu }_2^{\left(1\right)})∕{\pi }_i^{\left(1\right)}(X_{1i},Y_{1i},X_{2i})=0$, yielding the estimator for ${\mu }_2^{\left(1\right)}$,

$$\begin{array}{cc}\hfill & n_{RZ\left(1\right)}^{-1}\sum _{i=1}^n{R}_i{Z}_i{Y}_{2i}∕{\pi }^{\left(1\right)}(X_{1i},Y_{1i},X_{2i}),\hfill \\ \hfill & n_{RZ\left(1\right)}=\sum _{i=1}^n{R}_i{Z}_i∕{\pi }^{\left(1\right)}(X_{1i},Y_{1i},X_{2i}),\hfill \end{array}$$ (9)

and analogously for ${\mu }_2^{\left(0\right)}$. It is straightforward to show that such inverse weighting yields consistent estimators for ${\mu }_2^{\left(c\right)}$, c = 0, 1; for example, for (9) (c = 1), using (6) and (7),

$$\begin{array}{cc}\hfill & E\left\{\frac{RZ{Y}_2}{{\pi }^{\left(1\right)}(X_1,Y_1,X_2)}\right\}\hfill \\ \hfill & =E\left\{Z{Y}_2\frac{E(R\mid X_1,Y_1,X_2,Y_2,Z)}{{\pi }^{\left(1\right)}(X_1,Y_1,X_2)}\right\}\hfill \\ \hfill & =E\left(Z{Y}_2\right)=E\{ZE(Y_2\mid Z)\}=\delta E(Y_2\mid Z=1),\hfill \end{array}$$

and similarly E{RZ/π⁽¹⁾X₁,Y₁,X₂)} = δ, so that (9) converges in probability to $E(Y_2\mid Z=1)={\mu }_2^{\left(1\right)}$. Subtracting ${\mu }_2^{\left(c\right)}\text{and multiplying by}{n}^{1∕2}$ for each of c = 0, 1, the associated influence functions are seen to be

$$\begin{array}{cc}\hfill & \frac{RZ(Y_2-{\mu }_2^{\left(1\right)})}{\delta {\pi }^{\left(1\right)}(X_1,Y_1,X_2)}\text{and}\hfill \\ \hfill & \frac{R(1-Z)(Y_2-{\mu }_2^{\left(0\right)})}{(1-\delta ){\pi }^{\left(0\right)}(X_1,Y_1,X_2)},\hfill \end{array}$$ (10)

which have the form of the corresponding full-data influence functions in (3) weighted by 1/π^(c), c = 0, 1, for the complete cases only (R = 1). The IWCC be applied to any RAL estimator with influence function in class (3), including popular ones. However, although such simple IWCC leads to consistent inference, methods with greater efficiency are possible.

3.3 The Robins, Rotnitzky and Zhao Theory

As noted in Section 1.2, the pioneering advance of Robins, Rotnitzky and Zhao (1994) was to derive, for a general semiparametric model, the class of all observed data influence functions for estimators for a parameter β under complex forms of MAR and to characterize the efficient influence function. The theory reveals, perhaps not unexpectedly, that there is a relationship between full- and observed-data influence functions and that the latter involve inverse weighting.

Denote the subset of the full data V that is always observed for all subjects as O*; O* = (X₁,Y₁,X₂,Z) here. Under MAR, the probability that full data are observed depends only on O*, which we write as π(O*). Assuming π(O*) is known for now, if φ^F (V) is any full-data influence function, Robins, Rotnitzky and Zhao showed that, in general, all observed-data influence functions have the form Rφ^F (V)/π(O*) − g(O), where g(O) is an arbitrary square-integrable function of the observed data that satisfies E{g(O)|V} = 0. For situations like that here, where a particular subset of V (Y₂) is either missing or not for all subjects, this becomes

$$\frac{R{\phi }^F\left(V\right)}{\pi \left(O^{\ast }\right)}-\frac{R-\pi \left(O^{\ast }\right)}{\pi \left(O^{\ast }\right)}g\left(O^{\ast }\right),$$ (11)

where g(O*) is an arbitrary square-integrable function of the data always observed. In (11), the first term has the form of an IWCC full-data influence function; the second term, which has mean zero, depending only on data observed for all subjects, “augments” (e.g., Robins, 1999) the first, which leads to increased efficiency provided that g is chosen judiciously.

3.4 Observed-Data Influence Functions for the Pretest–Posttest Problem

In the special case of the pretest–posttest problem, focusing on estimation of the treatment mean ${\mu }_2^{\left(1\right)}={\mu }_2+\beta$, with O* = (X₁,Y₁,X₂,Z), (3) and (11) immediately imply that the class of all observed-data influence functions for estimators for ${\mu }_2^{\left(1\right)}$ when Y₂ is MAR is

$$\begin{array}{cc}\hfill & \frac{R\{Z(Y_2-{\mu }_2^{\left(1\right)})-(Z-\delta )h^{\left(1\right)}(X_1,Y_1)\}}{\delta \pi (X_1,Y_1,X_2,Z)}\hfill \\ \hfill & -\frac{R-\pi (X_1,Y_1,X_2,Z)}{\pi (X_1,Y_1,X_2,Z)}{g}^{\left(1\right)}(X_1,Y_1,X_2,Z)\hfill \end{array}$$ (12)

for arbitrary h⁽¹⁾ and g⁽¹⁾ such that var{h⁽¹⁾(X₁,Y₁)} < ∞ and var{g¹(X₁,Y₁,X₂,Z) < ∞. Defining g^(1)′ (X₁,Y₁X₂Z), we may write (12) equivalently in a way that is convenient in subsequent developments as

$$\begin{array}{cc}\hfill & \frac{RZ(Y_2-{\mu }_2^{\left(1\right)})}{\delta \pi (X_1,Y_1,X_2,Z)}-\frac{(Z-\delta )}{\delta }{h}^{\left(1\right)}(X_1,Y_1)\hfill \\ \hfill & -\frac{R-\pi (X_1,Y_1,X_2,Z)}{\delta \pi (X_1,Y_1,X_2,Z)}{g}^{{\left(1\right)}^{\prime }}(X_1,Y_1,X_2,Z);\hfill \end{array}$$ (13)

there is a one-to-one correspondence between (12) and (13).

As in the full-data problem, it is of interest to identify the optimal choices of h⁽¹⁾ and g⁽¹⁾, or, equivalently, h⁽¹⁾ and g^(1)′ , that is, those that yield the efficient observed-data influence function with smallest variance among all influence functions of form (12) or, equivalently, (13). In Appendix A.4 we show that the optimal choices of h⁽¹⁾ and g^(1)′ in (13) are

$$\begin{array}{cc}\hfill & h^{\mathrm{eff}\left(1\right)}(X_1,Y_1)\hfill \\ \hfill & =E(Y_2\mid X_1,Y_1,Z=1)-{\mu }_2^{\left(1\right)},\hfill \\ \hfill & g^{\mathrm{eff}{\left(1\right)}^{\prime }}(X_1,Y_1,X_2,Z)\hfill \\ \hfill & =Z\{E(Y_2\mid X_1,Y_1,X_2,Z)-{\mu }_2^{\left(1\right)}\}\hfill \\ \hfill & =Z\{E(Y_2\mid X_1,Y_1,X_2,Z=1)-{\mu }_2^{\left(1\right)}\}.\hfill \end{array}$$ (14)

The forms g^eff(1)′ and h^eff(1) show explicitly how augmentation exploits relationships among variables to gain efficiency. In ACTG 175, then, (14) shows that the optimal estimator for β involves knowledge of the true regressions of 96±5 week CD4 on baseline CD4 and other baseline covariates, and on this baseline information plus post-intervention CD4 and CD8 measures and off-treatment status, respectively.

To develop estimators for practical use with good properties, it is sensible to consider influence functions with form close to that of the efficient influence function. Accordingly, from the expression for g^eff(1)′ in (14) and the representation of π in (7), we restrict attention in the sequel to the subclass of (13) with elements of the form, for g^(1)′ (X₁,Y₁,X₂,Z) = Zq⁽¹⁾(X₁,Y₁,X₂) for arbitrary square-integrable q⁽¹⁾(X₁,Y₁,X₂),

$$\begin{array}{c}\hfill \psi (X_1,Y_1,X_2,R,R{Y}_2,Z)\hfill \\ \hfill =\frac{RZ(Y_2-{\mu }_2^{\left(1\right)})}{\delta {\pi }^{\left(1\right)}(X_1,Y_1,X_2)}-\frac{(Z-\delta )}{\delta }{h}^{\left(1\right)}(X_1,Y_1)\hfill \\ \hfill -\frac{\{R-{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\}Z}{\delta {\pi }^{\left(1\right)}(X_1,Y_1,X_2)}\hfill \\ \hfill \cdot q^{\left(1\right)}(X_1,Y_1,X_2).\hfill \end{array}$$ (15)

Equation (15) includes the optimal g^(1)′ , but rules out choices that cannot have the efficient form.

3.5 Estimation of the Missingness Mechanism

The foregoing results take π and, hence, π⁽¹⁾(X₁,Y₁,X₂) to be known, which is unlikely unless Y₂ is missing purposefully by design for some subjects in a way that depends on a subject's baseline and intermediate information. In practice, unknown π⁽¹⁾ is often addressed by positing a parametric model for π⁽¹⁾; intuition suggests that such a model be correctly specified, although we discuss this further in Section 4.2. For now, then, suppose that a parametric model π⁽¹⁾(X₁,Y₁,X₂;γ), say, for γ (s × 1) has been proposed and is correct, where γ₀ is the true value of γ so that evaluation at γ₀ yields the true probability π⁽¹⁾(X₁,Y₁,X₂). For definiteness, we focus henceforth on the logistic regression model

$$\begin{array}{c}\hfill {\pi }^{\left(1\right)}(X_1,Y_1,X_2;\gamma )\hfill \\ \hfill =\exp \left\{d^T(X_1,Y_1,X_2)\gamma \right\}\hfill \\ \hfill \cdot {[1+\exp \left\{d^T(X_1,Y_1,X_2)\gamma \right\}]}^{-1},\hfill \end{array}$$ (16)

where d(X₁,Y₁,X₂) is a vector of functions of its argument, but a development analogous to that below is possible for other choices (e.g., a probit model). In the ACTG 175 analysis in Section 6 we model the probability of observing CD4 at 96±5 weeks by a logistic function, where d(X₁,Y₁,X₂) includes functions of baseline and intermediate characteristics.

Under these conditions, a natural strategy is to derive an estimator for ${\mu }_2^{\left(1\right)}$ from an influence function of the form (15), assuming that π⁽¹⁾(X₁,Y₁,X₂) is known; estimate γ based on the i.i.d. data (X_1i,Y_1i,X_2i,R_i,Z_i), i = 1,...,n, and substitute the estimated value for γ in the (correct) parametric model π⁽¹⁾(X₁,Y₁,X₂;γ); and estimate ${\mu }_2^{\left(1\right)}$ acting as if π⁽¹⁾ were known. Robins, Rotnitzky and Zhao (1994) showed that, for any choice of h⁽¹⁾ and q⁽¹⁾ in (15), as long as an efficient procedure [e.g., maximum likelihood (ML)] is used to estimate γ , the resulting influence function for the estimator for β obtained by this strategy has the form

$$\begin{array}{c}\hfill \psi (X_1,Y_1,X_2,R,R{Y}_2,Z)\hfill \\ \hfill +d^T(X_1,Y_1,X_2)A_{\left(1\right)}^{-1}(b_{q\left(1\right)}-b_{\left(1\right)})\hfill \\ \hfill \cdot \frac{\{R-{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\}Z}{\delta },\hfill \end{array}$$ (17)

where

$$\begin{array}{c}\hfill b_{\left(1\right)}=E[(Y_2-{\mu }_2^{\left(1\right)})\{1-{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\}\hfill \\ \hfill \cdot d(X_1,Y_1,X_2)\mid Z=1],\hfill \end{array}$$

$$\begin{array}{c}\hfill b_{q\left(1\right)}=E[q^{\left(1\right)}(X_1,Y_1,X_2)\{1-{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\}\hfill \\ \hfill \cdot d(X_1,Y_1,X_2)\mid Z=1],\hfill \\ \hfill A_{\left(1\right)}=E[{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\{1-{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\}\hfill \\ \hfill \cdot d(X_1,Y_1,X_2)d^T(X_1,Y_1,X_2)\mid Z=1],\hfill \end{array}$$

and π⁽¹⁾(X₁,Y₁,X₂) is the true probability (i.e., the parametric model evaluated at γ₀). In Appendix A.5 we give the basis for this result. Thus, estimators for ${\mu }_2^{\left(1\right)}$ with influence functions in class (17) may be derived by finding estimators with influence functions in class (15) (so for “γ known” in the context of a correct parametric model for π⁽¹⁾) and substituting the ML estimator for γ . Thus, although influence functions of the form (17) are useful for understanding the properties of estimators for ${\mu }_2^{\left(1\right)}$ when γ is estimated, one need only work with influence functions of the form (15) to derive estimators.

When q⁽¹⁾(X₁,Y₁,X₂) has the efficient form $E(Y_2\mid X_1,Y_1,X_2,Z=1)-{\mu }_2^{\left(1\right)}$, b₍₁₎ = b_q(1). Hence, as long as the parametric model for π(1) is correct, even if γ is estimated, the last term in (17) is identically equal to zero, but this will not necessarily be true otherwise. This reflects the general result shown by Robins, Rotnitzky and Zhao (1994) that an estimator derived from the efficient influence function will have the same properties whether the parameters in a (correct) model for the missingness mechanism are known or estimated. For general h⁽¹⁾ and q⁽¹⁾ not necessarily equal to the optimal choices, the theory also implies the seemingly counterintuitive result that, even if γ is known, estimating it anyway can lead to a gain in efficiency; that is, for a specific (nonoptimal) choice of h⁽¹⁾ and q⁽¹⁾, the variance of (17) is at least as small as that of (15). In Appendix A.5 we give a justification of this claim.

3.6 Summary

By a development entirely similar to that above for influence functions for estimators for ${\mu }_2^{\left(1\right)}$, we may obtain similar influence functions for estimators for ${\mu }_2^{\left(0\right)}$. Here, influence functions in a subclass that contains the efficient influence function are of the form (15) with Z, π⁽¹⁾, δ, h⁽¹⁾ and q⁽¹⁾ replaced by 1 − Z, π⁽⁰⁾, (1 − δ) and analogous functions h⁽⁰⁾ and q⁽⁰⁾, respectively, with similar modifications in (17). The efficient influence function has, analogous to (14), h^eff(0) = E(Y₂|X₁,Y₁,Z = 0) − µ⁽⁰⁾ and $q^{\mathrm{eff}\left(0\right)}=E(Y_2\mid X_1,Y_1,X_2,Z=0)-{\mu }_2^{\left(0\right)}$. To deduce estimators for β when Y₂ is MAR, we derive estimators for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$ from these developments and take their difference, which is justified by the argument in Appendix A.3.

It may be shown that if the true missingness mechanism follows a parametric model π(X₁,Y₁,X₂,Z γ) inducing models π^(c)(X₁,Y₁,X₂;γ), c = 0, 1, correctly specifying this model and estimating γ by ML from the data for subjects with Z = 0 and 1 separately leads to estimators for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$ at least as efficient as those found by estimating γ by fitting π(X₁,Y₁,X₂,Z; γ) to all the data jointly. We recommend this approach in practice.

4. ESTIMATORS FOR β

4.1 Derivation of Estimators from Influence Functions

As a generic principle, based on (2), to identify an estimator from a given influence function, one sets the sum of terms that have the form of the influence function for each subject i = 1,...,n to zero, regarding the influence function as a function of the parameter of interest, and solves for this parameter, possibly substituting estimators for other unknown quantities. In complex models, particularly when p > 1, it may be impossible to solve for the parameter explicitly, and this and additional considerations can lead to computational and other challenges. However, for the simple pretest–posttest model, this strategy straightforwardly leads to closed-form estimators for β, as we now demonstrate.

The form of the efficient influence function is a natural starting point from which to derive estimators with good properties. Thus, focusing on ${\mu }_2^{\left(1\right)}$, applying this strategy to (15) with the optimal choices $h^{\left(1\right)}(X_1,Y_1)=E(Y_2\mid X_1,Y_1,Z=1)-{\mu }_2^{\left(1\right)}$ and $q^{\left(1\right)}(X_1,Y_1,X_2)=E(Y_2\mid X_1,Y_1,X_2,Y=1)-{\mu }_2^{\left(1\right)}$, simple algebra yields

$$\begin{array}{c}\hfill {\mu }_2^{\left(1\right)}={\left(n\delta \right)}^{-1}\sum _{i=1}^n\frac{R_i,Z_i,Y_{2i}}{{\pi }^{\left(1\right)}(X_{1i},Y_{1i},X_{2i})}\hfill \\ \hfill -{\left(n\delta \right)}^{-1}\sum _{i=1}^n(Z_i-\delta )\hfill \\ \hfill \cdot E(Y_{2i}\mid X_{1i},Y_{1i},Z_i=1)\hfill \\ \hfill -{\left(n\delta \right)}^{-1}\sum _{i=1}^n\frac{\{R_i-{\pi }^{\left(1\right)}(X_{1i},Y_{1i},X_{2i})\}{Z}_i}{{\pi }^{\left(1\right)}(X_{1i},Y_{1i},X_{2i})}\hfill \\ \hfill \cdot E(Y_{2i}\mid X_{1i},Y_{1i},X_{2i},Z_i=1),\hfill \end{array}$$ (18)

and similarly for ${\mu }_2^{\left(0\right)}$. Thus, to estimate β, one would take the difference of (18) and the analogous expression for ${\mu }_2^{\left(0\right)}$. In practice this is complicated by the fact that π(X₁,Y₁,X₂) must be modeled and fitted; moreover, it is evident that suitable regression models for E(Y₂|X₁,Y₁,Z) and E(Y₂|X₁,Y₁,X₂,Z) must be identified and fitted. We discuss strategies for resolving these practical challenges in Section 5.

4.2 Double Robustness

So far we have assumed that postulated models for π^(c), c = 0, 1, are correctly specified. If the postulated model is incorrect, substituting this incorrect model into an influence function of the form (15) or (17) when c = 1 with arbitrary h⁽¹⁾ and q⁽¹⁾ yields an expression that need not have mean zero; for example, the leading term in ψ(X₁,Y₁, X₂,R,RY₂,Z) in (15) has expectation zero only if P(R = 1|X₁,Y₁, X₂,Z = 1) = π⁽¹⁾ (X₁,Y₁,X₂), the true probability, and similarly for c = 0. Because a defining characteristic of an influence function is zero mean, estimators derived under such conditions need no longer be consistent. However, there is an exception when the optimal h⁽¹⁾ and q⁽¹⁾ are used as in (18), which we now describe.

In general, the augmentation in (11) induces the interesting property that estimators derived from (11) will be consistent if either (1) the choice g(O*) does not correspond to the optimal choice but π(O*) is correctly specified or (2) the optimal choice of g(O*) is used but π(O*) is misspecified. This property is referred to as double robustness (e.g., Scharfstein, Rotnitzky and Robins, 1999, Section 3.2.3; van der Laan and Robins, 2003, Section 1.6).

We may demonstrate the double robustness property for estimators for the pretest–posttest model; for definiteness, consider ${\mu }_2^{\left(1\right)}$. Under option 1, with any arbitrary choices for h⁽¹⁾ and q⁽¹⁾, if the model π⁽¹⁾(X₁,Y₁,X₂;γ) corresponds to the true mechanism, that (15) has mean zero is immediate. Thus, even if one models E(Y₂|X₁,Y₁,Z) and E(Y₂|X₁,Y₁, X₂,Z) incorrectly in (18), the resulting estimator still has a corresponding legitimate influence function in class (18) (assuming γ is estimated) and hence is consistent. Conversely, under option 2, suppose E(Y₂|X₁,Y₁,Z) and E(Y₂|X₁,Y₁,X₂,Z) are correctly specified in (18), but π⁽¹⁾(X₁,Y₁,X₂) is specified incorrectly by some π*(X₁,Y₁,X₂), say. Substituting π* for π⁽¹⁾ in (18), it is straightforward to show that the right-hand side converges in probability to ${\mu }_2^{\left(1\right)}$ (see Appendix A.6), suggesting that an estimator based on (18) would still be consistent. In fact, the second term in (18) converges in probability to zero even if E(Y₂|X₁,Y₁,Z = 1) is replaced by any arbitrary function of (X₁,Y₁), so that the double robustness property holds if only E(Y₂|X₁,Y₁,X₂,Z) is correct. Of course, if both π⁽¹⁾ and E(Y₂|X₁,Y₁,X₂,Z) are specified incorrectly, we cannot expect (18) to yield consistent inference in general.

As we discuss in Section 5, in practice one must develop and fit models for π^(c), E(Y₂|X₁,Y₁,Z) and E(Y₂|X₁,Y₁,X₂,Z), so the results above are somewhat idealized. However, if the analyst uses his or her best judgment and efforts to develop these models, the chance of coming very close to specifying at least one of them correctly may be high. The theoretical double robustness property suggests that, by using estimators like (18) based on the efficient influence function, the analyst has some protection against inadvertent mis-modeling. In our experience, even if both types of models are mildly incorrectly specified, valid inferences may be obtained; if one model is grossly incorrect, that with the mild misspecification error tends to dominate, so that reliable inferences are still possible.

5. PRACTICAL IMPLEMENTATION

To obtain estimators for β based on (18) and the analogous expression for ${\mu }_2^{\left(0\right)}$ suitable for practice, π^(c)(X₁,Y₁,X₂), E(Y₂|X₁,Y₁,Z = c) and E(Y₂ X₁,Y₁,X₂,Z = c), c = 0, 1, must be modeled and fitted. Given parametric models π^(c)(X₁,Y₁,X₂;γ), if γ is estimated by ML separately from the data for Z = 0 and 1 as at the end of Section 3.6, yielding estimators ${\widehat{\gamma }}^{\left(c\right)}$, c = 0, 1, we may form estimated probabilities ${\widehat{\pi }}_i^{\left(c\right)}={\pi }^{\left(c\right)}(X_{0i},Y_{1i},X_{1i};{\widehat{\gamma }}^{\left(c\right)})$, say. Similarly, given fits of some regression models E(Y₂|X₁,Y₁,Z = c) and E(Y₂|X₁,Y₁,X₂,Z = c), we may obtain predicted values ${\widehat{e}}_{h\left(c\right)i}$ and ${\widehat{e}}_{q\left(c\right)i}$, c = 0, 1, say, for E(Y_2i|X_1i,Y_1i,Z_i = c) and E(Y_2i|X_1i,Y_1i,X_2iZ_i = c), respectively. Letting $\widehat{\delta }=n_1∕n$, substituting in (18) and its analog for c = 0 then yields the estimator $\widehat{\beta }={\widehat{\mu }}_2^{\left(1\right)}-{\widehat{\mu }}_2^{\left(0\right)}$, where

$${\widehat{\mu }}_2^{\left(1\right)}=n_1^{-1}\left\{\sum _{i=1}^n{R}_i{Z}_i{Y}_{2i}∕{\widehat{\pi }}_i^{\left(1\right)}-\sum _{i=1}^n(Z_i-\widehat{\delta }){\widehat{e}}_{h\left(1\right)i}-\sum _{i=1}^n(R_i-{\widehat{\pi }}_i^{\left(1\right)})Z_i{\widehat{e}}_{q\left(1\right)i}∕{\widehat{\pi }}_i^{\left(1\right)}\right\}$$

and

$${\widehat{\mu }}_2^{\left(0\right)}=n_0^{-1}\left\{\sum _{i=1}^n{R}_i(1-Z_i)Y_{2i}∕{\widehat{\pi }}_i^{\left(0\right)}+\sum _{i=1}^n(Z_i-\widehat{\delta }){\widehat{e}}_{h\left(0\right)i}-\sum _{i=1}^n(R_i-{\widehat{\pi }}_i^{\left(0\right)})(1-Z_i){\widehat{e}}_{q\left(1\right)i}∕{\widehat{\pi }}_i^{\left(0\right)}\right\}.$$

Intuitively, replacing the unknown quantities in (18) and its analog for c = 0 by consistent estimators should not alter the implications for consistency of $\widehat{\beta }$ discussed earlier. We now review considerations involved in obtaining ${\widehat{\pi }}_i^{\left(c\right)}$, ${\widehat{e}}_{h\left(c\right)i}$ and ${\widehat{e}}_{q\left(c\right)i}$, c = 0, 1.

A natural approach to modeling E(Y₂|X₁,Y₁,Z = c) and E(Y₂|X₁,Y₁,X₂,Z = c) is to adopt parametric models based on usual regression considerations. For example, in ACTG 175, Y₂ = CD4 at 96±5 weeks is a continuous measurement, suggesting that standard linear regression models may be used. Because of the assumption of MAR, E(Y₂|X₁,Y₁,X₂,Z,R) does not depend on R; thus, E(Y₂|X₁,Y₁,X₂,Z) = E(Y₂|X₁,Y₁,X₂,Z,R = 1), implying that this model may be postulated and fitted based only on the complete cases. Thus, standard techniques for model selection and diagnostics may be applied to the data from subjects with R = 1. For example, inspection of plots like those in Figure 1, which shows only data for subjects for whom CD4 at 96±5 weeks is observed, may be used. Figure 1 suggests that such reasonable models might include both linear and quadratic terms in Y₁ = baseline CD4.

Considerations for developing and fitting models for E(Y₂|X₁,Y₁,Z = c) are trickier. Ideally, the chosen model for this quantity must be compatible with that for E(Y₂|X₁,Y₁,X₂,Z), as E(Y₂|X₁,Y₁,Z) = E{E(Y₂|X₁,Y₁,X₂,Z)|X₁,Y₁,Z}. Several practical strategies are possible, although none is guaranteed to achieve this property and hence yield the efficient estimators for ${\mu }_2^{\left(c\right)}$, c = 0, 1. One approach is to adopt a model directly for E(Y₂|X₁,Y₁,Z) that is likely “close enough” to be “approximately compatible.” For example, if E(Y₂|X₁,Y₁,X₂,Z) is a linear model in functions of (X₁,Y₁,X₂), one may be comfortable with a linear model for E(Y₂|X₁,Y₁,Z) that includes the same functions of X₁,Y₁. We demonstrate this ad hoc strategy for the ACTG 175 data in Section 6. If all of X₁,Y₁,X₂,Y₂ are continuous, assuming joint normality may be a reasonable approximation, in which case standard results may be used to deduce both models. Alternatively, one might use the relationship E(Y₂|X₁,Y₁,Z) = E{E(Y₂|X₁,Y₁,X₂,Z) X₁,Y₁,Z . For example, for low-dimensional X₂, a distributional model for X₂|X₁,Y₁,Z might be fitted based on the (X_1i,Y_1i,X_2i,Z_i), i = 1,...,n, which are observed for all subjects; integration with respect to this model would yield the desired conditional quantities for c = 0, 1. For univariate binary X₂, a logistic model for P(X₂ = 1|X₁,Y₁,Z) may be used; this is straightforward, but could be more challenging for mixed continuous and discrete and/or high-dimensional X₂. Instead, one might invoke an empirical approximation, for example, obtaining the predicted value ${\widehat{e}}_{h\left(c\right)i}$, c = 0, 1, for each i by averaging estimates of E(Y_2i|X_1i,Y_1i,X_2j ,Z_i = c) over subjects j that share the same values for (X₁,Y₁,Z) as i, which would likely be feasible only in specialized circumstances. A cruder version would be to average over all X_2j for j in the same group as i; this would yield the desired result only if X₂ is conditionally independent of (X₁,Y₁) given Z.

A further complication is that, for any chosen model for E(Y₂|X₁,Y₁,Z), it is no longer appropriate to fit the model based on the complete cases only. Ideally this fitting should be carried out by a procedure that accounts for the fact that Y₂ is MAR, such as an IWCC version of standard regression techniques. However, if the model is an approximation anyway, complete-case-only fitting may not be seriously detrimental. Even if the fit of the chosen model is not consistent for that model, the discussion of double robustness in Section 4.2 suggests that the resulting estimators ${\widehat{\mu }}_2^{\left(c\right)}$ and hence $\widehat{\beta }$ should be consistent regardless.

Another approach would be to use nonparametric smoothing to estimate E(Y₂|X₁,Y₁,X₁,Z) and E(Y₂|X₁,Y₁,Z) and obtain predicted values ${\widehat{e}}_{q\left(c\right)i}$ and ${\widehat{e}}_{h\left(c\right)i}$, for example, locally weighted polynomial smoothing (Cleveland, Grosse and Shyu, 1993) or generalized additive modeling (Hastie and Tibshirani, 1990). Ideally, smoothing for E(Y₂|X₁,Y₁,Z) should be modified to take into account that Y₂ is MAR, although this may not be critical by double robustness. Instead, an estimate of E(Y₂|X₁,Y₁,Z) could be derived from integration of the nonparametric fit of E(Y₂|X₁,Y₁,X₂,Z). Feasibility of smoothing might be limited in high dimensions.

However one approaches developing and fitting models for E(Y₂|X₁,Y₁,X₂,Z = c) and E(Y₂|X₁,Y₁,Z = c), c = 0, 1, we have found that it may be advantageous, at least for large n, to fit separate models for c = 0, 1. We also recommend including in all four models the same functions of components of X₁, Y₁ and X₂ (if appropriate) if they were found to be important in any one model, as it may be prudent to overmodel rather than undermodel.

Similarly, standard techniques for parametric binary regression may be used to fit models π^(c)(X₁,Y₁,X₂; γ) for each c = 0, 1, as all n subjects will have the requisite data. We recommend including in these models all covariates found to be important in any of the regression models above, as it may be shown that including covariates in this model that are correlated with Y₂, even if they are not associated with missingness, can lead to gains in efficiency. Lunceford and Davidian (2004) demonstrated this phenomenon in a simple related setting. Thus, we suggest developing this model after building and fitting of the models for E(Y₂|X₁,Y₁,X₂,Z = c) and E(Y₂|X₁,Y₁,Z = c) are complete.

Theoretically, if all of these models are correctly specified, then $\widehat{\beta }$ should be efficient in the sense described earlier. For parametric regression models for E(Y₂|X₁,Y₁,X₂,Z = c) and E(Y₂|X₁,Y₁,Z = c), although additional regression parameters must be estimated because of the geometry, there is no effect asymptotically; a similar phenomenon for nonparametric estimation of these quantities is suggested by the results of Newey (1990, pages 118−119) as long as this is at a rate faster than n^−1/4. The double robustness property discussed in Section 4.2 ensures that consistent estimators for β and ${\mu }_2^{\left(c\right)}$, c = 0, 1, will be obtained as long as either set of models is correct; however, efficiency is no longer guaranteed.

The asymptotic variance of $\widehat{\beta }$ is obtained from the expectation of the square of the difference of (15) and the analogous control influence function, given by

$$\begin{array}{cc}\hfill E& \left\{\frac{{(Y_2-{\mu }_2^{\left(1\right)})}^2}{{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\delta }\mid Z=1\right\}\hfill \\ \hfill & +E\left\{\frac{{(Y_2-{\mu }_2^{\left(0\right)})}^2}{{\pi }^{\left(0\right)}(X_1,Y_1,X_2)(1-\delta )}\mid Z=0\right\}\hfill \\ \hfill & -\delta (1-\delta )\cdot E\left[{\left\{\frac{E(Y_2\mid X_1,Y_1,Z=1)-{\mu }_2^{\left(1\right)}}{\delta }+\frac{E(Y_2\mid X_1,Y_1,Z=0)-{\mu }_2^{\left(0\right)}}{1-\delta }\right\}}^2\right]\hfill \\ \hfill & -\sum _{c=0,1}\left(\frac{I(c=1)}{\delta }+\frac{I(c=0)}{1-\delta }\right)\cdot E\left[\frac{1-{\pi }^{\left(c\right)}(X_1,Y_1,X_2)}{{\pi }^{\left(c\right)}(X_1,Y_1,X_2)}\cdot {\{E(Y_2\mid X_1,Y_1,X_2,Z=c)-{\mu }_2^{\left(c\right)}\}}^2\right].\hfill \end{array}$$ (19)

Implicit here is the assumption that the models for π^(c)(X₁,Y₁,X₂), E(Y₂|X₁,Y₂,X₂,Z = c) and E(Y₂|X₁,Y₁,Z = c) are correct. Equation (19) may be estimated by replacing the first two terms by ${\left(\widehat{\delta }{\widehat{n}}_{RZ\left(1\right)}\right)}^{-1}.{\sum }_{i=1}^n{R}_i{Z}_i{(Y_{2i}-{\widehat{\mu }}_2^{\left(1\right)})}^2∕{\widehat{\pi }}_i^{\left(1\right)2}$ and ${\left\{(1-\widehat{\delta }){\widehat{n}}_{RZ\left(0\right)}\right\}}^{-1}.{\sum }_{i=1}^n{R}_i(1-Z_i){(Y_{2i}-{\widehat{\mu }}_2^{\left(0\right)})}^2∕{\widehat{\pi }}_i^{\left(0\right)2}$, where ${\widehat{n}}_{RZ\left(c\right)}={\sum }_{i=1}^n{R}_{i}I(Z_i=c)∕{\widehat{\pi }}_i^{\left(c\right)}$, and replacing the remaining terms by sample averages with estimates substituted for needed quantities. Alternatively, var($\widehat{\beta }$) may be estimated by ${\sum }_{i=1}^n{\widehat{\phi }}_i^2∕n^2$, corresponding to the so-called sandwich technique, where ${\widehat{\phi }}_i$ is the difference of the influence functions with estimates substituted, that is,

$$\begin{array}{cc}\hfill {\widehat{\phi }}_i=& \frac{R_i{Z}_i(Y_{2i}-{\widehat{\mu }}_2^{\left(1\right)})}{\widehat{\delta }{\widehat{\pi }}_i^{\left(1\right)}}-\frac{(Z_i-\widehat{\delta })({\widehat{e}}_{h\left(1\right)i}-{\widehat{\mu }}_2^{\left(1\right)})}{\widehat{\delta }}\hfill \\ \hfill & -\frac{(R_i-{\widehat{\pi }}_i^{\left(1\right)})Z_i({\widehat{e}}_{q\left(1\right)i}-{\widehat{\mu }}_2^{\left(1\right)})}{\widehat{\delta }{\widehat{\pi }}_i^{\left(1\right)}}\hfill \\ \hfill & -\frac{R_i(1-Z_i)(Y_{2i}-{\widehat{\mu }}_2^{\left(0\right)})}{(1-\widehat{\delta }){\widehat{\pi }}_i^{\left(0\right)}}\hfill \\ \hfill & +\frac{(Z_i-\widehat{\delta })({\widehat{e}}_{h\left(0\right)i}-{\widehat{\mu }}_2^{\left(0\right)})}{(1-\widehat{\delta })}\hfill \\ \hfill & -\frac{(R_i-{\widehat{\pi }}_i^{\left(0\right)})(1-Z_i)({\widehat{e}}_{q\left(1\right)i}-{\widehat{\mu }}_2^{\left(0\right)})}{(1-\widehat{\delta }){\widehat{\pi }}_i^{\left(0\right)}}.\hfill \end{array}$$

If E(Y₂|X₁,Y₂,X₂,Z) and E(Y₂|X₁,Y₁,Z) are mismodeled, the influence function of ${\widehat{\mu }}_2^{\left(1\right)}$ would instead be of the form (17) to account for estimation of γ , and similarly for ${\widehat{\mu }}_2^{\left(0\right)}$. Although technically then the above formulae would seem to require modification, we have extensive empirical evidence to suggest that they yield reliable estimates of precision if incorrect models are used.

6. TREATMENT EFFECT IN ACTG 175

We now apply the proposed methods to the data from ACTG 175, where β is the difference in mean CD4 count at 96±5 weeks for subjects receiving ZDV (control) and those receiving any of the other three therapies (treatment), so that δ = 0.75. The analysis here is not definitive, but is meant to illustrate the typical steps in an analysis based on these techniques.

Following Section 5, we begin by modeling E(Y₂|X₁,Y₁,X₂,Z = c), c = 0, 1. As reviewed in Section 1.1, X₁ contains 11 baseline covariates in addition to baseline CD4 (Y₁). For X₂, we considered three covariates available for all subjects: CD4 at 20±5 weeks postrandomization, CD8 at 20±5 weeks and an indicator of whether the subject went off his/her assigned treatment prior to 96 weeks; reasons could include death, dropout or other patient or physician decisions. Because of the high dimension of X₁ and the fact that both X₁ and X₂ contain a mixture of continuous and discrete variables, we considered parametric linear regression modeling. Based on the 1342 of n = 2139 subjects that are complete cases, standard model selection techniques indicate that weight, indicators of HIV symptoms and prior antiretroviral therapy, Karnofsky score, CD8 count and CD4 count (linear and quadratic terms in CD4 and CD8) at baseline, CD8 and CD4 count at 20±5 weeks (linear and quadratic terms), and off-treatment status are associated with Y₂ = CD4 count at 96±5 weeks in one or both treatment groups. Thus, we fit separately for c = 0, 1, the models

$$\begin{array}{cc}\hfill & E(Y_2\mid X_1,Y_1,X_2,Z=c)\hfill \\ \hfill & ={\alpha }_0^{\left(c\right)}+{\alpha }_1^{\left(c\right)}\mathrm{wt}+{\alpha }_2^{\left(c\right)}\mathrm{HIV}+{\alpha }_3^{\left(c\right)}\mathrm{prior}\hfill \\ \hfill & +{\alpha }_4^{\left(c\right)}\mathrm{Karn}+{\alpha }_5^{\left(c\right)}\mathrm{CD}{8}_0+{\alpha }_6^{\left(c\right)}\mathrm{CD}{8}_0^2\hfill \\ \hfill & +{\alpha }_7^{\left(c\right)}\mathrm{CD}{4}_0+{\alpha }_8^{\left(c\right)}\mathrm{CD}{4}_0^2+{\alpha }_9^{\left(c\right)}\mathrm{CD}{8}_{20}\hfill \\ \hfill & +{\alpha }_{10}^{\left(c\right)}\mathrm{CD}{8}_{20}^2+{\alpha }_{11}^{\left(c\right)}\mathrm{CD}{4}_{20}+{\alpha }_{12}^{\left(c\right)}\mathrm{CD}{4}_{20}^2\hfill \\ \hfill & +{\alpha }_{13}^{\left(c\right)}\mathrm{offtrt}\hfill \end{array}$$ (20)

by ordinary least squares (OLS), obtaining predicted values ${\widehat{e}}_{q\left(c\right)i}$, c = 0, 1 for each i = 1,...,n. Adopting the ad hoc strategy in Section 5, we directly modeled E(Y₂|X₁,Y₁,Z = c), c = 0, 1, by including the same terms in X₁ and Y₁ as in (20), that is,

$$\begin{array}{cc}\hfill & E(Y_2\mid X_1,Y_1,Z=c)\hfill \\ \hfill & ={\alpha }_0^{\left(c\right)}+{\alpha }_1^{\left(c\right)}\mathrm{wt}+{\alpha }_2^{\left(c\right)}\mathrm{HIV}+{\alpha }_3^{\left(c\right)}\mathrm{prior}\hfill \\ \hfill & +{\alpha }_4^{\left(c\right)}\mathrm{Karn}+{\alpha }_5^{\left(c\right)}\mathrm{CD}{8}_0+{\alpha }_6^{\left(c\right)}\mathrm{CD}{8}_0^2\hfill \\ \hfill & +{\alpha }_7^{\left(c\right)}\mathrm{CD}{4}_0+{\alpha }_8^{\left(c\right)}\mathrm{CD}{4}_0^2,\hfill \end{array}$$

again fitting the model for each c by OLS and obtaining predicted values ${\widehat{e}}_{h\left(c\right)i}$, c = 0, 1 for all n subjects. Finally, based on standard techniques for logistic regression and the guidelines in Section 5, we arrived at

$$\begin{array}{cc}\hfill & \mathrm{logit}{\pi }^{\left(c\right)}(X_1,Y_1,X_2;{\gamma }^{\left(c\right)})\hfill \\ \hfill & ={\gamma }_0^{\left(c\right)}+{\gamma }_1^{\left(c\right)}\mathrm{wt}+{\gamma }_2^{\left(c\right)}\mathrm{HIV}+{\gamma }_3^{\left(c\right)}\mathrm{prior}\hfill \\ \hfill & +{\gamma }_4^{\left(c\right)}\mathrm{Karn}+{\gamma }_5^{\left(c\right)}\mathrm{CD}{8}_0+{\gamma }_6^{\left(c\right)}\mathrm{CD}{8}_0^2\hfill \\ \hfill & +{\gamma }_7^{\left(c\right)}\mathrm{CD}{4}_0+{\gamma }_8^{\left(c\right)}\mathrm{CD}{4}_0^2+{\gamma }_9^{\left(c\right)}\mathrm{CD}{8}_{20}\hfill \\ \hfill & +{\gamma }_{10}^{\left(c\right)}\mathrm{CD}{8}_{20}^2+{\gamma }_{11}^{\left(c\right)}\mathrm{CD}{4}_{20}+{\gamma }_{12}^{\left(c\right)}\mathrm{CD}{4}_{20}^2\hfill \\ \hfill & +{\gamma }_{13}^{\left(c\right)}\mathrm{offtrt},c=0,1,\hfill \end{array}$$

where γ was estimated separately by ML for each group.

Table 1 shows the estimate of $\widehat{\beta }$ and the estimated standard error obtained by the sandwich technique, and appears to provide strong evidence that mean CD4 at 96±5 weeks is higher in the treatment group relative to the control. Table 1 also presents the estimate of β obtained via the IWCC method. The IWCC estimated standard error is larger than that for the proposed methods, consistent with the implication of the theory that incorporation of baseline and intervening covariate information should improve precision. For comparison, Table 1 shows estimates of β obtained by the two most popular approaches in practice based on the complete cases only. These results suggest there may be nonnegligible bias associated with these naive methods, in this case suggesting an overly optimistic treatment difference.

Table 1.

Treatment effect estimates for 96±5 week CD4 counts for ACTG 175

	Estimate	SE
New method	57.24	10.20
IWCC	54.69	11.79
ANCOVA	64.54	9.33
Paired t test	67.14	9.23

Note. Standard errors for the new method and the IWCC estimate were obtained using the sandwich approach. ANOVA denotes ordinary analysis of covariance with no interaction term. Standard errors for the popular estimators based on complete cases were obtained from standard formulæ.

7. DISCUSSION

We have shown how the theory developed by Robins, Rotnitzky and Zhao (1994) may be applied to the ubiquitous pretest–posttest problem to deduce analysis procedures that take appropriate account of MAR follow-up data, yield consistent inferences and lead to efficiency gains over simpler methods by exploiting auxiliary covariate information. This perspective provides a general framework for pretest–posttest analysis with missing data that illuminates how relationships among variables play a role in both accounting for missingness and enhancing precision, thus offering the analyst guidance for selecting appropriate methods in practice. We hope that this explicit, detailed demonstration of this theory in a familiar context will help researchers who are not well versed in its underpinnings appreciate the fundamental concepts and how the theoretical results may be translated into practical methods.

We have carried out extensive simulations that show that the proposed methods lead to consistent inference and considerable efficiency gains over simpler methods such as IWCC estimators; a detailed account is available at http://www4.stat.ncsu.edu/∼davidian.

We considered the situation where only follow-up response is potentially missing; baseline and intermediate covariates are assumed observable for all subjects. In some settings covariate information in the period between baseline and follow-up may be censored due to dropout, leading to only partially observed X₂. The development may be extended to this case via the Robins, Rotnitzky and Zhao (1994) theory and is related to that for causal inference for time-dependent treatments, requiring assumptions similar to those of sequential randomization identified by Robins (e.g., Robins, 1999; van der Laan and Robins, 2003).

Although our presentation is in the context of the pretest–posttest study, it is evident that the results are equally applicable to the problem of comparing two means in a randomized study with adjustment for baseline covariates to improve efficiency, as discussed, for example, by Koch et al. (1998), because the pretest response Y₁ may be viewed as simply another baseline covariate. Thus, the developments also clarify how such optimal adjustment should be carried out to achieve efficient inferences on a difference in means in this setting; moreover, they provide a systematic approach to accounting for missing response.

APPENDIX

A.1. INFLUENCE FUNCTIONS AND SEMIPARAMETRIC THEORY

Correspondence between influence functions and RAL estimators

Before we describe semiparametric theory, we sketch an argument that more fully justifies why working with influence functions is informative for identifying (RAL) estimators. It is straightforward to show by contradiction that an asymptotically linear estimator [i.e., an estimator satisfying (2)] has a unique (almost surely) influence function. In the notation in (2), if this were not the case, there would exist another influence function φ*(W) with E{φ*(W)} = 0 that also satisfies (2). If (2) holds for both φ(W) and φ*(W), it must be that $A=n^{-1∕2}{\sum }_{i=1}^n\{\phi \left(W_i\right)-{\phi }^{\ast }\left(W_i\right)\}=o_p\left(1\right)$. Whereas the W_i are i.i.d., A converges in distribution to a normal random vector with mean zero and covariance matrix E[{φ(W) − φ*(W)}{φ(W) − φ*(W)}^T . Whereas this limiting distribution is o_p(1), it must be that ∑ = 0, implying φ(W) = φ*(W) almost surely.

Parametric model

We begin by considering fully parametric models. Formally, a parametric model for data V is characterized by all densities p(v) in a class $\mathcal{P}$ indexed by a q-dimensional parameter θ, so that $p\left(v\right)=p(v,\theta )\in \mathcal{P}$ is fully specified by θ. Suppose that interest focuses on a parameter β in this model. In the most familiar case, θ may be partitioned explicitly as θ = (β^T ,η^T)^T for β(p×1) and η(r×1), r = q − p, so that η is a nuisance parameter, and we may write p(v, β, η). Alternatively, β = β(θ) may be some function of θ, and identifying the nuisance parameter may be less straightforward, but the principles are the same. For simplicity, whereas β in the pretest–posttest problem is a scalar, we restrict attention to p = 1.

Maximum likelihood estimator in a parametric model

For definiteness, consider the case where θ = (β, η^T)^T. Define as usual the score vector $S_{\theta }(V,\theta )={\{S_{\beta }(V,\theta ),S_{\eta }^T(V,\theta )\}}^T=[\partial ∕\partial \beta \left\{\log p(V,\beta ,\eta )\right\}$, ∂/∂η^T {log|p(V, β, η)}]^T and let ${\theta }_0={({\beta }_0,{\eta }_0^T)}^T$ be the true value of θ. Then E{Sθ(V, θ₀)}= 0 and the information matrix is

$$\begin{array}{cc}\hfill \ell \left({\theta }_0\right)& =E\left\{S_{\theta }(V,{\theta }_0)S_{\theta }^T(V,{\theta }_0)\right\}\hfill \\ \hfill & =\left(\begin{array}{cc}\hfill {\ell }_{\beta \beta }\hfill & \hfill {\ell }_{\beta \eta }\hfill \\ \hfill {\ell }_{\beta \eta }^T\hfill & \hfill {\ell }_{\eta \eta }\hfill \end{array}\right),{\ell }_{\eta \eta }(r\times r),{\ell }_{\beta \eta }(1\times r),\hfill \end{array}$$

where expectation is with respect to the true density p(v, β₀,η₀). Writing $\widehat{\theta }={(\widehat{B},{\widehat{\eta }}^T)}^T$ to denote the maximum likelihood estimator for θ found by maximizing ${\sum }_{i=1}^n\log p(v_i,\beta ,\eta )$, it is well known (e.g., Bickel et al., 1993, Section 2.4) that, under regularity conditions,

$$\begin{array}{c}\hfill n^{1∕2}(\widehat{\beta }-{\beta }_0)=n^{-1∕2}\sum _{i=1}^n{\phi }^{\mathrm{eff}}\left(V_i\right)+o_p\left(1\right),\hfill \\ \hfill {\phi }^{\mathrm{eff}}\left(V\right)={\ell }_{\beta \beta •\eta }^{-1}\{S_{\beta }(V,{\theta }_0)\hfill \end{array}$$ (A.1)

$$\begin{array}{c}\hfill -{\ell }_{\beta \eta }{\ell }_{\eta \eta }^{-1}{S}_{\eta }(V,{\theta }_0)\},\hfill \\ \hfill {\ell }_{\beta \beta •\eta }={\ell }_{\beta \beta }-{\ell }_{\beta \eta }{\ell }_{\eta \eta }^{-1}{\ell }_{\beta \eta }^T,\hfill \end{array}$$ (A.2)

so that E{φ^eff(V)} = 0 and $\widehat{\beta }$ is RAL with influence function φ^eff(V). Whereas $S^{\mathrm{eff}}\left(V\right)=S_{\beta }(V,{\theta }_0)-{\ell }_{\beta \eta }{\ell }_{\eta \eta }^{-1}{S}_{\eta }(V,{\theta }_0)$ has variance ${\ell }_{\beta \beta •\eta }$, $\widehat{\beta }$ is consistent and asymptotically normal with asymptotic variance $E\left\{{\phi }^{\mathrm{eff}}\left(V\right){\phi }^{\mathrm{eff}T}\left(V\right)\right\}=1∕{\ell }_{\beta \beta •\eta }$, the well-known Cramér–Rao lower bound, the smallest possible variance for (regular) estimators for β. Thus, $\widehat{\beta }$ is the efficient estimator and, accordingly, S^eff(V) is often called the efficient score. Evidently φ^eff(V) is the efficient influence function, and these familiar results emphasize the connection between efficiency and the score vector.

We are now in position to place these results in a geometric context. Our discussion of this geometric construction for both parametric and semiparametric models is not meant to be rigorous and complete, but serves only to highlight the crucial elements.

Hilbert space

A Hilbert space $\mathcal{H}$ is a linear vector space, so that $a{h}_1+b{h}_2\in \mathcal{H}$ for $h_1,h_2\in \mathcal{H}$ and any real a, b, equipped with an inner product; see Luenberger (1969, Chapter 3). The key feature that underlies the geometric perspective is that influence functions based on data V for estimators for a p-dimensional parameter β in a statistical model may be viewed as elements in the particular Hilbert space H of all p-dimensional, mean-zero random functions h(V) such that E{h^T (V)h(V)} < ∞, with inner product $E\left\{h_1^T\left(V\right)h_2\left(V\right)\right\}$ for $h_1,h_2\in \mathcal{H}$ and corresponding norm ∥h∥ =[E{h^T (V)h(V)}]^1/2, measuring distance from h ≡ 0. Thus, the geometry of Hilbert spaces provides a unified framework for deducing results with regard to influence functions in both parametric and semiparametric models.

Some general results concerning Hilbert spaces are important. For any linear subspace M of $\mathcal{H}$, the set of all elements of $\mathcal{H}$ orthogonal to those in M, denoted M^⊥ (i.e., such that if h₁ ∈ M and h₂ ∈ M^⊥, the inner product of h₁,h₂ is zero), is also a linear subspace of $\mathcal{H}$. Moreover, for two linear subspaces M and N, M ⊕ N is the direct sum of M and N if every element in M ⊕ N has a unique representation of the form m + n for m ∈ M, n ∈ N. Intuitively, it is the case that the entire Hilbert space $\mathcal{H}=M\oplus M^{\perp }$. As we will see momentarily, a further essential concept is the notion of a projection. The projection of $h\in \mathcal{H}$ onto a closed linear subspace M of $\mathcal{H}$ is the element in M, denoted by Π(h|M), such that ∥h − Π(h|M)∥ < ∥h−m∥ for all m ∈ M and the residual h − Π(h|M) is orthogonal to all m ∈ M; such a projection is unique (e.g., Luenberger, 1969, Section 3.3).

In light of the pretest–posttest problem, we again take p = 1. Let θ₀ be the true value of θ.

Geometric perspective on the parametric model

Consider first the case where θ may be partitioned as θ = (β, η^T)^T, η (r × 1). Let Λ be the linear subspace of $\mathcal{H}$ that consists of all linear combinations of S_η(V, θ₀) of the form BS_η(V, θ₀), that is, Λ = {BS_η(V, θ₀) for all (1 × r) B}, the linear subspace of $\mathcal{H}$ spanned by S_η(V, θ₀). Whereas depends on the score for nuisance parameters, it is referred to as the nuisance tangent space. A fundamental result in this case is that all influence functions for RAL estimators for β may be shown to lie in the subspace Λ^⊥ orthogonal to Λ. Although a proof of this is beyond our scope, it is straightforward to provide an example by demonstrating that the efficient influence function in (A.2) lies in Λ^⊥. In particular, we must show that $E\left\{{\phi }^{\mathrm{eff}T}\left(V\right)B{S}_{\eta }(V,{\theta }_0)\right\}=E\left[{\{S_{\beta }(V,{\theta }_0)-{\ell }_{\beta \eta }{\ell }_{\eta \eta }^{-1}{S}_{\eta }(V,{\theta }_0)\}}^{T}B{S}_{\eta }(V,{\theta }_0)\right]∕{\ell }_{\beta \beta •\eta }=0$ for all B (1 × r). By taking B successively to be a vector with a 1 in one component and 0s elsewhere, this may be seen to be equivalent to showing that $E\left[\{S_{\beta }(V,{\theta }_0)-{\ell }_{\beta \eta }{\ell }_{\eta \eta }^{-1}{S}_{\eta }(V,{\theta }_0)\}{S}_{\eta }^T(V,{\theta }_0)\right]=0$, which follows immediately. Thus, one approach to identifying influence functions for a particular model with θ = (β, η^T)^T is to characterize the form of elements in Λ^⊥ directly.

Alternatively, other representations are possible. For general p(v, θ), the tangent space Γ is the linear subspace of $\mathcal{H}$ spanned by the entire score vector S_θ(V, θ₀), where S_θ(V, θ) = ∂/∂θ {log p(V, θ)}, that is, Γ = {BS_θ (V, θ₀) for all (1 × q) B}. We have the following key result.

Result A.1

Representation of influence functions

All influence functions for (RAL) estimators for β may be represented as φ(V) = φ*(V) + ψ(V), where φ*(V) is any influence function and ψ(V) ∈ Γ^⊥, the subspace of $\mathcal{H}$ orthogonal to Γ.

This may be shown for general β(θ); we demonstrate when θ = (β, η^T)^T. In this case, a defining property of influence functions φ(V) which is related to regularity is that (1) E{φ(V)S_β(V, θ₀) = 1 and (2) $E\left\{\phi \left(V\right)S_{\eta }^T(V,{\theta }_0)\right\}=0(1\times r)$; the proof } = is outside our scope here. Given this, we now show that all influence functions can be represented as in Result A.1. First, we demonstrate that if φ(V) can be written as φ*(V) + ψ(V ), where φ*(V) and ψ(V) satisfy the conditions of Result A.1, then φ(V) is an influence function. Letting Γ_β ={BS_β(V, θ₀) for all real B} be the space spanned by the score for β, it may be shown that Γ = Λ ⊕ Γ_β. Thus, if ψ ∈ Γ^⊥, ψ(V) is orthogonal to functions in both Λ and Γ_β, so that E{ψ(V)S_β(V, θ₀)} = 0 and $E\left\{\psi \left(V\right)S_{\eta }^T(V,{\theta }_0)\right\}=0(1\times r)$. Moreover, because φ*(V) is an influence function, it satisfies properties 1 and 2, whence it follows that φ(V) also satisfies properties 1 and 2 and, hence, is itself an influence function. Conversely, we show that if φ(V) is an influence function, it can be represented as in Result A.1. If φ(V) is an influence function, it must satisfy properties 1 and 2, and, writing φ(V) = φ*(V) + {φ(V) − φ*(V)} for some other influence function φ*(V), it is straightforward to use properties 1 and 2 to show that ψ(V) = {φ(V) − φ*(V)} ∈ Γ^⊥. Thus, in general, by identifying any influence function and Γ^⊥, one may exploit Result A.1 to characterize all influence functions.

Depending on the particular model and nature of β, one method for characterizing influence functions may be more straightforward than another. When using Result A.1 in models where θ = (β, η^T)^T, Γ may be most easily determined by finding Λ and Γ_β separately; for general β(θ), Γ may often be identified directly.

From Result A.1, we may also deduce a useful characterization of the efficient influence function φ^eff(V) that satisfies E{φ²(V)} − E{φ^eff2(V)} ≥ 0 for all influence functions φ(V). Whereas for arbitrary φ(V), φ^eff(V) = φ(V) − ψ(V) for ψ ∈ Γ^⊥ and E{φ^eff2(V)} = ∥φ − ψ∥ must be as small as possible, it must be that ψ = Π(φ|Γ^⊥). Thus, we have the following result.

Result A.2

Representation of the efficient influence function

The function φ^eff(V) may be represented as φ(V) − Π(φ|Γ^⊥)(V) for any influence function φ(V).

In the case θ = (β, η^T)^T, it is in fact possible to identify explicitly the form of the efficient influence function. Here, the efficient score is defined as the residual of the score vector for β after projecting it onto the nuisance tangent space, S^eff(V, θ₀) = S_β(V, θ₀) − Π(S_β|Γ), and the efficient influence function is an appropriately scaled version of S^eff given by φ^eff(V) = [E{S^eff2(V, θ₀)}]⁻¹S^eff(V, θ₀). It is straightforward to observe that φ^eff(V) is an influence function by showing it satisfies 1 and 2 above. Specially, by construction S^eff ∈ Λ^⊥, so property 2 holds. This implies E{φ^eff(V)Π(S_β|Λ)(V)} = 0, so that

$$\begin{array}{cc}\hfill & E\left\{{\phi }^{\mathrm{eff}}\left(V\right)S_{\beta }(V,{\theta }_0)\right\}\hfill \\ \hfill & =E\left\{{\phi }^{\mathrm{eff}}\left(V\right)S^{\mathrm{eff}}(V,{\theta }_0)\right\}+E\left\{{\phi }^{\mathrm{eff}}\left(V\right)\Pi (S_{\beta }\mid \Lambda )\left(V\right)\right\}\hfill \\ \hfill & =E\left\{S^{\mathrm{eff}2}(V,{\theta }_0)\right\}E\left\{S^{\mathrm{eff}2}(V,{\theta }_0)\right\}=1,\hfill \end{array}$$

demonstrating property 1. That φ^eff(V) has the smallest variance among influence functions may be seen by using the fact that all influence functions may be written as φ(V) = φ^eff(V) + ψ(V) for some ψ(V) ∈ Γ^⊥. Because S_β ∈ Γ_β and Π(S_β|Λ) ∈ Λ are both in Γ, it follows that E{ψ(V)φ^eff(V)} = 0. Thus, E{φ²(V)} = E[{φ^eff(V + ψ(V)}²] = Eφ^eff2(V)} + E{ψ²(V)}, so that any other influence function φ(V) has variance at least as large as that of φ^eff(V), and this smallest variance is immediately seen to be 1/S^eff2(V, θ₀).

Finally, we may relate this development to the familiar maximum likelihood results when θ = (β, η^T)^T . By definition, Π(S_β|Λ) ∈ Λ is the unique element B₀S_η ∈ Λ such that E[{S_β(V, θ₀) − B₀S_η(V, θ₀)} · BS_η(V, θ₀)] = 0 for all B (1 × r). As above, this is equivalent to requiring $E[\{S_{\beta }(V,{\theta }_0)-B_0{S}_{\eta }(V,{\theta }_0)\}\cdot S_{\eta }^T(V,{\theta }_0)]=0(1\times r)$, implying ${\beta }_0={\ell }_{\beta \beta }{\ell }_{\eta \eta }^{-1}$. Thus, $\Pi (S_{\beta }\mid \Lambda )={\ell }_{\beta \beta }{\ell }_{\eta \eta }^{-1}{S}_{\eta }(V,{\theta }_0)$ and $S^{\mathrm{eff}}(V,{\theta }_0)=S_{\beta }(V_i,{\theta }_0)-{\ell }_{\beta \eta }{\ell }_{\eta \eta }^{-1}{S}_{\eta }(V_i,{\theta }_0)$, as expected.

For a parametric model, it is usually unnecessary to appeal to the foregoing geometric construction to identify the efficient estimator and influence functions. In contrast, in the more complex case of a semiparametric model such results often may not be derived readily. However, as we now discuss, the geometric perspective may be generalized to semiparametric models, providing a systematic framework for identifying influence functions.

Geometric perspective on the semiparametric model

In its most general form, a semiparametric model for data V is characterized by the class $\mathcal{P}$ of all densities p{v, θ(·)} that depend on an infinite-dimensional parameter θ(·). Often, analogous to the familiar parametric case, θ(·) ={β, η(·)}, where β is (p × 1) and η(·) is an infinite-dimensional nuisance parameter, and interest focuses on β. For example, in the regression situation in Section 1.2, β specifies a parametric model for the conditional expectation of a response given covariates, and η(·) represents all remaining aspects, such as other features of the conditional distribution, that are left unspecified. Alternatively, interest may focus on a functional β{θ(·)} of θ(·). This is the case in the semiparametric pretest–posttest model, where θ(·) represents all aspects of the distribution of V = (X₁,Y₁,X₂,Y₂,Z) that are left unspecified and β is given in (1).

The key to generalization of the results for parametric models to this setting is the notion of a parametric submodel. A parametric submodel is a parametric model contained in the semiparametric model that contains the truth. In the most general case, with densities p{v, θ(·)} and functional of interest β{θ(·), there is a true θ₀(·) such that $p_0\left(v\right)=p\{v,{\theta }_0(\cdot )\}\in \mathcal{P}$ is the density that generates the data. A parametric submodel is the class of all densities ${\mathcal{P}}_{\xi }$ characterized by a finite-dimensional parameter ξ such that ${\mathcal{P}}_{\xi }\subset \mathcal{P}$ and the true density $p_0\left(v\right)=p\{v,{\theta }_0(\cdot )\}=p(v,{\xi }_0)\in {\mathcal{P}}_{\xi }$, where the dimension r of ξ varies according to particular choice of submodel. That is, there exists a density identified by the parameter ξ₀ within the parameter space of the parametric submodel such that p₀(v) = p(v, ξ₀). In Appendix A.2 below, we give an explicit example of parametric submodels in the pretest–posttest setting.

The importance of this concept is that an estimator is an (RAL) estimator for β under the semiparametric model if it is an estimator under every parametric submodel. Thus, the class of estimators for β for the semiparametric model must be contained in the class of estimators for a parametric submodel and, hence, any influence function for the semiparametric model must be an influence function for a parametric submodel. Now, if Γ_ξ is the tangent space for a given submodel p(v, ξ) with score vector S_ξ(v, ξ) = ∂/∂ξ {log p(v, ξ)}, by Result A.1 the corresponding influence functions for estimators for β must be representable as φ(V) = φ*(V) + γ(V), where φ*(V) is any influence function in the parametric submodel and $\gamma \left(V\right)\in {\Gamma }_{\xi }^{\perp }$. Thus, intuitively, defining to be the mean square closure of all parametric submodel tangent spaces [i.e., $\Gamma =\{h\in \mathcal{H}$ such that there exists a sequence of parametric submodels ${\mathcal{P}}_{{\xi }_j}$ with ∥h(V) − B_jS_ξ(V, ξ_0j)∥² → 0 as j → ∞}, where B_j are (1 × r_j) constant matrices], then it may be shown that Result A.1 holds for semiparametric model influence functions. That is, all influence functions φ(V) for estimators for β in the semiparametric model may be represented as φ*(V) + ψ(V), where φ*(V) is any semiparametric model influence function and ψ(V) ∈ Γ^⊥. Moreover, Result A.2 also holds: as in the parametric case, the efficient estimator with smallest variance has influence function φ^eff(V) and may be represented as φ^eff(V) = φ(V) − Π(φ|Γ^⊥)(V) for any semiparametric model influence function φ(V). In Appendix A.2 we use these results to deduce full-data influence functions for the semiparametric pretest–posttest model.

Although the pretest–posttest model may be handled using the above development, it is worth noting that a framework analogous to the parametric case ensues when θ(·) = {β, η(·), so that p(v) = p{v, β, η(·)}, with true values β₀,η₀(·) such that the true density is $p_0\left(v\right)=p\{v,{\beta }_0,{\eta }_0(\cdot )\}\in \mathcal{P}$. Here, a parametric submodel ${\mathcal{P}}_{\beta ,\xi }$ is the class of all densities characterized by β and finite-dimensional ξ such that ${\mathcal{P}}_{\beta ,\xi }\subset \mathcal{P},p\{v,{\beta }_0,{\eta }_0(\cdot )\}=p(v,{\beta }_0,{\xi }_0)\in {\mathcal{P}}_{\beta ,\xi }$. As a parametric model, a submodel has a corresponding nuisance tangent space and, as above, because the class of estimators for β for the semiparametric model must be contained in the class of estimators for a parametric submodel, influence functions for estimators for β for the semiparametric model must lie in a space orthogonal to all submodel nuisance tangent spaces. Thus, defining the semiparametric model nuisance tangent space Λ as the mean square closure of all parametric submodel nuisance tangent spaces, it may be shown that all influence functions for the semiparametric model lie in Λ^⊥. Moreover, the semiparametric model tangent space Γ = Λ ⊕ Γ_β, where Γ _β is the space spanned by S_β{V,β₀,η₀(·)} = ∂/∂β [logp{V,β,η₀(·,) evaluated parametric model efficient score S^eff is S_β{V,β₀,η₀(·)} − Π(S_β|Λ)(V) with efficient influence function φ^eff{V,β₀,η₀(·)} = E([S^eff{V,β₀,η₀(·)}]²)}⁻¹ · S^eff{V,β₀,η₀(·)}. The variance of φ^eff, {E([S^eff{V,β₀,η₀(·)}]²)}⁻¹, achieves the so-called semiparametric efficiency bound, that is, the supremum over all parametric submodels of the Cramér–Rao lower bounds for β.

A.2. DERIVATION OF FULL-DATA INFLUENCE FUNCTIONS

We apply the theory in Appendix A.1 to identify the class of all influence functions φ(V) for estimators for β depending on the full data V = (X₁,Y₁,X₂,Y₂,Z) under the semiparametric pretest–posttest model with no assumptions on p(v) beyond independence of (X₁,Y₁) and Z. By Result A.1, these may be written as φ(V) = φ*(V) + ψ(V), where ψ(V) ∈ Γ^⊥ and φ* is any influence function, so we proceed by identifying a φ* and characterizing Γ ^⊥.

To identify a φ* under the semiparametric model, consider the two-sample t test estimator ${\widehat{\beta }}_{2s}$ in (5). Using $n_c∕n\stackrel{p}{\to }{\delta }^c{(1-\delta )}^{1-c}$, c = 0,1, E(ZY₂) = E(ZE(Y₂|Z)} = δE(Y₂|Z = 1) and similarly for E{1 − Z)Y₂}, ${\widehat{\beta }}_{2s}$ is clearly consistent under the minimal assumptions on p(v), and from the ensuing expression for $n^{1∕2}({\widehat{\beta }}_{2s}-\beta )$, writing $\beta ={\mu }_2^{\left(1\right)}-{\mu }_2^{\left(0\right)}$ and using $n_c∕n\stackrel{p}{\to }{\delta }^c{(1-\delta )}^{1-c}$, it is straightforward derive the corresponding influence function

$$\begin{array}{cc}\hfill & {\phi }^{\ast }\left(V\right)=Z(Y_2-{\mu }_2^{\left(1\right)})∕\delta \hfill \\ \hfill & -(1-Z)(Y_2-{\mu }_2^{\left(0\right)})∕(1-\delta ),\hfill \end{array}$$ (A.3)

where we write this as a function of ${\mu }_2^{\left(0\right)}$ and ${\mu }_2^{\left(1\right)}$ following the convention noted after (3).

To find Γ^⊥, we consider the class $\mathcal{P}$ of all densities for our semiparametric model. Incorporating the only restriction on such densities of independence of (X₁,Y₁) and Z, it follows that $\mathcal{P}$ has elements of the form, in obvious notation, p(v) = p(X₁,y₁)p(X₂|x₁,y₁,z)p(y₂|x₁,y₁,x₂,z)p(z|x₁,y₁), where p(z|x₁,y = δ^z(1 − δ)^1−z and δ is known. The tangent space Γ is the mean square closure of the tangent spaces of parametric submodels

$$\begin{array}{cc}\hfill & p(x_1,y_1;{\xi }_1)p(y_2\mid x_1,y_1,z;{\xi }_2)\hfill \\ \hfill & \cdot p(x_2\mid x_1,y_1,y_2,z;{\xi }_3){\delta }^z{(1-\delta )}^{1-z},\hfill \end{array}$$ (A.4)

say. Each of the first three components of (A.4) must contain the truth. For example, if p₀(X₂|x₁,y₁,y₂,z) is the true conditional density of X₂ given (X₁,Y₁,Y₂,Z), then, for h₃ such that E{h₃(X₁,Y₁,X₂,Y₂,Z)|X₁,Y₁,Y₂,Z} = 0, a typical submodel for this component is

$$\begin{array}{cc}\hfill & p(x_2\mid x_1,y_1,y_2,z;{\xi }_3)\hfill \\ \hfill & =p_0(x_2\mid x_1,y_1,y_2,z)\hfill \\ \hfill & \cdot \{1+{\xi }_3{h}_3(x_1,y_1,x_2,y_2,z)\},\hfill \end{array}$$

where ξ₃ is sufficiently small so that p(X₂|x₁,y₁,y₂,z; ξ₃) is a density and the score with respect to ξ₃ may be shown to be h₃(X₁,Y₁,Y₂,Z), and similarly for the first two components of (A.4). Evidently Γ = Γ₁ ⊕ Γ₂ ⊕ Γ₃, where (e.g., Newey, 1990)

$$\begin{array}{cc}\hfill {\Gamma }_1& =\{\text{all}{h}_1(X_1,Y_1)\in \mathcal{H}\}[\text{so}E\left\{h_1(X_1,Y_1)\right\}=0],\hfill \\ \hfill {\Gamma }_2& =[h_2(X_1,Y_1,Y_2,Z)\in \mathcal{H}\hfill \\ \hfill & \text{such that}E(h_2(X_1,Y_1,Y_2,Z)\mid X_1,Y_1,Z\}=0],\hfill \\ \hfill {\Gamma }_3& =[h_3(X_1,Y_1,X_2,Y_2,Z)\in \mathcal{H}\hfill \\ \hfill & \text{such that}E(h_3(X_1,Y_1,X_2,Y_2,Z)\mid \hfill \\ \hfill & X_1,Y_1,Y_2,Z\}=0].\hfill \end{array}$$

It is easy to verify that Γ₁, Γ₂ and Γ₃ are all mutually orthogonal; e.g., for h₂ ∈ Γ₂,h₃ ∈ Γ₃,

$$\begin{array}{cc}\hfill & E\left\{h_2(X_1,Y_1,Y_2,Z)h_3(X_1,Y_1,X_2,Y_2,Z)\right\}\hfill \\ \hfill & =E[h_2(X_1,Y_1,Y_2,Z)\hfill \\ \hfill & \cdot E\left(h_3(X_1,Y_1,X_2,Y_2,Z)\mid X_1,Y_1,Y_2,Z\}\right]=0.\hfill \end{array}$$

Thus, Γ^⊥ is the space orthogonal to all of Γ₁, Γ₂ and Γ₃. It is straightforward to verify that the space ${\Gamma }_4=[h_4(X_1,Y_1,Z)\in \mathcal{H}$ such that E{h₄(X₁,Y₁,Z)|X₁,Y₁}= 0] is orthogonal to all of Γ₁, Γ₂ and Γ₃. Moreover, it may also be deduced that Γ₁ ⊕ Γ₂ ⊕ Γ₃ ⊕ Γ₄ is in fact the entire Hilbert space $\mathcal{H}$ of mean-zero functions of V. Thus, it follows that Γ₄ contains all elements of $\mathcal{H}$ orthogonal to Γ, so that Γ^⊥ = Γ₄. Because Z is binary, we may write any element in Γ^⊥ equivalently as Zh⁽¹⁾(X₁,Y₁)+(1−Z)h⁽⁰⁾(X₁,Y₁) for some h^(c)(X₁,Y₁), c = 0,1 with finite variance such that E{Zh⁽¹⁾(X₁,Y₁) + (1 − Z)h⁽⁰⁾(X₁,Y₁)|X₁,Y₁} = 0. This implies h⁽¹⁾(X₁,Y₁) = −h⁽⁰⁾(X₁,Y₁) · (1 − δ)/δ for arbitrary h⁽⁰⁾(X₁,Y₁), showing that elements in Γ^⊥ may be written as (Z − δ)h(X₁,Y₁) for h with var{h(X₁,Y₁) < ∞. Equivalently, may write these elements as −(Z − δ)h(X₁,Y₁), which proves convenient in later arguments.

Recalling that ${\mu }_2^{\left(1\right)}={\mu }_2+\beta$ and ${\mu }_2^{\left(0\right)}={\mu }_2$ and combining the foregoing results, we thus have that all influence functions for RAL estimators for β must be of the form

$$\begin{array}{cc}\hfill & \frac{Z(Y_2-{\mu }_2-\beta )}{\delta }\hfill \\ \hfill & -\frac{(1-Z)(Y_2-{\mu }_2)}{1-\delta }-(Z-\delta )h(X_1,Y_1),\hfill \\ \hfill & \mathrm{var}\left\{h(X_1,Y_1)\right\}<\infty ,\hfill \end{array}$$ (A.5)

which may also be expressed in the equivalent form given in (3).

We may in fact identify the efficient influence function φ^eff in class (A.5). By Result A.2 we may represent φ^eff(X₁,Y₁,Y₂,Z) = φ*(X₁,Y₁,Y₂,Z) − Π(φ*|Γ^⊥) for any arbitrary influence function φ*, and, from above, we know that Π(φ*|Γ^⊥) must be of the form −(Z − δ)h^eff(X₁,Y₁) for some h^eff. Projection is a linear operation; hence, taking φ* to be (A.3), the projection may be found as the difference of the projections of each term in (A.3) separately. Moreover, by definition the residual for each term must be orthogonal to Γ^⊥. Thus, we wish to find h^eff(c)(X₁,Y₁), c = 0, 1, such that

$$E\left(\left[\frac{Z(Y_2-{\mu }_2^{\left(1\right)})}{\delta }-\{-(Z-\delta )h^{\mathrm{eff}\left(1\right)}(X_1,Y_1)\}\right]\cdot (Z-\delta )h(X_1,Y_1)\right)=0,$$ (A.6)

$$E\left(\left[\frac{(1-Z)(Y_2-{\mu }_2^{\left(0\right)})}{1-\delta }-\{-(Z-\delta )h^{\mathrm{eff}\left(0\right)}(X_1,Y_1)\}\right]\cdot (Z-\delta )h(X_1,Y_1)\right)=0$$ (A.7)

for all h(X₁,Y₁). For (A.6), then, we require

$$E\left[\left\{\frac{Z(Y_2-{\mu }_2^{\left(1\right)})}{\delta }+(Z-\delta )h^{\mathrm{eff}\left(1\right)}(X_1,Y_1)\right\}\cdot (Z-\delta )\mid X_1,Y_1\right]=0\mathrm{a}.\mathrm{s}.,$$

and similarly for (A.7). Using independence of (X₁,Y₁) and Z, we obtain

$$\begin{array}{cc}\hfill & h^{\mathrm{eff}\left(c\right)}(X_1,Y_1)\hfill \\ \hfill & ={(-1)}^c\frac{\{E(Y_2\mid X_1,Y_1,Z=c)-{\mu }_2^{\left(c\right)}\}}{{\delta }^c{(1-\delta )}^{1-c}}\hfill \\ \hfill & c=0,1.\hfill \end{array}$$

For example, for c = 1 this follows from

$$\begin{array}{cc}\hfill & E\{Z(Z-\delta )(Y_2-{\mu }_2^{\left(1\right)})\mid X_1,Y_1\}\hfill \\ \hfill & =E[Z(Z-\delta )E\{(Y_2-{\mu }_2^{\left(1\right)})\mid X_1,Y_1,Z\}\mid X_1,Y_1]\hfill \\ \hfill & =(1-\delta )E\{(Y_2-{\mu }_2^{\left(1\right)})\mid X_1,Y_1,Z=1\}\hfill \\ \hfill & \cdot P(Z=1\mid X_1,Y_1),\hfill \end{array}$$

where P(Z = 1|X₁,Y₁) = δ, and similarly

$$\begin{array}{c}\hfill E\{{(Z-\delta )}^2{h}^{\mathrm{eff}\left(1\right)}(X_1,Y_1)\mid X_1,Y_1\}\hfill \\ \hfill =\delta (1-\delta )h^{\mathrm{eff}\left(1\right)}(X_1,Y_1).\hfill \end{array}$$

Substituting in φ*(X₁,Y₁,Y₂,Z) − Π(φ*|Γ^⊥), the efficient influence function is

$$\left[\frac{Z(Y_2-{\mu }_2-\beta )}{\delta }-\frac{(Z-\delta )\{E(Y_2\mid X_1,Y_1,Z=1)-{\mu }_2-\beta \}}{\delta }\right]-\left[\frac{(1-Z)(Y_2-{\mu }_2)}{1-\delta }+\frac{(Z-\delta )\{E(Y_2\mid X_1,Y_1,Z=0)-{\mu }_2\}}{1-\delta }\right].$$

A.3. REPRESENTATION OF OBSERVED-DATA INFLUENCE FUNCTIONS

Robins, Rotnitzky and Zhao (1994) derived the form of observed-data influence functions in (11) by adopting the geometric perspective on semiparametric models outlined in Appendix A.1. In contrast to the full-data situation of Appendix A.2, the relevant Hilbert space ${\mathcal{H}}^{\mathrm{obs}}$, say, in which observed-data influence functions are elements is now that of all mean-zero, finite-variance random functions h(O), with analogous inner product and norm, that is, such functions depending on the observed data. The key is to identify the appropriate linear subspaces of ${\mathcal{H}}^{\mathrm{obs}}$ (e.g., Γ^obs⊥ say) to deduce a representation of the influence functions, which in the general semiparametric model is a considerably more complex and delicate enterprise than for full-data problems.

We noted in Section 2.2 that, for purposes of deriving estimators for β based on the observed data, it suffices to identify observed-data influence functions for estimators for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$ separately. We now justify this claim. It is immediate from the definition (2) of an influence function that the differences of all observed-data influence functions for estimators for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$ are influence functions for observed-data estimators for β. Conversely, we may show that all observed-data influence functions for estimators for β can be written as the difference of observed-data influence functions for estimators for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$. In particular, if φ₁(O) and φ₀(O) are any observed-data influence functions for estimators for ${\mu }_2^{\left(1\right)}$ and ${\mu }_2^{\left(0\right)}$, respectively, then φ₁(O) − φ₀(O) is an influence function for β by the above reasoning. By Result A.1 it follows that any observed-data influence function for an estimator for β can be written as φ₁(O) − φ₀(O) + ψ(O), where ψ(O) ∈ Γ^obs⊥. We may rewrite this as {φ₁w(O) + ψ(O)} − φ₀(O). However, by Result A.1 {φ₁(O) + ψ(O)} is an observed-data influence function for an estimator for ${\mu }_2^{\left(1\right)}$, concluding the argument.

A.4. DERIVATION OF THE EFFICIENT OBSERVED DATA INFLUENCE FUNCTION

Robins, Rotnitzky and Zhao (1994) provide a general mechanism for deducing the form of the efficient influence function. In the pretest–posttest problem this approach may be used to find the optimal choices for h⁽¹⁾ and g^(1)′ in (13) given in (14). However, because this mechanism is very general, for a simple model as in the pretest–posttest problem it is more direct and instructive to identify these choices via geometric arguments, as we now demonstrate.

We wish to determine h^eff(1) and g^eff(1)′ such that the variance of (13) is minimized; that is, writing (13) as A − B₁ − B₂, as E(A − B₁ − B₂) = 0, we wish to minimize E{(A − B₁ − B₂)²}. Geometrically, this is equivalent to finding the projection of A onto the subspace of ${\mathcal{H}}^{\mathrm{obs}}$ of (mean-zero) functions of the form B₁ + B₂. It is straightforward to show that B₁ and B₂ are uncorrelated, whence it follows that, as E{(A−B₁−B₂)²)} = E{(A − B₁)²)} + E{(A − B₁)²)} − E(A²) under these conditions, this minimization is equivalent to minimizing the variances of A − B₁ and A − B₂ separately. Because B₁ and B₂ are uncorrelated, they define orthogonal subspaces of ${\mathcal{H}}^{\mathrm{obs}}$, so that these minimizations may be viewed as finding the separate projections of A onto these subspaces. Thus, as for the full-data case in Section A.2, we wish to find h^eff(1)(X₁,Y₁) and g^eff(1)′(X₁,Y₁X₂,Z) such that, for all h⁽¹⁾ and g^(1)′,

$$\begin{array}{cc}\hfill & E\left(\left[\frac{RZ(Y_2-{\mu }_2^{\left(1\right)})}{\delta \pi (X_1,Y_1,X_2,Z)}-\left\{\frac{(Z-\delta )}{\delta }{h}^{\mathrm{eff}\left(1\right)}(X_1,Y_1)\right\}\right]\cdot \frac{(Z-\delta )}{\delta }{h}^{\left(1\right)}(X_1,Y_1)\right)=0,\hfill \\ \hfill & E\left(\left[\frac{RZ(Y_2-{\mu }_2^{\left(1\right)})}{\delta \pi (X_1,Y_1,X_2,Z)}-g^{\mathrm{eff}(1{)}^{\prime }}(X_1,Y_1,X_2,Z)\cdot \frac{\{R-\pi (X_1,Y_1,X_2,Z)\}}{\delta \pi (X_1,Y_1,X_2,Z)}\right]\cdot g^{(1{)}^{\prime }}(X_1,Y_1,X_2,Z)\cdot \frac{\{R-\pi (X_1,Y_1,X_2,Z)\}}{\delta \pi (X_1,Y_1,X_2,Z)}\right)=0.\hfill \end{array}$$

A conditioning argument as in Section A.2 using E(R|X₁,Y₁,X₂,Y₂,Z) = π(X₁,Y₁,X₂,Z) under MAR then leads to (14). In (14), g^eff(1)′ does not depend on h^eff(1), and h^eff(1) is identical to the optimal full-data choice in (4). These features need not hold for general semiparametric models; in particular, the choice of φ^F (V) in (11) that yields the efficient observed-data influence function will not be the efficient full-data influence function in general. Here, this is a consequence of the simple pretest–posttest structure.

A.5. DEMONSTRATION OF (17)

The form of the influence function (17) when γ in (16) is estimated follows from a general result shown by Robins, Rotnitzky and Zhao (1994). In particular, Robins, Rotnitzky and Zhao showed precisely that, in our context, the influence function for the estimator for ${\mu }_2^{\left(1\right)}$ found by deriving an estimator for ${\mu }_2^{\left(1\right)}$ from the influence function ψ(X₁,Y₁,X₂,R,RY₂,Z) in (15) (assuming π⁽¹⁾ is known) and then substituting an estimator for γ , where γ is estimated efficiently (e.g., by ML), is the residual from projection of ψ(X₁,Y₁,X₂,R,RY₂,Z) onto the linear subspace of ${\mathcal{H}}^{\mathrm{obs}}$ spanned by the score for γ. To demonstrate this, consider the special case of IWCC in (10), that is, (15) with h⁽¹⁾ ≡ q⁽¹⁾ 0. Suppose γ is estimated by ML from data with Z = ≡ 1 only. The score for γ is S_γ(X₁,Y₁,X₂,Z;γ₀) = d(X₁,Y₁,X₂) · {R − π⁽¹⁾(X₁,Y₁,X₂;γ₀)}Z and the relevant linear subspace of ${\mathcal{H}}^{\mathrm{obs}}$ is {BS_γ(X₁,Y₁,X₂,Z;γ₀) for all (p × s) matrices B}. Here, b_q(1) = 0 and the projection of ψ onto this space, B₀S_γ(X₁,Y₁,X₂,Z,γ₀), say, must satisfy

$$E\left[\left\{\frac{RZ(Y_2-{\mu }_2^{\left(1\right)})}{\delta {\pi }^{\left(1\right)}(X_1,Y_1,X_2;{\gamma }_0)}-B_0{S}_{\gamma }(X_1,Y_1,X_2,Z,{\gamma }_0)\right\}\cdot B{S}_{\gamma }(X_1,Y_1,X_2,Z,{\gamma }_0)\right]=0$$

for all B. By a conditioning argument similar to those in Appendices A.2 and A.4, we may find B₀ and show the projection is equal to the second term in the influence function

$$\begin{array}{cc}\hfill & \frac{RZ(Y_2-{\mu }_2^{\left(1\right)})}{\delta {\pi }^{\left(1\right)}(X_1,Y_1,X_2)}\hfill \\ \hfill & -d^T(X_1,Y_1,X_2)A_{\left(1\right)}^{-1}{b}_{\left(1\right)}\hfill \\ \hfill & \cdot \frac{\{R-{\pi }^{\left(1\right)}(X_1,Y_1,X_2)\}Z}{\delta }\hfill \end{array}$$ (A.8)

and that (A.8) is (17) in this special case.

As noted in Section 3.5, for choices of h⁽¹⁾ and q⁽¹⁾ other than the optimal ones, estimating γ even if it is known leads to a gain in efficiency. Geometrically this is because (17) is the residual found from projection of ψ onto a linear subspace of ${\mathcal{H}}^{\mathrm{obs}}$.

A.6. DEMONSTRATION OF DOUBLE ROBUSTNESS PROPERTY 2

We must show that the right-hand side of (18) converges in probability to ${\mu }_2^{\left(1\right)}$ if the true π⁽¹⁾ is replaced by an incorrect model π*. Multiplying and dividing each term by n and using n₁/n → δ, that the second term converges in probability to zero is immediate by the independence of Z and (X₁,Y₁). The first term converges in probability to

$$\begin{array}{cc}\hfill & E\left\{\frac{RZ{Y}_2}{\delta {\pi }^{\ast }(X_1,Y_1,X_2)}\right\}\hfill \\ \hfill & =E\left\{\frac{Z{\pi }^{\left(1\right)}(X_1,Y_1,X_2)}{\delta {\pi }^{\ast }(X_1,Y_1,X_2)}{Y}_2\right\}\hfill \\ \hfill & =E\left\{\frac{Z{\pi }^{\left(1\right)}(X_1,Y_1,X_2)}{\delta {\pi }^{\ast }(X_1,Y_1,X_2)}E(Y_2\mid X_1,Y_1,X_2,Z)\right\}\hfill \end{array}$$

by a conditioning argument similar to those above. Similarly, the third term converges to

$$E\left[\frac{Z\{{\pi }^{\left(1\right)}(X_1,Y_1,X_2)-{\pi }^{\ast }(X_1,Y_1,X_2)\}}{\delta {\pi }^{\ast }(X_1,Y_1,X_2)}\cdot E(Y_2\mid X_1,Y_1,X_2,Z)\right],$$

using ZE(Y₂|X₁,Y₁,X₂,Z = 1) = ZE(Y₂|X₁,Y₁,X₂,Z). Thus, their difference converges to E{E(ZY₂|X₁,Y₁,X₂,Z)}/δ = E{ZE(Y₂|Z)}/δ = E(Y₂|Z = 1) as in Section 3.2.