Solvent dramatically affects protein structure refinement

Abstract

One of the most challenging problems in protein structure prediction is improvement of homology models (structures within 1–3 Å C^α rmsd of the native structure), also known as the protein structure refinement problem. It has been shown that improvement could be achieved using in vacuo energy minimization with molecular mechanics and statistically derived continuously differentiable hybrid knowledge-based (KB) potential functions. Globular proteins, however, fold and function in aqueous solution in vivo and in vitro. In this work, we study the role of solvent in protein structure refinement. Molecular dynamics in explicit solvent and energy minimization in both explicit and implicit solvent were performed on a set of 75 native proteins to test the various energy potentials. A more stringent test for refinement was performed on 729 near-native decoys for each native protein. We use a powerfully convergent energy minimization method to show that implicit solvent (GBSA) provides greater improvement for some proteins than the KB potential: 24 of 75 proteins showing an average improvement of >20% in C^α rmsd from the native structure with GBSA, compared to just 7 proteins with KB. Molecular dynamics in explicit solvent moved the structures further away from their native conformation than the initial, unrefined decoys. Implicit solvent gives rise to a deep, smooth potential energy attractor basin that pulls toward the native structure.

Experimental determination of protein structures is very expensive, costing U.S. $250,000 in 2000 (1) and $66,000 today (2) and can be a notoriously difficult task, especially for membrane proteins. With the continuing exponential growth of genome sequence data, there is an increasing need for methods that accurately compute the high-resolution native structure of a protein, for use in biological applications that include virtual ligand screening (3), structure-based protein function prediction (4) and structure-based drug design (5). Homology or template based modeling has been the most successful method for protein structure prediction in the critical assessment of protein structure prediction (CASP) experiments (6, 7). The power of this technique progressively increases as ever more structures are solved by world-wide structural genomics initiatives (8, 9). Nevertheless, obtaining a model with the same accuracy as a crystal structure is still an unsolved problem: structure refinement of a rough model (within 1–3 Å rmsd) to bring it closer to the native structure remains a major challenge (6, 10). Work on structure refinement has been ongoing for many decades, starting from the first Molecular Mechanics (MM) energy minimization (11, 12) and continuing to a recent study with knowledge-based (KB) statistically derived potentials (13). During this period many different potentials and a variety of simulation methodologies such as energy minimization, molecular dynamics, and replica exchange Monte Carlo have been used for structure refinement (14–20), but no method has emerged as a clear winner.

As protein molecules function in aqueous solution and crystals contain large amounts of water (21–23); it is appropriate to model the water environment for high resolution refinement of protein structures using explicit, implicit, or hybrid models. The most realistic way to include solvent effects is to immerse the protein in a periodic box of explicit water molecules and simulate the motion of the system by molecular dynamics (MD) as first done by Levitt and Sharon (24). Unfortunately, atomic motion inherent in MD introduces statistical noise that can only be removed by averaging over the many conformations generated to get a final refined structure. Solvent effects can also be included implicitly, where water is represented as a continuous medium and the effect of the solvent is represented by additional terms in the potential energy function of the protein. Because there are no explicit water molecules, energy minimization can be used in place of MD and there is no need to average over many conformations.

The many different ways to include solvent effects have been reviewed in (25, 26). Such methods extend from the early accessible surface areas (ASA) model by Lee and Richards (27), to the widely used generalized born surface area (GBSA) model (28, 29) and more recently to the screened coulomb potential implicit solvation model (30, 31). Even though implicit solvent models are less physically realistic than use of explicit solvent, their greater computational efficiency makes them an attractive choice for refinement. MD has been used for refinement but with limited success (14–17), although more recently better results was observed for refinement with spatial restraints (18–20). Such successes have been reported for a few isolated cases; as the methodologies can be computationally demanding, it is difficult to apply them broadly. Clearly, one needs to consider computationally less demanding refinement protocols involving minimization with MM and KB force fields that include implicit solvation.

In this work we test the role of solvent on protein structure refinement using energy minimization and MD on an extensive test set of 75 native proteins, each with 729 near-native decoys. This follows on from previous work (13), which used in vacuo energy minimization to compare the performance of various MM potentials such as optimized potential for liquid simulations (OPLS)-AA, AMBER99, GROMOS96, and ENCAD with a statistically derived KB potential. They found that the KB potential performed best of all and refined almost all proteins toward the native structure; AMBER99 was second-best, performing better than the other MM potentials, which generally moved the decoys away from the native state. The KB potentials include the effect of solvent implicitly, in that the distribution of distances between atoms in protein crystals is effected by the water in the unit cell.

We model implicit solvent, using energy minimization with the GBSA implicit solvent model (29), as implemented in Tinker 3.9 (32) with the all-atom OPLS (OPLS-AA) force field (33). We also model explicit water molecules, using MD simulation done with the SPC water model (34), and the OPLS-AA force field (35) as implemented in Gromacs (36–38). We used the same stringent testing criterion for refinement as before (13) for better comparison between simulations in solvent and in vacuo. Namely, a good refinement protocol must not perturb the native state, and at the same time must move decoys structures closer to the native state.

We find that Tinker energy minimization with implicit solvent performs better than KB energy minimization in that it moved the decoys much closer to the native state. Gromacs MD with explicit solvent performs much less well, generally moving decoys away from the native state. Visualizing the potential energy surface near the native state helps explain these differences in behavior.

Results

Energy Minimization of Native Structure.

Energy minimization was run on all 75 native proteins in implicit and explicit solvent. These results were compared to in vacuo energy minimization, using the KB potential (13). In all cases, we used the weighted C^α rmsd (wRMS) as a measure of deviation from the native structure (see Materials and Methods) to compensate for flexibility of loops and chain termini (Fig. 1). For all 75 native proteins, the mean wRMS value (see Fig. S1) was 0.89 ± 0.36 Å for GBSA implicit solvent, 0.38 ± 0.14 Å for KB, and 0.14 ± 0.01 Å for OPLS bulk explicit solvent. Although it may seem that bulk explicit solvent is working best as it perturbs the native structure least, this is not true. Energy minimization fails to move away from the native structure because the bulk explicit solvent acts like ice and greatly restricts movement. This example indicates why energy minimization from the native structure cannot be used to assess potentials: complete lack of convergence would appear to be perfect behavior with a wRMS value of zero. It justifies our much more extensive tests.

Fig. 1.

Showing the PC values averaged over the 729 decoys for each of the 75 proteins' energy minimization runs with KB in Encad (40, 41), GBSA implicit solvent in Tinker (32) and OPLS explicit solvent in Gromacs (36–38). The 75 proteins are arranged in decreasing order of improvement for the KB potential. A negative value of PC corresponds to improvement in the wRMS value of the energy minimized structure compared with that of the starting structure. Best overall improvement is for KB with a mean overall PC (〈PC〉) of −11.56% compared with −4.0% for GBSA and −0.2% for OPLS. Of the 46 proteins improved by GBSA, 24 had a PC value better than −20%, compared with just 7 proteins with KB. Overall, GBSA performs better than KB for 30 of the 75 proteins. However, GBSA moved 29 proteins away from the native state, whereas KB moved just 3. The drawing beside the chart are colored by the B-factor (blue for a low value and red for a high value) to show the greater flexibility of loops and chain termini that is compensated by wRMS.

Energy Minimization of Decoys.

As a much more rigorous test of the refinement protocol, energy minimization was run on all of the 729 decoys of each of the 75 proteins (see SI Text), using the convergent limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm or l-BFGS (39). Clearly, methods that can move decoys toward the native state are better than those that simply do not perturb that state. The mean wRMS for all 729 decoys of one protein is denoted by 〈wRMS〉; the mean wRMS for all decoys of all 75 proteins is denoted by ≪wRMS≫. We measure the average amount of refinement of decoys from the native state, using the percentage change (PC) defined as PC = 100 × (〈wRMS_final〉 − 〈wRMS_initial〉)/〈wRMS_initial〉, where 〈wRMS_initial〉 and 〈wRMS_final〉 are the initial and final value of 〈wRMS〉.

For all initial decoys the value of ≪wRMS_initial≫ was 1.08 ± 0.14 Å. For all final decoys the value of ≪wRMS_final≫ was 1.078 Å for OPLS explicit solvent minimization, 1.020 Å for GBSA implicit solvent minimization and 0.960 Å for KB minimization. Fig. 1 shows the PC values for all 75 proteins. GBSA generally outperforms KB whereas OPLS moves decoys very little and performs worst (again, we do not expect much movement in minimization within explicit solvent). In the best cases GBSA gives a much more negative 〈PC〉 value than KB: compare −55.1% ± 24.6% for 1kpta with GBSA to −33.2% ± 19.6% for 1nkd with KB.

Assessing Decoys Using wRMS and GDT-HA.

As the rmsd value is sensitive to large shifts of a few atoms of a molecule, we use the wRMS and global distance test (GDT) score for a more robust measure of structural similarity measure (see Materials and Methods). We computed high accuracy GDT scores (GDT-HA) (42) for all decoys minimized with the KB and GBSA potentials. When GDT-HA equals 1, all residues of a decoy must match the native structure to better than 0.5Å rmsd. A set of 6 proteins having large negative PC values with both GBSA and KB were selected for comparison (Fig. 2A). Here, the measure of improvement used is the difference between GDT-HA scores for final minimized and the initial unminimized decoy (GDT-HA_final − GDT-HA_initial) for all 729 decoys averaged over binned GDT-HA_initial values (Fig. 2). For both GBSA and KB, greater improvement is seen for decoys with smaller values of GDT-HA_initial, showing that decoys further from the native structure are improved more.

Fig. 2.

Comparison of the GDT-HA scores for energy minimization with KB (solid) and GBSA (dashed). (A) The change in GDT-HA between final minimized structure and the initial decoy GDT-HA_final − GDT-HA_initial is plotted against GDT-HA_initial for all 729 decoys of each of the 6 proteins that show large negative percentage change (PC) for the KB and GBSA potentials. Values of GDT-HA_final − GDT-HA_initial are averaged over GDT-HA_initial bins of width 0.1. A higher value of GDT-HA_final − GDT-HA_initial indicates an improvement in the decoy (gets closer to the native structure). Overall 〈GDT-HA_final − GDT-HA_initial〉 is higher for GBSA indicating that this method improves the decoy structure more than KB. (B) Showing 1pne, a good case with GBSA, that is less good with KB. The native structure of 1pne is shown in gray, the best decoy minimized with KB in red, and the best decoy minimized with GBSA in purple. GBSA gives a better match to the native structure than does KB. (C) Showing 1nkd, a good case with KB. The lowest GDT-HA_initial value is better (≈0.7) than for 1pne (≈0.5). For 1nkd, GBSA and KB do equally well.

For proteins with good PC values (large, negative), the GDT-HA improvement with GBSA is higher than with KB suggesting a better match to native. Also, the maximum improvement in GDT-HA of 0.3 is observed for GBSA, which is higher than the maximum improvement in KB of 0.2. In Fig. 2B, 1pne, a good case with GBSA, shows a better match to the native structure for GBSA as the GDT-HA curve for GBSA is significantly above KB for lower values of GDT-HA_initial. Moreover, the PC value of −36.7% ± 21.7% for GBSA is also better than the value of −12.5% ± 5.2% observed for KB, confirming wRMS as a good structural similarity measure. For 1nkd, a good case with KB, the GDT-HA curve for KB is not significantly higher than GBSA (Fig. 2C) and both GBSA and KB improve the structure equally well for higher values of GDT-HA_initial (Figs. S3 and S4). Nevertheless, 1nkd has a PC value of −33.2% ±19.6% with KB, which is better than the value of −19.2% ± 23.2% for GBSA. Moreover, the minimum value of GDT-HA_initial for 1nkd is 0.7, which is >0.5 for 1pne. Thus, similar improvement with GDT-HA is seen for good cases of GBSA and KB when most residues match well (high GDT-HA_initial value) but GBSA outperforms KB when low fraction of residues match the native with high accuracy.

Molecular Dynamics vs. Energy Minimizations of Decoys.

As MD is computationally expensive, we selected a subset of 20 of the 75 proteins, chosen to minimize bias with a mix of PC values for KB energy minimization. The selected proteins were: 1ail, 1bkra, 1c1ka__1, 1dsl, 1ge8a02, 1gvda, 1h99a1, 1ift, 1ift___2, 1lvfa, 1lwba, 1mf7a, 1mgta1, 1ntea, 1o0xa__1, 1pdo, 1qhva, 1tml___2, 1whi and 4euga0. MD was run for 200 ps on all 729 decoys of each of these 20 proteins (see SI Text). With a total simulation time of 2,916 ns, this represents a large increase in computational resources compared with energy minimization. The mean initial wRMS for all decoys of these 20 proteins was 1.02 ± 0.15 Å, which was not too different from the value of 1.08 ± 0.14 Å for all 75 proteins. Fig. 3 compares MD with energy minimization with KB and GBSA.

Fig. 3.

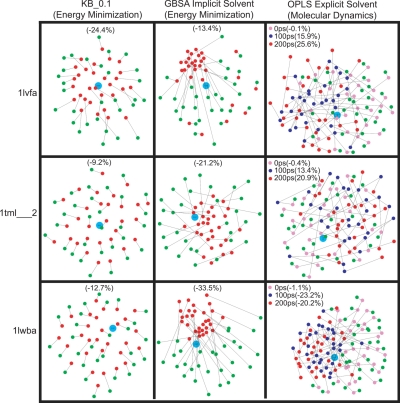
Showing MD of decoys in explicit solvent compared to energy minimization with the GBSA and KB potentials. (A) The PC values (y axis) are shown for the sampled set of 20 proteins, sorted in ascending order and plotted against their rank in the sort. Note, that the indicator at rank 1 does not necessarily reference the same protein for every condition. Negative values of PC correspond to improvement of the structure. For the 20 proteins, KB gives the largest number of improved proteins. Some proteins run with GBSA have better PC values than for KB, whereas others do worse. There is almost no change for MD at 0 ps and additional MD moves the structure away from the native, in that the 200-ps curve is always above those of 100 ps and 0 ps. (B) Diagram of 1lwba showing most improvement for OPLS explicit solvent MD. Red, high-value B-factor; blue, low-value B-factor. (C) Diagram of 1lwba showing that, after 100 ps of MD (orange), the decoys moved closer to the native structure (gray) with a PC value of −23.2% ± 25.8% compared with −20.2% ± 27.9% at 200 ps (blue). (D) Diagram of 1h99a1, which shows least improvement for OPLS explicit solvent MD, colored by B-factor with high values in red and low value in blue. (E) Diagram of 1h99a1 shows how MD moves the structure away from the native structure (gray) as time progresses, with PC value of 75.3% ± 36.5% at 100 ps (orange) compared with 98.4% ± 40.3% at 200 ps (blue). Note the flexibility of the chain termini.

We observe that KB minimization gives most improvement over all these 20 proteins with 〈PC〉 value of −9.6% compared with +7.14% with GBSA. However, GBSA improved 9 of 20 proteins with a 〈PC〉 value of −18.74% compared with −10.75% for 19 proteins with KB (see plot in Fig. 3A). There is almost no change for OPLS explicit solvent MD at 0 ps, with ≪wRMS≫ of 1.01 Å; these structures are a result of the preparatory energy minimization in the presence of explicit solvent and move very little. Specifically, for explicit water, the 〈PC〉 value at 0 ps was −0.32% for all 20 proteins with an improvement of −1.32% for 10 proteins. Unfortunately, additional MD moves the structure far away from the native (see Fig. 3A). The 〈PC〉 value for all proteins at 100 ps was 21.30% with ≪wRMS≫ of 1.22 Å, which is much worse than the 〈PC〉 value after preparatory energy minimization of −0.32%. More simulation makes the situation worse: at 200 ps the 〈PC〉 value is 29.76% with final ≪wRMS≫ of 1.31 Å. Thus, on average, decoys move away from native as the MD trajectory progresses from 100 to 200 ps (see Fig. S2). In contrast, 4 of 20 proteins improved with MD, in that the decoys moved closer to the native state. These are 1lwba, 1whi, 1bkra and 1ift with a 〈PC〉 value of −15.41% at 100 ps and −13.05% at 200 ps. Even in these “good” cases most improvement occurs in the first 100 ps and the situation deteriorates with additional MD (see Fig. S2).

Movement of Decoys on GBSA Potential Energy Surface.

The basic assumption for all of the refinement methodologies described here is that the native structure occurs at a minimum of the potential energy and is surrounded by a smooth attractor basin. How does solvent influence the downhill energy path from a decoy to the native state? Fig. 4 shows the near-native potential surface for GBSA energy minimization. For good cases with GBSA (1kpta, 1ln4a, and 1o0xa), the native state is located at a well-defined minimum of the potential energy surface (pink disk in Fig. 4). Energy minimization moves toward the native state and results in a low wRMS value; there is a clear attractor basin, which is most apparent for 1kpta, where the final energy minimized decoys cluster together and come very close to the native state. For these good cases, GBSA solvation gives rise to a well-defined energy basin with the native structure at its minimum; initial decoys on hills surrounding the basin move toward the native state upon minimization. The topography of the energy surface limits the improvement possible for a particular method. This is shown for the bad cases with GBSA (1ge8a01, 1h99a1, and 1pdo), where the native structure is not in the major energy basin containing all energy minimized decoys for 1ge8a01 (Fig. 4). For 1h99a1 and 1pdo, the native is located in a valley surrounded by one or more hills separating it from the major energy basin. For these bad cases, the nature of the energy surface causes large shifts from the native structure upon minimization. Often energy minimization moves from the initial decoys to a region far from the native state but with similar energy values as the native state. For bad cases, the region in which minimized decoys cluster is much larger than it is in the good cases, which often show a compact cluster.

Fig. 4.

Showing directed movement on the potential energy surface for GBSA energy minimization. The green points mark the positions of the initial decoy structures, the red points mark the positions of the final energy minimized structures, and the line connecting them indicates the movement. These contoured projections of multidimensional energy surface are made by selecting a random subset of 30 decoys before and after minimization including the native structure (big pink disk) to construct a 61 × 61 matrix of pairwise wRMS value. The energy contours are filled with color that varies from blue for low energy to red for high energy. In this plot, points close on paper are generally also similar with a small rmsd value, whereas points far apart on paper are different with a large rmsd value. Good and bad cases are selected using the PC values for each of the protein shown in parenthesis. The good cases show an attractor basin; seen most clearly for 1kpta. For the bad cases, the arrangement of the hills and valleys separates the native structure from the major energy basin where all of the decoys end up after energy minimization. Multidimensional scaling is done using Graphviz to get the clearest 2D representation of the 61-dimensional space defined by the wRMS matrix. We generate the contour plots using the potential energy at each point and MATLAB's 4-point smoothing.

Discussion

Improvement upon Minimization with GBSA Implicit Solvent.

Energy minimization in GBSA implicit solvent yields the largest negative PC and performs refinement better than both KB energy minimization and MD in explicit solvent. Moreover, GBSA energy minimized decoys correctly identify the native basin by clustering together, as shown by the good cases in Fig. 4. An X-ray structure is not perfectly accurate and it is useful to estimate when a near-native structure cannot be distinguished from the actual native state. Two studies (43, 44) have estimated the “accuracy limit” of the crystal structures, i.e., the maximum coordinate deviation after superposition of structures of the same protein determined experimentally in different crystal packing arrangements. These were estimated to be between 0.80 Å cRMS (44) and 0.95 Å (43) rmsd for heavy atoms. Thus, we can assume that a model within 0.8 Å rmsd is indistinguishable from the native state. For a very favorable case with GBSA minimization (1kpta), the PC value is −55.1% ± 24.6%, 〈wRMS_initial〉 is 1.15 Å and 〈wRMS_final〉 is 0.51 Å, which is indistinguishable from the native state. A value of 〈wRMS_final〉 <0.8 Å was observed for 18 proteins by GBSA energy minimization and 12 proteins by KB energy minimization. Moreover, GBSA outperforms KB when tested on the near-native decoys, which were energy minimized, using the ENCAD potential (40) to remove any bad contacts due to the decoy generation procedure (see SI Text, and Figs. S3 and S4). Clearly minimization with GBSA implicit solvent is an excellent refinement method.

Along with the good examples that show large improvement with GBSA, there are some very bad cases where decoys move far away from the native state upon minimization. What are the reasons for these bad cases? Is it a failure of the minimization method or of the potential function? Because GBSA minimization can cause large movements toward the native state, we are convinced that Tinker 3.9 uses a very good minimization protocol. Performance seems to depend on the accuracy with which GBSA implicit solvent mimics the solvent present in the crystals. For the good cases in Fig. 4 we see that the energy basin is smooth and has the native state at the minimum. For the bad cases in Fig. 4 we see a flat energy landscape where no correlation exists between the energy and the distance to the native state. Such bad cases seem to occur when the protein chain has long loops and chain termini with high B-factors (1ge8a01, 1h99a1 and 1pdo in Fig. 1). We believe that a more accurate representation of the energy surface is needed for these bad cases with GBSA. It is also possible that crystal contacts affect the position of these chain segments. It seems clear that GBSA implicit solvation removes the ruggedness around the native state by giving rise to a smooth energy basin in good cases or a flat energy landscapes in bad cases.

Molecular Dynamics in Explicit Solvent Moves Away from Native.

For the subset of 20 of 75 proteins simulated using MD in explicit solvent, only 4 proteins were refined (PC < 0) by MD compared to 9 with GBSA and 19 with KB energy minimization. For all 20 proteins, the mean PC value increased from −0.32% to 21.30% from 0 ps to 100 ps of MD; worsening to 29.76% was observed from 100 ps to 200 ps (Fig. 3A). Additional MD simulations of 10 ns in explicit solvent also moves the decoys away from the native structure (see SI Text, Fig. S5, and Table S1). This does not prove that MD tends to deform the native state; with sufficient averaging over long runs the native state might be reached, as shown for few isolated cases (14–17) where the refined structures were ≈2 Å rmsd from native. MD is a very popular method used to describe pathways of folding and unfolding. This technique is fundamentally different from energy minimization, in that MD introduces random noise and can get stuck in a minimum, which could be far from the native state. Given infinite time, it could find the native state provided it was in a sufficiently deep energy basin. We conclude that use of MD with periodic boxes of explicit water is not a good refinement method in that it is out-performed by both Tinker GBSA implicit solvent and Encad KB minimization.

It has recently been shown that MD does not help discriminate the native state from its decoys, in that the correlation between energy and rmsd vanishes after MD simulation with AMBER and a GB potential (45). Other recent work used replica exchange sampling with CHARMM22/GBSW potential to refine homology modeling targets with spatial restraints; it worked well but it is unclear whether this would have happened without the restraints (20). The use of accurate potentials with the native state as a global minimum is a necessary but not sufficient condition for extensive sampling methods to work for refinement. MD simulation is strongly dependent on random thermal perturbations involved in heating and we expect it to move all over a flat energy surface (Fig. 5). In addition, it seems that the potential surface used in MD is very rugged as can be seen by the energy minimized decoys (pink dots) in Fig. 5 (a plethora of local minima around the initial decoys). It seems that we need better sampling or significantly more computer time for MD to move out of these local minima.

Fig. 5.

Comparing the directed movement on the potential energy surface for energy minimization with KB and GBSA and MD with OPLS in explicit solvent. The starting decoy structures are green points and the native structure is shown as a cyan disk. For KB and GBSA, the final energy minimized decoys are red points. For OPLS explicit MD, the pink points are the energy minimized structure at 0 ps, the blue points are the decoys at 100 ps and the red points are the decoys at 200 ps. These projections of the multidimensional energy surface are made using a random subset of 30 decoys for each protein. For KB and GBSA energy minimization, a 61 × 61 matrix of pairwise wRMS values is used (30 initial decoys, 30 corresponding energy minimized decoys, and the native structure). For OPLS explicit MD a 121 × 121 matrix is used (30 initial starting decoys; 30 corresponding decoys at 0 ps, 100 ps, and 200 ps, respectively; and the native structure). Good cases with KB energy minimization (1lvfa), GBSA energy minimization (1tml___2) and OPLS explicit MD (1lwba) are selected using the PC values for each of the protein (shown in parenthesis). For each of these 3 proteins, we compare directed movement on the energy surface caused by energy minimization with KB and GBSA and MD with OPLS. An attractor basin is seen for KB and GBSA energy minimization for all 3 proteins, but only with GBSA do the final decoys come very close to each other and to the native structure. For KB energy minimization of 1tml___2 and 1lwba, the energy surface contains many local minima near the native state preventing it from being reached; in both these cases a clear attractive basin is seen with GBSA. For the best case with OPLS explicit MD (1lwba), initial simulation moves the protein closer to the native structure but more simulation (100 to 200 ps) moves away again. For the less good cases with OPLS explicit MD (1lvfa and 1tml___2) simulation moves the structure all over the energy surface with the 200-ps points (red), father apart from the native structure than the 100-ps points (blue) or the initial decoy points (green).

Nature of Energy Surfaces for Various Potentials.

Our 2D visualization of the energy surface for a representative set of decoys gives a clear picture of the nature of the near-native potential energy surface. The arrangement of hills and valleys around the native state limits the extent of refinement. The energy surface for KB potential is more rugged than GBSA, but most ruggedness is seen with explicit solvent (red points for KB and pink and blue points for OPLS explicit solvent in Fig. 5). For KB energy minimization the decoys gets stuck before reaching the native state minimum, which limits refinement. An ideal potential for refinement would have a smooth basin-shaped energy surface with the native state of the protein at a minimum. Such an energy surface is clearly seen for the good cases with the GBSA implicit model in Fig. 4. For the bad cases with GBSA the energy basin is not compact; it has a flat energy landscape with no correlation between energy and the distance to the native state. It is possible that better modeling of nonpolar solvation and charge effects would overcome the problem of flat landscapes. It might also indicate parts of the protein that are not well-defined in the absence of the crystal lattice.

Materials and Methods

Weighted C^α rmsd and High Accuracy GDT.

Normally protein structural deviation from the native state is measured by the rmsd of coordinates after optimum rigid body superposition of all atoms. This measure can over-emphasize deviations in chain termini or surface loops, which are often more flexible than the rest of the protein as seen by their large B-factors in X-ray structures (Fig. 1). Use of wRMS compensates for this flexibility by down-weighting the flexible residues identified by fewer contacts. It uses the far contact count value averaged over 5 adjacent residues centered on the residue of interest as that residue's weight. The far contact count is the number of contacts between atoms i and j such that the respective residues are further than 3 apart along the sequence. A contact occurs when the accessible surface area between atoms i and j is >0. For the proteins we analyze, the contact counts vary from 0.0 for the most exposed residues to 7.2 for the most buried residues. A simpler distance-based definition of contact would likely give the same results but we used the list of contacts as provided by Encad (40, 41). The wRMS value is calculated by a standard weighted coordinate superposition method (46) [we did not use the Kabsch method (U3BEST) (47). The GDT-HA is used to measure the similarity to the native state. The GDT method (48) computes the maximum percentage of noncontiguous residues with C^α rmsd from native state (cRMS) values <0.5, 1, 2, and 4 Å, respectively, and then averages these 4 percentages. The term “HA” refers to high-accuracy with cRMS threshold given above; normal GDT uses thresholds of 1, 2, 4, and 8 Å.