A DELIVERABLE FOUR-DIMENSIONAL INTENSITY MODULATED RADIATION TREATMENT PLANNING METHOD FOR DYNAMIC MULTILEAF COLLIMATOR TUMOR TRACKING DELIVERY

Abstract

Purpose

To develop a deliverable 4D IMRT planning method for DMLC tumor tracking delivery.

Methods and Materials

The deliverable 4D IMRT planning method involves aligning MLC leaf motion parallel to the major axis of target motion and translating MLC leaf positions by the difference in the target centroid position between respiratory phases of the 4D CT scan. This method ignores non-linear respiratory motion and deformation. A 3D optimal method where an IMRT plan on each respiratory phase of the 4D CT scan was independently optimized was used for comparison. For 12 lung cancer patient 4D CT scans, individual phase plans and deformable dose-summed 4D plans using the two methods were created and compared.

Results

For each of the individual phase plans, the deliverable method yielded similar isodose distributions and DVHs. The deliverable and 3D optimal methods yielded statistically equivalent dose-volume metrics for both individual phase plans and 4D plans (p > 0.05 for all metrics compared). The deliverable method was affected by 4D CT artifacts in one case. Both methods were affected by high vector field variations from deformable registration.

Conclusions

The deliverable method yielded similar dose distributions for each of the individual phase plans and statistically equivalent dosimetric values compared to the 3D optimal method, indicating the deliverable method is dosimetrically robust to the variations of fractional time spent in respiratory phases on a given 4D CT scan. Non-linear target motion and deformation did not cause significant dose discrepancies.

INTRODUCTION

Radiation treatment that explicitly accommodates temporal changes of anatomy, called four-dimensional (4D) radiotherapy, is an intense area of study in radiation oncology (1, 2). Recent development of 4D computed tomography (CT) provides better understanding of anatomic motion. How to use this extra information to further improve target coverage and spare normal tissue in an optimal way is still challenging.

Intensity modulated radiation treatment (IMRT) is shown to have better normal tissue sparing and target dose conformality, compared to conventional treatment techniques (3), and use of the dynamic multileaf collimator (DMLC) is shown to be a reliable and efficient IMRT delivery technique (4). DMLC also has been investigated to deliver 4D IMRT, and several techniques to incorporate anatomic changes into DMLC IMRT have been proposed (5–21). However, the finite mechanical motion capabilities of an MLC impose constraints on the leaf sequence of 4D radiotherapy since the MLC leaves need to both follow the tumor motion during treatment, as well as move to modulate the beam fluence to perform IMRT.

The complexity of IMRT using the DMLC delivery technique on 4D CT data sets has been investigated (5–21). Trofimov et al. (16) compared different 4D IMRT optimization schemes, with respect to the full optimization, and showed tumor tracking to be marginally better than other techniques. They showed a good framework of formulating a 4D IMRT planning problem. However, their investigations did not account for the design specifications of delivery devices and additional complexities of leaf motion constraints. Webb et al. (6, 8, 17–19) showed strategies to find the optimal leaf trajectories by minimizing the geometrical mismatch of MLC leaf and organ motion in 1D and 2D, including leaf motion constraints for the motion-compensated DMLC IMRT planning. They applied their strategies to a motion model constructed from a patient 4D CT, but did not demonstrate implementation beyond a single patient. Papiez et al. (7, 10–14) developed algorithms for DMLC leaf-pair optimal control IMRT delivery to moving and deforming targets. They demonstrated their algorithms for the target motion in real time and when a priori motion information is known for 1D, but as of yet not for 3D. Zhang et al. (20, 21) investigated plan optimization incorporating respiratory target motion and deformation with helical tomotherapy, but with only one lung case. Schlaefer et al. (15) showed feasibility of an approach to consider the relative motion of organs during treatment planning for robotic radiosurgery. Their study was based on the assumptions of perfect target tracking and regular respiratory motion, and was not applied to real patients. Due to the complexity of the 4D IMRT problem, an optimal IMRT planning method based on the 4D CT scan that combines MLC leaf motion constraints and MLC transport characteristics with an approach robust to respiratory-induced motion during treatment has not yet been developed.

In order to incorporate the MLC leaf motion constraints into 4D IMRT planning using DMLC, this study is focused on a simplification of rigid body target translation. Only target motion along the MLC leaf motion direction is considered, whereas target motion perpendicular to the MLC leaf motion caused by target deformation/rotation and motion non-linearity/hysteresis is ignored. This approach yields a planning scheme that is not optimal but importantly, is deliverable with currently available technology. For comparison, a 3D optimal scheme also is shown in which the dose distribution in each phase of the 4D CT scan is independently optimized. A given phase represents what could be achieved using respiratory gating. The 3D optimal approach accounts for target deformation/rotation and motion non-linearity/hysteresis, but ignores MLC leaf motion constraints and thus, is deliverable only if the MLC leaf velocity is infinite.

METHODS AND MATERIALS

Formalism for 4D IMRT planning optimization

The aim of 4D IMRT planning optimization for DMLC tumor tracking is to find the deliverable leaf sequence, L(MU,θ), as a function of monitor unit, MU, and respiratory phase, θ, to satisfy min {f[D(L(MU,θ))]}, where f is a mathematical cost function representation of a clinical objective, and D is the prescribed dose distribution:

$$D={\displaystyle \sum _{\theta =0}^P{\lambda }_{\theta }{D}_{\theta }\left(I(\theta ),I_{\text{ref}},u(\theta ),L(MU,\theta )\right),}$$ (1)

where λ_θ is time spent per each phase, D_θ is dose for a given phase, I is a 4D CT image of anatomy where I(θ) represents a given 3D instance for phase θ and I_ref the image used for dose summation, and u is a displacement vector field computed using deformable registration mapping images from a given to the reference phase. To obtain D_θ, the dose is computed on I(θ) based on L(MU,θ), and then deformed to I_ref using u(θ).

A deliverable 4D IMRT planning method to solve equation (1) proposed in this study is to account for rigid body target motion along the MLC leaf direction only, as well as to ensure that MLC leaf motion does not exceed the maximum leaf velocity (25). The deliverable method finds the deliverable leaf sequence on the reference phase, L(MU,θ_ref) to satisfy min {f[D(L(MU,θ_ref))]}, where D=D_θref(I_ref, L(MU,θ_ref)) and θ_ref is the reference phase. For the rigid body target translation, the solutions for other phases become L(MU,θ)=L(MU, θ_ref)+g(θ), where g(θ) is the target centroid displacement from the reference phase to phase θ along the major axis of target motion in a given beam’s eye view (BEV).

A benchmark method is a 3D optimal method, which finds the optimal leaf sequence, L(MU,θ), to satisfy min {f[D_θ(L(MU,θ))]} for each phase independently.

4D CT data and patient characteristics

The 4D CT data of 12 lung cancer patients acquired on a 16-slice CT scanner in a cine mode (GE Healthcare Technologies, Waukesha, WI) were used (26, 27). The acquisition was performed as a part of an IRB-approved study (protocol 00–202) at University of Texas MD Anderson Cancer Center. Based on the respiratory signal from a respiration-monitoring system (RPM, Varian Medical Systems, Palo Alto, CA), the respiratory cycle was divided into 10 phases of equal time length, with phase 0 representing end inhale and phase 5 approximately end exhale. The tumor classifications ranged from T1N0 to T4N0, and tumors were located in the upper lobes for 9 patients and in the lower lobes for 3 patients with peripheral (3 patients) and central (9 patients) tumor localizations. The means of gross tumor volume (GTV) and GTV centroid motion range were 49.2 cm³ and 0.7 cm, respectively (Table 1).

Table 1.

Patient gross tumor volume (GTV), GTV centroid motion range, and motion range in major axis.

Patient #	GTV volume (cm3)	GTV centroid motion (cm)	Motion in major axis (cm)
1	3.0	2.1	1.6
2	61.0	0.4	0.4
3	12.5	0.5	0.5
4	1.0	0.6	0.6
5	20.4	0.1	0.1
6	5.2	0.4	0.4
7	323.6	0.2	0.2
8	23.0	0.3	0.2
9	6.1	0.2	0.2
10	7.5	0.5	0.4
11	119.2	1.3	1.1
12	7.5	1.1	0.9
Mean (min, max)	49.2 (1.0, 323.6)	0.7 (0.1, 2.1)	0.6 (0.1, 1.6)

Contouring and IMRT planning

Contouring and planning were performed using a commercially available planning system (Pinnacle 7.9, Philips Medical Systems, Milpitas, CA). Based on the manually segmented contours on phase 0, the contours on the other 9 phases of the 4D CT scan were automatically generated using large deformation diffeomorphic image registration (28, 29). The GTV was expanded by an 8 mm margin to yield the clinical target volume (CTV) (30), and a 5 mm margin was added to create the planning target volume (PTV). The prescribed dose to PTV was 74 Gy, and beam arrangements were six coplanar non-opposed predominantly anterior-posterior, with beam angles adjusted depending on the tumor locations. Further details in planning and optimization are described in elsewhere (26).

Methods of the deliverable and 3D optimal IMRT planning on the 4D CT scans

The deliverable 4D IMRT planning method involves four steps for each patient (Fig. 1). From steps 1 through 3, individual phase plans were created and in step 4, deformable dose-summed 4D plans were created.

1. Appropriate beam angle arrangement for an IMRT plan was determined. The target centroid position for each phase was quantified from a 4D CT image set. The major axis of target motion was determined in each BEV. Then, for each beam, the collimator was rotated to align MLC leaf motion parallel to the major axis. Figure 2 shows this key step in the deliverable 4D IMRT planning method. The same target motion in 3D (Fig. 2[a]) has different 2D motion in the BEVs of different beam angles (Fig. 2[b]). Based on the target positions in a given BEV, the major axis (dashed arrows in Fig. 2[b]) of target motion was automatically determined for each beam using a least-squares fit.

2. For the reference phase (end exhale was used as the most stable phase during respiration [23]), an appropriate IMRT plan was created with the rotated collimator, creating MLC leaf positions for each beam.

3. For each of the other phases, an IMRT plan was created by copying the MLC leaf positions for the reference phase and translating them by the relative displacement of target centroid for each phase, while keeping the collimator angle for each beam the same. For example, for a given phase plan, a beam aperture was shifted from the reference phase (dashed red in Fig. 2[c]) to the given phase (solid red in Fig. 2[c]) by the difference in the target centroid position between the two phases, as seen in the BEV. All 10 individual phase plans for a given patient using the deliverable method were exactly the same except for the MLC leaf positions translated.

4. For each patient, a deformable dose-summed 4D plan was created by accumulating the resultant doses from all individual phase plans on phase 0 CT image using deformable dose summation (5, 20, 28, 29).

Fig. 1.

Flowchart of the methods of deliverable and 3D optimal IMRT planning on the 4D CT scans.

Fig. 2.

Determination of the major axis of target motion. (a) The same target motion in 3D has (b) different 2D motion in the BEV of different beam angles, such as gantry angles of 0° and 120°. Based on the target positions in a given BEV, the major axis (dashed arrows) of target motion is automatically determined for each beam: collimator angles are 41° and 106° for the gantry of 0° and 120°, respectively. (c) For the gantry angle of 0° in (b), the collimator is rotated by 41° to align MLC leaf motion parallel to the major axis. For a given phase plan, a beam aperture is translated from the reference (dashed red) to a given (solid red) phase by the difference in the target centroid position between the two phases, as seen in the BEV.

For comparison, the 3D optimal method, which was the same as the deliverable method except for step 3, was also applied (Fig. 1). For the other phases, with the same IMRT beam angle arrangement and collimator angles as the deliverable plans, the 3D optimal method was independently optimized an IMRT plan on each phase of the 4D CT images. All 10 individual phase plans for a given patient using the 3D optimal method can be different except for beam and collimator angles.

The deliverable method was compared with the 3D optimal method using composite objective values and dose-volume evaluation metrics derived from the dose-volume histogram (DVH). The composite objective value, a single number, is an indicator of plan quality that takes into account the actually achieved dose distribution for the PTV and organs at risk (OARs) after plan optimization, relative to the initial constraints (26). The smaller the composite objective value, the better the plan. For individual phase plans, the mean and standard deviation of dose-volume metric ratios were averaged over all 10 phases for all 12 patients: $\overline{\overline{X_{opt}^{del}}}=\frac{{\displaystyle \sum _i^M{\displaystyle \sum _j^N\raisebox{1ex}{$X_{del}^{i,j}$}\!\left/ \!\raisebox{-1ex}{$X_{opt}^{i,j}$}\right.}}}{M·N}$ and ${\sigma }_{\overline{\overline{X_{\text{opt}}^{\text{del}}}}}=\sqrt{\frac{{\displaystyle \sum _i^M{\displaystyle \sum _j^N{\left(\raisebox{1ex}{$X_{\text{del}}^{i,j}$}\!\left/ \!\raisebox{-1ex}{$X_{\text{opt}}^{i,j}$}\right.-\overline{\overline{X_{\text{opt}}^{\text{del}}}}\right)}^2}}}{M·N}}$, where X was a dose-volume metric computed from the DVHs of plans using the deliverable (X_del) or 3D optimal (X_opt) methods, i was a patient number, and j was a phase number. For 4D plans, those were averaged over all 12 patients: $\overline{X_{opt}^{del}}=\frac{{\displaystyle \sum _i^M\raisebox{1ex}{$X_{del}^i$}\!\left/ \!\raisebox{-1ex}{$X_{opt}^i$}\right.}}{M}$ and ${\sigma }_{\overline{X_{opt}^{del}}}=\sqrt{\frac{{\displaystyle \sum _i^M{\left(\raisebox{1ex}{$X_{del}^i$}\!\left/ \!\raisebox{-1ex}{$X_{opt}^i$}\right.-\overline{X_{opt}^{del}}\right)}^2}}{M}}$. A one-tailed student’s t-test with the null hypothesis of H₀ : X_opt=X_del and the alternative hypothesis of H_A: X_opt>X_del was used to evaluate whether two methods were statistically different (statistically different if 0.05 p < 0.05).

RESULTS

Individual phase plans

Figure 3 shows the composite objective values of individual phase plans using the deliverable and 3D optimal methods for each patient. The two methods have identical objective values for phase 5. For the other phases, the 3D optimal method always yields smaller values (better plan quality). Variation in plan quality is generally larger for phase-to-phase compared to that for method-to-method.

Fig. 3.

Composite objective values of individual phase plans using the deliverable (solid) and 3D optimal (dashed) methods and those of 4D plans using the deliverable (Del, filled circles) and 3D optimal (Opt, empty circles) methods for each patient. The smaller the value, the better the plan. The two methods have identical objective values for phase 5. For the other phases, the 3D optimal method always yields better plans. The 4D composite objective values for each method are similar to the average values over individual phase plans per patient.

Patient 1 shows significant discrepancy in the composite objective values between the two methods for some phases (red in Fig. 3). There are artifacts in the 4D CT image set for this patient, including division of the tumor into two parts for three phases. The artifacts deteriorate target coverage when the deliverable method is used, resulting in discrepancy in both PTV coverage and OAR sparing between the two methods (Fig. 4[a]). Figure 4(a) shows the DVHs and isodose distributions for patient 1, which illustrates the second worst agreement case in terms of the composite objective values (value ratio of 18.1). Patient 4 also shows significant discrepancies in the composite objective values between the two methods throughout the phases (blue in Fig. 3), which is explained by the largest variation in tumor volume during the respiratory cycle. Even though phase 0 plans using the two methods for patient 4 show the worst agreement in terms of the composite objective value (value ratio of 18.4), there is discrepancy only in the DVHs of PTV (Fig. 4[b]). The 74 Gy isodose curve (blue) does not cover the whole PTV in the deliverable plan unlike in the 3D optimal plan. Patient 7, whose tumor has almost no motion during respiration, shows the best agreement of the composite objective values between the two methods for all phases (grey in Fig. 3).

Fig. 4.

DVHs and isodose distributions of individual phase plans showing discrepancy in the composite objective values between the two methods: (a) the second worst agreement case (objective value ratio of 18.1) due to the artifacts in the 4D CT scan; and (b) the worst agreement case (objective value ratio of 18.4) due to significant variation in tumor volume during the respiratory cycle. Solid DVHs are for the deliverable method and dashed for the 3D optimal method. The PTV is shaded in red, and blue isodose curves indicate 74 Gy, green 40 Gy, and pink 20 Gy.

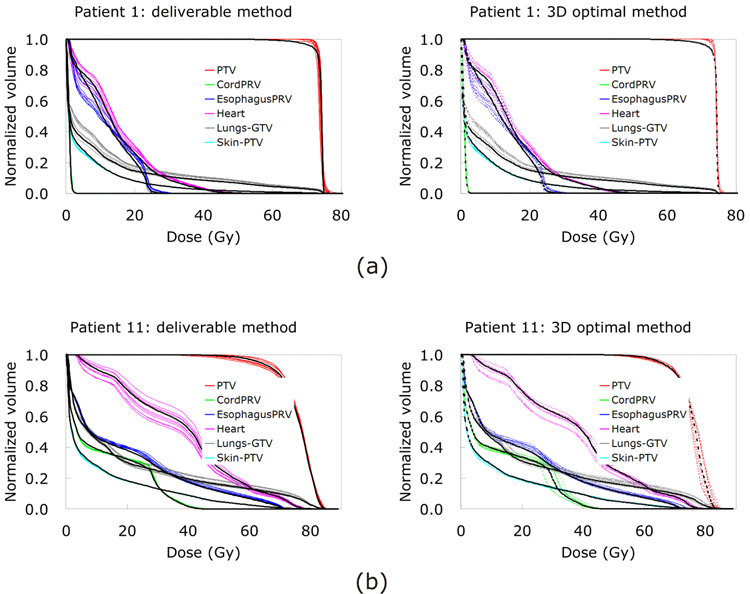
Figure 3 also shows phase-to-phase variation in plan quality. While the composite objective values for the 3D optimal method do not vary much from phase to phase, those for the deliverable method do vary. There is significant phase-to-phase variation in plan quality using the deliverable method for patients 1 and 4 (red and blue in Fig. 3). Again, patient 1 has artifacts in the 4D CT images, and patient 4 has the largest tumor volume variation. Patient 4 also shows a trend in that the farther the respiratory phases are from phase 5, the worse the deliverable plan quality becomes (blue in Fig. 3). The significant variation in tumor volume causes inferior PTV coverage in the deliverable plans, especially for the phases further away from phase 5. Figure 5(a) shows the DVHs of all 10 individual phase plans using the two methods for patient 1. Although the composite objective values do not vary significantly, there are phase-to-phase variations of the DVHs in the 3D optimal plans, especially for the OARs.

Fig. 5.

DVHs of all 10 individual phase plans with 4D plans (black thick curves) for the deliverable (left column) and 3D optimal (right column) methods: (a) significant phase-to-phase variation with degraded PTV coverage in 4D plans; and (b) significant phase-to-phase variation, but with reasonable DVHs (about the averages over individual phase plans) in 4D plans. Solid DVHs are for the deliverable method and dashed for the 3D optimal method.

Since the composite objective value is a numerical indicator of plan quality and does not indicate the plan details, a patient showing the most discrepancy in the DVHs between methods and between phases is chosen by visually inspecting the DVHs. Despite relatively good agreement of plan quality (pink in Fig. 3), patient 11 shows the most discrepancy in the DVHs between methods and between phases (Fig. 5[b]) because the tumor shows the most hysteresis during respiration (23, 27), the second biggest volume, and the second most motion. These attributes also cause the largest difference in PTV D_95% (dose received by 95% of the PTV) and lung D_mean (mean dose to the lungs) between the two methods.

Table 2 shows dose-volume metric ratios of individual phase plans. All mean values of the dose and volume metric ratios are very close to 1.00, indicating that the deliverable and 3D optimal methods yield similar dose-volume characteristics. No evaluated dose-volume metric is statistically different between the methods (p > 0.05 for all metrics compared), while PTV coverage shows more variation than OARs.

Table 2.

A comparison of the dose-volume metrics of individual phase plans using the deliverable and 3D optimal methods: the mean and standard deviation (SD) of the dose-volume metric ratios averaged over all 10 phases for all 12 patients; and p -values testing whether two distributions are statistically different. D_mean represents the dose received by mean volume of the PTV or OARs, D_A% the dose received by A% of volume of the PTV or OARs, and V_B the total volume of OARs receiving at least B Gy.

	PTV		Lungs-GTV		Spinal cord
	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{95\%}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(V_{20}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{0.1\%}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$
Mean ± SD	1.001 ± 0.004	0.992 ± 0.016	1.00 ± 0.02	1.01 ± 0.03	1.00 ± 0.05
min, max	0.988, 1.021	0.916, 1.010	0.93, 1.05	0.90, 1.12	0.88, 1.31
p	0.11	0.09	0.48	0.46	0.48
	Esophagus		Heart		Thorax-PTV
	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(V_{55}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(V_{40}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$
Mean ± SD	1.00 ± 0.03	1.02 ± 0.07	1.01 ± 0.05	0.96 ± 0.20	1.00 ± 0.02
min, max	0.88, 1.10	0.96, 1.56	0.87, 1.26	0.00, 1.17	0.93, 1.03
p	0.50	0.44	0.49	0.45	0.50

Deformable dose-summed 4D plans (4D plans)

Figure 3 also shows the composite objective values of 4D plans using the two methods for each patient. The 3D optimal method always yields better plans. The 4D composite objective values for each method are similar to the average values over individual phase plans per patient.

However, 4D plans for patient 1 are significantly worse than individual phase plans for both methods (red in Fig. 3). Degraded 4D plans for patient 1 also are evident in Fig. 5(a), mainly due to inferior PTV coverage. Figure 6 shows the isodose distributions of individual phase plans on phase 0 and phase 5, as well as 4D plans for patient 1. While the dose distributions for phase 0 and phase 5 plans look reasonable (Fig. 6[a] and [b]), 4D plans have inconsistent dose distributions (Fig. 6[c]) for both methods. This is explained by large gradients of the deformation vector field across the PTV. Since the tumor of patient 1 is next to the chest wall and moves 2.1 cm, the vector field, which differs significantly across the PTV, is used for deformable image registration and dose summation. As shown schematically in Fig. 6(d), the vector field tends to be large in the lungs (white arrows) and small in the chest wall (black arrows). As a result, some portion of the PTV (in the chest wall) deforms differently from its other portion (in the lungs). Thus, deforming the PTV differs from deforming the GTV and expanding it to create the PTV, since the former may generate unrealistic appearance of the PTV after deformable image registration (aqua star in Fig. 6[d]). However, when the dose is deformed back to phase 0, the latter may result in inconsistent dose distributions after deformable dose summation (green star in Fig. 6[d]). Because this occurs in both methods, the composite objective values for the two 4D plans are similar (red in Fig. 3) and the DVHs do not show significant discrepancy, especially for PTV coverage (Fig. 7[c]).

Fig. 6.

Isodose distributions for (a) phase 0 plans and (b) phase 5 plans, and (c) 4D plans (on phase 0 CT image) using the two methods in a sagittal view for patient 1. Note that phase 5 plans are identical for both methods. While the dose distributions of phase 0 and 5 plans look reasonable ([a] and [b]), the 4D plans have inconsistent dose distributions (c) for both methods. (d) This is due to large gradients of the deformation vector field across the PTV. Since the vector field is large in the lungs (white arrows) and small in the chest wall (black arrows), deforming the PTV generates unrealistic appearance of the PTV after deformable image registration (aqua star). Deforming the GTV and expand it to create the PTV results in inconsistent dose distributions after deformable dose summation (green star). See text for more details. In (a), (b), and (c), the PTV is shaded in red and the GTV in yellow, and blue isodose curves indicate 74 Gy, green 40 Gy, and pink 20 Gy. In (d), the GTV is shaded in red, blue indicates the PTV, and pink illustrates the isodose curves.

Fig. 7.

DVHs of 4D plans using the two methods for the patients with various tumor characteristics: (a) most hysteresis (0.35 cm); (b) least hysteresis (0 cm); (c) most motion (2.1 cm); (d) least motion (0.1 cm); (e) largest volume (323.6 cm³); and (f) smallest volume (1.0 cm³). Solid DVHs are for the deliverable method and dashed for the 3D optimal method.

On the other hand, patient 4 shows the largest difference in the composite objective values between the two 4D plans (blue in Fig. 3), while the composite objective value for each 4D plan is an average of individual phase plans, respectively. Again, this is due to the most variation in tumor volume, which results in poor PTV coverage in the deliverable plans (Fig. 7[f]).

As shown in Fig. 5(b), patient 11 has significant phase-to-phase variation in the DVHs for individual phase plans, but shows reasonable DVHs for the two 4D plans, each of which is an approximate average of the DVHs for individual phase plans. The composite objective values for the two 4D plans are better than the average of those values over individual phase plans (pink in Fig. 3). Between the two 4D plans, however, patient 11 shows the most discrepancy in the DVHs (Fig. 7[a]). The tumor of this patient has the most hysteresis (0.35 cm) (27), while patient 9 with the least hysteresis (0 cm) shows two DVH sets on the top of each other indicating good agreement between the two 4D plans (Fig. 7[b]). Patient 9 actually shows the best agreement between the two methods (Fig. 7[b]).

In terms of tumor motion, both of the patients with the most motion (2.1 cm) (Fig. 7[c]) and the least motion (0.1 cm) (Fig. 7[d]) show discrepancies in the DVHs. In terms of tumor volume, both of the patients with the largest tumor volume (323.6 cm³) (Fig. 7[e]) and the smallest tumor volume (1.0 cm³) (Fig. 7[f]) show relatively good agreement in the DVHs.

Table 3 shows dose-volume metric ratios of 4D plans. As in Table 2, all mean values are very close to 1.00, indicating that two methods yield similar dose-volume characteristics. Again, no evaluated dose-volume metric is statistically different between the methods (p > 0.05 for all metrics compared), while PTV coverage shows more difference than OARs. The difference in PTV coverage between the two methods is smaller than that for individual phase plans.

Table 3.

A comparison of the dose-volume metrics of 4D plans using the deliverable and 3D optimal methods: the mean and standard deviation (SD) of the dose-volume metric ratios averaged over all 12 patients; and p -values testing whether two distributions are statistically different. D_mean represents the dose received by mean volume of the PTV or OARs, D_A% the dose received by A% of volume of the PTV or OARs, and V_B the total volume of OARs receiving at least B Gy.

	PTV		Lungs-GTV		Spinal cord
	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{95\%}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(V_{20}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{0.1\%}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$
Mean ± SD	1.001 ± 0.002	0.995 ± 0.009	1.00 ± 0.02	1.01 ± 0.03	1.00 ± 0.02
min, max	0.999, 1.007	0.974, 1.009	0.97, 1.03	0.97, 1.08	0.96, 1.04
p	0.32	0.39	0.49	0.49	0.50
	Esophagus		Heart		Thorax-PTV
	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(V_{55}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(V_{40}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$	${\left(D_{\mathit{\text{mean}}}\right)}_{\mathit{\text{opt}}}^{\mathit{\text{del}}}$
Mean ± SD	1.00 ± 0.02	1.02 ± 0.05	1.01 ± 0.03	1.00 ± 0.10	1.00 ± 0.01
min, max	0.96, 1.03	0.97, 1.11	0.95, 1.05	0.77, 1.20	0.97, 1.02
p	0.50	0.48	0.50	0.49	0.50

DISCUSSION

An “ideal” 4D IMRT planning would be one optimized over the continuous motion of target and surrounding normal tissues, which may be deliverable; however, there are no solutions for this type of deliverable-based optimization yet. This study proposed a “deliverable” 4D IMRT planning method. The reason for taking this approach is that it provides a feasible solution that uses current planning technology and thus, has a clear path to clinical application. Though this approach is clearly not optimal, given the assumption made, Trofimov et al. (16) showed that tumor tracking yielded better results than the gated technique, and both methods improved treatment compared to the motion-inclusive technique. The planned clinical application involves integrating the linac with a real-time target position monitoring system. As the target position information is obtained, the appropriate corrections are made to the leaf positions in real time. A “3D optimal” method that involved an independent 3D IMRT optimization for each phase of the 4D CT scan also is proposed as a benchmark method. It is important to note that the sum of individually-optimized dose distributions does not guarantee an optimal dose distribution since min{f[D(L(MU, θ))]} is a subset of ${\displaystyle \sum _{\theta }\text{min}\{f[D_{\theta }(L(MU,\theta ))]\}}$.

“Deliverable” means that the plan does not have MLC leaf motion exceeding the maximum velocity of the MLC leaves. The average maximum leaf velocity at the isocenter plane ranges from 3.3 to 3.9 cm/s (25). In this series of patients, this velocity is exceeded by only 3/10 phase transitions in 1/12 patients. In patient 1, the displacement of 2.1, 1.6, and 1.6 cm was observed in subsequent phases (0.4 s apart), corresponding to the velocities of 5.3, 4.0, and 4.0 cm/s for a 4-sec period, respectively. A beam hold mechanism will be a part of DMLC tracking implementation. It is not be advisable to follow sharp position changes or coughing, providing that the beam hold is not applied so frequently as to significantly affect efficiency, which in this case would be 100% for 11/12 patients and 70% for patient 1. The collimator rotation is not planned to be changed on a daily basis. The deliverable implementation would account for some motion perpendicular to the MLC leaf direction by readjusting the MLC positions based on the plan and the estimated or measured target positions. However, if this algorithm is included in an online 4D adaptive therapy strategy, the collimator rotation could be changed day to day. Also, the algorithm for collimator rotation and MLC shift is not manufacturer-specific. Important MLC parameters required to implement this algorithm are a maximum leaf velocity and a fast secondary position feedback system that allows for real-time control of leaf positions.

The deliverable and 3D optimal methods were applied to 12 lung cancer patient 4D CT image sets. Two important findings are as follows. First, the deliverable method is dosimetrically robust to the variations of fractional time spent in respiratory phases on a given 4D CT scan. The deliverable method has the same λ in equation (1) for all phases. Given that the dose distributions of individual phase plans using the deliverable method are very similar to one another (Table 2), the deliverable method would result in the dose distribution close to the planned dose distribution even when a patient spends more time on one phase (e.g., end exhale) than other phases during treatment. In addition, for 4D plans, the deliverable method yields statistically similar dosimetric values to the 3D optimal method (Table 3). This indicates that not only is the deliverable method dosimetrically robust but also, the target deformation/rotation and hysteresis generally have little dosimetric impact for the 12 patient series studied. For each beam, the collimator is rotated to align the MLC leaf motion parallel to the major axis of target motion, which is determined from the target motion in a given BEV. Therefore, the target motion perpendicular to the MLC leaf motion is relatively small (0.13 cm at the most), resulting in negligible impact on plan quality.

However, patient 11 shows the most discrepancy in DVHs for 4D plans between the two methods (Fig. 7[a]), indicating that in the presence of hysteresis, the deliverable method is susceptible to plan quality degradation. In terms of target deformation/rotation, patient 4 shows discrepancy in 4D plans between the two methods, especially for target coverage (Fig. 7[f]), indicating that target deformation/rotation has some dosimetric impact when the deliverable method is used.

The second important finding is that the PTV concept can cause problems in 4D IMRT planning. The 4D plans for patient 1 are significantly inferior to individual phase plans for both methods (red in Fig. 3), mostly due to PTV coverage (Fig. 5[a]). Large gradients of the deformation vector field across the PTV cause unrealistic appearance of the PTV after deformable image registration and inconsistent dose distributions after deformable dose summation (Fig. 6). This problem occurred in 1/12 patients in this study. Therefore, care should be taken when there is a possibility that large deformation gradients across the PTV could occur. Eliminating the PTV by using probabilistic planning approaches (31–33) is one of the solutions.

As for individual phase plans, phase-to-phase variation is generally larger than the difference between the two methods, in terms of plan quality. A more important result is the comparison of 4D plans. The 4D plan quality is similar to average quality over individual phase plans, although three patients have issues. Patient 1 shows degraded 4D plans for both methods due to large deformation gradients across the PTV (Fig. 7[c]), and patient 4 shows a degraded deliverable 4D plan due to significant tumor volume variation (Fig. 7[f]). Given that patient 11 with the most hysteresis shows the most discrepancy in the DVHs between the two 4D plans (Fig. 7[a]) while patient 9 with the least hysteresis shows the best agreement (Fig. 7[b]), having motion hysteresis affects deliverable 4D plans. On the other hand, no marked differences between the two 4D plans with tumor motion or volume indicate that both tumor motion and volume do not have a significant effect on 4D plans using the deliverable method (Fig. 7[c–f]).

CONCLUSIONS

A deliverable 4D IMRT planning method was developed and applied to 12 patient 4D CT image sets. This method yields similar dose distributions for each of the individual phase plans and statistically equivalent dosimetric values compared to the 3D optimal method, indicating the deliverable method is dosimetrically robust to the variations of fractional time spent in respiratory phases on a given 4D CT scan. Non-linear target motion and deformation do not cause significant dose discrepancies.

The deliverable 4D IMRT planning method has a clear path to clinical implementation. The clinical application and integration with DMLC tumor tracking delivery research is the subject of ongoing development.