Abstract
Submovements that are frequently observed in the final portion of pointing movements have traditionally been viewed as pointing accuracy adjustments. Here we re-examine this long-lasting interpretation by developing evidence that many of submovements may be non-corrective fluctuations arising from various sources of motor output variability. In particular, non-corrective submovements may emerge during motion termination and during motion of low speed. The contribution of these factors and the factor of accuracy regulation in submovement production is investigated here by manipulating movement mode (discrete, reciprocal, and passing) and target size (small and large). The three modes provided different temporal combinations of accuracy regulation and motion termination, thus allowing us to disentangle submovements associated with each factor. The target size manipulations further emphasized the role of accuracy regulation and provided variations in movement speed. Gross and fine submovements were distinguished based on the degree of perturbation of smooth motion. It was found that gross submovements were predominantly related to motion termination and not to pointing accuracy regulation. Although fine submovements were more frequent during movements to small than to large targets, other results show that they may also be not corrective submovements but rather motion fluctuations attributed to decreases in movement speed accompanying decreases in target size. Together, the findings challenge the traditional interpretation, suggesting that the majority of submovements are fluctuations emerging from mechanical and neural sources of motion variability. The implications of the findings for the mechanisms responsible for accurate target achievement are discussed.
Keywords: arm kinematics, discrete, continuous, accuracy, variability
1. Introduction
Small irregularities that often appear in the final portion of the smooth, bell-shaped velocity profile during arm movements to a target have been referred to as secondary submovements. Starting from a seminal study by Woodworth (1899), the role of secondary submovements during pointing and reaching movements has been a focus of many investigations (Abrams & Pratt, 1993; Chua & Elliott, 1993; Crossman & Goodeve, 1983; Elliott et al., 2001; Keele, 1968; Khan & Franks, 2003; Meyer et al., 1988; Novak et al., 2002; Pratt & Abrams, 1996; Pratt et al., 1994; Walker et al., 1997; Woodworth, 1899). The common assumption has been that the major portion of distance to the target is covered in a primary, ballistic submovement characterized by smooth acceleration and deceleration. If the primary submovement misses the target, secondary, corrective submovements are performed. The major support for this interpretation is provided by an observation that decreases in target size are usually accompanied with more frequent emergence of secondary submovements.
Dounskaia, Wisleder, and Johnson (2005) questioned the traditional interpretation of submovements. They suggested that secondary submovements are not homogeneous and that they can be related to different subtasks included in the pointing task. In addition to the obvious subtask of accurate target achievement that may require corrective submovements, motion termination was considered as another possible source of velocity fluctuations, i.e. submovements. Motion termination is a movement component that is necessary to perform in addition to motion deceleration to stop at the target. Indeed, during deceleration, the limb approaches the target with negative, distinct from zero, acceleration. However, acceleration needs to be nullified as soon as the target has been achieved. In other words, the arm needs to be arrested and stabilized at the target, which requires specific component of control, i.e. motion termination. The existence of the stabilizing component of control has been recognized in electromyographic studies in which the third phase of the tri-phasic pattern of muscle activity has been interpreted as responsible for limb stabilization (Berardelli et al. 1996). Apparently, the limb stabilization may be accompanied with small fluctuations, specifically during fast movements that require high negative acceleration while approaching the target and quick reduction of this acceleration to zero when the target has been achieved.
The influence of motion termination on submovement emergence was examined by Dounskaia et al. (2005) with use of movement mode manipulations. Submovement incidence (that characterizes the probability of emergence of secondary submovements) was compared between discrete and reciprocal pointing movements. The discrete mode required termination of motion at the target and dwelling in this position for a period of time. In other words, it required arresting and stabilizing the arm at the target. The reciprocal mode included motion to the target and immediate reversal back to the home position without dwelling on the target. In this mode, the stabilization of the arm at the target was not performed (Guiard, 1993; Meulenbroek & Thomassen, 1993; Meulenbroek et al., 1998). Quantitatively, the difference between the two modes was that both velocity and acceleration were nullified at the target during discrete movements, whereby reciprocal movements involved nullification of velocity only, while acceleration remained non-zero during the reversal.
It was found that submovement incidence was higher during the discrete than reciprocal mode, supporting the influence of motion termination. Also, manipulations of target size were performed that resulted in the traditional observation that submovements emerge more frequently during movements to small than to large targets, suggesting that the accuracy regulation subtask also contributed to the submovement production. Furthermore, it was found that the two manipulations were associated with distinct submovement types. Submovements representing gross changes in the velocity profile (revealed as zero-crossings of the first and second motion derivative, i.e. velocity and acceleration) were responsive to the movement mode manipulations and not to changes in target size. In contrast, fine submovements (revealed as zero-crossings of the third derivative of displacement, jerk) were more frequent with decreases in target size, and their incidence was independent of movement mode. These results suggested that if any corrective adjustments of pointing accuracy were performed, they were limited predominantly to the fine submovements.
The finding that gross submovements are associated with motion termination was supported by Wisleder & Dounskaia (2007) who compared submovement incidence between discrete and cyclic movements. In addition, a hypothesis was tested that fine submovements are related to low movement speed rather than small target size, and that more frequent emergence of them with decreases in target size is a result of the speed-accuracy tradeoff (Fitts, 1954). Support for this possibility was obtained by examining cyclic movements at two distinct frequency levels. It was found that incidence of fine submovements increased with decreases in movement frequency, and it was independent of target size. Nevertheless, when cyclic frequency was self-paced, correlation of incidence of fine submovements with movement duration was rather low. Thus, the validity of the traditional interpretation in application to fine submovements remained uncertain and requires additional investigations.
The purpose of the present study is to contribute to the revision of the traditional submovement interpretation by examining possible sources of submovements. This is achieved by testing three movement modes. In addition to the discrete mode that requires motion termination at the target and reciprocal mode during which motion is reversed at the target without a dwell period, and hence, without motion termination, a passing mode is included in the present experiment. The passing mode requires crossing the target and terminating motion after that. Thus, it includes both subtasks, motion termination and accuracy regulation. However, in contrast to the discrete mode during which the two subtasks are performed simultaneously while approaching the target, they are performed separately from each other during passing movements. Accuracy regulation is performed prior to the target passing, and the remaining movement portion includes only the motion termination subtask. To isolate submovements not related to accuracy regulation, submovements will be analyzed in the passing mode only after passing the target. The role of accuracy constraints will be further emphasized by using small and large targets. If the conclusion of the previous studies that gross submovements emerge due to motion termination is correct, these submovements will appear in the discrete and passing mode and not in the reciprocal mode, and there will be no increase in their incidence with decreases in target size. If fine submovements are corrective adjustments performed to accurately achieve the target, they will be observed during the discrete and reciprocal mode and not during the passing mode, and they will be more frequent during movements to small than large targets. However, if fine submovements are related to decreases in movement speed, they will be observed in all three modes but more frequently for small than large targets. Thus, the comparison of submovements among the three modes provides new means for examining the contribution of different factors to submovement production.
2. Material and Methods
2.1. Participants
Sixteen right-handed subjects (10 males, 6 females, mean age 24.7 years, SD 4.9 years) participated in the study. Subjects were volunteers from the Arizona State University campus. After an explanation of the experiment, each participant signed an informed consent form approved by the Human Subjects Institutional Review Board (IRB) of Arizona State University.
2.2. Procedure
The experimental set-up is shown in Fig. 1. Subjects sat at a horizontal table on a top of which a Wacom Intuos 12×18 digitizer was positioned. The height of the table was adjusted to provide movement of the right arm right above the table in the horizontal plane at the shoulder level. A digitizer stylus was attached beneath the stretched index finger so that the tip of the stylus was located below the fingernail. The upper arm was suspended in a sling to decrease friction between the arm and the table and to prevent fatigue. While the stylus tip could slide across the table surface, the sling allowed the arm to move freely above the table. Motion was restricted to shoulder and elbow rotations. Wrist rotation was prevented by a brace. The trunk position was fixed between the chair back and the edge of the table.
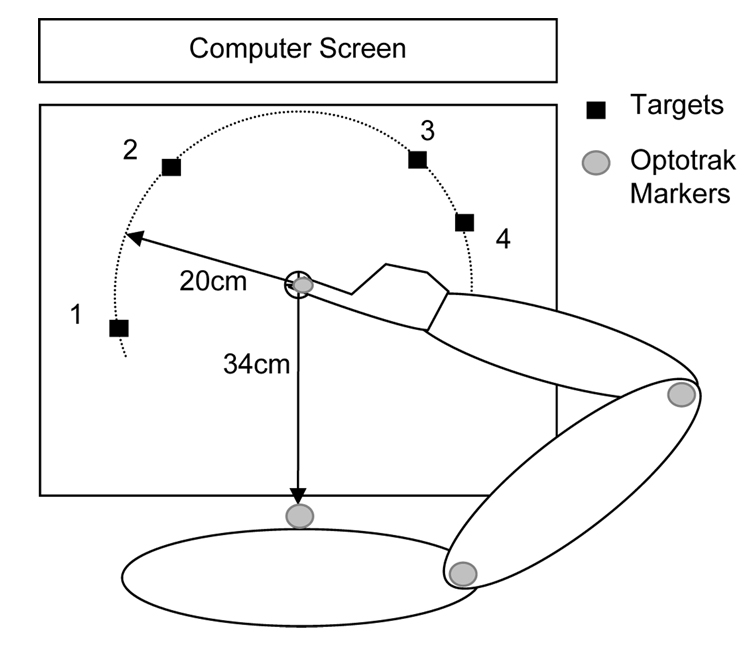
Figure 1.
Schematic representation of the experimental setup. Subjects moved the fingertip to one of the four targets on the horizontal table. The arm was positioned horizontally above the table. Movements were performed via the shoulder and elbow rotations with the immobilized trunk and wrist. Although the targets are shown in the plane of motion, they were presented on the computer screen and not on the table. In addition to the targets, the computer screen showed a cursor that represented motion of the fingertip.
Subjects performed pointing movements by sliding the stylus across the digitizer table from a home position to a target. Stylus motion on the digitizer was represented with a cursor on a large (24 inches) computer screen positioned in front of the subject at 70 cm distance. The home position and the target were also shown on the screen. The distance between the home position and the targets on the screen was the same as on the digitizer. Although subjects could see the arm, they were instructed to focus on the cursor motion and the target presented on the screen.
The home position was located at 34 cm from the trunk. The targets were squares of two sizes, small (1.0×1.0 cm) and large (3.5×3.5 cm). Four equidistant targets located in different directions from the home position were used. The target locations were chosen individually for each subject to provide four different joint coordination patterns. Target 1 enabled movement performed with shoulder flexion and no rotation at the elbow. Shoulder flexion and elbow extension was performed to achieve Target 2. Target 3 was chosen to enable elbow extension and no rotation at the shoulder. Finally, achieving Target 4 required extension at both joints. This method of the choice of target locations was similar to that used in the previous studies (Dounskaia et al., 2005; Wisleder & Dounskaia, 2007). The purpose of these manipulations was to test whether inter-segmental dynamics influence submovement production. The premise for this possibility was provided by Sainburg et al. (1993; 1995) who argued that inter-segmental dynamics regulation is specifically challenging during the deceleration movement phase. No evidence for this influence was found in our previous studies. This result was again verified in the present study. Preliminary analysis did not reveal a significant main effect of joint coordination pattern on submovement production or a significant interaction involving this factor. The data from the four targets were therefore combined and the factor of joint coordination/target location was not included in the subsequent analyses.
Movements to the targets were initiated by an auditory signal. Reaction time was not studied, and therefore, subjects were not required to initiate movement as fast as possible. Movements to the targets were performed in three different modes: discrete, reciprocal, and passing. The discrete mode required moving the cursor to the target and terminating motion within the target. The reciprocal mode involved moving the cursor to the target and returning to the home position without dwelling on the target. The passing mode required moving the cursor through the target and then stopping anywhere within the digitizer surface. The conditions of target size, target location, and movement mode were randomized across subjects.
Subjects were instructed to perform motion to the target as fast as possible in all movement conditions. In addition, bringing the cursor within the target was an ultimate requirement. Specifically, discrete movements consisted of reaching the target and staying within the target bounds with cursor velocity being lower than 5% of its peak for at least 150 ms. Reciprocal movements required bringing the cursor within the target and reversing motion back to the home position. To exclude dwelling on the target, the period before the initiation of the reversal motion during which velocity could stay below 5% of the peak velocity was limited to 60 ms. During the passing mode, subjects had to move the cursor through the target and to terminate motion after that anywhere within the digitizer area. Proper performance of this task was verified by controlling that the target was passed with velocity higher than 5% of its peak. These requirements were controlled by a computer program during movement performance. If any of these requirements were not satisfied, a high-tone auditory signal was produced to notify the subject that the performed movement is not acceptable. In this case, the experimenter verbally explained what requirements were violated, and the trial was repeated. Only successful trials were stored in the computer for future analysis. Usually, two-three practice trials in each movement condition were sufficient for subjects to learn the requirements and to perform subsequent trials successfully. Eight successful trials were recorded in each condition.
2.3. Data Recording and Analysis
Motion of the stylus was recorded by the digitizer at a sampling frequency of 100 Hz and with spatial resolution of 0.1 mm. These data were used to represent motion with the cursor on the computer screen in real time and for automatic control of fulfillment of the movement requirements. In addition to the digitizer, a three-dimensional, optoelectronic tracking system (Optotrak, Northern Digital) was used to record arm motion at a 100 Hz sampling rate. Four reflective markers were attached to the sternum, shoulder joint, elbow joint, and the tip of the index finger. The data from the fingertip marker were used to analyze fingertip motion. The data from the rest of the markers were employed to verify that movements were performed with shoulder and elbow coordination patterns required by each target. To obtain target representation in the Optotrak coordinates, the location of the fingertip marker was recorded when the subject accurately positioned the fingertip on the target.
Velocity, acceleration, and jerk profiles of the fingertip were calculated as derivatives of fingertip displacement. In addition to signed velocity (positive values of which corresponded to motion towards the target) unsigned velocity was computed. A sliding window technique was used to compute the derivatives. This method provides approximation of the data within a window with a quadratic polynomial. The coefficients of the quadratic polynomial are then used to calculate the analytic derivative at the window's center. This method of calculation also provides data smoothing. The width of the sliding window was 12 data points.
To determine the beginning of the movement, the moment of time was found at which the unsigned velocity of the fingertip marker exceeded 5% of peak velocity after staying below this threshold for at least 150 ms. Then, a backward-tracing algorithm was used to determine the last preceding moment at which signed velocity was zero. Similarly, the end of the discrete and passing movements was determined based on the moment of time at which unsigned velocity was lower than 5% of peak velocity and stayed under this threshold for at least 150 ms. The moment at which signed velocity became zero after crossing the 5% threshold was considered as the movement end. Only the movement from the home position to the target was considered during the reciprocal mode. The end of movement to the target in the reciprocal condition was defined as the moment of the initiation of motion from the target to the home position. To determine this moment, the velocity peak during the movement from the target to the home position was detected. Starting from this velocity peak, a backwards-tracing algorithm was then used to detect the time moment of the first local minimum of the unsigned velocity. In addition, passing the target was defined during the passing mode as the moment of time when the distance between the fingertip and the target center was minimal.
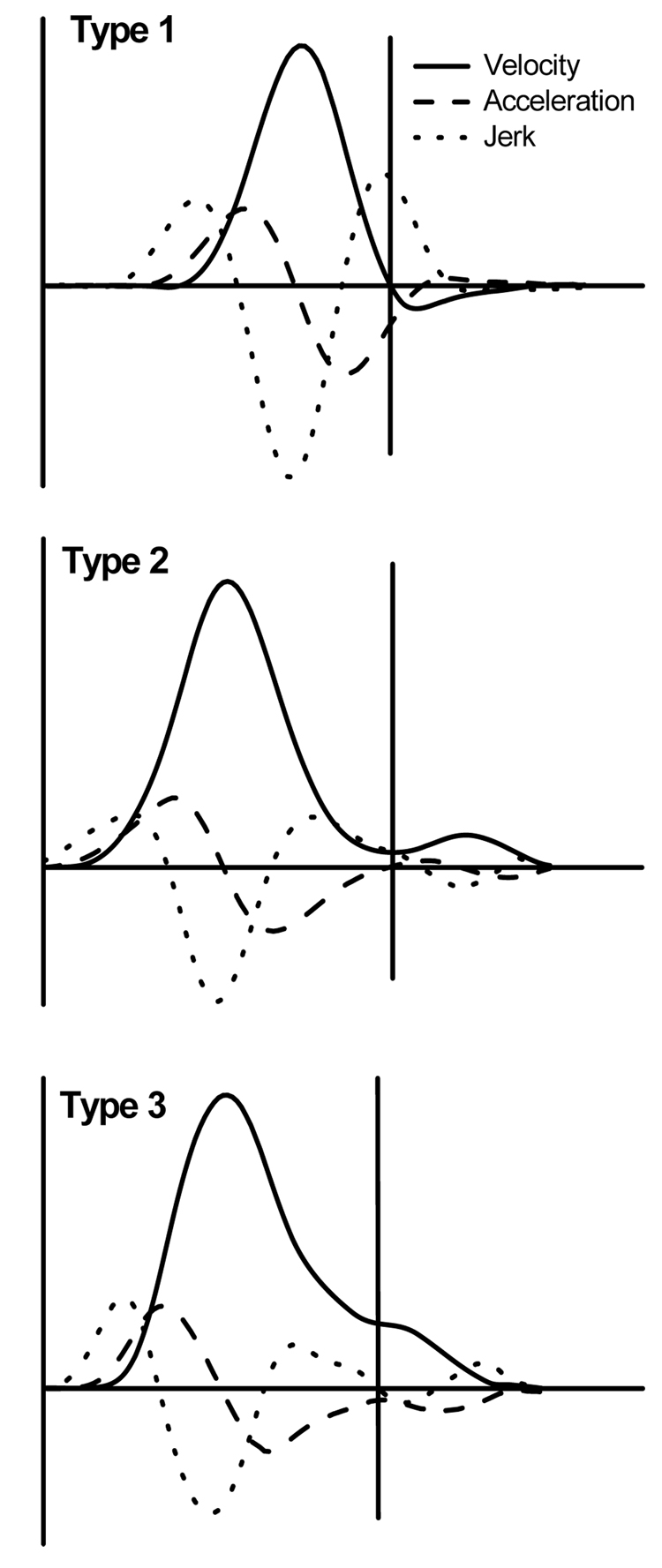
Each movement to the target was parsed in the primary and secondary submovement with use of the method adopted from Meyer et al. (1988). Although other methods of submovement detection have also been suggested (Milner, 1992; Novak et al., 2002; Rohrer & Hogan, 2003, 2006), the majority of studies promoting the interpretation of secondary submovements as corrective adjustments employed the method of Meyer and colleagues. Since the goal of the present study was to re-examine this interpretation, we also used this method. Namely, the initial smooth, bell-shaped portion of the velocity profile was defined as a primary submovement. The end of the primary submovement, which was also the beginning of the secondary submovement, was determined as the moment of time within the deceleration phase at which one of the following events occurred: a zero-crossing from positive to negative value occurred in the signed velocity profile (type 1 submovement); the acceleration profile crossed zero from a negative to a positive value (type 2 submovement); the jerk profile crossed zero from a positive to a negative value (type 3 submovement). Examples of the three submovement types during discrete movements are shown in Fig. 2.
Figure 2.
Examples of discrete movements with secondary submovements of type 1, 2, and 3. The vertical line marks the end of the primary submovement and the beginning of the secondary submovement. Type 1 submovement emerged when the smooth primary submovement was interrupted by a velocity zero-crossing from positive to negative values. Type 2 submovement was characterized by an acceleration zero-crossing from negative to positive values. A jerk zero-crossing from positive to negative values was indicative of a type 3 submovement.
The analysis was limited to the first fluctuation in the velocity profile, thus focusing on the interruption of the smooth velocity profile and factors causing this interruption. Accordingly, the movement portion comprised between the end of the primary submovement and the end of the entire movement to the target was defined as a secondary submovement. Although one or two velocity fluctuations emerged after the first irregularity in the velocity profile in 26% of trials with a submovement, these subsequent fluctuations were not analyzed as separate submovements, first, because the subsequent fluctuations were not a consistent feature of movements with submovements and emerged relatively rarely, and second, because the subsequent fluctuations may be not independent from the type of the first fluctuation.
Only secondary submovements emerging during the deceleration phase were analyzed, since corrective adjustments are likely to emerge during this phase. Frequency of emergence of the irregularities depending on movement mode and target size was studied. During the passing mode, only submovements initiated after passing the target were considered. Since the target had been passed before initiation of these submovements, none of them were corrective adjustments performed with a purpose to provide accurate target achievement. As subsequent analysis demonstrated, the target passing always occurred during the deceleration phase. Namely, it occurred when about 33% and 13% of deceleration duration elapsed when the targets were small and large, respectively. Due to this factor, frequency of submovement emergence could be lower in the passing mode than in the other modes during which submovements initiated at any moment of the deceleration phase were considered.
To assess frequency of submovement emergence, total submovement incidence was computed for each subject in each condition as the number of movements with secondary submovements of any of the three types divided by the total number of movements performed in this condition. Total submovement incidence has been the cardinal characteristic used in support of the traditional submovement interpretation because the common finding is that total submovement incidence increases with decreases in target size. In addition to the total submovement incidence, we follow Dounskaia et al. (2005) and Wisleder & Dounskaia (2007) and analyze submovement incidence separately for each type. The distinction of the three submovement types is justified by a consideration that if different factors may cause the interruption of the smooth, bell-shaped velocity profile, the degree of the perturbation in smooth motion (i.e., the type of submovement) may be different for different factors. This expectation was supported by a finding of our previous studies that gross (type 1 and 2) submovements were related to motion termination and fine (type 3) submovements were associated with pointing accuracy regulation. For this reason, the separate analysis of each submovement type was included here. The incidence of secondary submovements by type was computed for each condition as the number of movements with a secondary submovement of the respective type divided by the total number of movements performed in this condition. In addition to submovement incidence, peak velocity as a characteristic of movement speed was computed.
2.4. Statistical Analysis
A 2×3 (Size × Mode) repeated measures factorial analysis of variance (ANOVA) was applied to the computed characteristics. Size corresponded to the small and large targets and mode corresponded to the discrete, reciprocal, and passing mode. Bonferoni post-hoc tests were conducted to perform pairwise comparisons between the modes. The 0.05 significance level was used to define statistically significant effects.
2.5. Dependence of Submovements on the Differentiation and Filtering Procedure
To establish robustness of results reported in the next section, it was investigated whether the differentiation and smoothing procedure used to compute velocity, acceleration, and jerk influenced the emergence of the three types of submovements. With this purpose, submovement incidence obtained with use of the differentiation procedure was compared with this characteristic obtained with use of two other smoothing methods complimented with a MATLAB 2-point signal differentiation procedure. The first smoothing method was a 5th-order dual-pass low-pass Butterworth filter with a cut-off frequency of 7 Hz. The second method was a MATLAB cubic smoothing spline procedure csaps. Although using the different smoothing procedures resulted in slight variations in the values of submovement incidence in each condition, the statistical influence of target size and movement mode on the total submovement incidence and incidence of each submovement type was the same for all three methods. This demonstrated that the majority of submovements of all three types were not an artifact of the differentiation and smoothing procedure. Instead, they were inherent features of movement kinematics and their emergence depended on movement conditions, as presented next.
3. Results
3.1. Total Submovement Incidence
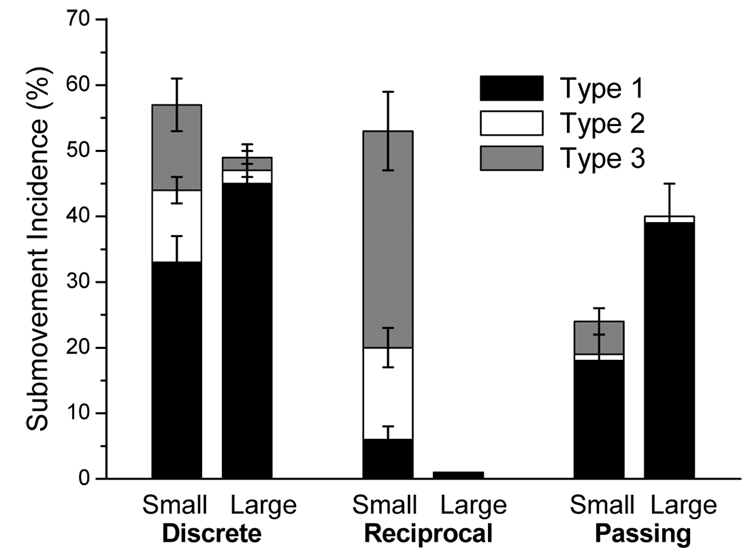
Submovements were found in 40% of all recorded movements. Mean and SE values of total submovement incidence (without distinction of the type) are presented in Table 1. The results of ANOVA applied to this characteristic are summarized in Table 2. The mean values of total submovement incidence are also shown in Fig. 3 as the sum of submovement incidence of the three types in each movement condition, i.e. as the height of each column. Both main effects were significant for this characteristic. Submovements were more frequent in movements to small than large targets. With respect to the main mode effect, the post hoc testing revealed that submovements were more frequent during the discrete mode than during any of the two other modes (p < 0.001 for both comparisons). The interaction was also significant. Fig. 3 shows that the effect of target size was different for the three modes. First, the inverse relationship between submovement incidence and target size took place during the discrete and reciprocal mode but not during the passing mode. Furthermore, the discrete and reciprocal mode also differed from each other with respect to the target size effect. For large targets, submovements were frequent in the discrete mode and they were basically absent during the reciprocal mode. This difference between the two modes suggests that in the discrete mode, submovements emerged not only due to decreases in target size but also due to motion termination. Motion termination as a source of submovements was further supported by the submovements observed in the passing mode, and specifically, by more frequent emergence of these submovements during movements to large than small targets. Together, the results obtained for the total submovement incidence show that the traditional interpretation is not sufficient to account for all observed effects. Other factors, and in particular, motion termination, also contributed to the submovement production.
Table 1.
Total submovement incidence (mean ± SE).
| % | Discrete | Reciprocal | Passing |
|---|---|---|---|
| Small Targets | 57 ± 4 | 53 ± 7 | 24 ± 4 |
| Large Targets | 49 ± 6 | 1 ± 0 | 40 ± 6 |
| Total | 53 ± 4 | 27 ± 4 | 32 ± 5 |
Table 2.
Statistical results (F-values).
| Size | Mode | Size ×Mode | |
|---|---|---|---|
| Degrees of Freedom | 1, 15 | 2, 30 | 2, 30 |
| Total SM Incidence | 8.9** | 13.8*** | 51.4 *** |
| Type 1 SM Incidence | 9.7** | 36.3*** | 13.8 *** |
| Type 2 SM Incidence | 31.0*** | 11.2*** | 11.2*** |
| Type 3 SM Incidence | 20.5*** | 25.1*** | 24.7*** |
| Peak Velocity | 182.0*** | 81.5*** | 7.2** |
p<0.05
p<0.01
p<0.001, SM - Submovement
Figure 3.
Mean submovement incidence by type expressed in percentage of the total number of movements in each condition defined by target size (small and large) and movement mode (discrete, reciprocal, and passing). The height of each column represents total submovement incidence in the corresponding condition. The error bars represent standard error (SE). Type 1 submovements emerged predominantly during the modes including motion termination, i.e. during the discrete and passing mode. Also, they were more frequent for large than small targets. In contrast, type 2 submovements occurred during the discrete and reciprocal mode and primarily when the target was small. Similar results were obtained for type 3 submovements. However, they were observed also in the passing mode (i.e. after crossing the target) during which they also emerged only when the target was small.
3.2. Submovement Incidence by Type
The effects of target size and movement mode on submovement production become clear when the three submovement types are considered separately from each other. The two main effects and interaction were significant for all three submovement types (Table 2). Fig. 3 helps to interpret these statistical results. Type 1 submovements emerged predominantly during discrete and passing and not reciprocal movements. This result points to a relation of these submovements to motion termination. Furthermore, type 1 submovements observed in these two modes were more frequent when the target was large than when it was small. These results are consistent with the association of these submovements with motion termination because movements to bigger targets usually have higher speed, and therefore, emergence of a type 1 submovement during arm stabilization was more likely. Further, post hoc testing revealed that type 1 submovements were more frequent during discrete than passing movements (p < 0.001). This suggests that simultaneous performance of motion termination with accuracy regulation increases chances of emergence of type 1 submovements. No statistical difference was found in type 1 submovement incidence between the two target sizes in the reciprocal mode (p>0.1).
Type 2 submovements were present in the discrete and reciprocal mode but not in the passing mode. This observation together with the fact that these submovements emerged predominantly during movements to small and not to large targets points to the association of these submovements with the accuracy regulation subtask. The same relationship with target size was obtained for type 3 submovements, offering the traditional interpretation to these submovements as well. However, this inference is questioned by the presence of type 3 submovements in the passing mode. Moreover, post hoc testing revealed that during the passing mode, type 3 submovements emerged more frequently for small than for large targets (p<0.001), even though they emerged after crossing the target, i.e. when no corrective submovements were needed. This result is remarkable because it shows that the inverse relationship between type 3 submovement incidence and target size does not necessarily mean that these submovements are directly related to accuracy regulation. Rather, they may be a by-product of mechanisms involved in accuracy regulation, for instance, of decreases in movement speed. The more frequent emergence of type 3 submovements with decreases in movement speed hypothesized here may also account for the higher incidence of these submovements during the reciprocal mode if movement speed was lower during this mode as compared to the other two modes. The differences in movement speed across the three modes are analyzed further.
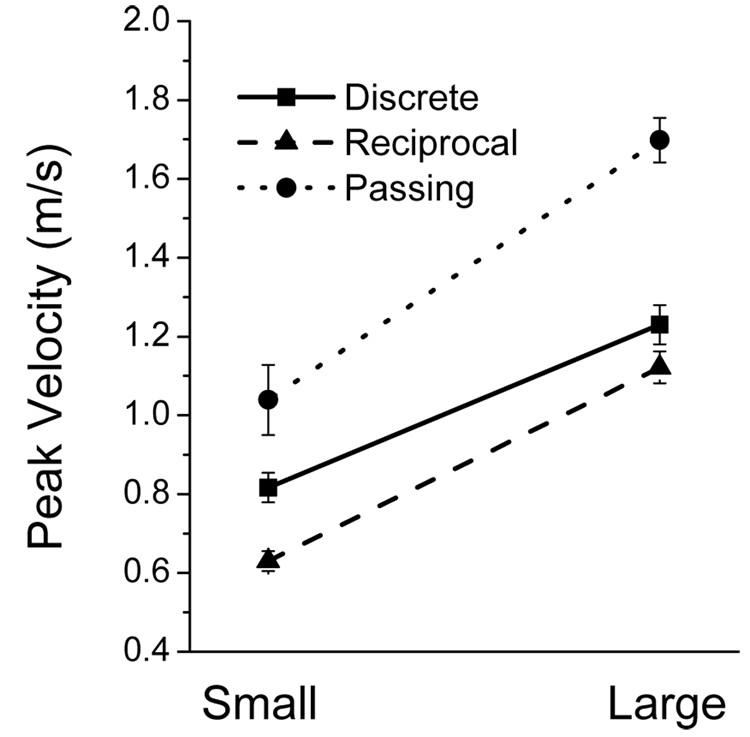
3.3. Peak Velocity
To explore the hypothesis that incidence of some of the three submovement types increases with decreases in movement speed, peak velocity and the dependence of submovement incidence on it was analyzed. Mean values of peak velocity in each condition are shown in Fig. 4. Table 2 shows that both main effects and interaction were significant. Peak velocity was lower during movements to the small than large targets, which is in agreement with the speed-accuracy tradeoff (Fitts, 1954). A distinct level of peak velocity was achieved in each mode. Velocity was the highest in the passing mode and the lowest in the reciprocal mode (p < 0.001 for all three comparisons). The interaction was significant because the velocity increases caused by the increases in target size were lower in the discrete than in other two modes.
Figure 4.
Mean values of peak velocity for the two target sizes and three movement modes. Velocity increased with increases in target size. Velocity was the highest in the passing mode and the lowest in the reciprocal mode, achieving distinct intermediate values during the discrete mode. The error bars represent SE.
The results of the peak velocity analysis confirm the assumption that speed was higher during movements to large than small targets, which was used in section 3.2 to account for more frequent type 1 submovements observed for large than small targets. However, the peak velocity results also show that movement speed may be not the only factor influencing emergence of submovements during motion termination because type 1 submovements were more frequent in the discrete than in the passing mode even though the former movements were slower than the latter. Rather, simultaneous performance of motion termination and accuracy regulation may account for the increased incidence of type 1 submovements during discrete movements. The decreases in peak velocity with target size were also consistent with the hypothesis that type 3 submovements were fluctuations that emerge during low speed movements, and that the dependence of these submovements on target size was a by-product of the speed-accuracy tradeoff.
The dependence of each submovement type on movement speed was further investigated via a regression analysis between submovement incidence and peak velocity. Since the purpose of this analysis was to examine the nature of each submovement type, passing movements were not included due to the selective method of submovement analysis applied to this mode that a priory excluded any corrective submovements. Thus, only discrete and reciprocal movements were analysed. Taking into account that our previous studies revealed dependence of temporal movement characteristics on the target location (Dounskaia et al., 2005; Wisleder & Dounskaia, 2007), incidence of each submovement type computed separately for each of the four targets was used for the regression analysis. Thus, mean values obtained during the sixteen conditions emerging from the combinations of the two movement modes (discrete and reciprocal), two target sizes, and four target locations were used.
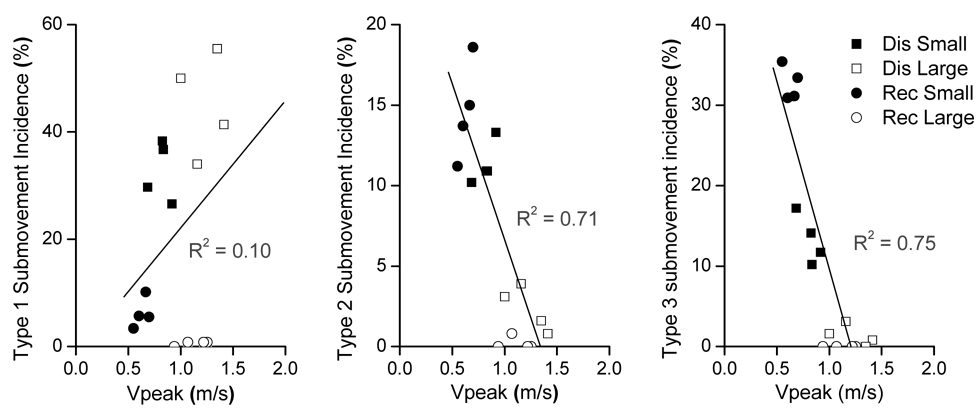
The results of the regression analysis for the three submovement types are shown in Fig. 5. Correlation between type 1 submovement incidence and peak velocity was low (R2 = 0.10, p > 0.1) suggesting that there was no consistent, linear relationship between type 1 submovements and movement speed. In contrast to type 1, submovement incidence was significantly (p < 0.05) and negatively correlated with peak velocity for type 2 and 3 (R2 = 0.71 and R2 = 0.75, respectively). These results support the conclusion of the analysis of submovement incidence by type that submovements of type 1 differ in nature from submovements of type 2 and 3. Furthermore, they are consistent with the possibility that submovements of type 3, and perhaps type 2 as well, were directly related to low movement speed, and that the dependence of these submovements on target size was a result of the speed-accuracy tradeoff.
Figure 5.
Results of linear regression between the velocity peak and incidence of type 1, 2, and 3 submovements. The analysis was applied to the discrete (Dis) and reciprocal (Rec) mode. Each panel includes sixteen data points corresponding to the combinations of the two movement modes, two target sizes, and four target locations.
4. Discussion
The traditional interpretation of secondary submovements suggests that they are visually guided adjustments performed to achieve required accuracy at the target (Crossman & Goodeve, 1983; Keele, 1968; Meyer et al., 1988; Woodworth, 1899). Here, we re-examined this long-lasting interpretation and studied whether there are submovements that cannot be interpreted as corrective submovements. The results suggest that submovements observed during pointing to a target are not homogeneous and that different factors may contribute to their production. In particular, strong evidence was obtained for type 1 submovements emerging due to motion termination. Other results point to a possibility that type 3 and perhaps type 2 submovements are not corrective adjustments for accuracy but are an attribute of low speed produced during movements to small targets. These findings are discussed next.
4. 1. Motion Termination and Submovement Production
To distinguish submovements caused by motion termination, we compared submovement incidence among the three modes, discrete, reciprocal and passing. It was expected that submovements related to motion termination would appear in the discrete and passing and not in the reciprocal mode because pointing in the latter mode does not include motion termination. The analysis pointed to type 1 submovements as those related to motion termination. Indeed, the traditional interpretation of these submovements is that they are corrections for target overshooting. This interpretation predicts that type 1 submovements would emerge equally during the discrete and reciprocal mode, and they would be more frequent during movements to small than large targets. However, type 1 submovements were abundant in discrete movements and were scarce in reciprocal movements. This result is not consistent with the interpretation of them as corrective submovements. Rather, it points to motion termination as a possible source of these submovements. This alternative interpretation is further supported by the finding that, in addition to the discrete mode, type 1 submovements were frequent during the passing mode that also included motion termination. In addition, type 1 submovements were more frequent during movements to large than small targets. This result is also consistent with the interpretation of these submovements as emerging from motion termination because movements to large targets were characterized by higher speed, and hence, were prone to oscillations during stabilization of the arm at the target.
The conclusion that type 1 submovements emerge from motion termination rather than being corrective adjustments was also derived in our previous studies (Dounskaia et al., 2005; Wisleder & Dounskaia, 2007). Similar to the present findings, type 1 submovements were frequent in the discrete mode and almost absent in the continuous modes that did not include motion termination. Also, incidence of these submovements did not increase with decreases in target size. A difference between the present and the previous studies is that in those studies, type 2 submovements demonstrated the same dependence on the experimental manipulations as type 1 submovements. Reasons why type 2 submovements had a different nature in the present experiment is discussed further. In spite of this difference, all three studies converge on the finding that the majority of gross submovements (revealed by zero-crossings in the motion derivatives of low order) are not corrective adjustments but rather are caused by motion termination.
Although mechanisms underlying motion termination are unknown, two origins for emergent submovements can be proposed, active and passive. The active origin implies that submovements are a kinematic consequence of muscle activity that provides motion termination. Specifically, submovements might emerge due to the third phase of the tri-phasic muscle activation pattern revealed with use of electromyographic analysis. This phase is often interpreted as stabilization of the limb in the final position (Berardelli et al., 1996; Hallett et al., 1975; Hannaford & Stark, 1985) referred here as motion termination. Spinal reflexes may play the cardinal role in the active component of motion termination. However, the same reflexes may also be involved in providing pointing accuracy (Osu et al., 2004), which would explain why type 1 submovements were more frequent in the discrete mode during which motion termination was performed simultaneously with pointing accuracy regulation than during the passing mode during which the final movement stage included only motion termination.
A possible passive origin of submovements during motion termination is the viscoelastic properties of the muscle-tendon complex that could cause oscillations of the limb during motion termination. However, it might be difficult to distinguish the active and passive origin from each other since stiffness of the muscle-tendon complex might be actively regulated (Bennett, 1993; Hogan, 1985; Latash & Gottlieb, 1991). Nevertheless, both origins suggest that submovements related to motion termination are not centrally programmed in response to pointing error but rather are a consequence of physical properties of the limbs and of control responsible for halting motion at the target.
4. 2. Origins of Type 2 and 3 Submovements
The major support of previous research for the traditional submovement interpretation has been the more frequent emergence of submovements with decreases in target size. This dependence on target size was obtained here for type 2 and 3 submovements. In addition, type 2 submovements were present only during the discrete and reciprocal and not during the passing mode from which corrective submovements were excluded by the analysis methods. These results point to type 2 submovements as the primary candidates in the present study for satisfying the traditional interpretation, i.e. for being visually-guided adjustments performed to fulfill pointing accuracy requirements. However, in the studies of Dounskaia et al. (2005) and Wisleder & Dounskaia (2007), type 2 submovements were classified as emerging from motion termination because their incidence did not depend on target size and they were more frequent during discrete than during continuous movements. The differences in the behavior of type 2 submovements between this and the previous studies may be attributed to differences in the experimental conditions. For instance, indirect vision conditions were used in the present experiment in which motion and the targets were presented on a vertical computer screen instead of natural vision conditions used in our previous experiments. Also, there was an ultimate requirement to terminate motion within the target in the present study. In contrast, subjects were instructed to achieve the target as accurately as possible but were allowed to end motion anywhere near the target in our previous studies. Apparently, type 2 submovements may be related either to motion termination or to accuracy regulation, depending on experimental conditions. Thus, careful analysis of the incidence of type 2 submovements is required for each experimental set-up prior to making conclusions about the nature of these submovements.
Similar to type 2, type 3 submovements were more frequent during movements to small than large targets. Nevertheless, the interpretation of type 3 submovements as corrective adjustments was challenged by frequent emergence of them in the passing mode, also in the inverse proportion to target size. An alternative interpretation is that many of type 3 and perhaps type 2 submovements may have been not corrective submovements but motion fluctuations that emerged during movements of high accuracy.
One possible source of motion fluctuations during movements to small targets is increased muscle co-contraction accompanying decreases in target size (Gribble et al., 2003). Also, fluctuations may be a characteristic of low movement speed while their dependence on target size is a by-product of speed-accuracy tradeoff (Fitts, 1954). This hypothesis is consistent with decreases in smoothness of movement trajectory with decreases in movement speed reported by Doeringer and Hogan 1998. Wisleder & Dounskaia (2007) provided support for this hypothesis specifically in application to type 3 submovements finding that incidence of these submovements was independent of target size during cyclic movements of controlled frequency. Instead, type 3 submovement incidence depended on cyclic frequency. In addition, regression analyses in that study revealed strong correlation of type 3 submovement incidence with movement duration. The results of the regression analysis performed here were consistent, revealing strong correlation between submovement incidence and peak velocity for submovements of both type 2 and 3. Thus, it is possible that at least a substantial portion of these submovements represented motion fluctuations that emerged more frequently with decreases in movement speed.
Fluctuations as a feature of slow movements and isometric production of low force levels have been recognized and accounted for with unsteady production of muscle force (Burnett et al., 2000; Galganski et al., 1993; Laidlaw et al., 2000; Moritz et al., 2005). The coefficient of variability (the ratio between the standard deviation and the mean of the signal) of force production is in the inverse relationship with the contraction intensity, and therefore, with movement speed. Variability of the discharge rate of motor units have been proposed as the critical factor causing unsteady force production (Moritz et al., 2005). Other mechanisms, such as motor unit synchronization, discharge rate, specific characteristics of low-threshold motor units, and oscillation in excitatory drive have also been discussed as possible contributors to the variability of motor output (Taylor et al., 2003). These neurophysiological findings support the hypothesis that fine submovements are a characteristic feature of slow movements.
To summarize, the results of this study challenge the traditional interpretation of submovements as corrective adjustments performed to improve pointing accuracy. Rather, many of submovements are fluctuations associated with motion variability that may have various mechanical and neural origins. Specifically, two possible sources of motion variability have been recognized. The first source is motion termination that may result in fluctuations represented by gross submovements. The second source is low movement speed that provides conditions for the emergence of fine submovements. Although our data do not exclude the possibility that some submovements were performed to correct motion to the target, the dominant portion of submovements likely represents the two types of motion fluctuations.
This finding in particular suggests that the submovement detection method by Meyer et al. (1988) may be the most appropriate to study submovements during pointing and reaching tasks. This method detects changes in the velocity represented by specific zero-crossings in the first three derivatives of the displacement profile. Thus, if submovements are irregular fluctuations of velocity, in addition to detecting submovements, this method also provides information about the degree of irregularities of the velocity profile. More recent methods detect submovements by fitting the velocity profile with series of bell-shaped functions with scaled duration and amplitude (Milner 1992; Novak et al. 2002; Rohrer et al. 2004; Rohrer and Hogan 2006). The degree of velocity irregularities can be assessed with these methods only indirectly, as the amount of submovement overlap. For instance, a type 2 submovement would be characterized by smaller overlap with the primary submovement that a type 3 submovement. A type 1 submovement would be characterized as a submovement in the direction opposite to the direction of the main movement. Apparently, these methods are oriented on detecting corrective submovements and therefore would be more appropriate for tasks during which corrective submovements frequently emerge.
For instance, these methods may be more suitable for studying submovements during tracking tasks. In these tasks, submovements are of type 2 and 3. These submovements may be corrective in contrast to the majority of type 2 and 3 submovements during pointing. The possibility for a distinct nature of submovements during tracking and pointing is supported by findings of Pasalar et al. (2005), Roitman et al. (2004), and Selen et al. (2006a) that submovements during tracking become more pronounced with increases in movement speed, whereas they disappear during fast pointing movements to large targets. Further, according to results of Selen et al. (2006a), submovements observed during tracking increase with increases in target size. It is likely that during tracking, submovements are performed to compensate for constantly emerging deviations of motion from the target trajectory, while the target size determines “safety margins” for these deviations. Previous research did not distinguish submovements emerging in pointing and tracking tasks, assuming that all of them were corrective. The results of our study suggest that submovements observed in these two tasks may have different nature, which points to the need to study these differences.
4. 3. Implications for Pointing Accuracy Regulation Mechanisms
Our findings question the long-standing interpretation of the mechanism of pointing accuracy regulation as a series of visually guided corrective submovements. Indeed, the data show that type 1 and 3 submovements may be not corrective submovements. Even type 2 submovements that were found to be primary candidates for corrective submovements are unlikely to represent the accuracy regulation mechanism. These submovements constituted only 14% of all submovements. Taking into account that only 40% of all movements included submovements, type 2 submovements were performed in 6% of all movements. This shows that even if these submovements were performed to improve pointing accuracy, they could not be a major mechanism of accuracy regulation.
An alternative possibility is that modifications in the trajectory are produced smoothly, in a continuous process (Elliott, 1992; Elliott et al., 1991). This possibility was supported in experiments in which the target or the cursor representing hand motion shifted after movement initiation (Desmurget et al., 2003; Saunders & Knill, 2003, 2005). Another mechanism that may play an important role in pointing accuracy regulation is modulation of arm stiffness (Lametti et al. 2007; Osu et al., 2004; Selen et al., 2006b; Van Galen and Schomaker 1992). These studies suggest that stiffness is increased during movements to smaller targets to prevent deviations from the required trajectory that may emerge due to possible external perturbations and noise in the neuromuscular control signals. While the stiffness regulation hypothesis is appealing, our results point to a question associated with this hypothesis. Namely, this hypothesis implies that increased stiffness results in decreased variability not only at the target but also while approaching the target. This however contradicts to our finding that incidence of type 2 and 3 submovements (that represents trajectory variability) increases with decreases in target size. Another doubt related to this hypothesis is that although increased stiffness may help to prevent deviations from the required trajectory, it would also hinder corrections of the trajectory if they are needed.
The findings of the present study contribute to understanding of multiple processes involved in pointing accuracy regulation by making implications for regulation of movement speed depending on the target size. Gross submovements emerging during motion termination endanger pointing accuracy, and therefore, they favor decreases in movement speed, specifically during the deceleration phase. However, slow movements are prone to fine submovements, which may impose limitations on decreases in movement speed. Together, the findings for gross and fine submovements propose that speed of voluntary movements is a result of a trade-off between the two types of motion fluctuations. This optimization process may constitute an important component of the accuracy regulation mechanism during self-paced movements to a target.
Acknowledgement
The study was supported by NIH grant NS 43502. We are grateful to Neville Hogan and anonymous reviewers for helpful comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
PsyclNFO classification: 2330, 2323
References
- Abrams RA, Pratt J. Rapid aimed limb movements: Differential effects of practice on component submovements. Journal of Motor Behavior. 1993;25(4):288–298. doi: 10.1080/00222895.1993.9941650. [DOI] [PubMed] [Google Scholar]
- Bennett DJ. Torques generated at the human elbow joint in response to constant position errors imposed during voluntary movements. Experimental Brain Research. 1993;95:488–498. doi: 10.1007/BF00227142. [DOI] [PubMed] [Google Scholar]
- Berardelli A, Hallett M, Rothwell JC, Agostino R, Manfredi M, Thompson PD, et al. Single-joint rapid arm movements in normal subjects and in patients with motor disorders. Brain. 1996;119:661–674. doi: 10.1093/brain/119.2.661. [DOI] [PubMed] [Google Scholar]
- Burnett RA, Laidlaw DH, Enoka RM. Coactivation of the antagonist muscle does not covary with steadiness in old adults. Journal of Applied Physiology. 2000;89(1):61–71. doi: 10.1152/jappl.2000.89.1.61. [DOI] [PubMed] [Google Scholar]
- Chua R, Elliott D. Visual regulation of manual aiming. Human Movement Science. 1993;12:365–401. [Google Scholar]
- Crossman ER, Goodeve PJ. Feedback control of hand-movement and Fitts' law. The Quarterly Journal of Experimental Psychology. A, Human Experimental Psychology. 1983;35(Pt 2):251–278. doi: 10.1080/14640748308402133. [DOI] [PubMed] [Google Scholar]
- Desmurget M, Grafton ST, Vindras P, Grea H, Turner RS. Basal ganglia network mediates the control of movement amplitude. Experimental Brain Research. 2003;153(2):197–209. doi: 10.1007/s00221-003-1593-3. [DOI] [PubMed] [Google Scholar]
- Doeringer JA, Hogan N. Intermittency in preplanned elbow movements persists in the absence of visual feedback. Journal of Neuroscience. 1998;80:1787–1799. doi: 10.1152/jn.1998.80.4.1787. [DOI] [PubMed] [Google Scholar]
- Dounskaia N, Wisleder D, Johnson T. Influence of biomechanical factors on substructure of pointing movements. Experimental Brain Research. 2005;164(4):505–516. doi: 10.1007/s00221-005-2271-4. [DOI] [PubMed] [Google Scholar]
- Elliott D. Intermittent versus continuous control of manual aiming movement. In: Proteau L, Elliot D, editors. Vision and motor control. North-Holland: Amsterdam; 1992. pp. 33–48. [Google Scholar]
- Elliott D, Carson RG, Goodman D, Chua R. Discrete vs. Continuous visual control of manual aiming. Human Movement Science. 1991;10:393–418. [Google Scholar]
- Elliott D, Helsen WF, Chua R. A century later: Woodworth's (1899) two-component model of goal-directed aiming. Psychological Bulletin. 2001;127(3):342–357. doi: 10.1037/0033-2909.127.3.342. [DOI] [PubMed] [Google Scholar]
- Fitts PM. The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology. 1954;47(6):381–391. [PubMed] [Google Scholar]
- Galganski ME, Fuglevand AJ, Enoka RM. Reduced control of motor output in a human hand muscle of elderly subjects during submaximal contractions. Journal of Neurophysiology. 1993;69(6):2108–2115. doi: 10.1152/jn.1993.69.6.2108. [DOI] [PubMed] [Google Scholar]
- Gribble PL, Mullin LI, Cothros N, Mattar A. Role of cocontraction in arm movement accuracy. Journal of Neurophysiology. 2003;89(5):2396–2405. doi: 10.1152/jn.01020.2002. [DOI] [PubMed] [Google Scholar]
- Guiard Y. On fitts's and hooke's laws: Simple harmonic movement in upper-limb cyclical aiming. Acta Psychologica. 1993;82(1–3):139–159. doi: 10.1016/0001-6918(93)90009-g. [DOI] [PubMed] [Google Scholar]
- Hallett M, Shahani BT, Young RR. Emg analysis of stereotyped voluntary movements in man. Journal of Neurology, Neurosurgery, and Psychiatry. 1975;38(12):1154–1162. doi: 10.1136/jnnp.38.12.1154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hannaford B, Stark L. Roles of the elements of the triphasic control signal. Experimental Neurology. 1985;90(3):619–634. doi: 10.1016/0014-4886(85)90160-8. [DOI] [PubMed] [Google Scholar]
- Hogan N. The mechanics of multi-joint posture and movement control. Biological Cybernetics. 1985;52(5):315–331. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- Keele SW. Movement control in skilled motor performance. Psychological Bulletin. 1968;70:387–403. [Google Scholar]
- Khan MA, Franks IM. Online versus offline processing of visual feedback in the production of component submovements. Journal of Motor Behavior. 2003;35(3):285–295. doi: 10.1080/00222890309602141. [DOI] [PubMed] [Google Scholar]
- Laidlaw DH, Bilodeau M, Enoka RM. Steadiness is reduced and motor unit discharge is more variable in old adults. Muscle Nerve. 2000;23(4):600–612. doi: 10.1002/(sici)1097-4598(200004)23:4<600::aid-mus20>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- Lammetti DR, Houle G, Ostry DJ. Control of movement variability and the regulation of limb impedance. Journal of Neurophysiology. 2007;98:3516–3524. doi: 10.1152/jn.00970.2007. [DOI] [PubMed] [Google Scholar]
- Latash ML, Gottlieb GL. Reconstruction of shifting elbow joint compliant characteristics during fast and slow movements. Neuroscience. 1991;43(2–3):697–712. doi: 10.1016/0306-4522(91)90328-l. [DOI] [PubMed] [Google Scholar]
- Meulenbroek RG, Thomassen AJ. Exploitation of elasticity as a biomechanical property in the production of graphic stroke sequences. Acta Psychologica. 1993;82(1–3):313–327. doi: 10.1016/0001-6918(93)90018-m. [DOI] [PubMed] [Google Scholar]
- Meulenbroek RG, Vinter A, Desbiez D. Exploitation of elasticity in copying geometrical patterns: The role of age, movement amplitude, and limb-segment involvement. Acta Psychologica. 1998;99(3):329–345. doi: 10.1016/s0001-6918(98)00018-3. [DOI] [PubMed] [Google Scholar]
- Meyer DE, Abrams RA, Kornblum S, Wright CE, Smith KJE. Optimality in human motor performance: Ideal control of rapid aimed movements. Psychological Review. 1988;95:340–370. doi: 10.1037/0033-295x.95.3.340. [DOI] [PubMed] [Google Scholar]
- Milner TE. A model for the generation of movements requiring endpoint precision. Neuroscience. 1992;49(2):487–496. doi: 10.1016/0306-4522(92)90113-g. [DOI] [PubMed] [Google Scholar]
- Moritz CT, Barry BK, Pascoe MA, Enoka RM. Discharge rate variability influences the variation in force fluctuations across the working range of a hand muscle. Journal of Neurophysiology. 2005;93(5):2449–2459. doi: 10.1152/jn.01122.2004. [DOI] [PubMed] [Google Scholar]
- Novak KE, Miller LE, Houk JC. The use of overlapping submovements in the control of rapid hand movements. Experimental Brain Research. 2002;144(3):351–364. doi: 10.1007/s00221-002-1060-6. [DOI] [PubMed] [Google Scholar]
- Osu R, Kamimura N, Iwasaki H, Nakano E, Harris CM, Wada Y, et al. Optimal impedance control for task achievement in the presence of signal-dependent noise. Journal of Neurophysiology. 2004;92(2):1199–1215. doi: 10.1152/jn.00519.2003. [DOI] [PubMed] [Google Scholar]
- Pasalar S, Roitman AV, Ebner TJ. Effects of speeds and force fields on submovements during circular manual tracking in humans. Experimental Brain Research. 2005;163(2):214–225. doi: 10.1007/s00221-004-2169-6. [DOI] [PubMed] [Google Scholar]
- Pratt J, Abrams RA. Practice and component submovements: The roles of programming and feedback in rapid aimed limb movements. Journal of Motor Behavior. 1996;28(2):149–156. doi: 10.1080/00222895.1996.9941741. [DOI] [PubMed] [Google Scholar]
- Pratt J, Chasteen AL, Abrams RA. Rapid aimed limb movements: Age differences and practice effects in component submovements. Psychology and Aging. 1994;9(2):325–334. doi: 10.1037//0882-7974.9.2.325. [DOI] [PubMed] [Google Scholar]
- Rand MK, Stelmach GE. Effect of orienting the finger opposition space in the control of reach-to-grasp movements. Journal of Motor Behavior. 2005;37:65–78. doi: 10.3200/JMBR.37.1.65-78. [DOI] [PubMed] [Google Scholar]
- Rohrer B, Hogan N. Avoiding spurious submovement decompositions: A globally optimal algorithm. Biological Cybernetics. 2003;89(3):190–199. doi: 10.1007/s00422-003-0428-4. [DOI] [PubMed] [Google Scholar]
- Rohrer B, Hogan N. Avoiding spurious submovement decompositions ii: A scattershot algorithm. Biological Cybernetics. 2006;94(5):409–414. doi: 10.1007/s00422-006-0055-y. [DOI] [PubMed] [Google Scholar]
- Roitman AV, Massaquoi SG, Takahashi K, Ebner TJ. Kinematic analysis of manual tracking in monkeys: characterization of movement intermittencies during a circular tracking task. Journal of Neurophysiology. 2004;91:901–911. doi: 10.1152/jn.00261.2003. [DOI] [PubMed] [Google Scholar]
- Sainburg RL, Ghilardi MF, Poizner H, Ghez C. Control of limb dynamics in normal subjects and patients without proprioception. Journal of Neurophysiology. 1995;73:820–835. doi: 10.1152/jn.1995.73.2.820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Poizner H, Ghez C. Loss of proprioception produces deficits in interjoint coordination. Journal of Neurophysiology. 1993;70:2136–2147. doi: 10.1152/jn.1993.70.5.2136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saunders JA, Knill DC. Humans use continuous visual feedback from the hand to control fast reaching movements. Experimental Brain Research. 2003;152(3):341–352. doi: 10.1007/s00221-003-1525-2. [DOI] [PubMed] [Google Scholar]
- Saunders JA, Knill DC. Humans use continuous visual feedback from the hand to control both the direction and distance of pointing movements. Experimental Brain Research. 2005;162(4):458–473. doi: 10.1007/s00221-004-2064-1. [DOI] [PubMed] [Google Scholar]
- Selen LP, van Dieen JH, Beek PJ. Impedance modulation and feedback corrections in tracking targets of variable size and frequency. Journal of Neurophysiology. 2006a;96:2750–2759. doi: 10.1152/jn.00552.2006. [DOI] [PubMed] [Google Scholar]
- Selen LP, Beek PJ, van Dieen JH. Impedance is modulated to meet accuracy demands during goal-directed arm movements. Experimental Brain Research. 2006b;172(1):129–138. doi: 10.1007/s00221-005-0320-7. [DOI] [PubMed] [Google Scholar]
- Taylor AM, Christou EA, Enoka RM. Multiple features of motor-unit activity influence force fluctuations during isometric contractions. Journal of Neurophysiology. 2003;90(2):1350–1361. doi: 10.1152/jn.00056.2003. [DOI] [PubMed] [Google Scholar]
- Van Galen GP, Schomaker LRB. Fitts Law as a Low-Pass Filter Effect of Muscle-Stiffness. Human Movement Science. 1992;11:11–21. [Google Scholar]
- Walker N, Philbin DA, Fisk AD. Age-related differences in movement control: Adjusting submovement structure to optimize performance. The Journals of Gerontology. Series B, Psychological Sciences and Social Sciences. 1997;52(1):P40–P52. doi: 10.1093/geronb/52b.1.p40. [DOI] [PubMed] [Google Scholar]
- Wisleder D, Dounskaia N. The role of different submovement types during pointing to a target. Experimental Brain Research. 2007;176(1):132–149. doi: 10.1007/s00221-006-0603-7. [DOI] [PubMed] [Google Scholar]
- Woodworth RS. The accuracy of voluntary movement. Psychological Review. 1899;3(3) suppl. 13:1–119. [Google Scholar]