QM/MM Minimum Free Energy Path: Methodology and Application to Triosephosphate Isomerase

Abstract

Structural and energetic changes are two important characteristic properties of a chemical reaction process. In the condensed phase, studying these two properties is very challenging because of the great computational cost associated with the quantum mechanical calculations and phase space sampling. Although the combined quantum mechanics/molecular mechanics (QM/MM) approach significantly reduces the amount of the quantum mechanical calculations and facilitates the simulation of solution phase and enzyme catalyzed reactions, the required quantum mechanical calculations remain quite expensive and extensive sampling can be achieved routinely only with semiempirical quantum mechanical methods. QM/MM simulations with ab initio QM methods, therefore, are often restricted to narrow regions of the potential energy surface such as the reactant, product and transition state, or the minimum energy path. Such ab initio QM/MM calculations have previously been performed with the QM/MM-Free Energy (QM/MM-FE) method of Zhang et al.¹ to generate the free energy profile along the reaction coordinate using free energy perturbation calculations at fixed structures of the QM subsystems. Results obtained with the QM/MM-FE method depend on the determination of the minimum energy reaction path, which is based on local conformations of the protein/solvent environment and can be difficult to obtain in practice. To overcome the difficulties associated with the QM/MM-FE method and to further enhance the sampling of the MM environment conformations, we develop here a new method to determine the QM/MM minimum free energy path (QM/MM-MFEP) for chemical reaction processes in solution and in enzymes. Within the QM/MM framework, we express the free energy of the system as a function of the QM conformation, thus leading to a simplified potential of mean force (PMF) description for the thermodynamics of the system. The free energy difference between two QM conformations is evaluated by the QM/MM free energy perturbation method. The free energy gradients with respect to the QM degrees of freedom are calculated from molecular dynamics simulations at given QM conformations. With the free energy and free energy gradients in hand, we further implement chain-of-conformation optimization algorithms in the search for the reaction path on the free energy surface without specifying a reaction coordinate. This method thus efficiently provides a unique minimum free energy path for solution and enzyme reactions, with structural and energetic properties being determined simultaneously. To further incorporate the dynamic contributions of the QM subsystem into the simulations, we develop the reaction path potential of Lu, et al.² for the minimum free energy path. The combination of the methods developed here presents a comprehensive and accurate treatment for the simulation of reaction processes in solution and in enzymes with ab initio QM/MM methods. The method has been demonstrated on the first step of the reaction of the enzyme triosephosphate isomerase with good agreement with previous studies.

Introduction

With the overwhelming details of real-time atomic motions, computer simulations have provided unprecedented insight into the puzzle of chemical reaction processes.^3–5 Complementary to experimental studies, simulation methods can provide information that is often not easily accessed by conventional experimental approaches. For example, simulations can determine the transition state structure of a reaction process, which is difficult to obtain from experimental methods. Simulations can also reveal the site-specific interactions influencing an enzymatic reaction process for which experimental studies are more costly or are often derived from indirect evidence.^6–13 However, challenging problems persist in simulating reaction processes in solution and in enzymes because of many technical limitations such as the accuracy of the force field and the convergence of the statistical sampling.

For reactions in solution or enzymes, quantum mechanical (QM) treatment for the whole molecular system is computationally prohibitive in general because there are too many electronic degrees of freedom. On the other hand, classical molecular mechanics (MM) is incapable of describing the electron redistribution during the bond breaking/forming events in reactive processes. To address this difficulty, a method was proposed to combine quantum mechanics and molecular mechanics in the simulations.¹⁴ In this hybrid approach, only a small portion of the molecular system that is important to the reaction is treated by QM, while the rest of the system is simulated by simplified MM force fields. Presumably, the QM treatment accurately captures the most important changes at the site of the chemical reaction, while the MM treatment takes into account the contributions of the environment as an approximate, yet computationally economic, solution.^{14, 15}

Since there is no restriction on the choice of the QM level of theory in the QM/MM approach, many different QM methods have been used in QM/MM simulations of reaction processes. The QM methods vary from the semiempirical level Empirical Valence Bond (EVB),³ MNDO,¹⁶ AM1,¹⁷ PM3,^{18, 19} and Self-Consistent Charge Density Functional Tight Binding (SCC-DFTB),^{20, 21} to ab initio Hartree-Fock, MP2, and Density Functional Theory (DFT).^22–24 Compared with the plentiful choices of QM methods, the MM subsystems vary much less between simulations and often assume the form of common classical MM force fields which are comprised of empirical covalent terms (i.e., bond, bond angle, dihedral, and improper dihedral terms), and nonbonded van der Waals and electrostatic interactions. With such flexible combinations of QM and MM methods, simulation studies of many reaction processes have demonstrated that within current computational capabilities, the QM/MM method has become the most effective way for simulating condensed phase reactions.^{5, 9–13, 25–28}

Different QM methods usually possess correspondingly different levels of accuracy and computational cost, both of which may vary significantly for a given simulation. Consequently, depending on the implementation of a specific QM level of theory, specific applications of QM/MM methods have followed different routes to maximize the effectiveness of the QM/MM method. Each route essentially evolves into a distinct QM/MM method with each method focusing on different aspects of the reaction process. As each method possesses different advantages and disadvantages, a brief review of these QM/MM methods will be given to set the stage for presenting our new development.

In general, when semiempirical methods such as EVB, MNDO, AM1, PM3, and SCCDFTB are used as the QM model, the computational cost is low with the currently available computational capacity. As a result, classical approaches such as umbrella sampling,²⁹ PMF calculations, and thermodynamic integration (TI) can be applied in a straightforward manner to the calculation of the structural and energetic properties of a reaction. Usually, a reaction coordinate is chosen as a combination of geometric and/or energetic terms. The conformations are then sampled and the free energy changes of the molecular system along this reaction coordinate is computed. Because broad sampling of phase space is attainable in this situation, the convergence of the results is satisfactory. However, the results may be less accurate and reliable compared to ab initio QM calculations because of the well known deficiencies in semiempirical QM methods, a problem which originates in the approximations made both in the theory and in the parameterization process. It is thus highly desirable to use high-level, accurate QM methods. This demand has in fact motivated the development of several QM/MM free energy simulation techniques based on ab initio quantum mechanics.

Jorgensen’s group has developed the quantum mechanical free energy (QM-FE) approach.^30–34 In this approach, the reaction path is optimized for a model reaction system in gas phase. To compute the free energy of the reaction process, free energy perturbation (FEP) is applied along the pre-optimized gas-phase reaction path with the inclusion of the QM/MM interactions. The interactions between the QM and MM subsystems are treated classically by either taking them directly from MM force fields or by fitting to a QM calculation for a molecular cluster in gas phase. This approach has been successfully applied to many solution reactions and some enzymatic reactions.³⁵ However, since the reaction path is pre-determined in gas phase, it is not clear whether the solution reaction will follow the same path. The results would most likely be more reliable if the path were determined in situ.

Warshel’s group pioneered in the development and application of QM/MM methods and has recently constructed several approaches to calculate accurate ab initio QM/MM free energies.^{25, 26} A strategy for combing those approaches, namely the hybrid ab initio quantum mechanics/molecular mechanics (QM(ai)/MM) method,^36–40 was developed for the study of condensed phase reaction processes. The first step, and also the essence of this method, is to build an EVB potential that approximates the potential energy surface from ab initio QM methods. In the second step, the EVB potential is used to perform long timescale dynamic sampling of the whole molecular system which ensures the convergence of statistical sampling in phase space. The free energies are also calculated on this EVB surface using standard sampling approaches. The final step of this method is to recover the free energy difference between the EVB surface and the ab initio surface. Free energy perturbation combined with the linear response approximation (LRA) is used to evaluate this term. The application of this method to a wide range of problems has demonstrated its success. There are, however, several technical concerns. The first is that the construction of the EVB potential is a non-trivial problem and often requires clear and clever understanding of the chemical process. The second relates to how well the EVB potential approximates the ab initio surface. The third concern is that this method does not provide direct determination of the transition state structure. Nevertheless, the idea of using a reference potential has proven to be successful and applicable in general, from which several more recent approaches share a similar spirit.⁴¹

Our group has developed a combined quantum mechanics/molecular mechanics free energy perturbation (QM/MM-FE) method for the simulation of enzymatic reaction processes.^{1, 10, 42, 43} Our approach consists of three major components: the pseudobond ab initio QM/MM method which provides a smooth interface between the QM and MM subsystem and thus a well-defined potential energy surface, the efficient iterative optimization procedure which determines the reaction paths within a realistic enzyme environment, and free energy calculations which take into account the fluctuation of the enzyme system. To calculate the free energy of activation (or the potential of mean force) in the QM/MM-FE method, we made two assumptions: (1) the dynamics of the QM and MM subsystems is independent of each other and (2) the QM subsystem fluctuations are harmonic. Then, we calculated the contribution to the free energy from the fluctuations in the MM subsystem with the FEP method, and approximated the contribution to the free energy from the fluctuations in the QM subsystem with harmonic frequency calculations. In addition, we approximate the QM/MM electrostatic interactions by the interactions between point charges of MM atoms and point charges of QM atoms; the latter being fitted to the QM electrostatic potential (ESP). This approximation leads to pairwise interactions that are separable and cost much less in the calculations. Therefore, the reaction path for the entire enzyme system can be iteratively optimized by this simplified QM/MM description.^{1, 43} To further include the dynamical contribution of the QM subsystem, the reaction path potential (RPP) method was developed.² The applications of this QM/MM-FE method have been shown to be successful.^{11, 12, 44, 45} The accuracy of the QM/MM-FE method has been tested against full free energy simulations in two other laboratories^{41, 46} and has been shown to be excellent. By employing the idea of reference potentials, further efforts have also been made to improve the accuracy in the construction of the thermodynamic cycle and FEP simulations. The main limitation of the QM/MM-FE method is, however, that the optimization of the reaction path depends on the choice of the initial conformation,⁴⁷ although it is debatable how much this dependence can bias the results in the simulations of enzymatic reactions (Cisneros and Yang, to be submitted). In solution reactions, nevertheless, this dependence becomes the main obstacle in applying the static, iterative optimization to the calculation of reaction paths^{1, 43} because of the disorder and rapid change of the positions of solvent molecules.

Extending the capability of the QM/MM-FE approach thus requires eliminating the conformational dependence of the reaction path. To do so, a naïve approach would be to carry out a set of several QM/MM-FE simulations with different starting conformations and then average over the individual simulation results. Although logically sound, this idea becomes practically intractable for two reasons. First, when the MM environments undergo significant conformational change during the reaction process, there is no guarantee that a converged reaction path can be obtained for given starting conformations. Second, averaging over results of a set of simulations is not trivial, because proper weighting is required for each simulation. To make the result meaningful, a rigorous theory is required to guide the selection of starting structures and the averaging of results. This theory is currently lacking.

To solve this problem, the conformational dependence of the QM/MM-FE method must be traced back to its origin. Like many other ab initio QM/MM methods, the potential energy surface is sampled first in the QM/MM-FE method, and the free energy profile is built afterwards for selected points on that energy surface. Consequently, the results depend on the selection of the initial conformation whose energy surface is used for reaction path optimization. To remove this dependence, the reaction path must be determined on a free energy surface in which the contributions of the MM conformations are appropriately included by ensemble averaging. The choice of an initial conformation thus becomes irrelevant in constructing the reaction path. Optimizing the reaction path on the free energy surface also possesses another advantage. That is, the interpretations of experimental studies are primarily based on classical transition state theory which relates the reaction rate constant with the free energy change. Thus, a theoretical free energy description of the reaction process correlates naturally with experimental study. In other words, the reaction path is computed on the free energy surface so that there is no need to map between different surfaces; the structures of the reactant state, transition state, and product state determined in this manner genuinely match the definitions in the classical transition state theory. For this purpose, methods for sampling the free energy surface of the reaction system must be developed.

Simulation methods have been proposed for exploring the free energy (as opposed to the potential energy) reaction path for small molecular reaction systems in gas phase, since the calculation of the free energy is achievable for those systems even with high level QM methods.^48–50 In this case, the full system is treated quantum mechanically and the free energy is simulated with the “brute-force” approach, i.e., direct sampling of the phase space of the entire QM/MM system. The free energy path is determined with the assistance of a pre-defined reaction coordinate. It is obvious that such methods cannot be applied to reactions in condensed phases for which the direct phase space sampling of the QM system is prohibitive. For those complicated reaction systems, methods have been proposed to explore the free energy surface of the system under the QM/MM framework, mainly with semi-empirical QM methods.^51–55 Applications have been reported, but are limited mainly to the optimization of the transition state structure of aqueous reactions. Thus, a complete, practical, and effective treatment based on ab initio quantum mechanics is still lacking.

We develop here an ab initio QM/MM minimum free energy path (QM/MM-MFEP) method to achieve dual goals in a single simulation, i.e., optimization of the reaction path on a free energy surface and calculation of the free energy profile of the reaction process. The essence of this method is to calculate the reaction path on the PMF surface of the QM/MM system. To accomplish these goals, we develop formulas to compute both the free energies and the free energy gradients of the system so that we are able to use all the degrees of freedom of the QM subsystem to define the reaction coordinate and hence optimize the reaction path and calculate the associated free energy changes. The relative free energies between different QM conformations are computed by the QM/MM-FE approach previously developed in our laboratory; the free energy gradients of the QM subsystem are computed through molecular dynamics sampling of the MM environment. The reaction path is then optimized by means of a chain-of-conformation approach. Compared with other approaches, this method has several distinct features: it drastically minimizes the computational need of the QM calculations which then allows the use of very accurate high-level QM method; it uses all of the QM degrees of freedom to define the reaction coordinate which relieves the bias from improper choice of reaction coordinate; it naturally generates a one-dimensional reaction profile without the need of converting from a high-dimensional potential energy surface; most importantly, the reaction path is optimized on the free energy surface, thus there is no longer a dependence on the choice of the initial molecular conformations.

The paper is organized as follows: We will first review the QM/MM approach with approximate QM/MM electrostatic interactions. We will then show how to approximate the free energy as a function of the degrees of freedom of a selected subset and how to calculate the free energy gradients which allows conformation/path minimization on a free energy surface. With the QM/MM free energy perturbation approach, we then show how to optimize the reaction free energy path with available chain-of-conformation methods such as the nudged elastic band (NEB) method,⁵⁶ the Ayala-Schlegel second order minimal energy path (MEP) method,⁵⁷ both having been adapted and extended by our laboratory for application to QM/MM simulations of large and complex systems.^{10, 58} We can also use most recent and very efficient quadratic string method (QSM)⁵⁹ for reaction path determination. We further introduce a RPP method² using the mean-field approximation for the contribution of the effects of the MM environment. Finally, we present an application of this method to the first step of the reaction catalyzed by triosephosphate isomerase (TIM).

Theory

QM/MM Hamiltonian with ESP charge simplification

For simulating complex reaction processes in the condensed phase, we describe a reaction system by the combined QM/MM approach: we select a small structural part of the system to be described by the QM method and the rest by an MM force field. The total energy of the whole system is then

$$E({\mathit{r}}_{QM},{\mathit{r}}_{MM})=E_{QM}({\mathit{r}}_{QM})+E_{QM/MM}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{MM}({\mathit{r}}_{MM})$$ (1)

where r_QM and r_MM represent the coordinates of the QM and MM subsystems, respectively. The three terms on the right hand side are the quantum mechanical energy of the QM subsystem, the interaction between the QM and MM subsystems, and the molecular mechanical energy of the MM subsystem, respectively. The interaction between the QM and MM parts is comprised of electrostatic, van der Waals, and covalent QM/MM link terms. The bonds connecting the QM and MM parts, which are usually present in enzymatic reaction system, are described by the pseudobond method.⁴² Thus, one can decompose the total energy of the system into the sum of different components as

$$E({\mathit{r}}_{QM},{\mathit{r}}_{MM})=E_{QM}({\mathit{r}}_{QM})+E_{\mathit{QMMM},\mathit{ele}}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{\mathit{QMMM},\mathit{vdw}}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{\mathit{QMMM},cov}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{MM}({\mathit{r}}_{MM})$$ (2)

The first two terms on the right hand side, the QM energy and the electrostatic interactions between the QM and MM parts, are obtained together via a combined QM/MM Hamiltonian in a self-consistent electronic structure calculations. In order to calculate the free energy, we follow the QM/MM-FE approach developed previously,¹ and make an approximation here that the QM/MM interaction can be further decomposed as

$$\begin{array}{l}{E}_{QM}({\mathit{r}}_{QM})+E_{\mathit{QMMM},\mathit{ele}}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{QM}^{\prime }({\mathit{r}}_{QM})+\sum _{j\in MM}\sum _{i\in QM}\frac{q_j{Q}_i}{\mid {\mathit{r}}_i-{\mathit{r}}_j\mid }\\ =E_{QM}^{\prime }({\mathit{r}}_{QM})+E_{\mathit{QMM},\mathit{ele}}^{\prime }({\mathit{r}}_{QM},{\mathit{r}}_{MM})\end{array}$$ (3)

where q and Q are the point charges of the MM and QM atoms, respectively. The former is taken from the MM force field, and the latter must be determined by fitting the ESP from QM calculations^{60, 61} in a proper MM environment. The underlining assumption here is that the fluctuation of the electrostatic potential of the QM subsystem caused by the fluctuation of the MM conformations can be neglected because it is small compared to the magnitude of the QM electrostatic potential. It should be noted that the QM electrostatic potential has already been polarized by the MM environment at a well-defined conformational state. This assumption can be further improved as discussed later. When the geometry of the QM subsystem is frozen and the MM subsystem is fluctuating, as in the case of the QM/MM-FE approach, it is not efficient to calculate the ESP charges for every MM conformation. On the other hand, QM ESP charges determined in a single MM environment are strongly influenced by the particular MM conformation, so the use of this set of QM ESP charges in the calculation of the electrostatic interactions with other MM conformations will thus be biased.

To reduce this bias in the original QM/MM-FE approach, we develop here the following strategy: we will use the mean field of the electrostatic potential from the MM subsystem to generate the QM ESP charges. That is, given multiple MM conformations, the effective way to determine the best set of ESP charges would be to use the mean electrostatic field of the MM conformations. The QM Hamiltonian is then

$$H=H_{QM}({\mathit{r}}_{QM})+\frac{1}{N}\sum _{n=1}^N\sum _{j\in MM}\sum _{i\in QM}\frac{q_j}{\mid {\mathit{r}}_i-{\mathit{r}}_{n,j}\mid }$$ (4)

where N is number of MM conformations recorded in the trajectory, r_n,j represents the coordinates of MM atom j of the n-th MM conformation. Within this averaged electrostatic field, the wave function of the QM system is solved and ESP charges are obtained. For this scheme, the best way to determine the QM ESP charges will be an iterative self-consistent approach: starting from a set of ESP charges (from a single MM conformation perhaps), sample the MM conformations by molecular dynamics (MD) or Monte Carlo (MC) simulation and record the trajectories, calculate the ESP charges using the mean electrostatic field from trajectories as in Eq. 4, and repeat the MM sampling and recalculate the ESP charges until they are converged. In practice we have found that the ESP charges from a short MD simulation of the MM subsystem are usually acceptable and we therefore did not pursue this self-consistent scheme any further. This simplified QM/MM approach with ESP charges solved within the mean-field approximation now provides us a feasible force field for efficient simulation of the reaction system.

Potential of Mean Force of the QM Coordinates

For calculating thermodynamic properties, an accurate force field and a converged phase space sampling are both necessary. For a complex system of interest, e.g., a chemical reaction in solution or an enzyme, the enormous number of degrees of freedom makes it inefficient and often impossible to treat the whole system with high accuracy. An effective scheme would involve focusing on a small number of degrees of freedom thought to be the most important to the reaction process, and modeling the remaining contributions by a simplified description. Therefore, we would expect to reach a balance between accessible precision and affordable complexity by combining fine and coarse grained methods together. This idea of combining theories of different levels has been proposed and applied in many ways in the simulation studies. For instance, the hybrid QM/MM method is an implementation of this idea in the construction of simulation force field and its effectiveness is well appreciated. Likewise, one would also like to seek a simplified thermodynamic description of the system based only on a small number of important degrees of freedom. This is toward the potential of mean force description of a reaction system in which the contribution of a large number of less important degrees of freedom have been ensemble-averaged out in the free energy expression of the whole system. It is obvious that such a PMF description of the reaction system bears two advantages compared with conventional approaches based on the exploration of the potential energy surface: the state of the system is consistently defined in a much simpler way without the complications from the environment, and the thermodynamic properties are genuinely obtained without extra effort. There have been applications reported for the sampling of PMF surfaces, either for small molecular systems in gas phase,^48–50 or for systems in the condensed phase but with simplified QM approaches.^51–55.

Here, we focus on the calculation of such a PMF with ab initio QM/MM methods. We derive below a PMF description of a reaction system within the QM/MM framework, although the theory is not dependent on the QM/MM method. The partition function of a QM/MM system is

$$Z_0=\int exp(-\beta E({\mathit{r}}_{QM},{\mathit{r}}_{MM}))d{\mathit{r}}_{QM}^{M}d{\mathit{r}}_{MM}^{M\prime }$$ (5)

in which E is the total energy of the system as a function of both r_QM and r_MM; M and M′ represent the number of degree of freedom of the QM and MM subsystems, respectively. The free energy of the system is then

$$A_0=-\frac{1}{\beta }ln(Z_0)$$ (6)

If we focus on the conformation of a selected subset of the system, e.g., the QM subsystem, we have a free energy expression of r_QM which is also regarded as a potential of mean force of r_QM, that is,

$$\begin{array}{l}{Z}_0({\mathit{r}}_{QM})=\int exp(-\beta E({\mathit{r}}_{QM},{\mathit{r}}_{MM}))d{\mathit{r}}_{MM}^{M\prime }\\ A_0({\mathit{r}}_{QM})=-\frac{1}{\beta }ln(Z_0({\mathit{r}}_{QM}))\end{array}$$ (7)

The integration of the potential of mean force in the r_QM space recovers the complete free energy of the system:

$$A_0=-\frac{1}{\beta }ln\left[\int exp(-\beta A_0({\mathit{r}}_{QM}))d{\mathit{r}}_{QM}\right]$$ (8)

With the MM contributions averaged out, the conformational space of the whole reaction system has been reduced to the potential of mean force surface of the QM subsystem. The problem of determining the reaction path and the activation free energy in a very complicated phase space of the whole system becomes a greatly simplified problem of exploring the PMF surface of the QM degrees of freedom.

Before proceeding, we like to make two comments on this PMF expression. First, with the assumption of the ergodicity of MD (MC) simulation, this PMF surface takes into account the complete thermodynamic contribution of the MM environment, while the direct dynamic (thermal) contribution of the QM part is not considered. For the latter term, the only rigorous way to compute is direct ab initio QM sampling, which is obviously too expensive to accomplish in the near future. However, with the equations derived below, one may either estimate the contribution of the dynamics of the QM part by computing the (thermodynamic) frequencies of the QM subsystem, or employing the reaction path potential method to carry out synergized dynamics sampling between the QM and MM parts. Second, in this expression, the reaction coordinate is defined in Cartesian space. Of course one can use more general geometrical coordinates to describe the reaction process and derive correspondingly the PMF expression for those coordinates. However, as we will discuss in later sections, cautions need to be taken to handle the mass-metric term which requires the evaluation of the inertial forces.

To sample the PMF surface of the QM conformation, the gradients for the PMF surface, i.e., the derivatives of the PMF with respect to the coordinates of the QM subsystem must be calculated. The free energy gradient acting on QM atom i is computed as.

$$\begin{array}{l}\frac{\partial A_0({\mathit{r}}_{QM})}{\partial {\mathit{r}}_{QM,i}}=\frac{\partial \left[-\frac{1}{\beta }ln(Z_0({\mathit{r}}_{QM}))\right]}{\partial {\mathit{r}}_{QM,i}}\\ =\frac{\int \frac{\partial E({\mathit{r}}_{QM},{\mathit{r}}_{MM})}{{\partial \mathit{r}}_{QM,i}}exp(-\beta E({\mathit{r}}_{QM},{\mathit{r}}_{MM}))d{\mathit{r}}_{MM}^{M\prime }}{Z_0({\mathit{r}}_{QM})}\\ ={\langle \frac{\partial E({\mathit{r}}_{QM},{\mathit{r}}_{MM})}{\partial {\mathit{r}}_{QM,i}}\rangle }_{{\mathit{r}}_{MM}}\end{array}$$ (9)

where the bracket represents ensemble averaging and the subscript r_MM represents an ensemble of MM conformations. Therefore, the gradient of the PMF is in fact an ensemble average of the gradients of the QM atoms, which must be evaluated by sampling the phase space of the MM subsystem with the QM conformation frozen. Similarly, when the second derivatives (i.e. Hessian) of the QM atoms are desired for computing the entropic contributions, for example, the formula is

$$\frac{{\partial }^2{A}_0({\mathit{r}}_{QM})}{\partial {\mathit{r}}_{QM,i}\partial {\mathit{r}}_{QM,j}}={\langle \frac{{\partial }^{2}E}{\partial {\mathit{r}}_{QM,i}\partial {\mathit{r}}_{QM,j}}\rangle }_{r_{MM}}-\beta \left[{\langle \frac{\partial E}{\partial {\mathit{r}}_{QM,i}}\frac{\partial E}{\partial {\mathit{r}}_{QM,j}}\rangle }_{r_{MM}}-{\langle \frac{dE}{d{\mathit{r}}_{QM,i}}\rangle }_{r_{MM}}{\langle \frac{dE}{d{\mathit{r}}_{QM,j}}\rangle }_{r_{MM}}\right]$$ (10)

To implement the calculation of the PMF force, we take the expression of the QM/MM energy as defined in Eq. 2 and also assume the QM density is frozen as defined in Eq. 3. The force is then

$$\frac{\partial A_0({\mathit{r}}_{QM})}{\partial {\mathit{r}}_{QM,i}}=\frac{\partial E_{QM}^{\prime }({\mathit{r}}_{QM}^0)}{{\partial \mathit{r}}_{QM,i}^0}+{\langle \frac{\partial E_{\mathit{QMMM},\mathit{ele}}^{\prime }({\mathit{r}}_{QM}^0,{\mathit{r}}_{MM})}{{\partial \mathit{r}}_{QM,i}^0}+\frac{\partial E_{\mathit{QMMM},\mathit{vdw}}({\mathit{r}}_{QM}^0,{\mathit{r}}_{MM})}{{\partial \mathit{r}}_{QM,i}^0}+\frac{\partial E_{\mathit{QMMM},\mathit{cova}}({\mathit{r}}_{QM}^0,{\mathit{r}}_{MM})}{{\partial \mathit{r}}_{QM,i}^0}\rangle }_{{\mathit{r}}_{MM}}$$ (11)

Accordingly, the second derivatives are written as

$$\begin{array}{l}\frac{{\partial }^2{A}_0({\mathit{r}}_{QM})}{\partial {\mathit{r}}_{QM,i}\partial {\mathit{r}}_{QM,j}}=\frac{{\partial }^2{E}_{QM}}{\partial {\mathit{r}}_{QM,i}\partial {\mathit{r}}_{QM,j}}{\langle \frac{{\partial }^2{E}_{QM/MM}}{\partial {\mathit{r}}_{QM,i}\partial {\mathit{r}}_{QM,j}}\rangle }_{r_{MM}}\\ -\beta \left[{\langle \frac{\partial E_{QM/MM}}{\partial {\mathit{r}}_{QM,i}}\frac{\partial E_{QM/MM}}{\partial {\mathit{r}}_{QM,j}}\rangle }_{r_{MM}}-{\langle \frac{\partial E_{QM/MM}}{\partial {\mathit{r}}_{QM,i}}\rangle }_{r_{MM}}{\langle \frac{\partial E_{QM/MM}}{\partial {\mathit{r}}_{QM,j}}\rangle }_{r_{MM}}\right]\end{array}$$ (12)

The availability of the first and second derivatives allows us to explore the phase space of the QM subsystem much more efficiently by conventional methods such as energy minimization and MD.

Reaction Path Minimization

Eq. 7 essentially represents a multi-dimensional PMF: additional procedures are required to convert it into the quantity (activation free energy) directly measured in experiments, which consisted of one and only one canonical order parameter to characterize the reaction progress. Therefore, to employ this equation in the QM/MM free energy simulation of the reaction process, a proper set of (Cartesian or internal) geometric or energetic coordinates is usually identified such that their combination closely mimics the canonical order parameter. This set of coordinates is commonly known as the reaction coordinate. In practice, the determination of the reaction coordinate is non-trivial, especially for many complicated reactions catalyzed by enzymes. Instead of choosing a reaction coordinate more or less arbitrarily and always bearing the risk of it being incomplete or inappropriate,⁶² we allow the reaction coordinate to be described by the coordinates of the entire QM subsystem, which eliminates the risk of it being improperly defined to the largest extent possible. Moreover, to efficiently employ the QM coordinates as the reaction coordinate, we select a series of discrete conformations parallel to the reaction process. The distance vectors between two adjacent conformations are used as a local reaction coordinate; while many local reaction coordinates are pieced together to constitute the global reaction coordinate. The chain of conformations is then optimized by means of well-established methods^{43, 56–59} with the free energy profile of the reaction process determined simultaneously via FEP.

To carry out the minimization for a chain of conformations efficiently, the free energy gradients, and maybe even the second derivatives, must be computed for the individual QM conformations. The relative free energies between adjacent QM conformations must also be computed. The former step is achieved by Eqs. 11 and 12, while the latter may be performed by using previously developed QM/MM-FE methods.¹ In this method, the free energy difference ΔA between two adjacent QM conformations is computed as

$$\mathrm{\Delta }{A}_{i\to j}=-\mathit{kT}ln{\langle exp(-\mathrm{\Delta }{E}_{i\to j}/kT)\rangle }_i$$ (13)

where the subscripts i and j are the indices of two adjacent conformations, the brackets represent an

$$\mathrm{\Delta }{E}_{i\to j}=E_j-E_i$$ (14)

We now outline our QM/MM-MFEP method as follows

1. Generate an initial set of discrete conformations for the QM subsystem connecting the reactant state to the product state using any interpolation scheme. Relax the MM environment for each QM conformation, if necessary. These intermediates states, plus the reactant and product states, form a chain of conformations.

2. For each conformation, compute the QM energy, ESP point charges, and forces for the QM subsystem using a standard QM/MM scheme.

3. Perform an MD simulation on the MM subsystems of each image with the QM conformations frozen. The QM/MM interactions employed in MD simulation are described by Eq. 3. During each MD step, the QM/MM forces on the QM atoms and the energy differences between a given QM conformation and its adjacent QM conformation(s) are computed and recorded for computing the free energy difference.

4. After a period of MD simulation, calculate the free energy difference between two adjacent conformations, as well as the free energy forces. Then apply one step of coupled optimization with a method such as NEB, Ayala-Schlegel MEP, or QSM to optimize all conformations on the chain.

5. Exit the optimization process if the path is converged by the pre-defined criteria. Otherwise, go to step 2 and continue for another cycle.

As discussed in previous sections, to obtain the highest quality ESP charges, the best approach would be to repeat steps 2 and 3 in an iterative, self-consistent manner. However, in practice we have found that ESP charges obtained after one MD simulation are accurate enough for future calculations. To reduce the computational time required, we have also made the approximation of using the MM conformations sampled during the MD simulation of the previous minimization step as the electrostatic background for the QM calculation, instead of self-consistently calculating them during the current minimization step. In practical simulations where the step size of the optimization can be controlled, we have found that this approximation works effectively (Data not shown).

Since one minimization cycle of the QM/MM-MFEP method consists of only one QM energy and force calculation, a certain length of MD simulation, and a single optimization step, the computational need for the QM calculations has been significantly reduced. The time spent on the QM calculations becomes minor compared to that of the MD simulations. For a typical QM/MM simulation of an enzyme reaction, the number of QM atoms is usually on the order of 10¹ ~ 10², while the number of MM atoms varies drastically between 10⁴ and 10⁶. In such a case, one ordinary hybrid DFT such as B3LYP^{63, 64} calculation with a double-zeta basis set for the QM subsystem takes only minutes to a few hours, while the MD simulation of 10² ps will take several tens of CPU hours. Because the MD simulation competes as the computational bottleneck and the time required for the QM calculation is relatively small, very high level ab initio QM methods may be used to improve the accuracy. On the other hand, the MD simulations may be carried out with well-established parallel algorithms to speed up the MD sampling.

To facilitate the convergence of the reactant path optimization, it appears to be practically more efficient if the reactant and product states are optimized prior to the iterative MD sampling/optimization procedure and their QM conformations frozen during the subsequent path optimization process.

Reaction Path Potential with a Mean MM Field

In the QM/MM-MFEP method, the QM subsystem is frozen for reducing the computational cost of the QM calculations. This treatment essentially removes the dynamics of the QM part and decouples any possible dynamic correlation between the active site and the conformational change of the enzyme environment. However, it should be noted that the coupling between the chemical reaction process and the large amplitude conformational motion of the enzyme can be seamlessly interfaced with the QM/MM-MFEP method (Hu et al., unpublished). Therefore, the only approximate term is the harmonic approximation of the QM subsystem. Since the details of the dynamics of the QM active site associate directly to the question of whether or not the enzyme achieves its catalytic function through coupling between the dynamics of the active site and other structural components, it is very important to simulate the dynamics of the QM subsystem.

In order to achieve the goal of QM dynamic sampling with a computationally affordable approach, we extend the previously developed RPP method² in the framework of a mean-field approach. The RPP originates from the idea of the reaction path Hamiltonian,⁶⁵ which expands the exact quantum mechanical Hamiltonian of a reaction system to different orders of perturbations, thus allowing the inexpensive yet accurate calculation of energetics for the region of phase space around the reaction path. In our method, the QM subsystem is spatially embedded in a buffer of atoms sampled during MD simulation. That is, the QM subsystem experiences the mean field of the MM environment. For each QM atom α, the external electrostatic field is

$${\nu }_{MM}({\mathit{r}}_{\alpha })=\frac{1}{N}\sum _{n=1}^N\sum _{m=1}^{M_n}\frac{q_m}{r_{\alpha m}}$$ (15)

where r_a represents the coordinates of QM atom α, N is the number of snapshots recorded during MD simulation, M_N is the number of MM atoms recorded in the N-th snapshot, q_m is the atomic charge of MM atom m, and r_am is the distance between MM atom m and QM atom α. Because the changes of the ESP-fitted charges of the QM atoms can be represented by the response to the perturbations, by truncating the response to the first order of perturbations, we can calculate the change of the ESP charges with respect to the changes in the geometries and external electrostatic potentials. To do so, we compute two response kernels for the QM atoms, namely, the changes of the QM ESP charges in response to the change of the external electrostatic potential

$${\chi }_{\alpha \beta }={\left(\frac{\partial Q_{\alpha }}{\partial {\nu }_{\beta }}\right)}_N$$ (16)

and the changes of the QM ESP charges in response to changes in the QM geometries

$${\kappa }_{\alpha \beta }={\left(\frac{\partial Q_{\alpha }}{\partial {\mathit{r}}_{\beta }}\right)}_N$$ (17)

where Q_α is the ESP-fitted change of QM atom α, ν_β is the mean electrostatic potential of QM atom β defined in Eq. 15, and the subscript N defines the constraint that the number of electrons must remain constant N. The first response kernel χ_αβ was introduced by Kato and coworkers,⁶⁶ and the second kernel κ_αβ by our group.² With these response properties, the polarized charge of QM atom α is computed as

$$Q_{\alpha }(\mathit{r},{\nu }_{MM})=Q_{\alpha }^{\mathit{ref}}+\sum _{\beta \in QM}{\chi }_{\alpha \beta }[{\nu }_{MM}({\mathit{r}}_{\beta }^{\mathit{ref}})-{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\beta }^{\mathit{ref}})]+\sum _{\beta \in QM}{\kappa }_{\alpha \beta }[{\mathit{r}}_{\beta }-{\mathit{r}}_{\beta }^{\mathit{ref}}]$$ (18)

The superscript ref designates the reference state in the absence of the perturbation. The electrostatic interaction between the QM and MM subsystems is the simple Coulombic interaction between point charges

$$E_{\mathit{QMMM},\mathit{ele}}^{\mathit{ESP}}=\sum _{m\in MM}\sum _{\alpha \in QM}\frac{q_m{Q}_{\alpha }(\mathit{r},{\nu }_{MM})}{\mid {\mathit{r}}_{\alpha }-{\mathit{r}}_m\mid }=\sum _{\alpha \in QM}{Q}_{\alpha }(\mathit{r},{\nu }_{MM}){\nu }_{MM}({\mathit{r}}_{\alpha })$$ (19)

The intenial energy of the QM sub system is defined as

$$E_1({\mathit{r}}_{QM},{\nu }_{MM})=\langle \mathrm{\Psi }\mid H_{\mathit{eff}}\mid \mathrm{\Psi }\rangle -E_{\mathit{QMMM},\mathit{ele}}^{\mathit{ESP}}$$ (20)

which can be computed as²

$$\begin{array}{l}{E}_1({\mathit{r}}_{QM},{\nu }_{MM})=E_1({\mathit{r}}_{QM}^{min},{\nu }_{MM}^{\mathit{ref}})\\ +\sum _{\alpha \in QM}\left({\frac{\partial \langle \mathrm{\Psi }\mid H_{\mathit{eff}}\mid \mathrm{\Psi }\rangle }{\partial {\mathit{r}}_{\alpha }}\mid }_{{\mathit{r}}_{QM}^{min},{\nu }_{MM}^{\mathit{ref}}}-\sum _{\beta \in QM}{\kappa }_{\beta \alpha }{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\beta }^{min})-Q_{\alpha }^{min}\frac{\partial {\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\alpha }^{min})}{\partial {\mathit{r}}_{\alpha }^{min}}\right)\mathrm{\Delta }{\mathit{r}}_{\alpha }\\ +\frac{1}{2}\sum _{\alpha ,\beta \in QM}\mathrm{\Delta }{\mathit{r}}_{\alpha }\left({\frac{{\partial }^2\langle \mathrm{\Psi }\mid H_{\mathit{eff}}\mid \mathrm{\Psi }\rangle }{\partial {\mathit{r}}_{\alpha }\partial {\mathit{r}}_{\beta }}\mid }_{{\mathit{r}}_{QM}^{min},{\nu }_{MM}^{\mathit{ref}}}-{\kappa }_{\alpha \beta }\frac{\partial {\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\alpha }^{min})}{\partial {\mathit{r}}_{\alpha }^{min}}-{\kappa }_{\beta \alpha }\frac{\partial {\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\beta }^{min})}{\partial {\mathit{r}}_{\beta }^{min}}-Q_{\alpha }^{\text{min}}\frac{{\partial }^2{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\alpha }^{min})}{\partial {\mathit{r}}_{\alpha }^{min}\partial {\mathit{r}}_{\beta }^{min}}{\delta }_{\alpha \beta }\right)\mathrm{\Delta }{\mathit{r}}_{\beta }\\ -\sum _{\alpha \in QM}\sum _{\beta \in QM}{\chi }_{\alpha \beta }{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\alpha }^{min})[{\nu }_{MM}({\mathit{r}}_{\beta }^{min})-{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\beta }^{min})]\\ -\frac{1}{2}\sum _{\alpha \in QM}\sum _{\beta \in QM}[{\nu }_{MM}({\mathit{r}}_{\alpha }^{min})-{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\alpha }^{min})]{\chi }_{\alpha \beta }[{\nu }_{MM}({\mathit{r}}_{\beta }^{min})-{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\beta }^{min})]\\ -\sum _{\alpha \in QM}\sum _{\beta \in QM}({\mathit{r}}_{\alpha }-{\mathit{r}}_{\alpha }^{min})\frac{\partial {\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\alpha }^{min})}{{\partial \mathit{r}}_{\alpha }^{min}}{\chi }_{\alpha \beta }[{\nu }_{MM}({\mathit{r}}_{\beta }^{min})-{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\beta }^{min})]\end{array}$$ (21)

That is, the energy is expanded to second order of perturbations around the initial conformation (denoted as ${\mathit{r}}_{QM}^{min}$) and the initial electrostatic potential it bears denoted as ${\nu }_{MM}^{\mathit{ref}}$). With the definitions of Eq. 18 and 19, the total energy of the system is then defined in a similar manne 150r to Eq. 2 as

$$E_{\mathit{RPP}}=E_1({\mathit{r}}_{QM},{\nu }_{MM})+E_{\mathit{QMMM},\mathit{ele}}^{\mathit{ESP}}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{\mathit{QMMM},\mathit{vdw}}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{\mathit{QMMM},\mathit{cov}}({\mathit{r}}_{QM},{\mathit{r}}_{MM})+E_{MM}({\mathit{r}}_{MM})$$ (22)

The derivation of the RPP allows dynamic sampling of the QM subsystem without the need for expensive QM calculations at every step, and also allows the direct simulation of the free energy difference between different conformational states through well-established classical or quantum free energy simulation techniques.^{44, 45}

Simulation Details

To examine the validity and effectiveness of the minimum free energy path method proposed here, we have studied the first reaction step catalyzed by the enzyme TIM. As shown in Figure 1, the reaction involves a proton transfer from the substrate to the sidechain carboxylate group of Glu 164. This reaction step has been studied many times previously.^{1, 2, 7} Since our intention here is to examine the applicability of the QM/MM-MFEP method, we have carried out the simulation under a setup similar to studies previously reported.

Figure 1.

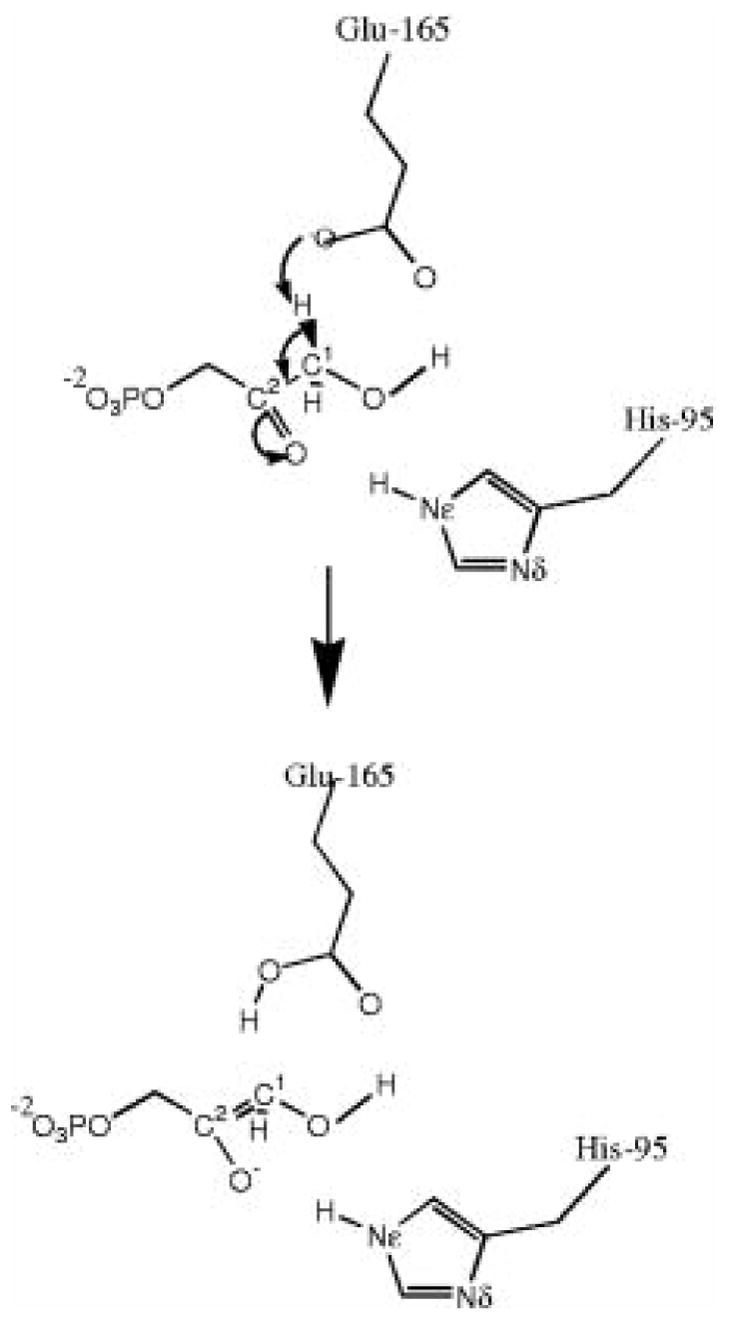
Active site and the reaction catalyzed by the enzyme triosephosphate isomerase (TIM).

For this system, all protein atoms were included in the simulation, and a solvation sphere of 21 Å was created around the C1 atom of the substrate molecule. Any residues or water molecules in which all atoms are greater than 16 Å away from all atoms of the substrate were restrained by a harmonic force of 10 kcal mol⁻¹ Å⁻² with respect to their initial minimized positions. A flat-bottomed restraint was added to all free water molecules to prevent them from crossing the restrained shell of atoms and escaping into the vacuum space. This restraint potential takes no effect until the distance between a specific water molecule and the C1 atom of the substrate is greater than 16.5 Å. The final system was comprised of 6618 atoms, of which 3795 belong to the protein and the substrate molecule, and 2823 belong to the 941 water molecules.

The parameters of the AMBER force field⁶⁷ incorporated into the TINKER program⁶⁸ were used to model the classical MM interactions. In all simulations, a dual cutoff of 9 and 15 Å was used to separate the short- and medium-range interactions. The non-bonded pair lists were updated every 16 fs. The multi-timestep method was used for integration,^{69, 70} with time steps of 1 and 4 fs for the short- and medium-range forces, respectively. The temperature of the system was kept at 300 K by a Berendsen thermostat.⁷¹ The medium-range QM/MM electrostatic interactions were modeled as pure classical interactions between the ESP point charges on the QM atoms and the point charges on the MM atoms; only the short-range neighboring MM atoms were included in the quantum mechanical calculation for the energy, gradient, and ESP charges. In other words, only the polarization effects from the short-range MM atoms were considered for the QM atoms.

The MD simulations and minimizations were carried out with the program Sigma,^72–74 which was interfaced with Gaussian 03³⁴ for performing the QM calculations. For the QM calculations, the HF/3-21G method was used while the QM/MM hybrid bonds were modeled with the pseudobond method.⁴² These choices were made for ease of comparison with previous studies, with no attention paid to the effect of the level of theory and basis set on the actual reaction mechanism.

For this model reaction system, the initial structures of the reactant and product states were obtained from previous studies.^{1, 2} The reaction process was modeled by linear interpolation between the reactant and product geometries to yield 13 intermediate conformational states. These 15 structures were used for all optimization and simulation studies. As described in the methods section, the QM part was frozen during the dynamics sampling of the MM part, i.e., their positions are not changing, and their velocities are set to zero. The SHAKE algorithm⁷⁵ was completely turned off for the protein molecule, which means the interactions of all protein bonds were explicitly computed, including the crossing bonds between the QM and MM atoms.

Beginning from the interpolated structures, the reaction path was determined by a three-stage optimization: standalone free energy minimization of the reactant and product states, NEB optimization,⁵⁶ and Ayala-Schlegel MEP optimization⁵⁷ on the QM/MM free energy surface.^{11, 43} After the first minimization step, the QM structures of the reactant and product states were kept frozen in the subsequent NEB and Ayala-Schlegel MEP optimizations.

All optimizations were carried out with the algorithm outlined in previous section. In general, each optimization cycle consists of one QM calculation which yields QM energies, gradients, and ESP charges, followed by MD simulations for calculating the free energy gradients of the QM subsystem and the free energy differences between adjacent conformations. After that, a optimization step is made on the basis of the free energies and the free energy gradients of the chain of conformations. The length of MD simulation in each optimization step has vital impact on the quality and efficiency of the global optimization process. Longer simulations yield better convergence of the energies and gradients. Because there is no easy and automated tool to determine the required length of the MD simulations, the convergence properties of the free energies and free energy gradients of each QM atom must be determined from trial simulations.

Nevertheless, to speed up the calculation, MD simulations of different lengths can be carried out in the NEB optimization process. In the current system, each NEB optimization step in the beginning stage consisted of one QM calculation followed by 40 ps of MD simulation for the computation of the free energies, free energy gradients. After 20 steps of optimization, the MD simulation time was extended to 80 ps for better convergence. An additional 40 steps of NEB optimization were then carried out and yielded a reaction path which was used as the input for the Ayala-Schlegel MEP optimization in the next stage. We observed slow convergence in the later stage of the NEB optimization, consistent with the observations of many others.

Starting from the last NEB path, Ayala-Schlegel MEP optimization was performed to determine the exact reaction path and most importantly, the structure of the transition state. In all MEP optimizations, the MD simulation time was 128 ps to ensure good convergence of the free energies and free energy gradients. The MEP convergence criteria were loosened to 1 × 10⁻³ hartree for energy and 1 × 10⁻³ hartree bohr⁻¹ for the gradients. Different sets of optimizations were carried out with different maximum step sizes, but all optimizations converged to nearly identical transition state structures and activation free energies.

After we obtained the exact MEP path, reaction path potential calculations with the mean-field approximation were carried out for the reactant state and the transition state, respectively, and each yielded an RPP function that allowed us to simulate the dynamics of the QM subsystem just as the same as carrying out ordinary MM simulations. The free energy difference between the transition state and the reactant state was then simulated by slow-growth free energy simulation method.^76–78

Results

All the optimization algorithms implemented here depend on the evaluation of the relative QM/MM free energies between different conformational states and the free energy gradients defined in Eq. 9. The convergences of both quantities are crucial for the effectiveness of the optimization process.⁷⁹ To demonstrate how the free energy gradients converge in a simulation, we plotted the evolution of the free energy gradient components of all QM atoms in a course of a simulation of 128 ps, (Figure 2) with first 12 ps disregarded as an equilibrium process. It was clear that most components achieved good convergences within 30 ps. After 80 ps, all components reached stable plateau. The free energy perturbations between different conformational states converged in general faster than the gradients. One in fact can examine the correctness of the free energy gradients by carrying out free energy perturbations with numerical differentiation of the QM coordinates.

Figure 2.

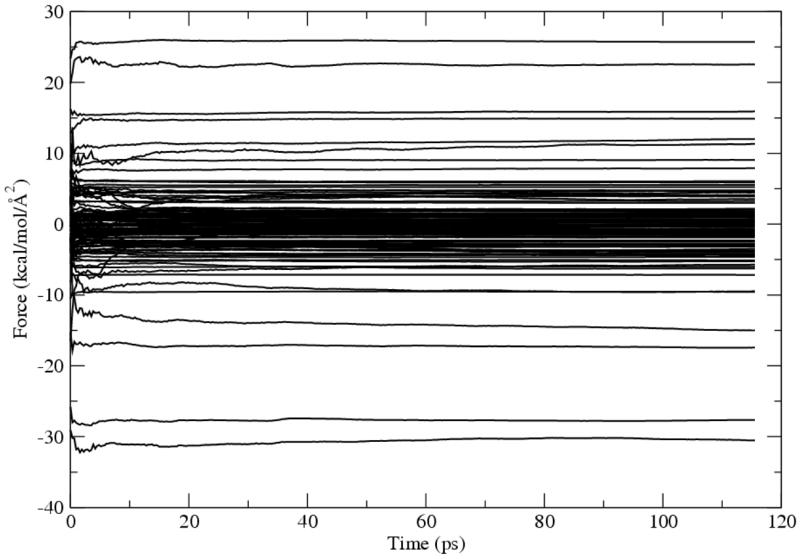
Convergences of the free energy gradients of all QM atoms in the TIM system. The X-axis is the simulation time, while the Y-axis is the free energy gradient defined in Eq. 9.

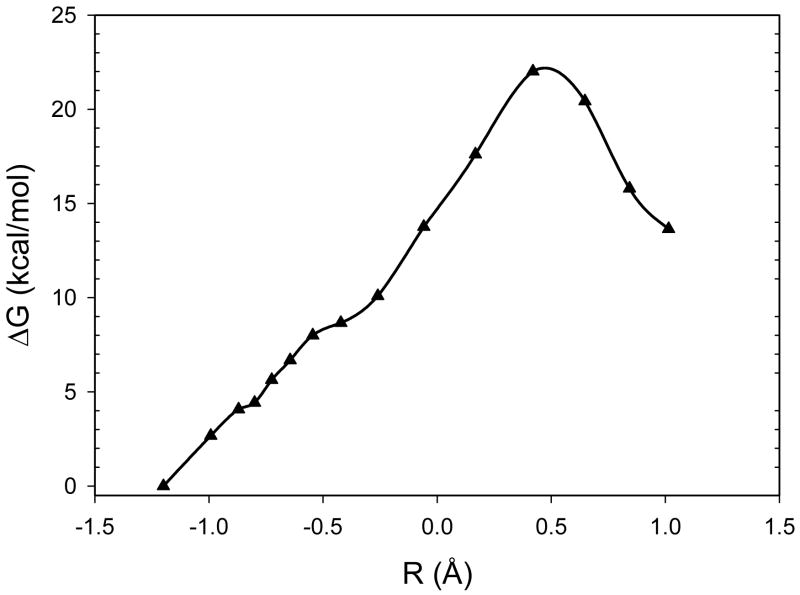
To illustrate the effectiveness of our approach, Figure 3 plots the final free energy profile for the NEB/FEP optimization. The final optimized activation free energies were 22.0 and 8.4 kcal mol⁻¹ for the forward and backward reactions, respectively. Not surprisingly, these numbers are larger than those of previously reported similar studies.^{1, 2} Since NEB converges very slowly when the path gets close to the exact path, it is very difficult to locate the exact reaction path and transition state. For this reason, we did not pursue other complicated NEB schemes to improve the accuracy of the results.

Figure 3.

Free energy profile from NEB optimization by the QM/MM-MFEP method for the proton transfer reaction in TIM. To make the results comparable to previous studies, the X-axis R is defined as the distance differences R_C–H – R_O–H, instead of the indices of the conformations used in the simulations.

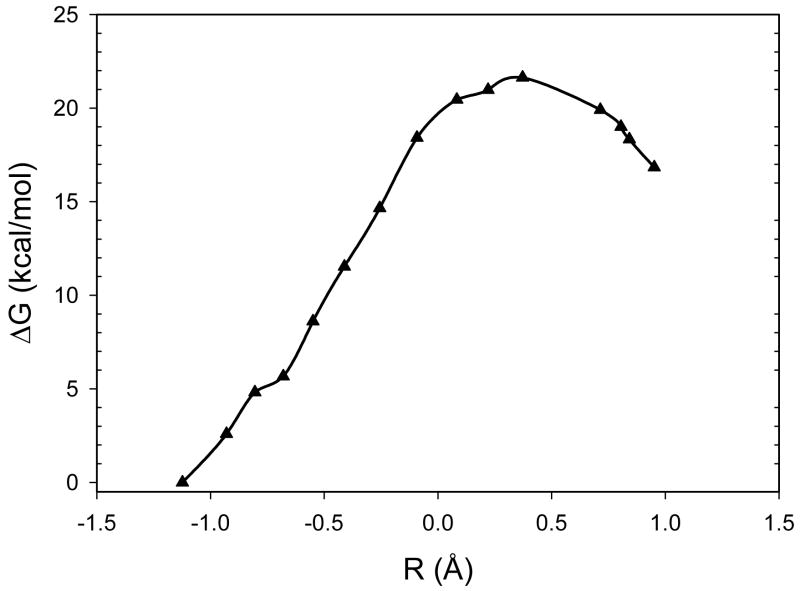
Figure 4 illustrates the free energy profile determined in the MEP/FEP optimizations. The activation free energies were 21.6 and 4.8 kcal mol⁻¹ for the forward and backward reactions, respectively. These values are close to what reported previously at the same QM level of theory. The structure of the transition state is also close to the one previously reported.¹ At the transition state, the difference between the C1-H1 and H1-O2 bond lengths was 0.37 Å. In previous studies, this distance difference was used as the reaction coordinate and was determined to be 0.4 Å at the transition state.

Figure 4.

Free energy profile from Ayala-Schlegel MEP optimizations by the QM/MM-MFEP method for the proton transfer reaction in TIM. The X-axis is defined in the same way as in Figure 2.

The free energy difference between the reactant state and the transition state was determined by the slow growth method with the reaction path potentials. The latter was computed from the reaction path optimized in the MEP/FEP simulations. The activation free energy was 19.8 kcal determined in this way. This value is slightly lower than those obtained previously. Such a difference may be attributed to the subtle difference between the reaction paths determined by different methods, or the longer MD relaxation of the MM environment in current study.

Discussion

Comparison with Related Studies on TIM

In current study, there is an apparent resemblance between the activation free energies obtained from NEB/FEP and MEP/FEP optimizations. It should be noted, however, that such a resemblance has no implications on the effectiveness of each method. Instead, it is well known that for complicated systems, the NEB method converges slowly and often fails to locate the exact position of the transition state. In addition to the slow convergence, the errors from two other known problems of the NEB method, straddling and corner-cutting the true transition state, tend to cancel out. As a result, the similar free energy barriers in both calculations come from the fact that the NEB optimization doesn’t locate the true transition state; otherwise, a higher barrier would be expected for the NEB method. It would be interesting to use the recently developed QSM method⁵⁹ which displays superlinear convergence and has been shown to be significantly more efficient than NEB.

For the model reaction step of TIM we have investigated here, the results of the present study are in good agreement with previous studies employing the same QM level of theory.^{1, 2} The structures of the reactant state, transition state, and product state are very similar to those previously obtained. The only notable difference is that the activation free energy of the forward reaction process obtained here is ~ 2 kcal mol⁻¹ lower than previous results. Several factors may contribute to this difference, including: extensive MD sampling of the enzyme MM subsystem in this study, minimization on the free energy surface rather than the potential energy surface. The fact that the structural differences between the current and previous studies are small tells us that the results from the current approach are consistent with previous work.

Compared with many other QM/MM simulation methods, the current QM/MM-MFEP method uses all of the QM degrees of freedom as a reaction coordinate, and thus does not require the explicit choice of the reaction coordinate prior to the simulation process. This considerably reduces the risk of incorrectly choosing the reaction coordinate, as it has been shown that improper choice of the reaction coordinate will bias the simulation and slow down the convergence.⁶² The problem of the inappropriate choice of the reaction coordinate is more severe in simulations using coordinate driving types of techniques in which the choice of the reaction coordinate not only strongly influences the ability to sample phase space correctly, but also causes technical difficulties when the changes of specific geometrical properties are stepwise or nonlinearly correlated. With the coordinates of the whole QM subsystem naturally utilized as the reaction coordinate, one no longer bears those problems.

Of course this method of constructing a reaction coordinate is an advantage but not a unique feature for the QM/MM-MFEP method. It is obvious that there is no need to explicitly specify the geometrical reaction coordinate in any QM/MM simulation of a reaction, as long as the global reaction coordinate is pieced together from a chain of conformations such as those implemented in the NEB, Ayala-Schlegel MEP, and QSM algorithms. On the other hand, the QM/MM-MFEP approach does not exclude the use of a well-defined reaction coordinate. If a reasonable reaction coordinate is available, one could by all means use this reaction coordinate in the QM/MM-MFEP simulation. In this situation, the known reaction coordinate will speed up the convergence of the free energy simulation, simplify the definition of the free energy gradients, and subsequently allow the use of other free energy simulation techniques.

The most important improvement of the QM/MM-MFEP approach compared with the original QM/MM-FE approach is that the results of the simulation no longer depend on the choice of the initial conformations, thus eliminating the bias from the initial structure. In many simulation methods previously proposed, including the QM/MM-FE method, the reaction path is usually determined with a static enzyme structure, i.e., on a single zero-temperature potential energy surface. Even though the enzyme structure is energetically minimized during the process of determining the reaction path, the configuration of the protein molecule is nearly immobile structurally, i.e. large-scale conformational changes such as domain motions or even the transition of sidechain rotamer states are almost completely prohibited. This dilemma causes two problems in the simulation of enzymatic reactions. On one hand, when specific MM groups undergo significant conformational change during the reaction process, it is technically difficult to obtain a converged reaction path. On the other hand, since in the native state an enzyme molecule can access an enormous number of conformational minima, choosing a particular minimum state will bias the results. According to the rigorous statistical mechanics principle, it is incorrect to use a reaction path obtained within one particular enzyme conformation to represent the thermodynamic behavior of the enzyme. Moreover, a reaction path determined on the zero-temperature potential energy surface is not the thermodynamic path as measured in experiments. Those problems were overcome by the QM/MM-MFEP method in a theoretically sounded way.

It may appear that the agreement between the results of the current and previous study is at odds with the idea that the results of QM/MM-FE method were strongly dependent on the choice of the initial structure model. It has been shown that this dependence can lead to some uncertainties in the simulation studies.⁴⁷ Since the dependence was removed in current approach, one is expected to see a clear difference between the current and previous results. To resolve this discrepancy, we note that the setup of the current model system does have a significant impact on the results. The numerous positional restraints applied to those atoms outside the active sphere of atoms to a large extent limits the sampling of phase space of the protein molecule, and subsequently the phase space of the QM atoms of the active site. In spite of these structural restraints, we still see a significant difference between the computed activation free energies of the potential energy and minimum free energy paths.

Connection to Previous Studies of Sampling the Free Energy Surface

The idea of representing the structural and thermodynamic properties of a molecular system in terms of the PMF surface of a few variables is a quite general idea in statistical mechanics.^{76, 80} Past simulation study often focused on building the PMF surface in simulations through various techniques such as umbrella sampling,²⁹ free energy perturbation,⁸¹ and thermodynamic integration.⁷⁶ Only recently it was proposed to explore the phase space of the system by directly walking the PMF surface.^52–55 Several groups have extended the theory and the simulation techniques, and have also reported several example applications to different reaction systems.^{48–50, 79} The work reported here should still be regarded as an important further improvement and enrichment of the idea because of several key differences between this work and those reported previously.

The QM/MM-MFEP method was built within the ab initio QM/MM framework, and thus is appropriate for simulating reaction processes in enzymes and in solution. In our method, the contribution of the MM environment has been explicitly considered. On the contrary, for other previously reported applications,^{48–50, 79} either the reaction process took place in the gas phase or semiempirical QM methods were used. Therefore, the QM/MM-MFEP is better suited for simulating complicated reaction systems with higher accuracy.

The difference in the means by which the reaction coordinate is chosen also results in different implementations of the free energy simulation approaches in the QM/MM-MFEP and other methods. In many other methods, the calculation of the free energy relies on the determination of a reaction coordinate which is usually defined as a set of geometrical variables. The free energy is computed by umbrella sampling or by computing the effective forces acting on the reaction coordinate, and then the work and/or the free energies along the reaction path are computed. Even though those approaches are still applicable in the QM/MM-MFEP method, our QM/MM model also allows the free energy to be computed through direct free energy perturbation on a chain of conformations. This provides additional flexibility when the reaction coordinate is not so easily defined by geometrical terms.

One more important improvement in the QM/MM-MFEP method is the application of the mean-field approximation. This approximation was used in modeling the electrostatic interactions from the MM environment to the QM system in both the optimization of the reaction path and the generation of the reaction path potential. The use of a mean MM field has improved the numerical stability and quality of the ESP charges, thus speeding up the convergence of the QM/MM-MFEP calculations. The reaction path potential has been also derived within the mean field of the MM atoms. This allows the dynamics of the QM system to be simulated without using the straightforward yet expensive full QM-MD methods.

The PMF surface of the QM/MM-MFEP method is built by means of molecular dynamic simulation with frozen QM atoms. The freezing of the QM subsystem makes the current method resemble some other methods such as the “blue moon sampling” which was developed with the constrained dynamics sampling approach.^82–84 It is clear that all these methods share the same origin as from thermodynamic integration.^{76, 85} Interestingly however, the use of Cartesian coordinates of the QM subsystem as the reaction coordinate of the QM/MM-MFEP method again leads to the difference in the ways of carrying out simulation and analyzing the results. When the reaction coordinate is chosen as a combination of general geometric variables such as bonds, bond angles, and/or dihedral angles, the PMF expression of those variables is still valid and takes a similar form to Eq. 7.^{82, 84} However, the calculation of the free energy gradients with respect to those variables is not as simple as we derived here in Eq. 9. In fact, it was shown that an additional term has to be included to count the metric tensor effect, caused by the overconstraint on the momentum space.^{82, 84, 86–88} Previous work also indicated the importance of this term.^{2, 79} On the contrary, when Cartesian coordinates are used as the reaction coordinate, the metric matrix becomes a unit matrix, thus makes no contribution to the evaluation of the free energy gradients.⁸⁴.

Like many other methods for locating the reaction path, the QM/MM-MFEP method developed here also has limitations. Apparently, the solution of the QM/MM-MFEP method depends on the effectiveness of the optimization algorithms. As the NEB, Ayala-Schlegel MEP, and QSM methods implements here are all developed for locating local minima, the QM/MM-MFEP will also be a localized minimal path. This feature often does not become a serious problem because in many systems good chemical intuitions often exist for the reaction mechanism. Abundant structural and biochemical information is usually available for enzymatic reactions from extensive biochemical experiments which will guide the simulation study. In such a case, the computed path will be (at least) very close to global minimal path and the essence of the chemistry will be captured to large extent with caution. Yet another factor that will impact the accuracy of the results is the issue of timescale. As we derived the free energy force as an ensemble-average of the forces bore in MD simulation (Eq. 9), we take the well-known ergodicity assumption of MD sampling and also assume the results converge within routine simulation period. As shown in Fig. 2, this assumption may hold well in the case of TIM. There are, however, many examples in the enzyme-catalyzed reactions that long-time conformational dynamics play significant roles in the reaction process.^{89, 90} For those molecules, apparently even nano-second MD simulations will not be enough to characterize the slow conformational dynamics. To combat this problem, new methods which combine the advantages of the QM/MM-MFEP method and other enhanced sampling approaches must be sought.

Further Improvements and Extensions to the QM/MM-MFEP Method

Even though we have shown here the effectiveness of the QM/MM-MFEP method, the precision of the method can still be improved by better modeling of the QM/MM interactions. Specifically, the abilities and accuracy of this method could be enhanced in at least two ways:

(a) Improving the electrostatic representation of the QM atoms in the MD simulation

Consistent with the QM/MM-FE approach, a simple ESP-fitted charge is used for each QM atom in the MD simulations. This is equivalent to the case where the whole QM electron density is approximated by electrostatic monopoles at the atomic positions. It is obvious that adding higher order electrostatic multipoles such as point dipoles to each QM atom will greatly improve the quality of the ESP fitting, thus improving the precision of the results. For enzymes, the improvement from atomic dipole moments may not be significant because the large structural environment of the MM subsystem will overwhelmingly modulate the motion of the small QM subsystem. For reactions in solution, however, dipoles become more important since the structure of the solute-solvent cluster is strongly influenced by the how correctly the local electrostatic interactions between the QM solute and MM solvents are described.

(b) Improving the accuracy of the QM/MM calculation by surmounting the frozen density assumption

For a given QM conformation, the electron density is assumed to be frozen during the subsequent MD simulation process in the current method. We have reported that the effect on the energetics is small for frozen electron densities. Still, the description of the QM electron density may be improved by allowing it to fluctuate in response to changes in the MM environment. Without any loss in efficiency, the linear response polarizable charge model developed in the RPP method may be employed. Since the QM atoms are frozen, the charges in Eq. 18 are simplified to

$$Q_{\alpha }(\mathit{r},{\nu }_{MM})=Q_{\alpha }^{min}+\sum _{\beta \in QM}{\chi }_{\alpha \beta }[{\nu }_{MM}({\mathit{r}}_{\beta }^{min})-{\nu }_{MM}^{\mathit{ref}}({\mathit{r}}_{\beta }^{min})]$$ (23)

For higher quality reference charges and the response kernel, the mean-field approach should be used. To show the validity of this polarizable charge model of the QM atoms, we compared the QM/MM energies from two sources of a frozen QM structure with a set of different MM environments in Fig. 5. One is computed from direct QM/MM calculation for each MM environment, and the other from the classical electrostatic interaction between the MM atoms and the polarized QM charges defined in Eq. 23. The response kernel here was computed by employing the mean field of the collection of all MM atoms. The results clearly indicated that the polarizable QM charge model can accurately reproduce the fluctuating QM density and thus the QM/MM interactions. The excellent agreement between the energies calculated from both methods also supports the use of the MM mean field in the QM/MM-MFEP method.

Figure 5.

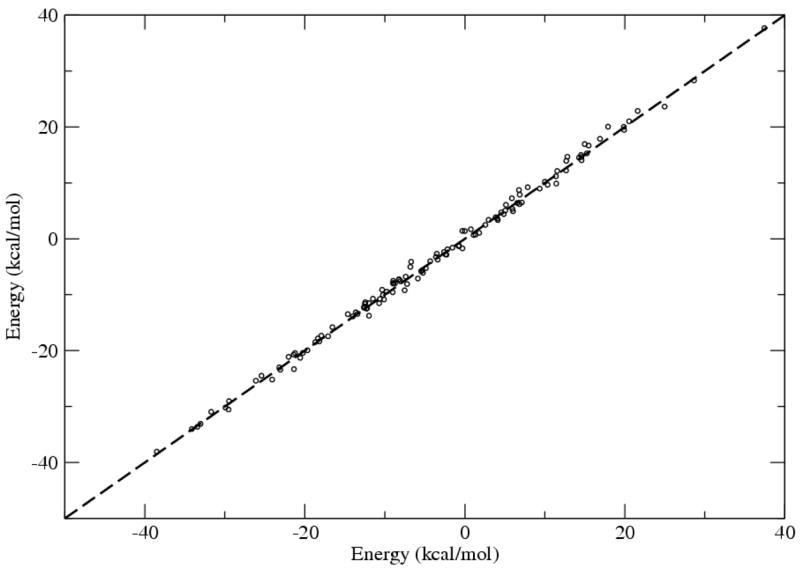
Comparison between the energies calculated for different MM environments with the same QM conformation. The X-axis is the energy calculated by direct QM/MM method in which the exact QM electron density is solved for each QM/MM conformation; the Y-axis is the energy calculated by the RPP method with polarizable QM charges. The RPP is constructed using the mean-field of all MM charges as the external electrostatic potential for the QM part. For better display, the energies on both axes have been shifted by the same amount.

Significance of the QM/MM-MFEP Method

The conventional way of determining the chemical reaction path relies on the techniques of exploring the energy surface of a small, isolated molecular system. For those systems, the conformational states are often very well defined and the number of conformational states is small enough so that it is possible to carry out exhaustive calculations for every state. When the reaction process occurs in the condensed phase, e.g., solution reactions and enzymatic reactions, the many degrees of freedom make it impossible to evaluate all conformational states one by one. Furthermore, the dynamics are hierarchically organized in proteins make it difficult to define the micro-conformational states with the canonical reaction process for complicated enzymatic reactions.^{91, 92} For this purpose, a PMF description of the reaction system with a small number of degrees of freedom will reduce much of the complexity of the phase space and simplify the simulation study of reaction processes.

The QM/MM-MFEP method allows the determination of reaction paths on the free energy surface, rather than the potential energy surface. It has been shown that dynamics can play an important role in the selection of the reaction path. The free energy path is one and only one path that corresponds exactly to the macroscopic thermodynamic reaction process. Therefore, it is crucial to develop simulation methods with the capability of sampling the free energy surface, as in the QM/MM-MFEP approach.

Conclusions

The accuracy of the simulations of condensed phase reaction processes depends on two factors: the ability of the method to faithfully describe the reactivity of the system under study, and the convergence of the statistical sampling of phase space. The former is solved by introducing quantum mechanics into the classical force field, while the latter can only be achieved by long timescale MD simulation (or MC). For reaction processes in the condensed phase, the complexity of the problem makes it difficult if not impossible to achieve the quantum mechanical treatment for the entire system. For this reason, the hybrid QM/MM method has been developed to reduce the computational cost. Even so, the excessive expense of high accuracy ab initio QM calculation still remains the bottleneck of the simulation and prevents the widespread application of the technique.

To reduce the cost of the QM calculations and bridge the gap between expensive ab initio QM calculations and long timescale MD sampling, we have developed the QM/MM-MFEP method to simulate reaction processes in the condensed phase, the essence of which to sample the dynamic free energy surface rather than the static potential energy surface. Distinct features of this method include the expression of the free energy profile of the system as a PMF surface along a chain of conformations described by hybrid ab initio quantum mechanics and classical molecular mechanics, with the contribution of the MM environment properly simulated by classical MD simulation and the relative free energies between distinct conformational states by computed QM/MM FEP. The method can be applied to numerous research projects, from the optimization of a reaction path by the NEB or second order Ayala-Schlegel MEP method to the simulation of the full energetics including the correlation between the dynamics of the QM active site and the MM environment by the reaction path potential method. Therefore, it provides a complete stepwise recipe for simulating reactions under the framework of the QM/MM approach. The example application of the QM/MM-MFEP method on the TIM system illustrates its validity and effectiveness.

Appendix: Potential of Mean Force as a Mean Field Approximation to the Free Energy

We give here a different derivation of the PMF expression through a mean field approximation to the free energy, providing an interesting interpretation of the PMF and also the minimum on the PMF surface.

The partition function Z₀ of a system (with momentum part factoring out) is written as

$$Z_0=\int exp(-\beta E)d{r}^N$$ (24)

in which E is the energy of the system, r the coordinate. It is noted that E is a function of r. The equilibrium configuration density/distribution is then defined as

$${\rho }_0=\frac{exp(-\beta E)}{Z_0}$$ (25)

which obviously is normalized as

$$\int {\rho }_{0}d{r}^N=1$$ (26)

The free energy of the system is

$$\begin{array}{l}{A}_0=\frac{-1}{\beta }ln(Z_0)\\ =\int {\rho }_0\left[E+\frac{1}{\beta }ln({\rho }_0)\right]d{r}^N\end{array}$$ (27)

We can define a free energy functional of an arbitrary distribution ρ

$$A[\rho ]=\int \rho \left[E+\frac{1}{\beta }ln(\rho )\right]d{r}^N.$$ (28)

It is clear that if ρ = ρ₀, A[ρ] approaches its minimal value as A(ρ₀) = A₀. This equation, known the textbook of statistical mechanics, then serves as the variational principle for determining the equilibrium distribution.

Suppose we have a system that is described by QM/MM force field. The energy of the system is written as E(R, r), again with R the coordinates of the QM subsystem and r the coordinates of the MM subsystem. By taking the mean-field approximation, we have

$${\rho }_{MF}(R,r)={\rho }_R(R){\rho }_r(r)$$ (29)

If we further assume that the QM atoms are frozen in space ρ_R (R) = δ(R − R₀), then we have

$$\begin{array}{l}A[\rho ]=\int {\rho }_{MF}(R,r)\left[E(R,r)+\frac{1}{\beta }ln({\rho }_{MF}(R,r))\right]d{R}^{M}d{r}^{M\prime }\\ =\int {\rho }_r(r)E(R_0,r)dr+\frac{1}{\beta }\int {\rho }_r(r)ln({\rho }_r(r))dr+\mathit{const}\end{array}$$ (30)

Omitting the constant term, which is independent of the choice of R₀, we now seek the condition for the minimization of A[ρ] from all possible ρ_r (r), which gives

$${\rho }_r^0(r)=\frac{exp(-\beta E(R_0,r))}{\int exp(-\beta E(R_0,r))dr}$$ (31)

Using ${\rho }_r^0(r)$ in Eq. (30), we obtain the free energy as a function of R₀, the QM fixed coordinates in the frozen QM approximation:

$$A(R_0)=-\frac{1}{\beta }ln\int exp(-\beta E(R_0,r))dr+\mathit{const},$$ (32)

which is just the potential of mean force (PMF) in the QM coordinate, Eq. (7) of the text. Therefore, the PMF A(R₀) is the approximation to the free energy under the mean field and the frozen QM approximation. The minimum of the PMF A(R₀) thus provides the best estimate to the free energy of the QM/MM system under the same approximations with optimal QM frozen coordinates. This appears to be an interesting interpretation of PMF and the minimum on the PMF.