Abstract
How focal adhesions (FAs) convert retrograde filamentous actin (F-actin) flow into traction stress on the extracellular matrix to drive cell migration is unknown. Using combined traction force and fluorescent speckle microscopy, we observed a robust biphasic relationship between F-actin speed and traction force. F-actin speed is inversely related to traction stress near the cell edge where FAs are formed and F-actin motion is rapid. In contrast, larger FAs where the F-actin speed is low are marked by a direct relationship between F-actin speed and traction stress. We found that the biphasic switch is determined by a threshold F-actin speed of 8–10 nm/s, independent of changes in FA protein density, age, stress magnitude, assembly/disassembly status, or subcellular position induced by pleiotropic perturbations to Rho family guanosine triphosphatase signaling and myosin II activity. Thus, F-actin speed is a fundamental regulator of traction force at FAs during cell migration.
Introduction
Directed cell migration requires that cell-generated traction stresses exerted on the ECM are spatially and temporally coordinated (Lauffenburger and Horwitz, 1996). Traction stresses are thought to originate in the F-actin cytoskeleton and be transmitted to the ECM through focal adhesions (FAs; Balaban et al., 2001; Beningo et al., 2001; Bershadsky et al., 2003). The intimate coupling of F-actin and FA dynamics suggests a mechanism for their coordination of traction stresses (Le Clainche and Carlier, 2008). F-actin polymerizes near the leading edge plasma membrane, followed by coherent retrograde motion of the F-actin networks away from the leading cell edge toward the cell center. This F-actin “retrograde flow” is driven by F-actin polymerization force in the lamellipodium and myosin II activity in the lamella and cell center (Lin et al., 1997; Ponti et al., 2004). Meanwhile, FAs originate as protein clusters in the lamellipodium (Choi et al., 2008) and subsequently grow and disassemble in the lamella or cell rear (Webb et al., 2004). The retrograde flow of F-actin in the lamellipodium slows at sites of FA assembly (Giannone et al., 2004; Hu et al., 2007; Alexandrova et al., 2008), and an inverse relationship between F-actin flow in the lamellipodium and leading edge protrusion has been observed (Lin and Forscher, 1995; Jurado et al., 2005).
The relationship between F-actin motion, FAs, and leading edge protrusion has led to the suggestion that FAs within the lamellipodium act like a mechanical clutch to impede actin motion, such that further actin polymerization contributes to leading edge protrusion (Lin and Forscher, 1995; Jurado et al., 2005). Based on this “molecular clutch” model, we hypothesize that the slowing of F-actin motion by FAs should generate traction force on the ECM. Here, we test this hypothesis by simultaneous measurement of F-actin retrograde flow and traction force impinged on the ECM via FAs in migrating cells.
Results and discussion
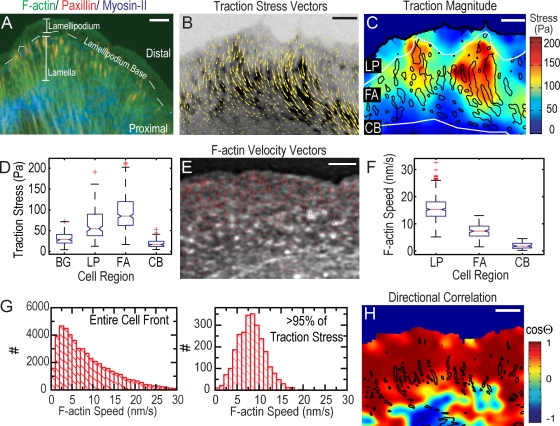
For simultaneous measurement of F-actin dynamics and traction on the ECM at FAs, we developed high-resolution traction force microscopy (Dembo et al., 1996) compatible with quantitative fluorescent speckle microscopy (FSM; Danuser and Waterman-Storer, 2006). We used migrating PtK1 epithelial cells because their F-actin organization and dynamics are well characterized (Fig. 1 A and Fig. S1, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1; Ponti et al., 2004). Cells expressing GFP-fused paxillin (GFP-paxillin) to mark FAs (Webb et al., 2004) and microinjected with x-rhodamine–conjugated actin were plated on 10–20-μm-thick compliant (1.5–6 kPa) fibronectin-coated polyacrylamide (PAA) substrates that were embedded with a high density of far-red fluorescent 40-nm spheres (∼10 spheres/μm2). Time-lapse images of GFP-paxillin, x-rhodamine–actin, and spheres were acquired by spinning-disk confocal microscopy (Video 1). Cellular traction stress (force/area) vector fields were reconstructed from cell-induced bead displacements using either boundary element or Fourier transform traction cytometry methods to provide ∼1.5-μm spatial resolution (Fig. 1 B and Video 2; Sabass et al., 2008).
Figure 1.
Traction stresses across the cell front. (A) Immunofluorescence of paxillin (red), serine-19–phosphorylated myosin II light chain marking activated myosin II (blue), and phalloiden staining of F-actin (green). Locations of lamellipodium, lamellipodium base, and lamella are indicated; distal and proximal directions are defined. (B) GFP-paxillin (inverted contrast) with traction stress vectors superimposed (Video 2, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). (C) Heat-scale plot of traction stress magnitude; segmented FAs indicated by black outlines (Video 2). White lines delineate boundaries between lamellipodium (LP), FAs, and cell body (CB). (D) Box plots of traction stresses in the lamellipodium, FAs, cell body, and background (BG) measured directly outside the cell. Box and whisker plots in all figures indicate the 25% (lower bound), median (middle line), and 75% (upper bound) nearest observations within 1.5 times the interquartile range (whiskers), 95% confidence interval of the median (notches) and near (+) and far (0) outliers. (E) FSM image of x-rhodamine F-actin with F-actin velocity vectors superimposed (Video 1). (F) Box plots of F-actin speed in the lamellipodium (LP), FAs, and cell body (CB). (G) Histograms of the F-actin speed across the entire cell front (left) and in areas of highest (>95%) traction stresses (right). (H) Heat scale plot of directional coupling, cosine of angle θ, between F-actin velocity and traction stress vectors; segmented FAs indicated by black outlines. Bars: (A) 10 μm; (B, C, and E) 3 μm; (H) 5 μm.
We first examined the relationship between traction stress and FAs. Consistent with previous results, the largest stresses were localized at FAs (Fig. 1, C and D; and Video 2; Balaban et al., 2001; Beningo et al., 2001). We also observed low (<25 Pa), but significant, stresses within the lamellipodium where there was unclustered GFP-paxillin intensity and nascent FAs engage (Wiseman et al., 2004; Choi et al., 2008). However, there was no strong correlation between stress magnitude and intensity of either fluorescent actin or paxillin (Fig. S2, B and C, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1) in the lamellipodium, lamella, or within FAs. The apparent contradiction to Beningo et al. (2001), comparing traction to FA protein density, may be caused by the use of paxillin versus zyxin as FA markers, since the relationship between traction and FA density may be protein specific. Thus, these results indicate that local densities of paxillin or F-actin are not primary determinants of traction stress.
To determine if F-actin motion is related to traction stress, we computed vector maps of F-actin velocity from FSM images (Fig. 1 E; Ji and Danuser, 2005). F-actin speeds ranged from 0 to 30 nm/s, with rapid retrograde flow (∼25 nm/s) in the distal lamellipodium that slowed to ∼2 nm/s in the lamella (Fig. 1, E–G; and Video 1), with a sharp gradient at the lamellipodium base, where F-actin motion transitions from polymerization driven to myosin II driven (Ponti et al., 2004). To establish if the direction of F-actin velocity is related to the direction of traction stress, we interpolated the two vector fields onto a common grid and used the cosine of the angle subtending the vector pairs to indicate directional correlation (Hu et al., 2007). In the cell body, where both measurements approached our resolution limit, the directional correlation was poor (Fig. 1 H). However, across the lamellipodium and within FAs, the directional correlation was uniformly high (Fig. 1 H). Thus, traction stresses on the ECM are directionally correlated with F-actin motion within the cell.
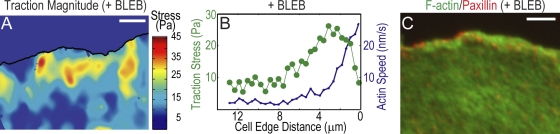
To determine if traction stresses are spatially restricted to cellular regions of F-actin motion, we selectively abrogated myosin II–driven F-actin flow in the lamella with 50 μM blebbistatin, leaving F-actin motion driven by filament elongation in the lamellipodium intact (Straight et al., 2003; Ponti et al., 2004; Fig. 2 B and Video 3, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). Surprisingly, stresses in the lamellipodium of blebbistatin-treated and control cells were similar (Fig. 2, A and B). Small FAs were primarily concentrated at the lamellipodium base where stresses peaked, but were also present in the lamella where stresses were negligible (Fig. 2 C and Fig. S1). Thus, traction stresses are spatially correlated with FAs in regions with coherent F-actin motion. Further, actin polymerization forces in the lamellipodium are sufficient to generate traction and mediate leading edge protrusion independent of myosin II activity.
Figure 2.
Inhibition of myosin II activity constrains traction to the lamellipodium. (A–C) Cells were treated with 50 μM blebbistatin (+BLEB). (A) Heat scale plot of traction stress magnitude. (B) Mean traction stress (green) and F-actin speed (blue) as a function of distance from leading cell edge. (C) Immunofluorescence image of paxillin (red) and F-actin (green). Bars, 5 μm.
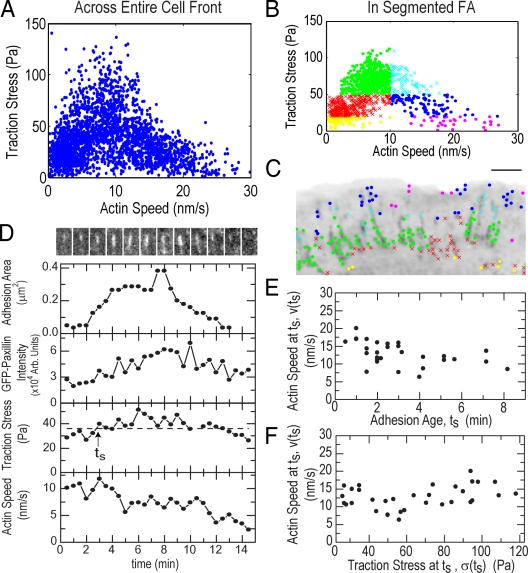
To determine the relationship between traction stress and F-actin speed magnitudes, we plotted the values from a time-lapse series for all grid positions throughout the cell front. This revealed a biphasic relationship, with highest stresses exerted at intermediate F-actin speeds (8–12 nm/s) and lower stresses exerted at the highest and lowest F-actin speeds (Fig. 3 A). Surprisingly, the distribution of F-actin speeds at the highest (>95%) stresses was Gaussian distributed around a mean of ∼8 nm/s (Fig. 1 G). Data from only within segmented FAs exhibited a similar biphasic relationship (Fig. 3 B). To identify where data populations of similar mean stress and F-actin speed were localized, we grouped the data in “stress/speed space” and mapped the points from each data group to their respective subcellular locations (Fig. 3 C and Video 4, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). Interestingly, data groups mapped to distinct cell regions with specific FA morphology. The fastest F-actin speeds associated with low traction stresses (Fig. 3 C, magenta and navy) localized to small FAs in the lamellipodium and distal tips of larger FAs; the highest traction stresses at intermediate F-actin speeds (Fig. 3 C, cyan and green) mapped to distal and central portions of large FAs; slower F-actin speeds and lower traction stresses (Fig. 3 C, red and yellow) mapped to the central and proximal portions of large FAs. Thus, there is a biphasic relationship between F-actin speed and traction stress in FAs that changes from inverse to direct across the leading edge.
Figure 3.
Traction stress is biphasically correlated with F-actin speed in FAs. (A) Traction stress versus F-actin speed for all points throughout the cell front over 25 frames of a time-lapse movie. (B) Subset of traction stress versus F-actin speed from A for data located within segmented FAs. Data were grouped by F-actin speed (greater or less than 10 nm/s) and three values of traction stress (<20, 20–50, and >50 Pa) to obtain six “stress-speed” groups identified by different colors/symbols. (C) Inverted GFP-paxillin image with spatial location of stress-speed data groups plotted in B (Video 4, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). Bar, 3 μm. (D, top) Montage of GFP-paxillin images of a single FA over 15 min (Video 5). For each time point, the integrated area (second row), GFP-paxillin intensity (third row), traction stress (fourth row), and local F-actin speed (bottom) were determined. In the fourth row, the dashed line indicates 75% of maximum stress; the arrow indicates time (ts) when traction stress exceeds this threshold. (E) F-actin speed at ts (v(ts)) as a function of ts. Mean of v(ts) = 12.7 ± 3 nm/s. Mean of ts = 3 ± 2 min. (F) v(ts) as a function of traction stress at ts, σ(ts). Mean of σ(ts) = 65 ± 28 Pa. Data in E and F are from 26 FAs in four cells.
The spatial distribution of traction stress and F-actin speed suggests that FAs may go through a cycle of stress strengthening and weakening that is modulated by F-actin speed. Over the assembly/disassembly lifecycle of single FAs (as monitored by GFP-paxillin intensity and FA area), stress increased, reached a peak, and then decreased (Fig. 3 D; Fig. S2, E–H; and Video 5, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). In nascent FAs, stress increase was concomitant with speed decrease as FAs grew (Fig. 3 D and Fig. S2, E–G). In contrast, in large FAs, decreased F-actin speed was concomitant with decreased stress, whereas FA size stayed constant or decreased (Fig. 3 D and Fig. S2, F–H). We also observed a biphasic change in correlation between stress and F-actin speed from the distal to proximal edges of single FAs (Fig. S2 D). Thus, as traction strengthens in assembling and distal tips of FAs, F-actin speed slows. Maximal traction by FAs occurs at intermediate F-actin speed, and the transition to traction weakening in mature and disassembling FAs is characterized by a direct relationship between F-actin speed and stress.
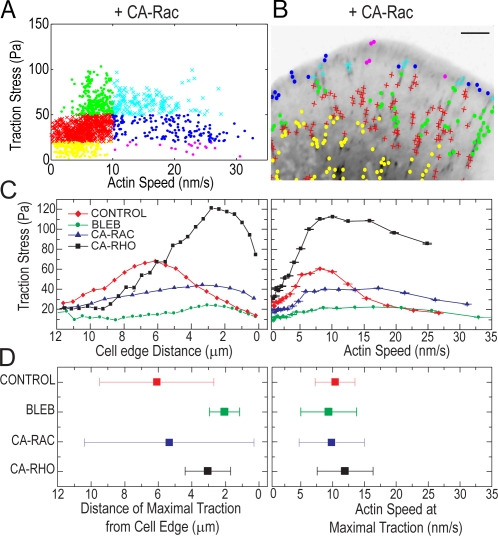
To establish if the transition from an inverse relationship to a direct relationship between F-actin speed and traction stress requires FA disassembly, we inhibited FA turnover dynamics by expressing constitutively active Rac1 (CA-Rac; Webb et al., 2004). CA-Rac also induces a wide lamellipodium with small FAs near the lamellipodium base and long, narrow FAs that extend into the cell body and do not disassemble in 30 min (Fig. S1 and Video 6, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). The magnitude of stresses in cells expressing CA-Rac was lower than control cells, possibly because of Rac-mediated down-regulation of myosin II activity (Sanders et al., 1999) or other changes in FA protein composition or posttranslational modification (Zaidel-Bar et al., 2007). F-actin speeds at FAs ranged from 0 to ∼30 nm/s, with the highest speeds in distal FAs near the cell edge and lowest speeds in FAs toward the cell body. Remarkably, in the absence of FA turnover, we still observed a biphasic relationship between stress and F-actin speed across FAs, with peak stresses exerted at intermediate speeds (Fig. 4, A and B; and Video 7). Thus, maximal traction stresses and the transition to a direct relationship between stress and F-actin speed occurs at intermediate F-actin speed, independent of FA disassembly.
Figure 4.
The switch from an inverse to a direct correlation between F-actin speed and traction stress does not require FA disassembly and occurs at a specific F-actin speed. (A) Traction stress versus F-actin speed for data within FAs for 15 frames of a time-lapse video of a cell expressing CA-Rac. Data are grouped as in Fig. 3 B. (B) Inverted GFP-paxillin image with spatial location of stress/speed data points plotted in A. Bar, 3 μm. See Video 7, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1. (C) Mean traction stress as a function of distance from cell edge (left) and F-actin speed (right). Characteristic data are shown for a control cell, treatment with 50 μM blebbistatin (BLEB), expression of CA-Rac, and expression of CA-Rho. (D) The mean (squares) and standard deviation (error bars) of the distance away from the cell edge (left) and F-actin speed (right) associated with peak (>95%) traction stresses. Data reflects the mean of >100 data points from three cells.
To determine if FA age or traction stress magnitude regulates the transition from an inverse to a direct relationship between F-actin speed and stress, we identified the time after initiation of individual FAs (ts) when stress peaked (Fig. 3 D). To minimize the effects of measurement noise inherent in picking a single peak value from a small dataset, attainment of peak stress was estimated as the mean of the top quantile of stresses measured for each FA. Values of ts were broadly distributed (Fig. 3 E), varying from ∼5 to 50% of the ∼17-min FA lifetime (Gupton and Waterman-Storer, 2006). In addition, the stress magnitude at the transition from strengthening to weakening was also broadly distributed (Fig. 3 F). However, the F-actin speed at ts was narrowly distributed (Fig. 3, E and F). Thus, achievement of maximal stress at FAs and the transition to a direct relationship between traction stress and F-actin speed is not determined by a timer triggered after FA initiation or by an absolute stress magnitude, but is well correlated with an intermediate F-actin speed.
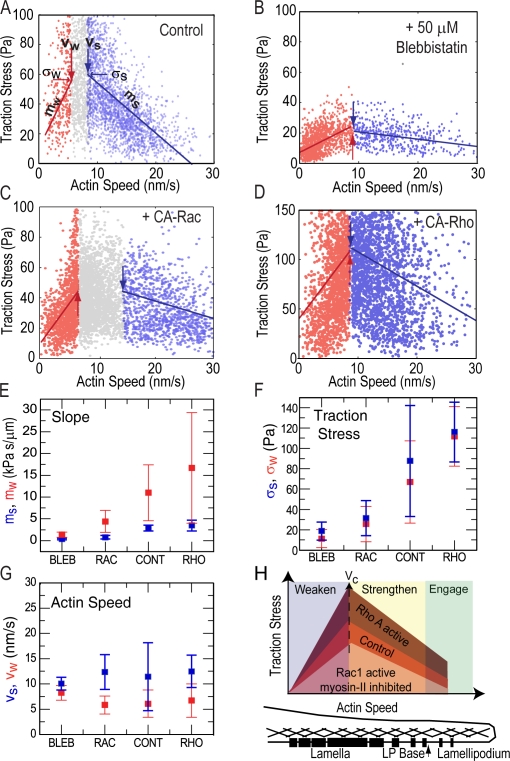
To address if aspects of FA function regulated by contractility and Rho family GTPase signaling, such as FA subcellular position or cytoskeletal morphology, control the switch in correlation between traction stress and F-actin speed, we analyzed traction stresses and F-actin dynamics under a range of perturbations. In addition to inhibiting myosin II ATPase activity and expression of CA-Rac as above, we also expressed constitutively active RhoA (CA-Rho), which promotes myosin II–dependent stress fibers and large FAs close to the cell edge (Bershadsky et al., 2003; Video 8, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). The locations and magnitudes of peak stresses varied significantly with these perturbations. For example, RhoA activation and myosin II inhibition had opposite effects on peak stress magnitude, yet the location of the peak stresses relative to the cell edge was similar. Rac1 activation produced similar peak stresses to control cells, yet the locations of peak stresses with respect to the cell edge were different. (Fig. 4, C and D, left). Despite these pleiotropic perturbations to contractility, cytoskeletal morphology, and signaling, maximal stresses were always associated with a similar F-actin speed (Fig. 4, C and D, right) and cells exhibited a biphasic relationship between F-actin speed and traction stress that changed from inverse to direct across the leading edge (Fig. S3, A–D; and Videos 9 and 10).
We next quantitatively characterized the biphasic relationship between traction stress and F-actin speed. We determined the range of F-actin speeds over which the data exhibited the strongest inverse (Fig. 5, A–D, blue; and Fig. S3, E and F, blue) and direct (red) linear correlations, although the data does not preclude the possibility of higher-ordered polynomial fits. The absolute values of the slopes (ms and mw) represent the efficiency of conversion of F-actin motion into traction stress by FAs. σs and σw are the mean peak stresses at the F-actin speeds, vs and vw (Fig. 5, A–D, arrows), over which the strongest inverse and direct correlations between stress and F-actin speed are found. In cells treated with blebbistatin or expressing CA-Rac, σs and σw were lower than those in controls, whereas in cells expressing CA-Rho, σs and σw were higher than controls (Fig. 5 F). Interestingly, ms was weakly sensitive, but mw was highly sensitive to perturbation (Fig. 5 E). Thus, myosin II activity and/or Rho GTPase signaling do not affect the conversion efficiency of rapid F-actin motion to traction stress during FA initiation, but do so at lower F-actin speeds in larger FAs. Remarkably, vs and vw were not significantly altered (Fig. 5 G) across perturbations. Thus, the F-actin speed where force transmission through FA change from an inverse relationship with F-actin speed to a direct relationship is constant and independent of contractility and Rho GTPase signaling.
Figure 5.
Inverse and direct correlations between traction stress and F-actin speed occur over similar ranges of F-actin speed despite perturbations to myosin II and Rho GTPase signaling. (A–D) Data ranges indicating the strongest inverse (blue) or direct (red) correlation between traction stress and F-actin speed (Fig. S3, available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1). Large blue and red arrows mark vs and vw, the F-actin speed delineating the upper and lower bounds, respectively, of the speed ranges. Gray symbols represent data outside the ranges; lines with slopes ms and mw show linear fits to data within the ranges. Small blue and red arrows mark σs and σw, the traction stress at vs and vw. Characteristic data are shown for control (A), blebbistatin-treated cells (B), and overexpression of CA-Rac (C) and CA-Rho (D). Mean slopes ms (E, blue) and mw (E, red), traction stresses σs (F, blue) and σw (F, red), and velocities vs (G, blue) and vw (G, red) for different conditions. In E–G, data reflects a mean of >1,000 data points for n = 3 cells. (H) Model for how F-actin dynamics are variably coupled to traction stress by initiation and assembly of FAs across the cell front; differently shaded regions reflect changes in the magnitude of traction stress measured at similar F-actin speeds for different conditions. Position within the cell front shown below; black bars represent FAs and crosshatching represents F-actin.
We demonstrate that F-actin retrograde flow in the cell is correlated with traction stress on the ECM and implicate F-actin dynamics in regulating cellular traction. The directional correlation between F-actin motion and traction stress suggests that F-actin motion may steer cell movement. We find an unexpected and remarkably robust biphasic relationship between F-actin speed and traction stress that persists in spite of pleiotropic perturbations that alter FA biochemical composition, signaling, and morphology. Although the magnitude of traction stress is altered by myosin II inhibition and activation of Rac1 or RhoA (Fig. 5 H), the F-actin flow speed where traction switches from strengthening to weakening at FAs remains constant and is not well correlated with many proposed or known regulators of FAs, including age, stress magnitude, disassembly, subcellular position, or cytoskeletal organization.
Our results suggest that the shear rate between F-actin and proteins within FA determines their association and dissociation kinetics and, thus, modulates force transmission through FAs. The inverse relationship between traction stress and F-actin speed during FA assembly is consistent with the fast shear rate either limiting the time available for local bond formation or driving bond breakage (Fig. 5 H, Engage). Because the conversion efficiency of F-actin motion into traction stress during FA strengthening (ms; Fig. 5 H, Strengthen) was only weakly dependent on myosin II activity and Rho family GTPase signaling, force transmission may be mediated by the same high-affinity protein bond during FA initiation across these conditions. At a critical F-actin speed (Vc), FAs stabilize and transition to speed-dependent weakening of traction stress (Fig. 5 H, Weaken), suggesting a viscous-like coupling between F-actin and the ECM (Cuvelier et al., 2007). In this regimen, the low shear rate could allow dissipative binding and dissociation between F-actin and FA proteins of a range of affinities. Indeed we find that mw, the efficiency of conversion of F-actin motion into traction stress, is dependent on perturbations to Rho family signaling and myosin II activity known to affect FA biochemical composition (Fig. 5 E). Together, our results suggest that variation in F-actin speed, or strain rate, may be a general mechanism for regulating integrin-mediated traction on the ECM at FAs in migrating cells.
Materials and methods
PAA substrates for traction microscopy
Fibronectin-coupled PAA substrates containing fluorescent microbeads were prepared on coverslips (Sabass et al., 2008) with a 7.5% acrylamide/0.1% bis-acrylamide gel, with a shear elastic modulus (G′) of 2,800 Pa for measurements of control cells and cells expressing CA-Rac. We used a 7.5%/0.05% gel, with G′ of ∼1,500 Pa, for cells treated with 50 μM blebbistatin and a 7.5%/0.2% gel, with G′ of ∼5,400 Pa, for cells expressing CA-Rho. These combinations of stiffnesses and cell conditions ensured that cell-induced deformation at the PAA surface was <10% of the thickness of the gel.
Cell culture and microinjection
Ptk1 cells were cultured (Gupton and Waterman-Storer, 2006) on PAA substrates for 24–48 h. Plasmid DNA encoding eGFP-paxillin (gift of A.R. Horwitz, University of Virginia, Charlottesville, VA), RhoAG14V (CA-RhoA), and/or RacQ61L (CA-Rac1) were co-microinjected with 1–2 mg/ml of x-rhodamine G–actin into the cell nucleus.
Live cell microscopy
Cells bound to PAA substrates were mounted in a perfusion chamber (Warner Instruments) in media supplemented with 30 μl/1 ml Oxyrase (Oxyrase, Inc.). Cells were imaged at 37°C 3–5 h after microinjection on a multispectral spinning disk confocal microscope (Gupton and Waterman-Storer, 2006) consisting of a TE2000 with a 60× 1.2 NA Plan Apo WI objective (Nikon) and a CSU10 scanner (Yokogawa) using a 1.5× optovar and an HQ2 cooled charged coupled device camera (Roper Scientific) controlled with Metamorph acquisition software (MDS Analytical Technologies). After imaging, 0.5% trypsin was perfused to detach cells from the PAA substrate and an image of unstrained bead positions was obtained. Cells treated with 50 μM blebbistatin (∼1 h) could not be repeatedly imaged with 488-nm light, thus only one to two GFP-paxillin images could be obtained.
Immunofluorescence
Immunofluorescence of serine-19–phosphorylated myosin light chain (Cell Signaling Technology), paxillin (Santa Cruz Biotechnology, Inc.), and phalloidin staining of F-actin in cells plated on PAA substrates was performed as described previously (Gupton and Waterman-Storer, 2006).
Image analysis
x-Rhodamine F-actin speckles and fluorescent beads were tracked separately in image series of each channel using time-integrated cross-correlation tracking as described previously (Ji and Danuser, 2005; Hu et al., 2007). Templates were placed on the positions of significant F-actin speckles (Ponti et al., 2003) and beads (Crocker and Grier, 1996), and template size was adaptively chosen between 0.67 × 0.67 and 1.6 × 1.6 μm. Approximately 1,000–3,000 vectors of bead displacements and F-actin speckle velocities were obtained for each image.
Modified boundary element and Fourier transform traction cytometry methods (Sabass et al., 2008) were used to estimate traction stress from bead displacements. Boundary element methods optimized the spatial resolution to ∼1.5 μm. Traction stress background, as shown in Fig. 1 D and Fig. S4, was measured outside the cell within 5 μm of the cell edge.
The F-actin velocity vector field was interpolated onto the grid of traction stress vectors using a distance-weighted mean based on a Gaussian kernel (width of 10 μm). The cosine of the angle subtended by these vectors was used as a measure of their directional coupling (Hu et al., 2007). Stress versus speed plots shown reflect data points obtained from four to five frames of a movie.
FAs were segmented by thresholding the background-subtracted GFP-paxillin images in Metamorph, and the centroid of segmented regions with an area >0.078 μm2 were determined. The stress and F-actin velocity vectors were interpolated onto the FA centroid. In videos, FAs were linked in time by finding centroids in successive frames separated by no more than 2 μm.
Cell edge distance was binned such that each bin contained ∼30–50 data points. The median of the traction stress and F-actin speed magnitude in each bin was determined.
Images for presentation were processed with a 5 × 5-pixel low pass filter followed by unsharp mask.
Online supplemental material
Fig. S1 shows localization of F-actin, paxillin, and serine-19–phosphorylated myosin II light chain. Fig. S2 shows traction stress versus paxillin or actin intensity (B and C), variation of traction and F-actin speed across single FAs (A and D) and evolution of traction and F-actin speed in assembling and disassembling FAs (E–H). Fig. S3 shows traction stress versus F-actin speed in blebbistatin-treated cells (A and B) and cells with CA-Rho overexpression (C and D). Method for determining correlation coefficients is shown in Fig. S3 (E and F). Video 1 shows simultaneous imaging of actin speckles, GFP-paxillin, and fluorescent beads. Video 2 shows reconstructed traction stresses. Video 3 shows actin speckles and fluorescent beads of a cell treated with blebbistatin. Video 4 shows GFP-paxillin overlaid with color-encoded groups of similar mean traction stress and F-actin speed. Video 5 identifies the FAs used for analysis in Fig. 4 and Fig. S2. Video 6 shows actin, paxillin, and beads of a cell where CA-Rac1 is overexpressed. Video 7 shows GFP-paxillin in cell expressing CA-Rac, overlaid with color-encoded groups of similar mean traction stress and F-actin speed. Video 8 shows actin speckles, GFP-paxillin, and beads of a cell expressing CA-Rho. Video 9 shows actin speckles in a blebbistatin-treated cell, overlaid with color-encoded groups of similar mean traction stress and F-actin speed. Video 10 shows GFP-paxillin in a cell expressing CA-Rho, overlaid with color-encoded groups of similar mean traction stress and F-actin speed. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.200810060/DC1.
Acknowledgments
This work was supported by the intramural research program of the National Institutes of Health (NIH)/National Heart, Lung, and Blood Institute (C.M. Waterman); Burroughs Wellcome Fund Career Award at the Scientific Interface, Jane Coffin Childs Fellowship, and NIH Director's Pioneer Award (DP10D00354) to M.L. Gardel; grant R01 GM71868 to G. Danuser; and the Center for Modelling and Simulation in the Biosciences at Heidelberg (U.S. Schwarz).
Abbreviations used in this paper: CA-Rac, constitutively active Rac1; FA, focal adhesion; FSM, fluorescent speckle microscopy; PAA, polyacrylamide.
References
- Alexandrova, A.Y., K. Arnold, S. Schaub, J.M. Vasiliev, J.J. Meister, A.D. Bershadsky, and A.B. Verkhovsky. 2008. Comparative dynamics of retrograde actin flow and focal adhesions: formation of nascent adhesions triggers transition from fast to slow flow. PLoS ONE. 3:e3234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balaban, N.Q., U.S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi, and B. Geiger. 2001. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell Biol. 3:466–472. [DOI] [PubMed] [Google Scholar]
- Beningo, K.A., M. Dembo, I. Kaverina, J.V. Small, and Y.L. Wang. 2001. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J. Cell Biol. 153:881–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bershadsky, A.D., N.Q. Balaban, and B. Geiger. 2003. Adhesion-dependent cell mechanosensitivity. Annu. Rev. Cell Dev. Biol. 19:677–695. [DOI] [PubMed] [Google Scholar]
- Choi, C.K., M. Vicente-Manzanares, J. Zareno, L.A. Whitmore, A. Mogilner, and A.R. Horwitz. 2008. Actin and alpha-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nat. Cell Biol. 10:1039–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crocker, J.C., and D.G. Grier. 1996. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 179:298–310. [Google Scholar]
- Cuvelier, D., M. Thery, Y.S. Chu, S. Dufour, J.P. Thiery, M. Bornens, P. Nassoy, and L. Mahadevan. 2007. The universal dynamics of cell spreading. Curr. Biol. 17:694–699. [DOI] [PubMed] [Google Scholar]
- Danuser, G., and C.M. Waterman-Storer. 2006. Quantitative fluorescent speckle microscopy of cytoskeleton dynamics. Annu. Rev. Biophys. Biomol. Struct. 35:361–387. [DOI] [PubMed] [Google Scholar]
- Dembo, M., T. Oliver, A. Ishihara, and K. Jacobson. 1996. Imaging the traction stresses exerted by locomoting cells with the elastic substratum method. Biophys. J. 70:2008–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannone, G., B.J. Dubin-Thaler, H.G. Dobereiner, N. Kieffer, A.R. Bresnick, and M.P. Sheetz. 2004. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 116:431–443. [DOI] [PubMed] [Google Scholar]
- Gupton, S.L., and C.M. Waterman-Storer. 2006. Spatiotemporal feedback between actomyosin and focal-adhesion systems optimizes rapid cell migration. Cell. 125:1361–1374. [DOI] [PubMed] [Google Scholar]
- Hu, K., L. Ji, K.T. Applegate, G. Danuser, and C.M. Waterman-Storer. 2007. Differential transmission of actin motion within focal adhesions. Science. 315:111–115. [DOI] [PubMed] [Google Scholar]
- Ji, L., and G. Danuser. 2005. Tracking quasi-stationary flow of weak fluorescent signals by adaptive multi-frame correlation. J. Microsc. 220:150–167. [DOI] [PubMed] [Google Scholar]
- Jurado, C., J.R. Haserick, and J. Lee. 2005. Slipping or gripping? Fluorescent speckle microscopy in fish keratocytes reveals two different mechanisms for generating a retrograde flow of actin. Mol. Biol. Cell. 16:507–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauffenburger, D.A., and A.F. Horwitz. 1996. Cell migration: a physically integrated molecular process. Cell. 84:359–369. [DOI] [PubMed] [Google Scholar]
- Le Clainche, C., and M.F. Carlier. 2008. Regulation of actin assembly associated with protrusion and adhesion in cell migration. Physiol. Rev. 88:489–513. [DOI] [PubMed] [Google Scholar]
- Lin, C.H., and P. Forscher. 1995. Growth cone advance is inversely proportional to retrograde F-actin flow. Neuron. 14:763–771. [DOI] [PubMed] [Google Scholar]
- Lin, C.H., E.M. Espreafico, M.S. Mooseker, and P. Forscher. 1997. Myosin drives retrograde F-actin flow in neuronal growth cones. Biol. Bull. 192:183–185. [DOI] [PubMed] [Google Scholar]
- Ponti, A., P. Vallotton, W.C. Salmon, C.M. Waterman-Storer, and G. Danuser. 2003. Computational analysis of F-actin turnover in cortical actin meshworks using fluorescent speckle microscopy. Biophys. J. 84:3336–3352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponti, A., M. Machacek, S.L. Gupton, C.M. Waterman-Storer, and G. Danuser. 2004. Two distinct actin networks drive the protrusion of migrating cells. Science. 305:1782–1786. [DOI] [PubMed] [Google Scholar]
- Sabass, B., M.L. Gardel, C.M. Waterman, and U.S. Schwarz. 2008. High resolution traction force microscopy based on experimental and computational advances. Biophys. J. 94:207–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders, L.C., F. Matsumura, G.M. Bokoch, and P. de Lanerolle. 1999. Inhibition of myosin light chain kinase by p21-activated kinase. Science. 283:2083–2085. [DOI] [PubMed] [Google Scholar]
- Straight, A.F., A. Cheung, J. Limouze, I. Chen, N.J. Westwood, J.R. Sellers, and T.J. Mitchison. 2003. Dissecting temporal and spatial control of cytokinesis with a myosin II Inhibitor. Science. 299:1743–1747. [DOI] [PubMed] [Google Scholar]
- Webb, D.J., K. Donais, L.A. Whitmore, S.M. Thomas, C.E. Turner, J.T. Parsons, and A.F. Horwitz. 2004. FAK-Src signalling through paxillin, ERK and MLCK regulates adhesion disassembly. Nat. Cell Biol. 6:154–161. [DOI] [PubMed] [Google Scholar]
- Wiseman, P.W., C.M. Brown, D.J. Webb, B. Hebert, N.L. Johnson, J.A. Squier, M.H. Ellisman, and A.F. Horwitz. 2004. Spatial mapping of integrin interactions and dynamics during cell migration by image correlation microscopy. J. Cell Sci. 117:5521–5534. [DOI] [PubMed] [Google Scholar]
- Zaidel-Bar, R., S. Itzkovitz, A. Ma'ayan, R. Iyengar, and B. Geiger. 2007. Functional atlas of the integrin adhesome. Nat. Cell Biol. 9:858–867. [DOI] [PMC free article] [PubMed] [Google Scholar]