Abstract
We derive a mathematical theory to explain the subthreshold resonance response of a neuron to synaptic input. The theory shows how a neuron combines information from its intrinsic resonant properties with those of the synapse to determine the neuron’s generalized resonance response. Our results show that the maximal response of a postsynaptic neuron can lie between the preferred intrinsic frequency of the neuron and the synaptic resonance frequency. We compare our theoretical results to parallel findings on experiments of the crab pyloric central pattern generator.
1 Introduction
Coherent rhythmic activity in the brain has been proposed to rely on the intrinsic tendency of neurons to produce a preferred subthreshold response to signals of a fixed frequency [2]. This property of neurons, known as membrane or cellular resonance, has been extensively studied in relationship to subthreshold network oscillations and signal processing [2][4]. Recently, it was demonstrated that synapses with short-term dynamics can also respond preferentially to signals arriving at a given frequency and have an attenuated response to signals at lower or higher frequencies [3]. This property is termed synaptic resonance [3] and can occur, for example, if the synapse demonstrates both short-term facilitation and depression. At this time little is known about the interaction between cellular and synaptic resonant properties in producing network activity.
Our analysis of neurons and synapses of a rhythmically active network, the pyloric central pattern generator of the crab Cancer borealis, shows that both neurons and synapses in this network demonstrate resonance properties. We focus on the connection between pacemaker and follower neurons and show that the follower neuron LP has a cellular resonance at a peak frequency that is distinct from the resonant frequency of the synapse it receives from the pacemaker neurons AB and PD. These distinct resonant frequencies point to a more general question: if cellular and synaptic resonances occur at different frequencies, do they interact to produce a net output resonance and, if so, at what frequency does this combined resonance occur?
In this study we examine how cellular and synaptic resonance properties interact to determine the resonant properties in a feed-forward network. Specifically, we examine the response of a postsynaptic cell that exhibits cellular resonance when it receives input from a resonant synapse. The network is driven by a fixed-frequency input that mimics input from a presynaptic cell. Of particular interest is the stimulus frequency that results in the largest subthreshold postsynaptic amplitude. We refer to this frequency as the generalized resonant frequency of the network. In this work, we do not consider supra-threshold behavior of the postsynaptic cell.
2 The Model
We consider the response of an excitable cell to periodic synaptic input. The cell model used is the Hodgkin-Huxley (HH) model [1]. The motivation for our choice is that when the HH model is in its resting state, it exhibits subthreshold resonance. Sufficiently large synaptic inputs can result in supra-threshold behavior; however, we shall not consider such inputs in this study.
The Hodgkin Huxley model with synaptic input is given by
where x = h, m, n. The gating functions, α and β and associated parameter values are standard [1]. The variable s represents the ratio of the total possible neurotransmitter being used by the synapse.
We use two different models for synaptic input s. In Model 1, we assume that synaptic strength is a Gaussian function of input frequency and use this theoretical construct to examine the effects of such a synapse on resonance properties of the postsynaptic neuron. In Model 2, we implement the frequency-dependent changes in synaptic strength by assuming that the synapse exhibits short-term facilitation and depression. This more realistic synapse is used to demonstrate the biological application of our theoretical construct.
Model 1 is given by the equation
| (1) |
where κ(f) denotes maximum synaptic transmission, determined by short-term synaptic dynamics. Vpre is the presynaptic voltage. The functions αsyn and βsyn are Heaviside functions that satisfy αsyn(V) = Heav(V −Vθ) and βsyn = Heav(Vθ − V), where Vθ is the synaptic release threshold. We assume that κ(f) is a Gaussian function:
| (2) |
This is a dimensionless variable so that σ has units ms2.
In Model 2, we utilize the model of a depressing/facilitating synapse given in [8]. The equations for this synapse are
| (3) |
where x is fraction of total synaptic resources available, s is the fraction of resources currently in use, and z is the fraction in the recovery state. The parameter τ1 is the synaptic decay time and τrec is the recovery time. tsp is the time that a presynaptic spike occurs. To incorporate facilitation we let u evolve according to
| (4) |
where τfacil is the time it takes for the facilitation to wear off and U represents the contribution of each presynaptic spike to facilitation.
We quantitatively describe the synaptic and cellular resonance properties using a pair of functions of the presynaptic firing rate. The synaptic response curve (SRC) is denoted by κ(f). This function determines the synaptic strength, relative to a maximum, for a given frequency. In Model 1 this function is explicitly given by (2). For Model 2, κ(f) is computed numerically. In particular, a presynaptic neuron activates the synapse given by equations (3) and (4) at different assigned frequency. The maximal steady-state value of s is then plotted for each value of f to obtain the SRC. The cellular resonance curve (CRC), denoted by A(K, f), measures the amplitude of subthreshold oscillations. K is a frequency-independent stimulus strength and f is the input frequency. To obtain the CRC for the HH equations we determine the amplitude for a stimulus of fixed frequency and repeat the stimulus at different frequencies. The CRC is defined as the trough-to-peak amplitude of the response.
We define the generalized response curve (GRC), to be the amplitude of subthreshold oscillations in the postsynaptic cell as a function of presynaptic frequency. The function that describes this curve can be written as A(κ(f), f) where A(K, f) and κ(f) are the CRC and SRC, respectively.
Biological Methods
Experiments were carried on adult male crabs (C. Borealis) purchased from local distributors (Newark, NJ). Details of experimental measurements are identical to those described in [5]. Spontaneous activity in the pyloric network was blocked by superfusion with saline containing 0.1 μM TTX (Biotium, CA). (TTX does not block graded synaptic release in this system.) For measurements of synaptic resonance the presynaptic neuron was voltage clamped with two electrodes (TEVC) and a ZAP function waveform, a constant amplitude input where the frequency of oscillations is slowly increased in time, was used as the voltage command. The ZAP waveforms were injected with the software Scope on a PCI-6070-E board (National Instruments, Austin, TX). Data were acquired using the same software and board as well as a Digidata 1332A board with the PClamp 9.2 software (Molecular Devices, Union City, CA). Acquired data were saved as binary files and were analyzed with Readscope and PClamp software. Scope and Readscope are software developed in the Nadim lab (http://stg.rutgers.edu/software/index.htm). Peaks of the IRC, SRC and GRC in the biological recordings were obtained using FFT filter smoothing.
3 Results
Experimental
The PD and LP neurons are members of the pyloric central pattern generator network in the crab Cancer borealis. The PD neurons are members of the pyloric pacemaker group and produce inhibitory synapses to the LP neuron. We measured the CRC in the LP neuron by injecting a ZAP current waveform and recording of the membrane voltage response. The CRC of the LP neuron peaked at 1.5 Hz indicating the membrane resonance frequency (Fig. 1). For measurement of the SRC, the presynaptic PD neuron was voltage clamped with a ZAP function voltage waveform while the synaptic current was measured in the postsynaptic LP neuron which was voltage clamped at a holding potential of −60 mV. The SRC exhibited a peak synaptic response at 0.3 Hz (Fig. 1). The GRC was measured by voltage clamping the PD neuron using a ZAP waveform (as in the SRC measurement) but recording the postsynaptic response in the LP neuron in current clamp mode. Thus, the voltage response in the postsynaptic LP neuron was determined by both the synaptic input it received from the PD neuron and its own intrinsic dynamics. The GRC showed a peak response at 0.6 Hz (Fig. 1). These results showed distinct peak frequencies of the SRC and CRC and also that the GRC peak frequency fell between these two peaks.
Figure 1.
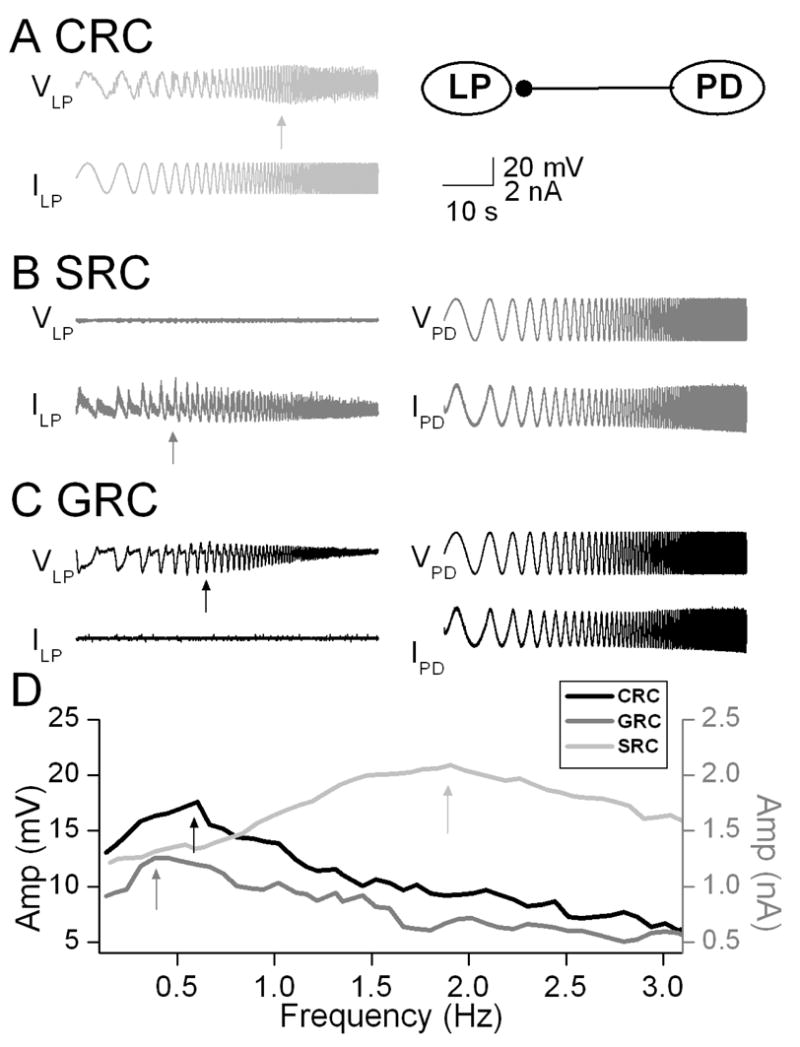
Measurement of CRC, SRC and GRC in the crab pyloric network. A. The CRC of the LP neuron was measured by injection a ZAP current of amplitude +/−2 nA sweeping frequencies between 0.1 and 5 Hz and indicated a resonance frequency at 1.9 Hz. Inset shows schematic diagram indicating the synaptic connection from the PD neuron to the LP neuron. B. The SRC was measured by voltage-clamping the PD neuron with a ZAP function waveform and measuring the synaptic current in the LP neuron. The LP neuron was voltage clamped at a holding potential of −60 mV. The SRC showed a peak value at 0.3 Hz. C. The GRC was measured by injecting a ZAP function waveform into the voltage-clamped PD neuron while the postsynaptic response of the LP neuron was measured in current clamp. The GRC showed a peak value at 0.6 Hz D. The CRC, SRC and GRC plotted as a function of frequency indicate the distinct peaks of the CRC and the SRC and that the GRC peak falls between these two values.
Modeling
We now determine how the location of the local maximum of the GRC depends on the properties of the CRC and SRC. This will be a local maximum for the function A(κ(f), f) which can be found by solving
The local maximum of the SRC occurs at the so-called resonant frequency of the synapse which we denote by fs. Similarly, the local maximum of the CRC occurs at resonant frequency of the cell, denoted by fc. We assume, without loss of generality, that fc < fs. We also assume that κ(f) and A(K, f) are monotone functions on the interval I = [fc, fs] and that they are each differentiable functions of f and K; see Fig 2.
Figure 2.
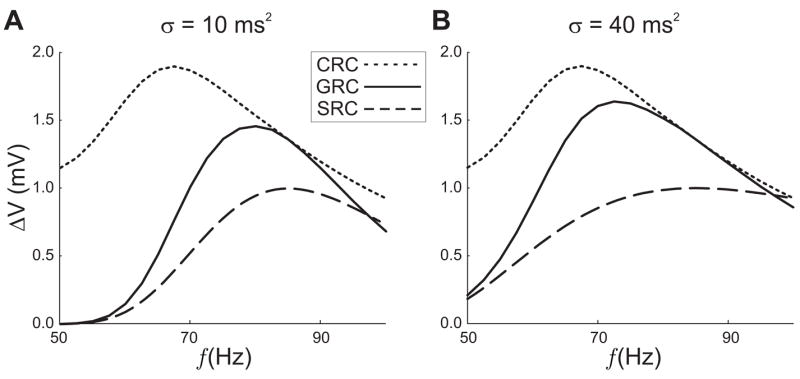
The response curves corresponding to equations (1–2). The CRCs (dotted curves) are the amplitude of oscillations for the given frequency (horizontal axis). The GRCs (solid curves) are the oscillation amplitude of the postsynaptic response when the signal is generated using a resonant synapse. The SRCs (dashed) are unitless curves superimposed so that the preferred resonant frequency can be seen. The maximum network response occurs for a frequency that is neither the resonant frequency for the cell nor the preferred frequency for the synapse. In the left panel σ = 10 ms2, resulting in a steeper profile for the SRC than in the right panel. The peak of the GRC is located closer to the peak of the SRC than in the right panel (σ = 40 ms2).
Note
The assumption that fc < fs is the opposite of what occurs in the experiments, however these results apply regardless of which resonant frequency is larger.
A generic property of most neurons is that the amplitude of subthreshold oscillations increases with stimulus strength. Making this assumption, here, yields
| (5) |
As a function of frequency, however, the CRC A(K, f) is monotone decreasing on I (Fig. 2a) since it attains it local maximum at f = fc. Therefore for f ∈[fc, fs],
| (6) |
Similarly, the assumptions on the synaptic profile imply that on the interval I, the SRC obeys
| (7) |
Note that equality holds in (6) when f = fc and in (7) when f = fs. Next differentiate to obtain
| (8) |
We can show that the location of the local maximum of the GRC lies between fc and fs by showing that the derivative dA/df = 0 for some f ∈(fc, fs). At f = fc, from (6), . Equations (5) and (7) then imply that the right-hand side of (8) is positive when f = fc. Thus near f = fc as frequency increases, the amplitude of subthreshold oscillations increases. Similarly, at f = fs, κ′ (fs) = 0 from (7) and from (6), ∂A/∂f < 0. Thus the right-hand side is negative at f = fs and A(κ(f), f) is decreasing near this value. Since A(κ(f), f) is increasing at f = fc (dA/df) < 0) and decreasing at f = fs (dA/df > 0), there must be an intermediate frequency at which dA/df = 0, corresponding to a local maximum of A(κ(f), f), the GRC.
This theoretical argument shows that the presynaptic frequency corresponding to the (locally) maximum response occurs for neither the resonant frequency of the synapse nor the resonant frequency for the cell, but between them. If we assume a fixed CRC, then the location, within I, of the GRC maximum depends on the steepness of the synaptic profile and the location of its peak (fs). For very steep synaptic profiles (κ′ (f) large on I), the preferred frequency of the network will be very close to that of the synapse. For flat synaptic profiles (κ′(f) ≈ 0 on I), the preferred network frequency will be near the that of the cell.
We now turn our attention to the synaptic models described earlier. To demonstrate the dependence of the GRC on the shape of the SRC curve, we consider Model 1 where the synapse evolves according to equation (1) and κ(f) is simply a Gaussian. In Figure 2 the GRC is shown along with the numerically computed CRC and the Gaussian κ(f) for σ = 10 sec−1. Most important to note is the location of the maximum of the GRC which clearly lies between the local maxima of the CRC and SRC. In Fig. 2, we demonstrate how the steepness of the synaptic profile influences the preferred network frequency. In this case, we compare the SRC with σ = 40 ms2 to a SRC with σ = 10 ms2 in equation (2). The smaller value of σ results in a much flatter SRC. The resonant frequency of the GRC is shifted toward the peak of the CRC, as predicted by the theory.
In Model 2, the synapse is governed by equations (3) and (4) and the SRC has a frequency dependent peak due to the combination of short-term facilitation and short-term depresssion. the SRC, CRC and GRC shown in Fig. 3 (with parameter values given in the caption) demonstrate that the prediction of the location of the GRC peak is also valid for a biologically realistic synaptic input. As predicted, the peak of the GRC lies slightly to the right of the peak of the CRC and to the left of the peak of the SRC. Because the SRC is rather flat, resonant network frequency is much closer to that of the cell than the synapse.
Figure 3.
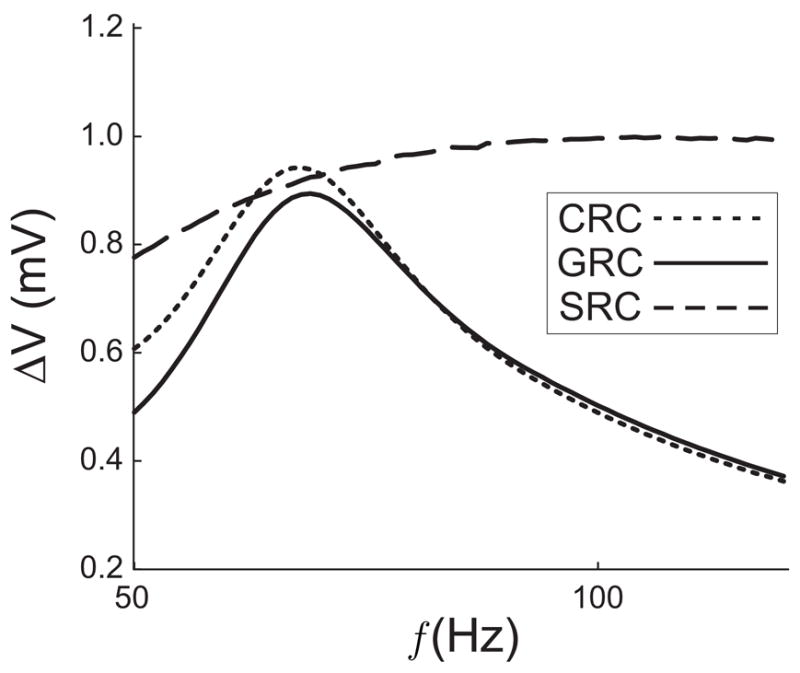
The SRC, CRC, and GRC when the synapse described by (3) (4) is used. The Hodgkin-Huxley parameters are the same as in Fig. 2. Parameter values for the synapse in this figure are τrec = 125, τ1 = 3, τfacil = 100 and U = 0.01. The peak of the SRC is hard to discern in the figure, but lies near 130 Hz.
4 Discussion
Many neurons and synapses respond optimally at a preferred resonant frequency. How resonance properties of neurons and synapses interact in a network setting remains an interesting and challenging question. We have shown that in the crab pyloric network, cellular and synaptic resonances interact to produce a maximum-amplitude subthreshold response at an intermediate frequency. This led us to develop a mathematical framework to examine whether this interaction between cellular (CRC) and synaptic (SRC) response curves holds in general. Our results show that the resonant frequency of a feed-forward network indeed lies between the resonant frequencies of the synapse and the postsynaptic neuron. We also demonstrate that by changing the shape of the CRC or SRC, while keeping the location of the resonant frequencies associated with these curves fixed, the shape of the combined response (GRC) can be changed and its resonant frequency can be shifted. In general, these results suggest that resonance properties can interact in non-intuitive ways. The central result is that synaptic resonance and cellular resonance combine to create a network resonance. This result provides a theoretical tool to simplify networks that contain a resonant synapse that is connected to a resonant cell. The individual properties of the synapse and the cell can be merged into as single curve, given here as the GRC.
Biological confirmation of the theoretical results presented in this study requires a demonstration that a shift in CRC curve peak or slopes would affect the GRC with a corresponding pattern. We are currently examining this prediction using ion channel blockers and dynamic clamp techniques.
It is important to note that the theoretical location presented here only identifies local maxima for the GRC. It is possible, and not uncommon, for the CRC to have multiple local maxima typically located at integer multiples of the resonant frequency. The auxillary peaks are not as large as the original since the trajectory has more time each cycle to relax toward rest. The SRC, on the other hand, can only have a single local maximum. Thus, there will always be an interval with the peaks of the GRC and SRC as endpoints that satisfies the hypothesis of our analysis such that the desired interval I exists. It is on this interval that our analysis applies.
A future step to be undertaken is to use mathematical analysis to understand how sub-threshold resonance relates to the spiking behavior of neurons [7]. We are currently studying this problem in the context of feedback networks modeled on the PD-LP neuron loop of the crab.
Acknowledgments
Supported by an NJIT Strategic Initiative Grant to the Department of Mathematical Sciences (JDD), NIH grant MH-60605 (FN) and NSF grant DMS-0315862(AB).
References
- 1.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–44. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hutcheon B, Yarom Y. Resonance oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 2000;23:216–22. doi: 10.1016/s0166-2236(00)01547-2. [DOI] [PubMed] [Google Scholar]
- 3.Izhikevich EM, Desai NS, Walcott EC, Hoppensteadt FC. Bursts as a unit of neural information: selective communication via resonance. Trends Neurosci. 2003;26:161–7. doi: 10.1016/S0166-2236(03)00034-1. [DOI] [PubMed] [Google Scholar]
- 4.Lampl I, Yarom Y. Subthreshold oscillations of the membrane potential: a functional synchronizing and timing device. J Neurophysiol. 1993;70:2181–6. doi: 10.1152/jn.1993.70.5.2181. [DOI] [PubMed] [Google Scholar]
- 5.Manor Y, Nadim F. Synaptic depression mediates bistability in neuronal networks with recurrent inhibitory connectivity. J Neurosci. 2001;21:9460–70. doi: 10.1523/JNEUROSCI.21-23-09460.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Puil E, Meiri H, Yarom Y. Resonant behavior and frequency preferences of thalamic neurons. J Neurophysiol. 1994;71:575–82. doi: 10.1152/jn.1994.71.2.575. [DOI] [PubMed] [Google Scholar]
- 7.Richardson MJ, Brunel N, Hakim V. From subthreshold to firing-rate resonance. J Neurophysiol. 2003;89:2538–54. doi: 10.1152/jn.00955.2002. [DOI] [PubMed] [Google Scholar]
- 8.Tsodyks M, Uziel A, Markram H. Synchrony generation in recurrent networks with frequency-dependent synapses. J Neurosci. 2000;20:1–5. doi: 10.1523/JNEUROSCI.20-01-j0003.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]


