Temperature dependence of salt-protein association is sequence specific

Abstract

Molecular dynamics (MD) simulations are used to probe the origin for the unexpected temperature dependence of salt accumulation in the C-terminal region of the protein human Lymphotactin. Similar to previous MD simulations, sodium ions are observed to have enhanced accumulation near the C-terminal helix at the lower temperature while the temperature dependence of chloride accumulation is much weaker and slightly positive. In a designed mutant in which all positively charged residues in the C-terminal helix are replaced by neutral polar groups (Ser), the unexpected temperature dependence of the sodium ions is no longer observed. Therefore, the current simulations convincingly verified the previous hypothesis that the temperature dependence of ion-protein association is sensitive to the local sequence. This is explained qualitatively in terms of the association entropy between charged species in solution. These findings have general implications on the interpretation of thermodynamic quantities associated with binding events where ion release is important, such as for protein-DNA interactions.

Biomolecules exist in a heterogeneous cellular environment to play their functional roles. It has been widely recognized that environmental factors such as temperature and the presence of small solutes and ions can influence the conformational stabilities of biomolecules and therefore their function.(1-3) For example, a vast amount of literature has shown that different salt ions preferentially stabilize the native or denatured state of proteins and therefore modulate the folding/unfolding equilibrium. (4-7) Small solute effects have also been proposed to be relevant to the long-range communication of biomolecules in cellular environments.(2) A quantitative theory that is capable of predicting the effect of identity and concentration of small solutes on the structure and stability of biomolecules, however, is not yet available. Therefore, it is of interest to employ atomistic simulations to reveal detailed descriptions for the interaction between biomolecules and small solutes as well as how the interaction depends on environmental variables such as temperature. The insights will provide essential clues regarding the molecular mechanism that biomolecules employ to respond and adapt to environmental variations.

A remarkable example in this context is the human Lymphotactin (hLtn). Recent NMR experiments have shown that hLtn converts between two distinct folds upon different salt and temperature conditions and it also tends to dimerize under the high-temperature (∼45°C) and low-salt condition.(8) In our recent molecular dynamics (MD) simulation study of hLtn,(9) an intriguing finding is that sodium ions, and chloride to a lesser degree, tend to increase their association with the C-terminal region of hLtn as temperature decreases. This is unexpected since the dehydration free energies of both ions and charged sidechains are lower at higher temperature and thus ion-protein association is expected to be stronger at the higher temperature, (10) which is indeed what was observed for most regions of hLtn except the C-terminal helix. Thus the result hinted at the sequence sensitivity for the temperature dependence of ion-protein association, although influence from other factors such as structural fluctuations could not be ruled out. (9)

A specific hypothesis raised in that study (9) is that the unexpected temperature dependence is due to the presence of residues of mixed charges in the C-terminal region (see below). To explicitly test this hypothesis without other complicating factors, we carry out MD simulations for the hLtn C-terminal helix itself and a designed mutant. The wild type sequence is ATWVREVVRSMDRKSN (charged residues are underscored) with a net charge of +2. In the mutant, all positively charged residues are replaced by neutral polar residues, resulting in the sequence ATWVSEVVSSMDSSSN with a net charge of −2. The expectation of the design is that the unusual temperature dependence of the salt-peptide association is observed only in the wild type but not the mutant peptide.

Methods

1. Molecular dynamics simulations

All simulations are carried out using the program CHARMM. (11) The starting structure for the wild type C-terminal helix is taken from the NMR structure of hLtn (PDB code 1J9O). For the designed mutant, the sidechains of positively charged residues are replaced by that of serine. The peptide is solvated in a Rhombic Dodecahedron solvent box and sodium and chloride ions are added to keep the charge neutrality of the system with an approximate concentration of 200 mM. The simulation set-up details are listed in Table 1. The SHAKE algorithm (12) is used to allow an integration time step of 2 fs. A switching (13) scheme for interatomic distances between 10 and 12 Å is used for van der Waals interactions. For electrostatic interactions, the particle mesh Ewald scheme (14) is used. After system assembly, heating is done with the peptide atoms harmonically restrained using a force constant of 40 kcal/mol/Ų. Twenty pico-seconds of equilibration and ∼23 nano-seconds of production runs are performed with constant temperature and pressure; peptide backbone atoms are always harmonically restrained to avoid large structural variations thus minimizing the number of variables that affect the ion-peptide association. The temperature is controlled using the Nose-Hoover algorithm,(15, 16) using a mass of 250 kcal·ps² for the thermostat and a reference temperature equal to the desired system temperature (10 or 45°C). The pressure is controlled with the Anderson algorithm,(17, 18) using a mass of 500 amu for the pressure piston, a reference pressure of 1 atm, a Langevin piston collision frequency of 10 ps⁻¹ and a Langevin piston bath temperature equal to the desired system temperature.

Table 1.

Simulation setup for all molecular dynamics calculations.

System	Statea	Number of Cl− ions	Number of Na+ ions	Average Box lengthb (Å)	Simulation time (ns)
Wild type	s10	10	8	47.7	23
Wild type	s45	10	8	48.2	23
Mutant	s10	8	10	47.7	23
Mutant	s45	8	10	48.2	24

^as10, s45 refer to salt condition [NaCl] =200 mM, 10 °C and 45°C, respectively.

^bthe average box lengths are for the Rhombic Dodecahedron periodic system.

2. Calculation methods for the radial distribution function g(r) and its integration N(r) based on MD simulations

For the calculations of ion-peptide-surface radial distribution function, g(r), the shortest distances between a specific type of ions (sodium or chloride) to the peptide atoms are collected from MD simulation trajectories and binned (δN(r)). The volume factor (δV) corresponding to the bin (r, dr) is estimated using the volume function in CHARMM (COOR VOLU) with all the peptide atoms (irrespective of atom type) having a radius of either r+dr/2 or r-dr/2; i.e. δV=V(r+dr/2)-V(r-dr/2). The ion-surface radial distribution function is then calculated as,

$$g\left(r\right)=\frac{\delta N\left(r\right)1}{\delta V\left(r\right){\rho }_{\infty }}$$ (1)

in which the ‘bulk number density’ (ρ_∞) is estimated by dividing the number of ions by the average volume of the simulation box.

The radial distribution functions are also integrated over the distance from the peptide surface to provide a more explicit description for the average number of ions N(r) accumulated around the peptide.

3. Non-linear poisson-boltzmann (PB) calculations

The non-linear Poisson-Boltzmann calculations are also carried out to explore the temperature dependence of ion-protein association to compare with MD simulations. Peptide snapshots are collected from the explicit simulations and the ion distributions at different temperatures are calculated. The set of atomic radii established by Roux and co-workers (19) is used together with a solvent probe radius of 1.4 Å and a stern ion-exclusion layer of 2 Å. The partial charges are those in the standard CHARMM 22 force field for proteins.(20) The grid consists of 201³ points spaced by 0.2 Å. As to the value of the dielectric constant, a value of 2 is used for the protein and assumed to be independent of temperature. The dielectric constant of bulk water, however, is taken as a function inversely dependent on the temperature;(10) specifically, the value is 83.9 and 71.6 at 10°C and 45°C, respectively.

Once the electrostatic potential is solved using PB, the ion distribution can be obtained by the Debye-Hückel expression,

$${\rho }_{N{a}^{+}∕C{l}^{-}}\left(\overrightarrow{r}\right)={\rho }_{\infty }\exp [-\beta q_{N{a}^{+}∕C{l}^{-}}\varphi \left(\overrightarrow{r}\right)]$$ (2)

where ρ_∞ is the bulk salt concentration, β the inverse temperature and q the charge of a specific type of ion.

4. Multiple Sequence Alignment

Multiple sequence alignment for several hLtn orthologs in different organisms is performed using the program MUSCLE (21) and the sequence conservation in the C-terminal helix is investigated.

Results and Discussion

1. Ion-peptide association from molecular dynamics simulations

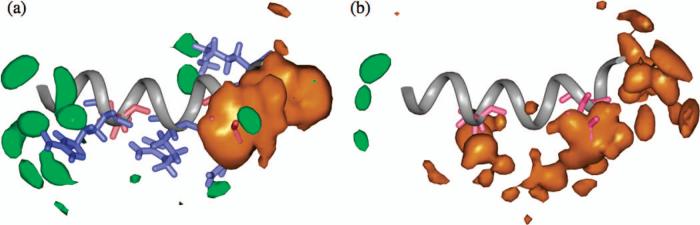
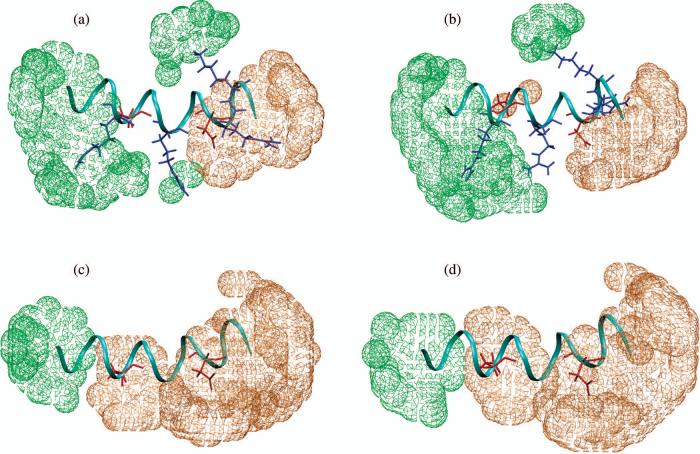
At a given temperature (Fig. 1, 10°C), the sequence dependence of ion-peptide association follows expectation. The wild type peptide has both positively and negatively charged residues thus both sodium and chloride associate to a notable degree. The mutant, by contrast, has only negatively charged residues and therefore only sodium ions accumulate significantly.

Figure 1.

Three dimensional ion density contours around (a) wild type and (b) mutant C-terminal helix of hLtn from MD simulations at 10°C. Chloride and sodium are shown in green and orange, respectively; positively and negatively charged residues are shown in blue and red, respectively. Density cutoff is 0.8 ions/nm³.

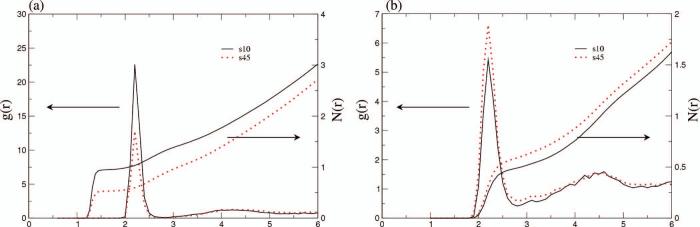
The temperature dependence of the salt-peptide association largely follows the trend suggested by the hypothesis (9) that motivated this study. For the wild type system, sodium ions weakly associate with the peptide; the integrated ion radial distribution function relative to the peptide surface, N(r), reaches about 1.0 at r=3.0 Å in the 10°C simulation and decreases to about 0.5 at the same distance in the 45°C simulation (Fig. 2a; for the convergence behavior of N(r), see Supporting Materials). For chloride-peptide association, the value of N(r) seems lower than that for sodium up to r=6.0 Å in the 10°C simulation and shows very little variation (slight increase) as the temperature increases to 45°C (Fig. 2b).

Figure 2.

The radial distribution function, g(r), of ions to the peptide surface, and its integration, N(r), for the wild type C-terminal helix of hLtn at 10°C and 45°C from MD simulations. (a) sodium and (b) chloride. Labels s10, s45 refer to 200mM NaCl at 10°C and 45°C, respectively. Note the difference in the y-axis scales.

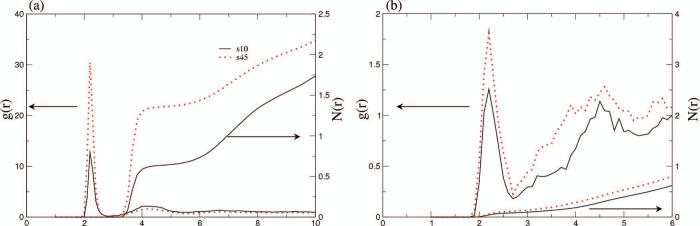
For the mutant peptide, since there are no positively charged residues there is little chloride-peptide association (Fig. 1b). At 10°C, the sodium-peptide N(r) at short distances is slightly lower than that calculated for the wild type peptide (compare Fig. 3a and Fig. 2a). Remarkably, the temperature dependence of N(r) for the mutant is “normal”; i.e., the N(r) increases as the temperature increases to 45°C (Fig. 3a). We note that the different temperature dependence of ion-peptide association can't be reproduced in Poisson-Boltzmann calculations where both solvent and ions are treated implicitly (see below).

Figure 3.

The radial distribution function, g(r), of ions to the peptide surface, and its integration, N(r), for the mutant C-terminal helix of hLtn at 10°C and 45°C from MD simulations. (a) sodium and (b) chloride. Labels s10, s45 refer to 200mM NaCl at 10°C and 45°C, respectively. Note the difference in the y-axis scales.

Regarding the ion association at a given temperature, it is somewhat surprising that chloride association is consistently lower than sodium regardless of the peptide sequence because sodium ion has a larger solvation free energy than chloride and therefore is expected to prefer solvated.(22-25) This might reflect a deficiency of the current CHARMM force field for ions, and it would be of particular interest in the future to compare results to simulations using polarizable force fields.(26, 27)

Regarding the different temperature dependence on the sodium-peptide association, since the structure of the peptide is held to be rather rigid except for the fully flexible sidechains, the drastically different temperature dependence of ion-peptide association in the wild type and mutant systems has to be caused by sequence variation. In our previous study, (9) we noted that the C-terminal helix is clustered with both positively and negatively charged residues; accordingly, the unexpected temperature dependence for ion accumulation in this region was rationalized qualitatively based on the association entropy of charged species in solution. For example, previous integral equation analysis (28) showed that the association of opposite-charge species in solution has a significant entropic driving force since water release during the association process is favorable entropically. Association of like-charge species, by contrast, has a significant enthalpic driving force and is entropically unfavorable, since the enhanced local electric field upon association restricts the mobility of nearby water molecules. In fact, these trends are easy to see qualitatively from the perspective of continuum electrostatics in which the potential of mean force and entropy for ion (A,B)-association have simple forms,

$$W(r;T)=q_A{q}_B∕\left[\epsilon \left(T\right)r_{AB}\right]$$ (3a)

$$S(r;T)=-\partial W∕\partial T=q_A{q}_B∕\left[{\epsilon }^2\left(T\right)r_{AB}\right]\partial \epsilon \left(T\right)∕\partial T$$ (3b)

Since the temperature derivative of the water dielectric constant is negative, the entropy of association is positive for opposite-charge species but negative for like-charge species.

Since the hLtn C-terminal peptide is clustered with five positively charged groups and three negatively charged groups (including the N, C-termini), the negative association entropies between sodium ions and positively charged groups overwhelm the positive association entropies between sodium and negatively charged groups, thus resulting in decreased sodium-peptide association as temperature increases. For chloride ions, there are only three like-charge groups but five opposite-charge groups in the wild type peptide and therefore the “normal” temperature dependence is maintained; the presence of the like-charge groups nevertheless makes the temperature dependence very weak. In the mutant peptide without any positively charged sidechains, larger and normal temperature dependence for sodium-peptide association is expected and observed.

Although the above argument seems to explain the qualitative findings from the simulations, it is important to realize that the decomposition of protein-ion association into the entalphic and entropic components is complex at a quantitative level. Even for the interaction between simple ions in solution, it has been well established that enthalpic and entropic components vary as a function of the inter-ionic distances.(29) It is perhaps possible to perform a deeper analysis in terms of the Kirkwood-Buff integrals,(30, 31) which we leave to future work. More importantly, it is worth pointing out (as emphasized by an anonymous referee) that many processes in a multi-component solution may be sensitive to temperature. Therefore, it is of interest to examine whether the unexpected temperature dependence of sodium-peptide association in fact reflects other processes such as sodium-chloride association and salt-bridge formation between peptide sidechains.

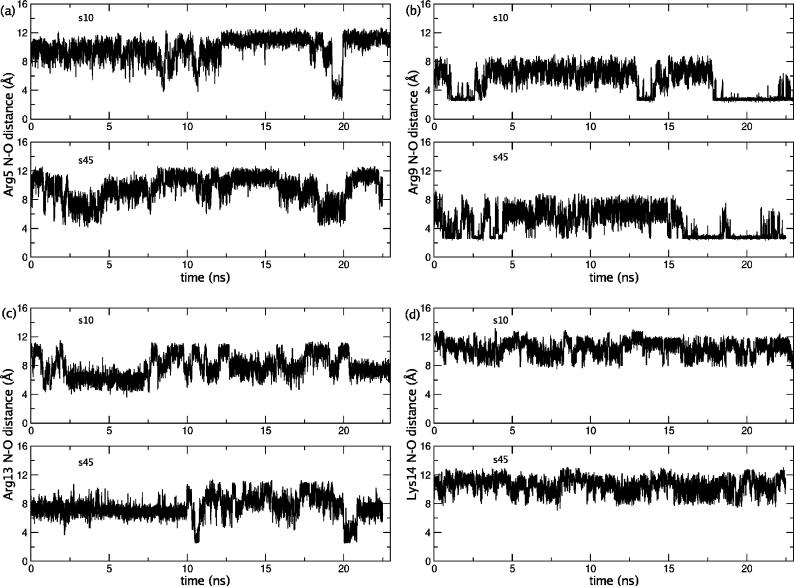
As shown in the Supporting Information, the sodium-chloride association exhibits the expected temperature dependence in both the wild type and mutant peptide simulations. Regarding the salt-bridge dynamics associated with the wild type peptide sidechains (no salt-bridge is possible in the mutant), the minimal distance between four positively charged sidechains and all negatively charged sidechains (including the C-terminus) are monitored throughout the simulation. The salt bridge is regarded as formed if the distance between the nitrogen atom of positively charged residues (NH1, NH2 for Arg and NZ for Lys) and the oxygen atom of negatively charged residues (OD1, OD2 for Asp and Glu, OT1, OT2 for the C-terminus) is less than 4.0 Å.(32) It is shown in Fig.4 that Lys14 is not involved in any salt bridge whereas Arg5 and Arg13 only form salt bridge sporadically (several hundred ps out of ∼23 ns). Arg9 is the only positively charged residue that forms relatively stable salt bridges (with Asp6) at both temperatures. The interaction appears stronger at the higher temperature based on the life-time of the salt-bridge interactions although it is difficult to quantify with only ∼23 ns of simulations. Nevertheless, we note that the salt bridge between Arg9 and Asp6 is mainly formed after 12 ns, when the distribution of sodium and chloride ions around the peptide has largely converged (see the convergence plot in Supporting Information), implying that the formation of salt bridge does not have a major effect on the salt-peptide association in our simulations. In short, we conclude that neither sodium-chloride association or salt-bridge dynamics is a major factor that leads to the unexpected temperature dependence of sodium-peptide association in the wild type system, which further supports our hypothesis(9) based on the association entropies of different ionic pairs in solution.

Figure 4.

The minimal N-O distance (see text) between four positively charged sidechains and all negatively charged sidechains (including the C-terminus) along the simulation trajectory for the wild type peptide at different temperatures. (a) Arg5, (b) Arg9, (c) Arg13, (d) Lys14. Labels s10 and s45 refer to 200mM NaCl at 10°C and 45°C, respectively.

2. Ion-peptide association from non-linear PB calculations

The temperature dependences of ion distribution around the wild type peptide and the mutant peptide from PB calculations are shown in Fig. 5. As temperature increases from 10°C to 45°C, both ions accumulate more around both two peptides. Since peptide backbones are held rigid during simulations, only results for two snapshots for each peptide are shown (though calculations averaged over snapshots are done and the results are similar). Clearly, PB calculations cannot reproduce the abnormal temperature dependence of ion distribution around the wild type peptide since PB treats the solvent as a dielectric continuum without properly taking into account the solvent entropy. Therefore, the different temperature dependence for ion-peptide association in the wild type and mutant peptides can't be understood as a result of the difference in the net charge (+2 vs. −2) and further supports our entropy-based explanation. We emphasize that the failure of PB in this case is likely due to the implicit treatment of the ions in solution. Indeed, as shown in Supporting Information, PB calculations can successfully capture the different temperature dependence for the interaction between ion-sidechain pairs of different charges, provided that the ion is represented explicitly and the temperature dependence of the water dielectric is taken into account.(10) In other words, there is no conflict between the failure of PB as illustrated in Fig. 5 and using Eq. 3 to rationalize the sign of association entropy for different ion-sidechain pairs.

Figure 5.

Ion distribution difference Δρ_{Na⁺ /Cl⁻} (ρ₄₅°_C-ρ₁₀°_C) by non-linear PB calculations around (a), a wild type peptide snapshot from s10 simulation; (b), a wild type peptide snapshot from s45 simulation and (c) a mutant peptide snapshot from s10 simulation and (d) a mutant peptide snapshot from s45 simulation. Sodium density increase is shown in orange, and chloride density increase is shown in green. Density difference cutoff is 0.1*ρ_∞ for both ions.

3. Multiple Sequence Alignment

All the trends observed in the current set of MD simulations can be explained by considering association entropy of charged species in solution, which highlights the importance of local sequence in determining the temperature dependence of ion-protein association. Whether hLtn takes advantage of this interesting behavior for its function remains debatable, although it is interesting to note that the result of multiple sequence alignment reveals that the feature of alternating positively and negatively charged residues in the C-terminal region is conserved among several lymphotactin family members (Fig. 6), which seems to imply that this design is related to hLtn stability and function. However, it may also simply reflect that dimerization, which was found to be sensitive to temperature salt concentration,(8) has an important electrostatic component.(9)

Figure 6.

Multiple Sequence Alignment for several hLtn orthologs in different organisms. Only the C-terminal helix region is shown. Positively charged residues are shown in blue and underscored by “+” and negatively charged residues are shown in red and underscored by “−”.

Concluding Remarks

Using the C-terminal helix of hLtn and its designed mutant, we show that the temperature dependence of ion-protein association is highly dependent on the distribution of charged residues. This sequence specificity can be qualitatively explained by taking into account the association entropy of charged species in solution and cannot be captured by PB calculations that treat solvent and ions in an implicit manner. The association between sodium-chloride ions in solution and the salt-bridge dynamics in the wild type peptide also exhibit temperature dependence, although neither is likely to have a major influence on the ion-peptide association in the present simulations.

Although the current work focuses on protein-salt association, our discussion on the association entropy of charged species have general implications for bimolecular association involving significant electrostatic components, such as protein-DNA interactions. (33) For example, since ion release upon binding is an important component in binding thermodynamic quantities such as heat capacity change, (1-7) the finding that ion distribution around the protein may have variable temperature dependence sensitive to the local sequence suggests that additional complexity may arise that further complicates the thermodynamic analysis. Finally, we encourage direct experimental probe of ion-protein association as functions of temperature and local sequence, which might be possible with recent developments of x-ray spectroscopy techniques using liquid microjets. (34)

Abbreviations

MD

Molecular Dynamics

hLtn

human Lymphotactin

PB

Poisson-Boltzmann