Abstract
Hierarchical (or multilevel) statistical models have become increasingly popular in psychology in the last few years. We consider the application of multilevel modeling to the ex-Gaussian, a popular model of response times. Single-level estimation is compared with hierarchical estimation of parameters of the ex-Gaussian distribution. Additionally, for each approach maximum likelihood (ML) estimation is compared with Bayesian estimation. A set of simulations and analyses of parameter recovery show that although all methods perform adequately well, hierarchical methods are better able to recover the parameters of the ex-Gaussian by reducing the variability in recovered parameters. At each level, little overall difference was observed between the ML and Bayesian methods.
Bayesian and maximum likelihood estimation of hierarchical response time models
Given the importance of the dynamics of behavior to theories of cognition, it is unsurprising that a number of methods have recently been developed to facilitate and simplify application of mathematical models of response times (e.g., Cousineau, Brown, & Heathcote, 2004; Vandekerckhove & Tuerlinckx, 2008; Wagenmakers, van der Maas, & Grasman, 2007). Such models are capable of providing a much richer characterization of the effect(s) of some experimental manipulation compared to an analysis of just central tendency (Andrews & Heathcote, 2001). However, stable estimation of distribution parameters is often hindered by the relatively small number of observations collected in psychology. In this context, one important development has been the introduction, by Rouder and colleagues, of a hierarchical Bayesian model to estimate the parameters of a response time (RT) model (Rouder, Lu, Speckman, Sun, & Jiang, 2005; Rouder, Sun, Speckman, Lu, & Zhou, 2003). In this multilevel approach, parameters are estimated for individual participants, and these parameters are themselves assumed to be drawn from distributions defining variation across individuals. In the approach advocated by Rouder and colleagues, posterior probability densities are estimated for individuals and populations in a Bayesian framework. Rouder et al. (2005) demonstrated the wide applicability of their approach, and showed that their Bayesian hierarchical method gave more accurate estimates of the parameters of individuals than classical single-level (i.e., non-hierarchical) maximum likelihood (ML) estimates. These benefits came from using population distributions as priors to constrain (or “shrink”) more extreme estimates that would otherwise be obtained at the level of individuals, particularly when the number of observations is relatively small.
In recognition of the promise of the hierarchical approach to RT distribution estimation, our aim was to compare the hierarchical Bayesian approach to multilevel ML estimation when estimating parameters of a commonly used model for RT, the ex-Gaussian. We present simulations to assess the accuracy of both approaches with respect to each other and in comparison to single-level ML and Bayesian estimation. Finally, we discuss practical and statistical issues in the application of each approach.
Bayesian and maximum likelihood multilevel models
In standard single-level approaches (e.g., Cousineau et al., 2004; Wixted & Rohrer, 1994; Van Zandt, 2000), a set of parameters is obtained for each person by fitting a model to that individual's data. The two well-known methods for single-level estimation are maximum likelihood (here denoted CML, referring to classical maximum likelihood) and Bayesian estimation (here referred to as SLB, for single-level Bayes). There exist a number of philosophical differences between the two approaches, including whether statistics (i.e., probabilities) are treated as the expected outcome from a large number of independent trials—the frequentist interpretation, usually associated with ML—or as a measure of subjective belief as in the Bayesian framework (MacKay, 2003). For our purposes, two important computational differences exist between Bayesian and ML estimation. As implied by the name, CML is concerned with finding that set of parameter values θ that maximizes the probability of observing the data y given those parameters, p(y|θ) ; in ML estimation, this is usually rephrased as maximizing the likelihood of the parameters given the data, ℓ(θ|y). In contrast, Bayesian estimation is concerned not merely with finding a single value for each parameter, but rather with returning a posterior (i.e., after the data) probability distribution for that parameter. That is, given some data have been observed, what is the new probability associated with each possible parameter value (this being a posterior density for a continuous distribution)? This concept of updating probabilities requires some probability for the parameters to exist prior to data observation in the Bayesian approach, a second computational difference between the Bayesian and maximum likelihood approaches. This gives a formal description of Bayesian estimation:
| (1) |
where p(θ) gives the prior probabilities for parameter values. CML (e.g., Cousineau et al., 2004; Heathcote, Brown, & Cousineau, 2004; Van Zandt, 2000) and variants (Heathcote, Brown, & Mewhort, 2002) have been extensively applied in estimating response time models, particularly in the case of the ex-Gaussian. In contrast, application of SLB to response time distributions is rare (for a recent development, see Lee, Fuss, & Navarro, 2007), although the Bayesian perspective generally is gaining popularity in psychology (e.g., Lee, 2008, Rouder & Lu, 2005).
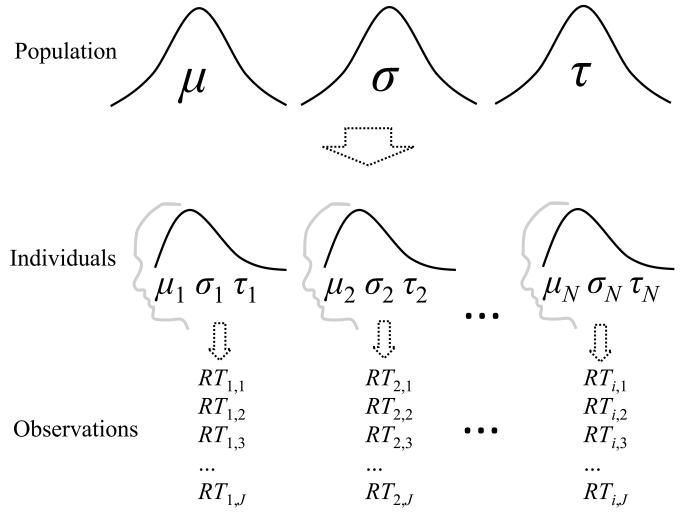
These single-level approaches to response time estimation can be extended by assuming a random-effects model for latencies (Rouder et al., 2003, 2005). Specifically, we can assume a multilevel model in which the parameters of individuals are assumed to be randomly distributed in the population according to some parent distributions. Figure 1 illustrates such a sampling scheme for the ex-Gaussian distribution. The ex-Gaussian is a popular and commonly used model for response times (e.g., Hockley, 1984; Hohle, 1965; Kieffaber et al., 2006; Ratcliff, 1979; Spieler, Balota, & Faust, 2000; Schmiedek, Oberauer, Wilhelm, Süss, & Wittmann, 2007). This distribution is obtained when each RT is assumed to be the sum of a random variate drawn from a Gaussian distribution and an another, independent variate drawn from an exponential distribution. The Gaussian component is taken to reflect encoding and motor processes, and is parameterized by the parameters μ and σ . The exponential component is taken to reflect information-processing or attentional processes (e.g., Rohrer & Wixted, 1994; Schmiedek et al., 2007), and is captured by the single parameter τ . Accordingly, single-level modeling would return an estimate of μi ,σi and τi for each individual i based only on that person's data. However, in multilevel models we assume the parameters of individuals are randomly distributed in the population according to some parent distributions, where each parent distribution is itself defined by a set of parameters. Thus, the parent distributions (top) specify how μ, σ, and τ are distributed across individuals in the population, and a sample of individuals is effectively a set of random draws from these parent distributions.
Figure 1.
A typical multilevel model for a response time experiment with a single condition. Parameters of response time distributions (here, ex-Gaussian) for individuals are sampled from population-level distributions, and these then determine the sampling of individual observations for each individual.
The benefit of assuming such a sampling scheme is that variability within participants can be estimated separately from variability between participants. Rouder and colleagues assumed such a random-effects model for the Weibull distribution (Rouder et al., 2005, 2003), and employed Bayesian parameter estimation to derive marginal posterior densities for the parameters of interest, both at the individual level and at the population level. In a number of simulations, Rouder and colleagues showed that their Weibull hierarchical Bayesian (HB) procedure produced more accurate estimates of the parameters of individuals than classical single-level maximum likelihood (CML) estimation (Rouder et al., 2003, 2005). This advantage mostly came from a reduction in the variability of estimates, with the CML estimates being overdispersed compared to both the known parameter values used to generate data in the simulations, and the estimates obtained from the HB procedure. The “shrinkage” in the Bayesian hierarchical model arises from information in the priors provided by the parent distributions, which are themselves informed by the estimates for all individuals, and higher-level priors placed on the parameters of these parent distributions.
The multilevel model is usefully employed in a Bayesian framework because the assumed parent distributions serve as priors for the estimation of posterior parameter densities of participants, but where those priors themselves are essentially informed by the data (Gelman, Carlin, Stern, & Rubin, 2004; Rouder & Lu, 2005). However, there also exist techniques for multilevel modeling using maximum likelihood estimation, an approach which has not been considered for response times. Hierarchical (or multilevel) maximum likelihood (HML) modeling is generally carried out with linear (e.g., Raudenbush & Bryk, 2002) and non-linear (e.g., Pinheiro & Bates, 2000) regression models. In psychology, multilevel ML models have been applied to such diverse areas as autobiographical memory (Wright, 1998); sentence processing (Blozis & Traxler, 2007); the speed-accuracy tradeoff (Hoffman & Rovine, 2007); serial and temporal recognition (Farrell & McLaughlin, 2007); and interference in working memory (Oberauer & Kliegl, 2006). The differences between Bayesian and ML multilevel modeling mirror those for estimation at a single level. Specifically, Bayesian parameter estimation aims to obtain a joint posterior probability density for the parameters given the observed data, while the HML approach gives modal estimates of the population-level parameters that maximize the likelihood of the model given the data.
More formally, in the Bayesian method we wish to obtain p(θ,B|y), where B and θ are vectors of parameters characterizing the individual- and population-level distributions, respectively. Although obtaining the joint posterior probability of parameters at different levels in the HB procedure may seem daunting, our job is made easier by the fact that θ only affects the data via B (see Figure 1); accordingly, the joint posterior can be obtained from (is proportional to):
| (2) |
where the first term is the joint prior probability ofθ and B (Gelman et al.., 2004). In contrast, rather than estimating B, ML estimation accounts for the non-observable variation in B by integrating it out (Pinheiro & Bates, 1995, 2000):
| (3) |
where ℓ(θ|y) is the likelihood of the parameters given the data. We are then concerned only with obtaining estimates of the population-level parameters inθ . Having obtained these, we can determine values of individuals' parameters in B by finding ML estimates for individuals given the estimated population-level parameters and the data.
Given classic maximum likelihood methods have been utilized successfully for many types of multilevel models, we wished to determine the applicability of the HML method to response time data. We were concerned with its ease of application, and with its performance compared to both HB and CML, the two methods that have thus far been given the majority of attention for response time modeling. We also examined the performance of single-level Bayesian estimation. Examining SLB will assist in determining whether the virtues of HB arise from its multilevel structure or from the use of Bayesian estimation (or both). For the simulations reported below, we focus on the ex-Gaussian distribution given its popularity in psychology. In the discussion, we return to consider the applicability of these methods to other distributions.
Statistical modeling of response times
All four approaches (CML, SLB, HML and HB) assume the same ex-Gaussian distribution function at the level of individual participants. For individual i the probability density function of response time on trial j, yij, is given by
| (4) |
where Φ is the cumulative Gaussian function, μi and σi are the mean and standard deviation of the Gaussian, and τi is the scale of the exponential. To estimate the ex-Gaussian in the hierarchical approaches it is useful to re-express this in terms of precision (i.e., inverse variance) rather than variance:
| (5) |
where φi = 1/σ2 and λi = 1/τ. This formulation was used in all the modeling below; results are reported forσ and τ as these are the parameters generally reported in the literature.
We now turn to how individuals' parameters are estimated or predicted under single-level and multi-level, Bayesian and maximum likelihood methods.
Classical maximum likelihood (CML)
CML estimation proceeds by assuming Equation 5 as a likelihood function, and finding those parameter values (μi, φi and λi) that maximize the likelihood of the parameters given the data (Cousineau et al., 2004; Van Zandt, 2000) for each individual i,
| (6) |
Equation 6 presents two useful relations. The first is that the likelihood of the parameters given the model is given by the same function that gives the probability density; however, in the case of the likelihood the data yi are fixed and the parameters vary, whereas for the probability density function the parameters are fixed and yi varies. The second useful relation in Equation 6 is that the joint likelihood for a set of observations is simply the product of the likelihoods for the individual observations (assuming the observations are independent).
Single-level Bayesian (SLB)
In the single-level Bayesian model, we wish to obtain the posterior probability density for μi, φi and λi for the data of each participant i, yi, given by
| (7) |
The first factor in the numerator is the joint probability , and the following three factors are the prior densities for μi, φi and λi (which we assume to be independent here). We assumed the following priors for μi, φi and λi:
| (8) |
| (9) |
| (10) |
where N and Gamma respectively denote the normal density function (with mean and inverse variance, or precision, as parameters) and the Gamma density function. The denominator in Equation 7 is the probability of observing the data; although this component is useful for model comparison as it can be treated as the evidence for the model being fit (MacKay, 2003), we ignore it here as we are only concerned with the posterior density of the parameters given the ex-Gaussian model. An important role of p(yi) in parameter estimation is to ensure that the posterior density integrates to 1; the procedures we use below perform this normalization without explicitly calculating p(yi).
For estimation in the Bayesian methods we used Gibbs sampling, a procedure in which samples are iteratively drawn from the posterior density of one parameter given the current values of all other parameters (and the data), to obtain the posterior densities for each parameter (see, e.g., Rouder & Lu, 2005, for more details). The posterior densities for each parameter are given in the Appendix, along with further details for the SLB.
Hierarchical maximum likelihood (HML)
In the HML procedure, we do not directly estimate individuals' parameters, but instead estimate parameters at the population level. As for SLB, we assumed a normal population distribution for μi, and a Gamma distribution parent for φi and λi (for convenience, we also use the same parameter labels). A joint likelihood ℓ(γ1,γ2,δ1,δ2,ε1,ε2|yi) can then be defined for the parent distribution parameters γ1, γ2, δ1, δ2, ε1, and ε2:
| (11) |
where yi is the vector of latencies for participant i and P is the number of participants, and p(yi|μ,φ,λ) is given by Equation 6. Accordingly, we do not estimate parameters for individual participants, but only estimate parameters for the parent distributions by maximizing Equation 11.
Once those parameters have been estimated in the HML procedure, the parameters for individuals (μi,φi,λi) can be predicted on the basis of these estimates. Following the literature on random effects (e.g., Pinheiro & Bates, 2000, p. 71), we obtain these predictors by finding modal (i.e., ML) estimates conditional on the parent distribution estimates. Specifically, for the model implemented here we calculate:
| (12) |
where Bi is the parameter vector [μi, φi, λi].
One computational consideration is the calculation of the integrals in Equation 11. These integrals were calculated using fourth-order Gauss-Lobatto quadrature, with 20 points along each parameter, and integration limits at the .01 and .99 quantiles of each parent distribution. We minimized the negative log-likelihood (i.e., summing across participants in Equation 12) using the SIMPLEX algorithm (Nelder & Mead, 1965).
Hierarchical Bayesian (HB)
In the HB method, we wish to obtain marginal posterior density estimates for all parameters of interest. These parameters include those defining the parent distributions, and also include the parameters of individuals themselves (i.e., μi, φi, λi). Following Rouder and Lu (2005) and Rouder et al. (2005), and as for SLB, we use Gibbs sampling to obtain these posteriors (e.g., Gelfand, Hills, Racine-Poon, & Smith, 1990; Gelman et al.., 2004). This requires defining conditional posterior densities or distributions for the parameters of individuals, and those parameters defining the parent distributions. As for HML, we assumed a normal parent distribution (i.e., prior) for the μi, and Gamma parents for φi and λi following standard treatment in Bayesian analysis (e.g., Gelman et al., 2004; Rouder & Lu, 2005). By assuming the same densities for the prior distributions in SLB and the parent distributions in HB, we can use the equations for posterior densities from the SLB procedure in HB. Additionally, we need to specify posterior densities for the parameters of the parent distributions, based on priors for these parameters. The full ex-Gaussian HB model, including specification of priors on the hyperparameters and the full set of conditional posteriors, is presented in the Appendix.
Simulations
In each simulation “observed” latencies were generated from a “true” sampling regime (e.g., Figure 1), and parameter estimation was then conducted on these generated latencies using the four approaches. The parent distributions from which the ex-Gaussian parameters were sampled and used to generate the data had parameters μμ = 0.9 s, σμ = 0.2 s, αφ = 7, βφ = 60, αλ = 20, and βλ = 0.5. For σ and τ this gave means of .052 s and 0.11 s, and standard deviations of .011 s and .025 s. The means approximated those used by Cousineau et al. (2004).
A number of different types of experiments were simulated. To reflect standard psychology experiments, three simulations were run that assumed 20 participants were tested, with the number of observations per participant being set at 20, 80, or 500. We also examined two cases typical in specific experimental domains. To reflect research in more low-level domains such as visual psychophysics or oculomotor physiology, where typically few participants are tested extensively, we assumed 5 participants generated a large number of responses (500). To reflect research using an individual differences approach, we assumed 80 participants, who each generated a small number of responses (20). For each simulation, 200 such data sets were generated and subjected to parameter estimation, with results being collected across runs within each simulation. For the Bayesian methods, which return an estimate of the full posterior distribution, parameter estimates were obtained by averaging across samples to obtain an expected value (see Appendix).
Table 1 summarizes the performance of the four approaches by showing the root mean squared deviation (RMSD) between the estimates and generated values. The two hierarchical methods gave more accurate estimates for the simulated participants, although this advantage is mostly restricted to small or medium numbers of observations (N=20 or N=80). There was little noticeable difference between the two single-level methods (CML and SLB), though SLB had a tendency to be more accurate for a small number of observations, while CML was slightly more accurate for larger N (particularly in the P=20, N=80 condition). Similarly, the HML and HB procedures performed equally well on average, with some slight differences according to the parameter and condition being examined.
Table 1.
Root mean squared deviations (RMSDs;×100) in seconds between observed parameter estimates of individuals, and those estimated or predicted from the three model estimates. P is the number of simulated participants, and N is the number of observations per participant.
| μ | σ | τ | ||
|---|---|---|---|---|
| CML | 4.34 | 2.97 | 4.78 | |
| P=20, N=20 | SLB | 3.80 | 2.72 | 4.10 |
| HML | 3.15 | 1.15 | 2.45 | |
| HB | 2.44 | 1.84 | 2.63 | |
| CML | 1.69 | 1.24 | 2.02 | |
| P=20, N=80 | SLB | 2.01 | 1.34 | 2.30 |
| HML | 1.29 | 0.80 | 1.47 | |
| HB | 1.32 | 0.83 | 1.58 | |
| CML | 0.62 | 0.46 | 0.75 | |
| P=20, N=500 | SLB | 0.73 | 0.48 | 0.84 |
| HML | 0.59 | 0.42 | 0.71 | |
| HB | 0.60 | 0.42 | 0.72 | |
| CML | 4.27 | 2.97 | 4.72 | |
| P=80, N=20 | SLB | 3.76 | 2.68 | 4.04 |
| HML | 2.25 | 1.01 | 2.03 | |
| HB | 2.44 | 1.12 | 2.29 | |
| CML | 0.60 | 0.45 | 0.72 | |
| P=5, N=500 | SLB | 0.64 | 0.46 | 0.76 |
| HML | 0.58 | 0.41 | 0.70 | |
| HB | 0.60 | 0.43 | 0.72 | |
Table 2 breaks these results down in more detail, by presenting the mean bias (the average deviation between each parameter estimate and the true value) and the standard deviation of the estimates, for μ ,σ and τ. The values have been multiplied by 100 in the table to enhance readability. An unbiased estimate will return a bias of 0, and the standard deviation of the estimates should ideally match that of the true values (for reference, these are 20, 1.1 and 2.5 when multiplied by 100). Table 2 shows that the hierarchical procedures show substantially less bias for small to medium N (N=20 and N=80). The hierarchical procedures also give less variable estimates, replicating Rouder et al.'s (2005) observation of “shrinkage” in their HB procedure for the Weibull distribution. The estimates from the HML procedure appear to be somewhat underdispersed for small N (cf. HB estimates), and are less biased than those from the HB procedure; there is little difference between the two procedures for medium and large N, except for a slight tendency to under-dispersement in HML. For small N, the SLB procedure is biased when compared to CML, but does give a reduction in variance. For medium N, SLB estimates tend to be more biased and slightly more variable; little difference is evident for large N.
Table 2.
Bias (“B”, ×100) and standard deviation (“SD”, ×100) of the estimates of μ, σ and τ, in seconds.
| μ | σ | τ | |||||
|---|---|---|---|---|---|---|---|
| B | SD | B | SD | B | SD | ||
| CML | 1.27 | 19.97 | −0.47 | 3.05 | −1.23 | 5.08 | |
| P=20, N=20 | SLB | 2.28 | 19.75 | 1.87 | 2.10 | −1.89 | 4.06 |
| HML | 0.26 | 19.24 | 0.08 | 0.52 | −0.26 | 1.45 | |
| HB | 0.45 | 19.60 | 0.33 | 1.07 | −0.20 | 2.79 | |
| CML | 0.19 | 19.95 | −0.14 | 1.59 | −0.19 | 3.09 | |
| P=20, N=80 | SLB | 0.65 | 19.94 | 0.43 | 1.65 | −0.54 | 3.29 |
| HML | 0.11 | 19.84 | 0.05 | 0.75 | −0.08 | 1.95 | |
| HB | 0.10 | 19.88 | 0.04 | 0.96 | −0.03 | 2.53 | |
| CML | 0.01 | 19.78 | −0.03 | 1.15 | −0.02 | 2.53 | |
| P=20, N=500 | SLB | 0.05 | 19.78 | 0.04 | 1.17 | −0.04 | 2.58 |
| HML | 0.02 | 19.76 | 0.01 | 1.00 | −0.03 | 2.33 | |
| HB | 0.00 | 19.77 | 0.00 | 1.04 | 0.00 | 2.46 | |
| CML | 1.18 | 20.47 | −0.54 | 3.08 | −1.21 | 5.14 | |
| P=80, N=20 | SLB | 2.19 | 20.20 | 1.81 | 2.14 | −1.87 | 4.14 |
| HML | 0.22 | 20.00 | 0.08 | 0.53 | −0.11 | 1.55 | |
| HB | 0.20 | 19.21 | 0.16 | 0.83 | −0.10 | 2.48 | |
| CML | 0.02 | 18.20 | −0.02 | 1.06 | −0.01 | 2.33 | |
| P=5, N=500 | SLB | 0.05 | 18.18 | 0.04 | 1.05 | −0.02 | 2.35 |
| HML | 0.02 | 18.19 | 0.02 | 0.89 | −0.01 | 2.12 | |
| HB | 0.02 | 18.19 | 0.02 | 0.99 | 0.01 | 2.31 | |
Finally, Table 3 shows the mean correlation between the true parameter values and those obtained from the four procedures. Strikingly, for μ the correlation is near-perfect for all models, irrespective of N and P. For σ and τ, correlations increase with N, and are also slightly larger with the increase in P between the P=20, N=20 and P=80, N=20 simulations. Overall, there is little difference between the approaches in the correlations for σ, with the exception that these correlations are somewhat smaller for CML. For τ, a small increase in correlations is witnessed when moving from SLB to HML or HB.
Table 3.
Correlations between true parameter values and estimates from the four procedures (averaged across replications).
| μ | σ | τ | ||
|---|---|---|---|---|
| CML | 0.98 | 0.3 | 0.43 | |
| P=20, N=20 | SLB | 0.99 | 0.38 | 0.47 |
| HML | 0.98 | 0.39 | 0.55 | |
| HB | 0.99 | 0.39 | 0.55 | |
| CML | 1.00 | 0.64 | 0.76 | |
| P=20, N=80 | SLB | 1.00 | 0.64 | 0.73 |
| HML | 1.00 | 0.67 | 0.8 | |
| HB | 1.00 | 0.67 | 0.79 | |
| CML | 1.00 | 0.91 | 0.95 | |
| P=20, N=500 | SLB | 1.00 | 0.91 | 0.95 |
| HML | 1.00 | 0.92 | 0.96 | |
| HB | 1.00 | 0.92 | 0.96 | |
| CML | 0.98 | 0.33 | 0.46 | |
| P=80, N=20 | SLB | 0.99 | 0.4 | 0.51 |
| HML | 0.99 | 0.44 | 0.6 | |
| HB | 0.99 | 0.43 | 0.58 | |
| CML | 1.00 | 0.87 | 0.94 | |
| P=5, N=500 | SLB | 1.00 | 0.86 | 0.93 |
| HML | 1.00 | 0.87 | 0.94 | |
| HB | 1.00 | 0.87 | 0.94 | |
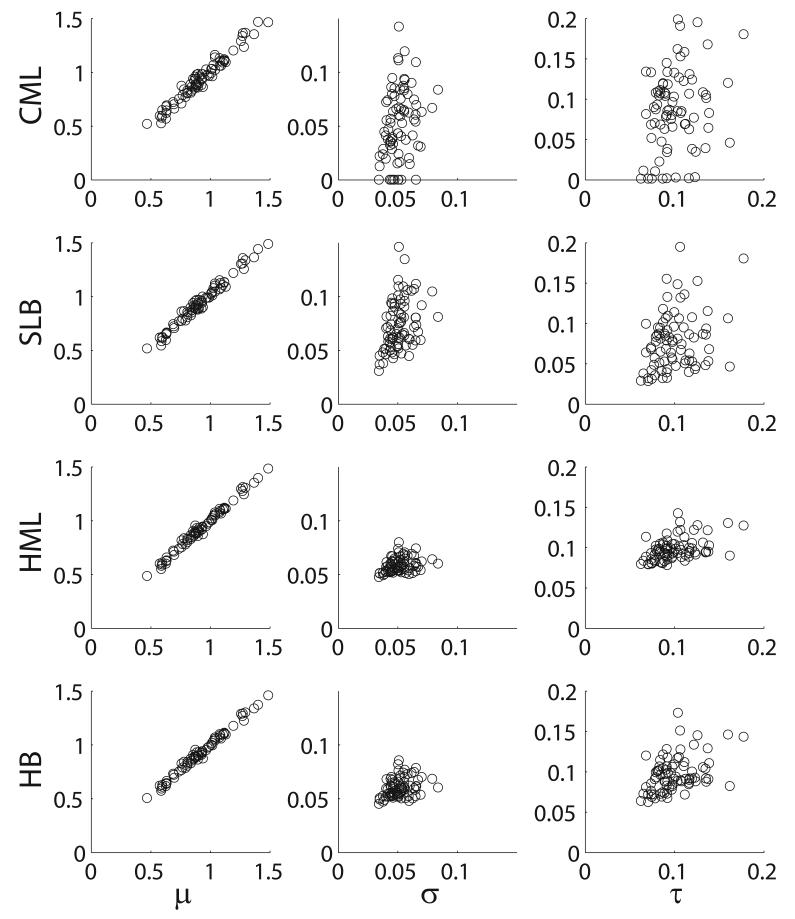
As a summary of the differences in estimation obtained from the differences in procedures, Figure 2 presents scatterplots of estimates from the four procedures against the true values for an instance from the P=80, N=20 simulations. For μ, all the procedures provide very accurate results. The advantages of hierarchical modeling are clearly seen for σ and τ, with the parameter estimates from both HML and HB less variable than those for CML and, to a slightly lesser extent, SLB, illustrating the “shrinkage” obtained from hierarchical methods.
Figure 2.
Scatterplots for a typical simulation run for P=80, N=20, plotting the “true” parameter values against the estimates obtained from the CML (top row), SLB (second row), HML (third row) and HB (fourth row) procedures. The three columns correspond to the three estimated parameters μ, σ and τ.
Discussion
The results show that although the methods all perform considerably well, HML and HB give a comparable improvement over single-level methods (CML and SLB) when estimating parameters of the ex-Gaussian distribution. This benefit comes both from a reduction in the bias of estimates, and from a reduction in variability of the estimates, with fewer extreme estimates (“shrinkage”). Although there were some differences between the maximum likelihood and Bayesian estimates at the single level (CML vs SLB) and in the hierarchical models (HML vs HB), the Bayesian and ML methods performed almost equally well (Table 1).
These results lead to the obvious question: when is it appropriate to use each of the methods investigated? Hierarchical modeling is arguably always more appropriate as it will more accurately reflect the sampling regime that holds in typical experiments, where individual differences will usually be random effects. In practice, if we are just concerned with estimation, there is generally little to discriminate hierarchical and non-hierarchical methods with large numbers of observations per participant, as is sometimes the case (e.g., Carpenter & Williams, 1995; Ratcliff & Rouder, 1998). For small number of observations, hierarchical models give an appreciable benefit and can be recommended.
The choice between HML and HB (and, indeed, between CML and SLB) seems to be partly dictated by the choice of inferential framework, and partly by computational concerns. A major difference between the approaches is their underlying philosophy. Bayesian modeling is concerned with delivering posterior densities by updating priors with likelihoods, while ML is concerned with point estimates of likelihoods. In terms of the inferential framework HB thus makes explicit, and estimates, the uncertainty of the model parameters, which is ignored when obtaining point estimates by averaging across distributions. Another difference is HB's requirement that priors be set on parameters of the parent distributions. The setting of priors generally is not arbitrary and requires some experience with the models being employed, and with Bayesian analysis. In the hierarchical case there is an added complication that we must consider the potential effects of the priors both on the parent distributions, and the downstream effects on the posterior densities at the level of individuals. This involves examining marginal prior distributions at the individual level, an additional step that is not required in HML. On the other hand, these priors give us the freedom to incorporate information about the latency domain into our models, an arguable benefit of Bayesian analysis (see, e.g., Rouder et al., 2005).
Another issue in considering the application of any of these methods is the ease with which they are implemented and carried out. CML is clearly the simplest and easiest of the four methods, requiring only a function for the latency distribution (e.g., Equation 4) and a minimization routine (these can be found in most statistical and mathematical packages). HML is surprisingly straightforward to program; the only technical difficulties are the integration in Equation 11, for which any number of numerical integration methods could be used, and that Equation 11 can return values outside the range of the double data type on computers when fitting large amounts of data per participant; we have found it useful to return a large dummy number to the minimization routine (e.g., 100000) when encountering this problem. We found the two Bayesian methods slightly more demanding; although the general algorithm is straightforward and useful introductions to Bayesian modeling and Gibbs sampling exist (e.g., Gelman et al., 2004; Rouder & Lu, 2005), some of the sampling from posterior densities required sampling from some log-densities using adaptive rejection sampling, which we then needed to compile into our own code for our log-density functions. Additionally, we encountered problems with small numbers of data, where the log-density function is relatively flat and a careful choice of upper and lower limits for the envelope for sampling from this function is required. Having done this, the SLB is effectively subsumed under HB which saved some time in implementation.1 Generally, as researchers having some experience with likelihood estimation we found the Bayesian methods most challenging to implement (particularly, the selection of priors and the technical challenges already detailed).
A final factor that should be mentioned is HML's limitations in the face of data-dependent bounds. Bounded distributions such as the log-normal and the Weibull (e.g., Heathcote et al.., 2004, ), which are undefined for latencies ≤ 0, often incorporate a parameter equivalent to μ that shifts the distribution away from 0. Estimation of this parameter is not straightforward in HML: for each participant, this shift parameter cannot exceed the shortest observed latency for that person. This means that integration across a common set of parameter bounds for all participants in Equation 3 is not possible. In simulations assuming a constant shift for all participants, we have found HML to perform poorly compared to CML and HB in estimating parameters of the Weibull distribution. 2 Modifications might exist for HML, such as introducing a Gaussian contaminant distribution to remove the effective bound on parameter estimates; nevertheless, HB has the advantage that such fixes are not required as we can sample from the posteriors for individual participants regardless of whether the prior is dependent on the estimates for individual participants. In the case of the ex-Gaussian distribution, where the Gaussian is explicitly incorporated into our latency model, we are able to integrate across all parent distributions in HML (Equation 11) and obtain accurate estimates; there is little to distinguish between HML and HB in this case.
Acknowledgments
This research was supported by Wellcome Trust grant 079473/Z/06/Z to S. Farrell, C. J. H. Ludwig, I. D. Gilchrist and R. H. S. Carpenter. The second author additionally received support from EPSRC grant EP/E054323/1. We thank Jeff Rouder for making available R code for Gibbs sampling for the multilevel Weibull; for suggesting the simulations of the single-level Bayesian analysis; and for his helpful responses to our queries on the method developed by him and his co-authors. We additionally thank Jeff Rouder, Denis Cousineau and an anonymous reviewer for their comments on a previous version of this manuscript. Correspondence should be addressed to Simon Farrell, Department of Psychology, University of Bristol, 12a Priory Road, Clifton, Bristol BS8 1TU, UK; e-mail: Simon.Farrell@bristol.ac.uk.
Appendix
Single-level and hierarchical Bayesian method for the ex-Gaussian distribution
Single-level Bayes
Given a normal prior (parent) distribution on μi, and Gamma distributions on φi and λi, the conditional posteriors (with constant of proportionality excluded) are :3
| (A1) |
| (A2) |
| (A3) |
The parameters for the prior distributions were set to vaguely informative values of γ1 = 0.2, γ2 = 2.6, δ1 = 0.1, δ2 = 0.001, ε1 = 0.1, and ε2 = 0.001.
Hierarchical Bayes
Second-level priors on the parameters of the parent distributions were specified as follows:
| (A4) |
| (A5) |
| (A6) |
| (A7) |
| (A8) |
| (A9) |
We chose values for the parameters of the second-level priors that were relatively non-informative, and gave acceptable marginal priors at the individual level; these values were a1 = 0.2, b1 = 2.0, a2 = 0.5, b2 = 0.5, c1=1, c2 = 0.1, d2 = 0.1, e1 = 1, e2 = 0.1, f2 = 0.1.
The resulting posteriors at the second level are:
| (A10) |
where
| (A11) |
and
| (A12) |
| (A13) |
| (A14) |
| (A15) |
| (A16) |
| (A17) |
For the simulations reported below (for both HB and SLB), we used a “burn-in” of 2500 iterations in the Gibbs sampling, and then estimated posteriors from a further 2500 iterations. This was found to give fairly stable results. Only a single Markov chain was run per simulated sample; prior testing showed that the burn-in and estimation iterations generally gave acceptable results in testing using multiple chains, in that autocorrelations decreases fairly quickly with lag (<0.1 within 10 lags), and the Gelman-Rubin statistic was close to 1 (Gelman & Rubin, 1992). In cases where the procedure returned wildly implausible estimates (specifically, where σ >1, which was associated with a τ close to 0), further chains were run to provide a more reasonable solution, as would be done in practice. The first four priors listed above are conjugate with their respective likelihoods, meaning we can sample from standard distributions in the Gibbs sampling. For all other functions, we sampled posterior values using adaptive rejection sampling with a Metropolis step (ARMS; Gilks, Best, & Tan, 1995), using code obtained from the website of W. Gilks. 4 We used ARMS rather than an alternative without the Metropolis step (ARS; Gilks & Wild, 1992) because the equations for the posterior of φi and λi are not log concave for δ1 < 1 and ε1 < 1, respectively, and because we found ARMS to be more stable than ARS: densities that are log-concave still sometimes failed using the ARS code, but not the ARMS code. The same envelope values for ARMS were used on each iteration (within each conditional density).
Footnotes
A related factor not discussed is the time taken to run these analyses. Unsurprisingly, CML runs much faster than the other methods. SLB and HB differ little in their speed, as they have a great deal of overlap in the required number of samples. The HML procedure as programmed was the slowest procedure, especially for a large number of observations. However, after running the simulations we realized that our adoption of quite conservative convergence criteria for the minimization routine for HML may have excessively lengthened the convergence time.
Heathcote et al. (2004) have noted additional problems when using CML to estimate the parameters of bounded distributions such as the log-normal.
The hyperparameters here are expressed for latencies measured in units of seconds.
References
- Andrews S, Heathcote A. Distinguishing common and task-specific processes in word identification: A matter of some moment? Journal of Experimental Psychology: Learning, Memory, and Cognition. 2001;27:514–44. doi: 10.1037/0278-7393.27.2.514. [DOI] [PubMed] [Google Scholar]
- Blozis SA, Traxler MJ. Analyzing individual differences in sentence processing performance using multilevel models. Behavior Research Methods. 2007;39:31–38. doi: 10.3758/bf03192841. [DOI] [PubMed] [Google Scholar]
- Carpenter RHS, Williams MLL. Neural computation of log likelihood in control of saccadic eye movements. Nature. 1995;377:59–62. doi: 10.1038/377059a0. [DOI] [PubMed] [Google Scholar]
- Cousineau D, Brown S, Heathcote A. Fitting distributions using maximum likelihood: Methods and packages. Behavior Research Methods Instruments & Computers. 2004;36:742–756. doi: 10.3758/bf03206555. [DOI] [PubMed] [Google Scholar]
- Farrell S, McLaughlin K. Short-term recognition memory for serial order and timing. Memory & Cognition. 2007;35:1724–1734. doi: 10.3758/bf03193505. [DOI] [PubMed] [Google Scholar]
- Gelfand AE, Hills SE, Racine-Poon A, Smith AFM. Illustration of Bayesian inference in normal data models using Gibbs sampling. Journal of the American Statistical Association. 1990;85:972–985. [Google Scholar]
- Gelman A, Carlin JB, Stern HS, Rubin DB. Bayesian data analysis. 2nd, Ed. London, UK: Chapman & Hall; 2004. [Google Scholar]
- Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statistical Science. 1992;7:457–511. [Google Scholar]
- Gilks WR, Best NG, Tan KKC. Adaptive rejection metropolis samping within Gibbs sampling. Applied Statistics. 1995;44:455–472. [Google Scholar]
- Gilks WR, Wild P. Adaptive rejection sampling for gibbs sampling. Applied Statistics. 1992;41:337–348. [Google Scholar]
- Heathcote A, Brown S, Cousineau D. QMPE: Estimating Lognormal, Wald, and Weibull RT distributions with a parameter-dependent lower bound. Behavior Research Methods Instruments & Computers. 2004;36:277–290. doi: 10.3758/bf03195574. [DOI] [PubMed] [Google Scholar]
- Heathcote A, Brown S, Mewhort DJK. Quantile maximum likelihood estimation of response time distributions. Psychonomic Bulletin & Review. 2002;9:394–401. doi: 10.3758/bf03196299. [DOI] [PubMed] [Google Scholar]
- Hockley WE. Analysis of response time distributions in the study of cognitive processes. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1984;10:598–615. [Google Scholar]
- Hoffman L, Rovine MJ. Multilevel models for the experimental psychologist: Foundations and illustrative examples. Behavior Research Methods. 2007;39:101–117. doi: 10.3758/bf03192848. [DOI] [PubMed] [Google Scholar]
- Hohle RH. Inferred components of reaction times as functions of foreperiod duration. Journal of Experimental Psychology. 1965;69:382–386. doi: 10.1037/h0021740. [DOI] [PubMed] [Google Scholar]
- Kieffaber PD, Kappenman ES, Bodkins M, Shekhar A, O'Donnell BF, Hetrick WP. Switch and maintenance of task set in schizophrenia. Schizophrenia Research. 2006;84:345–358. doi: 10.1016/j.schres.2006.01.022. [DOI] [PubMed] [Google Scholar]
- Lee MD. Three case studies in the Bayesian analysis of cognitive models. Psychonomic Bulletin & Review. 2008;15:1–15. doi: 10.3758/pbr.15.1.1. [DOI] [PubMed] [Google Scholar]
- Lee MD, Fuss IG, Navarro DJ. A bayesian approach to diffusion models of decision-making and response time. In: Schölkopf B, Platt JC, Hofmann T, editors. Advances in neural information processing systems. Vol. 19. Cambridge, MA: MIT Press; 2007. pp. 809–816. [Google Scholar]
- MacKay DJC. Information theory, inference, and learning algorithms. Cambridge, UK: Cambridge University Press; 2003. [Google Scholar]
- Nelder JA, Mead R. A simplex method for function minimization. Computer Journal. 1965;7:308–313. [Google Scholar]
- Oberauer K, Kliegl R. A formal model of capacity limits in working memory. Journal of Memory and Language. 2006;55:601–626. [Google Scholar]
- Pinheiro JC, Bates DM. Approximations to the log-likelihood function in the nonlinear mixed-effects model. Journal of Computational and Graphical Statistics. 1995;4:12–35. [Google Scholar]
- Pinheiro JC, Bates DM. Mixed-effects models in S and S-Plus. New York, NY: Springer; 2000. [Google Scholar]
- Ratcliff R. Group reaction time distributions and an analysis of distribution statistics. Psychological Bulletin. 1979;86:446–461. [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling repsonse times for two-choice decisions. Psychological Science. 1998;9:347–356. [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical linear models: Applications and data analysis methods. 2nd ed. Thousand Oaks, CA: Sage; 2002. [Google Scholar]
- Rohrer D, Wixted JT. An analysis of latency and interresponse time in free recall. Memory & Cognition. 1994;22:511–524. doi: 10.3758/bf03198390. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Lu J. An introduction to bayesian hierarchical models with an application in the theory of signal detection. Psychonomic Bulletin & Review. 2005;12:573–604. doi: 10.3758/bf03196750. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Lu J, Speckman P, Sun D, Jiang Y. A hierarchical model for estimating response time distributions. Psychonomic Bulletin & Review. 2005;12:195–223. doi: 10.3758/bf03257252. [DOI] [PubMed] [Google Scholar]
- Rouder JN, Sun D, Speckman PL, Lu J, Zhou D. A hierarchical Bayesian statistical framework for response time distributions. Psychometrika. 2003;68:589–606. [Google Scholar]
- Schmiedek F, Oberauer K, Wilhelm O, Süss HM, Wittmann WW. Individual differences in components of reaction time distributions and their relations to working memory and intelligence. Journal of Experimental Psychology: General. 2007;136:414–429. doi: 10.1037/0096-3445.136.3.414. [DOI] [PubMed] [Google Scholar]
- Spieler DH, Balota DA, Faust ME. Levels of selective attention revealed through analyses of response time distributions. Journal of Experimental Psychology: Human Perception and Performance. 2000;26:506–526. doi: 10.1037//0096-1523.26.2.506. [DOI] [PubMed] [Google Scholar]
- Vandekerckhove J, Tuerlinckx F. Diffusion model analysis with MATLAB: A DMAT primer. Behavior Research Methods. 2008;40:61–72. doi: 10.3758/brm.40.1.61. [DOI] [PubMed] [Google Scholar]
- Van Zandt T. How to fit a response time distribution. Psychonomic Bulletin & Review. 2000;7:424–465. doi: 10.3758/bf03214357. [DOI] [PubMed] [Google Scholar]
- Wagenmakers EJ, van der Maas HLJ, Grasman RPPP. An EZ-diffusion model for response time and accuracy. Psychonomic Bulletin & Review. 2007;14:3–22. doi: 10.3758/bf03194023. [DOI] [PubMed] [Google Scholar]
- Wixted JT, Rohrer D. Analyzing the dynamics of free recall: An integrative review of the empirical literature. Psychonomic Bulletin & Review. 1994;1:89–106. doi: 10.3758/BF03200763. [DOI] [PubMed] [Google Scholar]
- Wright DB. Modelling clustered data in autobiographical memory research: The multilevel approach. Applied Cognitive Psychology. 1998;12:339–357. [Google Scholar]