Multisensory integration in macaque visual cortex depends on cue reliability

Summary

Responses of multisensory neurons to combinations of sensory cues are generally enhanced or depressed relative to single cues presented alone. We examined integration of visual and vestibular self-motion cues in area MSTd. We presented unimodal as well as congruent and conflicting bimodal stimuli across a full range of headings in the horizontal plane. This broad exploration of stimulus space permitted evaluation of hypothetical combination rules employed by multisensory neurons. Bimodal responses were well fit by weighted linear sums of unimodal responses, with weights typically less than one (sub-additive). Importantly, weights change with the relative reliabilities of the two cues: visual weights decrease and vestibular weights increase when visual stimuli are degraded. Moreover, both modulation depth and neuronal discrimination thresholds improve for matched bimodal as compared to unimodal stimuli, which might allow for increased neural sensitivity during multisensory stimulation. These findings establish important new constraints for neural models of cue integration.

Introduction

Multisensory neurons are thought to underlie the performance improvements often seen when subjects integrate multiple sensory cues to perform a task. In their groundbreaking research, Meredith and Stein (1983) found that neurons in the deep layers of the superior colliculus receive visual, auditory and somatosensory information and typically respond more vigorously to multimodal than to unimodal stimuli (Kadunce et al., 1997; Meredith et al., 1987; Meredith and Stein, 1986a, b, 1996; Wallace et al., 1996). Multimodal responses have often been characterized as enhanced versus suppressed relative to the largest unimodal response, or as super-versus sub-additive relative to the sum of unimodal responses (see Stein and Stanford, 2008 for review).

Because the superior colliculus is thought to play important roles in orienting to stimuli, the original investigations of Stein and colleagues emphasized near-threshold stimuli, thus focusing on detection, one important function of multisensory integration. As a result, many subsequent explorations, including human neuroimaging studies, have focused on super-additivity and the principle of inverse effectiveness (greater response enhancement for less effective stimuli) as hallmark properties of multisensory integration (e.g., Calvert et al., 2001; Meredith and Stein, 1986b) (but see Beauchamp, 2005; Laurienti et al., 2005). However, use of near-threshold stimuli may bias outcomes toward a non-linear (super-additive) operating range in which multisensory interactions are strongly influenced by a threshold non-linearity (Holmes and Spence, 2005). Indeed, using a broader range of stimulus intensities, the emphasis on super-additivity in the superior colliculus has been questioned (Perrault et al., 2003; Stanford et al., 2005; Stanford and Stein, 2007), and studies using stronger stimuli in behaving animals more frequently find sub-additive effects (Frens and Van Opstal, 1998; Populin and Yin, 2002).

In recent years, these investigations have been extended to a variety of cortical areas and sensory systems, including auditory-visual integration (Barraclough et al., 2005; Bizley et al., 2007; Ghazanfar et al., 2005; Kayser et al., 2008; Romanski, 2007; Sugihara et al., 2006), visual-tactile integration (Avillac et al., 2007), and auditory-tactile integration (Lakatos et al., 2007). These studies have generally observed a mixture of super-additive and sub-additive effects, with some studies reporting predominantly enhancement of multimodal responses (Ghazanfar et al., 2005; Lakatos et al., 2007) and others predominantly suppression (Avillac et al., 2007; Sugihara et al., 2006). The precise rules by which neurons combine sensory signals across modalities remain unclear.

Rather than exploring a range of stimuli spanning the selectivity of the neuron, most studies of multisensory integration have been limited to one or a few points within the stimulus space. This approach may be insufficient to mathematically characterize the neuronal combination rule. A multiplicative interaction, for instance, can appear to be sub-additive (2×1 = 2), additive (2×2 = 4), or super-additive (2×3 = 6) depending on the magnitudes of the inputs. Because input magnitudes vary with location on a tuning curve or within a receptive field, characterizing sub-/super-additivity at a single stimulus location may not reveal the overall combination rule. We suggest that probing responses to a broad range of stimuli that evoke widely varying responses is crucial for evaluating models of multisensory neural integration.

In contrast to the concept of super-additivity in neuronal responses, psychophysical and theoretical studies of multisensory integration have emphasized linearity. Humans often integrate cues by weighted linear combination of the unimodal cue estimates, with weights proportional to the relative reliabilities of the cues as predicted by Bayesian models (Alais and Burr, 2004; Battaglia et al., 2003; Ernst and Banks, 2002). Although linear combination at the level of perceptual estimates makes no clear prediction for the underlying neuronal combination rule, theorists have proposed that neurons could accomplish Bayesian integration via linear summation of unimodal inputs (Ma et al., 2006). A key question is whether the neural combination rule changes with the relative reliabilities of the cues. Neurons could accomplish optimal cue integration via linear summation with fixed weights that do not change with cue reliability (Ma et al., 2006). Alternatively, the combination rule may depend on cue reliability, such that neurons weight their unimodal inputs based on the strengths of the cues.

This study examines neuronal multisensory integration from the viewpoint of this theoretical framework, and we address two fundamental questions. First, what is the combination rule used by neurons to integrate sensory signals from two different sources? Second, how does this rule depend on the relative reliabilities of the sensory cues? We have addressed these issues by examining visual-vestibular interactions in the dorsal portion of the medial superior temporal area (MSTd) (Duffy, 1998; Gu et al., 2006b; Page and Duffy, 2003). To probe a broad range of stimulus space, we characterized single MSTd neuron responses to eight directions of translation in the horizontal plane using visual cues alone (optic flow), vestibular cues alone, and bimodal stimuli including all 64 (8 × 8) combinations of visual and vestibular headings, both congruent and conflicting. By modeling responses to this array of bimodal stimuli, we evaluated two models for the neural combination rule, one linear and one non-linear (multiplicative). We also examined whether the combination rule depends on relative cue reliabilities by manipulating the motion coherence of the optic flow stimuli.

Results

We recorded from 112 MSTd neurons (27 from monkey J and 85 from monkey P). We characterized their heading tuning in the horizontal plane by using a virtual reality system to present 8 evenly spaced directions, 45° apart. Responses were obtained during three conditions: inertial motion alone (vestibular condition), optic flow alone (visual condition) and paired inertial motion and optic flow (bimodal condition). For the latter, we tested all 64 combinations of vestibular and visual headings, including 8 congruent and 56 incongruent (cue-conflict) presentations. In all conditions, monkeys were simply required to maintain fixation on a head-fixed target during stimulus presentation.

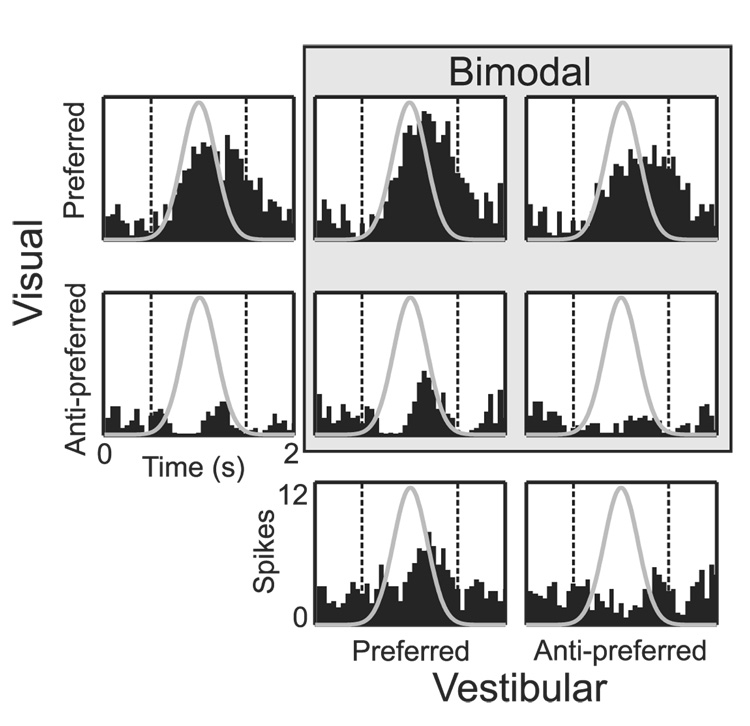
Raw responses are shown in Fig. 1 for an example MSTd neuron, along with the Gaussian velocity profile of the stimulus (gray curves). Peri-stimulus time histograms (PSTHs) are displayed for the response to each unimodal cue at both the preferred and anti-preferred headings. In addition, PSTHs are shown for the 4 bimodal conditions corresponding to all combinations of the preferred and anti-preferred headings for the two cues. Note that the bimodal response is enhanced when both individual cues are at their preferred values, and that the bimodal response is suppressed when either cue is anti-preferred. To summarize these observations, responses to each stimulus were quantified by taking the mean firing rate over the central 1 s of the 2 s stimulus period when the stimulus velocity varied the most (dashed vertical lines in Fig. 1; see also Materials and Methods). Using other 1 s intervals, except ones at the beginning or end of the trial, led to similar results (see also Gu et al., 2007).

Fig. 1.

Peri-stimulus time histograms (PSTHs) of neural responses for an example MSTd neuron. Gray curves indicate the Gaussian velocity profile of the stimulus. The two leftmost PSTHs show responses in the unimodal visual condition for the preferred and anti-preferred headings. Analogously, the two bottom PSTHs represent preferred and anti-preferred responses in the unimodal vestibular condition. PSTHs within the gray box show responses to bimodal conditions corresponding to the 4 combinations of the preferred and anti-preferred headings for the two cues. Dashed vertical lines bound the central 1s of the stimulus period, during which mean firing rates were computed.

Of the 112 cells recorded at 100% visual coherence, 44 (39%) had significant heading tuning in both the vestibular and visual unimodal conditions (one way ANOVA P<0.05). Note that we always use the term “unimodal” response to refer to the conditions in which visual and vestibular cues are presented in isolation. However, visual and vestibular selectivity can also be quantified by examining the visual and vestibular main effects in the responses to bimodal stimuli (e.g., by collapsing the bimodal responses along one axis or the other). When computed this way from bimodal responses, the percentage of vestibularly-selective cells increased: 74 cells (66%) showed significant vestibular tuning in the bimodal condition (main effect of vestibular heading in two-way ANOVA P<0.05, see Suppl. Fig. S1). This result indicates that the influence of the vestibular cue is sometimes more apparent when presented in combination with the visual cue, as also reported in other multisensory studies (e.g.,Avillac et al., 2007).

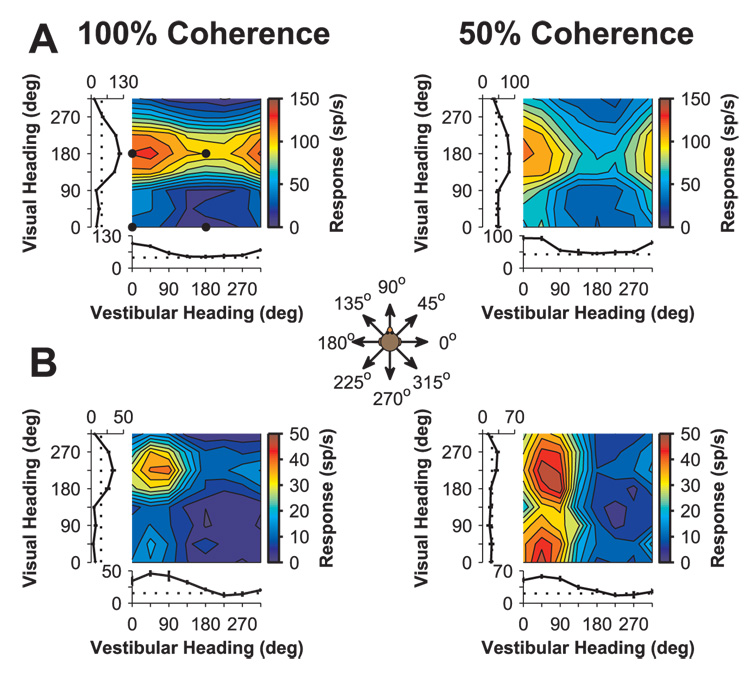
Data from two representative MSTd neurons that were significantly tuned under both unimodal conditions are illustrated in Fig. 2A and B. For each unimodal stimulus (visual and vestibular), tuning curves were constructed by plotting the mean response versus heading direction (Fig. 2, tuning curves along the left ordinate and abscissa). Both neurons had visual and vestibular heading preferences (computed as the direction of the vector sum of responses, see Materials and Methods) that differed by nearly 180° (Fig. 2A: vestibular: 10°, visual: 185°; Fig. 2B: vestibular: 65°, visual: 226°). Thus both cells were classified as “opposite” (Gu et al., 2006b). Note that heading directions in all conditions are referenced to physical body motion. For example, a bimodal stimulus in which both visual and vestibular cues indicate rightward (0°) body motion will contain optic flow in which dots move leftward on the display screen. Distributions of the difference in preferred directions between visual and vestibular conditions are shown in Suppl. Fig. S1 for the entire population of neurons. Neurons with mismatched preferences for different sensory cues have also been seen in other areas, including the closely related cortical area VIP (Bremmer et al., 2002; Schlack et al., 2002).

Fig. 2.

Examples of tuning for two “opposite” MSTd neurons. Color contour maps show mean firing rates as a function of vestibular and visual headings in the bimodal condition. Tuning curves along the left and bottom margins show mean (± SEM) firing rates versus heading for the unimodal visual and vestibular conditions, respectively. Data collected using visual stimuli (optic flow) having 100% and 50% motion coherence are shown in the left and right columns, respectively. (A) Data from a neuron with opposite vestibular and visual heading preferences in the unimodal conditions (same cell as in Fig. 1). Black dots indicate the bimodal response conditions corresponding to the PSTHs shown in Fig. 1. Bimodal tuning shifts from visually dominated at 100% coherence to balanced at 50% coherence. (B) Data from another “opposite” neuron. Bimodal responses reflect an even balance of visual and vestibular headings at 100% coherence, and become vestibularly dominated at 50% coherence. Inset: A top-down view showing the 8 possible heading directions (for each cue) in the horizontal plane.

For the bimodal stimuli, where each response is associated with both a vestibular heading and a visual heading, responses have been illustrated as two-dimensional color contour maps with vestibular heading along the abscissa and visual heading along the ordinate (Fig. 2, black dots in Fig. 2A indicate the bimodal conditions corresponding to the PSTHs in Fig. 1). At 100% visual coherence, bimodal responses typically reflected both unimodal tuning preferences to some degree. For the cell in Fig. 2A, bimodal responses were dominated by the visual stimulus, as indicated by the horizontal band of high firing rates. In contrast, the bimodal responses of the cell in Fig. 2B were equally affected by the visual and vestibular cues, creating a discrete and circumscribed peak centered near the unimodal heading preferences (54°, 230°).

Lowering visual coherence (by reducing the proportion of dots carrying the motion signal, see Materials and Methods) altered both the unimodal visual responses and the pattern of bimodal responses for both example cells. In both cases, the visual heading tuning (tuning curve along ordinate) remained similar in shape and heading preference, but the peak-to-trough response modulation was reduced at 50% coherence. For the cell of Fig. 2A, the horizontal band of high firing rate seen in the bimodal response at 100% coherence is replaced by a more discrete single peak centered around a vestibular heading of 8° and a visual heading of 180°, reflecting a more even mix of the two modalities at 50% coherence. For the cell in Fig. 2B, the well-defined peak seen at 100% coherence becomes a vertical band of strong responses, reflecting a stronger vestibular influence at 50% coherence. Thus for both cells, the vestibular contribution to the bimodal response was more pronounced when the reliability (coherence) of the visual cue was reduced.

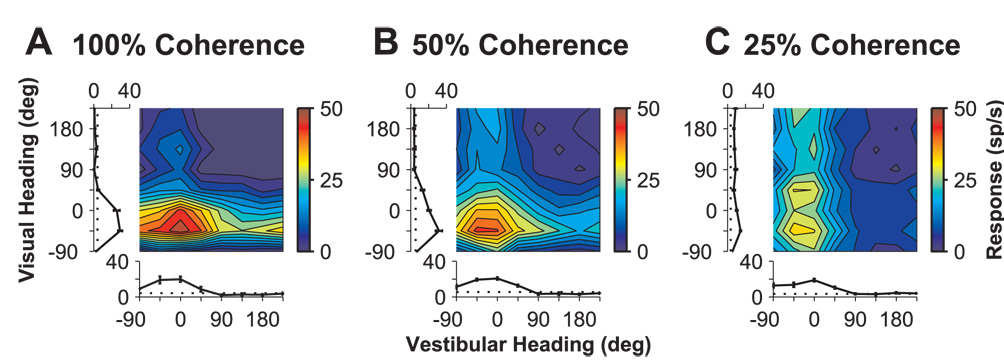
This pattern of results also held true for MSTd cells with “congruent” visual and vestibular heading preferences. Fig. 3 shows responses from a third example cell (with vestibular and visual heading preferences of −25° and −21°, respectively) at three visual coherences, 100%, 50% and 25%. Although vestibular tuning remains quite constant (tuning curves along abscissa), visual responsiveness declined as coherence was decreased (tuning curves along ordinate), with little visual heading tuning remaining at 25% coherence for this neuron. Simultaneously, the transition from visual dominance to vestibular dominance is clearly evident in the bimodal responses as a function of coherence. Bimodal responses were visually-dominated at 100% coherence (horizontal band in Fig. 3A), but became progressively more influenced by the vestibular cue as coherence was reduced. At 50% coherence, the presence of a clear symmetric peak suggests well-matched visual and vestibular contributions to the bimodal response (Fig. 3B). As visual coherence was further reduced to 25%, vestibular dominance is observed, with the bimodal response taking the form of a vertical band aligned with the vestibular heading preference (Fig. 3C). Data from 5 additional example neurons, tested at both 100% and 50% coherence, are shown in Suppl. Fig. S2.

Fig. 3.

Data for a “congruent” MSTd cell, tested at three motion coherences. Format is the same as in Fig. 2. (A) Bimodal responses at 100% coherence are visually dominated. (B) Bimodal responses at 50% coherence show a balanced contribution of visual and vestibular cues. (C) At 25% coherence, bimodal responses appear to be dominated by the vestibular input.

In the following analyses, we quantify the response interactions illustrated by these example neurons. First, we evaluate whether a linear summation of unimodal responses can account for bimodal tuning or whether a non-linear interaction is needed. Second, we explore how the relative contributions of visual and vestibular inputs to the bimodal response change with coherence. Third, we investigate whether the ability of neurons to discriminate small differences in heading improves when stimuli are aligned to match the visual and vestibular preferences of each neuron.

Linearity of cue interactions in bimodal response tuning

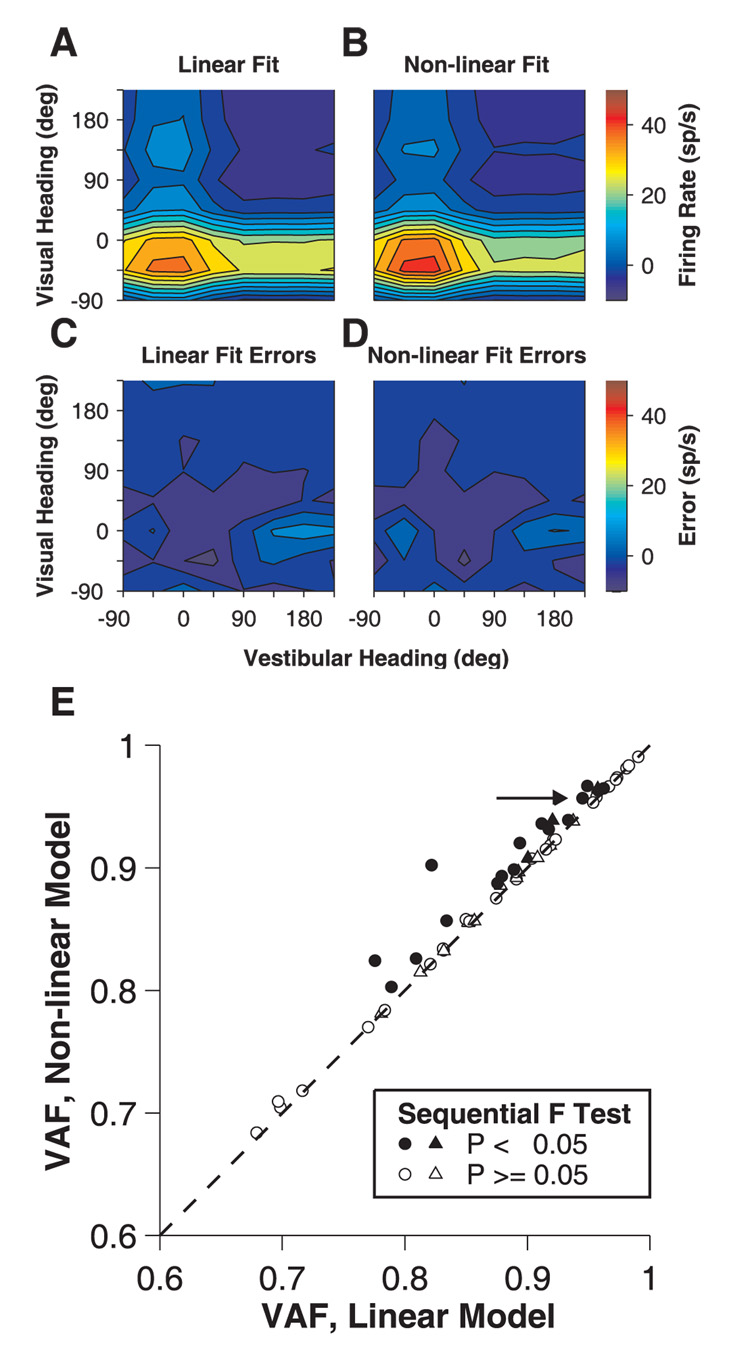
Approximately half of the MSTd neurons with significant visual and vestibular unimodal tuning (22 of 44 at 100% coherence, 8 of 14 at 50% coherence) had a significant interaction effect (two-way ANOVA) in the bimodal condition. This finding suggests that responses of many cells are well described by a linear model, whereas other neurons may require a non-linear component. To further explore the linearity of visual-vestibular interactions in these bimodal responses, we compared the goodness of fit for the simplest linear and non-linear interaction models (see Materials and Methods). In the linear model, responses in the bimodal condition were fit with a weighted sum of the responses from the vestibular and visual conditions. We also evaluated fits with a simple non-linear model, having an additional term consisting of the product of the vestibular and visual responses (see Materials and Methods). Both the linear and non-linear models provided good fits to the data, as illustrated in Fig. 4A and B, respectively, for the example congruent neuron of Fig. 3A. Although the non-linear model provided a significantly improved fit when adjusted for the additional fitting parameter (sequential F test, P=0.00013), the improvement in variance accounted for (VAF) was quite modest (94.5% versus 95.7%), and the patterns of residual errors were comparable for the two fits (Fig. 4C, D).

Fig. 4.

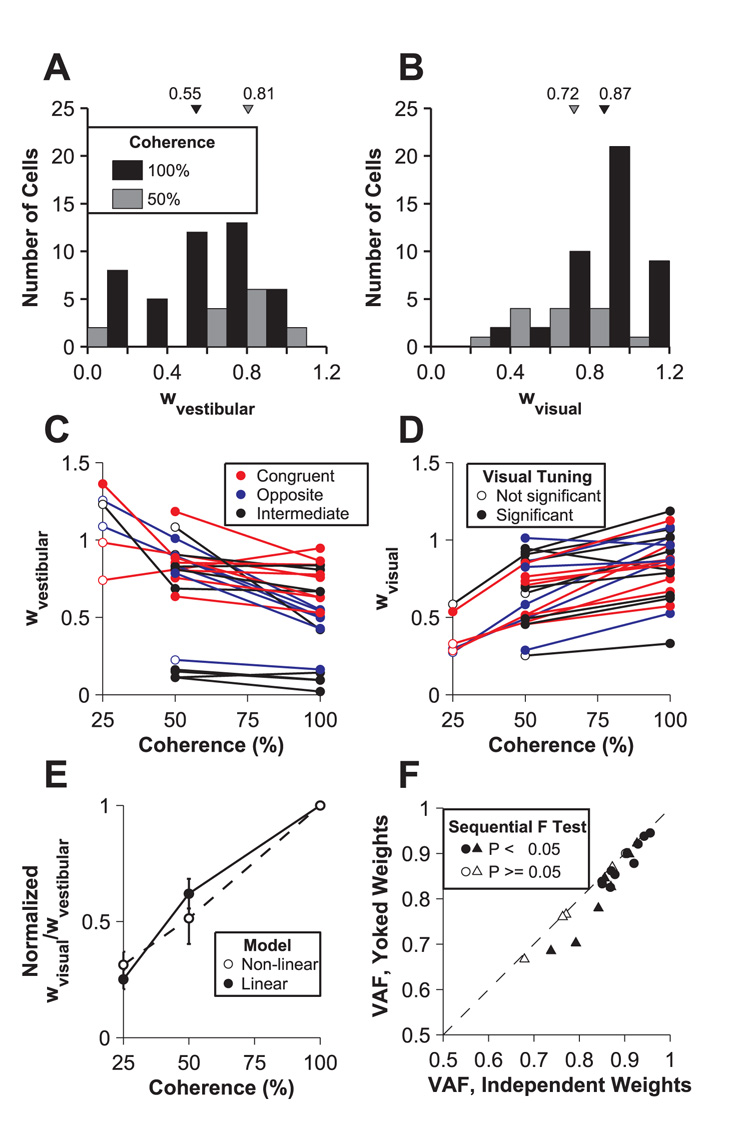
Fitting of linear and non-linear models to bimodal responses. (A–D) Model fits and errors for the same neuron as in Fig. 3. Color contour maps show fits to the bimodal responses using (A) a weighted sum of the unimodal vestibular and visual responses and (B) a weighted sum of the unimodal responses plus their product. (C), (D) Errors of the linear and non-linear fits, respectively. (E) Variance accounted for (VAF) from the non-linear fits is plotted against VAF from the linear fits. Data measured at 100% coherence are shown as circles; 50% coherence as triangles. Filled symbols represent neurons (16 of 44 neurons at 100% coherence and 8 of 14 at 50% coherence) whose responses were fit significantly better by the model including the product term (sequential F test, P<0.05).

Across the population of MSTd neurons, the linear model often resulted in nearly as good a fit as the non-linear model. For data collected at 100% coherence, the non-linear model provided a significantly better fit for 16 out of 44 (36%) neurons (sequential F test P<0.05, Fig. 4E, filled circles). At 50% coherence, this was true for 21% of the neurons (Fig. 4E, filled triangles). With the exception of a few cells, however, the improvement in VAF due to the non-linear term was quite modest. The median VAFs for the linear and non-linear fits were 89.1% versus 90.1% (100% coherence) and 89.2% versus 89.5% (50% coherence). Thus, linear combinations of the unimodal responses generally provide good descriptions of bimodal tuning, with little explanatory power gained by including a multiplicative component.

Sub-additive rather than super-additive interactions in bimodal responses

The weights from the best-fitting linear or non-linear combination rule (w_visual and w_vestibular, Eqn 1 and Eqn 2) describe the strength of the contributions of each unimodal input to the bimodal response. Visual and vestibular weights from the linear and non-linear models were statistically indistinguishable (Wilcoxon signed rank test P=0.407 for vestibular weights, P=0.168 for visual weights), so we further analyzed the weights from the linear model. The majority of MSTd cells combined visual and vestibular cues sub-additively, with both visual and vestibular weights being typically less than 1 (Fig. 5, A, B). We computed 95% confidence intervals for the visual and vestibular weights from the linear fits and found that, at 100% coherence, none of the vestibular weights was significantly larger than 1, whereas the majority (41 of 44) of the cells had vestibular weights that were significantly smaller then 1 (the remaining 3 cells had weights that were not significantly different from 1). Similarly, only 3 cells had visual weights significantly larger than 1, whereas 27 of 44 cells had weights significantly lower than 1. To further quantify this observation, we also performed a regression analysis in which the measured bimodal response was fit with a scaled sum of the visual and vestibular responses (after subtracting spontaneous activity). The regression coefficient was significantly lower than 1 for 37 of 44 cells, whereas none had a coefficient significantly larger than unity. For data obtained at 50% coherence, all 14 cells had regression coefficients that were significantly smaller than unity. Thus, in response to our stimuli, MSTd neurons most frequently exhibited sub-additive integration with occasional additivity and negligible super-additivity.

Fig. 5.

Dependence of vestibular and visual response weights on visual motion coherence. (A), (B) Histograms of vestibular and visual weights (linear model) computed from data at 100% (black) and 50% (gray) coherence. Triangles are plotted at the medians. (C), (D) Vestibular and visual weights (linear model) are plotted as a function of motion coherence. Data points are coded by the significance of unimodal visual tuning (open vs. filled circles) and by the congruency between unimodal vestibular and visual heading preferences (colors). (E) The ratio of visual to vestibular weights is plotted as a function of coherence. For each cell, this ratio was normalized to unity at 100% coherence. Errors bars show standard errors. Filled symbols and solid line: weights computed from linear model fits. Open symbols and dashed line: weights computed from non-linear model fits. (F) Comparison of variance-accounted-for (VAF) between linear models with yoked weights and independent weights. The filled data points (17 of 23 neurons) were fit significantly better by the independent weight model (sequential F test, P<0.05). Of 23 total neurons, 12 with unimodal tuning that remained significant (ANOVA P<0.05) at lower coherences are plotted as circles. Triangles indicate neurons that failed unimodal tuning criteria when coherence was reduced to 50% and/or 25%.

Dependence of visual and vestibular weights on relative cue reliabilities

Next, we investigated whether and how visual and vestibular weights change when the relative reliabilities of the visual and vestibular cues are altered by reducing the coherence of visual motion (see Materials and Methods). It is clear from the examples of Fig. 2 and Fig. 3 that the relative influences of the two cues on the bimodal response changes with motion coherence. This effect could arise simply from the fact that lower coherences elicit visual responses with weaker modulation and lower peak responses as a function of heading. Thus, one possibility is that the weights with which each neuron combines its vestibular and visual inputs remain fixed as coherence changes and that the decreased visual influence in the bimodal tuning is simply due to the weaker visual responses at lower coherences. In this scenario, each neuron would have a combination rule that is independent of cue reliability. Alternatively, the weights given to the vestibular and visual inputs could change with the relative reliabilities of the two cues. This outcome would indicate that the neuronal combination rule is not fixed, but may change with cue reliability. We addressed these two possibilities by examining how vestibular and visual weights changed as a function of motion coherence.

We used the weights from the linear model fits to quantify the relative strengths of the vestibular and visual influences in the bimodal responses. Fig. 5A and B summarize the vestibular and visual weights, respectively, for two visual coherence levels, 100% and 50% (black and gray filled bars; N=44 and N=14, respectively). As compared to 100% coherence, vestibular weights at 50% coherence are shifted toward larger values (median of 0.81 versus 0.55, one tailed Kolmogorov-Smirnov test P<0.001), and visual weights at 50% coherence are shifted towards lower values (median of 0.72 versus 0.87, one tailed Kolmogorov-Smirnov test P=0.037). Thus, across the population, the influence of visual cues on the bimodal responses decreased as visual reliability was reduced while simultaneously the influence of vestibular cues increased.

For neurons recorded at multiple coherences, we were able to examine how the vestibular and visual weights changed for each cell. Among the 44 neurons with significant tuning in both the vestibular and visual conditions at 100% coherence, responses were recorded at 50% and 100% coherences for 17 neurons, at 25% and 100% coherences for 3 neurons and at all three coherences for 3 neurons. All 23 cells showed significant visual tuning at all coherences in the bimodal condition (main effect of visual cue, two-way ANOVA P<0.05). Vestibular and visual weights have been plotted as a function of motion coherence for these 23 cells in Fig. 5C and 5D, respectively (filled symbols indicate significant unimodal visual tuning at each particular coherence, ANOVA P<0.05). Both weights depended significantly on visual coherence (ANCOVA P<0.005), but not on visual-vestibular congruency (P>0.05, Fig. 5C, D). Vestibular weights declined with increasing motion coherence whereas visual weights increased. In contrast, the constant offset term of the model (Eq. 1) did not depend on coherence (ANCOVA P=0.566).

The changes in relative weighting of the visual and vestibular cues in the bimodal response are further illustrated in Fig. 5E by computing the ratio of the weights, w_visual/w_vestibular. For ease of comparison (and because the magnitudes of the vestibular and visual weights varied among neurons, Fig. 5C, D), we normalized the w_visual/w_vestibular ratio of each cell to be 1 at 100% coherence. The normalized weight ratio declined significantly as coherence was reduced (ANCOVA, P≪0.001), dropping to a mean value of 0.62 at 50% coherence and to 0.25 at 25% coherence (filled symbols, Fig. 5E). Weights from the non-linear model fits showed a very similar effect (Fig. 5E, dashed line and open symbols). These results demonstrate that single neurons apply different weights to their visual and vestibular inputs when the relative reliabilities of the two cues change. In other words, the neuronal combination rule is not fixed.

Although weights vary significantly with coherence across the population, one might question whether a single set of weights adequately describes the bimodal responses at all coherences for individual neurons. To address this possibility, we also fit these data with an alternative model in which the visual and vestibular weights were common (i.e., yoked) across coherences. Fig. 5F shows the variance-accounted-for (VAF) for yoked weights versus the VAF for independent weights. We found that data from 17 of 23 cells were fit significantly better by allowing separate weights for each coherence (sequential F test, P<0.05). This result further demonstrates that the weights of individual neurons change with the relative reliabilities of the stimuli.

Because we have fit the bimodal responses with a weighted sum of the measured unimodal responses, one might question whether noise in the unimodal data (especially the visual responses at low coherence) biases the outcome of our analysis. To address this possibility, we first fit the unimodal responses with a family of modified wrapped Gaussian functions (see Materials and Methods and Suppl. Fig. S3). These fits were done simultaneously for all coherence levels, allowing the amplitude of the Gaussian to vary with coherence while the location of the peak remained fixed (see legend to Suppl. Fig. S3 for details). We found that this approach generally fit the unimodal data quite well, and allowed us to use these fitted functions (rather than the raw unimodal data) to model the measured bimodal responses. Results from this analysis, which are summarized in Suppl. Fig. S4, are quite similar to those of Fig. 5. As visual reliability (coherence) decreased, visual weights decreased and vestibular weights simultaneously increased. The change in normalized weight ratio as a function of coherence was again highly significant (ANCOVA P≪0.001). Thus, analyzing our data parametrically to reduce the effect of measurement noise did not change the results appreciably.

Modulation depth of bimodal tuning: comparison with unimodal responses

The analyses detailed above describe how visual and vestibular cues to heading are weighted by neurons during cue combination, but do not address how this interaction affects bimodal tuning. Does simultaneous presentation of vestibular and visual cues improve bimodal tuning compared to tuning for the unimodal cues? In the previous analyses we have shown that visual and vestibular weights and their dependence on visual coherence are similar for congruent and opposite neurons. However, it is logical to hypothesize that peak-to-trough modulation for bimodal stimuli should depend on both (1) the disparity in the alignment of the visual and vestibular heading stimuli and (2) each cell’s visual-vestibular congruency (Gu et al., 2006b; Takahashi et al., 2007). The present experiments, in which we have considered visual-vestibular stimulus combinations that are both aligned and mis-aligned, allow for a novel investigation of how bimodal stimuli alter the selectivity of responses in MSTd.

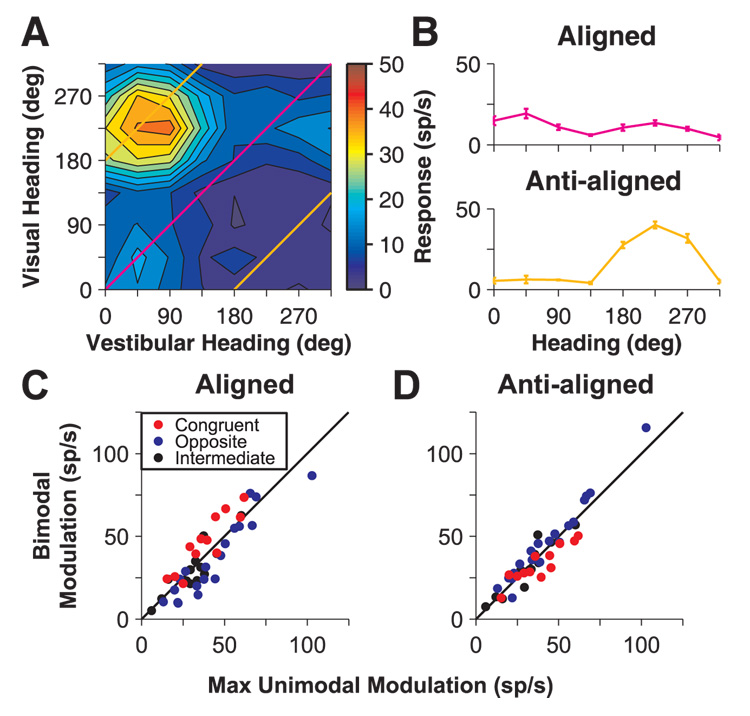
Consider two particular diagonals from the two-dimensional bimodal stimulus array: one corresponding to stimuli with aligned visual and vestibular headings and the other corresponding to stimuli with anti-aligned headings (Fig. 6A). We computed tuning curves for trials when vestibular and visual heading stimuli were aligned (Fig. 6A, magenta line) and tuning curves for trials when the visual and vestibular stimuli were anti-aligned (i.e., 180° opposite; Fig. 6A, orange lines). We then looked at how the modulation depths (maximum-minimum responses) for these bimodal response cross-sections (illustrated in Fig. 6B) differed from the modulation seen in the unimodal tuning curve (either vestibular or visual) with the largest modulation (max. unimodal modulation). Under the hypothesis that bimodal responses represent a near-additive combination of unimodal inputs, we expect that aligned bimodal stimuli should enhance modulation for congruent neurons and reduce it for opposite neurons. In contrast, when anti-aligned vestibular and visual heading stimuli are paired, the reverse would be true: modulation should be reduced for congruent cells and enhanced for opposite cells.

Fig. 6.

Modulation depth and visual-vestibular congruency. (A) Illustration of “aligned” (magenta) and “anti-aligned” (orange) diagonals through the bimodal response array (color contour plot). (B) Mean (± SEM) firing rates for aligned and anti-aligned bimodal stimuli (extracted from the data in A). The anti-aligned tuning curve is plotted as a function of the visual heading. (C), (D) Modulation depth (maximum-minimum response) for bimodal aligned and anti-aligned stimuli is plotted against the largest unimodal (vestibular or visual) response modulation. Color indicates the congruency between vestibular and visual heading preferences (red: congruent cells; blue: opposite cells; black: intermediate cells).

Results are summarized for aligned and anti-aligned stimulus pairings in Fig. 6C and 6D, respectively (data shown only for 100% visual coherence). As hypothesized, the relationship between modulation depths for bimodal versus the strongest unimodal responses depended on visual-vestibular congruency. For congruent cells, modulation depth increased for aligned bimodal stimuli (Wilcoxon signed rank test P=0.005) and decreased for anti-aligned stimuli (Wilcoxon signed rank test P=0.034; Fig. 6C and D, red symbols falling above and below the unity-slope line, respectively). The reverse was true for opposite cells: modulation depth decreased for aligned stimuli and increased for anti-aligned stimuli (aligned P=0.005, anti-aligned P=0.016; Fig. 6C and D, blue symbols falling below and above the unity-slope line, respectively).

Comparison of direction discriminability for bimodal versus unimodal responses

To further investigate the relationship between sensitivity in the bimodal versus unimodal conditions, we computed a measure of the precision with which each neuron discriminates small changes in heading direction for both the bimodal and unimodal conditions. Based on Fig. 6, the largest improvement in bimodal response modulation for each cell is expected to occur when visual and vestibular headings are paired such that their angular alignment corresponds to the difference between the heading preferences in the unimodal conditions. Greater response modulation should, in turn, lead to enhanced discriminability due to steepening of the slope of the tuning curve. To examine this for each MSTd neuron, we computed a “matched” tuning curve by selecting the elements of the array of bimodal responses that most closely matched the difference in heading preference between the unimodal conditions. This curve corresponds to a diagonal cross-section through the peak of the bimodal response profile, and it allows us to examine discriminability around the optimal bimodal stimulus for each MSTd cell, independent of visual-vestibular congruency. For the example neuron of Fig. 6A, the matched tuning curve would happen to be identical to the anti-aligned cross-section, since the latter passes through the peak of the bimodal response profile.

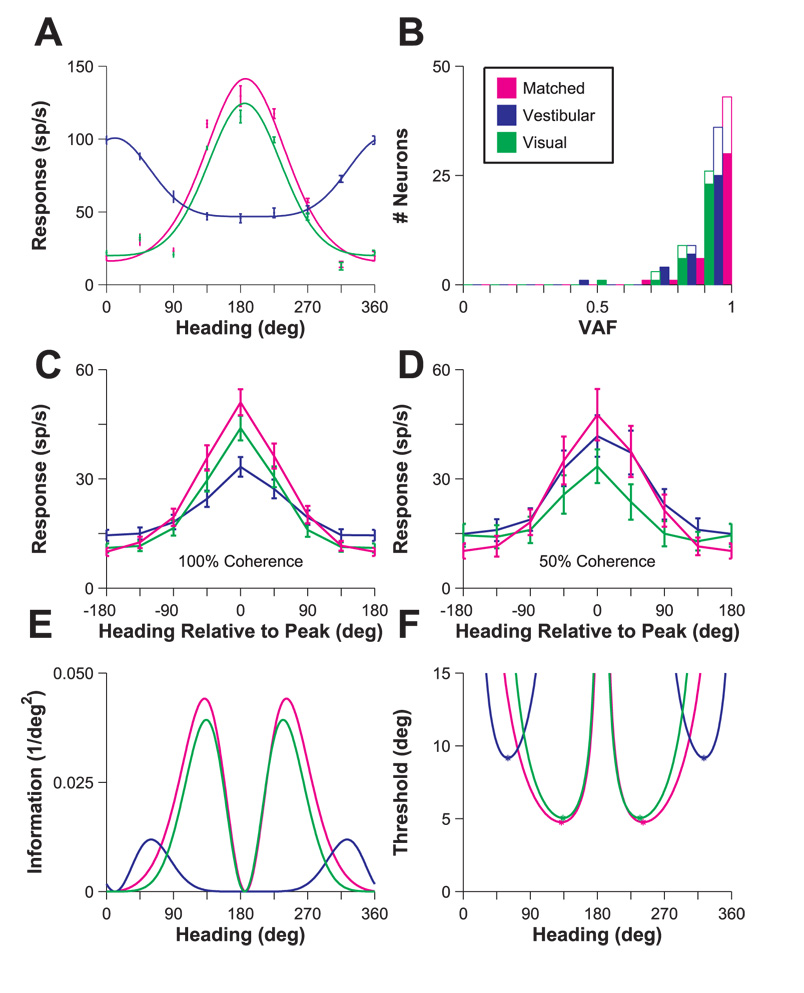
Theoretical studies (Pouget et al., 1999; Seung and Sompolinsky, 1993) have shown that, for any unbiased estimator operating on the responses of a population of neurons, the discriminability (d') of two closely spaced stimuli has an upper bound that is proportional to the square root of Fisher information (defined as the squared slope of the tuning curve divided by the response variance; see Materials and Methods). Thus, we computed minimum discrimination thresholds derived from estimates of Fisher information for both unimodal and matched bimodal stimuli. Because we sparsely sampled heading directions (every 45°), it was necessary to interpolate the heading tuning curves by fitting them with a modified Gaussian function. We fit the vestibular, visual and “matched” curves parametrically as shown in Fig. 7A for the same example cell as Fig. 2B. VAF from the fits across the population are shown in Fig. 7B. In general, the fits were quite good, with median VAF values > 0.9 in all three stimulus conditions. Fig. 7C and D plot the population tuning curves for 44 MSTd neurons at 100% coherence and 14 MSTd neurons at 50% coherence. Each tuning curve was shifted to have a peak at 0° prior to averaging. Matched tuning curves tend to show greater modulation than both vestibular (Wilcoxon signed rank test at 100% coherence: P≪0.001; 50% coherence: P=0.0012) and visual tuning curves (100% coherence: P≪0.001; 50% coherence: P=0.0012). Based on these modulation differences, one may expect lower discrimination thresholds for the matched tuning curves compared to the unimodal curves.

Fig. 7.

Fisher information and heading discriminability. (A) Example wrapped Gaussian fits to vestibular, visual, and “matched” tuning curves for the neuron shown in Fig. 2B. Error bars: ± SEM. (B) Population histogram of VAF for parametric fits to vestibular (blue), visual (green) and matched (magenta) tuning curves. Filled bars denote fits to 100% coherence data; open bars to 50% coherence data. (C), (D) Population vestibular (blue), visual (green) and matched (magenta) tuning curves for N=44 cells (100% coherence, C) and N=14 cells (50% coherence, D). Each curve was shifted to align the peaks of all tuning curves at 0° before averaging. (E) Fisher information versus heading. Using fits from A, Fisher information was computed as $I_F\left(\theta \right)=\frac{\mathrm{R\prime }{\left(\theta \right)}^2}{{\sigma }^2\left(\theta \right)},$, where R’(θ) is the derivative of the fitted tuning curve at a particular heading (θ), and σ²(θ) is the response variance. (F) Discrimination threshold versus heading for the same example neuron as in A and E. Thresholds were computed as $\mathrm{\Delta }\theta \left(\theta \right)=1/\sqrt{I_F\left(\theta \right)}.$ The two numerically computed minima for each curve are plotted as asterisks.

We used the parametric fits to calculate Fisher information as shown for the example cell in Fig. 7E. We calculated the slope of the tuning curve from the modified Gaussian fit and the response variance from a linear fit to the log-log plot of variance versus mean firing rate for each neuron. Assuming the criterion d’=1, one can use Fisher information to calculate a discrimination threshold as $\mathrm{\Delta }\theta =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{I_F(\theta )}$}\right.$ (Eqn 7). We thereby identified the lowest discrimination thresholds for the vestibular, visual and matched tuning curves (asterisks in Fig. 7F; see Materials and Methods for details).

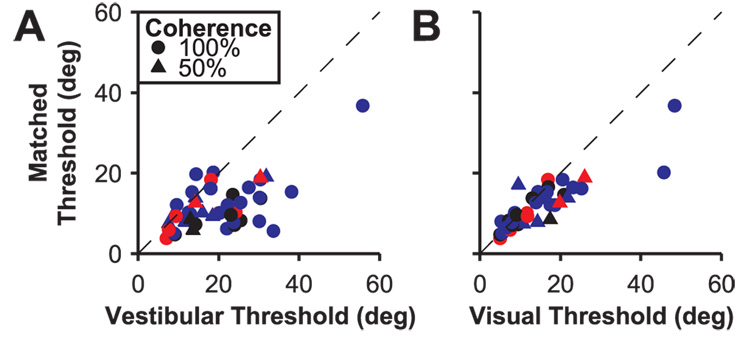
We examined how the addition of vestibular and visual inputs optimized for each cell’s direction preferences affected the discrimination thresholds derived from the bimodal responses relative to the unimodal responses. Fig. 8A and B show minimum thresholds derived from the matched tuning curves plotted against minimum thresholds for the unimodal tuning curves. In both comparisons, points tend to fall below the diagonal, indicating that cue combination improves discriminability (Wilcoxon signed rank test P<0.001). Thus, when slicing along a diagonal of the bimodal response array that optimally aligns the vestibular and visual preferences, improvements in threshold are common and do not depend on visual-vestibular congruency (congruent neurons in red, intermediate neurons in black, opposite neurons in blue). This is consistent with the finding above that the combination rule used by MSTd neurons does not appear different between congruent and opposite cells. As a result, all MSTd neurons are potentially capable of exhibiting improved discriminability under bimodal stimulation, though congruent cells may still play a privileged role under most natural conditions in which visual and vestibular heading cues are aligned.

Fig. 8.

Comparison of estimated heading discrimination thresholds for bimodal (matched) and unimodal (A, vestibular, B, visual) responses. Circles and triangles represent data collected at 100% and 50% coherence, respectively. Color indicates the congruency between unimodal heading preferences (red: congruent cells; blue: opposite cells; black: intermediate cells).

Discussion

We have characterized the combination rule used by neurons in macaque visual cortex to integrate visual (optic flow) and vestibular signals and how this rule depends on relative cue reliabilities. Using a virtual reality system, we studied MSTd neuron responses to eight directions of translation in the horizontal plane defined by visual cues alone, vestibular cues alone and all 64 possible bimodal combinations of visual and vestibular headings, both congruent and conflicting. We found that a weighted linear model provides a good description of the bimodal responses with sub-additive weighting of visual and vestibular inputs being typical. When the strength (coherence) of the visual cue was reduced while the vestibular cue remained constant, we observed systematic changes in the neural weighting of the two inputs: visual weights decreased and vestibular weights increased as coherence declined. In addition, response modulation depth increased and discriminability improved in the bimodal responses. Overall, these findings establish a neural combination rule that can account for multisensory integration by neurons and they provide important constraints for models of optimal (e.g., Bayesian) cue integration.

Linear combination rule for bimodal responses

We found that the firing rates of bimodal MSTd cells were described well by weighted linear sums of the unimodal vestibular and visual responses. Addition of a non-linear (multiplicative) term significantly improved fitting of bimodal responses for about one-third of MSTd neurons, but these improvements were very modest (difference in median VAF less than 1%). Our findings are consistent with recent theoretical studies which posit that multisensory neurons combine their inputs linearly to accomplish optimal cue integration (Ma et al., 2006). In the Ma et al. study, neurons were assumed to perform a straight arithmetic sum of their unimodal inputs, but the theory is also compatible with the possibility that neurons perform a weighted linear summation that is sub-additive (A. Pouget, personal communication). In psychophysical studies, humans often combine cues in a manner consistent with weighted linear summation of unimodal estimates where the weights vary with the relative reliabilities of the cues (e.g., Alais and Burr, 2004; Battaglia et al., 2003; Ernst and Banks, 2002). Although linear combination at the level of perceptual estimates does not necessarily imply any particular neural combination rule, our findings suggest that the neural mechanisms underlying optimal cue integration may depend on weighted linear summation of responses at the single neuron level.

It is important to relate our findings to previous physiological results regarding the combination rule used by multisensory neurons. In their pioneering studies of multimodal neurons in the superior colliculus, Stein and colleagues emphasized super-additivity as a signature of multisensory integration (Meredith and Stein, 1983,1986b, 1996; Wallace et al., 1996). While our findings lie in clear contrast to these studies, there are some important differences that must be considered, in addition to the fact that we recorded in a different brain area. First, the appearance of the neural combination rule may depend considerably on stimulus strength. The largest super-additive effects seen in the superior colliculus were observed when unimodal stimuli were near threshold for eliciting a response (Meredith and Stein, 1986b). Recent studies from the same laboratory have shown that interactions tend to become more additive as stimulus strength increases (Perrault et al., 2003, 2005; Stanford et al., 2005). Note, however, that the difference in average firing rate between the ”low” and “high” intensity unimodal stimuli used by Stanford et al. (2005) was less than two-fold and that responses were generally much weaker that those elicited by our stimuli. Linear summation at the level of membrane potentials (Skaliora et al., 2004) followed by a static nonlinearity (e.g., threshold) in spike generation will produce super-additive firing rates for weak stimuli (Holmes and Spence, 2005). Thus, the predominant sub-additivity seen in our study may at least partially reflect the fact that we are typically operating in a stimulus regime well above response threshold. Our finding of predominant sub-additivity is consistent with results of other recent cortical studies that have also used supra-threshold stimuli (Avillac et al., 2007; Bizley et al., 2007; Kayser et al., 2008; Sugihara et al., 2006), as well as other cortical studies which show that super-additive interactions tend to become additive or sub-additive for stronger stimuli (Ghazanfar et al., 2005; Lakatos et al., 2007).

Second, whereas most previous studies have examined multisensory integration at one or a few points within the stimulus space (e.g., visual and auditory stimuli at a single spatial location), our experimental protocol explored a broad range of stimuli, and our analysis used the responses to all stimulus combinations to mathematically characterize the neuronal combination rule. If nonlinearities such as response threshold or saturation play substantial roles, then the apparent sub-/super-additivity of responses can change markedly depending on where stimuli are placed within the receptive field or along a tuning curve. Thus, we have examined bimodal responses in MSTd using all possible combinations of visual and vestibular headings that span the full tuning of the neurons in the horizontal plane. This method allows us to model the combination of unimodal responses across a wide range of stimuli, including both congruent and conflicting combinations with varying efficacy. We suggest that our approach, which avoids large effects of response threshold yet spans the stimulus tuning of the neurons, provides a more comprehensive means of evaluating the combination rule used by multisensory neurons.

Dependence of weights on cue reliability

An important finding from human psychophysical studies is that the influence of a cue ina multisensory integration task depends on the relative reliability of that cue compared to others (Alais and Burr, 2004; Battaglia et al., 2003; Ernst and Banks, 2002). Specifically, a less reliable cue is given less weight in perceptual estimates of multimodal stimuli. Our findings suggest that an analogous computation may occur at the single neuron level, since we observe that MSTd neurons give less weight to their visual inputs when optic flow is degraded by reducing motion coherence. It must be noted, however, that such re-weighting of unimodal inputs by single neurons is not necessarily required to account for the behavioral observations. Rather, the behavioral dependence on cue reliability could be mediated by multisensory neurons that maintain constant weights on their unimodal inputs as a function of coherence. A recent theoretical study shows that a population of multisensory neurons with Poisson-like firing statistics and fixed weights on their unimodal inputs can accomplish Bayes-optimal cue integration (Ma et al., 2006). In this scheme, changes in cue reliability are reflected in the bimodal population response because of the lower responses elicited by a weaker cue, but the combination rule employed by the model neurons does not change. Our experiments provide a test of this theoretical framework.

Our findings may appear contrary to the assumption of fixed weights in the theory of Ma et al. (2006), as we have found that the weights in a linear combination rule change with stimulus reliabilty. When the reliability of the optic flow cue was reduced by noise, its influence on the bimodal response diminished while there was a simultaneous increase in the influence of the vestibular cue. This discrepancy may arise, however, because our neurons exhibit firing rate changes with coherence that violate the assumptions of the theory of Ma et al. Their framework assumes that stimulus strength (coherence) multiplicatively scales all of the responses of sensory neurons. In contrast, as illustrated by the example in Suppl. Figure S3B, responses to non-preferred headings often decrease at high coherence whereas responses increase at the preferred heading. When the theory of Ma et al. (2006) takes this fact into account, it may predict weight changes with coherence similar to those that we have observed (A. Pouget, personal communication).

It is important to point out that our finding of weights that depend on coherence cannot be explained by a static nonlinearity in the relationship between membrane potential and firing rate, since this nonlinearity is usually expansive (e.g., Priebe et al., 2004). Such a mechanism might predict that weak unimodal visual responses, such as at low coherence, would be enhanced in the bimodal response (Holmes and Spence, 2005). In contrast, we have observed the opposite effect, where the influence of weak unimodal responses on the bimodal response is less than one would expect based on a combination rule with fixed weights. The mechanism by which neuronal weights change with cue reliability is unclear.

We cannot speak to the temporal dynamics of this re-weighting because we presented different motion coherences in separate blocks of trials. Further experiments are necessary to investigate whether neurons re-weight their inputs on a trial by trial basis. Nevertheless, at least for the blocked design we have used, MSTd neurons appear to weight their inputs in proportion to their relative reliabilities. Another important caveat is that our animals were simply required to maintain visual fixation while stimuli were presented. Yet, cognitive and motivational demands placed on alert animals may affect the neuronal combination rule and the effects of variations in cue reliability. For example, the proportion of neurons with responses showing multisensory integration in the primate superior colliculus appears to depend on behavioral context. Compared to anesthetized animals (Wallace et al., 1996), multisensory interactions in alert animals may be more frequent when stimuli are behaviorally relevant (Frens and Van Opstal, 1998), but are somewhat suppressed during passive fixation (Bell et al., 2003). It is possible that the effects of cue reliability on weights in MSTd may be different under circumstances in which the animal is required to perceptually integrate the cues (as in Gu et al., 2006a). Thus, experiments in trained, behaving animals will ultimately be needed to confirm these findings.

An additional caveat is that our monkeys’ eyes and heads were constrained to remain still during stimulus presentation. We do not know whether the integrative properties of MSTd neurons would be different under more natural conditions in which the eyes or head are moving, which can substantially complicate the optic flow on the retina. In a recent study (Gu et al., 2007), however, we measured responses of MSTd neurons during free viewing in darkness and found little effect of eye movements on the vestibular responses of MSTd neurons.

Modulation depth and discrimination threshold

Another consistent observation in human psychophysical experiments is that subjects tend to make more precise judgments under bimodal as compared to unimodal conditions (Alais and Burr, 2004; Ernst and Banks, 2002). We see a potential neural correlate in our data, but with an important qualification. Simultaneous presentation of vestibular and visual cues can enhance the modulation depth and direction discrimination thresholds of MSTd neurons, but the finding depends on the alignment of the bimodal stimuli relative to the cell’s unimodal heading preferences. When the disparity between vestibular and visual stimuli matches the relative alignment of a neuron’s heading preferences, modulation depth increases and the minimum discrimination threshold decreases. For neurons with congruent unimodal heading preferences, these improvements occur when vestibular and visual headings are aligned, as typically occurs during self-motion in everyday life. For other neurons, modulation depth and discriminability are enhanced under conditions where vestibular and visual heading information is not aligned, which can occur for example during simultaneous self-motion and object-motion. Future research will need to examine whether congruent and opposite cells play distinct roles in self-motion versus object-motion perception. It also remains to be demonstrated that neuronal sensitivity improves in parallel with behavioral sensitivity when trained animals perform multi-modal discrimination tasks. Preliminary results from our laboratory suggest that this is the case (Gu et al., 2006a). In conclusion, our findings establish two new aspects of multisensory integration. We demonstrate that weighted linear summation is an adequate combination rule to describe visual-vestibular integration by MSTd neurons, and we establish for the first time that the weights in the combination rule can vary with cue reliability. These findings should help to constrain and further define neural models for optimal cue integration.

Experimental Procedures

Subjects and surgery

Two male rhesus monkeys (Macaca mulatta) served as subjects for physiological experiments. General procedures have been described previously (Gu et al., 2006b). Each animal was outfitted with a circular molded plastic ring anchored to the skull with titanium T-bolts and dental acrylic. For monitoring eye movements, each monkey was implanted with a scleral search coil (Robinson, 1963). The Institutional Animal Care and Use Committee at Washington University approved all animal surgeries and experimental procedures, which were performed in accordance with National Institutes of Health guidelines. Animals were trained to fixate on a central target for fluid rewards using operant conditioning.

Vestibular and visual stimuli

A 6 degree-of-freedom motion platform (MOOG 6DOF2000E; Moog, East Aurora, NY) was used to passively translate the animals along one of 8 directions in the horizontal plane (Fig. 2, inset), spaced 45° apart. It was controlled in real time over an Ethernet interface. Visual stimuli were projected onto a tangent screen, which was affixed to the front surface of the field coil frame, by a three-chip digital light projector (Mirage 2000; Christie Digital Systems, Cypress, CA). The screen measured 60 × 60 cm and was mounted 30 cm in front of the monkey, thus subtending ~90° × 90°. Visual stimuli simulated translational movement along the same 8 directions through a three-dimensional field of stars. Each star was a triangle that measured 0.15 cm × 0.15 cm, and the cloud measured 100 cm wide by 100 cm tall by 40 cm deep at a star density of 0.01 per cm³. To provide stereoscopic cues, the dot cloud was rendered as a red-green anaglyph using two OpenGL cameras and viewed through custom red-green goggles. The optic flow field contained naturalistic cues mimicking translation of the observer in the horizontal plane, including motion parallax, size variations and binocular disparity.

Electrophysiological recordings

We recorded action potentials extracellularly from two hemispheres in two monkeys. We stereotaxically fit a recording grid inside the head stabilization ring. In each recording session, a tungsten microelectrode was passed through a transdural guide tube. The electrode was advanced through the cortex using a micromanipulator drive. An amplifier, 8-pole bandpass filter (400–5000 Hz) and dual voltage-time window discriminator (BAK Electronics, Mount Airy, MD) were used to isolate action potentials from single neurons. Action potential times and behavioral events were recorded with 1 ms accuracy by a computer. Eye coil signals were low-pass filtered and sampled at 250 Hz.

Magnetic resonance image (MRI) scans and Caret software analyses were used to guide electrode penetrations to area MSTd (See Gu et al., 2006b for details). The targeted area was further verified by the depths of gray-to-white matter transitions. Neurons were isolated while presenting a large field of flickering dots. In some experiments, we further advanced the electrode tip into the lower bank of the superior temporal sulcus to verify the presence of neurons with middle temporal (MT) area response characteristics (Gu et al., 2006b). Receptive field locations changed as expected across guide tube locations based on the known topography of MT (Albright and Desimone, 1987; Desimone and Ungerleider, 1986; Gattass and Gross, 1981; Maunsell and Van Essen, 1987; Van Essen et al., 1981; Zeki, 1974).

Experimental protocol

We measured neural responses to 8 heading directions evenly spaced every 45° in the horizontal plane. Neurons were tested under three experimental conditions. (1) In vestibular trials, the monkey was required to maintain fixation on a central dot on an otherwise blank screen while being translated along one of these 8 directions. (2) In visual trials, the monkey saw optic flow simulating self-motion (same 8 directions) while the platform remained stationary. (3) In bimodal trials, the monkey experienced both translational motion and optic flow. We paired all 8 vestibular headings with all 8 visual headings for a total of 64 possible combinations. Eight of these 64 combinations were congruent, meaning that visual and vestibular cues simulated the same heading. These congruent bimodal stimuli correspond to the “combined” conditions in previous experiments (Fetsch et al., 2007; Gu et al., 2006b; Takahashi et al., 2007). The remaining 56 cases were cue-conflict stimuli. This relative proportion of congruent and cue-conflict stimuli was adopted purely for the purpose of characterizing the neuronal combination rule, and was not intended to reflect ecological validity. Each translation followed a Gaussian velocity profile. It had a duration of 2 s, an amplitude of 13 cm, a peak velocity of 30 cm/s and a peak acceleration of approximately 0.1 g (981 cm/s²).

These three stimulus conditions were interleaved randomly along with blank trials with neither translation nor optic flow. Ideally, 5 repetitions of each unique stimulus were collected for a total of 405 trials. Experiments with fewer than 3 repetitions were excluded from analysis. When isolation remained satisfactory, we ran additional blocks of trials with the coherence of the visual stimulus reduced to 50% and/or 25%. Visual coherence was lowered by randomly relocating a percentage of the dots on every subsequent video frame. For example, we randomly selected one quarter of the dots in every frame at 25% coherence and updated their positions to new positions consistent with the simulated motion while the other three-quarters of the dots were plotted at new random locations within the 3D cloud. Notice that each block consisted of both unimodal and bimodal stimuli at the corresponding coherence level. Whenever a cell was tested at multiple coherences, both the unimodal vestibular tuning and the unimodal visual tuning were independently assessed in each block.

Trials were initiated by displaying a 0.2° × 0.2° fixation target on the screen. The monkey was required to fixate for 200 ms. Then actual and/or simulated motion was presented. During all trials, the monkey was required to maintain fixation within a 3° × 3° window for a juice reward. Trials in which the monkey broke fixation were aborted and discarded.

Data analysis

Custom scripts written in Matlab (Mathworks, Natick, MA) were used to perform all analyses. We first computed the mean firing rate during the middle 1 s of each 2 s trial (Gu et al., 2006b). Subsequently, responses across stimulus repetitions were averaged to obtain a mean firing rate for each stimulus condition. These mean responses for the two unimodal cues (visual and vestibular) were used to compute tuning curves. One way ANOVA was used to assess the significance of tuning in the vestibular and visual conditions. For cells with significant tuning, preferred vestibular and visual headings were calculated using the vector sum of mean responses. Then the difference between preferred vestibular heading and preferred visual heading was computed for each neuron. We classified each cell as congruent, intermediate, or opposite based on the alignment between its vestibular and visual heading preferences. Cells having alignment within 60° were classified as congruent, and cells whose alignments differed by more than 120° were classified as opposite, with intermediate cells falling between these two conditions (Fetsch et al., 2007).

Modeling of bimodal responses

For the bimodal condition, we arranged the responses into two-dimensional arrays indexed by the vestibular heading and the visual heading (e.g., color contour maps in Fig. 2 and Fig. 3). Two-way ANOVA was used to compute the significance of vestibular and visual tuning in the bimodal responses, as well as their interaction. A significant interaction effect indicates non-linearities in the bimodal responses.

To further explore the linearity of visual-vestibular interactions in the bimodal condition, we also fit the data using linear and non-linear models. For these models, responses in the three conditions were defined as the mean responses minus the average spontaneous activity measured in the blank trials. For the linear model, the bimodal condition data were fit by a linear combination of the respective vestibular and visual responses.

$$r_{\mathit{\text{bimodal}}}\left(\theta ,\phi \right)=w_{\mathit{\text{vestibular}}}{r}_{\mathit{\text{vestibular}}}\left(\theta \right)+w_{\mathit{\text{visual}}}{r}_{\mathit{\text{visual}}}\left(\phi \right)+C$$ (Eqn 1)

In this equation, r_bimodal is the predicted response for the bimodal condition, and r_vestibular and r_visual are the responses in the vestibular and visual unimodal conditions, respectively. Angles θ and φ are the respective vestibular and visual heading preferences. Model weights w_vestibular, w_visual and the constant C were chosen to minimize the sum of squared errors between the bimodal prediction r_bimodal and the measured bimodal responses. In addition, responses were also fit by the following equation that includes a multiplicative non-linearity:

$$r_{\mathit{\text{bimodal}}}\left(\theta ,\phi \right)=w_{\mathit{\text{vestibular}}}{r}_{\mathit{\text{vestibular}}}\left(\theta \right)+w_{\mathit{\text{visual}}}{r}_{\mathit{\text{visual}}}\left(\phi \right)+w_{\mathit{\text{product}}}{r}_{\mathit{\text{vestibular}}}\left(\theta \right)·r_{\mathit{\text{visual}}}\left(\phi \right)+C$$ (Eqn 2)

where w_product is the weight on the multiplicative interaction term.

For each fit, the variance accounted for (VAF) was computed as

$$VAF=1-\frac{SSE}{SST}$$ (Eqn 3)

where SSE is the sum of squared errors between the fit and the data and SST is the sum of squared differences between the data and the mean of the data. As the number of free parameters was different between the linear and non-linear models, the statistical significance of the non-linear fit over the linear fit was assessed using a sequential F test. A significant outcome of the sequential F test (P < 0.05) indicates that the non-linear model fits the data significantly better than the linear model.

Visual and vestibular weights and cue reliability

Additional models were explored as we varied the coherence of the visual stimulus. Initially, the same two models as described above were used to fit data from different coherence blocks. That is, weights w_vestibular and w_visual were computed separately for each visual coherence (“independent weight” model). We also examined whether a single set of fixed weights for each cell is sufficient to explain the data at all coherences. For the latter pair of models (both linear and non-linear variants), weights w_vestibular and w_visual were common across coherences (“yoked weight” model). Note that for both the independent weight and yoked weight models, parameter C was allowed to vary with coherence. Thus, to fit the data across three coherences, the linear model would have 9 free parameters when weights are independent and 5 free parameters when weights are yoked. VAF was used to quantify whether fits were better using the model with independent weights versus the model with yoked weights. In addition, the sequential F test was used to assess whether allowing model weights to vary with coherence provides significantly improved fits.

Unimodal versus bimodal response tuning and discriminability

To illustrate how combining visual and vestibular cues alters responses in the bimodal condition, we computed tuning curves for two specific cross-sections though the array of bimodal responses. Using the main diagonal of the bimodal response array (Fig. 6A, magenta), we computed a tuning curve for trials when the vestibular and visual heading stimuli were aligned (i.e., congruent). We followed a similar procedure to obtain tuning curves for trials when the vestibular and visual headings were anti-aligned (i.e., 180° opposite; Fig. 6A, orange). For each of these tuning curves and the tuning curves from the unimodal conditions, we computed a modulation depth as the maximum mean response minus the minimum mean response. We then compared the best unimodal modulation depth to the modulation depth in the aligned and anti-aligned cross-sections for congruent, intermediate and opposite cells.

To further quantify how firing rates combine, we also derived a bimodal tuning curve along a single diagonal that was optimized for each cell to yield near-maximal bimodal responses. The difference in heading preference between the visual and vestibular conditions, which is used to define the congruency of each cell (see above), also specifies how disparate the visual and vestibular heading stimuli should be to produce maximum response modulation. From the array of bimodal responses, we constructed a “matched” tuning curve by selecting the diagonal that matched most closely this difference in heading preferences. For example, for vestibular and visual heading preferences within 22.5° of each other, the main diagonal would be selected. For vestibular and visual heading preferences that differ by 22.5° to 67.5°, the matched tuning curve would be derived from the diagonal along which the vestibular and visual headings differ by 45°. Selected this way, the matched tuning curve should be a diagonal cross-section through the peak of the bimodal response profile. After shifting each of the vestibular, visual and matched tuning curves to have a peak at 0°, we averaged across the population of neurons recorded at a given coherence to construct population tuning curves at different visual coherences.

We then used Fisher information to quantify the maximum discriminability that could be achieved at any point along the matched tuning curve and the unimodal curves. Because heading tuning was sampled coarsely, we interpolated the data to high spatial resolution by fitting the curves with a modified wrapped Gaussian function (Fetsch et al., 2007),

$$R\left(\theta \right)=A_1·\left[e^{\frac{-2\times (1-\text{cos}(\theta -{\theta }_0))}{{(\sigma ·\kappa )}^2}}+A_2·e^{\frac{-2\times (1-\text{cos}(\theta -{\theta }_0-\pi ))}{{\sigma }^2}}\right]+R_0$$ (Eqn 4)

where θ₀ is the angular location of the peak response, σ is the tuning width, A₁ is the amplitude and R₀ is the baseline response. The second term with amplitude A₂ is necessary to fit the tuning of a few MSTd cells that show a second response peak 180° out of phase with the first peak (with κ determining the relative widths of the two peaks; see Fetsch et al., 2007 for details). Goodness-of-fit was quantified using the VAF. Only fits having a full-width larger than 45° were used further to avoid situations in which the width of the peak (and hence the slope) was not well constrained by the data. Fits of the model to experimental data were carried out in Matlab using the constrained minimization function ”fmincon.”

From these tuning curves, we computed Fisher information using the derivative of the fits, R’, and the variance of the responses, σ².

$$I_F\left(\theta \right)=\frac{\mathrm{R\prime }{\left(\theta \right)}^2}{\sigma {\left(\theta \right)}^2}$$ (Eqn 5)

The variance at each point along the tuning curve was estimated from a linear fit to a log-log plot of response variance versus mean response for each cell. From the Fisher information, we computed an upper bound on discriminability (Nover et al., 2005).

$$\mathrm{d\prime }\left(\theta \right)=\mathrm{\Delta }\theta \sqrt{I_F\left(\theta \right)}$$ (Eqn 6)

For the criterion d’=1, the threshold for discrimination is

$$\mathrm{\Delta }\theta =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{I_F\left(\theta \right)}$}\right.$$ (Eqn 7)

We found the minimum discrimination threshold for each of the visual, vestibular and matched curves. For our population of cells, we plotted the minimum thresholds from the matched tuning curves against the minimum thresholds from each of the two unimodal tuning curves.