SUMMARY
Likelihood approaches for large irregularly spaced spatial datasets are often very difficult, if not infeasible, to implement due to computational limitations. Even when we can assume normality, exact calculations of the likelihood for a Gaussian spatial process observed at n locations requires O(n3) operations. We present a version of Whittle’s approximation to the Gaussian log likelihood for spatial regular lattices with missing values and for irregularly spaced datasets. This method requires O(nlog2n) operations and does not involve calculating determinants. We present simulations and theoretical results to show the benefits and the performance of the spatial likelihood approximation method presented here for spatial irregularly spaced datasets and lattices with missing values. We apply these methods to estimate the spatial structure of sea surface temperatures (SST) using satellite data with missing values.
Keywords: anisotropy, covariance, Fourier transform, periodogram, spatial likelihood, spatial statistics, satellite data, sea surface temperatures
1 Introduction
Statisticians are frequently involved in the spatial analysis of huge datasets. In this situation, calculating the likelihood function to estimate the covariance parameters or to obtain the predictive posterior density is very difficult due to computational limitations. Even if we can assume normality, calculating the likelihood function involves O(N3) operations, where N is the number of observations. However, if the observations are on a regular complete lattice, then it is possible to compute the likelihood function with fewer calculations using spectral methods (Whittle 1954, Guyon 1982, Dahlhaus and Küsch, 1987, Stein 1995, 1999). These spectral methods are based on the likelihood approximation proposed by Whittle (1954). Whittle’s approximation is for Gaussian random fields observed on a regular lattice without missing observations. In practice, very often the data are irregularly spaced or are not on a complete regular lattice, so we could not use Whittle’s approximation to the likelihood, and there is need for new methodology to overcome this problem.
Spectral methods for irregular time series have been studied, e.g. by Parzen (1963), Bloomfield (2000), Neave (1970), Clinger and Van Ness (1976), and Priestly (1981, p. 585), in the context of estimating the periodogram of a time series. However, little research has been done in terms of introducing spatial likelihood approximation methods using spectral tools for irregularly spaced spatial datasets. In a spatial setting it is worth mentioning that the simple likelihood approximation introduced by Vecchia (1988), which is based on partitioning the data into clusters, and assuming that the clusters are conditionally independent. Pardo-Igúzquiza et al. (1997) wrote a computer program for Vecchia’s approximation method. Stein et al. (2004) adapted Vecchia’s approach to approximate the restricted likelihood of a Gaussian process. Stein et al. (2004) showed that Vecchia’s approximation gives unbiased estimating equations. A similar clustering framework for likelihood approximation was presented by Caragea (2003), in which the clusters were assumed conditionally independent after conditioning on the cluster mean. For Markov fields, a coding method for parameter estimation was proposed by Besag (1974). Besag and Moran (1975) introduced an exact likelihood method for rectangular autonormal processes.
The new methods presented in this paper assume that the locations at which we have missing data are not random, but instead they are due to the spatial design of the data or other nonrandom phenomena, which seems to be the case in most environmental problems involving large spatial datasets with missing data. For instance, when working with monitoring air pollution data or meteorological data from weather stations, the location of the sites is not random, thus, the location of the sites without data is generally not random either. Another example is satellite data. For instance, satellite microwave radiometers that measure sea surface temperatures (SST) can not provide information over land (only water), and the locations with land surface, clearly, are not random. The important feature of microwave retrievals is that SST can be measured through clouds. In this work we apply our methods to estimate the spatial structure of sea surface temperature fields using the Tropical Rainfall Measuring Mission (TRMM) microwave imager (TMI) satellite data for the Pacific ocean. Likelihood methods are often not feasible because satellite data are very large datasets. Standard spectral methods can not be applied either because of the missing data over land surfaces.
In Section 3, we present an approach to approximate the likelihood for Gaussian lattice processes with missing values. In Section 4, we propose a method to approximate the Gaussian likelihood for irregularly spaced datasets. In Section 5 we apply our approximated likelihood method to estimate the spatial structure of sea surface temperature (SST) fields using TMI satellite data. We finish with a discussion.
2 Spectral Domain
A random field Z in ℝ2 is called weakly stationary, if it has finite second moments, its mean function is constant and it possesses an autocovariance function C, such that C(x − y) = cov{Z(x), Z(y)}. If the autocovariance function satisfies, ∫ℝ2 |C(x)|dx < ∞. Then, we can define the spectral density function, f, which is the Fourier transform of the autocovariance function:
If Z is observed only at N uniformly spaced spatial locations Δ units apart, the spectrum of observations of the sample sequence Z(Δx), for x ∈ℤ2, is concentrated within the finite frequency band −π/Δ ≤ ω< π/Δ (aliasing phenomenon). The spectral density fΔ of the process on the lattice can be written in terms of the spectral density f of the continuous process Z as
| (1) |
for .
We estimate the spectral density of a lattice process, observed on a grid (n1 × n2), where N = n1n2, with the the periodogram,
| (2) |
We compute (2) for ω in the set of Fourier frequencies 2πf/n where , and f ∈ JN, for
| (3) |
For large datasets, calculating the determinants that we have in the likelihood function can be often infeasible. Spectral methods could be used to approximate the likelihood and obtain the maximum likelihood estimates (MLE) of the covariance parameters: θ = (θ1, …,θr). These spectral methods are based on Whittle’s (1954) approximation to the Gaussian negative log likelihood:
| (4) |
where the sum is evaluated at the Fourier frequencies, IN is the periodogram and f is the spectral density of the lattice process. The approximated likelihood can be calculated very efficiently by using the fast Fourier transform. This approximation requires only O(Nlog2N) operations. Simulation studies conducted by the author seem to indicate that N needs to be at least 100 to get good estimated MLE parameters using Whittle’s approximation.
The asymptotic covariance matrix of the MLE estimates of θ1, …,θr is
| (5) |
this is much easier to compute than the inverse of the Fisher information matrix.
3 Incomplete lattices
In this Section we introduce spectral methods to approximate the likelihood for spatial processes observed on incomplete lattices. We propose an estimated spectral density for the process of interest on the incomplete lattice. We study the asymptotic properties of the estimated spectrum and the potential impact of this approximation on the likelihood approximation.
Consider Z a lattice process with spectral density fZ. We assume Z is a weakly stationary real-valued Gaussian process having mean zero and finite moments. The process Z is defined on a rectangle PN = {1, …, n1} × {1, …, n2} of sample size N = n1n2. The covariance c of the process Z satisfies the following condition:
[a.1] Σx[1 + ||x] || |c(x)| < ∞,
where c(x) = cov{Z(x + y), Z(y)}, and ||x|| denotes the l2-norm of a vector x =(x1, x2) on the 2-dimensional integer lattice. Thus, the spectral density of Z exits and has uniformly bounded first derivatives.
The process Z is not directly observed. Rather we observe Y, an amplitude modulated version of Z for the observations on the grid, we write
| (6) |
where x/n = (x1/n1, x2/n2).
The function g satisfies the following condition:
[a.2] g(u) is bounded in u, for any u in the 2-dimensional integer lattice, it is of bounded variation and vanishes for u outside a bounded domain A.
The results in this paper hold for general g functions satisfying condition [a.2], but without lost of generality in the remainder of this paper we consider g defined as:
| (7) |
The function g is assumed to be deterministic, which implies that the locations with missing values are not random.
We propose the following estimate of the spectral density of Z,
where , then , and
If g(xi/n) = 1 for all xi in PN, then Y ≡ Z on the lattice, and ĨN reduces to the standard definition of the periodogram. When g takes same zero values (due to missing data), the difference between the traditional periodogram for Z, IN as in (2), and the new definition given here, ĨN, is a multiplicative factor, (2π)2n1n2/H2(0). This is the bias adjustment that needs to be done to the periodogram function due to the missing values.
Let us study the asymptotic properties of this estimate of fZ, as N → ∞ (increasing domain asymptotics), under conditions [a.1] and [a.2]. The expected value of ĨZ is:
| (8) |
Thus, E[ĨZ (ω)] is a weighted integral of fZ (ω). Asymptotically,
| (9) |
This result is obtained by using (3.12) in Brillinger (1970), since ĨZ (ω) is the periodogram of a tapered version of Z.
Sharp changes in g make its Fourier transform and the squared modulus of its Fourier transform exhibit side lobes. The scatter associated with a large number of missing values creates very large side lobes in (8). Even if asymptotically the bias is negligible by (9), it could have some impact for small samples.
We obtain now the asymptotic variance for ĨZ,,
| (10) |
This can be proven by applying Theorem 5.2.8 in Brillinger (1981) to ĨZ (ω).
The quantity multiplying fZ in the expression (10) for the asymptotic variance is greater than 1 when we have missing values, and it is 1 when there are no missing values. Thus, a large number of missing values would increase the variance of the estimated spectrum.
We use now the estimated spectrum ĨZ (ω) to approximate the likelihood of the spatial process Z (zero mean). As we have seen in this Section, the impact of the missing values in the periodogram of Z is simply a multiplicative factor, (2π)2n1n2/H2(0), clearly this factor does not depend on ω. This new periodogram ĨZ (ω) is asymptotically uniformly unbiased (as a function of ω), assuming g satisfies [a.2]. The simplicity of this relationship between the periodogram with and without missing data, allow us to preserve the asymptotic properties of the Whittle approximated likelihood function (Guyon, 1982), when it is applied to processes with missing data. By proposition 1 in Guyon (1982), the estimated negative log-likelihood turns to be
which (as N → ∞) converges to the exact negative log-likelihood of Z (up to a constant),
We have
| (11) |
where Pθ is a prior distribution for θ. LZ requires only O(Nlog2N) operations. And by Guyon (1982, propositions 3 and 4), under assymptions b.1 and b.2 for fZ (see Appendix 3), our approximate maximum likelihood estimate (mle) is consistent and asymptotically normal.
3.1 Simulation study for incomplete lattices
To understand the performance with finite samples of our estimated likelihood function on an incomplete lattice, we conducted several simulation studies. We simulated a spatial lattice (15 × 15), with 15% missing values. The simulated process of interest is a stationary Gaussian spatial process with an exponential covariance function C, C(h) = σe−|h|/ρ, the sill parameter (σ) is 2, and the range (ρ) 3. We calculated ĨZ (with g being an indicator function, i.e. using zeros to fill in for the missing values) and obtained the approximated likelihood function of the range and sill parameters using the spectral approach introduced here. We repeated the experiment 50 times, by simulating 50 realizations of the spatial process. In the next Table we present results to study the performance of our likelihood estimates. We presented the estimated parameters (mean from 50 simulations), the Monte Carlo (MC) standard deviations (SD) from the 50 simuations, and the mean of the 50 estimated SD using (5).
With the filling-in approach, we tend to be a bit overoptimistic for the sill parameter (Table 1.a). But, overall the estimated pseudo-MLEs for the sill and range are practically the same. The fact that the MC SD and the estimated SD are simular, suggests that our estimates of the uncertainty associated to the parameters are also reliable. The standard errors for the sill and the range are around 0.02, which seems to indicate that in our setting 50 simulations might be enough.
Table 1.
| Table 1.a. Estimated covariance parameters using 50 simulations. We present the mean of the estimated parameters from the 50 simulations, the Monte Carlo standard deviations obtained from the 50 simulations, and the mean of the estimated standard deviations using asymtotic results. | ||||||||
|---|---|---|---|---|---|---|---|---|
| Exact Likelihood | Approximated likelihood | |||||||
| Parameter | MC Mean | MC SD | MC Mean | MC SD | ||||
| Sill | 2.1 | 0.09 | 0.09 | 1.8 | 0.12 | 0.18 | ||
| Range | 3 | 0.12 | 0.11 | 3.5 | 0.16 | 0.20 | ||
| Table 1.b. Estimated covariance parameters using 50 simulations. We present the mean of the estimated parameters in the 50 simulations, the values in parenthesis are Monte Carlo standard deviations obtained from the 50 simulations. | ||
|---|---|---|
| Parameters: | Range | Sill |
| TRUTH | 0.25 | 1 |
| MLE (exact likelihood) | 0.24 (0.05) | 0.91 (0.21) |
| MLE (Spectral gridded) | 0.30 (0.15) | 0.86 (0.30) |
We repeated this experiment with different percent of missing data, and when datasets had more than 20% missing values these results did not hold any longer.
4 Likelihood for irregularly spaced data
Assume Z is a continuous Gaussian spatial process of interest, observed at M irregularly spaced locations, and fZ is the stationary spectral density of Z. We define a process Y at location x as the integral of Z in a block of area Δ2 centered at x,
| (12) |
where for u = (u1, u2) we have,
Then, Y is also a stationary process with spectral density fY given by:
where ω = (ω1,ω2) and Γ(ω) = ∫ h(u)e−iωu = [2sin(Δ ω1/2)/ω1][2sin(Δω2/2)/ω2].
For small values of Δ, fY (ω) is approximately fZ (ω), since we have:
By (12), Y (x) can be treated as a continuous spatial process defined for all x ∈ D. But, here we consider the process Y only on a lattice (n1 × n2) of sample size N = n1n2 (i.e. the values of x in (12) are the centroids of the N grid cells in the lattice, where the spacing is Δ between neighboring sites (see Figure 1)). Then, we have that the spectral density of the lattice process Y
Figure 1.
Simulation: Irregularly spaced observations. We grid the observations in a 10×10 grid, with an average of 10 observations per grid.
| (13) |
In practice, we truncate the sum in (13) after 2N terms; The justification for this can be found in appendix A.1.
The idea is to apply Whittle likelihood to fΔ,Y, written in terms of fZ. Therefore, we can obtain the MLE for the covariance/spectral density parameters of Z by writing the likelihood of the process Y. It might help the reader to interpret this key idea in the spatial domain rather than the spectral domain.
-
Basic idea: interpretation in the spatial domain.
The covariance for the block averages (the lattice process Y) is defined as
where Cθ(u − v) is the covariance for the continuous underlying process Z, and θ are the covariance parameters. The continuous process Z is defined in terms of a pointwise covariance Cθ(h), but we then use the previous expression to derive the covariances of the block averages Y (xi), i = 1, …, N, in terms of the pointwise covariance Cθ. The pointwise covariance is then used to define a likelihood function for the parameters of the covariance function for the process Z in terms of the likelihood function of Y(x1), Y(x2), …, Y (xN).
To calculate the likelihood of Y, we first need to estimate fΔ,Y. With that purpose in mind we define YN as,
| (14) |
where for x = (x1, x2),
| (15) |
and the cardinal of this set is |Jx| = nx. For locations x, such that nx = 0, the value of YN (x) is not known.
As the observations become more dense, the covariance of YN converges to the covariance of Y, see Appendix (A.1). However, the approximation of YN to Y is lease reliable in grid cells with very few observations. Thus, we apply a data taper to YN that gives less weight to grid cells with less observations. We define g1(x) = nx/n, with n being the mean of the nx values. This g1 function plays a similar role to the g weight function (7) in the incomplete grid scenario.
We define Ig1YN (ω) to be the periodogram for the tappered process g1(x)YN (x),
| (16) |
where .
The peridogram Ig1YN(ω) is an asymptotically unbiased estimate of fΔ,Y. The bias is of order O(N−1)+O(n̄−1), where n̄ is the average of the values ( ):
The proof of this result is included in the Appendix (Theorem 1).
Thus, as long as O(N/n̄) is a faster or equal rate of convergence than O(1), we have that (see Appendix, Theorem 2)
| (17) |
converges to (exact negative log-likelihood for Y ). The order of convergence (in the sense of (11)) is N1/2.
If M is the total number of observations of the process Z, the calculation of LY requires O(Nlog2N + M) operations rather than O(M 3) for the exact likelihood of Z. We choose N ≤ M2/3 (with the equality only when there are not many empty cells) to satisfy that O(N/n̄) is a faster or equal rate of convergence than O(1). If we have N = M2/3, then the number of operations to obtain the likelihood function is O(M2/3log2M).
4.1 Simulation study for irregularly spaced datasets
To understand the performance of the proposed likelihood approximation for an irregularly spaced dataset, we simulated 1000 observations of a Gaussian spatial process with a stationary exponential covariance (range=0.25 and sill =1). We grided the observations in a 10× 10 lattice, and we obtained an average of 10 observations per grid. Figure 1 shows the grid. We want to emphasize the fact that in our approach we do not estimate the parameters of the block covariance for the gridded process. Instead, we write this block covariance (or the corresponding spectrum) in terms of the covariance parameters of the continuous underlying process Z, and then estimate the parameters of the point-covariance of Z. To study the performance of our approach, in the next table we compare the exact and approximate estimates of the sill and range parameters for 50 realizations of the process. There is not significant difference between the MLE and pseudo-MLE estimated parameters.
4.2 Modified version of the approximated likelihood function
The approach presented in this Section to approximate the spatial likelihood for irregularly spaced datasets (see expression (17)) performs well when there is no nugget effect (measurement error). But, we could improve the estimation of the nugget and also the smoothness parameter (that explains the degree of differentiability of Z, see Stein (1999)) by adding to the likelihood function of Y information about the behavior of the process Z(si) within grid cells.
Thus, we randomly choose m blocks (no more than 10%–15% of the blocks) and treat them as if nxi = 0 (i.e. we give them weight zero). We do not use the information from these m blocks in LY, the negative log-likelihood for Y.
Then, we add to the negative log-likelihood, LY, the negative log-likelihood of each one of the m blocks (treating the blocks as independent):
| (18) |
where Zj is a vector with the nxj observations within block j, and Σj is the covariance within the block written in terms of Cθ(h) (covariance of Z). The calculation of (18) is very fast, since the blocks are small, approximately of order M1/3.
4.3 Simulation study for irregular datasets
With the purpose of understanding the performance of the proposed likelihood approximation method with finite samples we present here several simulation studies. In our spatial approximated negative log-likelihood (18) we add a correction term with information within blocks. It is important to understand and study the impact on the pseudo-MLE parameters by choosing different number of blocks for the correction term.
We start by simulating 1000 observations from a Gaussian spatial process with a stationary Matérn covariance (nugget=.25, range=.25, smoothness parameter =3, and partial sill =1):
| (19) |
where
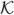 νs is a modified Bessel function and θ = (σ0, ν, σ1, ρ). I(h) is an indicator function; it takes the value 1 when h = (0, 0), and is zero otherwise. The nugget parameter is σ0 (microscale variation). The parameter ρ measures how the correlation decays with distance; generally this parameter is called the range. The partial sill, σ1, is the total variance of the process minus the nugget. The parameter ν measures the degree of smoothness of the process Z. The higher the value of ν the smoother Z would be; e.g. when
, we get the exponential covariance function. In the limit as ν→∞ we get the Gaussian covariance. We gridded the observations in a 10 × 10 lattice (as in Figure 1). We simulate 50 realizations of the spatial process. Each table in this section presents results based on 50 simulations, the parameters and standard deviations shown in Tables 3–7 and Table 9 are the mean and Monte Carlo standard deviations from 50 realizations.
νs is a modified Bessel function and θ = (σ0, ν, σ1, ρ). I(h) is an indicator function; it takes the value 1 when h = (0, 0), and is zero otherwise. The nugget parameter is σ0 (microscale variation). The parameter ρ measures how the correlation decays with distance; generally this parameter is called the range. The partial sill, σ1, is the total variance of the process minus the nugget. The parameter ν measures the degree of smoothness of the process Z. The higher the value of ν the smoother Z would be; e.g. when
, we get the exponential covariance function. In the limit as ν→∞ we get the Gaussian covariance. We gridded the observations in a 10 × 10 lattice (as in Figure 1). We simulate 50 realizations of the spatial process. Each table in this section presents results based on 50 simulations, the parameters and standard deviations shown in Tables 3–7 and Table 9 are the mean and Monte Carlo standard deviations from 50 realizations.
Table 3.
Approximated MLE for the nugget parameter and the Monte Carlo standard deviations in parenthesis. Using the proposed spectral likelihood method for irregular data. True nugget parameter = 0.25.
| Nugget | N=25 | N=100 | N=225 | N=400 |
|---|---|---|---|---|
| m=5% | 0.12 (0.31) | 0.14 (0.21) | 0.11 (0.12) | 0 (0.01) |
| m=10% | 0.27 (0.34) | 0.21 (0.24) | 0.14 (0.11) | 0.10 (0.01) |
| m=15% | 0.34 (0.40) | 0.30 (0.27) | 0.13 (0.12) | 0 (0.17) |
Table 7.
Mean of the relative absolute error for each design.
| MRAE | N=25 | N=100 | N=225 | N=400 |
|---|---|---|---|---|
| m=5% | 0.85 | 0.47 | 0.43 | 0.60 |
| m=10% | 0.44 | 0.27 | 0.43 | 0.68 |
| m=15% | 0.28 | 0.19 | 0.31 | 0.57 |
|
| ||||
| Average MRAE | 0.51 | 0.31 | 0.39 | 0.61 |
Table 9.
Estimated covariance parameters, the values in parenthesis are Monte Carlo standard deviations.
| Parameters: | Nugget | Partial Sill | Range | Smoothness | MRAE |
|---|---|---|---|---|---|
| TRUTH | 0.25 | 1 | 0.25 | 3 | 0 |
| MLE (exact likelihood) | 0.24 (0.2) | 0.9 (0.20) | 0.50 (0.25) | 2.0 (3.5) | 0.36 |
| Stein et al (2004) | 0.23 (0.1) | 0.79 (0.43) | 0.15 (0.4) | 7.8 (7.9) | 0.57 |
In the next simulations we study the impact on the approximated MLE parameters of the number of blocks used in the correction term in (18). We calculate the likelihood for the 50 realizations of the process, varying the two parameters of interest, the number of total blocks, N, and also m, the number of blocks used for the correction term. We considered N (number of blocks) to be 25 (corresponds to a 5 × 5 grid), 100 (10 × 10), 225 (15 × 15) and 400 (20 × 20). And in each case m represented 5% of blocks, 10% of blocks and 20% of blocks.
Table 2 shows the different designs used in our simulation study varying N and m. When N was 25, each block had approximately 40 observations, versus only 2 when N was 400.
Table 2.
Number of blocks used for the correction term in the spectral likelihood, in parenthesis we have an average of the number of points in each block.
| # of Blocks | N=25 | N=100 | N=225 | N=400 |
|---|---|---|---|---|
| 5% | 1 (40) | 5 (10) | 11 (4) | 20 (2) |
| 10% | 2 (40) | 10 (10) | 22 (4) | 40 (2) |
| 15% | 3 (40) | 20 (10) | 44 (4) | 80 (2) |
We present in Table 3 the approximated MLE for the nugget parameter using the 12 different designs introduced in Table 2. In parenthesis we show the Monte Carlo standard deviations from 50 simulations. The parameter has been obtained using the likelihood approximation proposed in Section 4.2. The designs with N smaller than 100 offer larger variability. On the other hand designs with N very large might not very helpful to estimate the nugget since the number of points within each block is too small. It seems that when the number of blocks for the correction term is 10% we obtain better results for any value of N.
In Table 4 we study the impact of N and m on the approximated MLE for the smoothness parameter. This parameter is always very difficult to estimate. It seems that is important to have a large enough number of observations within blocks to estimate this parameter, the designs with 10 and 40 observations within block seem to perform better. The results do not appear to be very sensitive to the value of m. N seems to play a more relevant role than m.
Table 4.
Approximated MLE for the smoothness parameter, in parenthesis the Monte Carlo standard deviationss. Using the proposed spectral likelihood method for irregular data. True smoothness parameter= 3.
| Smoothness | N=25 | N=100 | N=225 | N=400 |
|---|---|---|---|---|
| m=5% | 4.7 (5) | 5 (4.2) | 6 (4) | 0.1 (9) |
| m=10% | 3 (4.1) | 4.7 (3.2) | 1 (2) | 0.8 (4) |
| m=15% | 3.3 (3.8) | 3.9 (3.4) | 2 (3) | 5 (2) |
Table 5 shows the results for the partial sill parameter. The results for the sill parameter are similar to the results for the nugget, N needs to be at least 100, and designs with 10% of blocks perform always better. Except when N is too large, in that case the blocks only have 2 observations and this design does not perform very well either.
Table 5.
Approximated MLE for the partial sill parameter, in parenthesis the estimated standard deviation. Using the proposed spectral likelihood method for irregular data. True partial sill parameter=1.
| Partial Sill | N=25 | N=100 | N=225 | N=400 |
|---|---|---|---|---|
| m=5% | 0.47 (0.9) | 0.81 (0.14) | 0.89 (0.39) | 0.70 (0.20) |
| m=10% | 0.70 (0.4) | 0.90 (0.20) | 0.87 (0.30) | 0.63 (0.13) |
| m=15% | 0.72 (0.43) | 1.10 (0.11) | 0.79 (0.32) | 0.84 (0.21) |
In Table 6 we present the results for the range parameter. This parameter is not very well estimated when N is less than 100, also the variability associated to the nugget is larger for designs with N less than 100. The designs with 10 or 4 observations per block seem to perform better and the results in that setting do not seem to be so sensitive to the value of m.
Table 6.
Approximated MLE for the range parameter, in parenthesis the Monte Carlo standard deviations. Using the proposed spectral likelihood method for irregular data. True value of range parameter=.25.
| Range | N=25 | N=100 | N=225 | N=400 |
|---|---|---|---|---|
| m=5% | 0.77 (0.62) | 0.10 (0.11) | 0.23 (0.12) | 0.21 (0.19) |
| m=10% | 0.59 (0.31) | 0.32 (0.20) | 0.12 (0.15) | 0.51 (0.27) |
| m=15% | 0.15 (0.56) | 0.21 (0.39) | 0.19 (0.29) | 0.13 (0.80) |
As another way to compare the different designs, we calculate the mean relative absolute error (MRAE), defined as
where i is the index for the different covariance parameters (a total of 4). Table 7 presents the results. It seems that when N is 100 (10 observations per block) we obtain better results, and designs with m = 15% and m = 10% perform better.
Overall, it seems that we need to have at least 100 blocks, and the number of observations within each block should be around 10 (not less than 4). Using 10% or 15% of blocks for the correction term would be our recommendation, less than 10% does not seem to be enough.
4.4 Comparisons to other likelihood approaches for continuous spatial processes
In this Section we compare our spectral method to approximate the likelihood of a continuous Gaussian spatial processes to other know approaches proposed by Vecchia (1988) and Stein et al. (2004).
Vecchia (1988) proposed a simple approximation to the likelihood function for spatial processes by writing the probability density function as a product of conditional densitites. If p denotes the density function, assume Z = (Z(x1), …, Z(xn)) are the observed values of the process, then we denote the joint density p(z; θ), where θ are the unknown covariance parameters. We partition Z into k subvectors Z1, …, Zk, and we define Z(i) = (Z1, …, Zi). Thus, we have
Vecchia proposed to condition not on all components of z(i−1) to calculate p(z(i)|z(i−1); θ), but only of the nearest neighbors, thus,
where s(i−1) is a subset of z(i−1). Vecchia only considered prediction vectors z(i) of length 1.
In a recent paper by Stein et al. (2004), the authors propose a method to reduce the computation of Vecchia (1988) approach and improve the efficiency of the estimated parameters, by considering prediction vectors of longer length and conditioning sets s(i−1) that include not only the nearest neighbors but some rather distant observations from the prediction vectors.
One of the key contributions of Stein et al (2004) is the significant improvement obtained by adding in the conditioning set some other observations, rather than just the nearest neighbors, and also the reduction of the computational effort by using prediction vectors of length greater than 1. There is quite a lot of latitude about how one would select the prediction and conditioning sets. In our simulation study we use a design that seems to perform very well based on the results presented by Stein et al (2004).
We simulated 1000 irregularly spaced observations of a spatial Gaussian process. We gridded the data in 100 blocks. Each block (prediction set) had approximately 10 observations. All the observations were separated by at least a distance of 0.5 (to avoid numerical difficulties). This setting is similar to the one presented by Stein et al. (2004). The conditioning sets were of size 20, and following the recommendation given by Stein et al. we selected 50% of those as nearest neighbors. This design is the one that would minimize the computationally effort using Stein et al. (2004) method, and also based on the simulations presented by Stein et al. (2004) seems to be a good choice to obtain more reliable estimated covariance parameters. We simulated the same setting 50 times. The simulations presented by Stein et al. (2004) are based on an exponential model without nugget, and a power model with nugget. Here we study the exponential model but we also examine a more general model, the Matérn model with a smoothness parameter and a nugget effect. To calculate our approximated spectral likelihood we used the same 1000 observations gridded in 100 blocks, having 10% of the blocks for the correction term.
We used the computer code provided by Pardo-Igúzquiza and Dowd (1997) to calculate Vecchia (1988) approximated likelihood, with a conditioning set of size 20. We present the results in Table 8. The parameters in Table 8 are the mean from 50 realizations, and the Monte Carlo standard deviations (in parenthesis) from the 50 realizations. Our results are consistent with to the ones in Stein et al (2004), having some observations in the conditioning set that are not the nearest neighbors it does improve the performance of the approximated likelihood method. If in the conditioning sets of size 20 we select 10 observations that are not nearest neighbors, but instead they are among the “past” observations (and we use prediction sets of size 10), then we are able to reduce the MRAE from 0.45 to 0.34. The estimated range parameter (mean from 50 realizations) of an exponential covariance (Table 8) using Vecchia (1988) approach with 20 neighbors was 0.25 (truth is 0.25), when we reduced the number of neighbors to 10 we obtained a range of 0.44. Increasing the number of neighbors beyond 20 did not improve the results (estimated range was 0.20 with 30 neighbors). The main problem was estimating the sill parameter, we obtained a value of 0.59 (truth 1). When the number of neighbors increased to 30 the estimated sill parameter did not change (still 0.59).
Table 8.
Comparisons of Vecchia (1988) approach, Stein et al (2004) method, and the spectral likelihood method presented here to estimate the sill and nugget parameters of an exponential covariance. The parameters in this Figure are the mean from 50 realizations, and the Monte Carlo standard deviations (in parenthesis) from the 50 realizations.
| Sill | Range | Sill/Range | MRAE | |
|---|---|---|---|---|
| Truth | 1 | 0.25 | 4 | 0 |
| Exact likelihood | 0.97 (0.07) | 0.24 (0.1) | 4 | 0.07 |
| Spectral method | 0.90 (0.1) | 0.31 (0.14) | 2.9 | 0.34 |
| Stein’s method | 0.80 (0.32) | 0.20 (0.19) | 4 | 0.40 |
| Vecchia’s method | 0.59 (0.3) | 0.25 (0.1) | 2.3 | 0.45 |
The results obtained using Stein et al (2004) approach are very similar to the ones obtained using the spectral method, at least in terms of estimating the range and sill parameter. The MRAE was 0.34 for the spectral method and slightly larger for Stein et al (2004) method (0.40). However, if we consider the ratio of the sill to range, which is the important parameter for interpolation (Stein, 1999), then Stein et al (2004) approach has a much better performance. The truth is 4, the exact likelihood gives a value of 4, and Stein et al (2004) method gives also a value of 4 (Table 8).
In terms of capturing the behavior at very short distances, Stein et al (2004) method performs much better. The performance obtained with Vecchia (1988) approach at short distances is very poor.
We implemented the likelihood approximation approach proposed by Stein et al (2004) using the previous design (conditioning sets of size 20 and prediction sets of size 10), but having a Matérn covariance (as in Tables 3–7). We present here also results using the exact likelihood. We present in Table 9 the results for Stein et al (2004) approach (the results for the spectral method are in Tables 3–7). The estimated parameters are the mean of the results obtained using 50 simulations of an underlying Gaussian process with a Matérn covariance (1000 observations, prediction sets of size 10, conditioning sets of size 20 with 10 nearest neighbors). In parenthesis we present sample s.d. of the parameters from the 50 simulations. The MRAE obtained is 0.36 for the exact likelihood and 0.57 for Stein et al (2004) approach. The results obtained using the spectral method proposed here are presented in Tables 3–7 (for different designs). The design with 100 blocks and 10% of blocks for the correction term has an MRAE of 0.27.
In terms of computational considerations, Stein et al (2004) indicate that to minimize the computational effort of the approach they propose, the size of the conditioning sets (c) should be twice the size of the prediction sets (d). Thus, in our setting with 100 blocks and prediction sets of 10 observations, if the conditioning sets are chosen to be of size 20, with 10 nearest neighbors among these 20. Then, the number of floating point operations (flops) that are needed to calculate the likelihood approximation proposed by Stein et al (2004) is 9 * 105. To compare the efficiency of choosing the prediction sets with more than one observation to prediction sets of size 1 as proposed by Vecchia (1988), consider now d = 1 and c = 20 (versus d = 10 and c = 20). The flops needed are 3 * 106. Thus, the design suggested by Vecchia (1988) requires about 3 times the computation of the approach suggested Stein et al (2004). Our approach has a clear advantage in terms of computational effort, with our approach we need approximately only 104 flops (see Section 4.2).
5 Application
Global sea surface temperature (SST) fields are very useful for monitoring climate change, as an oceanic boundary condition for numerical atmospheric models, and as a diagnostic tool for comparison with the SST’s produced by ocean numerical models. SST’s can be estimated from satellites, for e.g. using the TRMM Microwave Imager (TMI). The spatial scales and structure of SST fields are the main factor to identify phenomena such as El Nino and La Nina, that occur in the equatorial Pacific and influence weather in the Western Hemisphere. Spatial patterns of SST’s in the Pacific ocean are also being used as one of the main climate factors to identify tropical cyclones (hurricanes), that form in the south of Mexico and strike Central America and Mexico from June to October. Studying the spatial structure of SST’s in the Pacific Ocean is also important to understand the exchange of water between the north equatorial current and the south equatorial current. A good understanding of the SST’s spatial variability is crucial for guiding future research on the variability and predictability of the world ocean SST and the climate that it influences.
In this work, we apply our methods to estimate the spatial structure of TMI SST data over the Pacific Ocean. Currently, most of the operational approaches to estimate the covariance parameters of the TMI SST fields, in particular the mesoscale and zone scale parameters (ranges of correlation) (Reynolds and Smith, 1994) are empirical methods and there is not a reliable measure of the uncertainty associated to the estimated parameters. Likelihood methods are difficult to implement because the satellite datasets are very large. Traditional spectral methods can not be applied directly because the data are not on a complete regular grid, since the TMI sensor only retrieves SST data from the surface through areas of open water (ocean or lakes) (see Figure 2). However, our methodology can be easily applied to these large satellite data.
Figure 2.
Satellite sea surface temperatures (in Celsius degrees) over the West Pacific Ocean. Missing values (in white) correspond to land surfaces (Central and South America and the Galapagos islands).
The satellite observations in this application are obtained from a radiometer onboard the Tropical Rainfall Measuring Mission (TRMM) satellite. This radiometer, the TRMM Microwave Imager (TMI) is well-calibrated and contains lower frequency channels required for sea surface temperature retrievals. The measurement of sea-surface temperature through clouds by satellite microwave radiometers has been an elusive goal for many years. The TMI data have a spatial resolution of 25km by 25km and are available on the web (http://www.remss.com/tmi/tmibrowse.html). We present here results for the month of March 1998. The study of the mesoscale spatial dependency for SST fields is generally done using SST Anomalies (SSTA), i.e. the SST field after removing the spatial trend. The SSTA fields here are obtained from the monthly SST values after substracting the yearly SST climatology (temporal mean for each year) at each location. In our analysis we have 4% of missing values that correspond to land surface (Central and South America and the Galapagos islands). The domain of interest is presented in Figure 2. In this image we have 9,600 pixels (120 × 80).
In our analysis, we first project the spatial coordinates using a Lambert projection to take into account the curvature of the Earth when calculating spatial dependencies. Some parameters of interest when studying the SSTA spatial structure are the meridional scale (range of correlation along the north-south direction) and the zonal scale (range of correlation along the east-west direction). These parameters explain the potential effect of directionality in the spatial dependency (anisotropy effect). We estimate this effect by allowing for geometric anisotropy in our covariance model, and estimating the rotation and strectching effects. First, we convert from cartesian coordinates x = (x1, x2) (spatial domain) and ω = (ω1, ω2) (spectral domain) to polar coordinates (r, θ) and (u, φ), respectively, where x1 = r cosθ, x2 = r sinθ, and ω1 = u cos φ, ω2 = u sin φ. Then, the covariance function of the SSTA process, C(x1, x2), and the corresponding spectral density f (ω1, ω2), become C(r, θ), and f(r, θ), respectively. We incorporate a parameter α that explains the stretching effect, and a parameter θ0 that explains the rotation. We estimate these two parameters and the rest of the covariance parameters (smoothness, nugget, range and partial sill) using the spectral likelihood approximation method presented here for incomplete regular lattices, that can be calculated very fast and efficiently for these large satellite datasets. The covariance function with the stretching and rotation parameters becomes C(αr, θ + θ0), and the corresponding spectral density is . Where f is a Matérn spectral density. The pseudo-MLE estimated parameters and their standard deviations (SD) (eq. (5)) have been obtained using the likelihood method proposed in this paper.
The anisotropy angle parameter is defined here as the azimuth angle (in radians) of the direction with greater spatial continuity, i.e. the angle between the y-axis and the direction with the maximum range. It is estimated as 0 radians ( 0 degrees ), the SD is 0.02. The anisotropy stretching parameter is defined here as the ratio between the ranges of the directions with greater and smaller continuity, i.e. the ratio between maximum and minimum ranges. Therefore, its value is always greater or equal to one. In this case is 1.05 (SD=0.2). Therefore, the fact that there is not a significant rotation and/or stretching effects indicate that there is not a meridional versus zonal effect in the spatial scales. This also suggests that the water exchange between the north Equatorial current and the south equatorial current is not affecting the mesoscale spatial dependency structure of the SSTA field. The nugget is zero, this is expected since the data are not real measurements. The range of correlation is 312 km, indicating that the SSTA field presents large spatial continuity. The variability of the process is relatively small 0.57 Celsius degrees2. The smoothness parameters is 1 (SD 1.2). The smoothness parameter tends to be a difficult parameter to estimate in practice, this is also the case here, since the uncertaintly associated to this parameter is quite large. The methods presented here are being applied to other time windows and oceans.
6 Discussion
In this paper we introduce a new spectral method for estimating the covariance parameters of a spatial process. Our approach is likelihood-based and offers enormous computational benefits. The first time that an extension of Whittle approximated likelihood can be applied to lattice data with missing values and irregularly spaced datasets. There are other alternative spectral approaches for irregularly sampled processes that are more computationally expensive:
a spectral likelihood based on a periodogram for irregularly sampled processes obtained using generalized prolate spheroidal sequences (Bronez, 1988),
the EM algorithm (Dempster, Laird, and Rubin 1977), which is a very well-known technique to find maximum likelihood estimates in parametric models with incomplete data. In the EM algorithm, we could first impute the values of the process at the locations in the grid where we have no data and then calculate the complete-data likelihood using spectral methods. We would need to iterate through these two steps.
The spectral likelihood approach presented here is attractive because of its simplicity and because it is very computationally efficient and fast compared to any other known likelihood approximation method for spatial data that gives consistent estimates.
The weight function g introduced here to handle incomplete lattices could have more sophisticated structures than the one used in this paper. For instance, instead of just taking values 1 and 0, g could go smoothly from 1 to 0 using a cosine function or a spline function to capture better the transition zones in the areas with missing values. This can be particularly helpful when we have missing values clustered together, e.g. clouds in AVHRR satellite data. Alternatively, we could use a moving average of the observations to fill in for the missing values of Z. Using then the approach introduced in Section 4 to obtain an approximation to the likelihood function of Z, by defining the process Y in equation (6) as a moving average of the observed values of Z (as in (14), rather than an amplitude modulated process.
In terms of calculating the likelihood for lattice processes, note that if we use a correlation function on the lattice rather than a continuous one, e.g. the Matérn and some other suggested in this paper. Then, there are other approaches to approximate the likelihood (e.g. Besag and Moran (1975), Rue (2001), Rue and Tjerlmeland (2002)) that can be evaluated using only O(n3/2) flops or O(n3/2logn) depending on the setup, rather than O(n3) using a continuous covariance. For a review of all these approximation techniques on the lattice, we recommend the new book by Rue and Held (2005, chapter 5).
In this paper we have assumed that the spatial process has a stationary covariance function. There are many models for nonstationary covariances (e.g. Sampson and Guttorp, 1992, Fuentes 2001 and 2002, and many others). In particular, by modeling the nonstationary process as a mixture of independent stationary processes (Fuentes, 2001, 2005), the likelihood framework presented here can be easily adopted, since then the likelihood function can be written in terms of stationary likelihood functions.
Table 9.
Estimated MLE parameters and standard deviations using the proposed likelihood approximation method for incomplete lattices.
| Parameters | Spectral MLE | SD |
|---|---|---|
| nugget | 0.001 | 0.002 |
| range | 312 km | 70 |
| partial sill | 0.57 | 0.02 |
| smoothness | 1 | 1.2 |
| Anisotropy rotation angle | 0 | 0.02 |
| Anisotropy stretching | 1.05 | 0.2 |
Acknowledgments
This research was partly sponsored by a National Science Foundation grant DMS 0353029, and by the U.S. National Oceanic and Atmospheric Administration Grant Award Number NAO3NES4400015 through a Cooperative Agreement (Climate & Weather Impacts on Society and the Environment) via the Charleston Coastal Services Center and the National Climatic Data Center.
1 Appendix
A. 1
Truncation of f Δ,Y
Let us assume that for large frequencies (as |ω| → ∞) the spectral density of a continuos spatial process Z satisfies:
| (20) |
The spectral density models generally used for continuous spatial processes (i.e. Matérn) satisfy condition (20). Under this condition, we need to prove that the residual term in the expression for f Δ,Y given in (13), when we truncate the sum the sum after 2N terms, is negligible compared to O(N−1), which is the bias of our estimated function of f Δ,Y (Section 4).
The spectral density of the lattice process Y, f Δ,Y (ω) for ω ∈ [−π/Δ, π/Δ]2, is defined in (13) in terms of fZ. Here we study the order of the residual term R,
| (21) |
where NY = {(q1, q2) ∈ ℤ2; −n1 < q1 < n1, −n2 < q2 < n2}. We have that,
| (22) |
We also have,
| (23) |
Similarly, the same bound is obtained for the other six subregions; when the pair (q1, q2) are in N1 = {(q1, q2) ∈ ℤ2; q1 > n1 and q2 < −n2}, N2 = {(q1, q2) ∈ ℤ2; q1 < −n1 and q2 > n2}, N3 = {(q1, q2) ∈ ℤ2; |q1| < n1 and q2 < −n2}, N4 = {(q1, q2) ∈ ℤ2; |q1| < n1 and q2 < −n2}, N5 = {(q1, q2) ∈ ℤ2; q1 < −n1 and |q2| < n2}, or N6 = {(q1, q2) ∈ ℤ2; q1 > n1 and |q2| < n2}.
Therefore, the order of convergence to zero of the residual term in (21) is faster than O(N−1), which is the bias of Ig1 YN (defined in (16)); it is our estimate of f Δ,Y.
A. 2
Definition
A spatially random pattern on a domain of interest D is synonymous with a homogeneous Poisson process in D, this means that any location on D has equal probability of receiving a point (see, e.g. Cressie (1993), page 586).
A spatially regular pattern on D indicates regular spacings between points (see, e.g. Cressie (1993), page 590).
Theorem 1
Consider a continuous weakly stationary spatial process Z observed at M locations in a domain D of interest. We define two lattice processes Y (as in (12)) and YN (as in (14)), both written in terms of the process Z, and defined on a lattice n1 × n2 covering D, with spacing Δ between neighboring observations. We define f Δ,Y, the spectral density of the process Y. We propose Ig1 YN defined in (16), as an estimate of f Δ,Y. As N → ∞ and n̄ → ∞, where and nxi is the number of observations of the process Z in the grid cell i. We assume the locations of the nxi observations within each grid cell i form a spatially random or regular pattern.
We have,
Proof of Theorem 1
First, we need to study the convergence of the second order moments of YN to the ones of the process Y as the observations become more dense, i.e. as each nxi → ∞. Assume Cθ(h) is the stationary covariance of the process Z at a distance h, with parameters θ. We have
where Jx is defined in (15), and
where . Clearly the covariance of Y is stationary. By the expressions above for the covariance functions of YN and Y, and the fact that the locations of the nxi observations within each grid cell i is spatially random or regular, we have that the covariance of YN between points x1 and x2, converges to cov(Y (x1), Y (x2)) as nx1 → ∞ and nx2 → ∞. The order of convergence is .
Thus, it is straighforward to see that the order of converge of the covariance of the tapered process g1 YN to the covariance of g1 Y is O(n−1 n−1), (n average of the nxi values). Then,
uniformly in x1, x2. This is a uniform convergence, because C is a uniformly bounded function, since we assume that the variance of Z is finite.
Thus, since
we have,
| (24) |
where Ig1 Y is the periodogram of the tapered process g1 Y. As N → ∞, E[Ig1 Y (ω)] in the expression above converges uniformly to f Δ,Y (ω),
and the residual term εN (ω) in expression (24) is of the following order,
Therefore,
A. 3
Let us assume that the spectral density of the lattice process Y (as in (12)), f Δ,Y with parameters ω, satisfies the following conditions:
(b.1) f Δ,Y (ω) is rational with respect to eiω, without zeros or poles,
(b.2) the second derivative of f Δ,Y in θ is continuous in θ.
All classical spectral density models satisfy these two conditions.
Theorem 2
Assume the order of convergence to zero of n̄ as N → ∞, is at least O(N−1). This means, O(N/n̄) is a faster or equal rate of convergence than O(1). Then, under conditions (b.1)–(b.2), we have that,
| (25) |
converges to (exact likelihood function for the lattice process Y), and if n1 and n2 are of the same order, the rate of approximation (in the sense of (11)) is N1/2.
Proof of Theorem 2
By the condition that O(N/n̄) is a faster or equal rate of convergence than O(1), the proposed peridogram function, Ig1 YN, approximates the spectral density f Δ,Y with a bias of the same order (Theorem 1) than if we use Ig1 Y, the periodogram of a tapered version of Y. Then, by Proposition 1 in Guyon (1982). In which the convergence of the spectral Whittle likelihood function for a tapered process g1 Y, to the exact likelihood of Y is proven. We obtain that (25) holds and the order is N1/2.
References
- Besag JE. Spatial interaction and the statistical analysis of lattice systems (with discussion) J R Statist Soc B. 1974;36:76–86. [Google Scholar]
- Besag JE, Moran PAP. On the estimation and testing of spatial interaction in Gaussian lattice processes. Biometrika. 1975;62:555–562. [Google Scholar]
- Bronez TP. Spectral estimation of irregularly sampled multidimensional processes by generalized prolate spheroidal sequences. IEEE Transactions on Acoustics, Speech, and Signal Processing. 1988;36:1862–1873. doi: 10.1109/29.9030. [DOI] [PubMed] [Google Scholar]
- Caragea P. Approximate Likelihoods for Spatial Processes. PhD Dissertation at UNC. 2003 http://www.stat.unc.edu/postscript/rs/caragea.pdf.
- Clinger W, Van Ness JW. On unequally spaced time points in time series. Ann Statist. 1976;4:736–745. [Google Scholar]
- Cramér H, Leadbetter MR. Stationary and related stochastic processes. Sample function properties and their applications. Wiley; New York: 1967. [Google Scholar]
- Dahlhaus R, Küsch H. Edge effects and efficient parameter estimation for stationary random fields. Biometrika. 1987;74:877–882. [Google Scholar]
- Bloomfield. Fourier Analysis of Time Series. Wiley; New York: 2000. [Google Scholar]
- Brillinger DR. The frequency analysis of relations between stationary spatial series. In: Pyke R, editor. Proceedings of the Twelfth Biennial Seminar of the Canadian Mathematical Congress. Montreal: Canadian Math. Congress; 1970. pp. 39–81. [Google Scholar]
- Brillinger DR. Time Series: Data Analysis and Theory. Expanded. Holden-Day, Inc; San Francisco: 1981. [Google Scholar]
- Fuentes M. A new high frequency kriging approach for nonstationary environmental processes. Envirometrics. 2001;12:469–483. [Google Scholar]
- Fuentes M. Spectral methods for nonstationary spatial processes. Biometrika. 2002;89:197–210. [Google Scholar]
- Fuentes M, Chen L, Davis JM. Modeling and predicting complex space-time structures and patterns of coastal wind fields. Environmetrics. 2005;16:449–464. [Google Scholar]
- Guyon X. Parameter estimation for a stationary process on a d-dimensional lattice. Biometrika. 1982;69:95–105. [Google Scholar]
- Letelier J, Pizarro O, Nez S, Arcos D. Spatial and temporal variability of thermal fronts off Central Chile (33-40S) Gayana. 2004;68(2):358–362. [Google Scholar]
- Marcotte D. Fast variogram computation with FFT. Computers and Geosciences. 1996;22:1175–1186. [Google Scholar]
- Matérn B. Medded Stat Skogsforkskinst, Lectures Notes in Statistics 36. 2. Vol. 49. New York: Springer; 1960. 1986. Spatial variation; p. 5. [Google Scholar]
- Neave HR. Spectral analysis of a stationary time series using initially scarce data. Biometrika. 1970;57:111–122. [Google Scholar]
- Pardo-Igúzquiza, Dowd AMLE3D: a computer program for the inference of spatial covariance parameters by approximate maximum likelihood estimation. Comput Geosci. 1997;23:793–805. [Google Scholar]
- Park KA, Chung JY. Spatial and Temporal Scale Variations of Sea Surface Temperature in the East Sea Using NOAA/AVHRR Data. Journal of Oceanography. 1999;55:271–288. [Google Scholar]
- Parzen E. On spectral analysis with missing observations and amplitude modulation. Sankhya, Ser A. 1963;25:383–392. [Google Scholar]
- Priestley MB. Spectral Analysis and Time Series. Academic Press; London: 1981. [Google Scholar]
- Reynolds RW, Smith TM. Improved global sea surface temperature analyses. J Climate. 1994;7:929–948. [Google Scholar]
- Rue H. Fast sampling of Gaussian Markov random fields. J R Statist Soc, B. 2001;63:325–338. [Google Scholar]
- Rue H, Tjelmeland H. Fitting Gaussian Markov random fields to Gaussian fields. Scandinavian Journal of Statistics. 2002;29:31–49. [Google Scholar]
- Rue H, Held H. Gaussian Markov random fields: Theory and applications. Chapman & Hall; London: 2005. [Google Scholar]
- Sampson PD, Guttorp P. Nonparametric estimation of nonstationary spatial covariance structure. Journal of the American Statistical Association. 1992;87:108–119. [Google Scholar]
- Stein ML. Fixed domain asymptotics for spatial periodograms. Journal of the Americal Statistical Association. 1995;90:1277–1288. [Google Scholar]
- Stein Chi, Welty Approximating likelihoods for large spatial data sets. Journal of the Royal Statistical Society, Series B. 2004;66:275–296. [Google Scholar]
- Stein ML. Interpolation of Spatial Data: some theory for kriging. Springer-Verlag; New York: 1999. [Google Scholar]
- Vecchia. Estimation and model identification for continuous spatial processes. Journal of the Royal Statistical Society, Series B. 1988;50:297–312. [Google Scholar]
- Whittle P. On stationary processes in the plane. Biometrika. 1954;41:434–449. [Google Scholar]
- Yaglom AM. Correlation theory of stationary and related random functions. Springer-Verlag; New York: 1987. [Google Scholar]




