Abstract
Tracer enrichment data are fitted by multicompartmental models to estimate rate constants and fluxes or transport rates. In apolipoprotein turnover studies, mass measurements are also available, e.g., apolipoprotein B (apoB) levels in VLDL, IDL and LDL, and are often essential to calculate some of the rate constants. The usual method to use mass measurements is to estimate pool masses along with rate constants. A systematic alternative approach is developed to use flux balances around pools to express some rate constants in terms of the other rate constants and the measured masses. The resulting reduction in the number of parameters to be estimated makes the modeling more efficient. In models that would be unidentifiable without mass measurements, the usual approach and the proposed approach yield identical results. In a simple two-pool model, the number of unknown parameters is reduced from four to two. In a published 5-pool model for apoB kinetics with three mass measurements, the number of parameters is reduced from 12 to 9. With m mass measurements, the number of responses to be fitted and the number of parameters to be estimated are each reduced by m, a simplification by 1/4 to 1/3 in a typical pool model. Besides a proportionate reduction in computational effort, there is a further benefit since the dimensionality of the problem is also decreased significantly, which means ease of convergence and a smaller likelihood of suboptimal solutions. While our approach is conceptually straightforward, the dependencies get considerably more complex with increasing model size. To generate dependency definitions automatically, a web-accessible program is available at http://biomath.info/poolfit/constraints.
Keywords: Apolipoproteins, tracer kinetics, rate constants, parameter estimation, parameter constraints, identifiability
1. Introduction
Multicompartmental models are used to fit tracer enrichment data to estimate metabolic parameters. A model typically has stationary, linear differential equations to describe the time behavior of tracer enrichments in the different pools in terms of rate constants, which are estimated by fitting the tracer enrichment data with the solutions to the differential equations. The model also has algebraic equations, stemming from material balances on total amounts (tracer plus the unlabeled tracee); these involve pool masses and the rate constants. Compartmental modeling is used to determine rates of secretion, interconversion, and fractional clearance of apolipoproteins in order to better understand plasma lipoproteins. An aspect of apolipoprotein metabolism is that lipoprotein fractions have plasma as their space of distribution, either in toto or as a significant part. This means that in turnover studies, plasma concentrations of apolipoproteins in different lipoprotein fractions (e.g., apoB in VLDL, IDL and LDL) are measured along with tracer enrichments in those fractions. The concentration or mass measurements are used to calculate certain direct removal rate constants that would not be a priori identifiable with tracer enrichment data alone, and sometimes to provide additional information on rate constants that are a priori identifiable otherwise. The goal of this paper is to develop a method to make optimal use of these mass measurements.
In early metabolic studies of drugs [1] or of molecules such as calcium, glucose or cholesterol whose equilibration outside the circulation is rapid with respect to sampling times [2–4], at best one mass measurement, e.g., total plasma concentration, was available. If only one mass is known, the algebraic equations from material balances can be used to calculate all the other pool masses in terms of the known pool mass and the rate constants estimated from fitting enrichment data [5]. Fluxes such as synthesis rates and other transport rates are calculated readily by multiplying the appropriate masses and rate constants. Modeling programs such as SAAM II routinely make these calculations [6,7].
As noted above, a distinctive aspect of apolipoprotein metabolism is that concentrations of an apolipoprotein in multiple lipoprotein fractions can be measured. For instance, VLDL, IDL and LDL levels of apolipoprotein B (apoB) are measured in most studies of apoB metabolism [8–10]. Indeed, Zheng et al. [11] have measured apoB in 21 subfractions based on apoE and apoC-III content. Since the systems are generally assumed to be in steady state, each mass is fairly accurate, being the average of several measurements. For instance, Packard and coworkers [12,13], Schaefer and colleagues [14–16], and Sacks and coworkers [11,17,18] routinely measure subfraction apoB levels from 4 to more than 10 times in the course of a turnover study.
The question arises, therefore, as to how mass measurements can be utilized. The most common approach in the literature, though seldom articulated [12,19–21], is (1) to calculate pool masses from rate constants using the abovementioned method developed in early studies when only one pool mass was known; (2) to compare the calculated values with the mass measurements; and (3) to adjust rate constants to fit the mass measurements and the enrichment data simultaneously. While this approach has the virtue of making use of preexisting features of modeling software, it does not make best use of the data.
An alternative approach would be to fix pool sizes at their measured values so that the model is simpler and there are fewer parameters to esimate. Publications on modeling methodology for lipoprotein kinetics [6,7,20–26] do not offer a method of procedure to do this. In what follows, we show how the algebraic equations relating masses and rate constants can be used to decrease the number of rate constants to be estimated and thus improve the efficiency and reliability of the parameter estimates.
2. Methods
The methods used in this paper are mathematical. While a few differential equations and matrices are used, the reader is not expected to know the theory of differential equations or to manipulate matrices. The methods used are those of basic algebra, pertaining to the solution of linear equations. The system under study is assumed to be in a steady state (the usual assumption in turnover studies), meaning that the total (tracer+tracee) pool masses and fluxes in and out of pools do not change during the study.
Concentrations or mass measurements correspond to sizes or masses of single or multiple pools in a multicompartmental model, and allow the calculation of fluxes and other transport rates from fractional catabolic rates (FCR) and other rate constants estimated from fitting the model to enrichment data. The calculations are trivial, equating each flux to the product of the appropriate mass and rate constant. But the fluxes must also satisfy material balances. Thus, for each pool, the total of all the individual fluxes into that pool must equal the total flux out of that pool and, in turn, the total of all the individual fluxes from that pool. The flux balances impose constraints in the form of relationships - sometimes simple and sometimes quite complex - among rate constants and pool masses. Some constraints involve one or more rate constants that would be a priori identifiable only from the constraints and the mass measurements. We will term these “identifying constraints.” Other constraints involve only rate constants that are a priori identifiable even without any mass measurements; these will be termed “nonidentifying constraints.” The approach proposed here will be shown to be of particular use with models containing identifying constraints.
The method is illustrated first with a simple model for the VLDL-IDL cascade, showing both types of constraints. The equivalence of the usual and proposed methods for models with only identifying constraints is shown with a numerical example. The problem is then stated for a general pool model, along with a systematic method of handling constraints that can be automated in modeling programs. An illustration is provided for a complex multicompartmental model for apoB kinetics.
A web-based system is presented that implements this automation using artificial intelligence techniques to solve algebraic equations symbolically. The software is written in C++ and the web interface in PHP. The C++ program contains about 2,500 lines of code but the executable is quite compact at 75 KB.
3. Results
3.1 A Very Simple Model for apoB in VLDL and IDL
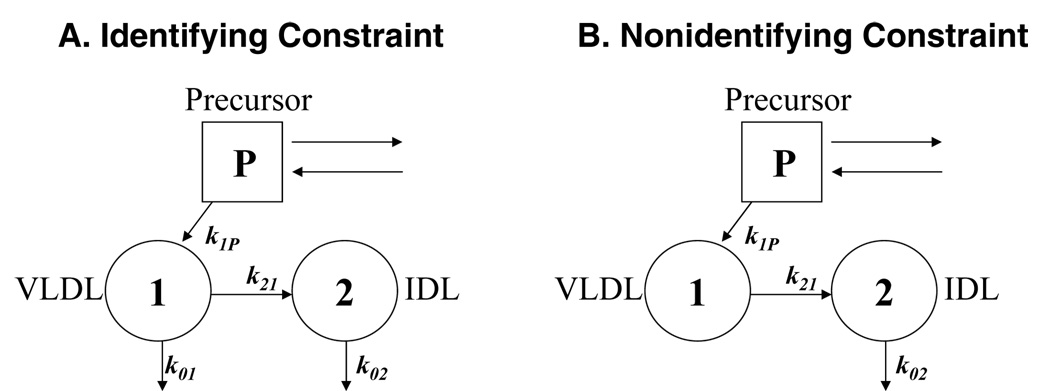
Figure 1A shows a model for apoB in VLDL and IDL that is very simple - a single pool each for VLDL and IDL, some VLDL being removed directly besides becoming IDL, and VLDL the sole source of IDL. The precursor, P, is shown by a square, instead of the usual circle for a pool, to indicate that it is used as a forcing function [7] known from precursor enrichment data, and that it is not necessarily a single pool. Rate constants are defined in the usual way [27] as fluxes divided by the source pool mass, and denoted by k with the first subscript indicating the destination and the second the source of the pathway (however, the term kii is used to designate the total flux into or out of the i-th pool divided by the mass of that pool). Thus, the fractional catabolic rate (FCR) of IDL apoB is k02, the rate constant into 0 (outside) from 2, and is equal to the removal flux out of 2 (IDL) divided by Q2, the mass of the source pool 2 (IDL). An extension of the usual notation [27] used here is that, when describing synthesis or other entry from outside, the second subscript is zero or P, and the division is by the destination pool mass. Thus, k1P is the VLDL apoB fractional synthesis rate (FSR), which equals the synthetic flux into 1 divided by Q1, the mass of pool 1 (VLDL).
Figure 1.
An extremely simple model for apoB turnover in VLDL and IDL with a labeled amino acid precursor as tracer. The square P denotes the precursor system, consisting of one or more pools. Pool 1 is for VLDL apoB and pool 2 for IDL apoB. The k symbols denote rate constants for the pathways, defined as fluxes divided by the source pool mass, with the first subscript indicating the destination and the second the source of the pathway. Thus, k02 is IDL apoB FCR, the rate constant into 0 from 2, equal to the mass flux to the outside from 2 (IDL) divided by Q2, the mass of the source pool 2 (IDL). The extension to this definition is that, when describing synthesis or entry from the outside, the second subscript is zero or P, and the division is by the destination pool mass. Thus, the FSR of VLDL apoB is k1P, the flux into 1 (VLDL) from P (the precursor) divided by Q1, the mass of the destination pool. A: The model has a direct removal pathway from VLDL (k01), making the relationship between the two masses an identifying constraint. B: The model has no direct removal pathway from VLDL (k01=0), making the relationship between the two masses a nonidentifying constraint.
Differential equations (also called state equations) can be written for the changes with time of q1 and q2, the tracer quantities in VLDL and IDL apoB, respectively:
| (1) |
| (2) |
The symbol (t) denotes that the concerned quantity (q1, q2, or w in the equations above) varies with time, and will be omitted when there is no ambiguity. The precursor enrichment, w(t), is the forcing function, and is multiplied by the synthetic rate k1PQ1 (or equivalently by k11Q1 since there is no other flux into pool 1) to obtain the rate of tracer entry into VLDL. The direct removal rate constant for VLDL is given by k01=k11–k21. The initial conditions for the state equations are that q1(0) and q2(0) are both zero. If the injected tracer were not a precursor but radiolabeled VLDL, there would be no “w” in the state equations and q1(0) would equal the initial activity in VLDL.
Enrichments in the two pools, y1(t)=q1(t)/Q1 and y2(t)=q2(t)/Q2, are observed along with Q1 and Q2 at a number of time points.
The constraints arise from flux balances around the two pools. The balance around pool 1 is already reflected in equation (1) by the use of k11Q1 instead of k1PQ1 multiplying the input enrichment w(t). The flux balance around pool 2 yields an algebraic relationship:
| (3) |
The popular software SAAM II, which has a built-in facility to use this equation to solve for Q2 as equal to k21Q1/k02, estimates four parameters (k11, k21, k02, Q1) by simultaneously fitting the tracer enrichment data (by model-predicted enrichment curves) and the mass measurements (by Q1obs=Q1, and Q2obs=k21Q1/k02). We term this the usual approach.
Our proposed approach is to use the actual mass measurements Q1obs and Q2obs in equation (3) to solve for k21 as equal to k02 Q2obs /Q1obs, and rewrite equation (2):
| (4) |
with equation (1) remaining unchanged. The mass ratio in equation (4) is set to the measured ratio of the masses and the enrichment data fitted to estimate two parameters, k11 and k02. The other rate constant k21 and the fluxes are easily calculated.
Thus, the proposed approach changes a problem of estimating four parameters (three rate constants and a mass) from four responses (two enrichments and two masses) to one of estimating two parameters (two rate constants) from two responses (two enrichments). This simple model illustrates how mass measurements can be used to simplify the estimation of kinetic parameters.
3.2 Identifying Constraints
The first question would be whether the two approaches yield the same values for the model parameters. The answer to the question depends on whether the constraint in equation (3) is of the identifying type. An identifying constraint is one with a rate constant that is unidentifiable without using that constraint. As the two rate constants in equation (3), k21 and k02, both appear in the differential equation (2), it is not immediately obvious whether equation (3) is an identifying constraint. It is necessary to look at the solution to the differential equations. Without loss of generality, we will assume a primed constant infusion study where w(t) is constant at c. It can be verified that the tracer enrichments in the two pools are given by:
| (5) |
| (6) |
These two equations can be fitted to the enrichment data to estimate c, k11 and k02. Interestingly, k21, and the masses as well, do not appear in the solutions, which means k21 cannot be estimated from the enrichment data alone. It has to be calculated from the constraint in equation (3), which makes it an identifying constraint as the constraint makes k21 a priori identifiable. In other words, k21 is identifiable only with mass measurements.
In this case, the usual and proposed approaches will yield the same parameter estimates. With either approach, the enrichment data lead to estimates for c, k11 and k02. Then, with our approach, the mass measurements Q1obs and Q2obs lead to
| (7) |
With the usual approach of fitting the mass measurements along with enrichments, since Q1, Q2 and k21 affect only the mass measurements, the modeling program will fit the mass measurements exactly by estimating Q1 as Q1obs and k21 as k02 Q2obs /Q1obs, regardless of the relative weights given to mass versus enrichment data. This means the result will be the same as with the approach proposed here. The approach proposed here is superior since it involves fitting fewer responses and estimating fewer parameters.
3.3 Numerical Example of Equivalence of Usual and Proposed Approaches
A simple numerical illustration can be constructed with the model in Figure 1A and a primed constant infusion. For ease of presentation, instead of working discrete enrichment data, we assume that the enrichment data are best fitted by sums of exponentials:
| (8) |
| (9) |
where time t is in days. Instead of estimating the model parameters by fitting the experimental data, we can equivalently fit the sums of exponentials. We also assume that the true pool masses are 10 and 5 mg/dL, respectively. The numbers are similar to literature values for VLDL and IDL apoB kinetics [28]. We consider five cases – one in which pool masses are measured with no error, and others in which each mass is measured with a significant error of +20% or −20%.
The proposed approach is first to calculate k11 and k02 by equating equation (5) to equation (8) and equation (6) to equation (9), so that k11=4 and k02=3 pools/day (mass and rate constant units are omitted below for clarity); and then to calculate k21 and k01 from equations (7). Table 1 shows the calculated values for the five cases. The first line shows that, with no error, Q2obs /Q1obs is 0.5, and that equations (7) lead to 1.5 for k21 and 2.5 for k01. The subsequent lines show the effects of substantial errors in the two mass measurements. The errors, if in opposite directions, lead to significant errors in k21 and k01.
Table 1.
Effects of Mass Measurement Errors on Model Parameter Estimates
| Error in Q1 | Error in Q2 | Q2obs /Q1obs | k21 = k02 Q2obs /Q1obs (pools/day) | k01=k11-k21 (pools/day) |
|---|---|---|---|---|
| 0 | 0 | 0.5 | 1.5 | 2.5 |
| +20% | +20% | 0.5 | 1.5 | 2.5 |
| −20% | −20% | 0.5 | 1.5 | 2.5 |
| +20% | −20% | 0.333 | 1.0 | 3.0 |
| −20% | +20% | 0.75 | 2.25 | 1.75 |
With the usual approach, k11, k21, k02, and Q1 are estimated by fitting the enrichment data and mass measurements simultaneously by equation (5), equation (6), and the relationship Q2=k21Q1/k02. It is easily verified that the best estimates with the usual approach are identical to those with the proposed approach:
| (10) |
These estimates lead to model-predicted enrichment curves given by equation (8) and equation (9), which best fit the enrichment data, and an exact fit to the observed pool masses.
Equations (10) are not just for the case with perfect mass data; they hold as well with mass measurement errors. Altering relative weights for the mass and enrichment data will not affect the estimates as the estimates in (10) provide the best fit to the enrichment data and fit the mass measurements exactly.
Thus, with either approach, errors in mass measurements lead to estimation errors in k21, k01, and all the fluxes; the enrichment data cannot compensate for mass errors. The numerical illustration shows how the two approaches yield identical parameter estimates in a model with identifying constraints.
3.4 Nonidentifying Constraints
There are, however, two situations where the two approaches may give different results. One is if a model constraint is nonidentifying. Consider the model in Figure 1B, a simplification of the model in Figure 1A, with no direct removal of VLDL (k01=0). Then, k21= k11, and is a priori identifiable from the enrichment data, without the need for mass measurements. Now the constraint in equation (3) is nonidentifying, providing an additional relationship between k21 and k02 in terms of the mass ratio. In this case, the two approaches may yield different parameter estimates, especially if the mass measurements are considered imprecise compared to enrichment data and given low weight.
The other exception is if the k21 calculated from the constraint in equation (3) is larger than k11, which would make k01=k11–k21 negative, an impossibility. The best estimates, then, would make k21= k11, which is the simpler model in Figure 1B with no direct removal of VLDL and a nonidentifiying constraint.
Thus, a nonidentifying constraint can lead to the usual and proposed approaches giving different parameter estimates. Otherwise, there should be no difference in the parameter estimates, whether the mass measurements are fitted along with the enrichment data or used to simplify the estimation process by decreasing the number of fitted responses and estimated parameters.
3.5 A General Pool Model
We now derive constraint equations for a general pool model. More complex models than that in Figure 1A are best analyzed using matrices and vectors. Matrix-vector notation is introduced by rewriting equation (1) and equation (2) for the simple model in Figure 1A:
| (11) |
where the square brackets denote vectors and a matrix.
The general n-pool model is:
| (12) |
where q(t) is the n-long tracer activity vector in units of concentration times mass (e.g., fractional enrichment multiplied by mass units), K is the nxn system matrix of rate constants (Kii = −kii is the negative of the total flux out of pool i divided by the mass of that pool, Kij = kij is the flux from pool j to pool i divided by the mass of pool j), Si is the direct labeled synthetic flux into pool i, w(t) is the precursor tracer enrichment function, z(t) is the vector of observed enrichments, and C is the observation matrix specifying the combination of pools that each observed variable represents. The model is assumed to be a priori identifiable [29].
For the general n-pool model,
| (13) |
By definition,
| (14) |
Si, the labeled synthetic flux into pool i, is given by Si=ki0Qi if all the flux into that pool is labeled. Some flux into pool i may be unlabeled, with unlabeled synthetic pathways or flux from pools that turn over too slowly to be traced; if so, Si will be smaller than ki0Qi, possibly zero. If zi is the enrichment in pool j, the i-th row of the observation matrix C has the value of 1/Qj in the j-th position and zero elsewhere. If zi is the enrichment in a combination of pools, as happens when an observed lipoprotein fraction is modeled by multiple pools, then the corresponding elements of the i-th row of C each equals the inverse of the total mass of those pools, with zeros elsewhere. This verbal description is perhaps simpler than the formal mathematical definition:
| (15) |
If zi is the enrichment in a single pool, the definition above simplifies to:
| (16) |
For the two-pool model in Figure 1A (equations (11)),
| (17) |
Equations (17) can be seen as a special case of equation (13) to equation (15) by noting that, since there is no path from pool 2 (IDL) to pool 1 (VLDL) in the simple model, k12 is zero so that k22 = k02. Also, C is simple since each observed variable is the enrichment in just one pool.
With these definitions in hand, we can study the constraints imposed by flux balances around each pool. One set of balances arises from setting the total flux out of each pool equal to the sum of the fluxes from that pool to all other pools as well as to the outside. Equation (14) ensures that these flux balances are always satisfied. Multiplying equation (14) throughout by Qi results in the following:
Total flux out of pool = Total flux from pool i to everywhere
| (18) |
A second set of balances arises from setting the total flux into each pool (from every other pool as well as from the outside) equal to the total flux out of that pool. Thus,
| (19) |
The constraints (18) and (19) may be written in a more compact form, noting that, by the model definition in equation (13), the diagonal elements of K equal -kii and the off-diagonal elements equal kij, as follows:
| (20) |
| (21) |
While the constraint equations may appear complex, they express two very simple requirements: Equations (20) state that each column of the system matrix K must add up to the fractional rate of removal from that pool to the outside; equations (21) state that the elements of each row, weighted by the corresponding pool masses, must add up to the flux into that pool from the outside.
If none of the masses are known, these constraints pose no difficulty. Tracer enrichment data can be fitted to estimate the rate constants, and equations (21) used to deduce relationships among the unknown masses. However, if some masses are measured, the constraints in (21) can be used to introduce the measured masses into the model equations in equations (13).
3.6 An Illustration from VLDL-IDL-LDL ApoB Kinetics
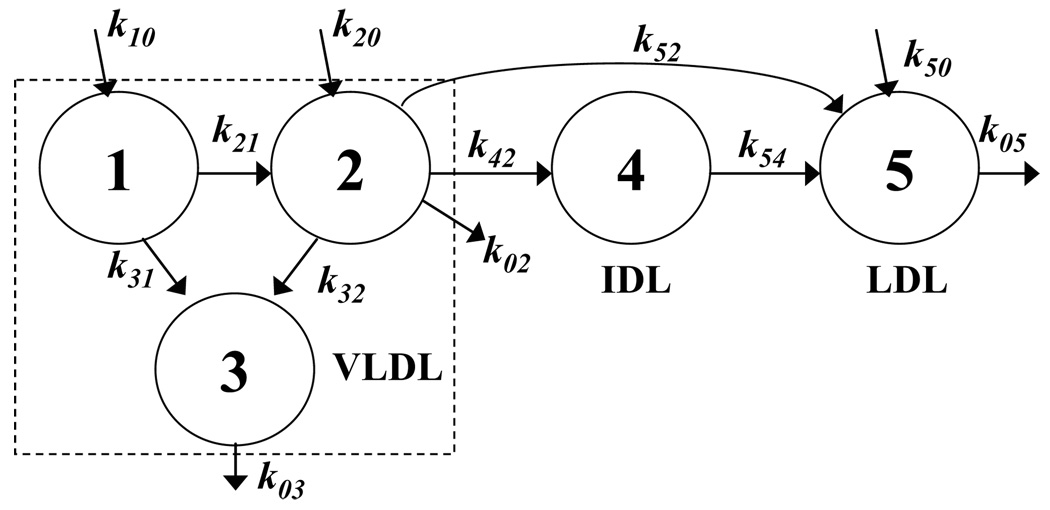
As an illustration, which will show the complex relationships generated by the constraints, we consider the model used by our group to study apoB turnover [28], shown in Figure 2. The system matrix is below:
| (22) |
The K matrix has been augmented by a column on the left to indicate pathways from the outside, and by a row at the top to indicate pathways to the outside. Pools 1, 2 and 3 constitute VLDL, pool 4 is IDL, and pool 5 is LDL. ApoB enrichments in VLDL, IDL and LDL are observed, as are the apoB masses in the three lipoproteins (MV is the VLDL mass). We begin with the most upstream pools, 1 and 2, and apply the row and column constraints, deriving relationships for some of the parameters in terms of the others, working downstream to pool 5:
| (23) |
Figure 2.
A five-pool model for apoB turnover, used in Nagashima et al. [28]. Pools 1, 2 and 3 constitute VLDL apoB, pool 4 is IDL apoB, and pool 5 is LDL apoB. The k symbols are as defined in Figure 1.
These eleven are dependent parameters, replaced in the model by the expressions in equations (23), while the remaining seven rate constants (k31, k20, k02, k32, k42, k52, k50) and two masses (Q2, Q3) are independent parameters to be estimated from the enrichment data.
3.7 General Principles in Incorporating Mass Measurements
The illustrative model helps to state some general concepts for combining mass measurements with tracer enrichment data:
Balances for fluxes around pools with measured masses result in equations to be satisfied by rate constants and pool masses;
These equations can be used to make some rate constants in the model dependent, i.e., to express them in terms of other rate constants and masses, thus introducing measured masses into the model equations;
Solving the model equations containing rate constants and measured masses to fit enrichment data results in parameter estimates that fit the enrichment data best while utilizing all the information in the mass measurements;
The dependent parameter definitions are unique and noncircular. There is a single equation for each dependent parameter, expressing it in terms of independent parameters and previously defined dependent parameters; thus, it is possible to begin with values for the independent parameters and evaluate equations (23) in sequence to get the values of all the dependent parameters. For example, k44 is expressed in terms of the independent parameters k42 and Q2 and the measured pool mass Q4, while k11 is expressed in terms of the independent parameter k31 and the just-defined dependent parameter k21. If care is not taken in choosing dependent parameters, circularity can happen. For instance, if the dependent parameters were k42 instead of k22 in the first equation and k52 instead of k55 in the penultimate equation (flux to 5), then there would be circularity in the first, eighth, ninth and tenth equations (k52 to k42 to k44 to k54 to k52), making it impossible to evaluate the dependent parameters.
3.8 Automation Considerations
The simple two-pool model in Figure 1A has a single constraint equation while the five-pool model in Figure 2 has eleven constraint equations defining eleven dependent parameters. With increasing model size, the number and complexity of the constraint equations increase. Care is also required to ensure noncircularity. Even someone comfortable with algebra has to be concerned with making mistakes and also with the effort required with each new model. It is desirable, therefore, to have the modeling program generate dependent parameter definitions automatically. The algorithm must satisfy the properties noted above for equations (23) – a unique definition for each dependent parameter, and noncircularity ensured by ordering of the definitions so that each uses only dependents already defined and independents. Some provision should be made for the user to guide the process: an investigator may wish to choose the parameters to be made dependent - for instance, to facilitate convergence of the iteration process, or to exclude from the dependent set any parameter that may be zero in a particular study.
We have incorporated a module to do this automatically for our modeling program Poolfit [28], with provisions for the user to guide the dependency selection partially or totally. Noteworthy features are: (1) The module generates flux balances as algebraic equations in symbolic terms; (2) it analyzes each equation in turn and applies a series of heuristics to choose the rate constant or mass to be made dependent from that equation; (3) its heuristics include making multiple initial passes over the balances in an effort to guide the later constraint construction; (4) it applies symbolic manipulation techniques to solve each flux balance equation for the corresponding dependent parameter symbolically; (5) it reorders the dependency equations to avoid circularity; and (6) if circularity cannot be avoided with the chosen dependency set, it repeats the whole process with different heuristics until there is no circularity, though the repetition is seldom necessary due to the logic built into the heuristics. The goal is to replicate what an experienced modeler might do.
For the benefit of users of other programs, the module is available as a stand-alone program accessed over the worldwide web at http://biomath.info/poolfit/constraints. When the user specifies the model pathways or connectivity of the pools, the program will generate a set of dependent parameters and an equation for each. It is possible to instruct the program to make one or more specific parameters dependent. The program output can be used to provide dependent parameter definitions to the user’s modeling program. To make it easier to learn to use the program, the models in Figure 1A and Figure 2 are available as illustrations at the website.
4. Discussion
We have used matrix-vector formulations to analyze general pool models for tracer enrichments. Matrix theory has long been used to study pool model properties. Closed form solutions are available from the eigenvalues and eigenvectors of the system matrix [30–32]. Berman and Schoenfeld [33] used matrix transformations to study invariants of pool models, their method applied later to the study of equivalent model structures [34,35], and extended to exhaustive modeling [36,37]. Basic theorems on net flux, mean residence time, etc., have been proved using matrix theory [38–43]. DiStefano and colleagues have used matrix theory to derive relationships among rate constants and also for pool sizes and fluxes [29,44], though the results are only for a catenary or mammillary pool model with a single input, a single observed pool, and no mass measurements.
We have shown here how mass measurements can be incorporated into a pool model used to fit enrichment data. This is done by writing two flux balances around each pool, one for the fluxes in and the other for the fluxes out. The mass balances cause some rate constants and unobserved masses to be expressed in terms of the other rate constants and the measured masses. The result is a model with fewer parameters to be estimated from the enrichment data.
With very simple models, this can be done manually. As model size increases, the number of dependencies increases rapidly and so does the complexity of the equations. It is useful for the modeling program to generate dependencies automatically. We have made available a web-accessible program to help investigators by generating dependency equations for use in their modeling programs.
4.1 Considerations in Choosing Parameters to be Constrained
A necessary requirement is that the constraint equations not be circular. That still leaves considerable room in choosing which parameters to make dependent. There are a few considerations that can go into the choice:
For a model to be physically realizable, the parameters must clearly be nonnegative. The rate constant for any pathway must be positive or zero. Modeling programs generally allow the user to specify limits for the parameters. However, some programs, including SAAM II, have no provision to set limits on derived or dependent parameters. Users of such programs, if possible, should make dependent only those parameters that can be expected to be positive in all studies. For instance, in the constraint equations (23) for the model in Figure 2, all the expressions except for the one for k21 involve no subtractions and so will always evaluate to nonnegative values. The expression for k21 does involve a subtraction but is unlikely to approach zero since that would imply that pool 1 is redundant. It can be verified that, for this model, every choice leads to at least one subtraction.
As a corollary, the rate constant for a pathway that may not be present in some subjects is best kept as a parameter to be estimated. In the model in Figure 2, direct synthesis into pools 2 and 5 and irreversible removal from pool 2 are pathways that may be absent in some studies. In equations (23), these parameters are kept as independent parameters.
- Speed or efficiency of convergence can be a consideration in choosing parameters to be constrained. If differential equations in a pool model are solved analytically or in closed form, the enrichments in different pools are given by sums of exponentials whose intercepts are complicated functions of the rate constants but, in the case of models with no reverse fluxes (that is, a molecule that leaves a pool can never re-enter it), the exponential rate constants equal some of the model rate constants. For instance, for the model in Figure 2, the exponential constants are k11, k22, k33, k44 and k55. The exponential constants are most directly estimated from the tracer data (analogous to slopes on semi-log plots or graphical peel-off methods) and so estimating model rate constants that equal exponential rate constants can improve convergence. For the model in Figure 2, the equations in (23) for k11, k22, k33, k44 and k55 can be replaced by equations for k31, k32, k42, k02 and k50:
(24)
The independent parameters are k11, k22, k33, k44, k55, k20, k52, Q2, and Q3.
This approach is not helpful if parameters such as k02 and k50 can be zero since convergence may be slow for a dataset if the best estimate of a dependent parameter is zero. The approach is also not helpful to SAAM II users since SAAM II does not allow diagonal elements kii to be independent parameters.
4.2 Generating Constraint Equations for SAAM II
Berman and coworkers [5,42] have shown that the K matrix can be inverted to relate the pool masses to the fluxes into the system in equations (21). Proceeding thus, SAAM II, the most popular software used in lipoprotein kinetic modeling, has a built-in facility that uses this approach to calculate the masses of all pools but one from numerical values for one pool mass and all the rate constants. The calculation is done not symbolically but arithmetically for specific numerical values.
Welty et al. [19] describe one clever work-around, explained in greater detail by Pont et al. [20]. The idea is to treat one mass measurement as error-free (LDL apoB in their example); utilize SAAM II’s built-in facility to calculate, at each iterative step in fitting the data, all other pool sizes in terms of the error-free mass and rate constants; and fit the other mass measurements along with enrichment data, using different data weights for masses. Other investigators [11,21] fit all the mass measurements, as illustrated here in Section 3.3 for the simple model in Figure 1A. These are two approaches to handle a SAAM II limitation. We have seen that, with identifying constraints, corresponding mass measurements are fitted exactly. It is not readily apparent if SAAM II can use more than one mass measurement to develop constraints on some rate constants as done here.
The method developed here can be used to generate constraint equations to be used with SAAM II. Our webpage has a SAAM option that produces equations specially for SAAM II, in particular taking into account that SAAM II always expresses the i-th diagonal element as the sum of all other elements in the i-th column. For instance, the second illustration on the webpage, corresponding to Figure 2 here, produces the following equations with the SAAM option:
SAAM II produces correct results when our webpage equations are entered into the Attributes box of the corresponding pathways, though it still refrains from calculating unobserved masses because it assumes that steady state is violated; there may be a work-around by using parameter names other than Q’s.
4.3 Improvement in Estimation Efficiency and Reliability
The method developed here will result in far fewer parameters and as many fewer responses to be fitted as there are measured masses, compared to a method that fits the mass measurements along with the enrichment data. We saw that, for the model in Figure 1A, with two pool masses being measured, four parameters estimated by fitting four responses was changed to two parameters estimated by fitting two responses. In general, if m is the number of masses measured, the number of responses is decreased by m and the number of parameters to be estimated is decreased by m as well, which is typically one-fourth to one-third the number of model parameters. For instance, for the model in Figure 2 with 3 mass measurements, the number of responses is reduced by 3 and the number of parameters by 3. In studies that involve more measured masses, the differences are larger - e.g., Zheng et al. [11] measured 21 subfraction masses, which means the approach developed here can be used to reduce the number of responses fitted by 21 and the number of estimated parameters by 21.
With any modeling program, estimation of parameters in a pool model involves a trial-and-error iterative scheme where the measured responses are fitted with the solutions to the model using the initial parameter guesses, the parameter guesses modified based on the fits, the measured responses refitted using the modified parameters, and so on until the fits cannot be improved. The process gets more complex as the number of parameters and the number of responses increase. The dimensionality of the problem is set by the number of parameters and so decreasing the number of parameters has a significant impact on the convergence characteristics of the estimation process. On the other hand, increasing the number of parameters not only slows down the convergence; it also increases the likelihood of converging to a local solution instead of to the best fit.
4.4 CheckingValidity of Parameter Estimates
One reason given for fitting mass measurements along with enrichment data is that masses are not known error-free; the errors could be due to imprecise assays, differential recoveries in different subfractions, differing assay sensitivities in different subfractions, or due to ignoring the extravascular part of a volume of distribution. However, we have seen, even with the simple two-pool model in Figure 1A and the numerical illustration in section 3.3, that if a model is unidentifiable without the mass measurements, that is, if all constraints are of the identifying type, it makes no difference whether the mass data are treated as error-free or inaccurate. The modeling program must fit the mass measurements exactly, regardless of the weights assigned. If the mass fits are not exact, it is likely to be due to convergence or other problems specific to the modeling program.
The concept of identifying and nonidentifying constraints developed here can be used to check the validity of the results from a modeling program that fits mass measurements along with enrichment data. If a measured pool mass is not fitted exactly by the model, there must be a nonidentifying constraint involving a flux into that pool, for instance, that there is no direct removal from that pool or from a pool that feeds directly to that pool. The model in Figure 1B with no direct removal from pool 1 (k01=0), as described in Section 3.4, would be an illustration.
However, if the model is a priori identifiable without the mass measurements, as in Figure 1B with no direct removal from VLDL (either postulated or found to be so for a particular study), the mass measurements do not provide essential information to estimate parameter values. In that case, it may be preferable, depending on the relative accuracy of mass versus enrichment data, to fit masses and enrichments simultaneously. However, the more likely scenario is that the model being used has pathways whose rate constants cannot be estimated without mass measurements, as in Figure 1A and Figure 2. In reviewing the literature, models for apoB kinetics typically have direct removal from the various VLDL and IDL pools [7,12,13,26,45–48], which means the models are not a priori identifiable without mass measurements. The recent model of Zheng et al, with 21 pools is an illustration – every subfraction pool has a direct removal pathway, which is identifiable only because subfraction masses were measured.
Investigators who find that mass measurements are not very accurate and fit the masses simultaneously with the enrichment data [11,12,20,21,49–52] should find the method developed here to be of use in generating good initial guesses by fixing the masses at the measured values and fitting just the enrichment data. Zheng et al. [11] measured apoB enrichments and masses in 21 subfractions. The apoB portion of their model has roughly 80 parameters to be estimated from fitting the 42 responses. By fixing the masses at the measured values and using equations generated from our webpage to constrain 21 rate constants, they can simplify the problem to estimating roughly 60 parameters from fitting 21 responses. The estimated parameters can then be used as initial guesses to fit the mass measurements along with the enrichments to estimate the 80-plus parameters. This two-step process should be much more efficient. Further, if it should turn out that all the constraints are of the identifying type, as when direct removal rate constants are nonzero, there would be no need for the second step.
To conclude, the formal description of the problem and the systematic approach presented here, as well as the webpage to generate constraint equations (http://biomath.info/poolfit/constraints), should be of use in fitting pool models to tracer data when mass measurements are also available and a steady state is assumed in the usual fashion.
Acknowledgments
The authors would like to acknowledge discussions with Henry Ginsberg, which greatly helped improve the clarity of presentation, helpful conversations with Chunyu Zheng and Bruce Patterson about SAAM II, Steve Holleran’s help with the figures and in testing the webpage, and anonymous reviewers whose questions led to our concept of identifying and nonidentifying constraints.
Grants
This work was supported by grants HL69190 and HL62705 from the National Heart, Lung and Blood Institute.
Abbreviations
- FCR
fractional catabolic rate
- FSR
fractional synthetic rate
- k
rate constant
- K
system matrix of rate constants
- Q
total (tracer+tracee) mass
- q
tracer mass or activity
- S
synthetic fluxes
- t
time
- w
precursor enrichment
- y
tracer enrichment or specific activity
- z
measured tracer enrichment
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Rescigno A, Segre G. Drug and Tracer Kinetics. Waltham: Blaisdell; 1966. [Google Scholar]
- 2.Neer R, Berman M, Fisher L, et al. Multicompartmental analysis of calcium kinetics in normal adult males. Journal of Clinical Investigation. 1967;46:1364–1379. doi: 10.1172/JCI105629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shames DM, Berman M, Segal S. Effects of thyroid disease on glucose oxidative metabolism in man. A compartmental model analysis. Journal of Clinical Investigation. 1971;50:627–641. doi: 10.1172/JCI106533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Goodman DS, Smith FR, Seplowitz AH, et al. Prediction of the parameters of whole body cholesterol metabolism in humans. Journal of Lipid Research. 1980;21:699–713. [PubMed] [Google Scholar]
- 5.Berman M. Kinetic analysis and modeling: Theory and applications to lipoproteins. In: Berman M, Grundy SM, Howard BV, editors. Lipoprotein Kinetics and Modeling. New York: Academic Press; 1982. pp. 3–36. [Google Scholar]
- 6.Cobelli C, Foster DM. Compartmental models: Theory and practice using the SAAM II software system. Advances in experimental medicine and Biology. 1998;445:79–101. doi: 10.1007/978-1-4899-1959-5_5. [DOI] [PubMed] [Google Scholar]
- 7.Barrett PHR, Bell BM, Cobelli C, et al. SAAM II: Simulation, Analysis, and Modeling Software for tracer and pharmacokinetic studies. Metabolism. 1998;47:484–492. doi: 10.1016/s0026-0495(98)90064-6. [DOI] [PubMed] [Google Scholar]
- 8.Packard CJ, Shepherd J, Joerns S, et al. Apolipoprotein B metabolism in normal, type IV, and type V hyperlipoproteinemic subjects. Metabolism. 1980;29:213–222. doi: 10.1016/0026-0495(80)90062-1. [DOI] [PubMed] [Google Scholar]
- 9.Arad Y, Ramakrishnan R, Ginsberg HN. Lovastatin therapy reduces low density lipoprotein apoB levels in subjects with combined hyperlipidemia by reducing the production of apoB-containing lipoproteins: implications for the pathophysiology of apoB production. Journal of Lipid Research. 1990;31:567–582. [PubMed] [Google Scholar]
- 10.Chan DC, Watts GF, Redgrave TG, et al. Apolipoprotein B-100 kinetics in visceral obesity: associations with plasma apolipoprotein C-III concentration. Metabolism. 2002;51:1041–1046. doi: 10.1053/meta.2002.33339. [DOI] [PubMed] [Google Scholar]
- 11.Zheng C, Ikewaki K, Walsh BW, et al. Rapid turnover of apolipoprotein CIII containing triglyceride-rich lipoproteins contributing to formation of LDL subfractions. Journal of Lipid Research. 2007;48 doi: 10.1194/jlr.P600011-JLR200. [DOI] [PubMed] [Google Scholar]
- 12.Demant T, Packard CJ, Demmelmair H, et al. Sensitive methods to study human apolipoprotein B metabolism using stable isotope-labeled amino acids. American Journal of Physiology-Endocrinology and Metabolism. 1996;270:E1022–E1036. doi: 10.1152/ajpendo.1996.270.6.E1022. [DOI] [PubMed] [Google Scholar]
- 13.Adiels M, Packard CJ, Caslake MJ, et al. A new combined multicompartmental model for apolipoprotein B-100 and triglyceride metabolism in VLDL subfractions. Journal of Lipid Research. 2005;46:58–67. doi: 10.1194/jlr.M400108-JLR200. [DOI] [PubMed] [Google Scholar]
- 14.Cohn JS, Wagner DA, Cohn SD, et al. Measurement of very low density and low density lipoprotein apolipoprotein (Apo) B-100 and high density lipoprotein Apo A-I production in human subjects using deuterated leucine. Effect of fasting and feeding. Journal of Clinical Investigation. 1990;85:804–811. doi: 10.1172/JCI114507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lichtenstein AH, Hachey D, Millar JS, et al. Measurement of human apolipoprotein B-48 and B-100 kinetics in triglyceride-rich lipoproteins using [5,5,5-2H3]leucine. Journal of Lipid Research. 1992;33:907–914. [PubMed] [Google Scholar]
- 16.Welty FK, Lichtenstein AH, Barrett PHR, et al. Interrelationships between human apolipoprotein A-I and apolipoproteins B-48 and B-100 kinetics using stable isotopes. Arteriosclerosis Thrombosis and Vascular Biology. 2004;24:1703–1707. doi: 10.1161/01.ATV.0000137975.14996.df. [DOI] [PubMed] [Google Scholar]
- 17.Walsh BW, Sacks FM. Effects of low dose oral contraceptives on very low density and low density lipoprotein metabolism. Journal of Clinical Investigation. 1993;91:2126–2132. doi: 10.1172/JCI116437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tomiyasu K, Walsh BW, Ikewaki K, et al. Differential metabolism of human VLDL according to content of ApoE and ApoC-III. Arteriosclerosis Thrombosis and Vascular Biology. 2001;21:1494–1500. doi: 10.1161/hq0901.094489. [DOI] [PubMed] [Google Scholar]
- 19.Welty FK, Lichtenstein AH, Barrett PHR, et al. Decreased production and increased catabolism of apolipoprotein B-100 in apolipoprotein B-67/B-100 heterozygotes. Arteriosclerosis Thrombosis and Vascular Biology. 1997;17:881–888. doi: 10.1161/01.atv.17.5.881. [DOI] [PubMed] [Google Scholar]
- 20.Pont F, Duvillard L, Verges B, et al. Development of compartmental models in stable-isotope experiments - Application to lipid metabolism. Arteriosclerosis Thrombosis and Vascular Biology. 1998;18:853–860. doi: 10.1161/01.atv.18.6.853. [DOI] [PubMed] [Google Scholar]
- 21.Chan DC, Barrett PHR, Watts GF. Lipoprotein transport in the metabolic syndrome: methodological aspects of stable isotope kinetic studies. Clinical Science. 2004;107:221–232. doi: 10.1042/CS20040108. [DOI] [PubMed] [Google Scholar]
- 22.Foster DM, Barrett PHR, Toffolo G, et al. Estimating the Fractional Synthetic Rate of Plasma Apolipoproteins and Lipids from Stable-Isotope Data. Journal of Lipid Research. 1993;34:2193–2205. [PubMed] [Google Scholar]
- 23.Demant T, Packard CJ, Stewart P, et al. Sensitive Mass-Spectrometry Techniques for Measuring Metabolism of Human Apolipoprotein-B In-Vivo. Clinical Chemistry. 1994;40:1825–1827. [Google Scholar]
- 24.Barrett PHR, Foster DM. Design and analysis of lipid tracer kinetic studies. Current Opinion in Lipidology. 1996;7:143–148. doi: 10.1097/00041433-199606000-00006. [DOI] [PubMed] [Google Scholar]
- 25.Cobelli C, Caumo A. Using what is accessible to measure that which is not: Necessity of model of system. Metabolism-Clinical and Experimental. 1998;47:1009–1035. doi: 10.1016/s0026-0495(98)90360-2. [DOI] [PubMed] [Google Scholar]
- 26.Barrett PHR, Chan DC, Watts GF. Design and analysis of lipoprotein tracer kinetics studies in humans. Journal of Lipid Research. 2006;47:1607–1619. doi: 10.1194/jlr.R600017-JLR200. [DOI] [PubMed] [Google Scholar]
- 27.Brownell GL, Berman M, Robertson JS. Nomenclature for tracer kinetics. International Journal of Applied Radiation and Isotopes. 1968;19:249–262. doi: 10.1016/0020-708x(68)90022-7. [DOI] [PubMed] [Google Scholar]
- 28.Nagashima K, Lopez C, Donovan D, et al. Effects of the PPARgamma agonist pioglitazone on lipoprotein metabolism in patients with type 2 diabetes mellitus. Journal of Clinical Investigation. 2005;115:1323–1332. doi: 10.1172/JCI23219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.DiStefano JJ., 3rd Complete parameter bounds and quasiidentifiability conditions for a class of unidentifiable linear systems. Mathematical Biosciences. 1983;65:51–68. [Google Scholar]
- 30.Hearon JZ. Theorems on linear systems. Annals of the New York Academy of Sciences. 1963;108:36–68. doi: 10.1111/j.1749-6632.1963.tb13364.x. [DOI] [PubMed] [Google Scholar]
- 31.Himmelblau DM, Bischoff KB. Process analysis and simulation – Deterministic systems. New York: Wiley; 1968. [Google Scholar]
- 32.Jacquez JA. Compartmental Analysis in Biology and Medicine. University of Michigan: Ann Arbor; 1985. [Google Scholar]
- 33.Berman M, Schoenfeld R. Invariants in Experimental Data on Linear Kinetics and the Formulation of Models. Journal of Applied Physics. 1956;27:1361–1370. [Google Scholar]
- 34.Walter E, Lecourtier Y. Unidentifiable compartmental models: What to do? Mathematical Biosciences. 1981;56:1–25. [Google Scholar]
- 35.Ramakrishnan R. An application of Berman’s work on pool-model invariants in analyzing indistinguishable models for whole-body cholesterol metabolism. Mathematical Biosciences. 1984;72:373–385. doi: 10.1016/0025-5564(84)90119-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vajda S. Structural equivalence and exhaustive compartmental modeling. Mathematical Biosciences. 1984;69:57–75. [Google Scholar]
- 37.Chapman MJ, Godfrey KR. Some extensions to the exhaustive modelling approach to structural identifiability. Mathematical Biosciences. 1985;77:305–323. [Google Scholar]
- 38.Hearon JZ. The washout curve in tracer kinetics. Mathematical Biosciences. 1968;3:31–39. [Google Scholar]
- 39.Hearon JZ. Interpretation of tracer data. Biophysical Journal. 1969;1363 doi: 10.1016/S0006-3495(69)86458-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hearon JZ. A note on open linear systems. Bulletin of Mathematical Biology. 1974;36:97–99. [Google Scholar]
- 41.Perl W, Lassen NA, Effros RM. Matrix proof of flow, volume and mean transit time theorems for regional and compartmental systems. Bulletin of Mathematical Biology. 1975;37:573–588. doi: 10.1007/BF02459526. [DOI] [PubMed] [Google Scholar]
- 42.Covell DG, Berman M, Delisi C. Mean residence time - theoretical development, experimental determination, and practical use in tracer analysis. Mathematical Biosciences. 1984;72:213–244. [Google Scholar]
- 43.Ramakrishnan R, Leonard EF, Dell RB. A proof of the occupancy principle and the mean transit time theorem for compartmental models. Mathematical Biosciences. 1984;68:121–136. doi: 10.1016/0025-5564(84)90076-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.DiStefano JJ, 3rd, Chen BC, Landaw EM. Pool size and mass flux bounds and quasiidentifiability relations for catenary models. Mathematical Biosciences. 1988;88:1–14. [Google Scholar]
- 45.Welty FK, Lichtenstein AH, Barrett PHR, et al. Human apolipoprotein (apo) B-48 and apoB-100 kinetics with stable isotopes. Arteriosclerosis Thrombosis and Vascular Biology. 1999;19:2966–2974. doi: 10.1161/01.atv.19.12.2966. [DOI] [PubMed] [Google Scholar]
- 46.Barrett PHR, Watts GF. Kinetic studies of lipoprotein metabolism in the metabolic syndrome including effects of nutritional interventions. Current Opinion in Lipidology. 2003;14:61–68. doi: 10.1097/00041433-200302000-00011. [DOI] [PubMed] [Google Scholar]
- 47.Lundahl B, Skoglund-Andersson C, Caslake M, et al. Microsomal triglyceride transfer protein –493T variant reduces IDL plus LDL apoB production and the plasma concentration of large LDL particles. American Journal of Physiology-Endocrinology and Metabolism. 2006;290:E739–E745. doi: 10.1152/ajpendo.00376.2005. [DOI] [PubMed] [Google Scholar]
- 48.Tremblay AJ, Lamarche B, Cohn JS, et al. Effect of Ezetimibe on the in vivo kinetics of ApoB-48 and ApoB-100 in men with primary hypercholesterolemia. Arteriosclerosis Thrombosis and Vascular Biology. 2006;26:1101–1106. doi: 10.1161/01.ATV.0000216750.09611.ec. [DOI] [PubMed] [Google Scholar]
- 49.Malmstrom R, Packard CJ, Caslake M, et al. Defective regulation of triglyceride metabolism by insulin in the liver in NIDDM. Diabetologia. 1997;40:454–462. doi: 10.1007/s001250050700. [DOI] [PubMed] [Google Scholar]
- 50.Malmstrom R, Packard CJ, Watson TDG, et al. Metabolic basis of hypotriglyceridemic effects of insulin in normal men. Arteriosclerosis Thrombosis and Vascular Biology. 1997;17:1454–1464. doi: 10.1161/01.atv.17.7.1454. [DOI] [PubMed] [Google Scholar]
- 51.Malmstrom R, Packard CJ, Caslake M, et al. Effect of heparin-stimulated plasma lipolytic activity on VLDL APO B subclass metabolism in normal subjects. Atherosclerosis. 1999;146:381–390. doi: 10.1016/s0021-9150(99)00153-7. [DOI] [PubMed] [Google Scholar]
- 52.de Roos B, Caslake MJ, Stalenhoef AFH, et al. The coffee diterpene cafestol increases plasma triacylglycerol by increasing the production rate of large VLDL apolipoprotein B in healthy normolipidemic subjects. American Journal of Clinical Nutrition. 2001;73:45–52. doi: 10.1093/ajcn/73.1.45. [DOI] [PubMed] [Google Scholar]